Demonstration of robust and efficient quantum property learning with shallow shadows

Abstract

Extracting information efficiently from quantum systems is crucial for quantum information processing. Classical shadows enable predicting many properties of arbitrary quantum states using few measurements. While random single-qubit measurements are experimentally friendly and suitable for learning low-weight Pauli observables, they perform poorly for nonlocal observables. Introducing a shallow random quantum circuit before measurements improves sample efficiency for high-weight Pauli observables and low-rank properties. However, in practice, these circuits can be noisy and bias the measurement results. Here, we propose the robust shallow shadows, which employs Bayesian inference to learn and mitigate noise in postprocessing. We analyze noise effects on sample complexity and the optimal circuit depth. We provide theoretical guarantees for the success of error mitigation under a wide class of noise processes. Experimental validation on a superconducting quantum processor confirms the advantage of our method, even in the presence of realistic noise, over single-qubit measurements for predicting diverse state properties, such as fidelity and entanglement entropy. Our protocol thus offers a scalable, robust, and sample-efficient method for quantum state characterization on near-term quantum devices.

Introduction

Classical shadow tomography¹ has emerged as a useful technique for efficiently characterizing quantum states with few measurements. This method leverages randomized measurements^2,3 to construct a classical approximation or “shadow” of a quantum state, enabling the estimation of various state properties without the need for costly protocols such as full-state tomography^4,5,6. This method is particularly attractive because it allows experimentalists to ‘measure first and ask questions later’³: the same dataset can be used multiple times to learn a wide class of state properties. As such, classical shadow tomography and its variations^{7,8,9,10,11,12,13,14,15,16,17,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36} have found applications in a broad spectrum of quantum information tasks, including state verification^37,38, device benchmarking^{39,40,41,42,43,44}, Hamiltonian learning^{45,46,47,48,49}, error mitigation^50,51,52,53, and quantum machine learning^54,55,56,57.

However, classical shadows are not a panacea: a poor choice of randomized measurement scheme can result in poor performance. For instance, although random Pauli measurements are experimentally friendly and perform well for recovering low-weight Pauli observables, they are known to require high sample complexities for predicting non-local Pauli observables and low-rank global observables such as fidelity¹. On the other hand, schemes that use fully global random twirling (i.e., global random Clifford unitaries) are well-suited for low-rank global observables, yet they are experimentally infeasible due to the long circuit depths required to implement a global twirling unitary. These limitations have motivated the exploration of alternative randomized measurement schemes that maintain experimental feasibility, yet achieve improved sample complexity scaling on a broader class of observables. To list just a few, these alternative schemes include Hamiltonian-driven systems^11,27,32, locally scrambled quantum dynamics^12,13,18, and shallow quantum circuits^14,15. Among these, measurement schemes using random finite-depth quantum circuits referred to as shallow shadows, have been shown to have considerably lower sample complexities for predicting non-local and low-rank observables.

While classical shadow tomography has been successfully demonstrated experimentally using random Pauli measurements^{42,58,59,60,61}, the shallow shadows protocol—which offers theoretical advantages for certain observables—has never been experimentally validated on real quantum devices. This is important because these devices are noisy: until now, it has remained unclear whether and to what degree the benefits of shallow shadows can persist even under the presence of noise. Indeed, a blind application of existing theoretical protocols, without accounting for the effects of noise, will produce biased results in real experiments.

In this work, we introduce the robust shallow shadows protocol, which is designed to be robust against the inherent noise in quantum systems. More specifically, our protocol aims to accurately predict a broad spectrum of quantum state properties from a single set of randomized measurements conducted on noisy, shallow quantum circuits. Our research advances the theoretical understanding of the shallow shadows protocol in three key ways. First, we introduce a robust shallow shadows protocol that produces unbiased classical shadows, enabling the efficient and noise-resilient prediction of many quantum state properties. This protocol requires only a simple calibration experiment and minimal assumptions. We also bound the sample complexity of the calibration and demonstrated that our method generalizes the robust classical shadow approach based on random Pauli or Clifford measurements. Second, we prove that incorporating a stochastic Pauli noise model in post-processing effectively captures time-independent experimental noise, and by combining this with Bayesian learning, we reduce the calibration sample overhead. Third, we explore the bias-variance tradeoff, showing that noise prevents the system from reaching the optimal noiseless circuit depth identified in ref. ⁶². We quantify how this optimal depth decreases with increasing noise strength.

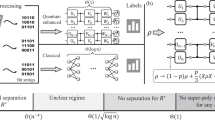
We apply these theoretical insights to conduct classical shadow experiments^{42,58,59,60,61} beyond Pauli measurements using 18 qubits on a 127-qubit superconducting quantum processor. We investigate three randomized measurement schemes using random brickwork circuits with $d\in \left\{0,2,4\right\}$ layers of twirled CNOT gates (see Fig. 1a). The case d = 0 serves as a benchmark, representing conventional noise-robust randomized Pauli measurements, while the other two schemes employ shallow random circuits of increasing depth of entangling gates. We test these schemes on application states such as the cluster state and the Affleck-Kennedy-Lieb-Tasaki (AKLT) resource state. Our analysis reveals two key findings. First, our robust protocol consistently produces accurate predictions for various physical observables across different circuit depths, demonstrating the success of our noise-resilient classical shadow approach. Second, we quantify the experimental sample complexity of the robust shallow shadows protocol. Comparing error-mitigated shallow random circuits to error-mitigated random Pauli measurements (both using our noise-robust framework), we find that shallow shadows reduce the sample complexity by up to five times for observables like fidelity and non-local Paulis. These improvements not only align with theoretical predictions but also persist in the presence of noise. Together, these results validate our theoretical framework and highlight the practical advantages of our protocol in enhancing the efficiency and robustness of quantum state learning.

Fig. 1: A schematic overview of the robust shallow shadow protocol.

a We show an example of our randomized measurement scheme for a shallow circuit with d = 2, which is a brickwork circuit comprised of twirled two-qubit gates. As shown b these twirled gates are CNOT gates sandwiched by single-qubit random Cliffords. Our noise model is the sparse Pauli-Lindblad model⁷⁴, which captures realistic noise effects such as qubit crosstalk. Upon twirling via single-qubit random Clifford gates, the effective noise channel simplifies from a full Pauli-Lindblad map (which has nine two-body terms on each edge and three one-body terms for each node) to the one illustrated in (c), which has only one parameter for each edge and one parameter for each node. The left half a shows the dataset collection process for both calibration and application states, and the right half shows our data postprocessing method. We use a Bayesian inference algorithm to estimate the noise parameters λ of the quantum device and use this to error mitigate our estimates of many different observables, ranging from fidelity to entanglement entropy.

Results

Preliminaries

We begin by reviewing the framework of randomized measurements and classical shadows. Each randomized measurement scheme is defined by an ensemble of unitary operators ${{\mathcal{E}}}$. A random unitary U_i is then sampled uniformly at random from ${{\mathcal{E}}}$ and applied to the state ρ, the evolved state is measured on a computational basis, and the measurement outcome ${| b\left.\right\rangle }_{i}$ is recorded. This evolve-and-measure scheme is repeated K times, choosing a new random unitary U_i each time. This forms the randomized measurement dataset ${{\mathcal{D}}}={\left\{{U}_{i},{| b\left.\right\rangle }_{i}\right\}}_{i=1}^{K}$. The aim is then to predict a large number of properties of ρ, all using the same dataset ${{\mathcal{D}}}$, a goal that we call multitasking.

To predict these properties, the dataset must first be classically postprocessed. The first step of this is to calculate the back evolution of the collapsed state ${| b\left.\right\rangle }_{i}$ by U_i to construct the associated classical snapshot ${\hat{\sigma }}_{i}={U}_{i}^{{\dagger} }{| b\left.\right\rangle }_{i}\left\langle \right.b{| }_{i}{U}_{i}$. This is possible when there are efficient classical algorithms for simulating ${U}_{i}^{{\dagger} }$; for instance, there are well-known algorithms for calculating ${\hat{\sigma }}_{i}$ when it is a Clifford circuit⁶³, matchgate circuit^64,65, or finite-time Hamiltonian evolution^66,67. The full set of classical snapshots can be viewed as a set of classical ‘shadows’ of the underlying quantum state ρ; although a single snapshot is not enough to fully specify the state, the full set of snapshots together proves sufficient, as we show below. The linearity of quantum mechanics implies that the expectation (over both random choices of the unitary U and random measurement outcomes $| b\left.\right\rangle$) of the classical snapshot is related to the original state ρ through a linear map ${{\mathcal{M}}}$: ${\mathbb{E}}[\hat{\sigma }]={{\mathcal{M}}}[\rho ]$. The precise details of this map are determined by the unitary ensemble ${{\mathcal{E}}}$. Importantly, when ${{\mathcal{E}}}$ forms a tomographically complete ensemble, ${{\mathcal{M}}}$ is an invertible map, so we can write $\rho={\mathbb{E}}[{{{\mathcal{M}}}}^{-1}(\hat{\sigma })]$, and of course any observable of ρ obeys ${{\rm{Tr}}}(\rho O)={\mathbb{E}}[{{\rm{Tr}}}({{{\mathcal{M}}}}^{-1}(\hat{\sigma })O)]$. This forms the basis of randomized measurement schemes: we can estimate ${\mathbb{E}}[{{\rm{Tr}}}({{{\mathcal{M}}}}^{-1}(\hat{\sigma })O)]$ with an empirical average over our dataset ${{\mathcal{D}}}$, hence allowing us to estimate ${{\rm{Tr}}}(\rho O)$. Notably, the dataset ${{\mathcal{D}}}$ was not tailored to a particular observable O, hence we can repeat the same classical postprocessing procedure to predict a large set of L observables $\left\{{O}_{l} \, | \, l=1,\ldots,L\right\}$ simultaneously. This flexibility extends beyond linear observables: since $\rho={\mathbb{E}}[{{{\mathcal{M}}}}^{-1}[\hat{\sigma }]]$ it follows that ${\tilde{\rho }}^{(2)}\equiv \frac{1}{K(K-1)}{\sum }_{i\ne j}{{{\mathcal{M}}}}^{-1}[{\hat{\sigma }}_{i}]\otimes {{{\mathcal{M}}}}^{-1}[{\hat{\sigma }}_{j}]$ is an unbiased estimator for ρ^⊗2. Remarkably, this means that the dataset ${{\mathcal{D}}}$, constructed using only single-copy measurements of ρ, can be used to learn non-linear properties of ρ: for instance, the purity can be estimated using the observable O = SWAP and evaluating ${{\rm{Tr}}}(O{\tilde{\rho }}^{(2)})$. However, the most useful property of classical shadows is that the sample complexity of achieving this multitasking has been shown¹ to be ${{\mathcal{O}}}(\log L\cdot {\max }_{i}{\left\Vert {O}_{i}\right\Vert }_{\,{\mbox{sh}}\,}^{2}/{\epsilon }^{2})$, which scales logarithmically in L instead of linearly. A critical component of this scaling is the shadow norm ${\left\Vert {O}_{i}\right\Vert }_{\,{\mbox{sh}}\,}^{2}$ of the operator O_i, which depends on the details of the unitary ensemble.

The shadow map ${{\mathcal{M}}}$ and its inverse can be efficiently calculated for a large family of unitary ensembles called locally scrambled unitary ensembles, where the unitary ensemble satisfies the local-basis invariance condition¹¹ (see Supplementary Note 1). Locally-scrambled unitary ensembles are easily realized experimentally: for example, as shown in Fig. 1b, any two-qubit gate sandwiched by random single-qubit Clifford gates satisfies the local-basis invariance condition. This procedure is also called single-qubit twirling^68,69,70. In the following, we will call these sandwiched two-qubit gates twirled gates for short. If the randomized quantum circuit is composed of twirled gates, as shown in Fig. 1a, then ref. ¹³ shows that ${{\mathcal{M}}}$ is diagonal in the Pauli basis. This means that ${{\mathcal{M}}}[P]=\omega (P)P$ for any Pauli P, where $\omega (P)\equiv {{\mathbb{E}}}_{U \sim {{\mathcal{E}}}}[{\left\langle \right.0| UP{U}^{{\dagger} }| 0\left.\right\rangle }^{2}]$ is called the Pauli weight. Here and throughout, we use $| 0\left.\right\rangle$ shorthand for the n-qubit product state ${| 0\left.\right\rangle }^{\otimes n}$. This implies that

$${\mathbb{E}}[\hat{\sigma }]={{\mathcal{M}}}[\rho ]= \frac{1}{{2}^{N}}\sum\limits_{P\in {{\mathbb{P}}}_{N}}\omega (P){{\rm{Tr}}}(\rho P)P;\\ \rho= {{{\mathcal{M}}}}^{-1}[{\mathbb{E}}[\hat{\sigma }]]=\frac{1}{{2}^{N}}\sum\limits_{P\in {{\mathbb{P}}}_{N}}{\omega }^{-1}(P){{\rm{Tr}}}({\mathbb{E}}[\hat{\sigma }]P)P$$

(1)

where ${{\mathbb{P}}}_{N}$ is the N-qubit Pauli group. We note that the local basis invariance of the unitary ensemble ${{\mathcal{E}}}$ effectively erases any information about the local basis for P. This means that ω(P) does not depend on the exact characters in the Pauli string P: if the position of all non-identity operators is the same for two Pauli operators, they share the same value of Pauli weights. Therefore, despite the fact that there are 4^N different Pauli operators, there are only 2^N distinct Pauli weights. As we show later, this fact makes it natural to use a ‘particle-hole’ basis for locally scrambled unitary ensembles. Although there are still exponentially many Pauli weights, in the next section and Methods section, we will show they can all be efficiently represented (i.e., using polynomial classical resources) with a simple tensor network representation.

So far, we have assumed that the state ρ can be evolved by U perfectly. However, real quantum circuits have noise, in which case the actual evolution will differ from the ideal unitary U. The actual evolution can be described by a channel ${{{\mathcal{C}}}}_{U,\lambda }[\rho ]$, where λ parameterizes the noise in the evolution. For unitary ensembles in which the set of unitaries U forms a group, such as those formed by the Clifford group or tensor products of single-qubit Clifford gates (i.e., random Pauli measurements), the noisy measurement channel takes a simple form when expressed in the Pauli basis^7,71,72:

$${{{\mathcal{M}}}}_{\lambda,{{\mbox{Clifford}}}}[P]= fP+\frac{(1-f)}{{2}^{N}}{{\rm{Tr}}}(P)I\\ {{{\mathcal{M}}}}_{\lambda,{\mbox{Pauli}}}[P]= {\otimes }_{i=1}^{N}\left({f}_{i}{P}_{i}+\frac{(1-{f}_{i})}{2}{{\rm{Tr}}}({P}_{i})I\right),$$

(2)

where $P={\otimes }_{i=1}^{N}{P}_{i}$ is a Pauli string, the tensor product of Pauli operators on each qubit, and f, f_i are noise-dependent parameters. These expressions allow for efficient noise characterization and mitigation^7,53.

However, for more general unitary ensembles, such as those involving shallow quantum circuits (which do not form a group), the form of the noisy measurement channel is not immediately apparent. For shallow quantum circuits that satisfy the local-basis invariance condition, we show the measurement channel is still diagonal in the Pauli basis: ${{{\mathcal{M}}}}_{\lambda }[P]={\omega }_{\lambda }(P)P$. The noisy Pauli weights are

$${\omega }_{\lambda }(P)={{\mathbb{E}}}_{U \sim {{\mathcal{E}}}}[\left\langle \right.0| UP{U}^{{\dagger} }| 0\left.\right\rangle \left\langle \right.0| {{{\mathcal{C}}}}_{U,\lambda }[P]| 0\left.\right\rangle ].$$

(3)

For a derivation of this, see Supplementary Note 1. Compared with Eq. (2), we see noisy Pauli weights are generalizations of noise parameters f_i and f when using noisy shallow circuits.

Bias-variance tradeoff

Understanding the bias-variance tradeoff is crucial for optimizing our robust shallow shadows protocol in practice. As we increase the depth of our shallow circuits, we gain the ability to estimate a broader class of observables efficiently. However, this comes at the cost of accumulating more noise, potentially biasing our results. This tradeoff directly impacts the choice of optimal circuit depth and the overall performance of our protocol.

Since the shadow map is diagonal in the Pauli basis, the expectation of any Pauli P is simply

$${{\rm{Tr}}}(\rho P)=\frac{1}{{\omega }_{\lambda }(P)}{\mathbb{E}}[{{\rm{Tr}}}(\hat{\sigma }P)].$$

(4)

Since $\left\vert {{\rm{Tr}}}(\hat{\sigma }P)\right\vert \le 1$, the inverse Pauli weight upper bounds the shadow norm of any Pauli P (i.e., the sample complexity of estimating P): ${\left\Vert P\right\Vert }_{\,{\mbox{sh}}\,}^{2}\le {\omega }_{\lambda }{(P)}^{-1}$. Therefore, to upper bound the sample complexity, it suffices to lower bound the Pauli weight ω_λ(P). In the noiseless case, the sample complexity scaling of shallow shadows was numerically investigated in refs. ^14,15. A theoretical understanding was given by ref. ⁶², where the expectation in Eq. (3) was calculated by mapping the evolution of P through the circuit to a classical random walk. The shadow norm depends on this random walk’s final set of configurations. We extend this analysis⁶² to the noisy case. Our analysis assumes that the noise is single-qubit depolarizing noise with site-independent strength λ. For a detailed analysis of more general noise models, including multi-qubit correlations and non-Markovian effects, see Supplementary Note 2.

As we show, the effect of noise on this random walk is simple. While we focus our analysis on Pauli operators comprised of k contiguous non-trivial characters (illustrated in Fig. 2a), the qualitative behaviors—operator spreading, density relaxation, and noise-induced damping—persist for non-contiguous operators. The main difference is that non-contiguous operators experience multiple independent spreading fronts, one from each cluster of non-trivial characters, leading to faster operator growth but maintaining similar asymptotic scaling. As depicted, there are three physical processes, and only a third of these depend on the noise. First, the average density of particles in the bulk will relax, owing to the fact that twirled two-qubit gates tend to reduce the weight of high-weight Pauli operators (for instance, a Haar random two-qubit gate maps a weight 2 Pauli operator to a weight 1 Pauli operator with probability $\frac{3}{5}$). Second, the domain of the observable will spread (shown in red) with some butterfly velocity v_B as a result of the entangling two-qubit gates which act on the edge of the Pauli’s support. Finally, each particle will have a damping factor of $\exp (-\lambda )$ during the stochastic process due to the depolarizing noise. The effects of each of these three processes can be bounded, and combining all of these bounds allows us to obtain an upper bound of the shadow norm for contiguous Pauli operators, hence bounding the requisite sample complexity to estimate these operators. The details of the theoretical analysis, as well as a numerical characterization of phenomenological parameters such as γ and v_B can be found in Supplementary Note 4.

Fig. 2: Sample complexity in robust shallow shadows (RSS) for Pauli observables with contiguous support of size k.

a We show a conceptual illustration of the three physical phenomena influencing sample complexity in the context of a classical random walk model: 1) operator spreading with a `butterfly velocity' v_B; 2) particle density relaxation; and 3) noise-induced damping with rate e^−λ. The hatched region represents the space-time domain where operator spreading and relaxation occur: as time progresses (vertically), the initial operator of size k (black dots) spreads ballistically (diagonal boundaries) while simultaneously relaxing to equilibrium density (vertical blue line). These phenomena collectively determine the sample complexity required for accurate observable estimation. b We illustrate the qualitative impact of noise on the sample complexity upper bound, illustrating that increased noise levels lead to a slight increase in the sample complexity upper bound and a reduction in the optimal circuit depth. This reduction is approximately linear in the noise strength λ, with a proportionality coefficient α. This is an example of the trade-offs involved in designing a noise-robust protocol. c We illustrate the RMS error of reconstructed Paulis inferred using 10⁴ different circuits with 100 shots each, as a function of the support size k. The dashed lines show the RMS error associated with direct calibration, while the solid lines correspond to the Bayesian learning protocol. The results demonstrate that Bayesian learning achieves comparable or better accuracy than direct calibration across all circuit depths d, while requiring significantly fewer calibration shots. This improved efficiency is particularly evident for larger support sizes, where the Bayesian approach maintains stable error rates even as k increases.

Theorem 1

(Sample complexity and optimal circuit depth, informal) Assuming single-qubit depolarizing noise with strength λ, for k ≫ d ≫ 1, the shadow norm of a Pauli operator support over k contiguous sites is upper bounded by

$${\log }_{3}{\left\Vert {P}_{k}(d)\right\Vert }_{{{\rm{sh}}}}^{2}\le \left(k+d\right)\left(\frac{3}{4}+\frac{\exp (-\gamma d)}{{t}^{3/2}}+\frac{d\lambda }{\log 3}\right),$$

(5)

where d is the circuit depth and $\exp (-\gamma )\equiv {(\frac{4}{5})}^{2}$. The circuit depth d ^* that minimizes this upper bound is

$${d}^{ * }=\frac{1}{\gamma }\left(\log \frac{k}{3\log 3+4k\lambda }+\ldots \right){=}_{(k\lambda \ll 1)}\frac{1}{\gamma }\left(\log \frac{k}{3\log 3}-\frac{4k\lambda }{3\log 3}+\ldots \right)$$

(6)

where … denotes subleading terms.

Equation (6) shows that the theoretical optimal circuit depth is shallower for noisy circuits compared to noiseless ones, a fact which we illustrate in Fig. 2b. Simultaneously, Eq. (5) shows that the noise also increases the associated sample complexity for estimating P_k. However, the sample complexity bounds in this theorem are overly pessimistic, and we can do significantly better using a phenomenological model that we detail in Supplementary Note 4.

The bias-variance tradeoff highlights the need for efficient and accurate calibration methods. To address this, we develop a Bayesian inference approach that allows us to characterize and mitigate the noise in our system, striking a balance between the benefits of increased circuit depth and the challenges posed by accumulated noise.

Efficient calibration with Bayesian inference

Equation (4) implies that an accurate estimate of ω_λ(P) is required to produce accurate estimates of Pauli expectation values. In this section, we describe an efficient Bayesian inference method to learn the Pauli weights. We begin with a cruder method: direct inference. Simply by inverting Eq. (4), we see that if we set $\rho=| 0\left.\right\rangle \left\langle \right.0|$ and P to be any Pauli operator formed of only I and Z operators, we get ${\omega }_{\lambda }(P)={\mathbb{E}}[{{\rm{Tr}}}(\hat{\sigma }P)]$. We can estimate ${\mathbb{E}}[{{\rm{Tr}}}(\hat{\sigma }P)]$ by preparing $| 0\left.\right\rangle$, evolving under a random shallow circuit U, and measuring on a computational basis. Theorem 2 shows that this calibration process requires no assumptions on the structure of noise in the circuit, and is asymptotically unbiased.

Theorem 2

(Informal, Learning noisy Pauli weights) Given ϵ > 0, a number of

$$R={{\mathcal{O}}}\left({\epsilon }^{-2}{\max }_{\left\vert {P}_{\alpha }\right\vert \le k}\parallel {P}_{\alpha }{\parallel }_{{{\rm{sh}}}}^{4}\right)$$

sample in the calibration process is enough for the following robust shallow shadow procedure to estimate any k—local observables to the following precision

$$\left\vert {{\rm{Tr}}}(\rho O)-{\widehat{O}}_{{{\rm{est}}}}\right\vert \, < \, \epsilon \,{2}^{k}{\left\Vert O\right\Vert }_{\infty }$$

(7)

with high success probability.

This direct calibration method allows us to learn individual Pauli weights efficiently. However, for predicting properties involving many noisy Pauli weights, knowing individual Pauli weights is insufficient. In practice, we require an efficient way to encode all 2^N Pauli weights. Although this is impossible in general, we can take advantage of certain structural features of our unitary ensemble: our random unitary ensemble consists of twirled two-qubit gates arranged in a brickwork structure. By leveraging this structural assumption, we prove that any time-independent device noise can be captured by a stochastic Pauli noise model. The proof idea is similar to the idea behind randomized compilation⁷³, wherein single-qubit random gates can effectively change physical noise to stochastic Pauli noise. This result is summarized in Theorem 3, the proof of which is in Supplementary Note 2.

Theorem 3

(Informal, Noise-robust shallow shadow on time-independent noise) In a noise-robust shallow shadow setting, a stochastic Pauli noise model can be used in the data post-processing to effectively capture the time-independent noise that happened in the physical circuit, including coherent errors, provided that the single-qubit gate errors are small. If the noise parameters are accurately learned, the predictions given by the robust shallow shadow remain unbiased.

By integrating this simple stochastic Pauli noise model with tensor network post-processing and Bayesian learning, we can achieve more efficient calibration and prediction, enabling the accurate prediction of a wide range of observables, including quantum fidelity. In light of Theorem 3, we model the noise channel Λ of an N-qubit system from the local interactions generated by a Lindbladian ${{\mathcal{L}}}(\rho )={\sum }_{k\in {{\mathcal{K}}}}{\lambda }_{k}\left({P}_{k}\rho {P}_{k}-\rho \right)$, where ${{\mathcal{K}}}$ is a set of Pauli operators that is defined by the local interactions between qubits. Given that the interactions are assumed to be geometrically local, the size of ${{\mathcal{K}}}$—and thus the number of noise parameters—scales linearly with N. While non-local Pauli errors may arise beyond nearest neighbors, this model has been shown to accurately describe realistic hardware noise, as demonstrated in ref. ⁷⁴. Furthermore, in Supplementary Note 2, we demonstrate that our protocol remains robust even in the presence of non-local correlated errors. Additionally, we extend Theorem 3 to other noise models, including non-Markovian noise, as detailed in the Methods. Specifically, if U represents a single layer of CNOT gates, the state after this layer evolves as ${\rho }^{{\prime} }={e}^{{{\mathcal{L}}}}[U\rho {U}^{{\dagger} }]$. Since ${{\mathcal{L}}}$ is a sparse Pauli-Lindbladian, ${e}^{{{\mathcal{L}}}}$ enjoys a particularly simple form when acting on Pauli operators:

$${e}^{{{\mathcal{L}}}}[P]=\exp \left(-\sum\limits_{k;[{P}_{k},P]\ne 0}{\lambda }_{k}\right)P,$$

indicating that P acquires a damping factor based on its non-commuting Lindbladian generators⁷⁴. We assume different noise parameters λ for the even and odd layers of CNOT gates, and model readout errors by absorbing them into the last layer of Pauli-Lindbladian noise. We note that although the Pauli-Lindbladian model has 9 two-body terms for each neighboring pair of qubits and 3 on-site terms for each qubit, the single-qubit twirling in our shallow circuit ensemble simplifies this noise significantly. The effect of these random single-qubit gates is to twirl the noise such that each edge, can be parameterized by three numbers: λ_PI, λ_IP, λ_PP. These represent the local action of the noise channel on a Pauli operator which has support on the first qubit, second qubit, or both qubits, respectively. The first two terms can be interpreted as single-qubit depolarizing noise.

In the post-processing, we aim to infer the ‘effective’ values of the noise parameters λ. We emphasize that the learned noise parameters are phenomenological, in the sense that we are concerned with their values only insofar as they affect the Pauli weights ω_λ(P). Indeed, as we show in Supplementary Note 2, this calibration method works well even if the device noise is not well-described by the Pauli-Lindblad model. The reason for this is that the noisy Pauli weights ω_λ(P) do not depend strongly on the particular structure of the device noise, hence our sparse Pauli-Lindblad ansatz is sufficiently flexible to represent the noisy Pauli weights of a wide variety of noise models.

To estimate the noise parameters λ more efficiently, we apply the framework of Bayesian inference. Although the learning framework in probabilistic error cancellation (PEC)⁷⁴ can be used for this estimation as well since the noise is twirled by random single-qubit Clifford gates, this results in a simplification of the effective noise channel. This simplification means that it is sufficient to use historical noise data (learned as part of PEC) as a loose prior and to use Bayesian learning to ‘fine-tune’ this prior. This Bayesian learning method requires less device time than the direct calibration method and Pauli-Lindblad learning, as the calibration dataset ${{{\mathcal{D}}}}_{c}$ we use for the parameter estimation is relatively simple. This calibration dataset is obtained by preparing the ${| 0\left.\right\rangle }^{\otimes N}$ state and applying our shallow shadows protocol. Using this data, we construct a likelihood function $p({{{\mathcal{D}}}}_{c}| \lambda )$ based on empirical estimates of Pauli weights. We then use a log-normal prior distribution p(λ) centered around historical noise data. The posterior distribution $p(\lambda | {{{\mathcal{D}}}}_{c})$ is sampled using Hamiltonian Monte Carlo, allowing us to infer the effective noise parameters λ. As shown in Fig. 2c, this Bayesian approach maintains significantly lower RMS errors compared to direct calibration, particularly for Pauli operators with larger support size k. While the direct calibration error grows rapidly with k, our Bayesian method shows remarkable stability, maintaining consistent error rates across different circuit depths and operator sizes. For details of this inference method, see Supplementary Note 2.

To further enhance our protocol’s efficiency, we complement our Bayesian inference method with a tensor network-based representation of the noisy Pauli weights. This approach allows us to efficiently encode all 2^N Pauli weights using polynomial classical resources. By recasting the Pauli weight calculation as an expectation over a random walk in the space of Pauli operators, we construct a matrix product operator (MPO) representation of the expectation ${\mathbb{E}}[{{{\mathcal{C}}}}_{2}[\cdot ]]$. This MPO, when applied to the all-plus state, yields a matrix product state (MPS) representation of the Pauli weights ω_λ(P) with bond dimension exponential in the circuit depth. For our log-depth circuits, this results in a polynomial-resource classical representation, enabling rapid estimation of a wide range of observables (see Supplementary Note 3 for details).

The full robust shallow shadow protocol with efficient Bayesian inference calibration is summarized in Box Box 1.

Box 1 noise-robust shallow shadows protocol

1: Fix a locally scrambled unitary ensemble ${{\mathcal{E}}}$. The circuits in this ensemble must be at most logarithmic depth.

Calibration

2: Prepare the $| 0\left.\right\rangle$ state with high fidelity and collect a calibration dataset ${{{\mathcal{D}}}}_{c}$ by sampling from the unitary ensemble ${{\mathcal{E}}}$.

3: Use Bayesian inference (see Methods) to find a MAP estimate of true noise parameters λ.

4: Construct a representation of the noisy Pauli weights ω_λ using the MPS formalism with λ, and variationally find an MPS representation of the inverse Pauli weights ${\omega }_{\lambda }^{-1}$ with gradient descent^14,15. Since empirically derived noise parameters are accounted for in ${\omega }_{\lambda }^{-1}$, these inverse Pauli weights mitigate the effects of experimental noise (e.g., qubit crosstalk, measurement error, etc.).

Application

5: Prepare the application state ρ and collect the dataset ${{\mathcal{D}}}$ by sampling from the unitary ensemble ${{\mathcal{E}}}$.

6: Find an MPS representation (on a Pauli basis) for the observables of interest. Examples of observables that admit an efficient MPS representation include any Pauli operator, subsystem purities, and overlaps with respect to MPSs.

7: Infer the values of the observables of interest by contracting the appropriate MPS (see Supplementary Note 3).

Experiments

In this section, we demonstrate the effectiveness of our robust shallow shadows protocol through a series of experiments on a superconducting quantum processor. Our goals are twofold: first, to show that our protocol can accurately recover various quantum state properties in the presence of noise, and second, to quantify the sample complexity advantages of our method compared to traditional approaches. We investigate three different circuit depths and apply our protocol to multiple quantum states, including the plus state, cluster state, and AKLT resource state.

There are a number of choices that an experimentalist is free to make in Box 1. The first is the choice of the unitary ensemble ${{\mathcal{E}}}$. As shown in the original classical shadow framework¹, the details of this ensemble can have a drastic impact on sample complexity, depending on the observables of interest. For instance, ensembles comprised of single-qubit random Cliffords are well-suited for predicting local observables, while ensembles comprised of global random Cliffords are useful for low-rank observables such as fidelity. In this section, we will provide experimental evidence showing that interpolating between these two regimes allows us to achieve, in a sense, the best of both worlds. By using shallow brickwork random Clifford circuits, we show that an extremely broad class of observables can be measured with relatively low sample complexity, including both local observables and low-rank observables such as fidelity. Concretely, we test three different ensembles which consist of $d\in \left\{0,2,4\right\}$ layers of single-qubit twirled CNOT gates. The d = 0 is simply the random single-qubit Clifford case initially proposed in ref. ¹, also known simply as randomized Pauli measurements. On the other hand, as shown in Fig. 1a, when d = 2, our circuits contain two layers of twirled CNOT gates (one even layer and one odd layer), so d = 4 contains four layers of twirled CNOT gates. The other remaining degrees of freedom in Box 1 are the size of the dataset ${{\mathcal{D}}}$, the application state ρ, and the observables of interest. For both the calibration and application dataset, we applied 10000 different random unitaries from ${{\mathcal{E}}}$ and took 100 shots for each unitary circuit, keeping the random twirling gates fixed across all 100 shots for a given unitary (see Supplementary Note 5 for experimental details). We then applied our multitasking protocol on both the plus state ${|+\left.\right\rangle }^{\otimes 18}$ and a cluster state. The cluster state we choose is $| \phi \left.\right\rangle={\prod }_{i=1}^{N-1}{{\mbox{CZ}}}_{i,i+1}{|+\left.\right\rangle }^{\otimes N}$, which is a ground state of a symmetry-protected topological Hamiltonian H = −∑_iZ_i−1X_iZ_i+1. Even though both are stabilizer states, we emphasize that our method doesn’t rely on any special properties of the stabilizer states (later in this section, we will demonstrate this by applying our protocol to the AKLT resource state). We show below that, using the same randomized measurement dataset, we can accurately predict a number of observables for each of these states, including fidelity, local and non-local Pauli observables, and subsystem purity.

Figure 3 summarizes our experimental results for the plus state and cluster state. The top panel shows the inferred overlap between the experimentally prepared state and the ideal application state. The hatched bars indicate recovered values without error mitigation, while the solid bars show inferred values when accounting for noise. To verify the correctness of our protocol, we also estimated some of these observables with direct measurement. For instance, the overlap of the experimentally prepared state with ${|+\left.\right\rangle }^{\otimes 18}$ was calculated by repeatedly measuring on the X basis, and the three Pauli observables were inferred similarly. The directly measured values are still subject to readout noise. Therefore, we use readout error mitigation⁷⁵ and use the mitigated results as the fiducial values (dashed black lines in Fig. 3a). Both our error-mitigated shadow predictions and these fiducial measurements agree within their respective statistical uncertainties, suggesting neither method has significant unmitigated systematic bias. We note that some error-mitigated estimates (like X₁X₂X₃X₄ at d = 4) slightly exceed the physical bound of 1. This is a known phenomenon in error mitigation: while our protocol guarantees unbiased estimates, statistical fluctuations combined with error mitigation can occasionally yield unphysical values. One could enforce physicality through additional constraints or renormalization, but this would introduce bias in the estimator. We choose to report the unbiased estimates directly, as their proximity to physical bounds suggests our error mitigation is working as intended without over-correction.

Fig. 3: We apply RSS to predict multiple quantities including fidelity, Pauli observables, and subsystem purities.

The hatched bars indicate recovered values without error mitigation, while the solid bars use error mitigation. a We infer the fidelity of the experimentally prepared plus state ${|+\left.\right\rangle }^{\otimes 18}$ and cluster state $| \phi \left.\right\rangle$ with respect to the ideal (i.e., perfectly prepared) state. For the plus state, predictions agree with fiducial values obtained via direct fidelity estimation (i.e., measurement in the X basis), showcasing the effectiveness of RSS in error mitigation. In contrast, predictions without error mitigation exhibit a decline in fidelity as circuit depth increases, underscoring the impact of noise. b Displays the predicted expectation values of Pauli observables, where RSS predictions maintain consistency and, for the plus state, agree with fiducial values. c We show different subsystem purity predictions for a cluster state, illustrating how purity values are contingent upon the number of cuts within a subsystem. For instance, a subsystem in the bulk (formed by two cuts) has a theoretical purity of 0.25, whereas a boundary subsystem, with one cut, has a theoretical purity of 0.5.

We can also use the dataset to predict non-linear properties, such as subsystem purity ${{\rm{Tr}}}{\psi }_{A}^{2}$, where ψ_A is the reduced density matrix of ψ on subsystem A. This purity is important because it encodes information about the entanglement entropy of a state—more specifically, it is related to the entanglement 2-Rényi entropy via ${S}_{2}=-{\log }_{2}{{\rm{Tr}}}({\psi }_{A}^{2})$. The entanglement entropy of a (perfectly prepared) cluster state is well-known. The degenerate boundary edge modes are broken in the state preparation for the cluster state, but if we cut the system into two pieces, this cut will create a degenerate edge mode, which in turn creates 1 bit of information. That is, we expect that each cut will reduce purity by a factor $\frac{1}{2}$. To be more concrete, if a subsystem is created with a single cut (e.g., subsystems $\left\{1,2\right\}$ and $\left\{1,2,3,4\right\}$), then the theoretically expected subsystem purity is $\frac{1}{2}$. If a subsystem is created with two cuts (e.g., subsystem $\left\{8,9,10,11\right\}$), we expect the subsystem purity to be $\frac{1}{4}$. In Fig. 3, we observe that, indeed, the predicted purity after error mitigation is close to these theoretical values. The small deviations away from theoretical values are due to imperfect state preparation: as shown in Fig. 3, the experimentally prepared cluster state has fidelity  ~80%. The performance improvement from shallow shadows varies across observables. For some local observables like the {1, 2} subsystem purity, unmitigated d = 0 performs as well as error-mitigated shallow shadows, indicating that shallow circuits provide minimal advantage for such local quantities. This aligns with theoretical expectations: random Pauli measurements (d = 0) are already optimal for local observables, while shallow shadows improve sample complexity primarily for more non-local (e.g., the purity of subsystem $\left\{1,2,3,4\right\}$) or low-rank observables.

One of the advantages of applying shallow circuits to classical shadow tomography is the reduction of sample complexity for both non-local and low-rank observables. To evidence this claim, we observe two competing effects. First, as shown in Theorem 1, increased depth is well-suited for non-local observables. It is also well-suited for low-rank observables such as fidelity, since we converge to the global Clifford ensemble (which is optimal for low-rank observables) with increased depth. This improved suitability reduces the standard deviation of the inferred values for these observables at larger depths: this effect is particularly evident for fidelity, as highlighted in Fig. 4.

Fig. 4: Since the number of samples required to achieve a certain statistical error is proportional to the variance (square of the standard deviation) of the estimator, we use the standard deviation to indicate sample complexity.

a The standard deviation of fidelity predictions decreases with increasing circuit depth, indicating reduced sample complexity. b The standard deviation for estimating Pauli operator expectations is plotted as a function of the Pauli weight k. We observe excellent agreement between experimental data (solid dots with error bars) and theoretical predictions (solid lines). Notably, shallow circuits (d = 2, 4) exhibit favorable sample complexity scaling for higher-weight Pauli operators, outperforming the d = 0 scaling (proportional to 3^k), as well as the theoretical upper bound of 2.28^k.

However, this effect competes against the increasing effects of noise. As can be seen in Fig. 3, when error mitigation is turned off, the recovered values become more biased with increasing depth d. This depth-dependent bias is most pronounced for fidelity because it is a global observable sensitive to all qubits, accumulating errors from the entire circuit. In contrast, local observables like X₁X₂ are affected only by errors in their local region, making them more robust to increasing circuit depth. As discussed in Section II C, this noise-induced bias can be corrected using Pauli weights ${\omega }_{\lambda }^{-1}$ that have been appropriately calibrated. However, this comes at the cost of slightly increased variance, which in turn increases the sample complexity. As with the bias, this increase in sample complexity also grows with depth d.

Using experimental data, we quantitatively study the competition between these two effects in Fig. 4. Using bootstrap estimates of the standard deviation σ of our recovered expectation values, we can study the effects of increased depth on a variety of observables, including fidelity and a set of Pauli observables with increasing weight. We observe that for high-weight Pauli observables, the two competing effects find an optimal tradeoff at d = 2. Although the upper bounds from Theorem 1 predict a standard deviation  ~2.28^k at the optimal depth in an ideal setting (already a significant improvement over σ ~ 3^k, which is the scaling for d = 0), we find that in practice, we can do much better than this, as evidenced by the d = 2 line compared to 2.28^k dashed line. Our MPS formalism allows us to calculate an exact prediction for the standard deviation of any Pauli observable, shown in solid lines, demonstrating excellent agreement with the bootstrapped standard deviations. Turning to fidelity estimation, we see, unlike Pauli observables, d = 4 is a strict improvement over d = 2. This contrasting behavior reflects the different scaling shown in Fig. 2b: while Pauli observables reach optimal sample complexity at moderate depths before noise degradation dominates, fidelity estimation continues improving with depth despite increased noise. This is expected, as random global Clifford shadows are the optimal setting for fidelity estimation in the noiseless limit¹. Regardless, for Pauli observables with contiguous support (like those shown here) and fidelity, using a shallow depth ensemble with error mitigation is always strictly better than using a d = 0 ensemble. While our experiments focus on contiguous Pauli strings for simplicity, theoretical analysis suggests similar advantages hold for non-contiguous strings (see Supplementary Note 2), though the optimal circuit depth may vary with the Pauli support pattern.

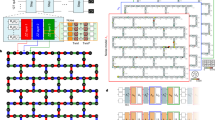
To further demonstrate the versatility of our protocol, we apply it to a more complex quantum state: the AKLT resource state. This state is particularly interesting as it is not a stabilizer state⁷⁶, unlike the plus and cluster states we examined earlier. By characterizing this state, we showcase our protocol’s ability to handle a broader class of quantum states, including those relevant to quantum simulation and quantum computational supremacy experiments. Specifically, we applied RSS with d = 4 to predict the purity of all size 1 and 2 subsystems for the AKLT resource state on 18 qubits. As shown in Fig. 5b, this state consists of 3 small clusters of AKLT states, which can eventually be merged into a 6-qubit AKLT state. The small clusters are knit together into a single global AKLT state by applying Bell measurements on the edge qubits of adjacent small AKLT states and applying a correction conditioned on the measurement outcome (this process is known as applying ‘fusion measurements’). However, in this work, we do not apply these fusion measurements, as this requires measurement feedforward, which is experimentally difficult to implement. Instead, we prepare the AKLT resource state on superconducting qubits and characterize its entanglement structure prior to fusion measurements using RSS. In Fig. 5a, we show theoretical and experimentally recovered values for every 1- and 2-qubit subsystem purity of the resource state. The theoretical predictions assume perfect state preparation and noiseless evolution, providing an idealized benchmark against which we can compare our error-mitigated experimental results. The mean relative error (compared to the theoretically predicted values) for the recovered purities without error mitigation is 6.4%, while the mean relative error with error mitigation is 3.2%, further evidencing the efficacy of our error mitigation method. Notably, the residual difference between mitigated and unmitigated results is consistently positive across all subsystems, indicating that our error mitigation protocol systematically reduces excess entropy introduced by experimental noise, particularly within the three AKLT clusters. Comparing the recovered purities shows excellent agreement with exact theoretical values: as expected, we clearly see three distinct entangled clusters in the experimental data, representing each of the local AKLT states.

Fig. 5: Prediction of subsystem purity in the AKLT resource state using RSS.

a We demonstrate how the RSS method can use a single dataset to concurrently predict the purity of all subsystems up to two qubits within AKLT resource states. We show theoretical predictions (left), experimental results with error mitigation (center), and the residual difference between mitigated and unmitigated results (right). The residual plot reveals that error mitigation systematically increases the predicted purities, bringing them closer to theoretical values, with the strongest corrections appearing in the three distinct AKLT clusters. The values at (i, j) represent the purity of the reduced density matrix ${{\rm{Tr}}}({\rho }_{ij}^{2})$. The AKLT resource state has three clusters, each representing a smaller AKLT state with two spin-1 particles before fusion measurement; experimental predictions clearly show this pattern as well, and closely align with theoretical predictions. b We show a schematic of the AKLT resource state before fusion measurements are applied to prepare the AKLT state.

Discussion

In this work, we executed an unbiased randomized measurement experiment that went beyond random Pauli measurements for large quantum systems. In these experiments, we showed that our robust shallow shadow protocol can efficiently recover unbiased estimates for a wide array of observables on unknown quantum states, even in the presence of noise. While our Bayesian noise characterization technique is general, we demonstrate its effectiveness using a sparse Pauli-Lindblad noise model well-suited to the IBM device’s heavy-hex architecture—other quantum platforms may require different device-specific noise models. We do this by providing a general noise characterization technique based on Bayesian inference that can account for realistic noise effects, such as qubit crosstalk and measurement error. Having characterized the noise on our device, we then introduced an efficient tensor network-based postprocessing technique that is naturally able to account for the effects of this noise. We provide evidence that this error mitigation technique is effective by demonstrating that our protocol gives unbiased predictions of low-rank observables (e.g., fidelity), non-local Pauli observables, and even nonlinear observables (e.g., subsystem purity) for a number of application states, including the cluster state and the AKLT resource state. Not only is our protocol able to recover unbiased estimators of these observables, but we also show that the standard deviation of these estimators improves with shallow circuits compared to d = 0, though the optimal depth varies by observable type. While fidelity estimates continue improving through d = 4, Pauli observables achieve minimum variance around d = 2 before noise effects begin to dominate. That is, we show how going beyond random Pauli measurements can give rise to improved sample complexities. Furthermore, we developed a theoretical framework that not only predicted improvements in sample complexity that agreed well with the empirically observed improvements, but our framework also showed that shallow shadows remain information-theoretically optimal, even in the presence of noise. Our new theoretical insights, combined with the experimental validation of our protocol, further underscore the practical relevance and effectiveness of our approach. The success of these experiments not only validates the theoretical underpinnings of our protocol but also showcases its potential for real-world quantum computing applications. Finally, we note that the framework developed in ref. ⁷⁷ could be used to characterize out-of-model errors in our noise model. When there is a significant mismatch between the effective Pauli noise model and the actual device noise, the Bayesian calibration procedure may fail, leading to biased predictions. In such cases, the direct calibration algorithm outlined in Section II C provides a model-agnostic method to estimate the relevant Pauli weights. In Supplementary Note 2, we evaluate the performance of our local Pauli-Lindbladian noise model in the presence of additional correlated non-local three-qubit noise. Across a wide range of strengths for these three-qubit errors, our framework remains robust, delivering unbiased predictions within statistical errors. Furthermore, in our experiments, comparisons between error-mitigated shadow predictions and fiducial values obtained from other direct measurement schemes show no deviations beyond statistical uncertainties.

We have presented a protocol that maintains the advantages of classical shadow tomography even in noisy quantum systems. This noise resilience is particularly important for the many applications of classical shadows in quantum machine learning, quantum chemistry, and quantum many-body physics. The randomized measurements dataset serves as a succinct classical description of a quantum state, and our robust protocol ensures these measurements remain reliable on real devices. By predicting many different Pauli observables efficiently, one can do unsupervised learning of conserved quantities, symmetries, and phases of matter for quantum many-body systems^56,78,79. A similar approach can be used for ansatz-free Hamiltonian learning and quantum device benchmarking^43,80,81. Measuring many low-rank observables simultaneously could also lead to new applications. For example, estimating the low eigenenergy spectrum is important for quantum many-body physics and quantum chemistry. Combining the idea of dynamic mode decomposition⁸² and measuring many low-rank observables simultaneously, one could have a better convergence rate in predicting eigenenergies⁸³.

To fully realize these potential applications and validate the broad applicability of our approach, future work should focus on extending these experiments to a wider range of quantum computing platforms and larger system sizes. While our current results demonstrate the effectiveness of robust shallow shadows on superconducting qubits, exploring its performance on other architectures such as trapped ions, neutral atoms, or photonic systems would be valuable. This cross-platform validation would not only further confirm the generality of our approach but also potentially reveal platform-specific optimizations. Additionally, investigating the scalability of our method to larger system sizes would be crucial for establishing its utility in future large-scale quantum applications.

In parallel with these experimental directions, it would be interesting to use modern machine learning techniques to further improve the inference and predictions of the proposed method⁸⁴ and also improve the sample complexity by tailoring unitary ensembles to special observables of interest^31,35. Lastly, by integrating the tensor network representation of the quantum noise model^85,86,87 with a robust shallow shadow dataset, it may be possible to mitigate quantum errors that occur during quantum simulation through data post-processing. This approach has the potential to improve the accuracy of quantum simulations on near-term quantum devices⁸⁸.

Note added—during the completion of this manuscript, we became aware of a related but independently developed work taking a randomized benchmarking approach to mitigate noise in randomized measurements⁸⁹.

Methods

Effective noise model

In the following, we summarize various effective noise models, including both Markovian and non-Markovian cases, after twirling by single-qubit Clifford gates. Detailed discussions and proofs are provided in Supplementary Note 2. We assume that single-qubit gates are either ideal or subject to gate-independent errors. As demonstrated in Supplementary Note 5, the noise associated with single-qubit gates is several orders of magnitude smaller than that of two-qubit gates or measurement operations, supporting the validity of this assumption in practical scenarios.

Theorem 4

(Noise-robust shallow shadow under time-independent Markovian noise) In a noise-robust shallow shadow setting, randomly sampling twirling gates independently in each round tailors the noise into a time-independent stochastic Pauli model, provided that the noise on single-qubit gates is gate-independent. This effective noise model can then be incorporated into data post-processing to mitigate the effects of time-independent Markovian noise. If the noise parameters are accurately learned, the predictions from the robust shallow shadow remain unbiased.

The key idea behind the proof of this theorem is that inserting single-qubit twirling gates into the randomized measurement circuit does not change the ensemble average of the noisy Pauli weight (Equation (3)), which defines the shadow map. These twirling gates symmetrize the Markovian noise in a manner similar to randomized compilation^90,91. This result provides the foundation for using the Pauli-Lindblad noise model to learn an effective noise representation and mitigate noise effects in robust shallow shadow protocols. Sometimes, quantum devices may also exhibit non-Markovian noise. The next theorem highlights the key distinction between Markovian and non-Markovian noise after twirling: in the latter case, classical correlations persist across different layers in the Pauli-Lindblad model⁹². These correlations can be incorporated into the post-processing step to further capture non-Markovian effects, using methods such as autoregressive machine learning models or tensor networks.

Theorem 5

(Noise-robust shallow shadow under non-Markovian noise) Consider a quantum channel where non-Markovian noise acts before and after a unitary operation U. This noise can be expressed in the Pauli basis as a general map ρ → ∑_i,j,k,l χ_ijkl P_jU(P_iρP_k)U^†P_l. After applying single-qubit Clifford twirling, the effective noise model reduces to a stochastic Pauli noise model with correlated error probabilities across layers, i.e. ρ → ∑_i,j p_i,j P_jU(P_iρP_i)U^†P_j with p_i,j = χ_ijij. In a noise-robust shallow shadow setting, this correlated Pauli noise model can be incorporated into data post-processing to mitigate the effects of non-Markovian noise. If the noise parameters and the classical correlations are accurately learned, the predictions from the robust shallow shadow remain unbiased.

In Fig. 6, we summarize the different effective noise models that emerge after applying single-qubit twirling.

Fig. 6: Effective channel after twirling with single-qubit random Clifford gates.

a Under time-independent Markovian noise, the effective channel is a stochastic Pauli noise channel with fixed Pauli probabilities, independent across layers. b For time-dependent Markovian noise, the effective channel is a stochastic Pauli noise channel, but with time-dependent Pauli probabilities, while different layers remain independent. c Under non-Markovian noise, the effective channel exhibits stochastic Pauli noise with joint Pauli probabilities correlated across layers.

Bayesian noise learning

The first step of our Bayesian noise learning method is to collect a calibration dataset ${{{\mathcal{D}}}}_{c}$ simply by running the shallow shadows protocol for a state $\rho=| 0\left.\right\rangle \left\langle \right.0{| }^{\otimes N}$, which we assume can be prepared with high fidelity. We then use this dataset to define a likelihood function $p({{{\mathcal{D}}}}_{c}| \lambda )$ for Bayesian inference as follows. We construct an estimator for the Pauli weights ${\tilde{\omega }}_{{{{\mathcal{D}}}}_{c}}(P)$ by inverting Eq. (4):

$${\tilde{\omega }}_{{{{\mathcal{D}}}}_{c}}(P)=\frac{1}{| {{{\mathcal{D}}}}_{c}| {{\rm{Tr}}}(| 0\left.\right\rangle \left\langle \right.0| P)}\mathop{\sum }_{i=1}^{| {{{\mathcal{D}}}}_{c}| }{{\rm{Tr}}}(\hat{{\sigma }_{i}}P),$$

(8)

where we always choose P to be some tensor product of identity and Z operators. Since any Pauli weight depends only on the support of P (thanks to the local-basis invariance of our ensemble) this subset of operators is sufficient to capture all Pauli weights. We calculate the standard deviations σ_P of these estimators using a standard bootstrap estimate, by resampling (with replacement) the empirical data 1000 times. The likelihood function is then simply

$$p({{{\mathcal{D}}}}_{c} \, | \, \lambda )\propto \exp \left(-\sum\limits_{P}\frac{{\left({\tilde{\omega }}_{{{{\mathcal{D}}}}_{c}}(P)-{\omega }_{\lambda }(P)\right)}^{2}}{2{\sigma }_{P}^{2}}\right),$$

(9)

where the sum runs over all Paulis P. We design a tensor network algorithm that efficiently encodes ω_λ(P) for all Paulis P given noise parameters λ as an MPS, which enables the efficient calculation of the likelihood function (details in Supplementary Note 3). In particular, we use the Pauli-Lindblad effective noise model, where each layer has independent noise parameters λ. While this model does not account for non-Markovian effects, one could, in principle, introduce parameterized classical correlations between these noise parameters to capture non-Markovian behavior. Rather than inferring these parameters layer by layer, we employ the tensor network method described in the next section to propagate the noise effects across all layers to the noisy Pauli weights, allowing us to infer them collectively. In practice, we choose all Pauli operators that are contiguous Z-strings up to weight 6 (beyond this weight, empirically recovered Pauli weights are too small to be resolved to within statistical significance). The prior p(λ) is given by a log-normal distribution with σ = 2, and centered around noise parameters $\tilde{\lambda }$ calculated via an independent inference process, namely that of ref. ⁷⁴. Together, the two fully specify the posterior distribution over the noise parameters:

$$p(\lambda \, | \, {{{\mathcal{D}}}}_{c})\propto p({{{\mathcal{D}}}}_{c} \, | \, \lambda )p(\lambda ).$$

(10)

We can then sample from this posterior distribution using Hamiltonian Monte Carlo^93,94. Although this method essentially gives us access to the full posterior distribution, in practice, we typically pick a fixed value of λ when inferring observables. This fixed value can be chosen in a number of ways, including by taking the mean or median of the posterior distribution samples, or simply using a maximum a posteriori probability (MAP) estimate (found by maximizing Eq. (10) via gradient descent). We find that each of these three methods for fixing λ produces almost identical results.

Although our Bayesian inference method makes an explicit assumption about the structure of the noise, in practice, this assumption turns out to be fairly weak. The reason is that the exact details of the noise channel are unimportant; only its effect on the Pauli weights ω_λ(P) is relevant. In Supplementary Fig. 4, we present evidence that ω_λ(P) depends only weakly on the detailed structure of the noise. To do this, we simulate a highly correlated and non-local noise source, which acts (with probability p) on random sets of three qubits with a random Pauli error at each layer of the circuit. Despite the fact that the sparse Pauli-Lindblad noise model cannot explicitly model this type of non-local noise, Supplementary Fig. 4 shows that after using our Bayesian inference method to obtain a phenomenological model for the noise, we are nevertheless able to recover unbiased estimates of various Pauli expectation values. In the future, it is also interesting to investigate the systematic error due to this model violation⁷⁷.

Tensor network post-processing for robust shallow shadow

We begin with noise-free shallow circuit shadows, where we use the ideal unitary channel ${{{\mathcal{C}}}}_{U}[\cdot ]=U\cdot {U}^{{\dagger} }$ for both physical processing and post-processing. For a system comprising a single qubit, the Pauli weight is given by

$$\omega (P)={{\mathbb{E}}}_{U}{{\rm{Tr}}}\left(| 0\left.\right\rangle \left\langle \right.0{| }^{\otimes 2}{U}^{\otimes 2}{P}^{\otimes 2}{U}^{{\dagger} \otimes 2}\right).$$

(11)

It is important to note that the tensor product of two replicas differs from that of different qubits. To distinguish between these cases, we use superscripts (1) and (2) to explicitly denote replicas and subscripts to denote qubit indices. For instance, ${P}_{(1,2)}^{\otimes 2}={X}_{1}^{(1)}\otimes {X}_{1}^{(2)}\otimes {Y}_{2}^{(1)}\otimes {Y}_{2}^{(1)}$.

To understand the evolution, it is helpful to track the “distribution" of Pauli operators (induced by our probability distribution P(U) over unitaries U) as we evolve forward under the random quantum circuit. For example, after applying one layer of single-qubit random Haar/Clifford twirling gates, a given Pauli operator, say Z, maps to an equal superposition of X, Y, and Z. Mathematically, this is expressed as

$${{\mathbb{E}}}_{U \sim {{\mbox{Haar}}}_{1}}\left[{U}^{\otimes 2}{Z}^{\otimes 2}{({U}^{{\dagger} })}^{\otimes 2}\right]= \frac{{X}^{(1)}\otimes {X}^{(2)}+{Y}^{(1)}\otimes {Y}^{(2)}+{Z}^{(1)}\otimes {Z}^{(2)}}{3} \\= -\frac{1}{3}I+\frac{2}{3}S,$$

(12)

where I is the identity operator, and S is the swap operator between two copies.

More generally, for global Haar/Clifford distributions of U, we have

$${{\mathbb{E}}}_{U \sim {{\mbox{Haar}}}_{n}}\left[{U}^{\otimes 2}{P}^{\otimes 2}{({U}^{{\dagger} })}^{\otimes 2}\right]= \left(\frac{{{\rm{Tr}}}(P)-{2}^{-n}\,{{\rm{Tr}}}(PS)}{{2}^{2n}-1}\right)I \\ +\left(\frac{{{\rm{Tr}}}(PS)-{2}^{-n}\,{{\rm{Tr}}}(P)}{{2}^{2n}-1}\right)S.$$

(13)

For locally scrambled ensembles of U, which do not distinguish between different Pauli bases, the coefficients of X, Y, and Z are equal. This makes it convenient to work on the I and S basis. We introduce a vector notation, $| I\left.\right\rangle$ and $| S\left.\right\rangle$, to denote the identity and swap basis (note that these are not superoperator notations). Using this notation, Eq. (12) becomes

$${{\mathbb{E}}}_{U \sim {{\mbox{Haar}}}_{1}}\left[{U}^{\otimes 2}{Z}^{\otimes 2}{({U}^{{\dagger} })}^{\otimes 2}\right]=-\frac{1}{3}| I\left.\right\rangle+\frac{2}{3}| S\left.\right\rangle=\left[\begin{array}{c}-\frac{1}{3}\\ \frac{2}{3}\end{array}\right].$$

(14)

Applying Eq. (13), we can verify that two-qubit random Haar/Clifford unitaries act as follows:

$$\begin{array}{rcl}| II\left.\right\rangle \, \to \,| II\left.\right\rangle \hfill \\ | SS\left.\right\rangle \, \to \,| SS\left.\right\rangle \hfill \\ | IS\left.\right\rangle \, \to \, \frac{2}{5}\left(| II\left.\right\rangle+| SS\left.\right\rangle \right)\\ | SI\left.\right\rangle \, \to \, \frac{2}{5}\left(| II\left.\right\rangle+| SS\left.\right\rangle \right),\end{array}$$

(15)

which we can express in matrix form as

$${T}_{12}=\left[\begin{array}{cccc}1&\frac{2}{5}&\frac{2}{5}&0\\ 0&0&0&0\\ 0&0&0&0\\ 0&\frac{2}{5}&\frac{2}{5}&1\end{array}\right].$$

(16)

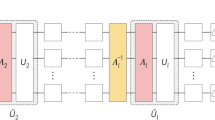
We call this action matrix T the transfer matrix. Using transfer matrices simplifies tracking the distribution of our Pauli operator P under random unitary gates. For shallow circuits comprising two-qubit random Haar unitaries with a brick wall structure, the transformation becomes a tensor network of nearest-neighbor transfer matrices T_i,i+1. The final state can be written as

$${{\mathbb{E}}}_{U}\left[{U}^{\otimes 2}{P}^{\otimes 2}{({U}^{{\dagger} })}^{\otimes 2}\right]\equiv | \Phi \left.\right\rangle={c}_{1}| II\ldots \left.\right\rangle+{c}_{2}| IS\ldots \left.\right\rangle+\cdots+{c}_{{2}^{n}}| SS\ldots \left.\right\rangle .$$

(17)

Since ${{\rm{Tr}}}\left(| 0\left.\right\rangle \left\langle \right.0{| }^{\otimes 2n}O\right)=1$ for any O that is a tensor product of identities and swaps, the Pauli weight of P simplifies to ω(P) = ∑_ic_i. This can be computed by evaluating the inner product $\left\langle \right.+| \Phi \left.\right\rangle$, where $|+\left.\right\rangle \equiv {\left[\begin{array}{c}1\\ 1\end{array}\right]}^{\otimes n}$.

When the two-qubit gates are not random Haar/Clifford, the distribution of Paulis after applying those gates will not be equally distributed in X, Y, and Z direction. For example, the two-qubit gates in our experiments are CNOT gates twirled by single-qubit random Clifford gates. Unlike Haar random unitaries, the CNOT gates pick a preferred direction for Paulis, in the sense that they treat X and Z differently. Furthermore, our locally correlated Lindbladian noise model treats different Pauli bases differently. So rather than working with identity I and SWAP S basis, we work with a four-state system, with basis states being the Paulis $| I\left.\right\rangle$, $| X\left.\right\rangle$, $| Y\left.\right\rangle$, $| Z\left.\right\rangle$. For instance, $| Z\left.\right\rangle \equiv {\left[\begin{array}{cccc}0&0&0&1\end{array}\right]}^{T}$. One should notice that the defined basis is different from the superoperator basis. Then, the transfer matrix of a single-qubit twirling gate is

$$T=\left[\begin{array}{cccc}1&0&0&0\\ 0&\frac{1}{3}&\frac{1}{3}&\frac{1}{3}\\ 0&\frac{1}{3}&\frac{1}{3}&\frac{1}{3}\\ 0&\frac{1}{3}&\frac{1}{3}&\frac{1}{3}\end{array}\right].$$

(18)

The transfer matrix of a CNOT gate is a 16 × 16 matrix defined by

$${T}_{{{\rm{CNOT}}}}[{P}_{i},{P}_{j}]=\left\{\begin{array}{ll}1\quad &{{\rm{if}}}\,{P}_{j}={{\rm{CNOT}}}\cdot {P}_{i}\cdot {{\rm{CNOT}}}\,\,{{\mbox{up}}} \, {{\mbox{to}}} \, {{\mbox{some}}} \, {{\mbox{phase}}}\,\\ 0\quad &\,{\mbox{otherwise.}}\hfill\,\end{array}\right.$$

(19)

Now, we also have a nice way of exactly solving Pauli distributions through the noise channel, since the noise model is diagonal in the Pauli basis. For instance, if a qubit has single-qubit error rates λ_X, λ_Y, λ_Z, the transfer matrix of the noise channel for this site is

$$\Lambda={{\rm{diag}}}\left(1,\exp (-2({\lambda }_{Y}+{\lambda }_{Z}))\right.,\exp (-2({\lambda }_{X}+{\lambda }_{Z}),\exp (-2({\lambda }_{X}+{\lambda }_{Y}))).$$

(20)

We can do the same for two-qubit noise, where our channel is then represented by a diagonal 16 × 16 matrix. At the end, our state $| \Phi \left.\right\rangle$ will be a superposition over all Paulis. The only nonzero contributions to (3) are those where all the Pauli characters are either I or Z. So, we can evaluate (3) with $\left\langle \right.+| \Phi \left.\right\rangle$ where

$$|+\left.\right\rangle={\left[\begin{array}{l}1\\ 0\\ 0\\ 1\end{array}\right]}^{\otimes n}.$$

(21)

This algorithm has also been implemented with PyClifford⁹⁵ and Tensornetwork⁹⁶.