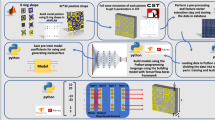
Abstract
Frequency transfer is a key challenge in machine learning as it allows researchers to go beyond in-range analyses of spectrum properties towards out-of-the-range predictions. Traditionally, to predict properties at a specific frequency, targeted spectrum is included in training data for a deep neural network (DNN). However, due to limitations of measurement or computation source, training data at some frequencies are hardly accessible, especially for multi-physics problems. In this work, we propose a multi-physics deep learning framework (MDLF) consisting of a multi-fidelity DeepONet, a Euler latent dynamic network, and a data-analytical inversion network. Without the knowledge about multi-physics response, MDLF is successfully generalized to unseen frequency bands for both parametric and free-form metasurface by dynamically utilizing a Euler latent space and single-physics information. Moreover, an inversion method is introduced to incorporate hybrid a priori in inverse design of metasurface. Under EM-thermal coupling, we verify the proposed MDLF numerically and experimentally.
Similar content being viewed by others
Introduction
Nowadays, artificial intelligence (AI) have attracted many interests in bioscience1, material science2, and energy science3, which improves the quality of detection and analysis4, accelerates new discoveries5,6, and achieves real-time control7. In particular, as a surrogate to full-wave simulation8,9,10, the data-driven artificial neural networks11,12,13 (ANNs) have shown extraordinary potential in speeding up design procedure14,15 and shortening the gap between measurement and design16,17, which greatly relieves the pressure of numerical simulations to obtain a suitable solution in inverse design18,19,20,21,22.
For example, variational auto-encoders (VAE)23,24 is thought to be a practical pre-processing method to compress the data space for better searching the design space by another optimization method. Developed from the generative adversarial network (GAN)25, conditional GAN (cGAN)26, as one of the most popular frames in inverse design these years, constructs both forward and inverse surrogate models by adversarial strategy, partly alleviating the problem of non-uniqueness.
In electromagnetic (EM) society27,28,29, a traditional ANN-based surrogate model builds a mapping from the material distribution of objects to the spectrum properties, in which the prediction range is determined by the training data and is fixed once the network is trained. However, due to the limitations of measurement or computation source, the training data sometimes are not complete to cover the scope of interest, and the performance of deep learning deteriorates dramatically when it comes to out-of-the-range tests, especially for complex systems or models, such as multi-physics coupling problems. Therefore, generalizations of the surrogate model, which allow researchers to go beyond in-range analyses of properties toward out-of-the-range predictions, are crucial.
Due to the unique ability to manipulate EM waves, metasurface has shown its promising abilities in hologram30,31, absorber32, semiconductors33, 5 G/6 G base station34,35,36, cloaking37, radome38 etc. Generalizations with respect to the operating state of the metasurface, like polarization transfer and dispersion transfer39, have attracted many attentions to relieve the burden of accumulating dataset and improve the applicability of the model. Similarly, frequency transfer, which is to predict the unknown spectrum given part of the frequency data, could be divided into two types according to the frequency range provided by the training dataset.
-
a.
In the first type, the range of training datasets already covers the predicted frequency: For example, the mapping relationship between the low-frequency and high-frequency wavefield is built in Geophysics fields40, where high-frequency data as the output is included in training data. Furthermore, in the field of metasurface, a data-driven spectra-to-spectra strategy is introduced to decode the unknown spectrum of metasurface from the latent space with the known spectrum41. By operator learning mechanism, the interpolation of frequency is achieved42.
-
b.
The second type of frequency transfer is out-of-distribution (OOD) generalization, i.e., the predicted spectrum is not seen in the training stage, which is the problem discussed in this work. There are two mainstream approaches, i.e., multi-fidelity modeling and fine-tuning43. For example, transfer learning is adopted in fine-tuning the backbone to achieve OOD with a sparse amount of data given in the extrapolation44. In addition, there are also physics-based approaches to extrapolation. Based on the correlation of metasurface size scaling and resonant wavelength, the generalizability in operation wavelength in the forward method is achieved39. Based on a prior provided by the equivalent circuit, spectral extrapolation of metamaterials is achieved45.
Despite the convincing achievement in the above literature, the mentioned works only focus on a single physical response. However, with the decreasing sizes and increasing power of electronic devices, forward modeling and inverse design of metasurface under multi-physics coupling46,47,48 becomes demanding. In the system where the EM-thermal effects dominate47, for example, as the power consumption increases, the temperature rise effects are unavoidable, which leads to the change of material constitutive parameters and further makes EM response deviate from the single-EM simulation, i.e., numerical calculation of object/system’s EM behaviors governed by Maxwell’s equations. However, modeling and designing metasurface considering both the EM and thermal multi-physical properties, i.e., multi-physical simulation, are challenging due to the complicated physical process and high computational costs. Specifically, to include EM propagation, heat loss, and heat transfer in the metasurface, Maxwell’s equations and heat conduction equation are alternately solved in the steady-state solution of the EM-thermal coupling49, between which temperature-varying parameters build the bridge.
Considering the difficulty in accumulating high-quality datasets, the key to a multi-physical surrogate model with high precision as well as frequency transfer is improving the data efficiency in the context of scientific machine learning (SciML). On the one hand, by explicitly introducing the governing equations into the loss function, physics-informed neural networks (PINNs)50,51,52 have made good practices in solving PDEs given specific questions. But, in this case, the multi-physical behaviors in the metasurface are governed by different partial differential equations (PDEs), which is hard to decouple. On the other hand, by learning operator mappings between functions, neural operators, such as deep operator networks (DeepONet)53,54,55, and Fourier neural operators (FNO)56, have shown tremendous success in modeling complex physical phenomena and engineering problem11,57,58, where the capability to achieve parameter efficiency59,60, small dataset training61,62,63, and to capture non-local interactions64 are witnessed. Compared with traditional ANNs, it is reported that DeepONet could learn operators accurately and efficiently from a relatively small dataset in practice61. Also, to alleviate the pressure of high-quality data accumulation, a multi-fidelity strategy is adopted62,63. In predicting the characteristics of time-varying systems, latent dynamics networks are developed to discover the system evolution of spatio-temporal processes, where non-Markovian effects are captured by tracking the system history64.
In this work, we propose a multi-physics deep learning framework (MDLF), as shown in Fig. 1. The forward networks consist of two parts, i.e., multi-fidelity DeepONet to predict EM S-parameter performance (\({S}_{M}\)) and a latent-dynamic network to predict temperature performance (\(T(f)\)), where both have considered EM-thermal multi-physics coupling effects. More specifically, since the computational cost is high when accumulating training data for predicting \({S}_{M}\), the multi-fidelity DeepONet65 is used to reduce the need of high-fidelity data (\({S}_{M}\)), where data of S-parameter performance without EM-thermal coupling effects (\({S}_{E}\)) are firstly accumulated to train a low-fidelity network, i.e., Net1 in Fig. 1. The output of the low-fidelity network is further input into the high-fidelity network (Net2) and formed as a residual part to reduce the difficulty in training Net2. Further, since obtaining thermal effects at high frequency is either computational or experimental challenging, we further developed a latent-dynamic network64 (Net3 & Net4) to predict temperature performance (\(T(f)\)) considering EM-thermal coupling effects. By using an Euler-method-based dynamic latent, the proposed network can predict temperature performance at a higher frequency not seen in training data, i.e., out-of-distribution (OOD) prediction. In the inverse method, since designing a metasurface considering both EM and thermal functionalities is a challenging multi-objective problem, hybrid regularizations66 are introduced in the inverse network (Net5) to boost the training process. More specifically, besides the loss defined on geometry parameters, forward solvers, including EM and thermal predictor and an analytical model, are further introduced to alleviate non-unique problems and constrain resonant points, respectively.
R represents requirement, Input-T represents temperature information of metasurface, \(G\) is geometry, \(G\hbox{'}\) is the predicted \(G\), \(T\) is temperature, \(f\) is frequency, \({S}_{E}\) is S-parameter by single EM simulation, \({S}_{M}\) represents S-parameter by multi-physics simulation, \({S}_{E}^{\prime}\) is the predicted \({S}_{E}\), \({S}_{M}^{\prime}\) is the predicted \({S}_{M}\), \({T}_{p}^{\prime}\) is the predicted temperature in inverse method, \(a(f)\) is latent space, \({f}_{R}\) is resonant frequency, \({f}_{R}^{\prime}\) is the predicted \({f}_{R}\), and \({S}_{R}\) = \({S}_{M}\) – \({S}_{E}\).
Results
Network architecture
We begin with a brief introduction of the vanilla DeepONet61 and multi-fidelity DeepONet65 proposed by Lu. et al. and describe some architectural choices in this work. Different from the traditional ANNs, a DeepONet consists of two sub-networks, i.e., branch net and trunk net, where the branch net encodes the input function at a fixed number and trunk net encodes the locations for the output functions61. Given the input function \(v\) and the locations \(\xi\), the output function can be approximated by merging the output of branch net and trunk net:
At the same time, to make full use of both low-fidelity and high-fidelity data, the multi-fidelity DeepONet is proposed with low-fidelity and high-fidelity models, in which it is recommended to append evaluation of low-fidelity in the trunk-net inputs and leave the branch-net unchanged, i.e., ref. 65,
where \({{{\mathscr{G}}}}_{H}\) represents the high-fidelity model, \({{{\mathscr{G}}}}_{L}\) represents the low-fidelity model.
In this case, by taking frequency \((f)\) as \(\xi\) in the trunk net and geometric input (\(G\)) as \(v\) in the branch net, DeepONet is a suitable frame to achieve a free sampling of frequency and a continuous representation of the spectrum in the metasurface. As shown in Fig. 2a, to predict \({S}_{M}\), the multi-fidelity DeepONet contains one low-fidelity network, Net1, and one high-fidelity network Net2, which are trained separately. Firstly, with the framework of unstacked DeepONet, the information from the geometry domain \(G\) of the multi-physic metasurface and frequency domain \(f\) are processed through two independent channels in Net1, and the S-parameter by single-EM simulation \({S}_{E}\) is predicted.
a The structure of multi-fidelity DeepONet, where Net1 predicts \({S}_{E}\) (S-parameter by single EM simulation) of geometry \(G\) at a specific \(f\) and Net2 predicts the residual between \({S}_{E}\) and \({S}_{M}\) (S-parameter by multi-physics simulation). FC represents the fully connected layer. \({L}_{E}\) and \({L}_{R}\) represent the loss in Net1 and Net2, respectively. b The structure of inverse design model, where \({L}_{G}\), \({L}_{S}\), \({L}_{T}\), and \({L}_{R}\) represent the loss by geometry data, EM forward model, thermal forward model, and analytical model. c The latent dynamics networks developed on the frequency flow, where Net3 is used to update the latent space \(a(f)\) and Net4 is used to predict the average temperature \(T(f)\). \({L}_{T}\) represents the loss in Net3 and Net4.
Then, the output of the trained Net1 is further input into the high-fidelity network (Net2) and formed as a residual part (\({S}_{R}\)) to reduce the difficulty in training Net2. In the trunk net, the EM response by Net1 corresponding to the current \(f\) is added, as well as that by two frequency points before and after the current frequency indicating the local features. Considering low fidelity Net1 provides a preliminary knowledge of space mapping and Net2 only learns a small value, it allows a sparse sampling in the training set of Net2, which reduces the pressure of multi-physical simulation. Moreover, in this work, the same geometric input (\(G\)) goes over the progressive feature extraction since the feature of \(G\) is not fully extracted in Net1, and there are totally different \({S}_{R}\) with the same input of \({S}_{E}\) and \(f\), but different \(G\), as shown in Supplementary Fig. 5.
In predicting the temperature performance (\(T(f)\)) under EM-thermal coupling, latent dynamics networks64 are developed in the frequency sequence flow. As presented in Fig. 2c, \(a(f)\) is computed from the parameters in the latent space, where no label of \(a(f)\) is provided in the whole training process, and the network automatically discovers a compact representation of the learning task, i.e., latent space. More specifically, similar with the frame of the encoder and decoder, Net3 in Fig. 2c encodes \({S}_{E}\) into latent space, and Net4 decodes \(a(f)\) into the temperature output \(T(f)\). In this way, the weights of Net3 are updated through the backpropagation of loss between the outputs of Net4 and its true value. Besides, given the initial state, i.e., \(a(f)\)= 0, the update of latent space in frequency sequence follows the Euler method,
where \(\triangle f\) represents the step in the frequency sequence, \(\beta\) is the hyperparameter for regularization, and \(\frac{\partial a}{\partial f}\) is the changing rate of latent space, which is also the output to Net3.
To conclude, given no label for the latent space, Net3 specifies the update rules of \(a\left(f\right)\) in the frequency sequence, Net4 ensures the effectiveness of \(a(f)\) in predicting the temperature at each frequency point, which together achieve frequency transfer to the unknow frequency. Besides, in Net4, we also use \({S}_{E}\) as one of the inputs because the temperature results and the EM results are highly correlated. However, \({S}_{E}\) is not the only determining factor to \(T(f)\). For instance, even with the same EM response at different frequencies, structure can appear in different thermal behaviors, as shown in Fig. 3c.
a The comparison between EM response by full-wave simulation considering multi-physical coupling, that by low-fidelity model Net1, and multi-fidelity model (Net1 & Net2). b Out-of-training test: The comparison between by full-wave simulation and that by multi-fidelity model. c Average temperature by latent dynamics networks, which are compared with full-wave simulation, where the arrows connect the different lines and their corresponding vertical axis. Left are parameterized metasurface structures with frequency transfer from 10.2 to 14 GHz. Middle are free-form and high-dimensional meta-atoms with extrapolated frequency bands from 11.2 to 14 GHz. Right are three-layer meta-atoms, in which the top and bottom layers are free-form and high-dimensional. d The comparison between the squared error in temperature prediction by the traditional DNN method and the proposed latent dynamics network, where results above 10 GHz are frequency transfer. e The comparison between the average temperature by full wave simulation, that predicted by the proposed method, and that by traditional DNN method.
In the inverse method, Net5 contains an inverse design network, an analytical model, and the above forward solvers including EM and thermal predictor, as shown in Fig. 2b. More specifically, the inverse design network produces the geometry \(G\hbox{'}\) from \({S}_{M}\) and temperature information (Input-T), i.e., value and position of maximum temperature within 2–8 GHz. The forward solver, on the contrary, puts the geometry \(G\hbox{'}\) back to the EM-thermal performance, in which the temperature predictor predicts the average temperature of the predicted geometry \(G\hbox{'}\) within 2–8 GHz. In addition, an analytical model is used to trace the position of resonant frequency points \({f}_{R}\) under the change of geometry. To be specific, the first and second extreme points of the EM response in the training set are extracted, and the numerical relationship between those points and the design variables is fitted by a polynomial function. In this way, hybrid regularizations are introduced to the training process of Net5, whose loss function is given below,
where the loss in total consists of mean square error (MSE) between the outputs and their corresponding truth value, \(G\) and \({G}^{\prime}\) represents the actual and predicted values of geometry, \({f}_{R}\) represents the resonant frequency points traced by the analytical model, \({S}_{M}\) represents the EM response predicted by the EM forward model, and \({T}_{p}\) represents the average temperature predicted by the thermal forward model. In this way, non-unique problem is alleviated and solutions that do not satisfy analytical equations are penalized. Besides, by adding Input-T to the input of Net5, we are targeted to constrain the thermal performance in the metasurface besides EM performance.
EM response by multi-fidelity DeepONet
Firstly, we consider parameterized metasurface structures, whose predefined topology is given in Supplementary Fig. 1. In total, with 720 individual geometries, low-fidelity data \({S}_{E}\) are obtained with a sample interval of 0.1 GHz within 2–14 GHz, high-fidelity data \({S}_{M}\) are obtained with a sample interval of 0.2 GHz, which are randomly divided into training set and validation set. As shown in Fig. 3a, for a typical geometry in the training set, a comparison between the \({S}_{M}\) by multi-physical full wave simulation and those by multi-fidelity model and low-fidelity model is given, which indicates the differences between \({S}_{E}\) and \({S}_{M}\). For the test out of the training set, the comparison between the full-wave simulation and the predicted \({S}_{M}\) is given in Fig. 3b, which matches well. It is noted that the sample interval in testing the multi-fidelity model is 0.1 GHz, which means frequency interpolation in \({S}_{M}\).
To quantify the overall accuracy for predicting EM response, relative error is used, i.e.,
where \({y}_{i}\) represents the true value and \(f\left({x}_{i}\right)\) is the predicted value. Tested with 106 random samples unseen in the training process, the multi-fidelity DeepONet obtains an average relative error of 0.036.
Then, the network trained only with high-fidelity data (single-fidelity DeepONet) is compared with the proposed multi-fidelity model to illustrate the importance of the proposed multi-fidelity DeepONet. More specifically, the trained single-fidelity DeepONet is tested with the same validation set with 106 random samples, where the relative error is 0.154.
By adjusting the sampling strategy of high-fidelity data, the influence of sampling interval ratio between low-fidelity model Net1 and high-fidelity model Net2 is studied. As indicated in the left of Table 1, as the sampling interval ratio increases from 2:1 to 12:1, the relative error in the validation set rises like a step. For example, the error in Case-R2 and Case-R3 is very close, however, from Case-R1 to Case-R2 and to Case-R4, the rise in error is more obvious, since their interval ratio increases exponentially. A similar situation can be found in Case-R3 and Case-R6. In addition, if the training data is randomly selected in the original high-fidelity data, which has 61 points in one single geometry, the influences of the sampling number in high-fidelity data are shown on the right of Table 1. Therefore, with a preliminary knowledge of space mapping provided by the low-fidelity model Net1, the multi-fidelity strategy allows a relatively smaller high-fidelity dataset.
Average temperature by latent dynamics networks
To illustrate the frequency transfer achieved by latent dynamics networks, we remove the data whose corresponding frequency is over 10 GHz from the training set, that is, the temperature prediction from 10.2 to 14 GHz is from frequency transfer. Similarly, relative error in Eq. (5) is used to quantify the overall accuracy for predicting average temperature. In the trained networks, \({E}_{R}\) for the temperature within 2 to 10 GHz is about 0.007, and for the temperature in 10.2 to 14 GHz is about 0.043.
As shown on the left of Fig. 3c, the comparisons between the average temperature of the geometry by full-wave simulation and prediction are given, where EM response as the inputs to Net3 and Net4 are also presented. From the figures, the extreme points of temperature have a high correlation with the extreme points of EM response in the frequency domain. Yet, even with the same EM response, geometry appears at different temperatures at different frequencies. For frequency transfer, in figures, the areas with background color are totally unseen in training, in which the simulation and prediction matches well. Besides, it is noted that the most dramatic temperature effect occurs near the extreme point.
To evaluate the contribution of latent space \(a(f)\) in temperature prediction as well as frequency transfer, a contrast test between the traditional method without the proposed latent space and the proposed method with latent space is conducted. In the traditional method, \(f\), EM response, and \(G\) are the inputs to DNN and \(T\left(f\right)\) is the output, which has a similar structure with Net2 but has a different output. Specifically, in the traditional method, with the same dataset, \({E}_{R}\) within 2–10 GHz is about 0.0281, and in 10.2–14 GHz is about 0.1643, which is much larger than the error in the proposed method. To further quantify the prediction error at each frequency point, square error is used. As shown in Fig. 3d, in the proposed model, part of the structure samples is used for training, which means out-of-range tests are carried out in both geometry and frequency range. Compared with the results from a traditional DNN method without latent space, the proposed method obtains a smaller test error. In addition, a typical example of temperature prediction is given in Fig. 3e, where the comparisons between the full-wave simulation, the proposed method, and the traditional method are conducted. From the figure, even if the curve by the traditional method meets the trend of the simulated result, the predicted temperature deviates from the simulation, when it comes to the extrapolated frequency points.
Furthermore, besides the parameterized metasurface structures, by changing full connected network to a convolutional neural network to deal with 2D patterns while keeping the framework of the prosed method unchanged, the frequency transfer of the proposed method on free-form meta-atoms with a higher degree of freedom are also tested. For example, the thermal performance of free-form single-layer meta-atoms are predicted, as shown in the middle of Fig. 3c, where the extrapolated frequency band is set to be 11.2–14 GHz with a relative error of 0.047. For more complex EM-thermal coupling effects, a three-layer meta-atom is studied in this work. In this case, the top and bottom layers are the same 2D pattern with a high degree of freedom, as shown on the right of Fig. 3c, where the simulation and prediction match well. The results from other geometries are given in Supplementary Fig. 8. From these experiments, it is shown that the frequency transfer of the proposed method still validates in higher dimension cases.
Inverse design by data-analytical networks
In the development of an inverse design network, the weights in Eq. (4) are important to direct the training. Under the same training epochs, as shown in Fig. 4a and b, the relative errors in the validation set are given under different training cases, in which the numbers from left to right in parentheses represent the weights of data-driven regularization \({w}_{1}\), analytical model regularization \({w}_{2}\), EM forward model regularization \({w}_{3}\), and temperature forward model regularizations \({w}_{4}\), respectively. Besides, E1 represents the relative error on geometry determined by data-driven regularization. E2 represents the relative error on the resonant frequencies determined by analytical-driven regularization, in which E21 and E22 represent the relative error on the first and second resonant frequencies, respectively. E3 represents the relative error on EM response predicted by the EM forward model. E4 represents the relative error on average temperature predicted by the thermal forward model.
a The relative errors in the validation set by an inverse model trained with different weights of regularizations, in which the numbers from left to right in parentheses represent \({w}_{1}\) to \({w}_{4}\). E1 represents the relative error on geometry determined. E21 and E22 represent the relative error on the first and second resonant frequency, respectively. E3 represents the relative error on EM response. E4 represents the relative error on average temperature. b Partial enlarged drawing of a, which emphasizes the error by analytical model and thermal forward model. c, d The effects of analytical-driven regularization in this work. e The comparison between the desired EM response and that inversely designed, where the desired one is a polyline connected with a few points available. f The inverse design example when real EM response curves from the simulation are available.
As shown in Fig. 4b, compared with Case3, driven by data and EM forward model, Case2, which is driven by data and analytical model, has a similar E21 and a lower E22, which means a better prediction in resonant frequency. From Case1 to Case3 and Case5, the EM forward model and analytical model are added into the traditional method in turn, in which a gradual accuracy improvement can be observed. In addition, Table 2 gives the detailed value in Fig. 4. From the table, Case5, which is adopted as the proposed data-analytical-driven model, performs the best in many indexes and has a very close value with the best performance in other index.
Furthermore, the effect of analytical-driven regularization is visualized in Fig. 4c and d. As shown in Fig. 4c, although the EM response in the passband obtained by Case2 (governed by the analytical model) is less accurate than that by Case3 (governed by the EM forward model), a higher accuracy in pole prediction is witnessed in Case2. From Fig. 4d, by adding analytical model to the model driven by data and EM forward method, the inverse design achieves more accurate local performance deign while ensuring the overall consistency.
In the inverse design scenario, usually, we do not have detailed performance distributions, i.e., desired EM performance, before we design. Instead, we usually have some incomplete requirement, for example, we want to find a geometry with two passbands at about 4 GHz and 8–10 GHz, thus a polyline of performance is draw according to these obscure requirements, as shown in Fig. 4e, indicating the desired passband location and bandwidth. Besides, the extra peak between the two passbands of the parameterized metasurface in Fig. 3c is eliminated for the purpose of achieving stability in EM and thermal performance. However, no one knows whether a metasurface structure satisfying the plotted polyline exists or not. In this case, the aim of inverse method here is to find a geometry to satisfy the fictitious performance as much as possible, deviations outside the required passband could be acceptable. Thereby, by applying Net5, a comparison between the desired EM response and the simulated response from the designed geometry is given in Fig. 4e, where a small increase can be found at the end of frequency, considering the EM properties of the geometry itself.
Furthermore, in the situation where real EM response curves from the simulation are available, consistency between the desired EM response and the EM response from the designed geometry is observed, as shown in Fig. 4f. Particularly, the characteristic of a peak at the end of the frequency is captured by the inverse method, and the inversely designed geometry can reproduce this feature.
To further consider both EM and thermal multi-physics functionality in optimizing metasurface structures, the proposed model with Input-T, i.e., the value and position of maximum temperature within 2–8 GHz, as one of the inputs, is compared with the model trained without Input-T. In this case, by adding Input-T, we are targeted to constrain the thermal performance in the metasurface besides EM performance under EM-thermal coupling effects. As shown in Supplementary Fig. 10, under the same training weights, the relative errors in the model trained without Input-T are larger than those in the proposed model, especially in thermal performance. Specifically, with the same desired EM response, the achieved performances by the results from the inverse model trained without Input-T (Option 1) and with Input-T (Option 2) are given in Fig. 5a, b, respectively, whose design parameters are given in Supplementary Note 4. As shown in Fig. 5a, Options 1 and 2 have similar passband frequency characteristics, which are very close to the desired one. However, as shown in Fig. 5b, by constraining the position of the maximum temperature near 4 GHz, Option 2 performs better in the average temperature compared to Option 1, where the maximum temperature rise occurs at a higher frequency in Option 1 meaning more serious thermal effects happen.
a The comparison of EM performance between the design results from the inverse model trained without Input-T (Option 1) and with Input-T (Option 2) under the same desired EM response. b The comparison of thermal performance between Option 1 and Option 2. c Infrared image of design Option 1 and Option 2 under 3 mins radiation d The measured temperature at the quarter of the samples (Line1) and at the half of the samples (Line2).
Experimental results
To verify the thermal performance by the inverse method experimentally, design results in Fig. 5a, b are fabricated with 4*2 units, whose total size are 40 mm * 20 mm, as shown in Supplementary Fig. 13c. Then, the fabricated samples are irradiated in the waveguide with power amplifier (PA) enhancing the microwave from vector network analyzer (VNA), whose measurement platform is given in Supplementary Fig. 12c in Supplementary Note 5. After 3 mins of continuous wave irradiation at 7.9–8 GHz and 20 W, the surface temperature distributions of samples are given in Fig. 5c, where the highest and average temperature of Option 1 (347.45 K, 321.22 K) are higher than those of Option 2 (331.85 K, 311.71 K), while the environment temperature is close. In addition, the measured temperature at the quarter and the half of the samples (Line1, Line2) are compared as shown in Fig. 5d, where the temperature of Option 1 (design without Input-T) is generally above that of Option 2 (design with Input-T), with similar measured EM response as shown in Supplementary Fig. 14c.
To verify the accuracy of the proposed method, a parameterized geometry inversely designed by Net5 is fabricated with 20*20 units, as shown in Supplementary Fig. 9 and 13a. Transmission (S21) under low-power input (\({S}_{E}\)) is measured and compared with simulated \({S}_{E}\), as shown in Fig. 6a.
a The measurement of S21 under low-power input (\({S}_{E}\)) compared with simulation. b The measurement results of the rise in temperature under high-power input (c) The infrared photo at 3.65 GHz. d The measurement of the EM response under high power irradiation in the waveguide. e The EM and thermal performance of a contrast sample under high power irradiation.
In addition, the temperature rises of the fabricated sample under higher power EM radiation are measured, in which the input to the horn antenna is about 40 dBm, as shown in Supplementary Fig. 12b. For each single investigated frequency, the radiation time is about 20 to 30 mins when the temperature rises from room temperature to a steady state. The measured results are calculated by averaging the temperature rise in the whole surface of the sample, as shown in Fig. 6b, whose trend is close to that predicted by Net3 and Net4. The main reason for the difference in the numerical scale is that the input power to one single metasurface unit cannot reach the level in multi-physical simulation. At 3.65 GHz, as shown in Fig. 6c, when the thermal effect is most salient, the maximum temperature is in the center of the sample surface, indicating the maximum power received is at the same position. At 3.2 and 5.2 GHz, however, when the temperature rise is less apparent, the temperature distribution is relatively uniform, as shown in Supplementary Fig. 15.
The measurement of the EM response under high-power irradiation is conducted in the waveguide with PA. The inversely designed result is fabricated with 4*2 units with the size of 40 mm * 20 mm, as shown in Supplementary Fig. 13b. After 9 mins continuous wave irradiation at 6–7.05 GHz and 20 W, the measured S21 are basically unchanged during irradiation, as shown in Fig. 6d since the heat effect in the design sample is designed to be not severe in the observed frequency, whose highest and average temperature after 10 mins irradiation are 314.15 K, 305.12 K. However, due to the difference in the EM behaviors of small samples in waveguides and periodic large arrays in free space, the measured S21 in waveguide is not compared with that in Fig. 6a, which is the measurement in free space.
To further highlight the importance of Net2, which is the importance of predicting the changes of EM response under multi-physical coupling, a contrast sample is further fabricated with the same size of the designed sample and measured in the same condition, as shown in Supplementary Fig. 13b. As shown on the left of Fig. 6e, after 10 mins irradiation under 20 W microwave of 6–7.05 GHz in waveguide, the surface temperature distribution of contrast sample is given, where the highest and average temperature is 360.15 K and 342.17 K. The increase of temperature further leads to the change of the EM properties of the sample. As shown on the right of Fig. 6e, it is obvious that S21 of the contrast sample is shifted to the left as the irradiation time increases and basically stable at about 9 min, where S21 at 0 min is \({S}_{E}\) and that at 9 mins is \({S}_{M}\). Therefore, it is seen that EM response is significantly affected by multi-physical coupling and Net2, that considers multi-physical coupling is important.
Discussion
Facing the challenge of frequency transfer and multi-physic coupling effects in AI for EM science, a novel multi-physics deep learning framework is proposed, which allows forward modeling and inverse design for multi-physics metasurface. In our scheme, the pressure of multi-physics data collection is relieved by a priori knowledge, and the properties at a frequency out of the training range are predicted with a latent space, benefiting vast applications involving multi-frequency and multi-physics domains.
More specifically, in predicting the EM response by multi-fidelity DeepONet, the residual between the data by multi-physical and single-EM simulation is learnt. From Table 1, the influence of the sampling strategy to the performance of the multi-fidelity model is studied, in which the relative error in the validation set increases slowly as the number of high-fidelity data decrease by randomly selecting training data in the original high-fidelity. In this way, with the knowledge provided by the built low-fidelity model, the number of heavy EM-thermal simulations could be reduced with a larger sampling interval, which is also helpful in other complex scenarios of field coupling. Besides, both low-fidelity and high-fidelity provide continuous representations of the input-output relationship, which allows the absence of unavailable data due to the limitations of measurement or computation source.
Furthermore, in the area of frequency transfer, our approach benefits from the latent space in the latent dynamics network, which has demonstrated its effectiveness for predicting the evolution, even in time-extrapolation scenarios, of dynamic system64. In this work, we introduced this strategy for frequency transfer, where instead of predicting temporal sequences, frequency sequences are predicted. The effectiveness of the latent space \(a(f)\) is due to the following reasons:
-
1.
Firstly, as also pointed out by ref. 64, the latent dynamics network enables the training algorithm to select a compact representation of the state that is functional in predicting its dynamics (i.e., frequency sequences in our work). An auto-encoder, conversely, when trained, extracts features on a purely statistical basis, being agnostic of the importance of each feature in determining a dynamic system. In other words, the latent states allow the propagation of nonlocal information across different frequency domains.
-
2.
Secondly, the proposed architecture enables the sharing of the trainable parameters across different frequency points and geometry parameters, where it has been demonstrated by our previous work59 and other literatures60 that weight sharing is extremely important for improving generalization abilities, i.e., frequency transfer in this work, of networks.
-
3.
The trajectories of the latent space are also an important factor. In Supplementary Fig. 7, given the training data from 2–10 GHz, we further present the evolution of latent space from the initial frequency \({f}_{0}\) = 2 GHz to the maximum observation frequency 14 GHz. It is found that the latent spaces are quite smooth across different frequency domain, where the smooth changes also boost extrapolation predictions.
However, there are also some weaknesses of the presented frequency transfer. In determining the bounds of the extrapolated frequency band, given an initial state of \(a\left({f}_{0}\right)\), from Eq. (3), the latent space can only be updated in one direction of increasing or decreasing frequency, which indicates the direction of frequency transfer. The simulated EM and thermal performance of a typical geometry are given in Supplementary Fig. 2a, where little information can be observed within the band below 2 GHz. Thereby, the prediction above 2 GHz is much more important.
For the frequency transfer beyond 14 GHz, as shown in Supplementary Fig. 2b, unexpected higher-order resonances occur at the frequency above 14 GHz, which is generally not of great concern in existing works. Deviations between the predicted temperature and the full wave simulation occur at these resonance points, as shown in Supplementary Fig. 11. It shows the limitation of frequency transfer based on the proposed method that the prediction of different physical phenomena is not accurate, which could be improved by means such as transfer learning. However, considering the grating lobe effect, the application frequency of the periodic array is limited by its period, i.e., \({f}_{T}=c/2d\,\)= 15 GHz in this case, where \({f}_{T}\) represents the minimum frequency grid-lobe effect may occur, \(c\) represents the speed of light, \(d\) represents the period of the array. Due to the grating lobe effect and high-order resonances, there is no need to take such a wide frequency band under consideration. Besides, the ablation studies in the forward model are given in Supplementary Note 4 to evaluate the necessity of each component of the networks, where the relative error of frequency transfer in the thermal forward model are given in Supplementary Table 2.
In the area of inverse design, hybrid regularization mechanisms are introduced to the inverse design method, where forward solvers and an analytical model are introduced to alleviate non-unique problems and penalize solutions that do not satisfy analytical equations in the training process, providing the paradigm of the same type of problem. From Table 2, E3 in Case2 and Case5 is 0.151 and 0.0811, respectively, which shows the role of the EM forward model in limiting the EM response. Comparing the E2 performance in Case3 and Case5, the role of the analytical model in limiting resonant frequency are witnessed. From Supplementary Fig. 10, in the cases without Input-T, Case7’ performs better than Case5’, which shows the necessity of a thermal forward model in inverse design.
To conclude, although we demonstrate our work with electromagnetic-thermal surface, we envision that this work provides an efficient way to implement a powerful and hybrid regularization, and thus can eventually serve as a generalized framework in various scientific fields where the synthesis of multi-physics and multi-frequency domains is needed.
Methods
Metasurface under EM-thermal coupling
Apart from energy flow considered in the traditional works, where some of the input energy is reflected or passes through the structure into the free space, in this work, the energy absorbed by the lossy materials and conductors is also analyzed, which is transferred into heat, as discussed in Supplementary Note 1. To quantify EM-thermal coupling, the temperature-related material model is established. For example, the relative dielectric constant of the substrate is descried by the Debye model, as given in Supplementary Equation (1). The relationships between temperature and the conductivities (including both electrical conductivity \({\sigma }_{{{\rm{Cu}}}}\) and thermal conductivity \({\kappa }_{{{\rm{Cu}}}}\)) are fitted in the form of polynomials according to the experimental data67, as given in Supplementary Equation (2, 3).
The unit structure of the parameterized metasurface contains three layers based on the substrate with a height of 4 mm, as shown in Supplementary Fig. 1. The metal patterns on the top and bottom layers are the same, and the pattern on the middle layer is a circular ring, where some of the structure parameters are fixed, and the other parameters are treated as design parameters, i.e., geometry (\(G\)).
The single-layer free-form meta-atoms in Fig. 3c are also based on the mentioned substrate with a height of 1 mm. The 2D random patterns are generated by Gaussian random fields15, where a center-symmetric pattern is produced by mirroring a one-eighth square pattern, as shown in Supplementary Fig. 3. The three-layer free-form meta-atoms in Fig. 3c are based on the mentioned substrate with the height of 4 mm, in which the top and bottom layers are the same 2D pattern and the middle layer is a circular ring, as shown in Supplementary Fig. 4.
Numerical simulation and training details
Both single-EM and EM-thermal simulations are carried out in the commercial software package COMSOL Multiphysics. For parameterized metasurface, design parameters are swept in the data collection, where 720 independent geometries are obtained. For single-EM data, frequency sampling from 2 to 14 GHz with an interval of 0.1 GHz (121 points) is adopted. For EM-thermal data, the sampling interval is 0.2 GHz (61 points), which costs about 7200 mins in total. On the contrary, the proposed learning-based solvers predict the results within 1 second. For free-form meta-atoms, COMSOL Multiphysics with MATLAB is used, where 544 independent single-layer meta-atoms and 648 independent three-layer meta-atoms are obtained. For the data pre-processing, the EM response is translated into the magnitude, and the average temperature is mapped by log10.
The multi-fidelity DeepONet Net1 and Net2 are developed with the DeepXDE library under Tensorflow 2.13. The latent dynamics networks Net3 and Net4 and the inverse design network Net5 are developed under Keras and Tensorflow 2.13. The details of the architectures, as well as the network training, can be found in Supplementary Note 2, 3, and Supplementary Table 1. The time of training the networks are about 62 mins, where the loss decreases as the training process is given in Supplementary Fig. 6. It is worthwhile to mention that both accumulating dataset and training the networks can be done offline, and accumulating dataset can be further done in parallel.
Data availability
Data are available at https://doi.org/10.5281/zenodo.14799160. Source data are provided in this paper.
Code availability
All the source codes to reproduce the results in this study are available on Zenodo at https://doi.org/10.5281/zenodo.14799160.
References
Rajpurkar, P., Chen, E., Banerjee, O. & Topol, E. J. AI in health and medicine. Nat. Med. 28, 31–38 (2022).
Lv, C. D. et al. Machine Learning: An advanced platform for materials development and state prediction in lithium-ion batteries. Adv. Mater. 34, 2101474 (2022).
Ahmad, T. et al. Artificial intelligence in sustainable energy industry: Status Quo, challenges and opportunities. J. Cleaner Prod. 289, 125834 (2021).
Nam, J. G. et al. AI improves nodule detection on chest radiographs in a health screening population: A randomized controlled trial. Radiology 307, e221894 (2023).
Ament, S. et al. Autonomous materials synthesis via hierarchical active learning of nonequilibrium phase diagrams. Sci. Adv. 7, eabg4930 (2021).
Wang, H. et al. Scientific discovery in the age of artificial intelligence. Nature 621, 47–60 (2023).
Elsheikh, A. H. Applications of machine learning in friction stir welding: Prediction of joint properties, real-time control and tool failure diagnosis. Eng. Appl. Artif. Intell. 121, 105931 (2023).
Alaee, R., Albooyeh, M. & Rockstuhl, C. Theory of metasurface based perfect absorbers. J. Phys. D Appl. Phys. 50, 503002 (2017).
Roberts, N. B. & Hedayati, M. K. A deep learning approach to the forward prediction and inverse design of plasmonic metasurface structural color. Appl. Phys. Lett. 119, 061101 (2021).
Zhu, R. C. et al. Phase-to-pattern inverse design paradigm for fast realization of functional metasurfaces via transfer learning. Nat. Commun. 12, 2974 (2021).
Lee, D., Zhang, L., Yu, Y. & Chen, W. Deep neural operator enabled concurrent multitask design for multifunctional metamaterials under heterogeneous fields. Adv. Opt. Mater. 12, https://doi.org/10.1002/adom.202303087 (2024).
Zhang, H. R. et al. Semantic regularization of electromagnetic inverse problems. Nat. Commun. 15, 3869 (2024).
Kim, B. & Shin, M. A novel neural-network device modeling based on physics-informed machine learning. IEEE Trans. Electron Dev. 70, 6021–6025 (2023).
Wang, P. et al. Pre-processing-based fast design of multiple EM structures with one deep neural network. IEEE Trans. Antennas Propag. 72, 4298–4310 (2024).
Bastek, J.-H. & Kochmann, D. M. Inverse design of nonlinear mechanical metamaterials via video denoising diffusion models. Nat. Mach. Intell. 5, 1466–1475 (2023).
Li, B. C. et al. Computational discovery of microstructured composites with optimal stiffness-toughness trade-offs. Sci. Adv. 10, eadk4284 (2024).
Ha, C. S. et al. Rapid inverse design of metamaterials based on prescribed mechanical behavior through machine learning. Nat. Commun. 14, 5765 (2023).
So, S. et al. Multicolor and 3D holography generated by inverse-designed single-cell metasurfaces. Adv. Mater. 35, 2208520 (2022).
Wang, Y. X. et al. End-to-end diverse metasurface design and evaluation using an invertible neural network. Nanomaterials 13, 2561 (2023).
Narendra, C., Brown, T. & Mojabi, P. Gradient-based electromagnetic inversion for metasurface design using circuit models. IEEE Trans. Antennas Propag. 70, 2046–2058 (2022).
Zhang, D. S., Liu, Z. Z., Yang, X. T. & Xiao, J. J. Inverse design of multifunctional metasurface based on multipole decomposition and the adjoint method. ACS Photonics 9, 3899–3905 (2022).
Xu, Z. L. et al. Arbitrary wavefront modulation utilizing an aperiodic elastic metasurface. Int. J. Mech. Sci. 255, 108460 (2023).
Wei, Z. H. et al. Equivalent circuit theory-assisted deep learning for accelerated generative design of metasurfaces. IEEE Trans. Antennas Propag. 70, 5120–5129 (2022).
Kingma, D. P. & Welling, M. Auto-encoding variational bayes. Preprint at https://doi.org/10.48550/arXiv.1312.6114 (2014).
Goodfellow, I. et al. Generative adversarial networks. Commun. Acm. 63, 139–144 (2020).
So, S. & Rho, J. Designing nanophotonic structures using conditional deep convolutional generative adversarial networks. Nanophotonics 8, 1255–1261 (2019).
Salucci, M., Arrebola, M., Shan, T. & Li, M. K. Artificial intelligence: New frontiers in real-time inverse scattering and electromagnetic imaging. IEEE Trans. Antenna Propag. 70, 6349–6364 (2022).
Nadell, C. C., Huang, B. H., Malof, J. M. & Padilla, W. J. Deep learning for accelerated all-dielectric metasurface design. Opt. Express 27, 27523–27535 (2019).
Ding, W., Chen, J. & Wu, R. X. A generative meta-atom model for metasurface-based absorber designs. Adv. Opt. Mater. 11, 2201959 (2022).
Wen, D. D. et al. Helicity multiplexed broadband metasurface holograms. Nat. Commun. 6, 8241 (2015).
Manu, G. et al. Full-colour 3D holographic augmentedreality displays with metasurface waveguides. Nature 629, 791–797 (2024).
Azad, A. K. et al. Metasurface broadband solar absorber. Sci. Rep. 6, 20347 (2016).
Hu, G. W. et al. Coherent steering of nonlinear chiral valley photons with a synthetic Au-WS2 metasurface. Nat. Photon. 13, 467–472 (2019).
Li, S. J. et al. Transmissive coding metasurface with dual-circularly polarized multi-beam. Opt. Express 30, 26362–26376 (2022).
Yu, S. X. et al. Generating multiple orbital angular momentum vortex beams using a metasurface in radio frequency domain. Appl. Phys. Lett. 108, 241901 (2016).
Shlezinger, N., Alexandropoulos, G. C., Imani, M. F., Eldar, Y. C. & Smith, D. R. Dynamic metasurface antennas for 6G extreme massive MIMO communications. IEEE Wirel. Commun. 28, 106–113 (2021).
Xu, H. X. et al. Polarization-insensitive 3D conformal-skin metasurface cloak. Light Sci. Appl. 10, 75 (2021).
Wang, S. J. et al. Janus metasurface for super radome with asymmetric diffusion and absorption. Adv. Opt. Mater. 12, 2302061 (2024).
Tanriover, I., Lee, D., Chen, W. & Aydin, K. Deep generative modeling and inverse design of manufacturable free-form dielectric metasurfaces. ACS Photonics 10, 875–883 (2023).
Song, C. & Wang, Y. H. High-frequency wavefield extrapolation using the Fourier neural operator. J. Geophys. Eng. 19, 269–282 (2022).
Chen, J. T., Qian, C., Zhang, J., Jia, Y. T. & Chen, H. S. Correlating metasurface spectra with ageneration-elimination framework. Nat. Commun. 14, 4872 (2023).
Peng, Z. et al. Rapid surrogate modeling of electromagnetic data in frequency domain using neural operator. IEEE Trans. Geosci. Remote Sens. 60, 2007912 (2022).
Zhu, M. et al. Reliable extrapolation of deep neural operators informed by physics or sparse observations. Comput. Methods Appl. Mech. Eng. 412, 116064 (2023).
Wang, Y. F., Zhang, H., Lai, C. S. & Hu, X. Y. Transfer learning Fourier neural operator for solving parametric frequency-domain wave equations. IEEE Trans. Geosci. Remote Sens. 62, 5923211 (2024).
Yan, Y. M. et al. Highly intelligent forward design of metamaterials empowered by circuit-physics-driven deep learning. Laser Photonics Rev. https://doi.org/10.1002/lpor.202400724 (2024).
Cai, Z. R., Ding, Y. T., Chen, Z. M., Zheng, Z. W. & Ding, F. Dynamic dual-functional optical wave plate based on phase-change meta-molecules. Opt. Lett. 48, 3685–3688 (2023).
Liu, Y., Chen, J., Li, J. X. & Xu, W. J. A study on the electromagnetic-thermal coupling effect of cross-slot frequency selective surface. Materials 15, 640 (2022).
Komlan, P., Kevin, X., Jun, H. C. & Jay, K. L. Multiphysics analysis of plasma-based tunable absorber for high-power microwave applications. IEEE Trans. Antennas Propag. 69, 7624–7636 (2021).
Qi, S. T. & Sarris, C. D. Electromagnetic-thermal analysis with FDTD and physics-informed neural networks. IEEE J. Multiscale Multiphys. Comput. Tech. 8, 49–59 (2023).
George, E. K. et al. Physics-informed machine learning. Nat. Rev. Phys. 3, 422–440 (2021).
Wang, S. F. & Perdikaris, P. in Knowledge Guided Machine Learning, 133–160 (Chapman and Hall/CRC, 2022).
Wang, S. F., Sankaran, Wang, H. W. & Perdikaris, P. An expert’s guide to training physics-informed neural networks. Preprint at https://arxiv.org/abs/2308.08468 (2023).
Lu, L., Meng, X. H., Mao, Z. P. & Karniadakis, G. E. DeepXDE: A deep learning library for solving differential equations. Siam Rev. 63, 208–228 (2021).
Lu, L., Jin, P. Z., Pang, G. F., Zhang, Z. Q. & Karniadakis, G. E. Learning nonlinear operators via DeepONet based on the universal approximation theorem of operators. Nat. Mach. Intell. 3, 218 (2021).
Wang, S. F., Wang, H. W. & Perdikaris, P. Improved architectures and training algorithms for deep operator networks. J. Sci. Comput. 92, 35 (2022).
Li, Z. et al. Fourier neural operator for parametric partial differential equations. Preprint at https://doi.org/10.48550/arXiv.2010.08895 (2020).
Jin, H. et al. Mechanical characterization and inverse design of stochastic architected metamaterials using neural operators. Preprint at https://doi.org/10.48550/arXiv.2311.13812 (2023).
Augenstein, Y., Taavi, R. & Carsten, R. Neural operator-based surrogate solver for free-form electromagnetic inverse design. ACS Photonics 10, 1547–1557 (2023).
Wang, Y., Zong, Z., He, S., Song, R. & Wei, Z. Push the generalization limitation of learning approaches by multi-domain weight-sharing for full-wave inverse scattering. IEEE Trans. Geosci. Remote Sens. 61, https://doi.org/10.1109/TGRS.2023.3303572 (2023).
Goodfellow, I., Bengio, Y., Courville, A. & Bengio, Y. Deep Learning, Vol. 1. (MIT Press Cambridge, 2016).
Lu, L., Jin, P. & Karniadakis, G. E. DeepONet: Learning nonlinear operators for identifying differential equations based on the universal approximation theorem of operators. Preprint at https://doi.org/10.48550/arXiv.1910.03193 (2019).
Howard, A. A. et al. Multifidelity deep operator networks for data-driven and physics-informed problems. J. Comput. Phys. 493, 112462 (2023).
Lyu, Y. et al. Multi-fidelity prediction of fluid flow based on transfer learning using Fourier neural operator. Phys. Fluids 35, 077118 (2023).
Regazzoni, F., Pagani, S., Salvador, M., Dede, L. & Quarteroni, A. Learning the intrinsic dynamics of spatio-temporal processes through latent dynamics networks. Nat. Commun. 15, 1834 (2024).
Lu, L., Pestourie, R., Johnson, S. G. & Romano, G. Multifidelity deep neural operators for efficient learning of partial differential equations with application to fast inverse design of nanoscale heat transport. Phys. Rev. Research 4, 023210 (2022).
Zhang, C. Y., Bengio, S., Hardt, M., Recht, B. & Vinyals, O. Understanding deep learning (still) requires rethinking generalization. Commun. ACM 64, 107–115 (2021).
Wang, X.-P., Yin, W.-Y. & He, S. L. Multiphysics characterization of transient electrothermomechanical responses of through-silicon vias applied with a periodic voltage pulse. IEEE Trans. Electron Devices 57, 1382–1389 (2010).
Acknowledgements
This work was supported by the National Key R&D Program of China (2023YFB3813100, Z.W.), NSFC Ye Qisen Joint Fund under Grant U2441232 (W.-Y.Y.), National Natural Science Foundation of China under Grant 62371417 (Z.W.), Zhejiang Provincial Natural Science Foundation of China under Grant LZ23F010005 (Z.W.), and National Natural Science Foundation of China under Grant 62101484 (Z.W.).
Author information
Authors and Affiliations
Contributions
Z. Wei conceived and supervised the entire study. Z. Wei and W.-Y. Yin suggested the designs. E. Zhu implemented the method and designed the metasurface. E. Zhu and Z. Zong wrote the code. Z. Wei, W.-Y. Yin, E. Zhu, Z. Zong, E. Li, Y. Lu, J. Zhang, H. Xie, and Y. Li carried out the measurements and data analysis. Z. Wei, W.-Y. Yin, E. Zhu, Z. Zong, E. Li, Y. Lu, J. Zhang, H. Xie, and Y. Li contributed to the writing of the paper. All authors discussed the models numerical simulations and reviewed the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Qianying Cao, Wei Chen, and the other anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Source data
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Zhu, E., Zong, Z., Li, E. et al. Frequency transfer and inverse design for metasurface under multi-physics coupling by Euler latent dynamic and data-analytical regularizations. Nat Commun 16, 2251 (2025). https://doi.org/10.1038/s41467-025-57516-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-025-57516-z