Introduction

Two-dimensional (2D) semiconductor materials have evolved into a versatile platform for exploring fundamental excitonic physics and developing functional optoelectronic devices1,2,3. When 2H transition metal dichalcogenides (2H-TMDCs) are thinned down from bulk to monolayers, they exhibit a band-gap transition from indirect to direct, large exciton binding energy and significantly improved carrier mobility4,5. Therefore, TMDCs monolayer exhibits superior excitonic optical response within a unit thickness. Nevertheless, the absolute excitonic responses are quite low, which limits their performance in optoelectronic applications. TMDCs multilayer van der Waals (vdW) artificial crystals emerge as promising candidates to address the aforementioned challenges. However, the bottom-up assembly of thick artificial crystals with maintained 2D excitonic performance remains a tough task.

The major challenge arises from the sensitive energy band evolution induced by interlayer coupling. To date, pioneering efforts have been invested in advancing the preparation and optical property exploration of vdW crystals6,7,8,9,10. The commonly employed bottom-up approach, chemical vapor deposition (CVD), can produce 3R multilayer homostructures of more than 17-layer (17L)6. Despite that increasing second harmonic generation (SHG) signal intensity with thickness was achieved, they still observed a decreased excitonic emission of thick crystal in comparison to that of 1L counterparts, resulting from direct-to-indirect bandgap transition in such synthesized crystals with strong interlayer coupling6.

Another extensively employed bottom-up method is layer-by-layer assembling of either CVD-grown7,8 or disassembled9 monolayers. In the latter case, the SHG intensity of well-aligned AA-stacked 5L MoS2 exhibits a square dependence on layer number9. However, so far superior excitonic emission has not yet been realized in such artificial crystals7,8. Moreover, the layer-by-layer assembly approach requires (n-1)-time operation for fabricating an n-layer crystal, which prevents the production of thick artificial crystals with high efficiency and high yield. Alternatively, electrochemical molecular intercalation seems to be a practical method to create TMDCs/molecule superlattices, in which the strong monolayer excitonic emission can be reserved10. This method is attractive for efficiently creating bulk single-component monolayer crystals for light-emitting devices, although in certain cases a pure inorganic superlattice or even multi-component crystal is preferred. Therefore, a method that is compatible with multiple application scenarios is pending to be developed for the design and exploration of excitonic behaviors in the 3D form.

Herein, motivated by the exponentially increasing character of origami, we demonstrated an approach named the “2N method” for constructing m∙2N-layer artificial crystals by only a number N of stacking operation, where N represents the stacking rounds, and m denotes the layer number of the initial material unit. As illustrated in Fig. 1a, b, starting from a heterobilayer (m = 2), a 32L heterostructure can be fabricated through only four cycles of “picking-up—pressing and dividing—picking-up”. Beyond the exponentially increasing thickness (Fig. 1c), the initial material unit can be freely selected, and their identical interlayer alignment can be precisely controlled (Fig. 1d). A millimeter-scale 16L-MoS2 single crystal and an 8L WSe2/(MoS2/WSe2)3/MoS2 superlattice were fabricated and their superior excitonic performance will be introduced in sequence. This study demonstrates the design and fabrication of emerging types of excitonic crystals, which hold potential for future advancements in photonics and optoelectronics.

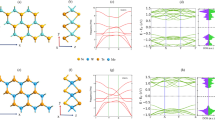
Fig. 1: Building m∙2N-layer artificial crystals with exponentially growing thickness.
figure 1

a The schematic concept of constructing an m∙2N-layer superlattice with N-time operation, where N represents the stacking rounds, and m denotes the layer number of the initial material unit. b The “picking-up—pressing and dividing—picking-up—restacking” procedure. c Crystal layer number (n) versus operation times (N) of this work (red symbols; the fit curve is n = 2N) and the layer-by-layer approach (gray symbols; the fit curve is n = 1 + N), for clearance, we take m = 1 as an example. d Schematic illustration of identical interlayer alignment with zero twist angle for the 2N method. Photos of a centimeter-scale MoS2 single crystal grown by chemical vapor deposition (CVD) (e), as-prepared ladder-like millimeter-scale 16 layers (16L) MoS2 crystal (f) and the corresponding schematic structure (g). Optical microscopy images of a near 0° WSe2/MoS2 heterobilayer (h), as-prepared 8L WSe2/(MoS2/WSe2)3/MoS2 heterogeneous superlattice (i) and corresponding schematic structure (j).

Full size image

Results

The 2N method

Following the above concept, we used self-cracked [100] edges of {100} silicon wafers and a Ni sacrificial layer to assist 2N fabrication. Take the 16L MoS2 single crystal as an example, the detailed fabrication process includes: (i) Initially, a centimeter-scale monolayer MoS2 single crystal on a sapphire substrate was obtained by CVD growth11 and then wet-transferred to a polydimethylsiloxane (PDMS) stamp; (ii) Subsequently, the MoS2 monolayer is positioned close to the edge of a Ni-sacrificial-layer coated SiO2/Si substrate (Ni/SiO2/Si substrate), leaving half MoS2 layer on the Ni/SiO2/Si substrate and the other half suspended; (iii) The interaction force between the monolayer and the sacrificial-layer exceeds that between the monolayer and the PDMS layer, resulting in half of the monolayer being transferred to the Ni/SiO2/Si substrate, while the other half staying on the elevated PDMS layer (Supplementary Fig. 1); (iv) After translation movement, the MoS2/PDMS layer is then restacked on top of the MoS2 monolayer on the Ni/SiO2/Si substrate, doubling the layer number of the homostructure sample; (v) Dissolving the sacrificial layer in diluted hydrochloric acid separates the homostructure from the substrate; (vi) By repeating steps ii to v three times, a 16L MoS2 crystal can be constructed and is ready to be transferred to a target substrate. Heating operation was avoided during the whole process to realize weak coupling between individual layers12. Since the single-crystal monolayers on the Ni/SiO2/Si substrate and PDMS are from the same parent, there is strictly no interlayer twist during the whole fabrication process (Fig. 1d). Figure 1e, f show the photos of a centimeter-scale monolayer MoS2 single-crystal by CVD and the as-prepared ladder-like MoS2 crystal, and a schematic structure was shown in Fig. 1g.

This method can be extended to the fabrication of heterogeneous superlattices. We used TMDCs monolayers obtained through exfoliation from bulk crystals. The layer number is confirmed by optical contrast, Raman spectroscopy, and photoluminescence (PL) spectroscopy (Supplementary Fig. 2). The lattice axes (armchair and zigzag directions) were determined by polarization-resolved SHG. Starting from a near 0° WSe2/MoS2 heterobilayer (Fig. 1h, the twist angle is confirmed by SHG, as will be discussed later), an 8L WSe2/(MoS2/WSe2)3/MoS2 heterogeneous superlattice can be assembled through only two rounds of stacking operation, as shown in the optical image (Fig. 1i) and the corresponding schematic structure (Fig. 1j). Notably, in 8L heterogeneous superlattice, we heated to 80 °C during each ii-iv step, for efficient interlayer charge transfer and potential interlayer exciton (IX) emission. We found that such a low annealing temperature is adequate, this is likely because we have chosen an interlayer twist angle of near 0° (or 60° as will be discussed later), which promotes close overlap in momentum space (K-K or K-K′) and results in a strong interlayer coupling. We did not use an even higher annealing temperature, mainly because of the purpose of minimizing thermal damage and possible substrate doping effects.

Optical properties of 16L ladder-like MoS2 crystal

We first focus on the optical properties of the millimeter-scale 16L MoS2 crystal. The AA-stacked feature with zero interlayer twist angle in 16L MoS2 crystal aligns well with the strong SHG response. The SHG intensity excited by fs-pulsed laser (0.79 eV, 80 MHz) increases steadily as the layer number increases, giving a maximum SHG intensity of ~35 times higher than that of a monolayer, surpassing previous results on AA-stacked single-component multilayer TMDCs6,9,13. The experimental results and corresponding calculation details considering the absorption and multiple-beam interference are summarized in Supplementary Section 1 and Supplementary Figs. 3 and 4.

To explore the excitonic behaviors in assembled 16L MoS2 crystal (shorted as this study), we conducted optical imaging and spectroscopic study on the ladder-like crystal with 1L, 2L, 4L, 8L, and 16L regions. Optical microscopy image (Fig. 2a) and PL mapping (Fig. 2b) show a monotonously increasing PL emission as layer number n increases. This is in stark difference to natural 2H-MoS2 crystal (purchased from HQ graphene), where the crystal exhibits the highest PL intensity at the monolayer region, then decreases quickly as the layer number n increases (Fig. 2c, d). Detailed transmission and PL spectra for 1L, 2L, 4L, 8L, and 16L MoS2 are presented in Fig. 2e. For all thicknesses, each transmission spectrum displays two dips at 1.901 ± 0.004 eV and 2.053 ± 0.001 eV with negligible peak shifts, corresponding to A and B excitons at the K point, respectively. As summarized in Supplementary Fig. 5, the A exciton absorption peak position for different layer numbers in the assembled MoS2 crystal remains unchanged, indicating the weak interlayer interactions and intact monolayer-like nature. On the contrary, the A exciton peak for the natural 2H-MoS2 crystal redshifts about 0.053 eV from 1L to 9L, mainly due to the changes in the interlayer-coupling-induced band structure4.

Fig. 2: Millimeter-scale monolayer-like excitonic crystal.
figure 2

Optical microscopy images (a, c) and steady-state photoluminescence (PL) mapping of A excitons (b, d) for as-prepared 16L MoS2 crystal (a, b) and natural 2H-MoS2 crystal (c, d). e Transmission and PL spectra of 1L, 2 L, 4L, 8L and 16L regions, respectively. Absorption (f), normalized integrated PL intensity as well as relative quantum yield (QY) (g) of A excitons with respect to layer numbers in the 16L MoS2 artificial crystal and the natural 2H-MoS2 crystal, with laser excitation at 2.33 eV. * marks the Raman signal of the polydimethylsiloxane (PDMS) substrate. The error bars in g represent the standard deviation of PL intensity measurements from different locations. The dashed lines in (f, g) are guided by eyes.

Full size image

Figure 2f, g summarize the absorption and integrated A exciton PL intensity for both the 16L MoS2 artificial crystal and the natural 2H-MoS2 crystal. The absorption follows a similar trend for both samples, for instance, the absorption value increases from 7% for 1L to 46% for 16L at the A exciton energy. Strikingly, unlike 2H-MoS2 crystals and existing studies on 3R-MoS2 crystals (Supplementary Fig. 2, Fig. 2g, and refs. 6,8,13), which show a decreased PL intensity with increased layer number resulting from the indirect Γ-K transition, the PL intensity of the ladder-like 16L MoS2 crystal exhibits a rapid increase and tends to saturate after 16L. The integrated A exciton PL intensity of the 16L MoS2 crystal is more than 300 times stronger than that of the bulk 2H-MoS2 crystal (Supplementary Fig. 6). When the integrated PL intensity is divided by the absorption value in Fig. 2f, the relative quantum yield (QY) of the ladder-like 16L MoS2 crystal (as compared to the monolayer parent) is calculated and plotted in Fig. 2g (right axis). The similar QY further indicated the monolayer-like characteristic of the as-prepared 16L MoS2 crystal, which holds promise for the wafer-scale light source. The weak interlayer coupling shall play a critical role in the monolayer-like excitonic feature, and we did observe a PL decrease if we annealed a 2L assembled MoS2 crystal at 120 °C for 30 min (Supplementary Fig. 7).

We then conducted time-resolved photoluminescence (TRPL) measurements to explore the excitonic dynamics in the as-prepared 16L MoS2 crystal. For comparison, Figure 3a, b show the normalized TRPL spectra for different regions of the MoS2 artificial crystal and 2H-MoS2 crystal, only 1L, 2L, and 16L for assembled MoS2 crystal and 1L, 3L, 9L for 2H-MoS2 crystal are displayed for clarity. Notably, multilayers in assembled MoS2 crystals have a monotonously increasing decay rate compared to 1L MoS2 (blue). This is in stark difference to 2H-MoS2, in which 1L-MoS2 has the fastest decay rate. A double-exponential decay function (\(I={A}_{1}{e}^{-\frac{t}{{\tau }_{1}}}+{A}_{2}{e}^{-\frac{t}{{\tau }_{2}}}\)) was applied to fit the TRPL curves after deconvolution with the instrument response function (IRF), where I is the PL intensity, τ1 and τ2 are the decay time constants, Α1 and Α2 are the amplitude coefficients, respectively. Amplitude-weighted averaged lifetime (\(\tau_{{{\rm{amp}}}}=\frac{{A}_{1}{\tau }_{1}+{A}_{2}{\tau }_{2}}{A}\)) versus the number of layers curves are plotted in Fig. 3c. The abruptly increased averaged lifetime τamp from 1L to multilayer in 2H-MoS2 is caused by the direct-to-indirect bandgap transition5. In contrast, we can unambiguously see that such bandgap transition is absent in the ladder-like MoS2 artificial crystal. Detailed thickness-dependent decay time constants (τ1 and τ2) and their amplitude coefficients are presented in Fig. 3d–g. In contrast to multilayer 2H-MoS2, monolayer MoS2 (either CVD-grown or mechanically exfoliated from 2H-MoS2 crystal) and multilayers in MoS2 artificial crystal exhibit similar PL lifetime characteristics. All decay curves include a dominant component τ2 with an amplitude coefficient of ~0.9 and a minor component τ1 with an amplitude coefficient of ~0.1, and the amplitude coefficients of τ1 and τ2 are almost unchanged with varying layer number n. More importantly, the dominant shorter component τ2 can be attributed to free excitons, which is also almost unchanged with n. These results demonstrate the monolayer-like excitonic characteristics of our MoS2 artificial crystal, which is essentially different from the longer lifetime in the natural multilayer crystal with an indirect bandgap. The minor longer component τ1 may be related to defect states or exciton-phonon scattering14.

Fig. 3: Excitonic dynamics in millimeter-scale MoS2 artificial crystal and 2H-MoS2 crystal.
figure 3

Normalized time-resolved photoluminescence (TRPL) spectra and fitting curves with respect to layer number for millimeter-scale MoS2 crystal (a) and 2H-MoS2 crystal (b). IRF is the instrument response function. c The averaged lifetimes for millimeter-scale MoS2 artificial crystal and 2H-MoS2 crystal. Fitted lifetimes (τ1 and τ2) and the amplitude coefficients of τ1 and τ2 lifetimes with respect to layer number for millimeter-scale MoS2 crystal (d, f) and 2H-MoS2 crystal (e, g). The blue-shadowed regions correspond to monolayers and monolayer-like crystals, and the gray-shadowed regions correspond to indirect bandgap crystals. Excitation condition: fs-pulsed laser at 3.18 eV, 80 MHz. The error bars in (c–g) represent the uncertainties obtained from the fitting process and are calculated in SymphoTime 64 software.

Full size image

Interlayer quadrupolar excitons and their evolution

One might question the necessity of strictly 0° alignment of layer components to achieve monolayer-like excitonic properties in 16 L MoS2 artificial crystal, as an increased interlayer distance diminishes the impact of the interlayer twist angle. In the following part, we will demonstrate another unique capacity of our method in vertical integration of multilayer heterogeneous superlattice emitting interlayer excitons. Interlayer excitons, with electrons and holes residing at each monolayer component in type II heterostructures with a staggered band alignment, hold significant potential in next-generation optoelectronic devices due to their long lifetime15 and engineerable energy states16,17. However, the bottom-up assembly of interlayer exciton crystals with highly consistent interlayer coupling states is challenging, and existing research is limited to bilayer15,18,19,20,21 or trilayer structures22,23,24,25. Recalling the 8L WSe2/(MoS2/WSe2)3/MoS2 superlattice we have fabricated (Fig. 1i), the design is mainly based on two considerations: (i) WSe2/MoS2 exhibits IX emission falling in the second near-infrared region (NIR-II) range21, which is crucial in fields like telecommunication and sensing; (ii) Strictly same interlayer-twist is adapted to precisely duplicate {WSe2/MoS2} units with identical interfacial electronic states.

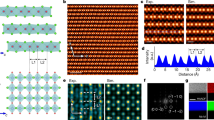
The high-resolution cross-sectional high-angle annular dark-field scanning transmission electron microscopy (HAADF-STEM) image shows the atomic structure of an 8L WSe2/(MoS2/WSe2)3/MoS2 superlattice, with alternant WSe2 and MoS2 layers (Fig. 4a). WSe2 and MoS2 can be clearly identified by the image contrast due to the atomic number difference, and their consistent lattice orientation for different layers can be distinguished. The alternant stacking can be further revealed by the energy dispersive spectrometer (EDS) elemental mapping images of W and Mo elements (Fig. 4b). The averaged interlayer distance Davg of 0.70 nm is close to an ideal vdW distance in TMD layers (Fig. 4c)7. The identical orientation of atomic layers of 8L WSe2/(MoS2/WSe2)3/MoS2 superlattices was further demonstrated by the well-aligned six-fold symmetry of the SHG patterns in monolayers and superlattices (Supplementary Fig. 8). A summed effective second-order nonlinear susceptibility χ(2) and stronger SHG response in superlattices indicate the angle offset between WSe2 and MoS2 monolayers is close to 0° rather than 60°15.

Fig. 4: Structural characterization of an 8L WSe2-(MoS2-WSe2)3-MoS2 superlattice.
figure 4

a High-angle annular dark-field scanning transmission electron microscopy (HAADF-STEM) image of a WSe2-(MoS2-WSe2)3-MoS2 superlattice with the corresponding atomic model overlaid. b The corresponding energy dispersive spectrometer (EDS) mapping images of W and Mo. c EDS intensity profiles for W (red) and Mo (blue) from (b). The dashed lines represent the positions of distinct atomic layers (W, red, and Mo, blue). The averaged interlayer distance Davg = 0.70 nm is calculated from the EDS data in (c). Scale bars in a, b are 2 nm.

Full size image

Multilayer superlattices allow for the existence of a wide variety of exciton species due to the degree of freedom of the exotic layer. According to the type II band alignment, electrons tend to be confined in the MoS2 layers and holes are localized in the WSe2 layers. It shall be clarified that, despite there being reports on indirect Γ-K IX transition at ~1.58 eV in WSe2/MoS2 heterobilayers, in this work, we focus on the lower-energy K-K(K′) IX transition at ~1.03 eV. Interlayer charge transfer leads to the formation of dipolar interlayer excitons in the bilayer heterostructure, as well as the quenching of intralayer excitons (Supplementary Fig. 9). In superlattices thicker than bilayers, the hole/electron confined to a middle layer can be bound to delocalized electrons/holes residing in the adjacent layers, forming new quasiparticles called quadrupolar interlayer excitons22,23,24,25. The quadrupolar excitons are the hybridization of two dipolar excitons, resulting in the two energy branches, where the lower energy branch has been observed experimentally22,23,24,25. In these works, the PL intensity of quadrupolar IXs in the trilayer is weaker than that of dipolar IXs in the bilayer.

The as-prepared 8L WSe2-(MoS2-WSe2)3-MoS2 superlattice using the 2N method provides a unique system for studying multiple quasiparticles, particularly for quadrupolar IXs. To conduct a careful investigation of the evolution of multi-body excitons, we also prepared a sample with four kind regions for comparison, i.e., 2L (WSe2/MoS2), 3L (MoS2/WSe2/MoS2, e−-h+-e− type), 3L (WSe2/MoS2/WSe2, h+-e−-h+ type), and 4L (WSe2/MoS2/WSe2/MoS2). Angle-resolved SHG measurements indicate an interlayer twist angle of near 60° (Supplementary Fig. 10).

Benefiting from identical interlayer twist angles, as we can see in Fig. 5a, all sample regions (2~4L superlattices) exhibit prominent interlayer exciton emission. The emission from the 2L (~60°) sample shows a single peak at 1.030 eV, which belongs to triplet dipolar IX from K(K′)-K′(K) transition26 (Supplementary Fig. 11). Excitation power and temperature-dependent experiments further suggest that this single peak is from neutral IXs rather than trions. Starting from 3L, it becomes a two-peak structure. Take the e−-h+-e− type of 3L as an example, the higher energy one at 1.018 eV belongs to redshifted dipolar IX, and the other lower energy one at 0.972 eV corresponds to quadrupolar IX. The redshift value of quadrupolar IX energy as compared to that of dipolar IX in the bilayer is observed to be 58 meV for 3L (e−-h+-e− type) and 54 meV for 3L (h+-e−-h+ type), respectively. A summary of dipolar and quadrupolar IX emission energies at 8.65 μW and 91.3 μW can be found in Supplementary Table 1. We attribute the dominant contribution to this redshift value to the formation of quadrupolar IXs. The validity of the assignment can be understood for the following reasons: (1) The emergent lower energy peak in 3L (both e−-h+-e− type, and h+-e−-h+ type) shall not be singlet IX (with higher energy than triplet IX)23, trion27 or phonon replica28, otherwise the dipolar IX in 2L would also not display a single-peak structure22; (2) Emergence of this lower energy peak is not redshifted dipolar IX due to increased dielectric screening. Were this the case, we would observe a single-peak structure in 3L. Actually, from Fig. 5a, we can calculate the dielectric screening-induced redshift of dipolar IX from 2L (1.030 eV) to 3L (1.018 eV) is less than 12 meV at an excitation power of 8.65 μW; (3) Power-dependent experiments of quadrupolar IX in 3L (4L) suggest a 1.83 (4.31) times smaller energy shift, than that of dipolar IX in 2L at a higher excitation power with increased excitonic density (Fig. 5b, c), in accordance with recent investigations on 3L WSe2/WS2/WSe223, which is another important feature of quadrupolar IX with reduced exciton-exciton repulsion. Furthermore, we have conducted spectral mapping on the WSe2/MoS2 superlattice with 2L, 3L, and 4L regions. We plot the spatial distribution of quadrupolar IX emission at 0.950–0.970 eV and dipolar IX emission at 1.090-1.120 eV in Fig. 5d-f, respectively. Noticeably, both 2L regions show prominent dipolar IX emission at 1.09-1.12 eV and the absence of quadrupolar IX emission at 0.950–0.970 eV. Since 3L, we can observe the occurrence of quadrupolar IX emission. More discussions can be found in Supplementary Section 2, and Supplementary Figs. 12 and 13.

Fig. 5: WSe2-(MoS2-WSe2)3-MoS2 superlattices with boosted quadrupolar interlayer excitons (IXs) emission.
figure 5

a The PL spectra and fitting curves with Viogt function of 2L (WSe2/MoS2), 3L (MoS2/WSe2/MoS2 and WSe2/MoS2/WSe2), and 4L (WSe2/MoS2/WSe2/MoS2), measured at 78 K and under laser excitation at 2.58 eV, 8.65 μW. The orange/blue circles with “+/–” symbols represent holes and electrons in different layers, respectively. PL spectra with different excitation powers for 2L WSe2/MoS2 (b) and 3L MoS2/WSe2/MoS2 (c), measured at 78 K and under laser excitation at 2.58 eV. Optical microscopy image (d) and steady-state spatial PL mapping of lower energy IXs (0.95–0.97 eV, quadrupolar IXs) (e) and higher energy IXs (1.09–1.12 eV, dipolar IXs) (f) for as-prepared 4L superlattice, measured at 78 K and under laser excitation at 2.58 eV with a galvo-scanning system with a step size of 1.2 μm, 78.8 μW. The solid blue, green, and red solid lines mark the 2L, 3L (MoS2/WSe2/MoS2), and 4L regions, respectively. g Schematic illustration of excitonic species in 8L WSe2-(MoS2-WSe2)3-MoS2 superlattice, including intralayer exciton, dipolar IX, and quadrupolar IX. h Transmission spectra of MoS2 monolayer, WSe2 monolayer, WSe2/MoS2 heterobilayer, and the WSe2-(MoS2-WSe2)3-MoS2 superlattice. The dashed lines represent the A exction peak energy of monolayer WSe2 and MoS2, respectively. i Low-temperature PL spectra in the second near-infrared region (NIR-II) region, measured at 78 K and under laser excitation at 2.33 eV, 0.782 mW. Data vertically offset for visualization in (a–c, i).

Full size image

The robust manifestation of multibody excitonic species in 2L, 3L, and 4L superlattice is inspiring, which benefits from the strictly identical interlayer twist angle ensured by our 2N method. The excitonic properties of the 8L WSe2/(MoS2/WSe2)3/MoS2 superlattice resemble that of the 4L superlattice, as displayed in Fig. 5g. We have conducted micro-area transmission spectroscopy on the 8L superlattice prepared in Fig. 1i, monolayers, 2L WSe2/MoS2 are also presented for reference. The characteristic dips at approximately 1.96, 2.11, and 2.91 eV in the MoS2 monolayer are attributed to A, B, and C intralayer excitons, respectively. The characteristic peaks at approximately 1.74, 2.18, 2.52, and 2.95 eV in the WSe2 monolayer correspond to A, B, A′, and B′ intralayer excitons, respectively29 (Fig. 5h). The transmission peak positions of superlattices are consistent with monolayers, with a slight redshift due to the hybridization of interlayer electronic wave functions.

In accordance with previous study, the different peak energy of dipolar IX emission (Fig. 5a, i) is likely due to their different interlayer twist angles30. Intriguingly, we observed a boost to 400% quadrupolar IX emission in the NIR-II region (Fig. 5i) compared to that of the dipolar IX emission in 2L WSe2/MoS2 heterobilayers. The redshifted peak position of IX in the 8L superlattice is mainly due to the contribution of the formation of dominant quadrupolar excitons. Notably, the presence of highly consistent WSe2/MoS2 repeating units in the 8L WSe2/(MoS2/WSe2)3/MoS2 superlattice shall play a critical role in providing a bright quadrupolar IX emission in the NIR-II range.

Discussion

In conclusion, we have developed a 2N approach for achieving bottom-up assembly of m∙2N-layer artificial crystals in an exponentially growing manner, with strictly identical replication and vertical integration of the initial functional unit. We have realized millimeter-sized homogeneous 16L ladder-like MoS2 crystal exhibiting boosted monolayer-like exciton emission and SHG performance. Furthermore, 2L, 3L, 4L, and 8L superlattices with alternating MoS2 and WSe2 layers exhibit robust IX emission and their layer-number-dependent dipolar and quadrupolar excitonic evolution have been investigated. Besides the above-demonstrated examples, our approach shall be especially useful in the construction and exploration of moiré and ferroelectric crystals which are domain-sensitive. Benefiting from the great success in synthesizing different types of wafer-scale 2D single crystals11,31, as well as progress in the robotic assembly technique8, our study offers the potential of scalable and rapid production of free-designed macroscale structures with exotic properties.

Methods

Bottom-up assembly of m∙2N-layer vdW artificial crystals by the 2N method

Centimeter-scale monolayer single-crystal MoS2 was prepared on sapphire by CVD growth11. Polymethylmethacrylate (PMMA) dissolved in anisole (950 K, 4 wt%, from MicroChem) was spin-coated onto the MoS2/sapphire (4000 r.p.m., 60 s) and baked at 125 °C for 1 min. After soaking in saturated KOH solution for 30 min, the PMMA/MoS2 was carefully peeled off with the assistance of a windowed scotch tape. The PMMA/MoS2 was transferred onto a PDMS film (Gel-Pak). The PMMA layer as well as the windowed scotch tape can be removed after soaking in acetone for 1 minute.

WSe2 and MoS2 crystals were purchased from HQ Graphene. We obtained high-quality monolayers via the mechanical exfoliation method. WSe2/MoS2 heterobilayers were prepared on the Ni/SiO2/Si substrate by the aligned dry transfer method.

Then, the homo- and heterogeneous multilayer artificial crystals were fabricated using our 2N method described in the main text. The Ni layer, approximately 80 nm thickness (at a rate of about 1 Å/s and at a pressure of about 10-4 Pa), was deposited via electron beam evaporation. To preserve the monolayer-like optical properties of MoS2 artificial crystals, we avoided any heating processes. In contrast, for the superlattice with strong interlayer charge transfer, we heated it at 80 °C for more than 15 min.

Optical spectroscopy measurements

Raman, transmission, steady-state PL, and SHG spectra were measured on the same confocal micro-Raman spectrometer (Horiba-LabRAM HR Evolution) if not otherwise noted. Measurements were implemented at room temperature and conducted with a ×100 objective lens (Olympus, numerical aperture 0.90) under ambient conditions if not otherwise noted. A 2.33 eV solid-state continuous-wave (CW) laser was used as the excitation source for Raman and PL measurements. We used 600 grooves/mm and 100 grooves/mm gratings for Raman and PL measurements, respectively. Power-dependent PL spectra in Fig. 4 were measured using a 2.58 eV ps-pulse laser (5 MHz, YSL Supercontinuum Source SC-Pro). The millimeter-scale PL mapping was measured using a motorized XYZ stage, with a step size of 30 μm. A halogen lamp was used as the white-light source for transmission measurement. The transmission spectra of a sample (T) and PDMS substrate (T0) were collected, and the final transmission spectra were obtained according to T/T0. The SHG was excited by a femtosecond-pulse laser (NPI Laser, Rainbow, 80 MHz, <80-fs pulse duration) with either 1.59 eV output or 0.79 eV output after passing through a frequency-doubling crystal. SHG responses were collected by parallel analyzer orientations relative to the incident light polarization. We measured polarization-resolved SHG by rotating the sample at 3–5° intervals. Low-temperature measurements were conducted in a liquid-nitrogen continuous-flow cryostat (Cryo Industries of America). For compensation for optical window thickness, a ×100 objective lens with a correction collar (Leica, numerical aperture 0.85) was used and adjusted in measurements. We used Labspec6 software for data processing. All optical spectra are reported without smoothing.

Time-resolved photoluminescence measurements

The TRPL measurements were conducted using the same femtosecond-pulse laser (1.59 eV) with 3.18 eV output after passing through a frequency-doubling crystal. Time-correlated single photon counting (TCSPC) was performed with PicoHarp 300 equipment (PicoQuant). The time resolution of this setup is ∼16 ps. The PL intensity decay curve was fitted to a bi-exponential deconvolution fitting model by SymPhoTime 64 software. The instrument response function was measured with a SiO2/Si substrate and under laser excitation at 1.59 eV.

Scanning transmission electron microscopy

High-quality cross-sectional samples were fabricated by the focused ion beam (FIB) technique using the FEI Helios 600i dual-beam system. Atomic resolution HAADF-STEM images were obtained on a double spherical aberration-corrected STEM/TEM FEI Titan G2 60–300 instrument at 300 kV with a field emission gun. The probe convergence angle on the Titan electron microscope was 22.5 mrad, and the angular range of the HAADF detector was from 79.5 to 200 mrad.