Towards fairness-aware and privacy-preserving enhanced collaborative learning for healthcare

Abstract

The widespread integration of AI algorithms in healthcare has sparked ethical concerns, particularly regarding privacy and fairness. Federated Learning (FL) offers a promising solution to learn from a broad spectrum of patient data without directly accessing individual records, enhancing privacy while facilitating knowledge sharing across distributed data sources. However, healthcare institutions face significant variations in access to crucial computing resources, with resource budgets often linked to demographic and socio-economic factors, exacerbating unfairness in participation. While heterogeneous federated learning methods allow healthcare institutions with varying computational capacities to collaborate, they fail to address the performance gap between resource-limited and resource-rich institutions. As a result, resource-limited institutions may receive suboptimal models, further reinforcing disparities in AI-driven healthcare outcomes. Here, we propose a resource-adaptive framework for collaborative learning that dynamically adjusts to varying computational capacities, ensuring fair participation. Our approach enhances model accuracy, safeguards patient privacy, and promotes equitable access to trustworthy and efficient AI-driven healthcare solutions.

Introduction

The increasing integration of AI algorithms in medicine and healthcare has raised significant ethical concerns, with privacy and fairness at the forefront^1,2,3,4. As these algorithms leverage vast amounts of sensitive patient data for training and inference, there is a heightened risk of privacy breaches and unauthorized access⁵. Safeguarding patient privacy becomes crucial to maintain trust in medicine and healthcare systems⁶. Additionally, concerns about fairness arise due to the potential biases in AI algorithms, especially when trained on datasets that may not be representative of diverse demographics^7,8. Biased algorithms can lead to unequal treatment and diagnostic inaccuracies, disproportionately affecting certain patient groups^9,10. Achieving a balance between the advantages of AI in medicine and healthcare and alleviating public concerns regarding ethical issues requires ongoing efforts to tackle privacy protection and biases in algorithmic decision-making. This underscores the ethical responsibility of stakeholders in the medicine and healthcare, as well as technology sectors.

Federated Learning (FL) has emerged as a groundbreaking collaborative learning approach to address the delicate balance between data sharing and privacy concerns^{11,12,13,14,15}. This innovative technique enables multiple institutions or devices to collaboratively train machine learning models without the need to centrally pool sensitive data. The practice of keeping data localized and conducting model updates on-site significantly reduces the risks associated with centralized data storage and processing. The decentralized nature of FL aligns seamlessly with stringent data protection regulations, such as the Health Insurance Portability and Accountability Act (HIPAA)¹⁶ in the United States or the General Data Protection Regulation (GDPR)¹⁷ in Europe. Moreover, FL serves as a promising approach to promoting algorithmic fairness in AI for medicine and healthcare. The decentralized training process of FL enables the inclusion of diverse datasets from various healthcare institutions and demographics, contributing to a more representative and equitable model. As the federated model learns from a broad spectrum of patient data without directly accessing individual records, the potential for bias is reduced, leading to fairer and more robust models^18,19,20.

However, despite its promise, FL faces critical challenges related to computational resource diversity, which introduces implicit fairness issues in participation. Healthcare institutions vary significantly in computational capabilities, with resource-constrained organizations such as hospitals in developing countries often lacking the infrastructure to handle the substantial demands of large-scale FL¹². In traditional model-homogeneous FL, where all clients train on the same large model, powerful clients benefit more because they can fully leverage their resources, while weaker clients are often excluded from participation due to their limited computational capacity. Conversely, when smaller models are used to accommodate weaker clients, the computational resources of stronger clients are underutilized, leading to a trade-off that undermines both fairness and efficiency. Even in heterogeneous FL methods, which aim to allow clients with varying resource levels to participate, significant performance disparities between strong and weak clients persist. Stronger clients typically achieve much higher model accuracy than weaker ones, creating a severe fairness issue that exacerbates existing healthcare inequalities. Addressing this problem is critical to ensuring that the benefits of FL are equitably distributed across healthcare providers with diverse resource capabilities.

We claim that, a fair and sustainable collaborative learning system should satisfy the following five key principles: 1) Equal Opportunity: All collaborators, irrespective of their resource strength, should have an equal opportunity to participate in the collaborative learning process. This includes equal opportunities for model updates and participation in communication. This helps avoid inequalities and biases between nodes, ensuring that each node’s voice is fully considered. 2) Fair Contribution: The FL system should encourage and accommodate contributions from all nodes. Even if nodes have different scales or types of data as well as computational resources, their contributions should be considered valuable. Technically, this might involve mechanisms to ensure that the contribution of each node influences the global model. 3) Shared Fruits: During the model training process, ensure that the learned global model is available to each node, and contributions from each node are equally reflected in the overall performance during the testing phase. This can be achieved by considering the impact of each node when aggregating the model. 4) Equal Model Test Accuracy: Emphasize that all nodes should have the same model test accuracy to prevent bias and unfairness resulting from unequal treatment. This may require the consideration of fairness metrics in the design of FL algorithms and incorporating these metrics during model evaluation and aggregation. 5) Sustainability: The system should be designed to be sustainable, ensuring that FL can continue in the face of dynamic changes in node participation, resource availability, and engagement levels. This might include smooth transition mechanisms when nodes dynamically join or leave and adaptive strategies for situations where node resources are insufficient.

From a technical perspective, the resource heterogeneity across different participating clients involves variations in processing power, memory and communication capabilities²¹. Ensuring effective coordination and resource allocation becomes intricate when dealing with such diversity. Despite this fact, traditional FL paradigms, such as FedAvg¹¹, adhere to the uniform model capacity assumption, where all participating clients share the same model architecture. In the era of large language models (LLM), training large models seems like an inevitable choice. A widely-adopted strategy to match this assumption is to employ a large-scale model as the uniform global model for collaborative training, which, however, results in the following challenges:

• Unfairness Issue. The utilization of a uniform large global model poses a significant barrier for clients with constrained computational resources, making their participation in collaborative training unfeasible. This exclusion is problematic as these clients may struggle to bear the costs associated with local training efforts. Resource budgets are often intertwined with the demographic and socio-economic status of the owners, exacerbating the issue of unfairness in terms of participation. The omission of such resource-constrained clients not only introduces training bias due to the absence of their data perspective but also exacerbates overall fairness concerns. Additionally, during the deployment phase, participating clients equipped with limited computational resources face challenges in accommodating large-scale models, further underscoring the need for a more resource-sensitive approach in the FL paradigm.

• Huge Communication Overhead. During the training phase, intensive communication between the server and participating clients occurs for exchanging local model updates across multiple rounds. The prohibitive cost of transmitting parameters, particularly with a large global model, emerges as a significant bottleneck in the training process²². This limitation not only hinders the participation of clients with weaker communication conditions in collaborative learning but also leads to substantial energy consumption, rendering the training procedure practically infeasible and environmentally unfriendly.

• Fragile Privacy Protection. The uniform model architecture introduces a vulnerability in terms of privacy protection. When coordinating model updates between the server and participating clients, a malicious server can exploit this uniformity to infer local data by analyzing stolen gradients–a threat commonly known as gradient inversion attack²³. This poses a considerable risk to the security and privacy preservation of FL.

The successful deployment of FL for medicine and healthcare in diverse computing resources hinges on overcoming these challenges to unlock the full potential of decentralized, privacy-preserving machine learning. A scheme that embodies fairness, communication-efficient characteristics, and enhanced privacy protection becomes essential for building a trustworthy and effective medicine and healthcare AI ecosystem that prioritizes patient well-being and confidentiality.

To address the heterogeneity of participating clients, it becomes imperative to develop an FL framework capable of accommodating a spectrum of diverse local models. Such a framework must exhibit adaptability to varying neural network complexities in accordance with computational resource budgets. However, this introduces a new challenge: How can knowledge be exchanged effectively across these heterogeneous local models to derive a unified global model? In the literature, some strategies tailored for heterogeneous FL have been explored, with notable works adopting either knowledge distillation-based approaches^24,25,26,27 or network pruning-based techniques^28,29,30. Knowledge distillation allows edge clients to train diverse local models, which are subsequently distilled into a uniform global model for aggregation. However, a well-known limitation is the inability of knowledge distillation to losslessly transfer knowledge across diverse network structures, resulting in a loss of model accuracy³¹. On the other hand, pruning-based approaches modulate the size of Convolutional Neural Networks (CNNs) by adjusting the width or depth of networks, offering a means to adapt model capacity. Yet, disparities in behavior between sub-networks and complete networks can lead to a mismatch of feature spaces.

While knowledge distillation and network pruning are popular strategies, they suffer from limitations such as lossy knowledge transfer and feature space mismatch. Consequently, exploring an alternative approach to unlock the full potential of all clients becomes imperative. This paper introduces an effective approach to heterogeneous FL through a unified framework. Specifically, we propose the Dynamic Federated Learning (DynamicFL) framework, which ensures fair participation of all clients in collaborative learning, allowing them to work at full capacity and ensuring lossless knowledge transfer across diverse local models. The overall process is illustrated in Fig. 1. The motivation of our scheme involves a thoughtful examination of two pivotal issues: 1) designing a resource-adaptive network architecture for each client to harness their complete strength and 2) projecting heterogeneous local models into a uniform model architecture to streamline the aggregation operation. In response to these considerations, the key components of DynamicFL are tailored, encompassing heterogeneous local training and homogeneous global aggregation:

Fig. 1: The overall framework of DynamicFL.

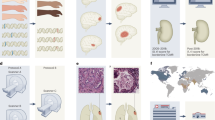
a, Healthcare institutions in developing and developed countries exhibit significant variations in accessing crucial computing resources, with resource budgets often linked to demographic and socio-economic factors, exacerbating unfairness in participation of collaborative learning for medicine and healthcare. b, The workflow of the proposed DynamicFL scheme. c, Fairness guaranteed collaboration: Comparison of test accuracy across clients with varying computational capabilities under different FL algorithms. Each column represents a distinct FL method, with the order of bars corresponding to the legend above for clarity. DynamicFL ensures consistent test accuracy across clients, fostering fairness in the distribution of training outcomes. d, Privacy guaranteed collaboration: DynamicFL can effectively counteract gradient inversion attacks, achieving enhanced privacy preservation capabilities, even in scenarios involving gradient leakage. Source data are provided as a Source Data file.

– Heterogeneous Local Training: Customizing the training approach for each client, DynamicFL dynamically expands local models to multi-branches based on the local computational resources, as shown in Fig. 1 (b). This expansion is achieved through re-parameterization, drawing capacity from the VGG-style plain global model. Each client operates on its modulated local model at full computational capacity, ensuring high accuracy in local training. A noteworthy distinction from conventional structural re-parameterization, such as those seen in^32,33, lies in our dynamic adjustment of computation workloads. This involves selecting operations with significant contributions to performance, striking a balance between training accuracy and efficiency.

– Homogeneous Global Aggregation: After local training, the heterogeneous local models undergo re-parameterization to transform back to the original global model structure. This ensures that all uploaded local models share the same structure, facilitating aggregation operations without incurring knowledge transfer overhead. The absence of intricate knowledge distillation on the server side streamlines the aggregation process, allowing for rapid execution.

Our proposed approach not only guarantees fair participation across diverse institutions, regardless of their computational strength, but also minimizes communication overhead. Furthermore, it strengthens the adherence to security and privacy standards, essential for building and sustaining trust in AI applications within the medicine and healthcare domain.

Results

In this section, we present extensive experimental results to illustrate the superiority of DynamicFL in terms of prediction accuracy, convergence speed, test accuracy variance (i.e., performance fairness among clients), and robustness to gradient attacks. We also demonstrate the advantage of DynamicFL as a plug-and-play module for enhancing the performance of existing methods.

Comparison Baselines

To evaluate the effectiveness of our proposed method, we compare it against several widely recognized and highly cited baselines spanning different categories of FL approaches. For knowledge distillation-based methods, we include DSFL²⁶, FedET²⁷, IncluFL³⁴, FedMD³⁵ and FedDF²⁵, which aim to achieve communication efficiency and model personalization through knowledge distillation. For network pruning-based methods, we evaluate HeteroFL²⁸, DepthFL³⁶, and FedRolex³⁷, which focus on adapting model complexity to clients’ heterogeneous resources. Furthermore, we extend the comparison to include three recently proposed methods, FCCL³⁸, pFedHR³⁹ and FedTGP⁴⁰, to benchmark our approach against the latest advancements in the field. It is worth noting that most of the original implementations of the compared methods did not include experiments on ViT, and many of them cannot be directly applied to ViT without significant modifications. Therefore, for the ViT-based experiments, we limit the baselines to knowledge distillation-based methods such as FedDF and FedMD, which can naturally scale to ViT.

Experiment Setup

Datasets

In our experiments, we conducted a thorough evaluation of DynamicFL’s performance using two well-known benchmark datasets, CIFAR-10 and CIFAR-100, as well as three specialized medical image datasets: CancerSlides^41,42, ChestXray^43,44, and BloodCell⁴⁵. Specifically, the CancerSlides dataset focuses on the prediction of survival outcomes in colorectal cancer, featuring 10,000 non-overlapping image patches extracted from hematoxylin & eosin-stained histological slides. Additionally, it includes a test set of 7180 patches sourced from a different clinical center. The ChestXray dataset consists of 3616 COVID-19 positive cases along with 10,192 normal, 6012 lung opacity (Non-COVID lung infection), and 1345 viral pneumonia images. Lastly, the BloodCell dataset comprises 17,092 images of single normal cells, collected from individuals without infection, hematologic or oncological diseases, and not under any pharmacological treatment at the time of blood draw. This dataset categorizes images into 8 distinct classes, facilitating a detailed analysis and classification. To align with the input requirements of different architectures, we resized all datasets to 32 × 32 for experiments involving convolutional neural networks (CNNs) and to 224 × 224 for transformer-based models.

Data & Clients Heterogeneity

To simulate statistical heterogeneity, we employ the Dirichlet distribution p_k ~ Dir_N(β) to construct Non-IID data partitions across clients. To simulate the heterogeneous device scenario, clients are categorized into three types—weak, medium, and strong clients. This classification is grounded on the capability of each client to run models of varying sizes.

Experimental Settings

For CNN models, the learning rate is set to 0.01, while for transformer models, the learning rate is set to 0.001. The batch size for all experiments is set to 16, except for ViT-1B, where the batch size is set to 3 due to the model’s large size. Unless otherwise specified, the number of clients in all experiments is 30, except for ViT-1B, which involves 9 clients. Our experiments are implemented using PyTorch and tested on various platforms, including several machines with 4 NVIDIA 3090 GPUs, several machines with 4 NVIDIA 4090 GPUs, and a machine with a single NVIDIA A100 GPU.

Evaluation Strategy

In our approach, we adapt the global model to more complex architectures, allowing for the accommodation of varying computational capabilities among the diverse clients participating in the FL process. Specifically, our global model is designed to be equivalent to the smallest local model, which corresponds to the weakest client. This strategy enables us to develop a lightweight neural network through FL. For a fair comparison, the knowledge distillation-based methods we compare against use the same local models as our method. However, their global model is the largest local model, corresponding to the strongest client. This distinction results in a significantly larger global model for the knowledge distillation-based methods compared to ours. The comparison with pruning-based methods presents a different challenge. Achieving identical local models as our method is difficult with pruning-based approaches. We align these methods’ global models with those used in the distillation-based methods, while employing pruned versions of these models as their local models. Consequently, both the knowledge distillation and pruning-based methods utilize a much larger global model than our approach. To evaluate the effectiveness of the compared FL methods, we focus on the accuracy of their global models on the test datasets.

Performance Evaluation Under Equal Wall-Clock Time

We evaluate the performance of DynamicFL compared to several baseline methods on three medical datasets (CancerSlides, ChestXray, and BloodCell) under the same wall-clock training time. The experiments are conducted under both IID and Non-IID data distributions, where Non-IID heterogeneity is introduced using a Dirichlet distribution Dir(β) with a concentration parameter β = 0.5. To simulate realistic heterogeneous environments, clients are divided into strong, medium, and weak categories in an equal ratio of 1:1:1. Each experiment is repeated five times to ensure statistical reliability, and results are reported as mean accuracy  ± standard deviation, with the best-performing results highlighted in bold.

As shown in Table 1, DynamicFL consistently outperforms all baseline methods across the three datasets under both IID and Non-IID settings. On the CancerSlides dataset, DynamicFL achieves an accuracy of 87.37% under IID settings, outperforming the strongest baseline FCCL by 5.54%, while under Non-IID settings, it achieves 80.26%, surpassing FCCL’s 74.65% by a significant margin. For the ChestXray dataset, DynamicFL achieves an accuracy of 87.92% under IID settings, which is 5.40% higher than FCCL’s 82.52%, and under Non-IID settings, it reaches 83.41%, significantly outperforming pFedHR’s 76.46% by 6.95%. On the BloodCell dataset, DynamicFL achieves an accuracy of 88.64% under IID settings, which is 5.91% higher than FedRolex’s 82.73%, and under Non-IID settings, it achieves 81.76%, outperforming FCCL’s 75.41% by 6.35%.

Table 1 Performance evaluation of DynamicFL on three medical datasets under the same wall-clock training time

These results demonstrate that DynamicFL is highly effective across datasets and consistently outperforms baseline methods in both IID and Non-IID scenarios. Its performance under Non-IID settings is particularly noteworthy, as it demonstrates superior robustness and adaptability to data heterogeneity, making it a strong solution for federated learning in realistic, heterogeneous environments.

Performance Evaluation Under Diverse Client Distributions

We conduct experiments with client distribution ratios: 7:2:1, 5:2:3, 4:1:5, 4:3:3, and 3:6:1. The results are summarized in Table 2, demonstrating that DynamicFL adapts effectively to diverse client distributions while maintaining superior performance and fairness across all configurations. In the most heterogeneous distribution (7:2:1), DynamicFL achieves 82.12% accuracy on ResNet-18, significantly surpassing the best baseline method (pFedHR, 74.45%) by 7.67%. In the balanced distribution (4:3:3), DynamicFL maintains its superiority with an accuracy of 83.45%, outperforming the best baseline (FCCL, 77.01%) by 6.44%. These results further underline the robustness of DynamicFL across varying levels of client heterogeneity, reinforcing its ability to adapt to real-world FL scenarios.

Table 2 Performance evaluation of DynamicFL and other methods on ResNet-18 and ViT-Base architectures

Performance Evaluation Across Diverse Network Architectures

Generalization on CNN Architectures

We systematically evaluate the performance of DynamicFL on different CNN network architectures, including LeNet-5, GoogLeNet, and ResNet-18, with ratios of 1:2:3. As shown in Table 3, DynamicFL consistently outperforms both distillation-based and pruning-based methods across these diverse network structures. For example, on the BloodCell dataset using LeNet-5, DynamicFL achieves an accuracy of 66.44%, surpassing the pruning-based method FedRolex (60.13%) and the distillation-based method (61.75%). This demonstrates the ability of DynamicFL to adapt to smaller network architectures while maintaining superior performance. Furthermore, by adopting a smaller network as the global model, our approach reduces communication costs compared to pruning-based methods, making it more practical for resource-constrained scenarios such as mobile devices.

Table 3 Performance evaluation of test accuracy (%) with different network structures

Generalization on Transformer Architectures

To further validate the scalability and generalizability of DynamicFL, we conduct experiments on transformer-based models, including ViT-Tiny, ViT-Small, ViT-Base, and ViT-1B, across two datasets: BloodCell and CancerSlides. These experiments are performed under both IID and non-IID settings, where non-IID heterogeneity is introduced using a Dirichlet distribution with a concentration parameter of 0.7. As summarized in Table 4, DynamicFL successfully scales across transformer architectures of varying sizes. Larger models, such as ViT-Base and ViT-1B, consistently outperform smaller models (ViT-Tiny and ViT-Small), particularly on clients with higher computational resources. For instance, on the BloodCell dataset under IID settings, ViT-1B achieves an accuracy of 94.77%, significantly outperforming ViT-Tiny, which achieves 73.11%. Even under non-IID settings, ViT-1B maintains a high accuracy of 91.26%, demonstrating its robustness in heterogeneous data distributions.

Table 4 Performance evaluation of transformer architecture

While our experiments demonstrate the scalability of DynamicFL across diverse architectures, we acknowledge that the absence of direct baseline comparisons for large-scale transformer models may introduce potential biases. Specifically, superior performance on smaller models does not necessarily guarantee the same level of improvement when scaling up to larger architectures. However, it is important to emphasize that our approach primarily focuses on lossless model transformation, enabling seamless collaboration among clients with varying computational resources. By minimizing accuracy degradation during global-to-local and local-to-global model transitions, DynamicFL ensures that knowledge transfer remains efficient and robust. Therefore, we believe that even for large-scale networks, our method can continue to deliver superior performance while maintaining fairness across heterogeneous clients.

Fairness Evaluation Among Clients of Varying Capacities

In this part, we conduct an analysis of test accuracy, i.e., the fairness among participating clients with respect to test accuracy. A fair and sustainable FL system should ensure that all nodes, regardless of their resource strength, have an equal opportunity to contribute their efforts to the collaborative learning process and share the fruits of FL equally, meaning they should achieve the same model test accuracy.To verify this point, we offer evaluation results in Fig. 2 (a), which show that DynamicFL consistently maintains identical test accuracy among strong, medium, and weak clients, while other methods show significant discrepancies in model accuracy between strong and weak clients. Taking the case of FedET as an example, the discernible discrepancy in accuracy, with a 6.31% superiority on strong clients, highlights the challenges faced by conventional approaches in mitigating the performance gap between different-sized clients. The implications of these findings are paramount in scenarios where weak clients significantly outperform their stronger counterparts, underscoring the need for methods such as DynamicFL to ensure fairness in FL applications. The equitable performance demonstrated by DynamicFL underscores its potential to address the pervasive challenges associated with model heterogeneity and provides a promising avenue for promoting fairness across diverse client profiles.

Fig. 2: Fairness & convergence evaluation.

a, Test accuracy of heterogeneous models obtained by three types of clients with different computational power on the same global test set. b, Convergence analysis of DynamicFL and other baselines on CancerSlides and BloodCell. c, Pie chart illustrating the proportions of strong, medium, and weak clients under different client distributions in the experiments. Source data are provided as a Source Data file.

Robustness Analysis Across Varying Non-IID Scenarios

To evaluate the robustness of DynamicFL under varying degrees of data heterogeneity, we conduct experiments using different values of the Dirichlet parameter β, including 0.1, 0.3, 0.5, 0.7, and 0.9. These values represent different levels of data distribution imbalance, where smaller β values correspond to more severe Non-IID scenarios, and larger β values approximate IID distributions. The experimental results, presented in Table 5, demonstrate that DynamicFL consistently outperforms all baseline methods across all Non-IID degrees and model architectures.

Table 5 Performance evaluation of DynamicFL and other methods on ResNet and ViT-Base architectures under the same wall-clock training time

DynamicFL achieves the highest accuracy in every scenario, with the performance gap being more pronounced in highly heterogeneous settings (e.g., β = 0.1 and β = 0.3). For instance, on the ResNet-18 architecture, DynamicFL surpasses the best baseline method by 1.73% under β = 0.5 and by 2.49% under β = 0.1. Similarly, on the ViT-Base architecture, DynamicFL achieves a remarkable improvement of 2.56% under β = 0.5 and 4.31% under β = 0.1. While the performance of all methods improves as the data distribution becomes closer to IID (i.e., larger β values), DynamicFL maintains a clear advantage over the baselines, demonstrating its adaptability to both IID and Non-IID scenarios.

These results highlight the robustness and generalizability of DynamicFL in FL environments with diverse levels of data heterogeneity. Its consistent performance across different β values confirms its ability to effectively address the challenges posed by Non-IID data distributions in real-world FL systems.

Scalability Evaluation with Increased Number of Clients

To evaluate the scalability of DynamicFL, we conduct experiments with 60, 120, and 180 clients on the BloodCell and CancerSlides datasets under both IID and non-IID settings. The results in Table 6 show that DynamicFL consistently outperforms baseline methods across all tested scenarios, demonstrating its robustness and scalability. As the number of clients increases, the overall accuracy of all methods decreases due to growing data heterogeneity, but DynamicFL maintains a significant performance advantage. For example, on the BloodCell dataset with 180 clients, DynamicFL achieves 72.69% accuracy with ResNet-18, outperforming the best baseline methods by 3.24%–8.91%, while on the CancerSlides dataset, it achieves 76.59% accuracy, maintaining a strong lead. DynamicFL also performs effectively across different model architectures, such as ResNet-18 and ViT-Base, with ViT-Base achieving 75.39% accuracy on the BloodCell dataset with 180 clients, significantly outperforming the 68.34% achieved by the best baseline method. These results confirm that DynamicFL scales effectively to larger numbers of clients while maintaining fairness and robustness, making it suitable for real-world FL applications.

Table 6 Performance evaluation of DynamicFL and other methods with more clients

Convergence Speed Evaluation

In Section Convergence Analysis, we present the theoretical convergence analysis of DynamicFL, indicating that DynamicFL shares the same convergence rate as the vanilla FedAvg. To further elaborate, we provide a comparison of the convergence speeds of the compared methods in Fig. 2 (b). The visualization underscores the superior convergence speed and stability exhibited by our method during the initial training phase when compared to existing approaches. This advantage arises from the intricacies inherent in model-heterogeneous FL, where knowledge transfer between two heterogeneous models occurs twice-first during aggregation and then during broadcasting. Specifically, in distillation and pruning based methods, knowledge transfer between local models of different clients has a profound impact on accuracy, leading to significant fluctuations in the accuracy of the global model during training for both approaches. In contrast, our method, thanks to the lossless knowledge transfer capabilities across heterogeneous models, demonstrates minimal accuracy fluctuations in the early stages of training. Furthermore, compared to distillation and pruning based methods, our approach exhibits swifter convergence and achieves a higher final accuracy.

Evaluation on the Ability of Enhanced Privacy Protection

In this subsection, we assess our method’s performance in terms of enhanced privacy protection. Originally, FL was predicated on the belief that sharing gradients, as opposed to raw data, would not substantially endanger client privacy. Nonetheless, recent studies^46,47 have unveiled the potential for a “gradient inversion attack". In this type of attack, an adversary monitoring a client’s communication with the server can start piecing together the client’s confidential data. This attacker could be a malicious entity within the FL protocols. This includes a server that is honest-but-curious and aims to reconstruct the private data of its clients, or a client with similar intentions, seeking to gather private information about other clients. Most current FL methodologies, including the commonly used vanilla FedAvg, operate under a uniform model capacity assumption, utilizing identical network architectures for both local and global models. This approach, however, is susceptible to gradient inversion attacks. Our method, by contrast, shows resilience against such attacks, thanks to the combination of heterogeneous local training and homogeneous global aggregation.

We follow the methodology presented in⁴⁶, replicating their experimental setup. This involves setting the local batch size to one and uploading the updates of a single batch gradient to the central server. The results of our experiments, as depicted in Fig. 3, provide insightful observations. It can be observed that the vanilla FedAvg method offers minimal protection against privacy breaches, with private data being almost entirely reconstructible from gradients. In contrast, our approach is designed to keep the central server in the dark regarding the intricate details of local models. This strategic design effectively hinders the reconstruction of local training data, thereby significantly bolstering the privacy of edge devices. This distinctive attribute of our method showcases its strength and efficiency in safeguarding against gradient inversion attacks within the realm of FL.

Fig. 3: Privacy evaluation.

The existing model-heterogeneous FL methods and Vanilla FedAvg are deficient in their defense against gradient inversion attacks. This shortcoming exposes a significant vulnerability: a malicious central server can easily exploit the received gradient information to reconstruct clients' private data, thereby posing a substantial privacy risk. These methods resort to implementing established encryption techniques within FL, but this approach often leads to reduced system efficiency and accuracy loss. DynamicFL, on the other hand, offers a more effective and robust solution. In the DynamicFL framework, the central server remains unaware of the specific private models employed by individual clients. This lack of information severely restricts the server’s capability to reconstruct semantic information, significantly reducing the potential for privacy breaches and thus bolstering the protection of client data. Source data are provided as a Source Data file.

Discussion

Advantages of Our Scheme

From a multi-objective optimization standpoint, the objective behind designing FL algorithms is to navigate the Pareto front within the model utility—data privacy—system efficiency space. Some studies, such as⁴⁸, posit the absence of a free lunch when addressing the three objectives in FL, suggesting that optimizing one objective may result in a decline in others. Our method challenges this claim, which achieves fair client participation, superior model utility, enhanced data privacy, and improved system efficiency simultaneously. The detailed discussion is offered as follows:

• Fair Clients Participation: DynamicFL ensures fair treatment for all clients, regardless of their computational strength, actively involving them in the learning process at their full operational capability. Unlike knowledge distillation based and network pruning based approaches, DynamicFL fully transfers global model knowledge even to resource-constrained clients, without the consumption seen in other methods. In our approach, every client contributes meaningfully, fostering sustainability in the FL ecosystem.

• Superior Model Accuracy: Attributing to that all clients work at full capacity and knowledge is losslessly transferred across heterogeneous models, our method achieves superior test accuracy. As demonstrated by experimental results, DynamicFL achieves much better performance than the state-of-the-art knowledge distillation based and network pruning based heterogeneous FL methods.

• Enhanced Privacy Protection: DynamicFL enjoys a side benefit of enhanced privacy preservation. Due to the dynamic construction of local models, the server remains unaware of the actual network structures, rendering gradient inversion attacks ineffective. Experimental results (see Fig. 3) underscore the effectiveness of this model-gradients separation mechanism in mitigating data leakage risks. Notably, compared with other privacy-preserving enhancement strategies like homomorphic encryption⁴⁹ and perturbation techniques^50,51, our strategy seamlessly integrates into the entire learning process without introducing additional computational burdens or performance degradation.

• Improved System Efficiency: In DynamicFL, the process of structural re-parameterization introduces additional computation costs as a trade-off, seemingly impacting system efficiency. However, the introduction of a lightweight global model mitigates this effect by reducing communication overhead. The experimental results (see Table 3) indicate that, within the same training time budget, our lightweight model outperforms state-of-the-art methods employing larger global models. Moreover, the theoretical convergence analysis provided in Convergence Analysis shows that DynamicFL achieves the same convergence performance with FedAvg, and empirical results (see Fig. 2 (b)) suggest that our method achieves swifter convergence compared with the state-of-the-art baselines.

Future Challenges and Outlook

While DynamicFL effectively enhances fairness in federated learning, real-world deployment presents additional challenges. One key issue is communication synchronization among participating healthcare institutions. Existing research has yet to explore asynchronous model-heterogeneous federated learning, meaning that all participating institutions must maintain synchronized communication during training. Additionally, frequent transmission of model parameters in federated learning imposes significant communication overhead, which could further strain network resources. Future work could explore adaptive scheduling mechanisms to mitigate communication overhead, ensuring more efficient federated learning in real-world deployments.

Methods

Ethical Statement

Our study utilizes publicly available datasets to conduct federated learning for collaborative training across clients with varying computational resources. As no human participants, personal data, or ethical concerns are involved, this research does not require ethical approval.

Overall Workflow

In this subsection, we elaborate the methodology of DynamicFL. We consider FL across N heterogeneous edge clients with diverse computational capabilities. Each client i can only access its own private dataset ${{{{\mathcal{D}}}}}_{i}=\{({{{{\bf{x}}}}}_{j}^{i},{y}_{j}^{i})\}$ where x and y denote the input features and corresponding class labels, respectively. The overall algorithmic workflow is summarized in 1 In the following, we elaborate the main steps of DynamicFL:

Initialization

Define the global model as the convolutional neural network, which is still widely used in real-world applications due to the advantage of parallel computing and lightweight memory footprint. The server initializes the model parameters and hyper-parameters and distributes the global model to all clients. In the first round, once the global model is received, the client i expands the K × K convolution layers to diverse branches adopted in DBB³² from bottom to top according to their computational resources:

$${\zeta }_{i}^{(0)}\leftarrow {{{\rm{REP}}}}({\omega }_{g}^{(0)}).$$

(1)

The stronger the client, the more layers it can expand. Upon the derived local model ${\zeta }_{i}^{(0)}$, we perform local training for E epochs:

$${\zeta }_{i}^{(0)} \leftarrow {\zeta }_{i}^{(0)}-\eta \nabla \ell ({\zeta }_{i}^{(0)};{{{{\mathcal{D}}}}}_{i}),\\ {S}_{i}^{l} \leftarrow \nabla \ell ({\zeta }_{i}^{(0)};{{{{\mathcal{D}}}}}_{i}).$$

(2)

We record the gradient of the last epoch as ${S}_{i}^{l}$, which reflects the sensitivity of each branch of the local model to local knowledge. The local model is then transformed back to the original plain structure and uploaded to the server. Since all uploaded local models have the same structure as the global model, we can perform the aggregation operation to derive the updated global model ${\omega }_{g}^{(0)}$.

Heterogeneous Local Training

The new global model is distributed to local clients, upon which the next round of local training is conducted. Considering local clients have diverse and limited computational resources, we dynamically adjust computational workloads by selecting operations that significantly contribute to performance, instead of re-parameterizing all candidate operations as done in DBB. The resource-adaptive models modulation is tailored according the local and global gradient information of FL. Specifically, in the t-th round, relying on the new global model ${\omega }_{g}^{(t-1)}$ and the stale local model ${\zeta }_{i}^{(t-1)}$ in the last round, we conduct structural re-parameterization to derive a temporary local model ${\epsilon }_{i}^{(t)}$ that has the same output as ${\omega }_{g}^{(t-1)}$ while with the same structure as ${\zeta }_{i}^{(t-1)}$:

$${\epsilon }_{i}^{(t)}\leftarrow {{{\rm{REP}}}}({\omega }_{g}^{(t-1)},{\zeta }_{i}^{(t-1)}),$$

(3)

where REP(⋅) represents the re-parameterization operation. We perform local training on ${\epsilon }_{i}^{(t)}$ along with the private dataset ${{{{\mathcal{D}}}}}_{i}$ for only one epoch, and obtain the gradient information ${S}_{i}^{g}$:

$${\epsilon }_{i}^{(t)} \leftarrow {\epsilon }_{i}^{(t)}-\eta \nabla \ell ({\epsilon }_{i}^{(t)};{{{{\mathcal{D}}}}}_{i}),\\ {S}_{i}^{g} \leftarrow \nabla \ell ({\epsilon }_{i}^{(t)};{{{{\mathcal{D}}}}}_{i}),$$

(4)

where ${S}_{i}^{g}$ reflects the sensitivity of each branch of the local model to the global knowledge, i.e., the aggregation result of all participants.

${S}_{i}^{g}$ and ${S}_{i}^{l}$ offer useful cues to reflect the contribution of branches to the global aggregation. According to them, we dynamically evolve the network structures of the local model to remove redundant operations with little contribution while further expanding important operations with significant contribution, and obtain the new local model ${\zeta }_{i}^{(t)}$:

$${\zeta }_{i}^{(t)}\leftarrow {{{\rm{DYMM}}}}({\epsilon }_{i}^{(t)};{S}_{i}^{g},{S}_{i}^{l}).$$

(5)

The details of DYMM(⋅) for how to use ${S}_{i}^{g},{S}_{i}^{l}$ to perform dynamic model modulation can be found in Section Dynamic Model Modulation.

Client i then performs local training along with its private data on the new local model ${\zeta }_{i}^{(t)}$ with full operational capability:

$${\zeta }_{i}^{(t)}\leftarrow {\zeta }_{i}^{(t)}-\eta \nabla \ell ({\zeta }_{i}^{(t)};{{{{\mathcal{D}}}}}_{i}).$$

(6)

where the number of epochs executed is E − 1, since one epoch has already been done in Eq. (4). The gradient information of the last epoch is recorded as the updated ${S}_{i}^{l}$:

$${S}_{i}^{l}\leftarrow \nabla \ell ({\zeta }_{i}^{(t)};{{{{\mathcal{D}}}}}_{i}).$$

(7)

It is worth mentioning a possible scenario: in this round, client i may have a smaller computational budget than in the last round due to other active routines, which makes it unable to afford the local model from the previous round. In this case, the steps correspond to Eq. (3), (4) and (5) cannot be performed. Instead, we conduct re-parameterization based on ${S}_{i}^{l}$ only to derive the new model:

$${\zeta }_{i}^{(t)}\leftarrow {{{\rm{REP}}}}({\omega }_{g}^{(t-1)},{S}_{i}^{l}).$$

(8)

Then, local training on ${\zeta }_{i}^{(t)}$ is performed for E epochs, as shown in Eq. (6).

Homogeneous Global Aggregation

Once Client i completes the local training, the local model ${\zeta }_{i}^{(t)}$ is transformed back to the original global model structure by re-parameterization:

$${\omega }_{i}^{(t)}\leftarrow {{{\rm{REP}}}}({\zeta }_{i}^{(t)},{\omega }_{g}^{(t-1)}),$$

(9)

${\omega }_{i}^{(t)}$ has the same output as the local model ${\zeta }_{i}^{(t)}$ while with the same structure as the global model ${\omega }_{g}^{(t-1)}$. After the central server receives the uploaded ${\{{\omega }_{i}^{(t)}\}}_{i=1}^{N}$ from all clients, the global aggregation can be done since ${\{{\omega }_{i}^{(t)}\}}_{i=1}^{N}$ share the same network structure:

$${\omega }_{g}^{(t)}\leftarrow \frac{1}{N}\sum\limits_{\omega _i}^{(t)}.$$

(10)

The equivalent transformations of operations during re-parameterization ensure lossless knowledge transfer across heterogeneous local models. The central server then distributes the new global model ${\omega }_{g}^{(t)}$ to local clients to start the next round of local training.

Algorithm 1

Dynamic Federated Learning

Dynamic Model Modulation

In this subsection, we present the details of the DYMM( ⋅ ) operator to perform dynamic model modulation based on the local knowledge from the local private dataset and the global knowledge from the global aggregation.

We dynamically identify the important operations and redundant operations of local models according to the gradient information. Some works in the literature^52,53 have shown that the gradient of each weight of the model in the training process can effectively reflect the sensitivity of the weight to data. Inspired by works^54,55, we use the following metric to measure the salience of each weight:

$${{{\mathcal{S}}}}\left({\theta }_{i}\right)=\frac{\partial \ell }{\partial \theta }\left({\theta }_{i}\right),$$

(11)

where θ_i ∈ θ is the parameter of the model.

Local knowledge in FL is easy to obtain during local training. In the (t − 1)-th round, we record the last local epoch gradient information by Eq. (7) and (11):

$${S}_{i}^{l}({{{{\boldsymbol{\theta }}}}}^{k})=\sum \limits_{j}^{n}\frac{\partial \ell }{\partial {\theta }_{j}^{k}}\odot {\theta }_{j}^{k},$$

(12)

where θ^k is the k-th branch in the local model ${\zeta }_{i}^{(t-1)}$, and ${\theta }_{j}^{k}$ is the j-th parameter of the branch k. ${S}_{i}^{l}({{{{\boldsymbol{\theta }}}}}^{k})$ is leveraged for dynamic model modulation in the next round.

The global knowledge in FL is implicitly encoded into the global model, which is the aggregation result of all participating clients. To extract global information, according to the received global model ${\omega }_{g}^{(t-1)}$ in the t-th round and the last round local model ${\zeta }_{i}^{(t-1)}$, re-parameterization is conducted to get the temporary model ${\epsilon }_{i}^{t}$ through Eq. (3). Here ${\epsilon }_{i}^{t}$ is a re-parameterized model of ${\omega }_{g}^{(t-1)}$, which has the same structure as ${\zeta }_{i}^{(t-1)}$. We use ${\epsilon }_{i}^{t}$ to perform one-epoch local training with the private dataset, from which the derived gradient information reflects the sensitivity of the branches in the local model ${\zeta }_{i}^{(t-1)}$ to the global information:

$${S}_{i}^{g}({{{\psi }}}^{k})=\sum \limits_{j}^{n}\frac{\partial \ell }{\partial {\psi }_{j}^{k}}\odot {\psi }_{j}^{k},$$

(13)

where ψ^k is the k-th branch in the local model ${\epsilon }_{i}^{(t)}$, and ${\psi }_{j}^{k}$ is the j-th parameter of branch k.

We regard branches with small ${S}_{i}^{l}$ and ${S}_{i}^{g}$ as redundant ones; the branches with a small ${S}_{i}^{l}$ but large ${S}_{i}^{g}$ as important ones since they are sensitive to global knowledge; the rest branches as common ones. In Eq. (5), we first merge redundant branches into common branches to reduce the size of the local model:

$${{{\psi }}}^{\left({{\rm{common}}}{\prime} \right)}\leftarrow {{{\psi }}}^{({{\rm{common}}})}+{{{\psi }}}^{({{\rm{redundant}}})},$$

(14)

where ${{{\psi }}}^{\left({{\rm{common}}}{\prime} \right)}$ is the new common branch after merging; ψ^(common) and ψ^(redundant) represent common and redundant branches, respectively. Then we expand the important branches to adapt the client’s computing capabilities:

$${{{\psi }}}^{\left({{\rm{important}}}{\prime} \right)}\leftarrow {{{\psi }}}^{({{\rm{important}}})}-({{{\psi }}}^{(1)}+\cdots+{{{\psi }}}^{(n)}),$$

(15)

where ${{{\psi }}}^{\left({{\rm{important}}}{\prime} \right)}$ are the expanded parameters of the important branch. In order to ensure the same output, we need to subtract the parameters of the new branch ${\{{{{\psi }}}^{(i)}\}}_{i=1}^{n}$ from the parameters of the original important branch ψ^(important). The parameters of the new branch are generated randomly.

To ensure the stability and effectiveness of training, we adopt a fixed local reparameterization strategy for transformer-based models throughout the training process, unless computational resources change. Transformer architectures are particularly sensitive to parameter variations, and frequent changes to the reparameterization strategy may adversely affect their convergence and performance.

Lossless Knowledge Transfer

This section introduces the re-parameterization techniques for CNNs and transformers, demonstrating how these methods enable flexible structural transformations while preserving model outputs.

Re-parameterization for CNN

As indicated by works^55,56, the 2D convolutions hold the property of additivity:

$${{{\boldsymbol{I}}}} \circledast {{{{\boldsymbol{F}}}}}^{(1)}+{{{\boldsymbol{I}}}} \circledast {{{{\boldsymbol{F}}}}}^{(2)}={{{\boldsymbol{I}}}} \circledast \left({{{{\boldsymbol{F}}}}}^{(1)}+{{{{\boldsymbol{F}}}}}^{(2)}\right).$$

(16)

where I, F⁽¹⁾ and F⁽²⁾ are the input and kernels, respectively. The above equation is satisfied even with different kernel sizes. Some widely used operations in CNN —- average pooling and batch normalization —- can be converted into a convolution operation. The above additivity property ensures that a single convolution can be equivalently transformed to multi-branch operations, and vice versa. The equivalent transformations of operations guarantee lossless knowledge transfer, since the model outputs are not changed along with the network structure adjustment.

Re-parameterization for Transformer

The re-parameterization technique can also be adapted to transformer architectures. In the case of transformers, the linear layers hold the property of additivity, similar to the convolution operation in CNNs:

$${{{\boldsymbol{X}}}}\cdot {{{{\boldsymbol{W}}}}}^{(1)}+{{{\boldsymbol{X}}}}\cdot {{{{\boldsymbol{W}}}}}^{(2)}={{{\boldsymbol{X}}}}\cdot \left({{{{\boldsymbol{W}}}}}^{(1)}+{{{{\boldsymbol{W}}}}}^{(2)}\right),$$

(17)

where X is the input feature matrix, and W⁽¹⁾ and W⁽²⁾ are the weight matrices of two linear layers. This equation implies that multiple parallel linear layers can be equivalently merged into a single linear layer, or vice versa.

Moreover, operations commonly used in transformer architectures, such as layer normalization and residual connections, can also be transformed into equivalent forms compatible with the re-parameterization technique. Specifically, layer normalization can be expressed as an affine transformation, which can be absorbed into the parameters of linear layers. Residual connections, being additive in nature, align naturally with the additivity property of linear operations.

The re-parameterization process for transformers involves expanding a single linear layer into multiple parallel linear layers, optionally combined with normalization layers (e.g., batch normalization or layer normalization). These parallel branches can then be merged back into a single equivalent linear layer without loss of information. This guarantees lossless knowledge transfer, as the outputs of the model remain unchanged before and after the structural reconfiguration:

$${{{\boldsymbol{X}}}}\cdot {{{\boldsymbol{W}}}}\,{{\rm{merged}}}\,={{{\boldsymbol{X}}}}\cdot ({{{{\boldsymbol{W}}}}}^{(1)}+{{{{\boldsymbol{W}}}}}^{(2)}),$$

(18)

where Wmerged is the weight matrix of the merged linear layer.

It is worth noting that, according to Eq. (16) and (17), the re-parameterization process in DynamicFL ensures mathematical equivalence between the original and transformed model structures, guaranteeing that the input-output mapping remains unchanged. As a result, when evaluating the model on the same test set, its accuracy remains identical, thereby ensuring fairness in the models obtained by institutions with different computational resources.

Convergence Analysis

In this subsection, we present the convergence analysis of DynamicFL. We consider the following standard assumptions commonly made in FL analysis^57,58,59:

Assumption 1

(L-smoothness and σ-uniformly bounded gradient variance).

(a) F is L-smooth, i.e., $F(u)\le F(x)+\left\langle \nabla F(x),u-x\right\rangle+\frac{1}{2}L{\left\Vert u-x\right\Vert }^{2}$ for any $u,x\in {{\mathbb{R}}}^{d}$.

(b) There exists a constant G_max > 0 such that: ${\mathbb{E}}[| | \nabla {F}^{(i)}(x)| {| }^{2}]\le {G}_{max}^{2},\quad \forall i\in [N],\forall {{{\bf{x}}}}\in {{\mathbb{R}}}^{d}$, where ∇ F⁽ⁱ⁾(x) is an unbiased stochastic gradient of f⁽ⁱ⁾ at x.

(c) ∇ f(x) has σ² -bounded variance, i.e., ${{\mathbb{E}}}_{\xi \sim {{{{\mathcal{S}}}}}_{i}}\Vert \nabla {F}_{i}({{{\bf{x}}}})-\nabla {f}_{i}({{{\bf{x}}}})\Vert \le {\sigma }^{2},\quad \forall i\in [N],\forall {{{\bf{x}}}}\in {{\mathbb{R}}}^{d}.$

Lemma 2

For any reparameterization of a convolutional layer l that can be represented as a summation of N convolutional branches with weights ${W}_{l,n}^{(t)}$ and binary receptive field mask M_l,n, for n = 1, …, N, its gradient descent update can be respresented as:

$${W}_{l}^{(t+1)}\Leftarrow {W}_{l}^{(t)}-{\lambda }^{(t)}f\left({{{{\mathcal{G}}}}}_{l}\odot \frac{\partial {{{\mathcal{L}}}}}{\partial {W}_{l}^{(t)}},{W}_{l}^{(t)},\ldots,{{{{\mathcal{G}}}}}_{l}\odot \frac{\partial {{{\mathcal{L}}}}}{\partial {W}_{l}^{(0)}},{W}_{l}^{(0)}\right),$$

(19)

where ${{{{\mathcal{G}}}}}_{l}={\sum }_{n=1}^{N}{M}_{l,n}$. Therefore, it can be seen as spatial gradient scaling applied to the original convolution. Here we assume ${{{{\mathcal{G}}}}}_{l}\le {{{\mathcal{G}}}}$. In FL, it can be expressed that for the local model ${\zeta }_{i,k}^{(t)}$ on edge client i,:

$${\zeta }_{i,k+1}^{(t)}\leftarrow {\zeta }_{i,k}^{(t)}-\eta \nabla \ell ({\zeta }_{i}^{(t+1)};{{{{\mathcal{D}}}}}_{i}).$$

(20)

Here, we note that the variable k denotes the current local epoch, and each client’s structure of ${\zeta }_{i,k}^{(t)}$ may differ from one another. We can reparameterize ${\zeta }_{i,k}^{(t)}$ as ${\phi }_{i}^{(t)}$ with the same structure as the global model. Specifically, we have:

$${\phi }_{i,k+1}^{(t)}\leftarrow {\phi }_{i,k}^{(t)}-{{{{\mathcal{G}}}}}_{i}^{(t)}\odot \eta \nabla \ell ({\phi }_{i}^{(t+1)};{{{{\mathcal{D}}}}}_{i}).$$

(21)

This reparameterization ensures that the structure of ϕ^(t)i is consistent across all clients, matching that of the global model. As a result, we can aggregate the virtual sequences on each client to obtain the global model ω^(g)t, which satisfies:

$${\mathbb{E}}\left[{\left\Vert {\phi }_{i,k}^{(t)}-{\omega }_{t}^{(g)}\right\Vert }^{2}\right]\le 4{\eta }^{2}{K}^{2}{{{{\mathcal{G}}}}}^{2}{G}^{2}\quad \forall t,k,i.$$

(22)

Theorem 3

The sequence generated by our method with stepsize  η ≤ 1L satisfies

$$\frac{1}{T}{\sum }_{t=1}^{T}{\mathbb{E}}\left[{\left\Vert \nabla f\left({w}_{t}^{(g)}\right)\right\Vert }^{2}\right]\le \frac{2}{\eta T}\left({\mathbb{E}}\left[f\left({w}_{1}^{(g)}\right)\right]-\right.\\ \left.f\left({w}_{T}^{(g)}\right)\right)+4{\eta }^{2}{{{{\mathcal{G}}}}}^{2}{L}^{2}{G}^{2}{K}^{2}+\frac{L}{N}\eta {\sigma }^{2}.$$

(23)

Corollary 4

When the function f is lower bounded with $f({w}_{1}^{(g)})-{f}^{*}\le \Delta$ and the number rounds T is large enough, then set the stepsize $\eta=\frac{\sqrt{N}}{L\sqrt{T}}$ yields

$$\frac{1}{TK}\sum _{t=1}^{T}\sum \limits_{k=1}^{K}{\mathbb{E}}\left[{\left\Vert \nabla f\left({w}_{t}^{(g)}\right)\right\Vert }^{2}\right]=O\left(\frac{2L\Delta+{\sigma }^{2}}{\sqrt{NT}}+\frac{N}{T}\right).$$

(24)

The dominance of the first term in our algorithm ensures that it shares the same convergence speed, $O(1/\sqrt{NT})$, as the vanilla FedAvg.

Statistics & Reproducibility

This study is based on a publicly available dataset. No statistical method was used to predetermine sample size. No data were excluded from the analyses. Since the dataset is pre-collected and publicly available, no randomization or blinding was applicable. The machine learning models were trained using standard procedures, and all experiments were conducted with fixed hyperparameters unless otherwise specified.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.