Introduction

The human brain constitutes a highly intricate network of interconnected regions that maintain ongoing communication, even during periods of rest1. Research employing functional magnetic resonance imaging (fMRI) has shown how distant brain regions exhibit synchronized fluctuations (functional connectivity) in their spontaneous activity, giving rise to distinct spatial patterns of temporal covariances known as resting-state networks (RSNs)2,3,4. The topographic organization of the seven canonical RSNs (visual, somatomotor, dorsal attention, anterior salience, limbic, frontoparietal, default mode networks5) has now been extensively replicated and validated across multiple species6,7,8 and data modalities9,10,11.

Given the significance of RSNs across cognitive and clinical domains, a question of central importance for contemporary neuroscience research is how these networks emerge from their anatomical and physiological underpinnings. Significant progress has been made on the anatomical underpinnings following the discovery that the seven canonical RSNs adhere to a distinctive spatial layout12 on both cortical and subcortical structures13,14. This layout encodes a hierarchical distinction15 between low-order networks (visual, somatomotor) associated with fundamental sensory/motor functions, and high(er)-order networks (limbic, frontoparietal, dorsal attention, ventral attention, default mode) associated with introspection, self-referential contemplation, and intricate cognitive processes12,16. However, gaps remain in our understanding of functional brain organization, particularly in the temporal dynamics (i.e., the time-varying activity patterns) and neurophysiology (i.e., the underlying cellular and circuit mechanisms) of RSNs17,18,19. A more comprehensive characterization of these systems can be expected to enhance brain stimulation techniques by improving targeting of network interactions, identifying biomarkers for treatment response, and enabling the development of personalized neuromodulation therapies20. This expectation is supported by evidence that targeting specific RSNs improves therapeutic outcomes and that network-level measures can predict individual responses to stimulation21,22. The cortical hierarchy of RSNs follows a principal gradient of organization, transitioning from unimodal (low-order) sensorimotor regions to transmodal (high-order) regions12. This gradient reflects fundamental differences in both structure and function: low-order networks primarily process specific sensory or motor information through local circuits, while high-order networks integrate information across multiple domains through distributed connections23. Recent evidence has revealed that this hierarchical organization is reflected in the cellular composition of these networks, with distinct cell-type distributions characterizing different positions along the functional gradient24. Our central research question focuses on whether low-order and high-order RSNs exhibit different information processing characteristics. We examine this through the networks’ stimulation-evoked responses, which capture how activity propagates through the network following external perturbation. While this measure represents a simplified indicator of network function, it provides key insights into how these networks process information and how these differences relate to network dynamics. This question is critical for understanding how brain function emerges across multiple spatial and temporal scales25,26. Specifically, we aim to understand how neural activity that is organized both in space (across distributed brain regions) and time (showing coordinated temporal patterns), which we conceptualize as coordinated RSN behavior, emerges from interactions between underlying micro-/meso-scale circuit mechanisms and the macroscale network structure of the anatomical connectome. It is widely believed, due mainly to analogies with task-activation studies, that each RSN plays a key role in one or more distinct neurocognitive processes27,28,29. These distinct functional roles necessarily require different types of neural computations—for instance, the processing of sensory information in primary sensory networks differs fundamentally from the integration of multiple information streams in higher-order networks15. Such functional specialization suggests that these networks may have evolved different local circuit properties and processing architectures to support their specific computational demands23,30. This architectural specialization may be expected to manifest in how these networks process and respond to incoming inputs, including external stimulation. Supporting this view, the fact that all brain regions have widespread long-range connections not restricted to adjacent regions within the same or neighboring hierarchical levels31,32, suggests that the RSNs should differ systematically in how they respond to their inputs.

A compelling modus operandi to causally study principles of brain organization is the perturbational approach, which combines precisely targeted neurostimulation with neuroimaging techniques. Interleaved TMS-fMRI has demonstrated significant activation changes within the targeted network33,34, emphasizing its utility in tracking large-scale network connectivity. Concurrent TMS-fMRI and TMS-PET studies have provided valuable insights into effective connectivity across extended brain networks by stimulating specific regions and mapping subsequent activity propagation, particularly within cortico–subcortical circuits35,36,37,38. However, TMS-fMRI lacks the temporal precision necessary to capture the rapid neural communication occurring within and between interconnected networks. Coupling neurostimulation with fast (electrophysiological) neural activity recordings39 overcomes this limitation, offering superior temporal resolution and providing a complementary view of the brain’s rapid dynamic responses to targeted stimulation (Fig. 1A).

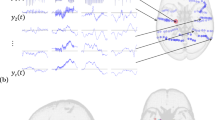
Fig. 1: Studying Resting-State Network (RSN) input processing strategies and the role of recurrent feedback with computational brain network models.
figure 1

Shown here is a schematic of the hypotheses, methodology, and general conceptual framework of the present work. A Intracerebral electrical stimulation (iES) applied to an intracortical target region generates an early (~20-30 ms) response (evoked-related potential (ERP) waveform component) at high-density scalp electroencephalography (hd-EEG) channels sensitive to that region and its immediate neighbors (red arrows). This also appears in more distal connected regions after a short delay due to axonal conduction and polysynaptic transmission. Subsequent second (~60–80 ms) and third (~140–200 ms) late evoked components are frequently observed (blue arrows). After identifying the stimulated network in this way, we aim to determine the extent to which this second component relies on intrinsic network activity versus recurrent whole-brain feedback. B Schematic of the hierarchical spatial layout of canonical RSNs as demonstrated in Margulies and colleagues12, spanning low-order networks showing greater functional segregation to high-order networks showing greater functional integration15. Networks are distributed based on their position along the first principal gradient. The stimulation sites are distributed across different levels of this gradient. C Schematic of virtual dissection methodology and key hypotheses tested. We first fit personalized connectome-based computational models of iES-evoked responses to the hd-EEG time series, for each patient and stimulation location. Then, precisely timed communication interruptions (virtual dissections) were introduced to the fitted models, and the resulting changes in the iES-evoked propagation pattern were evaluated. We hypothesized that lesioning would lead to activity suppression (C, right side) in high-order but not low-order networks.

Full size image

Recent studies employing this approach with concurrent transcranial magnetic stimulation and electroencephalography (TMS-EEG) have reported that stimulation-evoked responses exhibit a distinctive pattern of activity propagation, predominantly spreading to distal regions that are both structurally and functionally connected to the target site40,41,42. Importantly, these studies also demonstrate that stimulus-evoked activity preferentially propagates to, and exhibits sustained activity within, distal parts of the same (distributed, discontiguous) RSN that was used for the initial TMS targeting. Moreover, different networks can show distinct influences over brain dynamics, with evidence that the default mode network plays a unique role in organizing resting-state activity through its pronounced effects on alpha rhythm modulation43. In related work using intracerebral electrical stimulation (iES) in patients undergoing brain surgery, Veit and colleagues observed faster activation and spreading to regions within the stimulated RSN than those within non-stimulated RSNs44. Recent research has further bridged the gap between invasive and noninvasive techniques, showing that EEG responses to iES can reproduce features of TMS-EEG45, and that TMS induces specific downstream effects in regions functionally connected to the stimulation site46. While these studies established the network-specific nature of stimulation propagation, they did not examine how these responses might systematically vary based on the hierarchical position of networks along the cortical gradient.

In this study, we aim to explore how the interactions within and between different RSNs contribute to their modular and hierarchical organization, corresponding to their distance along the principal gradient12, which distinguishes between low-order and high-order networks (Fig. 1B). Are there qualitative differences between low-order and high-order RSNs in terms of their response to external stimulation? What is the level of cross-talk across RSNs in their stimulation responses? How necessary are these network-network interactions in determining a local brain response?

To address these questions, we analyzed brain activity patterns using simultaneous recordings of stereotactic electroencephalography (sEEG) and scalp high-density electroencephalographic (hd-EEG) data from patients undergoing presurgical iES. Evoked potentials elicited by iES provide high functional specificity47, signal fidelity48, and excellent spatial and temporal resolution49,50,51. These attributes make it ideal for studying the dynamics of brain networks and their hierarchical structures, as well as for examining how different regions respond to targeted perturbations. We then employed a whole-brain, connectome-based neurophysiological model for mechanistically investigating the level of recurrence in cortical networks. While standard analysis of noninvasive neuroimaging data can offer valuable insights into neural processes in the human brain, systematic brain stimulation techniques manipulate neuronal activity in a temporally and spatially specific manner, making them central tools for studying cause-effect relationships between neuronal activity and cognitive processes52,53. Mathematical modeling54,55 can complement these empirical methods by delving deeper into the underlying mechanisms of observed phenomena, offering insights into processes that are challenging to measure in-vivo in humans56,57. Connectome-based whole-brain modeling57 has been already utilized to both simulate the dynamics of RSNs58 and to investigate the effects of brain stimulation on neural activity patterns across different brain regions56,59,60. For example, Spiegler et al. explored how different stimulation sites impact the spatiotemporal propagation patterns in the mouse brain, demonstrating that spatial proximity does not necessarily predict induced activity similarity61.

This study uses our recent deep learning-based whole-brain modeling approach62, combining novel analytical techniques with subject-specific mathematical models of brain stimulation. Using combined iES and simultaneous recordings of sEEG and scalp hd-EEG, we mapped the response properties of seven canonical RSNs across 323 stimulation sessions from 36 patients. By fitting connectome-based neurophysiological models to each patient’s hd-EEG data, we replicated the observed response patterns accurately. In addition, we performed spatially specific “virtual dissections” on the models, isolating the stimulated network from surrounding activity while preserving its ability to propagate and receive information internally. Our main question was whether low-order and high-order RSNs show distinct patterns of information processing across their hierarchical organization. As shown in Fig. 1C, we hypothesized that activity patterns in the high-order networks would show a more integrated and cohesive level of organization63, where feedback connections are necessary to generate the observed iES responses. Conversely, low-order networks would show more segregated and localized behavior in their evoked activity dynamics64, with iES stimulation responses that are primarily dependent on intrinsic within-network activity- and thus relatively unchanged following virtual dissections. These network-specific differences in response to virtual dissections highlight the varying degrees of dependence on recurrent feedback across the cortical hierarchy. Understanding how recurrent feedback shapes RSN information flow enhances our ability to design more effective diagnostic and therapeutic strategies in psychiatry and neurology, particularly in optimizing brain stimulation protocols. This recurrent feedback represents the continuous and dynamic exchange of information between brain regions, where signals are sent back to the originating regions after being processed by other parts of the network, and it is crucial for maintaining and modulating the hierarchical structure of RSNs from high-order to low-order networks.

Results

A gradient of excitability from low-order to high-order brain networks

We evaluated the magnitude of stimulation-evoked global brain activation in concurrent hd-EEG and sEEG recordings as an index of neuronal excitability across the seven canonical RSNs (Visual network: VN, Somatomotor network: SMN, Dorsal attention network: DAN, Anterior salience network: SN, Limbic network: LN, Frontoparietal network: FPN, Default mode network: DMN). The assessment of which RSN each sEEG electrode stimulation site fell within demonstrated a high spatial resolution as indicated by an average distance of 0.52 cm ± 0.22 cm to the nearest parcel centroid (Fig. 2A). When examining the hd-EEG global mean field power (GMFP), we observed three response clusters at ~40 ms, ~80 ms, and ~370 ms (Fig. 2B). These peak response timings are consistent with results previously reported from invasive human electrophysiology recordings44. We observed a significant interaction between response timing and stimulated network (Fig. 2C, top row; (F(12, 927) = 2.539, P = 0.00266), indicating that the effect of stimulation on the overall response varied depending on both the timing at which the response was recorded and the network that was stimulated. This significant interaction was supported by significant main effects of both response timing (F(2, 927) = 93.792, P < 2e-16) and stimulated network (F(6, 927) = 3.641, P = 0.00141). For the first response cluster (0–37 ms), permuted Wilcoxon–Mann–Whitney U pairwise comparisons showed significant differences in AUC for the following network pairs: DAN-VN: W = 15881, P = 0.0003; SN-VN: W = 18156, P < 0.0001; SN-SMN: W = 20265, P < 0.0001; FPN-VN: W = 26141, P < 0.0001; FPN-SMN: W = 22234.5, P < 0.0001; DMN-VN: W = 27125, P < 0.0001; DMN-SMN: W = 25239.5, P < 0.0001. The comparison between LN-VN (W = 7083, P = 0.034) was not significant after adjustment for multiple comparisons. For the second response cluster (37–78 ms), no significant differences were observed across any network pairs (all P > 0.05). For the third response cluster (78–373 ms), significant differences in AUC were found for the following pairs: SN-SMN: W = 15881, P = 0.0002; SMN-FPN: W = 18162, P < 0.0001; SMN-DMN: W = 17835.5, P < 0.0001; SMN-LN: W = 14226, P = 0.0003; VN-FPN: W = 16125.5, P < 0.0001; VN-DMN: W = 15822.5, P < 0.0001. However, the following comparisons were significant before adjustment but not after correcting for multiple comparisons: DAN-FPN: W = 7125, P = 0.014; DAN-DMN: W = 6832.5, P = 0. 029.

Fig. 2: Empirical high-density electroencephalography (hd-EEG) and stereotactic electroencephalography (sEEG) signals show larger global activation patterns for high-order than low-order brain networks.
figure 2

A The histogram illustrates the distance in centimeters between the electrode’s centroid delivering the electrical stimulus and the center of the nearest Schaefer’s parcel87. The results indicate a high level of spatial precision, with 97.2% of sessions showing distances of less than 1 cm. B Global mean field power (GMFP) of hd-EEG averaged across all 36 subjects and 323 sessions, revealing three consistent response peaks/clusters within strict confidence intervals at ~40 ms, ~80 ms, and ~370 ms, consistent with prior electrophysiological research44. C GMFP of every stimulated Resting-State Network (RSN) for hd-EEG (top row) and sEEG (bottom row). The bar plot of the normalized area under the curve (AUC) of the three clusters revealed a significantly stronger global activation pattern when the stimulus targeted high-order networks, such as the Default mode network (DMN) and Frontoparietal Network (FPN), particularly for the late evoked responses (third cluster at ~370 ms). Data are presented as mean values ± standard error of the mean (SEM) (error bars), with individual subject data points overlaid (36 independent subjects, 323 stimulation sessions). In the GMFP time course plots, shaded areas represent ±SEM around the mean. Notably, this trend aligns with the “principal gradient” hierarchy reported in the functional magnetic resonance imaging (fMRI) literature12, which describes a general pattern from low-order to high-order regions15.

Full size image

When examining the sEEG data (Fig. 2C, bottom row), a significant interaction was also observed between response timing and stimulated network (F(12, 927) = 1.904, P = 0.03048). In line with the hd-EEG results, this interaction indicates that the impact of stimulation on the overall response varies depending on the network affiliation of the stimulation site. This significant interaction was supported by significant main effects in the sEEG data of both response timing (F(2, 927) = 41.961, P < 2e-16) and stimulated network F(6, 927) = 3.556, P = 0.00173).

For the first response cluster (0–37 ms), permuted Wilcoxon–Mann–Whitney U pairwise comparisons showed significant differences in AUC for: VN-DAN: W = 21128.5, P < 0.0001; VN-SN: W = 21212, P < 0.0001; VN-LN: W = 18721.5, P < 0.0001; VN-FPN: W = 28925.5, P < 0.0001; VN-DMN: W = 17003.5, P < 0.0001. SMN-DAN: W = 19458.5, P < 0.0001; SMN -SN: W = 18918.5, P < 0.0001; SMN-LN: W = 17998, P < 0.0001; SMN-FPN: W = 24221, P < 0.0001; SMN-DMN: W = 16121.5, P < 0.0001. For the second response cluster (37–78 ms), permuted Wilcoxon–Mann–Whitney U pairwise comparisons showed significant differences in AUC for: VN-DAN: W = 21345, P < 0.0001; VN-SN: W = 21089.5, P < 0.0001; VN-LN: W = 18902.5, P < 0.0001; VN-FPN: W = 29145, P < 0.0001; VN-DMN: W = 17232, P < 0.0001. SMN-DAN: W = 19285, P < 0.0001; SMN-SN: W = 19102.5, P < 0.0001; SMN-LN: W = 18100, P < 0.0001; SMN-FPN: W = 24500, P < 0.0001; SMN-DMN: W = 16400, P < 0.0001. For the third response cluster (78–373 ms), permuted Wilcoxon–Mann–Whitney U pairwise comparisons showed significant differences in AUC for: VN-DAN: W = 21512, P < 0.0001; VN-SN: W = 21401.5, P < 0.0001; VN-LN: W = 19110.5, P < 0.0001; VN-FPN: W = 29310, P < 0.0001; VN-DMN: W = 17415.5, P < 0.0001. SMN-DAN: W = 19532, P < 0.0001; SMN-SN: W = 19345.5, P < 0.0001; SMN-LN: W = 18375, P < 0.0001; SMN-FPN: W = 24712.5, P < 0.0001; SMN-DMN: W = 16634, P < 0.0001.

In addition, comparisons between high-order (LN, SN, DAN, DMN and FPN) and low-order (VN and SMN) networks consistently revealed significant differences for both hd-EEG (low-order-high-order: W = 4567.5, P = 0.0013) and sEEG (low-order-high-order: W = 5713, P = 0.0008). Overall, these findings demonstrate greater levels of excitability (as indicated by the magnitude of global activation) amongst high-order networks than in low-order networks. Moreover, as is also observed in both sEEG and hd-EEG data, this effect follows a continuous hierarchy over networks (Fig. 2C, right panels), that aligns closely with the well-known macroscale functional connectivity gradient12,16.

The results observed at the channel level in hd-EEG have been replicated at the source level. These findings are detailed in Supplementary Results 2.1 and Fig. S5, providing additional support for the robustness of our conclusions.

The contribution of recurrent feedback to stimulation responses mirrors the excitability gradient

Comparing the simulation runs with the intact versus those with the virtually dissected/lesioned structural connectome (for further details see methods), significant interactions between “response timing” (3 levels: first, second and third cluster) and “stimulated network” (F(12, 1854) = 1.78, P = 0.046) and between “condition” (2 levels: intact, lesion) and “response timing” (F(2, 1854) = 5.88, P = 0.002) were found.

Permuted Wilcoxon–Mann–Whitney U pairwise comparisons between intact and lesioned structural connectome simulations showed significant differences in AUC within the late (78–373 ms) response period for LN (W = 466.5, P = 0.003), DAN (W = 71.5, P = 0.005), FPN (W = 78.5, P < 0.001), and DMN (W = 1076, P < 0.001). No significant differences in these late-response AUCs were found for SN (W = 1704, P = 0.08), SMN (W = 2622.5, P = 0.21), and VN (W = 275.5, P = 0.47), and no significant differences were found for any network in the two earlier response windows (peak #1 at 0–37 ms, peak #2 at 37–78 ms).

To investigate the effects of virtual lesions on the network hierarchy, we compared low-order networks (VN and SMN) with high-order networks (LN, SN, DAN, FPN, and DMN) in both the intact and the lesioned structural connectome condition. A significant difference in the late-response AUCs was found (low-order-high-order: W = 28132, P < 0.0001), while no significant differences were found in the two earlier response windows.

Virtual dissections applied to isolate the stimulated network thus had a significant effect on high-order networks only, and only in the later component of their stimulation responses. Moreover, as shown in Fig. 3C, the impact of removing recurrent connections on stimulation response amplitudes follows a trend from low-order to high-order networks, similar to the reverse pattern of the excitability gradient observed in Fig. 2.

Fig. 3: Removing recurrent connections to isolate the stimulated network suppresses late evoked potentials for high-order networks.
figure 3

A Global mean field power (GMFP) for every stimulated network for model-generated high-density electroencephalography (hd-EEG) data run with both the intact (continuous line) and disconnected (dashed line) structural connectome. Findings show a more pronounced decrease in evoked late responses for high-order networks (LN Limbic Network, SN Salience Network, DAN Dorsal attention network, FPN Frontoparietal Network, DMN Default mode network). B Area under the curve (AUC) differences comparing the simulation run with the intact versus the lesioned structural connectome. The bar plot shows differences across three time windows (1st response: 0−37 ms, 2nd response: 37–78 ms, 3rd response: 78–373 ms). Data are presented as mean values ± standard error of the mean (SEM) (error bars), with individual subject data points overlaid (36 independent subjects, 323 stimulation sessions). A significant reduction in the AUC was found for late responses (78−373 ms) of high-order networks (LN, SN, DAN, FPN, and DMN) compared to low-order networks (Visual Network [VN] and Somatomotor Network [SMN]), indicated by asterisks (*P < 0.05). C Demonstration of the network recurrence-based theory for two representative sessions. Simulations of evoked dynamics are run using the intact (left) and lesioned (right) anatomical connectome. In the latter case, the connections were removed to isolate the stimulated networks for SMN (top) and DMN (bottom). In the case of the low-order network, this virtual dissection does not significantly impact the evoked potentials, while for the high-order network, a substantial reduction or disappearance of evoked components was observed.

Full size image

Discussion

Using a computational framework recently developed for personalized neurostimulation modeling62, in this work we examined scalp and intracerebral electrophysiology data as a window into feedforward and feedback response characteristics of intrinsic human brain networks. Uncovering the rules and structures according to which brain networks are organized and interact at a mechanistic physiological level is important not only as a basic question in systems and cognitive neuroscience, but also as a foundation for clinical applications aimed at customizing brain stimulation techniques to enhance network engagement, thereby promoting better clinical outcomes. Our results demonstrate that iES leads to downstream electrophysiological evoked responses whose spatiotemporal patterning follows the hierarchical cortical gradient structure commonly studied in structural and functional neuroimaging data12,15. Specifically, we found significantly stronger activation patterns when stimulating a high-order network (LN, SN, DAN, FPN, and DMN), particularly for the late evoked responses. Importantly, this trend in excitability levels was observed both in the scalp-recorded hd-EEG and the intracerebrally-recorded sEEG data, suggesting its replicability across different measurement modalities and scales of spatial resolution. Previous work has demonstrated that brain regions exhibit hierarchical gradients of activity timescales during task performance and resting state, with slower timescales found in regions most distant from sensory input and motor output65. These hierarchical timescales, it has been argued, serve as an intrinsic organizing principle of brain function, influencing large-scale networks and subcortical regions, across sensory and higher-order cortical regions, as well as subcortical structures.

There is growing awareness amongst neuroscientists that this hierarchical network structure of brain organization shapes the spatiotemporal propagation of activity evoked by brain stimulation31,40,41,66,67, and specifically that iES effects depend on the network connectivity profile of the region being stimulated49,68,69,70,71. A seminal recent study reported that patients’ self-reported perception of iES stimulation intensity depends on the stimulated region’s position in the cortical hierarchy, with simpler effects in lower-level networks and more complex, heterogeneous effects in higher-order networks72. Within this broader body of work, our empirical results reported here provide electrophysiological evidence that global patterns of hierarchical organization in the brain (cortical gradients) shape evoked-response dynamics. Specifically, we show that the position of the stimulated region along the cortical gradient is a potent predictor of iES-evoked activation dynamics, a finding that goes beyond the previously established network-specific propagation patterns reported in stimulus-evoked EEG studies40,41,42,44.

Building on these observations of an excitability gradient from our empirical sEEG+hd-EEG data analyses, we used connectome-based whole-brain modeling62 to obtain further insights into the role of recurrent feedback activity in stimulation-evoked brain responses. Specifically, we employed a “virtual dissection” approach73 to isolate and prevent the stimulated network from receiving feedback input from the rest of the other non-stimulated RSNs. This procedure allows us to evaluate the extent to which model-generated stimulation-evoked patterns relied on recurrent inputs from downstream brain areas that did not belong to the stimulated network. These in-silico interventions resulted in substantial reductions in the stimulation-evoked activity, with the magnitude of these reductions varying considerably depending on which network was perturbed. Virtual dissections designed to isolate the stimulated network significantly reduced the amplitude of late responses when the iES was delivered to high-order areas, as compared to low-order areas. Interestingly, in a recent work using the same virtual dissection methodology62, we have demonstrated that early transcranial magnetic stimulation-evoked responses are primarily driven by localized dynamics of the stimulated region, whilst later components are driven by large-scale recurrent feedback loops. In this study, we have expanded upon these earlier findings by studying network-level responses spread widely across the cortex (as opposed to primary motor cortex stimulation only), demonstrating that these network-driven late responses differ based on the position of the stimulated region along a canonical cortical gradient hierarchy. Findings showed that the late responses mainly depend on intrinsic within-network connections for low-order regions, and extrinsic between-network connections for high-order regions. This result suggests that varying strategies are employed by different brain networks in terms of how they send, receive, and process, and is in line with other results placing sensorimotor areas (with predominantly bottom-up outgoing connections) at the bottom of the hierarchy, and higher-order association areas (with mostly top-down outgoing connections) at the top of the hierarchy74,75. Recent studies have also analyzed network-based incoming and outgoing communication efficiencies, characterizing low-order cortical regions as primarily senders, and high-order networks as receivers76. This picture is consistent with reports of a developmentally driven shift in macroscale cortical organization during adolescence, progressing from a functional motif dominated by low-order regions (e.g., Sensorimotor, Visual) in children to an adult-like gradient, where the high-order regions are located at the opposite end of a spectrum77. Our findings expand this evidence base, demonstrating the existence of the macroscale functional gradients for stimulus-evoked electrophysiological data, and provide computational evidence of how this scaffold shapes information processing strategies characterized by functional segregation/integration for low-order/high-order networks, respectively.

In regard to the limitations of the study, a potential caveat is the derivation of the resting-state networks (RSNs) which, despite being based on individual anatomical images of the subjects, were not derived from resting-state functional MRI data. In addition, we did not have diffusion-weighted imaging sequences available for obtaining individual structural connectivity matrices. Although we estimated the individual structural connectome during the model fitting process, the posterior structural connectivity did not significantly deviate from the prior, thereby preserving the biological properties of the structural connectivity (please see supplementary methods for more details).

A key limitation is the variability in spatial sampling of sEEG, which affects intracerebral signal amplitudes. Due to differences in electrode placement, even within the same region, electrodes can be positioned in varying sub-regions or distances from active areas. Volume conduction effects further complicate interpretation. While we aimed to minimize these confounds by focusing on specific regions, this heterogeneity limits the generalizability of our findings. Ongoing efforts, such as those by Medina Villalon et al.78, are exploring source localization techniques to address these challenges.

In addition to this, we acknowledge that the variation in the number of stimulations across different functional networks presents a limitation in our study. While we have employed ANOVA to account for these differences, it is important to recognize that this statistical method, while robust, may not entirely eliminate the potential biases introduced by unequal stimulation counts. In addition, the inherent variability in patient responses to iES stimulation further complicates the direct comparability across networks. Future studies with more balanced stimulation protocols and larger sample sizes could provide more definitive insights into the effects of iES on different functional networks.

Furthermore, future studies could benefit from incorporating additional open datasets, such as the F-TRACT project (https://f-tract.eu/), which offers large cohort data and may provide further insights into brain gradients79,80,81.

Another limitation of our study is the reliance on a specific computational model (Jansen-Rit) and its parameters, which might not capture the full complexity of brain dynamics. Future work could explore the use of different models and parameter settings to validate and extend our findings.

Finally, our results were obtained from a population of epileptic patients whose clinical condition and specific treatment82,83 may affect both invasive and noninvasive recordings. To minimize such confounds, we did not include any sEEG contact located in the SOZ (as verified by surgical resection) or exhibiting sustained pathological interictal activity. Moreover, we excluded from the analyses all the CCEPs showing evoked epileptic activity at the sEEG and/or at the hd-EEG level84.

Our results, and the framework for investigating the scientific questions we are introducing here, have clear and practical relevance to basic and clinical research, as well as broader implications for the scientific understanding of functional brain organization. Using computational modeling and the virtual dissection approach allows us to ask and answer mechanistic questions around the necessity and sufficiency of various anatomical and physiological components in different aspects of local and global brain dynamics. It also provides a potential entry point for understanding brain disorders at a mechanistic level, possibly leading to novel, more effective therapeutic interventions.

Methods

The analyses conducted in this study consist of four main components: (i) measurement of stimulation-evoked responses in sEEG and hd-EEG data, (ii) construction of anatomical connectivity priors for our computational model using diffusion-weighted MRI tractography, (iii) simulation of whole-brain dynamics and stimulation-evoked responses with a connectome-based neural mass model, and (iv) fitting of the model to individual subject scalp hd-EEG data. A schematic overview of the overall approach is given in Fig. 4.

Fig. 4: Methodological workflow for characterizing the stimulated network and performing subject-specific connectome-based neurophysiological modeling of evoked potentials.
figure 4

A Simultaneous stereotactic electroencephalography (sEEG) and scalp high-density electroencephalography (hd-EEG) signals were recorded. The black triangle and dashed vertical line indicate the time at which intracerebral electrical stimulation (iES) was delivered. For further details on the methodology and data preprocessing please refer to refs. 45,85. B To pinpoint the brain network where the stimulus was delivered, we employed the Schaefer atlas87, which divides the brain into 1000 regions across seven distinct Resting-State Networks (RSNs): Visual Network, Somatomotor Network, Limbic Network, Dorsal attention network, Ventral Attention Network, Frontoparietal Network and Default Mode Network. Subsequently, we identified the parcellation region that overlapped with the intracerebral electrode responsible for delivering the stimulus, ultimately enabling us to determine the stimulated network. C To model individual stimulus-evoked time series, the Jansen-Rit model90, a neural mass model comprising pyramidal, excitatory interneuron, and inhibitory interneuron populations, was embedded in every parcel of the lower-resolution 200-region Schaefer atlas87 for simulating and fitting neural activity time series. The connectivity between regions was modeled using diffusion-weighted magnetic resonance imaging (MRI) tractography computed from a sample of healthy young individuals from the Human Connectome Project (HCP) Dataset94, and then averaged to give a grand-mean anatomical connectome. The iES-induced depolarization of the resting membrane potential was modeled by a perturbing voltage offset to the mean membrane potential of the excitatory interneuron population. Next, a lead field matrix was employed to project the time series from the cortical surface parcels into EEG channel space, resulting in the generation of simulated scalp hd-EEG measurements. The quality of fit (loss) was quantified by calculating the cosine similarity between the simulated and empirical stimulus-evoked time series. Optimization of model parameters was accomplished by leveraging the autodiff-computed gradient95 between the objective function and the model parameters, employing the ADAM algorithm96. Ultimately, the optimized model parameters were utilized to generate the fitted, simulated (optimized) stimulus-evoked hd-EEG activity.

Full size image

Simultaneous stereo and high-density EEG data

The data used in this study were taken from an open dataset collected at the Claudio Munari Epilepsy Surgery Center, Milan (https://doi.org/10.17605/OSF.IO/WSGZP), where sEEG and scalp hd-EEG were recorded following single-pulse intracerebral electrical stimulation (iES) on 36 patients (median age = 33 ± 8 years, 21 female). All subjects had a history of drug-resistant, focal epilepsy, and were candidates for surgical removal/ablation of the seizure onset zone (SOZ). For details regarding the data acquisition and the preprocessing steps, please refer to the original papers45,85. All the preprocessed sEEG and hd-EEG analyses were performed using the MNE software library86 (mne.tools/stable/index.html) running in Python 3.6.

Precise identification of the stimulated network

In order to identify the network stimulated for a specific session (Fig. 4B), the Schaefer atlas87, which divides the brain into seven canonical functional brain networks, subdivided at multiple spatial scales (100, 200, 300…1000 parcels), was mapped to the individual’s FreeSurfer parcellation. In this study we used finest-resolution (1000 brain regions) Schaefer parcellation for categorizing surgical stimulation sites, and a lower-resolution (200 brain regions) for whole-brain physiological modeling and network analysis.

The seven canonical networks correspond to the visual network: VN, Somatomotor network: SMN, Dorsal attention network: DAN, Anterior salience network: SN, Limbic network: LN, Frontoparietal network: FPN, Default mode network: DMN. We first projected the seven-network cortical atlas onto the subject’s cortical surface using the Freesurfer spherical registration parameters. The resulting maps were then resampled to native space structural T1w MRIs. Then, we identified the parcellation region overlapping with the intracerebral electrode responsible for delivering the stimulus, ultimately allowing us to determine the stimulated network. For a detailed overview of the number of sessions included for each stimulated network, please refer to Supplementary Fig. S4.

Analyzing differences in the activation dynamics dependent on the stimulated network

All statistical analyses were carried out using R version 2023.06.2, Build 561. We aimed to investigate whether the pattern of activation dynamics resulting from iES depends on the specific network that is stimulated. In order to explore this, the GMFP was extracted from every stimulation session

$${GMFP}\left(t\right)=\sqrt{{\sum }_{i}^{k}\frac{{\left({V}_{i}\left(t\right)-{V}_{{mean}}\left(t\right)\right)}^{2}}{K}}$$

where t is time, Vi(t) is the voltage at channel i at time t, Vmean is the mean of the voltage over all channels, and K is the number of channels. Upon examining the average scalp hd-EEG GMFP across subjects and sessions, we identified three clusters of response peaks in a time frame consistent with findings already reported in electrophysiological data from previous research using similar approaches44. We extracted the area under the curve (AUC)—which reflects cortical excitability88,89—for each one of these clusters (Fig. 3B; cluster 1: 0–37 ms; cluster 2: 37–78 ms; cluster 3: 78–373 ms), and subsequently grouped the AUC values belonging to the same stimulated network session. This allowed us to assess whether the overall activity evoked by the stimulation varies systematically as a function of the specific network that was perturbed. To address the varying number of sessions among participants, a mixed-design analysis of variance (ANOVA) was conducted. “response timing” was treated as a within-subjects factor with three levels corresponding to the three response clusters (first, second, and third clusters), based on previous literature44 and the results from our peak-finding analysis. “stimulated network” was treated as a between-subjects factor with seven levels corresponding to the stimulated networks (VN, SMN, DAN, SN, LN, FPN, DMN).

A Wilcoxon–Mann–Whitney U test was then conducted to evaluate pairwise comparisons between the different stimulated networks for each response cluster. Each comparison was assessed with a null distribution constructed from 1000 random permutations, with a significance threshold set at P < 0.007 (after adjusting for multiple comparisons). In addition, we compared low-order (VN, SMN) and high-order (LN, SN, DAN, FPN, DMN) networks using the same approach to investigate broader network hierarchy effects on the AUC. By comparing these conditions, we sought to determine statistically significant network-wise differences in AUC, without making any assumptions about the underlying distribution of the data.

Overview of computational modeling approach

We employed a whole-brain modeling57 approach to analyze hd-EEG data and study the physiological mechanisms of network excitability. The specific model we used here incorporated 200 distinct brain regions (as defined by the Schaefer 200 parcellation), connected with a set of inter-regional weights derived from the anatomical connectome. Jansen-Rit neural mass dynamics90 at each region described the process of stimulated activation and oscillatory responses resulting from local interactions within cortical microcircuits, with these effects propagating to regions distal to the stimulated site via the long-range anatomical connections. After specifying its structure and a common set of priors for all parameters, the model was fit to EEG data separately for each patient. This resulted in a set of individualized physiological and connectivity parameters, having a mechanistic influence on several spatial and temporal features of the brain stimulation response, which we subsequently interrogated to obtain further insight into our research questions around the topographic organization and network specificity. For details regarding the computational model and the parameter estimation, see refs. 62,91 and supplementary methods. For a graphical overview of all optimized parameters and their distributions, see Supplementary Figs. S1,  S2, and  S3.

Assessing the similarity between simulated and empirical evoked responses

To further assess the goodness-of-fit of the simulated waveforms arrived at after convergence of the ADAM algorithm, Pearson correlation coefficients and corresponding p-values between empirical and model-generated waveforms were computed for each subject. In order to control for type I error, this result was compared with a null distribution constructed from 1000 time-wise random permutations, with a significance threshold set at P < 0.05.

Dissecting the network-specific activation dynamics

The primary objective of this study is to determine the extent to which the activation patterns observed in sEEG and hd-EEG data depend on intrinsic dynamics within the stimulated network, or on contributions from other non-stimulated network regions. In order to explore this, simulations were re-run for each subject using their optimal parameters estimated from the original evoked potentials fitting step, but this time with specifically designed “virtual dissections” applied to the (otherwise intact) structural connectome. These virtual dissections were performed by setting to zero the weights of all connections returning to the stimulated network from other non-stimulated RSNs. In this way the stimulated network was still able to send information to the whole brain, and receive information from regions that belong to the same network. Once the whole-brain model was re-run with these new virtually dissected connectome weights, the evoked potential time series of each brain region were again projected to the hd-EEG channel space, and the AUC was extracted for the same clusters, and compared against the original model-generated evoked potentials’ AUC. For this comparison, a mixed-design ANOVA was run with “condition” as a within-subjects factor, corresponding to the 2 simulation runs with different connectomes (2 levels: intact, lesion); “response timing” as a within-subjects factor, corresponding to the 3 response clusters (3 levels: first, second and third cluster); and “stimulated network” as a between-subjects factor, corresponding to the seven Yeo networks (7 levels: VN, SMN, DAN, SN, LN, FPN, DMN). Then, the Wilcoxon–Mann–Whitney U test was conducted to evaluate pairwise differences between the two simulation conditions across different stimulated networks. In addition, comparisons between low-order (VN, SMN) and high-order (LN, SN, DAN, FPN, DMN) networks were made using the same statistical approach to investigate differences in response to virtual lesions along the cortical hierarchy. Every comparison was compared with a null distribution constructed from 1000 time-wise random permutations, with a significance threshold set at P < 0.05. We hypothesized that when the stimulus is delivered to high-order networks, these virtual dissections would significantly suppress later responses, as the activity of these networks is intricately integrated and heavily reliant on recurrent feedback from the rest of the brain. In contrast, we expect the propagation dynamics when the stimulus is delivered to low-order RSNs to remain largely unaltered, due to the fact that their activity is characterized by segregated communication strategies.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.