Introduction

MR is a fascinating magnetoelectric phenomenon that has attracted significant attention since decades ago due to its importance in both fundamental science and practical applications1,2,3,4,5,6,7. Researchers aim to develop MR sensors with low energy consumption and high sensitivity that can operate over a wide-temperature range. To achieve this, the MR of a variety of newcomer materials have been investigated in the past, including Dirac and Weyl semimetals8,9,10,11,12,13, strange metals14,15,16, etc. The most notable feature of these materials is the widespread unsaturated linear MR observed at cryogenic temperature. However, the MR usually maximizes at low temperature and decreases rapidly with increasing temperature9,10,11,12,13, which greatly limits their practical applicability. As a two-dimensional (2D) Dirac semimetal, graphene has been found to show unsaturated linear MR caused by spatial charge inhomogeneity inevitably seen in 2D systems at room temperature17,18,19,20,21, holding great promise for future applications.

The MR of pristine graphene is finite, leaving a large room for improvement. According to the effective medium theory22, the degree of disorder or charge inhomogeneity in graphene directly affects its MR. Therefore, various methods have been proposed to enhance the MR of monolayer graphene by increasing its disorder. For example, different nanoparticles, such as gold23, cobalt24 and nickel25, have been decorated on the surface of graphene. But, the enhancement of MR by such decoration method is not very effective. Alternative way to introduce extra disorder into graphene is to place it on exotic substrates such as lattice-mismatched black phosphorous26, surface-terraced SrTiO327 and BiFeO3 nano-island array28. By doing so, the room-temperature MR has been enhanced significantly. However, the MR in these systems still shows severe temperature instability, which could be attributed to the highly temperature-dependent extrinsic degree of disorder. Very recently, Dirac plasma has been generated in graphene through sophisticated hexagonal boron nitride (h-BN) encapsulation technique, which achieves an MR as large as 110% under 0.1 T and 8600% under 9 T at room temperature29. However, the Dirac plasma only forms at the vicinity of Dirac point and sustains down to only ~100 K, which makes the MR decrease dramatically at low temperature as well as away from Dirac point.

In order to achieve giant, stable MR in graphene in a broader temperature range, alternative strategy with temperature insensitivity needs to be introduced. Here, we propose a novel approach to enhance the MR of graphene by stacking the van der Waals ferromagnet FGT on a monolayer graphene to form an FGT/Gr heterostructure30,31. The FGT/Gr heterostructure can achieve a MR of up to ~9400% under 9 T at room temperature away from Dirac point, which is more than thirty-fold enhancement over the MR of pure graphene. More importantly, the giant MR sustains in the full temperature range studied from RT down to 4 K and even slightly increases with lowering temperature. DFT calculations show that when FGT is placed on graphene, the magnetism of FGT breaks the spin-degeneracy of graphene, where the spin majority carriers with low mobility contribute little conductivity while the spin minority carriers with high mobility dominates in transport. When an external magnetic field is applied, the density of spin minority carriers decreases rapidly, resulting in the reduction of conductivity and thus giant MR. Our work sheds light on the development of next generation MR sensors and relevant spintronic devices with high sensitivity and wide working-temperature range.

Results and discussion

Giant MR at room temperature

We fabricated the FGT/Gr heterostructure device by using a simple dry transfer method followed by standard electron-beam lithography and metal deposition procedure (see Methods for details). A typical device (Device A) is shown in Fig. 1a, where Hall-bar shaped electrodes are patterned directly on graphene ribbon, dividing the channel into two parts: pure graphene region and FGT/Gr heterostructure region. The MR for both regions were measured by recording the longitudinal resistance Rxx as a function of perpendicularly applied magnetic field B in a four-probe geometry and calculated as MR = (Rxx(B)-Rxx(0))/Rxx(0) × 100%, where Rxx(B) and Rxx(0) are the resistance values at finite field and zero field, respectively.

Fig. 1: Device structure and basic magneto-transport measurements at room temperature.
figure 1

a Optical microscope image of a typical FGT/Gr heterostructure device (Device A) and schematic illustration of measurement setup. The red dashed line in the photograph indicates the monolayer graphene. Scale bar is 10 µm. b I–V curves of the FGT/Gr heterostructure in Device A under different magnetic fields. c Room-temperature MR of the FGT/Gr heterostructure in Device A as a function of magnetic field. The MR curve of the pure graphene region is also shown for comparison. d Hall resistances Rxy of the FGT shown in the inset as a function of out-of-plane magnetic field at various temperatures ranging from 1.6 to 225 K. Scale bar is 5 µm.

Full size image

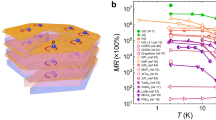
The four-probe current-voltage (I–V) curves across the FGT/Gr heterostructure region under different magnetic fields were first measured and shown in Fig. 1b. As can be seen, the inverse slope of the I–V curves, which corresponds to the longitudinal resistance Rxx, changes dramatically with increasing magnetic field, pointing to a large MR. Next, by scanning the magnetic field continuously under a constant sourcing current, the MR curves of both the graphene region and the FGT/Gr heterostructure region were measured, calculated and plotted in Fig. 1c. The MR of the FGT/Gr heterostructure reaches ~9400% under 9 T at room temperature, while that of the pure graphene is less than 300% which is comparable to previous reported values19,21. The more than thirty-fold enhancement of MR in our FGT/Gr heterostructure is appreciable and to the best of our knowledge, the absolute value sets a record as compared to previous reports on different graphene-based systems (refer to Fig. 4c and Supplementary Table 1)8,19,20,21,23,24,25,26,27,28,29.

The origin of the giant MR from FGT itself has to be ruled out first. The magneto-transport properties of FGT with comparable thickness (~40 nm) to that of the one used in Device A were characterized by making a Hall bar device as shown in the inset of Fig. 1d. The anomalous Hall effect measurement shows that the Curie temperature (Tc) of the van der Waals ferromagnet FGT is ~210 K with an out-of-plane easy axis32. The MR curves of the FGT both below and above Tc were measured in the same way as aforementioned and shown in Supplementary Fig. 1. The negligibly small MR agrees with previous report33, indicating that the FGT alone cannot contribute to the giant MR observed in our FGT/Gr heterostructure.

Temperature, angle and gate-dependence of MR

The MR curves at different temperatures in Device A were measured and shown in Fig. 2a. We note that the oscillatory and negative MR usually seen at cryogenic temperature in pure graphene (Supplementary Fig. 5) and other graphene based heterostructures is absent in our system. Instead, the MR increases monotonically with magnetic field in the whole temperature range studied. These features suggest that the weak (anti)localization and universal conductance fluctuation are suppressed in our system26,27. The temperature-dependent MR under fixed magnetic fields were further plotted in Fig. 2b. Strikingly, the giant MR observed at room temperature stays almost unchanged when temperature decreases, in stark contrast to the trend observed in previously studied graphene-based systems8,19,20,23,26,29, which implies that the giant MR in our FGT/Gr heterostructure may have a different origin. We emphasize that such temperature-insensitive MR favors magnetic sensor applications at both room temperature and cryogenic temperature regimes. Next, the angular dependence of the Rxx on magnetic field direction was routinely checked and shown in Supplementary Figs. 2 and 5. The Rxx is at its maximum (minimum) when the magnetic field is perpendicular (parallel) to the sample surface, following a cosine dependence. Therefore, our FGT/Gr heterostructure complies with the classical MR mechanism, where the Lorentz force takes effect34.

Fig. 2: Temperature- and gate-dependent MR of FGT/Gr heterostructure.
figure 2

a The MR curves of FGT/Gr heterostructure in Device A as a function of magnetic field at different temperature points. b Variation of MR with temperature under different magnetic fields in Device A. c Transfer curves of FGT/Gr heterostructure in Device C measured at room temperature under different magnetic fields. d Normalized MR of the FGT/Gr heterostructure in Device C under three representative magnetic fields as a function of gate voltage.

Full size image

Figure 2c shows the transfer curves of another device (Device C) under different magnetic fields. As can be seen, the Dirac point of graphene in the FGT/Gr heterostructure is at −2.5 V under zero magnetic field and remains almost unchanged up to high magnetic fields. The gate-voltage-dependent MR was calculated from Fig. 2c and plotted in Fig. 2d for three representative magnetic fields. Similar to previous reports19,23,26,29, the MR is maximized around the Dirac point and decreases gradually away from it. It is noted that the MR decreases faster under low field while slower under high field.

Understanding the origin of the giant MR

It is unclear why FGT, a ferromagnet with minimal MR on their own (less than 1% under 9 T), can increase the latter’s MR by more than an order of magnitude when formed into heterostructures with monolayer graphene. To understand the physical mechanism inside, we performed a density functional theory (DFT)35,36 calculation of FGT on monolayer graphene, as shown schematically in Fig. 3a. The spin resolution band structures projected to graphene and FGT are plotted in Fig. 3b, c, respectively. It can be seen from Fig. 3b that around Fermi energy (−0.08 eV), the spin-down bands (blue bands) of graphene are coupled with the spin-down bands of FGT, while the spin-up bands (red bands) of graphene almost keep its original linear dispersion, due to the lack of spin-up bands of FGT around the Fermi level, leading to strong hybridization of only one spin channel. Similar phenomenon has been reported in graphene proximitized by ferromagnetic insulator CrI3 recently37. Here, we regard spin-down with larger density of states (DOS) at Fermi level as majority spin and spin-up with smaller DOS at Fermi level as minority spin. As well known, the high mobility of graphene originates from its linear dispersion and pseudo-spin of Dirac cone. Therefore, the breaking of the linear dispersion of graphene spin-down bands makes the majority spin carriers scattered by FGT easily, resulting in much lower mobility of majority spin carriers as compared with that of minority spin carriers. The total conductivity of graphene proximitized by FGT can be written as: \({\sigma }_{{\rm{B}}}=e\left({n}_{\uparrow }{\mu }_{\uparrow }+{n}_{\downarrow }{\mu }_{\downarrow }\right)\), where \({n}_{\uparrow /\downarrow }\) and \({\mu }_{\uparrow /\downarrow }\) are the density and mobility of spin-up/down carriers, respectively. When there is no magnetic field, we have \({n}_{\uparrow } \, < \, {n}_{\downarrow }\) and \({\mu }_{\uparrow }\, \gg \, {\mu }_{\downarrow }\) as aforementioned, therefore the conductivity of graphene \({\sigma }_{B=0}\approx {{en}}_{\uparrow }{\mu }_{\uparrow }\). When an external magnetic field B is applied, the spin-down bands move downward, with larger DOS, while the spin-up bands move upward, with smaller DOS. Based on conservation of particle number, \({n}_{\uparrow }+{n}_{\downarrow }+{N}_{{\rm{FGT}},\downarrow }={Const}.\), we have \({\rm{\delta }}{n}_{\uparrow }={\rm{\delta }}{n}_{\downarrow }+{\rm{\delta }}{N}_{{\rm{FGT}},\downarrow }\left({\rm{\delta }}n\equiv \left|n\left(B\right)-n\left(B=0\right)\right|\right)\), which means that the density of spin-up (minority) carriers \({n}_{\uparrow }\) reduces much faster than spin-down (majority) carriers \({n}_{\downarrow }\) increases, resulting in rapid reduction of the conductivity of graphene \({\sigma }_{B}\approx {{en}}_{\uparrow }(B){\mu }_{\uparrow }\) and therefore the giant MR.

Fig. 3: Theoretical calculation.
figure 3

a Crystal structure of FGT/Gr heterostructure. b The spin-resolution band structure, projected to graphene. c The spin-resolution band structure, projected to FGT. The dashed lines in both (b, c) indicate the Fermi level.

Full size image

To demonstrate the uniqueness of FGT on the enhancement of the MR in graphene, we stacked CrGeTe3 (CGT)38, a 2D ferromagnetic semiconductor, on monolayer graphene to make a CGT/Gr heterostructure device. The device image and measurement results are presented in Supplementary Fig. 8. It is found that there is no MR enhancement at all and the MR of the heterostructure even decreases as compared to the pure graphene. DFT calculations on the CGT/Gr heterostructure were also performed and the results are shown in Supplementary Fig. 9. Different from the FGT/Gr case, the energy band hybridization between CGT and graphene is inappreciable, therefore spin-dependant orbital coupling induced MR enhancement effect is not expected as shown in Supplementary Fig. 8. Likewise, we also stacked MoS2, a 2D nonmagnetic semiconductor, with monolayer graphene to make a MoS2/Gr heterostructure device. The measurement results presented in Supplementary Fig. 10 also show negligible MR enhancement effect. The MR obtained from different heterostructures in our work are summarized in Fig. 4a, where only FGT/Gr shows giant MR as compared to others, pointing to the unique role of FGT on enhancing the MR in graphene as aforementioned.

Fig. 4: Statistics of MR in different devices.
figure 4

a Histogram of MR under 1 T magnetic field for different structures studied in this work. b Variation of MR under 9 T magnetic field with annealing temperature for different groups of devices. c Comparison of MR for different graphene-based systems reported in our work and literatures.

Full size image

We also note that vacuum annealing can help to improve the coupling between FGT and graphene, therefore enhance the MR of the heterostructure. It is a common way to do vacuum annealing in order to enhance the interfacial coupling in van der Waals heterostructures by driving out the trapped air/moisture as much as possible39,40,41,42, which depends on the annealing temperature and time. As shown in Fig. 4b and Supplementary Fig. 4c, the as-fabricated FGT/Gr heterostructure shows MR of only ~300% under 9 T (Device C), which is nevertheless still higher than that of pure graphene. After annealing in high vacuum at 170 °C (see Methods), the MR of the heterostructure drastically increased to ~760%. For devices with even higher annealing temperature (220 °C and 250 °C), the MR all reached above ~2000% with highest value of ~9400%. For pure graphene and other heterostructures studied in this work, however, vacuum annealing showed little enhancement of the MR. This further supports that the giant MR in FGT/Gr heterostructure originates from the unique interfacial coupling induced spin-split band hybridization between FGT and graphene, rather than other artificial effects.

In summary, giant MR of up to ~9400% under 9 T at room temperature has been observed in FGT/Gr heterostructure, in which the more than one order of magnitude enhancement of MR as compared to pure graphene originates from spin-dependent orbital coupling between FGT and graphene. While in graphene heterostructures formed with either ferromagnetic semiconductor CGT or nonferromagnetic semiconductor MoS2, such spin-dependent coupling is negligible, leading to little MR enhancement. Strong spin-dependent hybridization was recently predicted in CrI3/Gr heterostructure37, therefore similar MR enhancement effect may also exist, which needs to be further studied. More importantly, the giant MR of FGT/Gr heterostructure at room temperature stays almost unchanged with decreasing temperature, which is strikingly different from the temperature-dependent behavior in previously reported systems. With rapid advancement of growing large-area graphene and related 2D materials, our work holds an attractive prospect for fabricating highly sensitive graphene-based magnetic sensors with wide temperature operation ranges.

Methods

Heterostructure preparation and device fabrication

Monolayer graphene was prepared by mechanically peeling high-quality graphite (natural graphite from HQ Graphene) onto SiO2(285 nm)/Si substrate and identified by optical contrast as well as Raman spectra. Multilayer Fe3GeTe2 was exfoliated and transferred onto monolayer graphene by PDMS dry transfer technique in glove box (O2, H2O < 1 ppm). Electrodes were patterned by e-beam lithography and then Ti/Au (2 nm/50 nm) was deposited by an e-beam evaporator with base pressure of 10−7 Torr. Standard lift-off procedure was done subsequently and blowed dry with Ar gun. Finally, multilayer h-BN was exfoliated and transferred onto the device channel region to prevent Fe3GeTe2 from being oxidized in air. For CGT/Gr and MoS2/Gr heterostructure devices, same procedures were followed. For vacuum annealing, device was put into a tube furnace equipped with turbo pump station (base pressure: 10−6 Torr) and kept at different temperatures for 3 h.

Magneto-transport measurements

The magneto-transport measurements were carried out in a Cryofree superconducting magnet system (CFMS-12T-30VTI, Cryogenic Co.) with magnetic field up to 12 T by using two source meters (Model 2400 and Model 2450, Keithley Inc.). To apply back gate voltage, the source terminal was connected to the back gate and the leakage current through the SiO2 dielectric layer was monitored.

Theoretical calculation details

The first-principles calculations were performed using Vienna ab initio simulation package (VASP) based on the density function theory with LDA + U. The energy cut off of the plane wave basis was set as 400 eV, and the Brillouin zone was sampled by 6 × 6 × 1 k-mesh.