INTRODUCTION

Exceptional points (EPs) are special points in the parameter space of a non-Hermitian system where two or more eigenstates and their corresponding eigenvalues coalesce. At these points, compared to the Hermitian Hamiltonian, the eigenvalues of the underlying system’s Hamiltonian have complex values1,2,3,4,5. Recent studies have shown that open systems undergo phase transitions at EPs, leading to a variety of interesting physical phenomena, including chirality6,7, unidirectional transmission or reflection8,9, topological phase transition10,11, parity-time symmetry breaking12,13 and charge-conjugation parity (CP) symmetry breaking14, and supernormal sensitivity to perturbations15,16. These properties have become the focus of research on non-Hermitian systems associated with EPs, which opened the door to a series of experimental studies in optics17,18,19,20, electronics21,22, and enhanced sensing23,24,25,26,27 (where the sensor sensitivity is enhanced by energy bifurcation near the EPs). The combination between non-Hermiticity and many-body interaction enables the emergence of non-trivial effects28,29,30, thus providing a platform to study the emergent phases beyond few-body scenarios.

Due to the strong dipole interaction between Rydberg atoms31,32,33, they have become a versatile tool for studying many-body physics. This long-range interaction induces non-linearity and gives rise to a unique dissipation channel, enabling investigations into non-equilibrium phase transitions34,35,36,37,38,39,40, self-organization41,42,43,44, ergodicity breaking and time crystals45,46,47,48,49,50,51. The dissipation induced by interactions can cause energy to be exchanged between a many-body system and its external environment, thereby influencing the dynamics and symmetric properties of the system, i.e., non-Hermitian many-body physics. Thus, studying the relationship between many-body interactions and non-Hermiticity can provide a new framework to investigate non-Hermitian dynamics in many-body scenarios52. Studying these in Rydberg atom systems has advantages in precise control of interactions, offering valuable insights in finding new emergent phases in symmetry breaking14, which is the starting point of this work.

Here, we propose a paradigm for studying non-Hermitian physics in cold Rydberg atomic gases, where the non-Hermitian term arises from dissipation induced by long-range Rydberg-Rydberg interactions. In contrast to other systems characterized by different types of interaction, such as those involving electron-electron and cavity-coupled interactions discussed in previous studies19,53,54, our system features a different interaction and dissipation mechanisms. This leads to the unique non-Hermitian dynamics and provides a ideal platform for experimentally studying EPs. We observe a normal electromagnetically induced transparency (EIT) spectrum under weak Rydberg atom interactions, whilst the peak of EIT splits into two when in strong interaction, indicating that the system crosses the second-order EPs. Additionally, our theoretical model confirms the existence of the third-order EP. In this scenario, the interaction is a dominant resource for system to produce non-Hermitian features, leading to rich hysteresis trajectories by varying probe intensities. The area of hysteresis loops reveals energy loss due to non-Hermiticity, and the dynamics can be tuned in various time scales.

RESULTS

Physical model

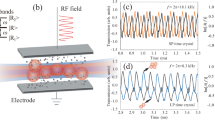
Our model is based on a three-level Rydberg atom system, as depicted in Fig. 1a. There are three atomic state manifolds of ground state \(\vert g \rangle\), metastable state \(\left\vert e\right\rangle\), and Rydberg state \(\left\vert r\right\rangle\). The probe field with Rabi frequency (detuning) Ωp (Δp) drives the transition \(\vert g\rangle \leftrightarrow \vert e\rangle\), and the coupling field with Rabi frequency (detuning) Ωc (Δc) drives the transition \(\left\vert e\right\rangle \leftrightarrow \left\vert r\right\rangle\). The spontaneous decay rates of the states \(\left\vert e\right\rangle\) and \(\left\vert r\right\rangle\) are Γ1 and γ, and γeff is the decay rate caused by Rydberg many-body interactions. A pair of atoms i and j at positions ri and rj excited to the Rydberg states \(\left\vert r\right\rangle\) interact with each other via a van der Waals (vdW) potential VvdW ∝ C6/R6, where C6 is the coefficient and R represents the distance between the Rydberg atoms.

Fig. 1: Schematic of many-body interaction induced EPs and hysteresis loops in Rydberg atoms.
figure 1

a Rydberg atomic energy level diagrams. Probe Ωp and coupling Ωc fields excite atoms with detunings Δp and Δc. Γ1 and γ are spontaneous decay rates of states \(\left\vert e\right\rangle\) and \(\left\vert r\right\rangle\), and γeff is the decay rate caused by Rydberg many-body interactions. b Schematic diagram of the experimental setup. The probe beam is incident opposite to the coupling beam through the lens and focused in a magneto-optic trap (MOT) trapping 85Rb atoms, and the transmission signals are detected using a photo-multiplier tube (PMT). c Measured transmission by positively (Up, pink) and negatively (Down, blue) scanning \({({\Omega }_{{{{\rm{p}}}}}/2\pi )}^{2}\) with the scan time Ts, and the trajectories connected by data points exhibit hysteresis loop.

Full size image

By the EIT theory of the ensemble of cold atoms, long-range interactions between atoms limit the medium to behave as a collection of superatoms (Rydberg polaritons), each containing a blockade volume that can hold at most one Rydberg excitation as shown in Fig. 1b. The experimental setup is depicted by Fig. 1b, and the scan of \({\Omega }_{{{{\rm{p}}}}}^{2}\) probes the dynamics of system response, as given in Fig. 1c. Here, the error bars are derived from the standard deviation calculated using three independent measurements, following the same estimation method used throughout the manuscript. The Rydberg polaritons display a dephasing feature when considering the interactions with each other, where the non-uniform distribution of the Rydberg atoms inside the polariton causes the position-dependent phase shifts55,56.

The interaction between polaritons accelerates the decay of Rydberg atoms and causes a broadening of the Rydberg energy levels. This creates an additional dissipation channel for the Rydberg state \(\left\vert r\right\rangle\) to its surrounding environment; further analysis can be found in the Methods section. In the rotating frame, the Hamiltonian of our system takes the form

$${H}_{1}=\left(\begin{array}{ccc}0&{\Omega }_{{{{\rm{p}}}}}/2&0\\ {\Omega }_{{{{\rm{p}}}}}/2&{\Delta }_{{{{\rm{p}}}}}&{\Omega }_{{{{\rm{c}}}}}/2\\ 0&{\Omega }_{{{{\rm{c}}}}}/2&{\Delta }_{{{{\rm{c}}}}}+{\Delta }_{{{{\rm{p}}}}}-i{\gamma }_{{{{\rm{eff}}}}}/2\end{array}\right),$$
(1)

where γeff = Vρrr donates the effective non-Hermitian term. In our theoretical model, V represents the interaction strength and ρrr represents the population of the Rydberg atoms, with both factors contributing to the overall decay rate of Rydberg atoms. Obviously, when Δp = Δc = 0, this system is protected by CP-symmetry, and the non-Hermitian Hamiltonian satisfies \({U}_{CP}{H}_{1}{U}_{CP}^{-1}=-{{H}_{1}}^{*}\) with UCP = diag(1, −1, 1)14.

The eigenvalues of H1 are calculated as E = E1, E2, E3. In this case, we can observe the Riemann surface showing real and imaginary parts of the eigenvalues of Hamiltonian H1 [see more details in the Methods section]. The non-zero γeff induces imaginary parts of eigenvalues and generates the non-Hermitian features. By increasing γeff, the coalesce of three eigenvalues emerges and results in complex singularities in energy spectrum, we called these points as EPs2,14.

Additionally, we reveal the existence of the third-order EP in our theoretical simulations, which shows promising potential for the application of precision measurement due to their enhanced sensitivity to perturbations23,27. At the third-order EPs, the real and imaginary parts of the eigenvalues exhibit a triple degeneracy. The three eigenvalues coalesce at a single point in both their real and imaginary components [see more details in the Methods section]. This unique degeneracy at the third-order EPs is different from the case at the second-order EPs in PT symmetry two-level system where the real and imaginary parts of the eigenvalues will degenerate simultaneously2,12,57.

The system also exhibits two second-order EPs, with a stable regime existing between these EPs [see more details in the Methods section]. In the scenario of the stable regime, a triple degeneracy of the eigenenergy exists in real space (Re[Ei] = 0, i ∈ {1, 2, 3}), while the corresponding imaginary parts separate into three distinct values. The eigenvalues satisfied E1 ≠ E2 ≠ E3 and \({E}_{i}\in i{\mathbb{R}}\), indicating CP-symmetry breaking14. Outside this regime, when the eigenvalues of real space are completely non-degenerate, the eigenvalues of imaginary space separate into two values where two of the three are degenerate. Here, \({E}_{1}=-{E}_{2}^{*}\) and \({E}_{3}\in i{\mathbb{R}}\) [or \({E}_{1}=-{E}_{3}^{*}\) and \({E}_{2}\in i{\mathbb{R}}\)], indicating the preservation of CP-symmetry.

We calculate the solution of master equation \(\dot{\rho }=-i[\hat{{H}_{1}},\rho ]+{{{\mathcal{L}}}}[\rho ]\) at the steady-state condition \(\dot{\rho }=0\). By the treatment of mean-field method, we map the spectrum of the normalized Im[ρeg] [corresponding to the transmission of EIT] versus the interaction strength V and detuning Δp, as shown by the down panel in Fig. 2a. With increase of V, for example, from V = 0 to V = 110γ, the peak of Im[ρeg] decreases and the neighbor two peaks emerge, as shown in Fig. 2b–e and the up panel in Fig. 2a. In this process, the system crosses the EPs, and the peak of Im[ρeg] splits into two, indicating that the degeneracy of one complex eigenvalue of system has been de-degenerated.

Fig. 2: Theoretical phase diagram.
figure 2

a Theoretical spectrum Im[ρeg] versus the interaction strength V and detuning Δp. As the interaction strength gradually increases, Im[ρeg] decreases, as shown in (b) and (c). With further increase in interaction strength, the system transits an EP (marked by the black arrow in the up panel of (a)) and two distinct transmission peaks emerge [marked by the two black arrows] in the spectrum, as depicted in (d) and (e). The frequency difference δΔp between these emergent two peaks is indicated by the red circles in the up panel in (a). A value of 0 means that the system does not exhibit two distinguishable peaks. In these simulations, we set Γ1 = 6γ, Δc = 0, Ωc = 3γ, and Ωp = γ.

Full size image

Non-Hermitian spectrum and exceptional point

The presence of strong interactions between Rydberg atoms leads to additional dissipation, which provides a platform to study non-Hermitian spectrum. In the experiment, we excite the ground state of a cold ensemble of 85Rb atoms to Rydberg state \(\vert 47{D}_{5/2},F=5,{m}_{F}=-5 \rangle\) by the EIT method, see more detailed information in Methods section. We measure the spectra by scanning probe detuning Δp from Δp = −2π × 15 MHz to Δp = 2π × 15 MHz under different probe intensities \({({\Omega }_{{{{\rm{p}}}}}/2\pi )}^{2}\).

As the probe intensity increases, the interaction between Rydberg atoms become progressively stronger. This enhanced interaction is similar to the effect of raising the interaction strength V in theoretical model, where both scenarios lead to an increase in the decay rate of Rydberg atoms due to enhanced interaction-induced dissipation [see more detail in Methods section]. By this way, we can map a phase diagram of system that responds to parameters of probe detuning Δp and intensity \({({\Omega }_{{{{\rm{p}}}}}/2\pi )}^{2}\). From \({({\Omega }_{{{{\rm{p}}}}}/2\pi )}^{2}\) = 9 MHz2 to \({({\Omega }_{{{{\rm{p}}}}}/2\pi )}^{2}\) = 64 MHz2, the dynamics of response are obtained. When the probe intensity \({({\Omega }_{{{{\rm{p}}}}}/2\pi )}^{2}\) is small [for example, \({({\Omega }_{{{{\rm{p}}}}}/2\pi )}^{2}\le 14.5\) MHz2], the EIT spectrum is normal as the interaction between Rydberg atoms is weak. In this process, the system has three eigenvalues as we can see only one peak and two dips in Fig. 3b [the peak and dips result from one zero energy and two symmetric eigenenergy as described in ref. 58], and this corresponds to the regime of Hermiticity approximately [as the interaction is ignored].

Fig. 3: Measured phase diagram.
figure 3

a Measured EIT transmission spectrum versus the probe intensity, which is proportional to \({\Omega }_{{{{\rm{p}}}}}^{2}\). The EIT spectrum shows a visible transmission peak when the probe intensity is low, which means that the interaction between Rydberg atoms are so weak that the system maintains Hermiticity, as shown in (b). As the probe intensity grows, non-Hermiticity of the Rydberg atoms system begins to emerge, which is manifested in the transmission spectrum as a weakening of the transmission intensity, as shown in (c). And as the probe intensity continues to increase, the strong interaction between the Rydberg atoms brings out the eigenenergy bifurcation, and two transmission peaks appear in the EIT spectrum, as shown in (d) and (e). The red circles in the upper panel of (a) indicate the frequency shifts δ of the two transmission peaks.

Full size image

When the probe intensity \({({\Omega }_{{{{\rm{p}}}}}/2\pi )}^{2}\) is large [for example, \({({\Omega }_{{{{\rm{p}}}}}/2\pi )}^{2} > 14.5\) MHz2], non-Hermiticity of system begins to emerge and the peak intensity of the EIT spectrum becomes weak, as shown in Fig. 3c. With a further increase of \({({\Omega }_{{{{\rm{p}}}}}/2\pi )}^{2}\), the peak of EIT spectrum splits into two peaks and the system undergoes the second-order EP [see the results in Fig. 3d, e]. At EP (\({({\Omega }_{{{{\rm{p}}}}}/2\pi )}^{2}\) = 36.5 MHz2), a sudden change in the physical parameters breaks symmetry of system, leading to a bifurcation where the real and imaginary parts of system eigenvalue coalesce and split respectively. In this scenario, the presence of spectrum splitting post-EPs signatures the breaking of CP-symmetry14. The peaks in Fig. 3e are asymmetric due to the small shift on Rydberg energy level.

Hysteresis trajectories

The dependence on the transmission on the probe intensity allows us to observe hysteresis trajectories, which reflects the interplay between Rydberg atoms’ response and theirs interaction. For all hysteresis trajectories measurements, the detuning values for both the coupling and probe beams were set to zero, which is consist with the conditions used in the theoretical calculations presented in the Methods section. Notably, all hysteresis trajectories measurements were conducted under weaker interaction strengths compared to the experimental conditions for observing EPs in Fig. 3, which required higher optical density. Hence, even at larger values of \({\Omega }_{{{{\rm{p}}}}}^{2}\), the system remained below the EPs during these measurements. Our investigation of hysteresis trajectories reveals the non-Hermitian characteristics of the Rydberg atom system, highlighting the dynamic behavior below the EPs and the emergence of hysteresis loops.

By scanning \({({\Omega }_{{{{\rm{p}}}}}/2\pi )}^{2}\) from 0 MHz2 to 140.6 MHz2 and vice versus, we can obtain a series of closed circles under different optical densities (ODs), as shown in Fig. 4a–d. In the regime with small atoms numbers (which corresponds to large atomic distance R), we can find that the invariance of the linearity of transmission to probe intensity. This implies the interaction-induced dissipation does not dominate by comparing the inherent decay rate γ of Rydberg state, corresponding to the physical process under the regime of Hermiticity, as given by the case of OD = 4.6 in Fig. 4a. When we increase OD, for example, from OD = 6.8 to OD = 8.9, the transmission for positive and negative scans undergoes behavior with different scaling. The physics behind this phenomenon is non-Hermiticity: at larger OD, the Rydberg atomic interaction-induced dissipation cannot be ignored and the response is no longer linear to probe intensity and results in the emergence of hysteresis loop, see the area between pink and blue data given in Fig. 4b–d.

Fig. 4: Measured hysteresis trajectories versus OD, Ωc, and n.
figure 4

a–d Measured transmission with scanning \({\Omega }_{{{{\rm{p}}}}}^{2}\) in positive (pink, up) and negative (blue, down) directions under optical densities of OD = 4.6 (a), OD = 6.8 (b), OD = 7.7 (c) and OD = 8.9 (d). The pink circle data represents the transmission when increasing \({({\Omega }_{{{{\rm{p}}}}}/2\pi )}^{2}\) from 0 MHz2 to 140.6 MHz2, and the blue circle data shows the transmission by scanning \({({\Omega }_{{{{\rm{p}}}}}/2\pi )}^{2}\) from 140.6 MHz2 to 0 MHz2 with the same sweep rate. e, f Measured transmission versus the coupling field’s Rabi frequency of Ωc = 2π × 13.3 MHz (e), Ωc = 2π × 27.8 MHz (f), Ωc = 2π × 38.6 MHz (g) and Ωc = 2π × 45.6 MHz (h). i–l Measured transmission versus the principal quantum number of n = 40 (i), n = 42 (j), n = 47 (k), n = 50 (l).

Full size image

We also model the trajectories of system using the Lindblad master equation \(\dot{\rho }=-i[\hat{{H}_{1}},\rho ]+{{{\mathcal{L}}}}[\rho ]\), where the operator \({{{\mathcal{L}}}}\) describes the decay rate of system. The theoretical results predict the hysteresis loops of Im[ρeg], see more details in Methods section. The phenomenon of hysteresis loop is counter-intuitive because the transmission does not overlap under the same probe intensity, in which the current state of system not only depends on its current inputs but also on its past states and inputs. The increase of atoms number through probe intensity forms structured Rydberg clusters by near neighbor interaction, the induced dissipation makes the clusters’ behaviour different from the case of few atoms. If the probe intensity is then reduced conversely, the atoms retains some level of dissipation. To completely release the dissipation of atoms, only small reduction of probe intensity is required in the reversal scanning, see more detailed information in Methods section. This asymmetry in the response of the Rydberg atoms to increasing and decreasing probe intensity is a clear manifestation of hysteresis.

The direction of hysteresis trajectories is reversal to magnetic hysteresis in ferromagnetic material59, but same with the normal elastic hysteresis of rubber60. The different directions of trajectories result from the distinct physical mechanism behind these hysteresis. In our experiment, different ODs (which relate to different numbers of atoms and interaction strengths) can alter how the system responds to changes in probe intensity, and influences the size (area) and shape of the hysteresis loop observed experimentally, as illustrated in Fig. 4a–d). In terms of energy, the area enclosed by the hysteresis loop quantifies the energy loss during scanning \({({\Omega }_{{{{\rm{p}}}}}/2\pi )}^{2}\).

The hysteresis loop also depends on the coupling Rabi frequency Ωc, as given in Fig. 4e–h. We can find that the hysteresis loop only appears within a range of Ωc. When we use a relative small Rabi frequency of Ωc = 2π × 13.3 MHz, the corresponding excited Rydberg atoms number cannot provide enough interaction strength between atoms, thus resulting in normal trajectories shown in Fig. 4e. When we set Ωc = 2π × 27.8 MHz, the interaction-induced dissipation affects the scaling of transmission to probe intensity, then generates a hysteresis loop given in Fig. 4f. If the system is driven under a large Ωc (for example, Ωc = 2π × 38.6 MHz and Ωc = 2π × 45.6 MHz) that the atoms have no time to respond, then the hysteresis loop shrinks and disappears.

Furthermore, we also investigated the effect of the principal quantum number n on the hysteresis loop while keeping OD and Ωc constant, which maintained an equal number of excited atoms, as shown in Fig. 4i–l. In Rydberg atom system, changes in the principal quantum number n directly influence the value of C6, thereby influencing the interaction strength V ∝ C6. At relatively low values of n [such as n = 40], the interactions between Rydberg atoms are weak, resulting in less energy dissipation. This leads to a smaller hysteresis loop in the EIT spectrum, as illustrated in Fig. 4i. As the principal quantum number increases, the interaction strength correspondingly intensifies, leading to greater energy dissipation within the system. This enhanced dissipation manifests as an expansion of the hysteresis loop, which further reveals the mechanism of interaction-induced dissipation in our system, as illustrated in Fig. 4j–l.

Hysteresis loops dynamics

The underlying mechanism behind the physical system is based on interaction-induced dissipation, which exhibits how quickly the system respond to changes in probe field. This enables us to capture the time-dependent behavior of system as it undergoes changes in external conditions. In the experiment, we record hysteresis loops versus the scanning time Ts and measure the area enclosed by hysteresis loop. The results are found in Fig. 5a. In this scenario, we consider two cases of OD = 8.0 (blue data in Fig. 5a) and OD = 4.5 (red data in Fig. 5a) and show the difference between them. We fit the measured areas using dashed lines, where the fit function is \(y=a{e}^{-b{(x-d)}^{\alpha }}\)+c (a = −64.9, b = 0.053, c = 65.3, d = 5, α = 1.5) for OD = 8.0 and the fit function is y = 0 for OD = 4.5. For OD = 4.5, the atoms are dilute, the linearity of transmission on \({({\Omega }_{{{{\rm{p}}}}}/2\pi )}^{2}\) is invariant to the scanning time Ts as the interaction is ignored. However, when we increase OD to 8.0, hysteresis loops appear and the area grows versus Ts.

Fig. 5: Hysteresis dynamics.
figure 5

a The measured area of hysteresis loops versus the scan time Ts under OD = 8 (blue circles) and OD = 4.5 (red circles). The blue data is fit by the function of \(y=a{e}^{-b{(x-d)}^{\alpha }}\)+c (a = −64.9, b = 0.053, c = 65.3, d = 5, α = 1.5), and the red data is fit by the function of y = 0. b, c are the measured transmission (OD = 8) in positive and negative scanning \({({\Omega }_{{{{\rm{p}}}}}/2\pi )}^{2}\) by setting Ts = 2 μs and Ts = 18 μs, respectively. d, e are the measured transmission (OD = 4.5) in positive and negative scanning \({({\Omega }_{{{{\rm{p}}}}}/2\pi )}^{2}\) by setting Ts = 2 μs and Ts = 18 μs, respectively.

Full size image

In our experiment, a fast scan accumulates a small number of Rydberg atoms within limited time interval to each data, which makes the interactions so weak that the effect from non-Hermiticity might not dominate, see the results shown in Fig. 5b. As Ts increases, this corresponds to more excited Rydberg atoms for a relatively large time interval and interactions between the Rydberg atoms cannot be ignored, thus the effect of non-Hermiticity emerges, as illustrated in Fig. 5c. For our experiment, there’s a characteristic measurement time of Ts ~ 5 μs, where shorter scan times capture system’s transient behavior, while longer scan times converge to the equilibrium value. The results in Fig. 5d, e show examples of small OD, the variance of scanning time do not affect the linearity of transmission to probe intensity.

DISCUSSION

Our experiment serves as a preliminary verification test for non-Hermitian many-body physics1,61, and promotes the applications towards studying high-order EPs and symmetry breaking in high-dimension systems. For example, according to ref. 14, both sides of third-order EPs have different signs of winding number, thus providing a platform to study the topological properties (such as topology stability, topological phase transition) around EPs in the Rydberg system. In addition, the phenomenon of hysteresis loops enables us to build an interface between hysteresis dynamics and non-Hermitian physics, this could provide an experimental correspondence to theory62.

In summary, we have observed interaction-induced second-order EPs and hysteresis loops in a cold Rydberg atomic gas. The interaction between Rydberg atoms endows system a dissipation channel, leading to non-Hermitian many-body dynamics. In the experiment, we observe interaction-induced hysteresis loops, in which the dynamics of the system is dramatically distinct by comparing with weak-interaction case. In the context of a cold Rydberg atomic gas, the emergence of EPs and the hysteresis loops due to many-body interactions help us to explore the rich dynamics between many-body interaction and the non-Hermitian physics.

Methods

Details of the experimental setup

To study non-Hermitian many-body dynamics, the emergence of EPs, and hysteresis trajectories, we prepare a cold ensemble of 85Rb atoms trapped in a three-dimensional magneto-optic trap (MOT). The atomic ensemble is prepared in the ground state \(\vert g \rangle=\vert 5{S}_{1/2},F=3,{m}_{F}=-3 \rangle\) by an optical pumping process. In experiment, we wrapped the MOT with a double-layer magnetic shield system. By this way, we can shield the system from external magnetic fields, and it can reduce the internal magnetic field to less than 10 mGauss. A guiding magnetic field is generated by a pair of Helmholtz coils symmetrically placed around the atomic ensemble, and the direction of the field is along the direction of beams propagation. By this way, the direction of the quantisation axis of the system is confirmed.

We used a two-photon transition scheme to excite 85Rb atoms from the ground state to the Rydberg state. The probe beam (ωp ≈ 10 μm) driving the atoms from the ground state \(\vert g \rangle\) to the intermediate excited state \(\vert e \rangle=\vert 5{P}_{3/2},F=4,{m}_{F}=-4 \rangle\), and the coupling beam (ωc ≈ 20 μm) then drives the transition from \(\left\vert e\right\rangle\) to the Rydberg state \(\vert r \rangle=\vert 47{D}_{5/2},F=5,{m}_{F}=-5 \rangle\), as shown in Fig. 1a in the main text. The probe beam and coupling beam are focused into the cold atomic ensemble, and we used the Pound-Drever-Hall method to lock probe and coupling beams frequency, thus constituting the EIT process. We use a beam splitter to split the coupled beam into two beams before focusing into the cold atomic ensemble, and the intensity of one of these beams was detected using a photodetector. This method allows us to monitor the intensity of the coupling beam in real time. The transmission signals are detected using a photo-multiplier tube.

In experiment, we loaded a triangular wave signal that was generated using a signal generator (RIGOL DG4102) onto the acousto-optic modulator. By this way, we produce the process of increasing beam intensity (Up process) and intensity reduction process (Down process). To better compare the Up and Down processes, we perform an inversion of the Down process, as shown in Fig. 1c in the main text.

Non-Hermitian Hamiltonian

The system of interest is schematically depicted in Fig. 1b, where two optical fields with spatial overlap comprise a counter-collinear weak-probe field and a strong-control field. The Rydberg atomic level structure is the three-level EIT configuration shown in Fig. 1a. The strong-control field with the Rabi frequency (Ωc) and detuning (Δc) drives the transition \(\left\vert e\right\rangle \leftrightarrow \left\vert r\right\rangle\); the weak-probe field with the Rabi frequency (Ωp) and detuning (Δp) drives the transition \(\vert g \rangle \leftrightarrow \left\vert e\right\rangle\), and the two-photon detuning between two counter-collinear fields is Δ = Δp–Δc. Under the Rydberg EIT configurations, the population is mainly distributed in \(\vert g \rangle\). The spontaneous decay of the state \(\left\vert e\right\rangle\) (\(\left\vert r\right\rangle\)) at a rate Γ1 (γ). The interactions between excited Rydberg atoms are reflected in the optical responses of atoms and the transmission of the probe field.

The Hamiltonian in the interaction picture and rotating-wave approximation reads (ℏ = 1),

$${H}_{many}= {\sum }_{j=1}^{N}\left[-({\Delta }_{{{{\rm{p}}}}}+{\Delta }_{{{{\rm{c}}}}}){\hat{\sigma }}_{rr}^{\,j}-\left({\Omega }_{{{{\rm{p}}}}}{\sigma }_{eg}^{\,j}+{\Omega }_{{{{\rm{c}}}}}{\sigma }_{re}^{\,j}+{{{\rm{H.c.}}}}\right)\right]\\ +{\sum }_{j=1}^{N}\left[-{\Delta }_{{{{\rm{p}}}}}{\hat{\sigma }}_{ee}^{\,j}+{\sum}_{j < k}{V}_{jk}{\sigma }_{rr}^{\,j}{\sigma }_{rr}^{k}\right],$$
(2)

where \({\sigma }_{\alpha \beta }^{j}=\vert {\alpha }_{j} \rangle \langle {\beta }_{j} \vert\) (α, β = e, g, r). We then consider the mean-field approximation, in which a single atom is immersed in a field generated by the interactions between itself and other atoms. Consequently, the problem of solving the dynamic many-body system is reduced to addressing the dynamics of one single atom within that field, treating the other atoms as part of the environment. The Hamiltonian can be written as

$${H}_{many}={H}_{1}\otimes {I}_{N-1}+{I}_{1}\otimes {H}_{N-1}+{H}_{I},$$
(3)

where HI describes the interaction between the single atom and the environment, H1 is the single atom Hamiltonian, HN−1 is the Hamiltonian of the environment, and I1 (IN−1) denotes the identity in the Hilbert space H1 (HN−1). Consider the two-body interaction between the Rydberg atoms, the interaction distance Rj represents the single atom between the atom in the environment. Then the total Rydberg state \(\vert {r}_{N} \rangle={\sum }_{j=1}^{N-1} \vert {r}_{1} \rangle \otimes \vert {r}_{j} \rangle\) evolves according to

$$\hat{U}(t)={\sum }_{j=1}^{N-1}{e}^{-i{V}_{j}t}\left(\left\vert {r}_{1}\right\rangle \otimes {\sum }_{i=1}^{N-1}{\left\vert {r}_{i}\right\rangle }_{j}\right)\left(\left\langle {r}_{1}\right\vert \otimes {\sum }_{i=1}^{N-1}{\left\langle {r}_{i}\right\vert }_{j}\right).$$
(4)

Since the distance between the single atom and the j-atom in the environment Rj is different, in regarding the energy shifts on \(\vert {r}_{1} \rangle\), it is necessary to consider the distinct contributions from the j-atom. The atom far away in the environment produces a small shift, otherwise the shift will be large, due to the form of van der Waals (vdW) potential VvdW ∝ C6/R6. Overall, this effect is to widen the energy level \(\vert {r}_{1} \rangle\) with an effective width γeff. Here, we consider the reduced density matrix of the single-atom system, and the non-Hermitian Hamiltonian has the form

$${H}_{1}= -{\Delta }_{{{{\rm{p}}}}}{\hat{\sigma }}_{ee}-({\Delta }_{{{{\rm{p}}}}}+{\Delta }_{{{{\rm{c}}}}}-\frac{i{\gamma }_{{{{\rm{eff}}}}}}{2}){\hat{\sigma }}_{rr}\\ -\left({\Omega }_{{{{\rm{p}}}}}{\sigma }_{eg}+{\Omega }_{{{{\rm{c}}}}}{\sigma }_{re}+{{{\rm{H.c.}}}}\right),$$
(5)

where γeff reveals the effective decay rate induced by the interaction of the environment. The eigenvalues of H1 are given by

$${E}_{1}=\frac{1}{6}\left(\frac{C} {\root 3 \of {B+iA} } - {\root 3 \of {4B+4iA} } -2i{\gamma }_{{{{\rm{eff}}}}}\right),$$
(6)
$${E}_{2}=\frac{1}{12}\left(\left(1-i\sqrt{3}\right) {\root 3 \of { 4B+4iA} } -\frac{\left(1+i\sqrt{3}\right)C} {\root 3 \of { B+iA} } -4i{\gamma }_{{{{\rm{eff}}}}}\right),$$
(7)
$${E}_{3}=\frac{1}{12}\left(\left(1+i \sqrt{3}\right) {\root 3 \of { 4B+4iA} } -\frac{\left(1-i\sqrt{3}\right)C}{\root 3 \of { B+iA} }-4i{\gamma }_{{{{\rm{eff}}}}}\right),$$
(8)

where

$$A=9{\gamma }_{{{{\rm{eff}}}}}\left({\Omega }_{{{{\rm{c}}}}}^{2}-2{\Omega }_{{{{\rm{p}}}}}^{2}\right)-2{\gamma }_{{{{\rm{eff}}}}}^{3},$$
(9)
$$B=3\sqrt{3} {\root 3 \of {\begin{array}{l}{\gamma }_{{{{\rm{eff}}}}}^{2}\left({\Omega }_{{{{\rm{c}}}}}^{4}+20{\Omega }_{{{{\rm{c}}}}}^{2}{\Omega }_{{{{\rm{p}}}}}^{2}-8{\Omega }_{{{{\rm{p}}}}}^{4}\right)\\ -4{\Omega }_{{{{\rm{p}}}}}^{2}{\gamma }_{{{{\rm{eff}}}}}^{4}-4{\left({\Omega }_{{{{\rm{c}}}}}^{2}+{\Omega }_{{{{\rm{p}}}}}^{2}\right)}^{3}\end{array}} },$$
(10)
$$C=2 {\root 3 \of 2} \left({\gamma }_{{{{\rm{eff}}}}}^{2}-3\left({\Omega }_{{{{\rm{c}}}}}^{2}+{{\Omega }_{{{{\rm{p}}}}}}^{2}\right)\right).$$
(11)

By setting the parameters Ωc = 3γ and Δp = Δc = 0, we obtain the real and imaginary parts of the system eigenvalues as a function of γeff and Ωp, as given in Fig. 6.

Fig. 6: Theoretical simulations of third-order EPs.
figure 6

a Real and b imaginary parts of the system eigenvalues as a function of Ωp and γeff. In these simulations, we set Δc = Δp = 0, Ωc = 3γ. c, d are the real and imaginary parts of the system eigenvalues as a function of Ωp with γeff = 10γ. e, f represent the system eigenvalues as a function of γeff with Ωp = 0.8γ. g, h represent the system eigenvalues as a function of γeff with Ωp = 1.061γ. The black dots represent the third-order EP of the system. The red, orange, and blue lines correspond to the values of E1, E2, and E3, respectively.

Full size image

From these results, for example in Fig. 6c, d, we can find that the second-order EPs appear. Before the EPs, the real parts of the three eigenvalues coalesce and the imaginary parts of the eigenvalues split, characterized by E1 ≠ E2 ≠ E3 and \({E}_{i}\in i{\mathbb{R}}\), indicating CP-symmetry breaking. In contrast, after the EPs, the eigenvalues satisfy \({E}_{1}=-{E}_{2}^{*}\) and \({E}_{3}\in i{\mathbb{R}}\) [or \({E}_{1}=-{E}_{3}^{*}\) and \({E}_{2}\in i{\mathbb{R}}\)], thereby preserving CP-symmetry14. In addition, when Ωp = 0.8γ, a second-order EPs first appear, and retain stable in a range of 5.77γ < γeff < 6.49γ (in the stable region, CP-symmetry breaking occurs) and then enter another second-order EPs (outside the stable region, the system preserves CP-symmetry), as shown in Fig. 6e, f. When Ωp = 1.061γ, the third-order EP appear, where both the real and imaginary parts of the system exhibit a triple degeneracy, and the system always preserving CP-symmetry, as shown in Fig. 6g, h).

Lindblad master equation

In the mean-field treatment, we solve the Lindblad master equation by adding the dissipation term Γ2 → γ + γeff = γ + Vρrr42,55,56,63,64,65,66, and obtain the following equations:

$${\dot{\rho }}_{gg}=i\frac{{\Omega }_{{{{\rm{p}}}}}}{2}({\rho }_{eg}-{\rho }_{ge})+{\Gamma }_{1}{\rho }_{ee},$$
(12)
$${\dot{\rho }}_{ee}=i\frac{{\Omega }_{{{{\rm{p}}}}}}{2}({\rho }_{ge}-{\rho }_{eg})+i\frac{{\Omega }_{{{{\rm{c}}}}}}{2}({\rho }_{re}-{\rho }_{er})-{\Gamma }_{1}{\rho }_{ee}+{\Gamma }_{2}{\rho }_{rr},$$
(13)
$${\dot{\rho }}_{rr}=i\frac{{\Omega }_{{{{\rm{c}}}}}}{2}({\rho }_{er}-{\rho }_{re})-{\Gamma }_{2}{\rho }_{rr},$$
(14)
$${\dot{\rho }}_{re}=i\frac{{\Omega }_{{{{\rm{c}}}}}}{2}({\rho }_{ee}-{\rho }_{rr})-i\frac{{\Omega }_{{{{\rm{p}}}}}}{2}{\rho }_{rg}-\left(i{\Delta }_{{{{\rm{c}}}}}+\frac{{\Gamma }_{2}}{2}+\frac{{\Gamma }_{1}}{2}\right){\rho }_{re},$$
(15)
$${\dot{\rho }}_{er}=i\frac{{\Omega }_{{{{\rm{c}}}}}}{2}({\rho }_{rr}-{\rho }_{ee})+i\frac{{\Omega }_{{{{\rm{p}}}}}}{2}{\rho }_{gr}+\left(i{\Delta }_{{{{\rm{c}}}}}-\frac{{\Gamma }_{2}}{2}-\frac{{\Gamma }_{1}}{2}\right){\rho }_{er},$$
(16)
$${\dot{\rho }}_{rg}=i\frac{{\Omega }_{{{{\rm{c}}}}}}{2}{\rho }_{eg}-i\frac{{\Omega }_{{{{\rm{p}}}}}}{2}{\rho }_{re}-\left(i({\Delta }_{{{{\rm{p}}}}}+{\Delta }_{{{{\rm{c}}}}})+\frac{{\Gamma }_{2}}{2}\right){\rho }_{rg},$$
(17)
$${\dot{\rho }}_{gr}=i\frac{{\Omega }_{{{{\rm{p}}}}}}{2}{\rho }_{er}-i\frac{{\Omega }_{{{{\rm{c}}}}}}{2}{\rho }_{ge}+\left(i({\Delta }_{{{{\rm{p}}}}}+{\Delta }_{{{{\rm{c}}}}})-\frac{{\Gamma }_{2}}{2}\right){\rho }_{gr},$$
(18)
$${\dot{\rho }}_{eg}=i\frac{{\Omega }_{{{{\rm{p}}}}}}{2}({\rho }_{gg}-{\rho }_{ee})+i\frac{{\Omega }_{{{{\rm{c}}}}}}{2}{\rho }_{rg}-\left(i{\Delta }_{{{{\rm{p}}}}}+\frac{{\Gamma }_{1}}{2}\right){\rho }_{eg},$$
(19)
$${\dot{\rho }}_{ge}=i\frac{{\Omega }_{{{{\rm{p}}}}}}{2}({\rho }_{ee}-{\rho }_{gg})-i\frac{{\Omega }_{{{{\rm{c}}}}}}{2}{\rho }_{gr}+\left(i{\Delta }_{{{{\rm{p}}}}}-\frac{{\Gamma }_{1}}{2}\right){\rho }_{ge}.$$
(20)

First, we consider the case of no-interaction (γeff = 0) and calculate the steady-state solution (\({\dot{\rho }}_{ij}\) = 0, where i, j represent the states of \(\left\vert g\right\rangle,\left\vert e\right\rangle\), and \(\left\vert r\right\rangle\)), we therefore obtained the element of density matrices ρeg and ρrr versus Δp and Γ2, with forms of ρeg(Δp, γ) and ρrr(Δp, γ), respectively. Then, by considering the interaction induced non-Hermiticity, we obtain the modified matrix element ρeg(Δp, γ + Vρrr) with the mean-field approximation Γ2 → γ + Vρrr. We plot Im[ρeg] versus Δp and V, the phase diagram and transmission lines are given by Fig. 2. In this framework, we keep Rydberg atom population ρrr fixed, assuming it behaves as in a non-interacting scenario where it varies only with Δp. By adjusting interaction strength V, we can effectively control the decay rate of Rydberg state.

To simulate hysteresis trajectories, the state of atoms is influenced not only by the external input but also by their previous states. In particular, the systematic evolution is dependent on the direction of scanning Ωp. Thus, we replace the time-dependent population ρrr(t) by the term \({\dot{\rho }}_{rr}(t)\) according to Eq. (14): \({\rho }_{rr}(t)=i{\Omega }_{{{{\rm{c}}}}}/2{\Gamma }_{2}({\rho }_{er}(t)-{\rho }_{re}(t))-{\dot{\rho }}_{rr}(t)/{\Gamma }_{2}\). Thus, the slope of Rydberg population \({\dot{\rho }}_{rr}(t)\) plays a crucial role in influencing the transient behavior of ρrr(t).

In the simulations, we treat the results ρij(t) at time t as the initial conditions for calculating ρij(t + Δt) at time t + Δt. This approach effectively captures the inherent memory effects in the system’s evolution. We specifically examined the time-dependent component Im[ρeg(t)] while scanning Ωp both positively and negatively, across various interaction strengths: V = 0, V = −400γ, and V = −1500γ. The corresponding results are presented in Fig. 7a–c. These results reveal intriguing behaviors of the scanned trajectories. In the case with no interaction (V = 0, Fig. 7a), the trajectories exhibit a coincident pattern, indicating that the system’s dynamics are symmetric. However, when considering interactions, specifically at V = −400γ and V = −1500γ, as depicted in Fig. 7b, c, the trajectories form closed loops.

Fig. 7: Hysteresis trajectories of Im[ρeg] versus interaction strength V.
figure 7

The simulated hysteresis versus interaction strength are given in (a) V = 0, (b) V = −400 γ, and (c) V = −1500 γ. The pink and blue arrows represents the positive and negative scanning Ωp. In these simulations, we set Γ1 = 12γ, Δc = Δp = 0, Ωc = 0.25γ, and ρre(t = 0) = 0.1.

Full size image

The emergence of these hysteresis loops underscores the critical role of interaction strength in shaping the dynamical properties of the system. Moreover, the observed dynamics align closely with experimental observations illustrated in Fig. 4a–l and Fig. 5a–e, which further corroborates the relevance of our simulation results. This consistency between theoretical predictions and experimental observations highlights the exact complex interplay between system memory and interaction, providing valuable insights into the underlying mechanisms governing the observed phenomena.