Introduction

Human activities have caused nitrate (NO3−) accumulation in aquatic ecosystems from various sources, including agricultural runoff, municipal sewage, industrial discharges, and the ammonia (NH3) cracking process when the byproduct nitrogen oxide dissolves in water1,2,3, which poses significant threats to both ecosystems and human health. The electrocatalytic NO3− reduction reaction (NO3−RR) to NH3, powered by renewable electricity under ambient conditions, offers significant promise for simultaneous NO3− removal and NH3 green synthesis2,4,5. However, real-world scenarios often involve polluted streams with low NO3− concentrations, such as textile wastewater ( ~ 7.4 mM) and industrial wastewater ( ~ 41.6 mM)2. Efficient conversion of low-concentration NO3− is challenging due to the complex eight-electron-nine-proton transfer process, limited mass diffusion, and the competitive hydrogen evolution reaction (HER)6,7. Therefore, developing electrocatalysts with high activity, selectivity, and stability for low-concentration NO3−RR to NH3 becomes imperative.

Inspired by the presence of iron active sites in both the industrial Haber−Bosch catalyst (a Fe-based compound) and the natural nitrogenase enzyme (which primarily contains a Fe-Mo cofactor), and given their low cost, Fe-based catalysts are considered as promising candidates for NO3−RR8,9,10. To further enhance their intrinsic catalytic activity, one effective strategy is to tune their electronic structures through strain engineering11. While less reported in Fe-based catalysts, strains have been shown to promote the NO3−RR-to-NH3 activity by improving NO3− adsorption and facilitating water dissociation to generate active hydrogen in several catalysts, such as tensile strain in Ru/O-doped Ru nanoclusters12, compressive strain in Bi nanocrystals13, and shear strain in Pd-CuO (ref. 14). However, strains in these catalysts are typically introduced manually prior to electrochemical reactions11,12,13,14. Considering the dynamic interactions between the catalyst surface and the electrolyte under external bias during electrolysis, pre-designed catalysts with precisely engineered structures may undergo undesirable in-situ changes15. Therefore, exploring whether the strain can be developed spontaneously during electrolysis in Fe-based catalysts is appealing to boost the NO3−RR performance and reveal the true catalytic active sites, facilitating a deeper understanding of the real structure-activity relationship.

In this context, two-dimensional (2D) FeM (M = Se, Te) chalcogenides present an excellent platform. While FeM chalcogenides have been studied extensively as magnets and superconductors16,17, their potential as electrocatalysts remains largely under-explored, primarily due to challenges such as anion dissolution and oxidation and the high exposure of Se/Te atoms18,19. However, these traditionally perceived limitations may offer opportunities for in-situ strain engineering, as the vacant Se/Te positions resulting from anion leaching can potentially be occupied by foreign anions with differing size and electronegativity, thereby inducing lattice distortion and modulating the electronic structure. Additionally, making catalysts into 2D morphology is equally important. The large specific surface area, abundant low-coordination atoms, and high flexibility of 2D materials20 enable facile structural modifications including strain engineering21,22. More importantly, thanks to their atomic thickness and large surface-area-to-volume ratio, surface modifications in 2D catalysts can potentially impact their entire volume, enabling concurrent surface and structural engineering23. For example, metal ions can be homogenously and controllably doped into 2D photocatalysts with minimal diffusion depth, whereas doping in bulk semiconductors is restricted to shallow surface layers23. Strain can be uniformly induced across the entire sheets of 2D materials like graphene24 and transition metal dichalcogenides25, affecting the properties of the entire materials, whereas strain in nanoparticles is often localized to specific regions, such as at edges, corners, or defects26. Given that the electrocatalytic process is a surface reaction, the abundance of unsaturated surface atoms in 2D catalysts allows for effective surface modifications during electrolysis. These surface changes can propagate throughout the entire sheet, enabling in-situ structural engineering of the entire material, rather than being limited to the surface alone. However, these considerations have been largely under-explored especially in the context of electrochemical NO3−RR, with recent studies primarily focusing on the development of Fe-based catalysts with pre-engineered structures prior to electrolysis8,9,10.

Here, we present a 2D Fe-based chalcogenide, i.e., iron telluride selenide (FeTeSe) nanosheets, and demonstrate the reaction-driven in-situ formation of anisotropic in-plane tensile and out-of-plane compressive strains to enhance low-concentration NO3− reduction to NH3 in alkaline media (Fig. 1a). Through a combination of ex-situ and operando synchrotron-based X-ray techniques including X-ray absorption fine structure (XAFS), X-ray diffraction (XRD), and X-ray scattering, we found that strain formation can be ascribed to the electrochemical generation of Se/Te vacancies, which facilitate the in-situ doping of oxygen species (i.e., O/OH) through OH− adsorption and NO3− adsorption followed by dissociation. Experimental investigations, in-situ attenuated total reflection infrared (ATR-IR) spectroscopy measurement, and density functional theory (DFT) calculations demonstrate that the strained Fe sites and surface hydroxyl groups work synergistically to promote the adsorption of NO3− and water, lower the energy barrier of the potential-determining step, and suppress the competing HER. Consequently, under a low NO3− concentration of 10 mM in 1 M KOH electrolyte, the FeTeSe nanosheets attain a maximum Faradaic efficiency (FE) for NH3 of 98.7 ± 2.2% at −0.55 V vs. reversible hydrogen electrode (RHE), a high NH3 yield rate of 42.14 ± 2.06 mg h−1 mgcat−1 at −0.75 V vs. RHE, and remarkable stability during cyclic and long-term operations, outperforming the FeTeSe bulk crystals, FeTe nanosheets, and many previously reported catalysts for low-concentration NO3−RR.

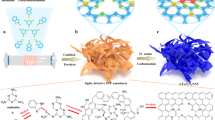
Fig. 1: Preparation and characterization of FeTeSe catalyst.
figure 1

a Schematic illustration for the synthesis of 2D FeTeSe nanosheets and the electrochemistry-induced formation of anisotropic strains. b, e Scanning electron microscopy (SEM) image (b) and XRD pattern (e) of FeTeSe bulk crystals. c, f TEM image (c) and XRD pattern (f) of the exfoliated FeTeSe nanosheets. d, g TEM image (d) and XRD pattern (g) of FeTeSe nanosheets on carbon paper after the alkaline NO3−RR. h WT contour maps of the Fe K-edge EXAFS of FeTeSe nanosheets, bulk crystals, FeSe, and Fe2O3. The color bars represent intensity with arb. units. Scale bars, b 2 µm; c 100 nm; d 200 nm. Source data are provided as a Source Data file.

Full size image

Results

Structural characterizations of catalysts

The formation of reaction-driven anisotropic strains in FeTeSe nanosheets involves three steps (Fig. 1a). Fe(TexSe1−x) is a typical layered material that crystallizes in a tetragonal structure (P4/nmm), with adjacent layers connected through the van der Waals (vdW) interactions (Supplementary Fig. S1), enabling the facile synthesis of 2D Fe(TexSe1−x) nanosheets from bulk crystals. First, bulk Fe0.90(Te0.60Se0.40) crystals were prepared via a high-temperature solid-state reaction, showing high crystallinity and a closely stacked lamellar layered architecture (Fig. 1b, e). Subsequently, a chemical lithium intercalation method (Supplementary Fig. S2) was employed to synthesize 2D wrinkled FeTeSe nanosheets with an average thickness of <3 nm (Fig. 1c, f and Supplementary Figs. S3, 4). The tetragonal phase of the exfoliated nanosheets is well preserved, as evidenced by the XRD pattern which displays the characteristic (001), (101), (002), (003), and (004) peaks without noticeable impurity peaks (Fig. 1f). The relative intensity of the (101) peak to the (001) peak increases, suggesting that some exfoliated nanosheets are no longer flat on the substrate, thus exposing more edge sites beyond the (001) basal plane (Fig. 1f). This finding is further corroborated by the transmission electron microscopy (TEM) and scanning TEM (STEM) images (Fig. 1c and Supplementary Figs. S3, 4), which show both flat and wrinkled nanosheets. Inductively coupled plasma optical emission spectroscopy (ICP-OES) confirms the composition as Fe0.92(Te0.70Se0.30) (Supplementary Table S1). The increased surface area of the exfoliated 2D nanosheets is demonstrated by the enhanced adsorption of oxygen-containing species during the water-involved exfoliation and subsequent material characterization processes27. X-ray photoelectron spectroscopy (XPS) analysis (Supplementary Fig. S5) reveals increased oxygen content in nanosheets compared to their bulk counterpart, as evidenced by the increased peak areas for Fe3+, Tex+, and Sex+ relative to the Fe2+, Te2−, and Se2− peaks that are characteristic of the FeTeSe lattice, along with the overall shift of all peaks to higher binding energies28,29. This increased oxidation is further supported by the Fe K-edge X-ray absorption near edge structure (XANES) spectra, which show a positive shift in the Fe K absorption edge with a general shift of its white line toward higher energy in the 2D FeTeSe nanosheets (Supplementary Fig. S6a). Wavelet transform (WT, Fig. 1h), Fourier-transformed (FT) k2-weighted extended X-ray absorption fine structure (EXAFS) spectra (Supplementary Fig. S6b), and the quantitative fitting results (Supplementary Fig. S6c–e and Table S2) further demonstrate an obvious increase in the Fe−O coordination, along with a decrease in the Fe−Se/Te coordination, which is attributed to the generation of Se/Te vacancies and the increased specific surface area during the exfoliation process30,31.

Then, in-situ anisotropic strains were induced in the 2D FeTeSe nanosheets by subjecting them to electrolysis in an electrolyte containing 1 M KOH and 10 mM KNO3 under negative bias (Fig. 1d, g). The emergence of lattice strain is demonstrated by conducting operando synchrotron-based XRD using a homemade electrolysis cell at an X-ray wavelength of 0.41 Å (Fig. 2a–c and Supplementary Figs. S7–9). Two characteristic peaks of the FeTeSe lattice are focused, i.e., the (001) peak at ~3.86° and the (101) peak at ~7.33°, which represent the planar distances of the out-of-plane (c-axis) and in-plane (ac-axis), respectively (Fig. 2b, c). The XRD patterns in Fig. 2a-c depict the average patterns obtained from multiple scans conducted before and during NO3−RR under the open-circuit potential (OCP) (Supplementary Figs. S8, 9), with chronoamperometry being performed in between under negative bias. Notably, an intriguing anisotropic strain phenomenon is observed. During electrolysis, the (001) peak shifts rightward to ~3.88°, while the (101) peak shifts leftward to ~7.31°, corresponding to a 0.52% compressive strain in the (001) plane and a 0.27% tensile strain in the (101) plane (Fig. 2b, c). Beyond these two peaks, other peaks corresponding to the (110) and (111) planes also exhibit slight leftward shifts (Fig. 2a), supporting the emergence of in-plane tensile strain within the FeTeSe nanosheets during electrolysis. Furthermore, ex-situ XRD using an X-ray wavelength of 1.54 Å was conducted on the catalyst-loaded carbon cloths taken out from two electrolyte conditions (i.e., 1 M KOH and 1 M KOH + 10 mM KNO3) after chronoamperometry. The results are consistent with those obtained using operando synchrotron-based XRD, showing a slight left shift of the peak corresponding to the (101) plane and a notable right shift of the peak indexed to (002) (Supplementary Fig. S10). Interestingly, the peaks continue to shift after electrolysis in 1 M KOH followed by 1 M KOH + 10 mM KNO3, suggesting that both OH− and NO3− ions contribute to the strain formation (Supplementary Fig. S10b). Additionally, selected area electron diffraction (SAED) patterns in TEM characterization obtained from a bunch of nanosheets demonstrate increased lattice spacings after NO3−RR for the (101), (110), and (111) planes (Fig. 2d, e), further confirming the emergence of in-plane tensile strain. Besides, the ex-situ XRD pattern of FeTeSe nanosheets after electrolysis reveals that the tetragonal phase is well preserved, showing no apparent crystalline impurities (Supplementary Fig. S11). The morphology and crystal structure of the FeTeSe nanosheets before and after NO3−RR were also examined using electron microscopy. TEM images of the pristine (Fig. 2f) and post-electrolysis (Fig. 2n) catalysts indicate that the wrinkled nanosheet morphology is well maintained. Both the high-resolution TEM (HRTEM) images (Fig. 2g, o) reveal a clear atomic lattice, and the corresponding fast Fourier transform (FFT) patterns (Fig. 2h, p) display a characteristic set of diffraction spots along the tetragonal [001] zone axis, confirming the preservation of the tetragonal phase after electrolysis. Energy-dispersive X-ray spectroscopy (EDS) elemental mappings confirm the homogeneous distribution of Fe, Te, Se, and O elements throughout the entire FeTeSe nanosheets before (Fig. 2i–m) and after (Fig. 2q–u) electrolysis. These findings collectively indicate the formation of in-plane tensile strain and out-of-plane compressive strain in the 2D FeTeSe nanosheets during NO3−RR, highlighting that the catalyst undergoes spontaneous strain engineering during electrolysis (Fig. 2v).

Fig. 2: Reaction-driven strain formation during alkaline NO3−RR.
figure 2

a Operando synchrotron-based XRD patterns of FeTeSe nanosheets before and during catalysis. OCP denotes open-circuit potential. b, c Enlarged regions of (a), showing the shift of (001) and (101) peaks. d, e SAED patterns of a bunch of FeTeSe nanosheets before (d) and after (e) catalysis. f, g TEM (f) and HRTEM (g) images of FeTeSe nanosheets before catalysis. h FFT pattern of (g). i–m STEM image (i) and the corresponding EDS elemental mappings (j–m) of FeTeSe nanosheets before catalysis. n, o TEM (n) and HRTEM (o) images of FeTeSe nanosheets after catalysis. p FFT pattern of (o). q–u STEM image (q) and the corresponding EDS elemental mappings (r–u) of FeTeSe nanosheets after catalysis. v Schematic illustration of the FeTeSe crystal structure along the b and c directions, where the strain directions are indicated by the orange arrows. Scale bars, d, e 2 1/nm; f 50 nm; g 1 nm; i 1 µm; n 100 nm; o 2 nm; q 500 nm. Source data are provided as a Source Data file.

Full size image

Origins and formation mechanisms of strains during alkaline NO3 −RR

The possible origins and formation mechanisms of the anisotropic strains developed during NO3−RR were investigated through a series of operando and ex-situ measurements, alongside theoretical calculations. First, operando synchrotron-based XAFS measurements were performed using a homemade electrolysis cell to reveal changes in the valence state and coordination environment of Fe during NO3−RR (Supplementary Fig. S12). The results are presented in the Fe K-edge XANES spectra (Fig. 3a–c and Supplementary Fig. S13) and the FT k2-weighted EXAFS spectra (Fig. 3d–f and Supplementary Fig. S14) for 2D FeTeSe nanosheets under varying reaction conditions: (i) 1 M KOH at OCP, (ii) 1 M KOH + 10 mM KNO3 at OCP, and (iii-v) during NO3−RR at −0.4 V vs. RHE for 20, 40, and 60 min.

Fig. 3: Origins and formation mechanisms of strains during alkaline NO3−RR.
figure 3

a Operando Fe K-edge XANES spectra of FeTeSe nanosheets in 1 M KOH under OCP, in 1 M KOH + 10 mM KNO3 under OCP, during NO3−RR at −0.4 V for 20, 40, and 60 min. b, c Enlarged regions of (a). d, e FT k2-weighted Fe K-edge EXAFS spectra (d), and the corresponding contour map (e). The color bar represents intensity with unit of Å−3. f Changes of the normalized X-ray absorption coefficient under different conditions for Fe−O, Fe−Se, Fe−Te, and second-shell Fe−Te scattering paths. g Total X-ray scattering of the FeTeSe nanosheets before (red) and after (blue) electrolysis, as well as their difference pattern (green). h Scheme illustrating the in-situ formation of strained catalyst due to chalcogen vacancies and oxygen dopants in 2D FeTeSe nanosheets. i O 1 s spectra of the pristine FeTeSe nanosheets and those after catalysis in 1 M KOH under OCP, in 1 M KOH + 10 mM KNO3 under OCP, in 1 M KOH + 10 mM KNO3 at −0.55 V for 1, 2, and 4 h. OCP denotes open-circuit potential. Source data are provided as a Source Data file.

Full size image

As shown in Fig. 3a–c, even without applying any potential bias (i.e., under OCP), the addition of 10 mM KNO3 into 1 M KOH results in a shift of the Fe K absorption edge toward higher energy, accompanied by an increase in the intensity of the white line peak. Subsequently, when a cathodic potential of −0.4 V vs. RHE is applied for 20, 40, and 60 min, the absorption edge continues to shift toward higher energies (Fig. 3a–c), indicating a distinct increase in the Fe valence state in FeTeSe nanosheets as the NO3−RR progresses over time. Notably, the positions of the absorption edges for samples measured under operando conditions still lie between those of the ex-situ-measured standard FeSe and Fe2O3 samples (Supplementary Fig. S13), suggesting that the average valence state of the Fe cations increases, while remaining within the range of +2 and +3 (i.e., Feδ+, where 2 < δ < 3). The continuous increase in the Fe valence states during NO3−RR at a cathodic potential of −0.4 V indicates a continuous incorporation of oxygen species from the electrolyte (e.g., OH− and NO3−), which possess a higher electronegativity (3.44 for O) than Se (2.55) and Te (2.10) chalcogens32. The interplay between the applied negative bias, which tends to lower the valence, and the favorable incorporation of the electronegative oxygen species, which tends to raise the valence, results in a net increase in the nominal Fe valence state. This finding challenges the stereotype that metal cations in transition metal chalcogenides tend to be reduced under cathodic overpotentials33. Only a few reports document unusual increases in metal valence states during cathodic reactions, but all at relatively positive potentials (e.g., −0.1 to 0 V)21,34,35.

The changes in the coordination environment of Fe are revealed by the Fe FT k2-weighted EXAFS spectra. Upon the addition of NO3−, the amplitude of the shell peak at ~1.44 Å, corresponding to the Fe−O scattering, shows a significant increase, while the peak intensities associated with Fe−Se at ~1.87 Å and Fe−Te at ~2.30 Å are reduced (Fig. 3d-f and Supplementary Fig. S14a). This trend continues during the NO3−RR at −0.4 V over a duration of 60 min, demonstrating an increase in the Fe−O coordination at the expense of Fe−Se/Te coordination (Fig. 3d-f and Supplementary Fig. S14b). The amplitude of the second-shell Fe−Fe scattering peak at ~2.76 Å also increases (Fig. 3e, f), further corroborating the loss of Se/Te chalcogens that likely reduces the electronic shielding effect. Additionally, an obvious loss of Se than Te during electrolysis is also noticed (Fig. 3e, f). As further confirmed by the ICP-OES analysis of the post-reaction electrolyte (Supplementary Table S3), Se and Te anions leach by 15.3% and 8.6% during electrolysis, respectively, resulting in the formation of Se/Te vacancies, which in turn provide abundant sites for the adsorption and diffusion of oxygen species in thin FeTeSe nanosheets36, thus promoting their incorporation. Furthermore, the Fe−O peaks exhibit a high-R shift from ~1.44 Å to ~1.47 Å, while the Fe−Se peaks display a low-R shift from ~1.87 Å to ~1.84 Å, indicating a distorted coordination environment for the Fe atoms (Fig. 3d)35,37.

The findings from XAFS measurements were further corroborated by total X-ray scattering analysis of the 2D FeTeSe nanosheets before (red line) and after (blue line) NO3−RR, along with their difference pattern (green line), offering comprehensive structural information at the atomic scale (Fig. 3g). For the 2D FeTeSe nanosheets before catalysis, the first peak top is located at ~1.94 Å, corresponding to the Fe−O pair. The second through fifth peak tops can be assigned as the collectivity of Fe−Fe/Se/Te or Se/Te−Se/Te bonding. The difference pattern reveals that the relative intensity of the first peak increases, while the intensities of the second through fifth peaks decrease. Moreover, the scattering pattern broadens after catalysis, and new peak tops emerge between the original peak tops in the difference pattern. This suggests a wider range of interatomic distances, which can be attributed to several factors, including the positional disorder of atoms38, the loss of Se/Te atoms that alters the relative bonding ratios of Fe/Te/Se−Fe/Te/Se, and the formation of new Fe−O bonds due to the replacement of Se/Te with O atoms. These observations correlate with the formation of Fe−O(H) species indicated by the operando XAFS results (Fig. 3a–f) and the dissolution of Se (by 15.3%) and Te (by 8.6%) as determined by the ICP-OES (Supplementary Table S3).

Based on the aforementioned synchrotron-based X-ray techniques, the electrochemistry-driven formation of chalcogen vacancies and incorporation of oxygen species could be linked to strains observed in the operando XRD patterns (Fig. 2a–c). DFT calculations were resorted to investigating the formation mechanism of strains (Supplementary Figs. S15-17). We first calculated the formation energies of chalcogen vacancies in FeTeSe, which show similar values for the formation of Se and Te vacancies (Supplementary Fig. S15). The chalcogen vacancies tend to be repaired by oxygen species from the electrolyte due to the stronger Fe−O bond compared to Fe−chalcogen bonds, rendering the coordination with oxygen species thermodynamically favorable39,40. Then, the formation energies of various oxygen species (i.e., O, OH, and NO3) at both substitutional and interstitial positions of the FeTeSe lattice were calculated (Supplementary Fig. S16). The doping of OH at both substitutional ( −0.73 eV) and interstitial ( −0.16 eV) positions is thermodynamically favorable, suggesting that OH− ions from the alkaline electrolyte contribute to the strain formation via doping. On the other hand, when the NO3− molecule enters the interstitial position, it spontaneously dissociates to form O-doped FeTeSe, inducing the formation of a strained lattice39. Moreover, theoretical investigations demonstrate that the type, concentration, and position of chalcogen vacancies and oxygen dopants can distort the original FeTeSe lattice in different directions and to different degrees (Supplementary Fig. S17). Therefore, combining the findings from operando measurements and DFT calculations, we conclude that the lattice strain arises from the formation of chalcogen vacancies in the thin 2D FeTeSe nanosheets, which facilitate the filling and diffusion of oxygen species from the electrolyte into the lattice vacancy sites36, creating the strained 2D FeTeSe-O(H) (Fig. 3h). The observed anisotropic strains likely result from a combined effect of Se/Te vacancies, interstitial/substitutional O(H) dopants, and distortion caused by *NO3 adsorption followed by dissociation (Supplementary Fig. S16, 17). In contrast, the electrochemistry-driven formation of strain is unobvious in FeTe nanosheets without Se doping (Supplementary Fig. S18) and FeTeSe bulk crystals with huge material volume (Supplementary Fig. S19). This indicates that both the presence of Se and 2D morphology contribute to the reaction-driven strain development. On one hand, the favorable leaching of Se promotes the creation of chalcogen vacancies during electrolysis, which in turn facilitates the backfill of oxygen, thereby promoting strain development. On the other hand, the high specific surface area and the capacity of 2D materials to sustain significantly larger mechanical strains compared to their bulk counterparts41 also promote the in-situ strain formation.

The surface oxygen environment of 2D FeTeSe nanosheets was investigated using XPS after reactions under various electrochemical conditions: (i) pristine catalyst, (ii) 1 M KOH at OCP, (iii) 1 M KOH + 10 mM KNO3 at OCP, and (iv-vi) after NO3−RR at −0.55 V for 1, 2, and 4 h (Fig. 3i and Supplementary Figs. S20-24). All samples display a broader O 1 s peak after immersion in the aqueous electrolyte (Fig. 3i). Deconvolution was performed to identify the different sources of oxygen: peaks at ~530.0 eV, ~531.5 eV, and ~533.0 eV are indexed to M − O, M − OH, and adsorbed water, respectively42. The relative percentages of these oxygen species were calculated and shown in Supplementary Fig. S22. The concentration of M − O slightly increases during NO3−RR, while the percentages of M − OH (adsorbed hydroxyl) and adsorbed water increase and reach their maxima when the catalyst is immersed in 1 M KOH electrolyte. This phenomenon occurs because in the absence of KNO3, the adsorption of H2O and OH− dominates. When KNO3 is introduced, its preferential adsorption on the catalyst surface reduces the amounts of surface-adsorbed H2O and OH−, thereby facilitating the NO3−RR. Furthermore, the dominant presence of M − OH based on the XPS analysis also indicates a significant abundance of surface-adsorbed hydroxyl groups (Supplementary Fig. S22), which form as a result of rich chalcogen vacancies, leading to the creation of a di-anionic surface (i.e., chalcogen vacancies and surface hydroxyl groups).

Electrochemical performance of catalysts

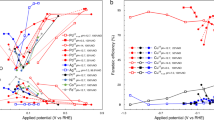
The catalytic performance of 2D FeTeSe nanosheets with in-situ developed strains toward NO3−RR-to-NH3 was evaluated and compared to two counterparts: FeTeSe bulk crystals and FeTe nanosheets without Se doping. Targeting a NO3− concentration relevant to industrial wastewater (10 mM)2, the electrochemical NO3−RR was conducted under ambient conditions in a standard three-electrode H-type cell (Fig. 4). The desired product, NH3, was quantified using the spectroscopic indophenol blue method (Supplementary Fig. S25). The main gaseous by-product, H2, was quantified via the online gas chromatography, while the main liquid by-product, nitrite (NO2−) (Supplementary Fig. S26a–c), and the reactant, NO3− (Supplementary Fig. S26d–f), were quantified via the ion chromatography. All potentials are referenced to the RHE. The NO3−RR activity of all catalysts was first assessed via linear sweep voltammetry (LSV) tests (Fig. 4a). All catalysts show a notable increase in cathodic current density upon the addition of 10 mM KNO3 into 1 M KOH electrolyte, with FeTeSe nanosheets demonstrating the highest current density and the most positive onset potential, suggesting the more effective reduction of NO3− ions. Product quantifications were performed using chronoamperometry over the potential range of −0.35 to −0.75 V vs. RHE (Fig. 4b-e and Supplementary Figs. S27, 28). The NH3 FE for FeTeSe nanosheets presents a volcano-type curve and peaks at 98.7 ± 2.2% at −0.55 V, with a corresponding NH3 yield rate of 21.16 ± 1.49 mg h−1 mgcat−1 (Fig. 4b). With more negative overpotentials, the NH3 FE starts to decline due to the stronger HER competition (Fig. 4c). The NO2− FE reaches a maximum of 18.6 ± 9.8% at −0.35 V, and continuously decreases to <1% at more negative potentials (Fig. 4c). The NH3 yield rate for FeTeSe nanosheets increases monotonically with more negative potentials, peaking at 42.14 ± 2.06 mg h−1 mgcat−1 at −0.75 V (Fig. 4b). In comparison, FeTeSe bulk crystals (maximum NH3 FE of 83.5 ± 2.9% with the corresponding yield rate of 9.97 ± 0.91 mg h−1 mgcat−1), FeTe nanosheets (maximum NH3 FE of 83.5 ± 4.2% with the corresponding yield rate of 8.18 ± 1.28 mg h−1 mgcat−1), and commercial Fe2O3 (maximum NH3 FE of 81.2% with the corresponding yield rate of 15.90 mg h−1 mgcat−1) exhibit inferior catalytic activities (Fig. 4d, e and Supplementary Fig. S29). Additionally, the performance of FeTeSe nanosheets exceeds that of most previously reported electrocatalysts for low-concentration ( ~ 10 mM) NO3−RR, excelling in both NH3 FE and yield rate (Supplementary Fig. S30 and Table S4).

Fig. 4: Nitrate reduction performance in 1 M KOH.
figure 4

a LSV curves of FeTeSe nanosheets, FeTeSe bulk crystals, and FeTe nanosheets with and without the addition of 10 mM KNO3 in 1 M KOH under Ar at a scan rate of 10 mV s−1. b NH3 yield rates and FEs at different potentials over FeTeSe nanosheets. c FEs of NH3, NO2−, and H2 at different potentials over FeTeSe nanosheets. d, e Comparisons of FeTeSe nanosheets with FeTeSe bulk and FeTe nanosheets toward electro-reduction of 10 mM NO3− in terms of the NH3 FE (d) and yield rate (e) at different potentials. f NH3 yield rates and FEs at −0.55 V under different concentrations of KNO3 over FeTeSe nanosheets. g NH3 FEs and yield rates for 10 consecutive cycles. h Concentrations of NO3−, NO2−, and NH3 with increasing time, as well as the NH3 FEs at different time points. Experimental conditions: A catalyst mass loading of 0.1 mg cm−2 on the Toray H-090 carbon paper (geometry area of 1×1 cm2) in a H-cell with Nafion 117 membrane separating two chambers under ambient conditions for nitrate electrolysis. Each chamber has 30 mL of Ar-saturated 1 M KOH and 10 mM KNO3 (pH = 13.98 ± 0.07). All potentials are not iR corrected. The solution resistance in 1 M KOH + 10 mM KNO3, determined by potentiostatic electrochemical impedance spectroscopy, was 2.53 ± 0.03, 2.39 ± 0.08, and 2.48 ± 0.27 for FeTeSe nanosheets, FeTeSe bulk, and FeTe nanosheets, respectively. Error bars denote the standard deviations calculated from three independent measurements. Source data are provided as a Source Data file.

Full size image

The catalytic performance of the best-performing 2D FeTeSe nanosheets for NO3−RR was further evaluated to assess its adaptability to various wastewater sources. Given the wide range of NO3− concentrations in real-world scenarios2, the performance of FeTeSe nanosheets was examined across a NO3− concentration spectrum of 1 to 100 mM (Fig. 4f and Supplementary Fig. S31). As KNO3 concentration increases, the current density also rises (Supplementary Fig. S31), indicating improved NO3−RR activity with greater reactant availability. Specifically, the FeTeSe nanosheets deliver impressive NH3 FEs of >90% within the KNO3 concentration range of 10-100 mM at −0.55 V, and the corresponding NH3 yield rate monotonically increases with rising NO3− concentration (Fig. 4f). The stability of the FeTeSe nanosheets was evaluated through long-term chronoamperometric test (Supplementary Fig. S32) and 10 consecutive cycle tests at −0.55 V (Fig. 4g and Supplementary Fig. S33). While the current density, NH3 yield rate, and NH3 FE fluctuate slightly in each cycle, the average results remain stable, confirming its remarkable stability. Additionally, the effectiveness of FeTeSe nanosheets for low-concentration NO3− remediation was evaluated by performing a batch conversion test using an initial concentration of 10 mM. Figure 4h illustrates that as the electrolysis time increases, the NO3−-N concentration gradually decreases, along with the gradual increase in NH3-N concentration, while the NO2−-N concentration remains negligible. The catalyst reduces NO3− levels to below the World Health Organization’s recommended maximum of 50 ppm for drinking water43 within 5 h, showing a high conversion rate of 93.4%.

Control experiments were performed to confirm the N source in the electrochemically produced NH3. NH3 is almost undetectable in electrolytes with the absence of KNO3 or potential bias, while the amount is trivial when pure carbon paper without the loading of FeTeSe catalyst is used as the working electrode (Supplementary Fig. S34a). Moreover, isotope labelling coupled with 1H nuclear magnetic resonance (NMR) measurements demonstrate characteristic triple and double peaks, corresponding to 14NH3 and 15NH3, when K14NO3 and K15NO3 are used, respectively (Supplementary Fig. S34b). These findings verify the generated NH3 derives from the FeTeSe nanosheet-catalyzed NO3−RR process under negative bias.

Mechanism studies of the strain effect on NO3 −RR

The reaction pathway of the NO3−RR-to-NH3 process was investigated using in-situ ATR-IR spectroscopy to capture potential reaction intermediates (Supplementary Fig. S35). Figure 5a presents the in-situ ATR-IR spectra collected over the FeTeSe nanosheets in an electrolyte containing 1 M KOH and 10 mM KNO3, with IR signal acquisition ranging from 1050 to 3600 cm−1 during a scan from OCP to −0.75 V vs. RHE. The spectra display characteristic peaks associated with the adsorbed NOx, water, and NH3. The upward and downward bands reflect the formation and consumption of the corresponding intermediates, respectively. Notably, a pair of downward peaks at ~1520 and 1340 cm−1 represent the asymmetric and symmetric vibration modes of the absorbed NO2 intermediate, respectively, while the downward peak at ~1120 cm−1 is attributed to the N − O bond or Si−O from the substrate44. The intensities of these downward peaks increase with more negative potentials, indicating the consumption of NOx species during NO3−RR. The emergence of upward bands corresponding to N − H bending and −NH2 wagging modes at ~3220 and 1380 cm−1, respectively, suggests the formation of NH3 (ref. 44,45). Additionally, the upward bands at ~3380 and 1640 cm−1 arise from the O − H stretching and bending modes of water, respectively, implying water adsorption on the catalyst surface44. These upward bands concurrently become more prominent with more negative potentials, suggesting intensified water adsorption to supply protons for the hydrogenation of N-involving intermediates. These findings demonstrate that the *NOx deoxygenation process is followed by a series of protonation steps during the NO3−RR-to-NH3 process, with water dissociation being essential to provide adequate protons for the hydrogenation of N-involving intermediates.

Fig. 5: Mechanism studies.
figure 5

a In-situ ATR-IR spectra of FeTeSe nanosheets under various potentials. OCP denotes open-circuit potential. b, c Calculated PDOS of strained FeTeSe-O/unstrained FeTeSe with NO3– (b) and H2O (c). d, e Gibbs free energy diagrams via the minimum energy pathway during NO3–RR-to-NH3 (d) and HER (e) over the strained FeTeSe-O (red) and unstrained FeTeSe (blue) surfaces. Source data are provided as a Source Data file.

Full size image

Then, the effects of strain on both the NO3−RR-to-NH3 and water dissociation processes were explored theoretically using DFT calculations. Structural models of both the unstrained surface and strained surface with the presence of chalcogen vacancies and oxygen dopants were constructed (Supplementary Fig. S36). The projected density of states (PDOS) for *NO3 (Fig. 5b) and *H2O (Fig. 5c) indicate that the Fe 2p and Oads 2p orbitals show greater overlap below the Fermi level on the strained FeTeSe-O surface, suggesting stronger binding between *NO3/*H2O and the Fe sites. This is further supported by the calculated binding free energies of NO3− and H2O on both surfaces, which show more negative values of −0.67 eV and −0.50 eV for the adsorption of NO3− and H2O, respectively, on the strained FeTeSe-O surface, as compared to those on the unstrained FeTeSe surface ( −0.39 eV for NO3− and 0.18 eV for H2O) (Supplementary Fig. S37). Subsequently, the free energy diagrams based on the Gibbs free energy changes (ΔG) and the corresponding adsorption configurations for all possible pathways from NO3− to NH3 on both the strained and unstrained surfaces were examined (Supplementary Figs. S38, 39a, b). Our calculations show that the minimum energy pathway begins with the adsorption of NO3−, followed by its reduction to *NOH, then to *N, and the subsequent hydrogenation of *N to produce NH3 on both surfaces (Fig. 5d and Supplementary Fig. S39a, b). The conversion from *NH2 to *NH3 is calculated to be the potential-determining step (PDS) for the strained FeTeSe-O surface, with a smaller uphill ΔG of 0.18 eV. In contrast, for the unstrained FeTeSe surface, the PDS is the conversion from *NH to *NH2, which has a larger ΔG of 0.40 eV (Fig. 5d). These results underscore the critical role of the strained surface in facilitating the adsorption of reactants (NO3− and H2O) and lowering the energy barrier of the PDS, thereby enhancing the NO3−RR activity.

Additionally, considering the critical role of water dissociation in supplying the necessary protons for the hydrogenation of N-involving intermediates during the alkaline NO3−RR, we also calculated the free energy diagrams for the alkaline HER on both the strained and unstrained catalyst surfaces (Fig. 5e and Supplementary Fig. S39c, d). For both the strained FeTeSe-O and unstrained FeTeSe surfaces, the PDS of the alkaline HER is the conversion from *H to H2, with an energy barrier of 0.42 eV and 0.51 eV, respectively, indicating the strong inhibition of H − H dimerization to H2. Meanwhile, on the strained FeTeSe-O surface, the binding free energy of H2O ( −0.50 eV) is less negative than that of NO3– ( −0.67 eV) (Supplementary Fig. S37), and the energy barrier for the PDS in alkaline HER (0.42 eV) is higher than that in NO3–RR (0.18 eV) (Fig. 5d, e). These findings suggest that, on the strained FeTeSe-O surface, the adsorption and activation of NO3– are energetically more favorable than HER, while the favorable dissociation of water into protons ensures a sufficient supply of protons for the hydrogenation process. In contrast, for the unstrained FeTeSe, the unfavorable H2O adsorption (0.18 eV, Supplementary Fig. S37) indicates its poorer ability to provide protons, which limits the hydrogenation process.

Other factors also contribute to the superior activity of 2D FeTeSe nanosheets, in addition to (i) the strain effect (Fig. 5). (ii) The presence of abundant hydroxyl groups on the surface, resulting from the rich chalcogen vacancies (Fig. 3i), facilitates the adsorption of NO3− by forming hydrogen bonds, as evidenced by the more negative adsorption energy of NO3− on the catalyst surface with hydroxyl groups (Supplementary Fig. S40), thereby creating a reactant-friendly interface that helps drag NO3− ions more effectively to the catalyst surface. Similar phenomena have been observed in metal (oxyhydr)oxide catalysts, where surface hydroxyl groups enhance the adsorption of NO3− (ref. 46) and CO2 (ref. 47) through hydrogen bonding. (iii) Upon intercalation and exfoliation, 2D FeTeSe nanosheets exhibit an increased surface area with more exposed active sites, as indicated by a larger electrochemical active surface area (ECSA) compared to the bulk counterpart (Supplementary Fig. S41a–c). After normalizing the LSV curves and NH3 partial current densities over ECSA, the FeTeSe nanosheets still exhibit higher NO3−RR-to-NH3 activity (Supplementary Fig. S41d), indicating that its superior performance is attributable not only to their larger surface area but also to their enhanced intrinsic activity. (iv) The charge transfer kinetics of the 2D FeTeSe nanosheets improve after exfoliation, as evidenced by the smaller charge transfer resistance compared to those of FeTeSe bulk crystals and FeTe nanosheets in the fitted electrochemical impedance spectroscopy (EIS) plots (Supplementary Fig. S42). Overall, a series of electrochemical studies, in-situ measurement, and theoretical investigations suggest that the superior catalytic activity of 2D FeTeSe nanosheets arises from the synergistic effects of strained Fe sites exposed due to the formation of Se/Te vacancies, the presence of surface hydroxyl groups that create a reactant-friendly interface via hydrogen bonding, and the increased surface area due to their 2D structure. Collectively, these factors enhance the adsorption and activation of NO3−, lower the energy barrier of the PDS, and promote the water dissociation process to supply protons while suppressing the HER side reaction, thereby boosting the low-concentration NO3−RR-to-NH3 activity of FeTeSe nanosheets.

Discussion

In conclusion, we have showcased the significant role of reaction-driven formation of anisotropic in-plane tensile and out-of-plane compressive strains in 2D FeTeSe nanosheets during alkaline NO3−RR to improve catalytic performance. A series of operando/ex-situ measurements and theoretical calculations were used to uncover the origins of the in-situ formed strains, revealing the essential roles of the partial leaching of Se/Te ions as well as the adsorption and dissociation of OH−/NO3− on the thin 2D FeTeSe catalyst. The combination of electrochemical studies and theoretical investigations further unveiled the vital contributions of the exposed strained Fe sites and surface hydroxyl groups in boosting the alkaline NO3−RR-to-NH3 activity. Our findings demonstrate how the conventionally perceived limitations in transition metal chalcogenides can be harnessed to realize electrochemistry-driven in-situ structural engineering of catalysts to enhance catalytic performance. Furthermore, given the dynamic chemistry of nano-catalysts during electrolysis, we anticipate that our comprehensive understanding of the catalyst structural evolution will inspire deeper investigations into the true structure-activity relationships necessary for the targeted design of effective electrocatalysts.

Methods

Chemicals

Iron ( ≥ 99%), tellurium (99.8% trace metals basis), selenium (99.99% trace metals basis), iodine ( ≥ 99.99% trace metals basis), n-butyllithium solution (2.0 M in cyclohexane), n-hexane (anhydrous, 95%), potassium hydroxide (KOH, 90%), potassium nitrate (KNO3, ≥99%), sodium hydroxide (NaOH, ≥97%), salicylic acid ( ≥ 99%), sodium citrate tribasic dihydrate ( ≥ 99%), sodium hypochlorite (NaClO, available chlorine 4.00–4.99%), sodium nitroferricyanide ( ≥ 99%), ammonium chloride (NH4Cl, 99.99% trace metals basis), deuterium oxide (D2O, 99.9%), dimethyl sulfoxide (DMSO, ≥99.9%), potassium nitrate-15N (K15NO3, 98 atom% 15N), boron nitride (BN, 98%), hydrochloric acid (HCl, 37%), and Nafion 117 solution ( ~ 5% in a mixture of lower aliphatic alcohols and water) were purchased from Sigma-Aldrich. Sulfuric acid (H2SO4, 95-97%) and nitric acid (HNO3, min. 69%) were purchased from Honeywell. Hydrogen peroxide solution (H2O2, 30-32%) was purchased from Quality Reagent Chemical. Ethanol (99.9%) was purchased from Merck (Nordic European Centre, Singapore). The Milli-Q water (18.2 MΩ·cm, Milli-Q System, Millipore, Billerica, MA) was used in all experiments. All the chemicals were used as received without further purification.

Synthesis of bulk Fe0.90(Te0.60Se0.40) and FeTe crystals

Bulk Fe0.90(Te0.60Se0.40) crystals were synthesized via a high-temperature solid-state reaction method. Fe, Te, and Se powders with stoichiometric amounts were loaded into a silica tube with a little iodine as flux. The silica tube was sealed under high vacuum ( < 10−2 Pa), and then transferred to the furnace, which was heated to 700 °C within 1 day and held for 2 days. Then, the furnace was ramped to 900 °C with a rate of 50 °C h−1 and kept at this temperature for 6 days. Finally, after cooling down to room temperature, Fe0.90(Te0.60Se0.40) bulk crystals were obtained with ingot shapes. Bulk FeTe (atomic ratio ~1) crystals were synthesized via a similar pathway, except for the absence of Se powders in this case.

Synthesis of Fe0.92(Te0.70Se0.30) and FeTe nanosheets

The chemical lithium intercalation method was used to prepare the Fe0.92(Te0.70Se0.30) and FeTe nanosheets from their corresponding bulk crystals. 30 mg of Fe0.90(Te0.60Se0.40) or FeTe bulk crystals were immersed in 3 mL of n-butyllithium solution (2.0 M in cyclohexane) for 24 h in a glove box under Ar atmosphere. After the reaction, the upper solution containing the unreacted n-butyllithium was removed using pipet, and the lithium-intercalated powder was rinsed with n-hexane several times to further remove the excessive n-butyllithium. After taking out the lithium-intercalated powder from the glove box, 60 mL of Ar-degassed H2O was added, followed by sonication for 30 min, to obtain a uniform solution with exfoliated products. The obtained suspension was centrifuged at 2,000 rpm (570 x g) for 15 min, and the supernatant was collected, while the precipitates containing the unreacted bulk crystals were discarded. The collected supernatant was washed with Ar-degassed H2O and centrifuged at 10,000 rpm (14,400 x g) for 30 min. The precipitates were collected and further washed three times. Finally, the intercalated Fe0.92(Te0.70Se0.30) and FeTe nanosheets were obtained.

Material characterizations

Transmission electron microscopy (TEM) characterization and energy dispersive X-ray spectroscopy (EDS) elemental mapping were performed on JEOL 2100 F (Japan) operated at 200 kV with an EDAX EDS detector. Scanning electron microscopy (SEM) image was obtained on FESEM 7600 F operated at 15 kV. Lab X-ray diffraction (XRD) patterns were collected using an X-ray diffractometer with Cu-Kα radiation and an X-ray wavelength of 1.54 Å (Bruker D8 Advance XRD) operated at 40 kV and 40 mA. Synchrotron XRD patterns were collected using SPring8 BL19b2 with an X-ray wavelength of 0.41 Å operated at 30 keV. The powder samples were sealed in Ф 5 mm Glassy capillary tubes. X-ray photoelectron spectroscopy (XPS) measurements were carried out on the Kratos AXIS Supra system. Inductively coupled plasma optical emission spectrometry (ICP-OES) was carried out with the Dual-view Optima 5300 DV ICP-OES system. Ultraviolet-visible (UV-Vis) absorption spectra were recorded on UV-Vis Spectrophotometer Shimadzu UV2700. Nuclear magnetic resonance (NMR) spectrometer was detected on JEOL ECA400 (ECA400SL) UltraShield 400 MHz magnet with the auto-tunable liquid probe, equipped with a 64-position auto-sampler. Total X-ray Scattering was applied at BL04b2, SPring-8 Japan.

Catalyst ink preparation

Catalyst inks were prepared by mixing 12 mg of catalyst powder, 6 mg of carbon black (Vulcan XC72R), 3200 µL of ethanol, and 60 µL of Nafion 117 solution (Sigma Aldrich, 5 wt%). The mixture was sonicated in iced water, until a homogeneous solution was obtained. The as prepared catalyst ink exhibited a concentration of 3.68 mg mL−1. To prepare the working electrode, 27 µL of catalyst ink was dropped on the Toray H-090 carbon paper, to achieve a mass loading of 0.1 mg cm−2 with an active area of 1 × 1 cm2.

Electrochemical measurements

Electrochemical nitrate reduction reactions (NO3−RR) were carried out in a Solartron Analytical 1470E electrochemical workstation with a standard three-electrode system at ambient conditions. Catalysts loaded on carbon paper clipped by the graphite electrode clamp (J110, Tianjin Aida), Hg/HgO (filled with 1 M KOH solution, Gaoss Union), and Pt mesh (1 × 1 cm2, Gaoss Union) were used as the working, reference, and counter electrodes, respectively. All potentials were measured and converted versus the reversible hydrogen electrode (RHE) scale by the Nernst equation:

$$E\left({{\rm{V\; vs}}}.\,{{\rm{RHE}}}\right)=E\left({{\rm{V\; vs}}}.\,{{\rm{Hg}}}/{{\rm{HgO}}}\right)+0.059\times {{\rm{pH}}}+0.098$$
(1)

The electrochemical NO3−RR measurements were acquired in Ar-saturated 1 M KOH with 10 mM KNO3 (pH = 13.98 ± 0.07, measured by Hanna precision pH meter), by using an H-type cell (Gaoss Union) with the cathode and anode chambers separated by a Nafion 117 membrane (DuPont, thickness of 183 µm, size of 3 cm in diameter). Each chamber contains an electrolyte volume of 30 mL. The Nafion 117 membrane was successively washed in H2O2 solution (5%), DI H2O, 0.5 M H2SO4 solution, and DI H2O at 80 °C for 1 h, and finally stored in DI H2O for further use. The 1 M KOH electrolyte was prepared by weighing 1 mol of KOH pellets into 1 L of DI H2O. The mixture was stirred until fully dissolved and cooled to room temperature, which was stored in a plastic bottle under ambient conditions for experimental use. Similar procedures were followed expect for the addition of specific amount of KNO3 powders into the solution for preparing the electrolyte containing 1 M KOH and KNO3.

Before testing, the electrolyte solution was purged with Ar gas for 30 min to remove O2/N2, and the Ar purging was maintained at a flow rate of 20 sccm throughout the electrochemical test. Prior to the NO3−RR test, cyclic voltammetry was conducted until the polarization curves stabilized, with a sweep rate of 100 mV s−1 from −0.5 to −2 V vs. Hg/HgO. Electrochemical NO3−RR measurements were performed using the linear sweep voltammetry method at a scan rate of 10 mV s−1 and chronoamperometry method in the potential range of −0.35 V and −0.75 V with an interval of 0.1 V for 1 h. The standard deviations come from three independent measurements. The electrochemical impedance spectroscopy (EIS) measurements were conducted in a frequency range from 105 to 0.01 Hz with an amplitude of 10 mV under the NO3−RR condition. Rs is related to the solution resistance, while Rct denotes the charge transfer resistance. The double layer capacitance (Cdl) was recorded from the cyclic voltammograms at varied scan rates (10, 20, 40, 60, 80, and 100 mV s−1) in an electrolyte of 1 M KOH + 10 mM KNO3 in the potential range from −0.4 to −0.5 V vs. Hg/HgO (non-Faradaic region), which could be used to calculate the ECSA using the equation:

$${{\rm{ECSA}}}={C}_{{dl}}/{C}_{S}\times A$$
(2)

where \({{{\rm{C}}}}_{{{\rm{S}}}}\) is the capacitance of an atomically smooth planar surface (40 µF cm⁻² in alkaline media), and \({{\rm{A}}}\) is the electrode area13. The long-term stability test was performed in a flow-system H-cell with an electrolyte flow rate of 2.5 mL min−1. The cyclic stability test was performed in a H-type cell at −0.55 V vs. RHE by replacing the electrolyte every 1 h, without changing the working electrode and ion exchange membrane. All potentials are not iR corrected.

Quantification of ammonia

Ammonia was quantified spectrophotometrically via the indophenol blue method. (i) Strock reagent preparation: Chromogenic reagent (A): 1 M NaOH aqueous solution containing 5 wt% salicylic acid and 5 wt% sodium citrate. Oxidizing reagent (B): 0.05 M NaClO aqueous solution. Catalyzing reagent (C): 1 wt% sodium nitroferricyanide aqueous solution. (ii) Ammonia calibration and quantification: NH4Cl dissolved in 1 M KOH aqueous solution was used to prepare a series of standard NH3 assays with varied concentrations in 1 M KOH. The UV-Vis spectra and the calibration curve by linear fitting (absorbance values at wavelength of 655 nm versus the NH3 concentration) were shown in Supplementary Fig. S25. To quantify the NH3 concentration in sample electrolyte, 2 mL of sample electrolyte diluted to the detection range using 1 M KOH solution was added to a glass vial, into which 2 mL of reagent (A), 1 mL of reagent (B), and 200 µL of reagent (C) were successively added. After homogeneously mixing the solution and keeping it under dark for 2 h, the solution was measured using UV-Vis spectrophotometer, and the concentration of NH3 was calculated based on the calibration curve.

Calculation of NH3 yield rate and FE

The ammonia yield rate was calculated using the following equation:

$${{{\rm{R}}}}_{{{\rm{NH}}}3}\left({{\rm{mg}}}{{{\rm{h}}}}^{-1}{{{{\rm{mg}}}}_{{{\rm{cat}}}}}^{-1}\right)=({C}_{{NH}3}\times V)/(t\times m)$$
(3)

where \({{{\rm{C}}}}_{{{\rm{NH}}}3}\) is the concentration of ammonia quantified by the indophenol blue method (mg mL−1), \({{\rm{V}}}\) is the volume of electrolyte (30 mL), \({{\rm{t}}}\) is the electrolysis time (h), and \({{\rm{m}}}\) is the catalyst mass loading (0.1 mg).

The ammonia FE was calculated using the following equation:

$${{{\rm{FE}}}}_{{{\rm{NH}}}3}\left(\%\right)=(8\times F\times {C}_{{NH}3}\times V)/(17\times Q)$$
(4)

where \({{\rm{F}}}\) is the Faraday constant (96485.3 C mol−1) and \({{\rm{Q}}}\) is the total charge during the reaction obtained by integrating current versus time (C).

Quantification of nitrite/nitrate ions

Nitrite (NO2−) and nitrate (NO3−) ions were quantified via the ion chromatography. NO2− and NO3− standard solutions were diluted using DI H2O to different concentrations. The ion chromatographs and calibration curves by linear fitting (peak areas versus NO2−/NO3− concentrations) were shown in Supplementary Fig. S26. To quantify the NO2−/NO3− concentration in sample electrolyte, sample electrolyte was diluted to the detection range using DI H2O and tested using the ion chromatography. The concentration of NO2−/NO3− were calculated based on the calibration curves.

Calculation of NO2 − FE

The nitrite FE was calculated using the following equation:

$${{{\rm{FE}}}}_{{{\rm{nitrite}}}}\left(\%\right)=(2\times F\times {C}_{{nitrite}}\times V)/(46\times Q)$$
(5)

where \({{{\rm{C}}}}_{{{\rm{nitrite}}}}\) is the concentration of nitrite quantified by the ion chromatography (mg mL−1).

Quantification and FE calculation of H2

The gaseous by-product H2 was detected and analyzed by online gas chromatography (GC2060, Shanghai Ruimin), which was equipped with flame ionization (FID) and thermal conductivity detector (TCD) detectors. The analysis time of each round was ~13 min. The H2 FE was calculated using the following equation:

$${{{\rm{FE}}}}_{{{\rm{H}}}2}=(2\times {C}_{H2}\times F\times v\times P)/(R\times T\times i)$$
(6)

where\(\,{{{\rm{C}}}}_{{{\rm{H}}}2}\) is the concentration of H2 quantified by the gas chromatography (ppm), \({{\rm{v}}}\) is the Ar gas flow rate (mL min−1), \({{\rm{P}}}\) is the ambient pressure, \({{\rm{T}}}\) is the ambient temperature, \({{\rm{R}}}\) is the gas constant, and \({{\rm{i}}}\) is the average current density during sampling time.

Isotope labelling experiment and 1H NMR measurement

The K15NO3 (98 atom%) was used as the feeding N-source for the isotopic labeling experiments to verify the source of ammonia. 1 M KOH was used as an electrolyte and K15NO3 with a concentration of 0.1 M was added into the cathode compartment as the reactant. After the reaction, the electrolyte with obtained 15NH3 was taken out and the electrolyte pH was adjusted to around 2 by adding HCl for 1H NMR measurement. Specifically, 400 µL of the pH-adjusted electrolyte, 100 µL of D2O, and 100 µL of 10 ppm DMSO aqueous solution as internal standard were homogeneously mixed. The prepared solution was tested by an NMR spectrometer (JEOL ECA400 (ECA400SL) UltraShield 400 MHz magnet with auto-tunable liquid probe, equipped with 64-position auto-sampler).

Ex-situ / operando synchrotron XAFS

XAFS experiments of the Fe K-edge were performed using a Si (111) monochromator crystal at the BL14B2 beamline at SPring-8, in Japan. All ex-situ XAFS experiments were recorded in transmission mode at room temperature. The operando experiments were conducted with a homemade electrochemical cell with a flow system. The electrolyte was Ar-saturated 1 M KOH with 10 mM KNO3 aqueous solution. The FeTeSe nanosheet catalyst with a loading amount of ~2 mg cm−2 loaded on 1*1 cm2 carbon cloth serves as the working electrode, while carbon rod and Hg/HgO were used as the counter and reference electrodes, respectively. The samples were measured in fluorescence mode. Subsequent data processing was performed via the ATHENA module implemented in the IFEFFIT software package.

Operando synchrotron XRD

Operando electrochemical-XRD was applied at BL19b2, SPring-8 Japan, using X-ray with a wavelength of 0.41326(9) Å (30 keV). The FeTeSe nanosheet catalyst was loaded on 1 × 1 cm2 carbon cloth with a loading amount of ~2 mg cm−2, serving as the working electrode. Carbon rod and Hg/HgO were used as the counter and reference electrodes, respectively. A homemade electrochemical cell with a thickness of liquid layer of 5 mm was used. The electrolyte containing Ar-purged 1 M KOH and 10 mM KNO3 was pumped during the test to minimize the mass transfer limit of KNO3 during test. To perform the experiment, before catalysis, under OCP, 10 scans of XRD patterns were obtained to generate an average pattern. Then, a negative bias of −0.45 V was applied. Afterwards, under OCP, another 7 scans of XRD patterns were obtained to generate an average pattern.

In-situ ATR-IR

In-situ ATR-IR experiments were carried out on the BRUKER-Fourier Transform Infrared Spectrometer-INVENIO equipped with a liquid nitrogen-cooled MCT detector. The customized cell was used to perform NO3−RR with the saturated Hg/HgO reference electrode and the Pt foil counter electrode. The electrolyte of 1 M KOH added with 10 mM KNO3 solution was purged with Ar for at least 30 min prior to test. For the chronopotentiometry measurement, the applied potential was set in the range between OCP to −0.75 V vs. RHE, and each spectrum was collected in a period of 30 s.

DFT calculations

All spin-polarized DFT calculations were conducted using the Perdew, Burke, and Ernzerhof (PBE) exchange-correlation functional48 implemented in Vienna Ab-initio Simulation Package (version 5.4)49. The projector augmented wave (PAW) method50 was used for describing the core-valence interaction. The kinetic energy cutoff for the plane-wave expansion was set at 600 eV. The Gamma sampling of a 5 × 5 × 5 and 5 × 5 × 1 k-point grids were used for the bulk structures and the slabs. The selected k-point grid and cutoff energy were tested and able to generate results with sufficient accuracy (Supplementary Table S5). The slab structures were constructed based on the optimized bulk structures. During geometry optimizations, both lattices and ions were fully relaxed in bulk structures, while for the slab structures, the bottom two layers of atoms were frozen and the rest of the ions were fully relaxed, until the total energy and absolute value of the forces acting on each atom were less than 1 × 10−6 eV and 1 × 10−2 eV Å−1, respectively. Dipole corrections and a vacuum layer of at least 15 Å were applied for the slabs. The DFT-D3 method51 was used to correct the dispersion interactions. The Gibbs free energies were calculated using the computational hydrogen electrode model with the equation:

$$\Delta G=\Delta E+(\Delta {ZPE}-T\Delta S)$$
(7)

where \(\Delta {{\rm{E}}}\) is the change of the total DFT energies of the reaction products and reactants, \({{\rm{ZPE}}}\) is the zero-point energy, and \({{\rm{TS}}}\) is the entropic term at room temperature. The \({{\rm{ZPE}}}\) corrections were calculated from vibrational frequencies derived from Hessians calculated from finite differences of analytic gradients on single molecules in vacuum or adsorbates on the slabs. The entropic terms for single molecules in vacuum were taken from standard thermodynamics tables52. Since the entropic terms for absorbed species on the slabs were small, they were typically omitted53,54. The (H+ + e−) pair at standard conditions (pH = 0, T = 298.15 K, and P = 1 atm) is equivalent to ½ H2 in the gas phase55. We adopted the computational hydrogen electrode model because of its simplicity and computational efficiency. Solvent effects were considered in the calculations using the implicit solvation model (water) implemented in VASPSol56. For the pH effects, the Gibbs free energy of (H+ + e−) pair was adjusted by the concentration dependence of the entropy using the formula (Supplementary Fig. S43):

$${G\left({{{\rm{H}}}}^{+}+{{{\rm{e}}}}^{-}\right)}_{{{\rm{pH}}}}={G\left({{{\rm{H}}}}^{+}+{{{\rm{e}}}}^{-}\right)}_{{{\rm{pH}}}=0}+{k}_{B}T{\mathrm{ln}}\left(10\right)\times {{\rm{pH}}}$$
(8)

whereas for the electrode potential effects, the Gibbs free energies of the reaction steps were adjusted by applying the term \(-{{\rm{eU}}}\), where \({{\rm{U}}}\) is the applied external potential (Supplementary Fig. S44)54,55. The defect formation energy (\({{{\rm{E}}}}_{{{\rm{for}}}}\)) of Se/Te-vacancies was calculated using the equation:

$${E}_{{for}}={E}_{{dFTS}}+{\mu }_{{Se}/{Te}}-{E}_{{FTS}}$$
(9)

where \({{{\rm{E}}}}_{{{\rm{dFTS}}}}\), \({{{\rm{\mu }}}}_{{{\rm{Se}}}/{{\rm{Te}}}}\), and \({{{\rm{E}}}}_{{{\rm{FTS}}}}\) are the total energy of the defected FeTeSe with a Se/Te vacancy, the chemical potential of Se/Te, and the total energy of the FeTeSe, respectively21. We considered neutral vacancy defect formation. We did not consider charged states because VASP treats charge as the background charge rather than the charge on the reactive site. Also, for a charged slab, the total energy would depend on the vacuum level, making the convergence of the calculations very challenging. We adopted the trigonal bulk structures of Se and Te with the space group of P3_121 as the reference states. The formation energy \(({{{\rm{E}}}}_{{{\rm{for}}}})\) of oxygen species was calculated using the equation:

$${E}_{{for}}={E}_{{Surf}+{Mol}}-({E}_{{Surf}}+{E}_{{Mol}})$$
(10)

where\(\,{{{\rm{E}}}}_{{{\rm{Surf}}}+{{\rm{Mol}}}}\), \({{{\rm{E}}}}_{{{\rm{Surf}}}}\), and \({{{\rm{E}}}}_{{{\rm{Mol}}}}\) are the total energies of the molecule binded surface, the surface, and the molecule, respectively.