Introduction

Many-body effects are at the heart of condensed matter physics. The celebrated Hubbard model is one of the most elegant theoretical models to capture the many-body interactions of quasiparticles1, which is yet difficult to be solved exactly and thus generally mimicked by various quantum simulators to reveal the inherent strong-correlation phenomena2,3. Recently, transition metal dichalcogenide (TMD) moiré superlattices have emerged as a booming platform to explore the rich physics of the triangular-lattice Hubbard model4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22. Strongly-correlated electronic states such as Mott and generalized Wigner crystal states have been well established on these triangular lattices to simulate the Fermi-Hubbard Hamiltonian4,5,6,7,8,9,10,11,12,13,14. For bosons, a few types of correlated bosonic states have also been demonstrated on these lattices to explore the Bose-Hubbard physics16,17,18,19,20. Moreover, correlated fermionic-bosonic mixtures, which were previously observed in optical lattices with atomic gases23,24,25, have recently been evidenced in an artificial square lattice of a semiconductor bilayer to implement the mixed Fermi-Bose-Hubbard Hamiltonian26. However, such studies in TMD triangular lattices27,28 remain largely unexplored. In addition, although correlated fermionic and bosonic states were observed independently in TMD bilayers, their coexistence and dynamical evolution on a single system have yet to be explored, which would be highly desirable for building a complete picture of the simulated many-body interactions.

Here, we demonstrate that the twisted WSe2/WS2/WSe2 hetero-trilayer hosts an unconventional fermionic complex, namely the charge-layer-locked (CLL) trion with the constituent two fermions locked in the outer two layers while the left one with opposite sign in the middle layer (Fig. 1a), which is distinctly different from the intra-layer trion in a monolayer and the asymmetric inter-layer trion in a hetero-bilayer. This CLL trion emerges as the lowest-energy excitonic state of the trilayer system with symmetric electric field response owing to its symmetric charge configuration. Notably, the spatially-indirect nature of this fermionic trion enables it to dynamically evolve into a bosonic inter-layer exciton (IX) plus a layer-separated carrier under an applied optical/electric field, which is challenging in hetero-bilayers where the opposite direction, namely the exciton-to-trion conversion, is the common scenario. This unique quasiparticle evolution makes the trilayer system a tunable platform to prepare fermions (CLL trions), fermionic-bosonic mixtures (CLL trions-IXs), and bosons (IXs) on demand. Importantly, these CLL trions themselves function as a reservoir for both charge and exciton fillings, where strongly-correlated states were emergent for each type of quasiparticles. Specifically, a fermionic insulating state related to the CLL trions correlated with the decomposed charge order was observed, which then evolved to a correlated fermionic-bosonic state when a preexisting background of CLL trion-IX mixtures was prepared, and then further to a correlated bosonic state after the background dominated by the bosonic inter-layer excitons. These results offer a unique perspective to simultaneously simulate the Fermi-, Fermi-Bose-, and Bose-Hubbard models on a single platform.

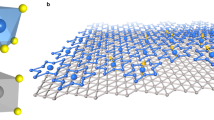
Fig. 1: Layer index engineering of the internal structure of three-body trionic systems.
figure 1

a Internal structure of the trion evolves from an intra-layer to an inter-layer and then to a charge-layer-locked (CLL) geometry. b Symmetric type-II band alignments in the WSe2/WS2/WSe2 hetero-trilayer, with the outer two WSe2 layers arranged in an AB configuration. Solid and dashed orange arrows indicate spin-up and spin-down states, respectively. VB (CB) denotes the valence (conduction) band. c Charge distributions of the CLL trion and inter-layer excitons (IXs) in the trilayer and bilayer regions, respectively (top panel). IX-top denotes the inter-layer exciton in the top bilayer (WSe2/WS2); IX-bottom denotes the inter-layer exciton in the bottom bilayer (WS2/WSe2); CLL trion denotes the charge-layer-locked trion in the trilayer (WSe2/WS2/WSe2). The optical microscope image of a WSe2/WS2/WSe2 hetero-trilayer is displayed in the bottom panel (Sample 1), where the regions of top WSe2 monolayer (dashed blue line), middle WS2 monolayer (dashed red line) and bottom WSe2 monolayer (dashed yellow line) are marked. I, II, and III denote the bottom bilayer, top bilayer and trilayer regions, respectively. The top bilayer of this hetero-trilayer structure is in an R-type stacking while the bottom bilayer in an H-type stacking. Scale bar is 20 μm. d Photoluminescence (PL) spectra of the top bilayer (Top BL: WSe2/WS2), bottom bilayer (Bottom BL: WS2/WSe2) and trilayer (WSe2/WS2/WS2) regions measured at 10 K from Sample 1. The PL intensity of inter-layer excitons in the top bilayer is multiplied by a factor of 0.2 for clarity. Excitation power is 5.64 μW.

Full size image

Results

Charge-layer-locked trions in twisted WSe2/WS2/WSe2 hetero-trilayers

Twisted WSe2/WS2/WSe2 hetero-trilayer structures were chosen to realize the target CLL trions because of the following two important reasons. First, this symmetric trilayer system can form a symmetric type-II band alignment between the two adjacent layers (Fig. 1b), enabling the electrons favoring in the middle WS2 layer while holes preferring in the outer two WSe2 layers. In such a scenario, inter-layer excitons with opposite dipole moments can be formed within top WSe2/WS2 bilayer and bottom WS2/WSe2 bilayer, while symmetric CLL trions are expected to have the opportunity to emerge in the trilayer region with inter-layer Coulomb interactions (Fig. 1c). Second, the stacking order of the outer two WSe2 layers was intentionally designed as the AB stacking, wherein the holes in the outer two WSe2 layers possess opposite spin states at the K valleys (Fig. 1b). This arrangement results in spin-forbidden transitions29 that inhibit efficient hole tunneling between the WSe2 layers, as altering their spin state would require additional energy. Such spin restrictions prevent layer hybridization required for quadrupolar exciton formation, but confine each hole to its respective WSe2 layer to favor the formation of CLL trions that consist of two holes in the WSe2 layers and one electron in the middle WS2 layer (Fig. 1c). Therefore, the expected CLL trions in our study can be easily distinguished from the recently reported quadrupolar excitons30,31,32,33,34,35 observed in similar trilayer systems but with a different stacking order (angle-aligned AA stacking) for the outer layers. In those reported cases30,31,32,33,34,35, inter-layer tunneling between the outer layers is crucial for hybridizing two oppositely-oriented inter-layer excitons into quadrupolar excitons, and hence the twist angle between the outer layers is restricted to be near zero. However, such an angle restriction is substantially released in the formation of CLL trions, which are principally bounded by Coulomb attractions between their constituent charges36. For these reasons, we chose the twisted WSe2/WS2/WSe2 hetero-trilayer with AB-stacked outer WSe2 layers to realize the desired CLL trions.

To verify the presence of charge-layer-locked trions in the WSe2/WS2/WSe2 hetero-trilayer (Supplementary Notes 1 and 2), we performed low-temperature photoluminescence (PL) measurements on the heterostructure (Fig. 1d). One can see two significant features in Fig. 1d. First, the PL emission energy obtained in top and bottom bilayer regions is around 1.46 eV, consistent with reported values for inter-layer excitons in WS2/WSe2 hetero-bilayers20,37. However, as the layer structure extending from the asymmetric bilayer to the symmetric trilayer, such inter-layer excitonic peak disappears in the WSe2/WS2/WSe2 hetero-trilayer, contrasting with the previous results on WSe2/MoSe2/WSe2 hetero-trilayers, where enhanced inter-layer excitonic emission was observed38. More interestingly, a distinct PL emission peak emerges in the hetero-trilayer at a lower energy of ~ 1.40 eV. This emerged excitonic state can be attributed to the CLL trions as discussed later. Second, the energy difference between the CLL trions and inter-layer excitons (exceeding 50 meV, Supplementary Note 3) is much larger than those between inter-layer trions and inter-layer excitons in WS2/WSe2 hetero-bilayers39, indicating that the CLL trions in hetero-trilayers are more energetically stable than the inter-layer trions in hetero-bilayers and further suggesting that the symmetric trilayer can stabilize the three-body entity as compared to the asymmetric bilayer cases. Note that the large energy difference ( > 50 meV) between the CLL trions and inter-layer excitons also implies the existence of a large binding energy between them. The origin of this binding energy is considered principally arising from the additional Coulomb attraction introduced in the symmetric CLL trion, as compared to that of asymmetric inter-layer exciton (Supplementary Note 4), and such a large binding energy is probably the reason why CLL trions can survive at room temperature as experimentally demonstrated in Supplementary Note 5. Additionally, we calculated the Coulomb potential energy for trions with various charge configurations and demonstrated that the vertically aligned charge-layer-locked trion is the most energetically stable configuration (Supplementary Note 6). One more thing that needs to be addressed is that the PL energies of those excitonic complexes vary slightly between different samples due to the sample discrepancies, with the energy peak of inter-layer excitons ranging from ~ 1.42 to 1.46 eV while that of CLL trions ranging from ~ 1.33 to 1.40 eV (Supplementary Fig. 7).

To confirm the formation of charge-layer-locked trions in the hetero-trilayer and distinguish it from inter-layer excitons in hetero-bilayer, we studied the PL emission spectra in a WSe2/WS2/WSe2 hetero-trilayer by applying an external out-of-plane electric field, denoted by VTG-VBG. Unless specified otherwise, the voltage values VTG-VBG mentioned in our study represent the applied electric field (Fig. 2a–c, Supplementary Notes 7 and 12). One can see in Fig. 2d that the PL emission in the bilayer regions shows a linear energy shift (a typical Stark shift) with increased electric field, but the energy shift slopes for the top and bottom bilayers are opposite (top and middle panels in Fig. 2d). This behavior is consistent with that of inter-layer excitons with an out-of-plane dipole moment, and their dipole orientations point exactly opposite in the top and bottom bilayers. The dipole moments p for inter-layer excitons are further estimated to be approximately 0.5 e • nm and 0.7 e • nm for the top and bottom bilayer regions, respectively, based on the slopes of the energy shifts with electric field (Supplementary Note 8), which are consistent with previous reports37,40,41 and further confirm that the electric field has been effectively applied to our trilayer heterostructures for tuning excitonic states.

Fig. 2: Charge-layer-locked (CLL) trions in the twisted WSe2/WS2/WSe2 hetero-trilayer.
figure 2

a Schematic geometry of the twisted WSe2/WS2/WSe2 trilayer in a dual-gate configuration. VTG and VBG: the top and bottom gate voltages; Gr: graphene; hBN: hexagonal boron nitride; CLL trion: charge-layer-locked trion; IX-Top: inter-layer exciton in the top bilayer; and IX-Bottom: inter-layer exciton in the bottom bilayer. b, c Photoluminescence (PL) mapping images with the PL energy of ~ 1.46 eV in the top and bottom bilayer regions and that of ~ 1.37 eV in the trilayer region at 10 K from Device 1. Dashed blue, yellow, and red outlines mark the top bilayer (Top BL), bottom bilayer (Bottom BL), and trilayer regions, respectively. Scale bar is 10 μm. Excitation power:1 mW. d PL emission as a function of the electric field in the trilayer and two bilayer regions at 10 K from Device 1. VTG-VBG corresponds to the out-of-plane electric field. Excitation power: 109 μW. e PL emission as a function of the electric field in the trilayer and two bilayer regions at 297 K from Device 7. Excitation power: 3.5 mW.

Full size image

In sharp contrast to the linear Stark shift observed in hetero-bilayers, the PL emission of CLL trions in the trilayer region exhibits energy redshifts with increasing electric fields along both positive and negative directions (bottom panel in Fig. 2d), which manifests as a superposition of two linear Stark shifts with opposite slopes (Supplementary Note 8). This phenomenon indicates that the CLL trion in the hetero-trilayer carries two oppositely oriented dipoles, resulting in the observed opposite Stark shifts. Considering the symmetric type-II band alignment of the WSe2/WS2/WSe2 hetero-trilayer, with the outer two WSe2 layers arranged in an AB configuration, where the electron prefers to stay in the middle WS2 layer while holes favor in the two outer WSe2 layers due to spin restriction (as discussed above), it is natural to form a trionic state with a unique hole/electron/hole (WSe2/WS2/WSe2) charge distribution. Obviously, in such a symmetric trilayer, the dipoles with opposite orientations are always associated to the unique internal structure of the trion with a charge-layer-locked geometry, which can give rise to the opposite Stark shifts as observed in the CLL trionic state in the trilayer. Although opposite Stark shifts have also been observed in quadrupolar excitonic states as recently reported31,32,33,34,35, the angle-aligned trilayers with outer layers in AA stacking are required to achieve inter-layer tunneling for realizing this four-body state. In our case, the CLL trionic state forms in trilayers with AB-stacked outer layers where the inter-layer tunneling has been reported to be negligible32. In addition, this CLL trionic state can even exist in the trilayer with a large twist angle, which further excludes the possibility of forming quadrupolar excitons in our system (Supplementary Notes 3 and 4). It is also worth mentioning that the PL emission of CLL trions as a function of the electric field at room temperature exhibits similar behavior to that observed at a lower temperature (Fig. 2e), suggesting the robustness of this charge-layer-locked trion to temperature variations (Supplementary Note 5).

Two other points need to be addressed in Fig. 2d. First, the PL intensity of CLL trions under a negative electric field is stronger than that under a positive electric field, indicating that the layer coupling in the top bilayer may be relatively stronger than that in the bottom bilayer. This observation is also evident in the PL intensity of inter-layer excitons, where the top inter-layer excitons exhibit stronger PL intensity than that of bottom inter-layer excitons. Such a phenomenon also hints a certain degree of dipole asymmetry in the CLL trions (Supplementary Note 8). Second, the PL spectra at room temperature were obtained at a significantly higher optical excitation power, where a coexistence of CLL trions and inter-layer excitons, rather than purely CLL trions, was observed in the trilayer region (Fig. 2e and Supplementary Fig. 8e in Supplementary Note 5). This finding may signal a transition from CLL trions to inter-layer excitons as the excitation power increases.

Optical- and electric-field-tunable charge-layer-locked trions

Optical-field-tunable charge-layer-locked trions

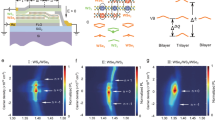
In order to verify the transition from CLL trions to inter-layer excitons, we studied the power-dependent PL emission of the trionic state in the hetero-trilayer. One can see in Fig. 3a that, within the emission energy range from 1.26 eV to 1.50 eV, only the CLL trion band (peaked at 1.37 eV) is present at low excitation power ( ~ 0.2 μW). However, when increasing the excitation power, an additional PL band centered at 1.42 eV (corresponding to the energy of inter-layer excitons) emerges. By analyzing the PL intensity ratios of the CLL trion band and the emerging inter-layer exciton band, one can find that the intensity ratio of the CLL trion band decreases while that of the inter-layer exciton band increases with increasing excitation power (Fig. 3d). This indicates a power-induced transition from CLL trions to inter-layer excitons. Notably, this transition occurs rapidly in the low power region ( < 1 μW) and then stabilizes over a wide power range ( ~ 1-100 μW, Fig. 3d). Such a phenomenon was consistently observed in different samples (Supplementary Note 9). Interestingly, in all samples, there exists a critical power at which the intensity ratio of the CLL trion band starts to stabilize around ~ 60%, while that of the inter-layer exciton band stabilizes around ~ 40%. That is, the intensity ratios between these two quasiparticles remain nearly constant or vary pretty slowly as the power exceeding the critical values (Fig. 3d and Supplementary Fig. 12a–c for other samples). This unusual behavior suggests that, beyond certain critical power values, the CLL trions and inter-layer excitons appear to be correlated with each other, to maintain their distributions within the trilayer at a roughly fixed ratio (60:40) over a wide power range (see the details in Supplementary Note 9). This 60:40 ratio stability appears to be an intrinsic feature of this many-body system, where additional excitation does not disrupt the established interactions.

Fig. 3: Optical- and electric-field-induced transition from CLL trions to inter-layer excitons.
figure 3

a–c Excitation power-dependent photoluminescence (PL) spectra and their contour plots at applied voltage VTG-VBG of 0 V (a), 2 V (b), and 4 V (c) at 10 K from Device 2. The measured power-dependent PL spectra are fitted to Gaussian peaks. CLL trion: charge-layer-locked trion; IX: inter-layer exciton; IXX: inter-layer bi-exciton; IX+: charged inter-layer exciton; and CLL trion+: charged CLL trion. d PL intensity ratios of CLL trions (shown in red) and inter-layer excitons (shown in blue) as functions of excitation power. The PL intensity ratio is defined as the ratio of the integrated PL intensity of the CLL trion band or inter-layer exciton band to the total integrated PL intensity of these two bands. VTG-VBG corresponds to the out-of-plane electric field. e Schematic illustration of field-induced transitions from CLL trions to inter-layer excitons and bi-excitons.

Full size image

Despite the excitation power-dependent PL intensity, the PL energies of CLL trions and inter-layer excitons also exhibit blueshifts with increasing power. One can find that the PL energy blueshift of CLL trions is nearly twice as large as that of inter-layer excitons (approximately seven times that of quadrupolar excitons (Supplementary Fig. 13)). This result aligns with our theoretical calculations of Coulomb interaction energies for these excitonic states (Supplementary Note 10), and highlights that CLL trions exhibit the stronger Coulomb interactions and thus a larger energy blueshift. Although the energy blueshift differs between CLL trions and inter-layer excitons, their PL energies follow similar power-dependence trends, where they initially exhibit a rapid blueshift with increasing power, followed by saturation at higher power levels (Fig. 3a, Supplementary Fig. 12d–f). Interestingly, this saturation appears around the critical power, marking the turning point in the power-dependent intensity ratios as discussed above (Supplementary Fig. 12). In other words, both the energy blueshifts and intensity ratios of CLL trions and inter-layer excitons start to vary slowly or remain constant when the power exceeds the critical value. Such a nonlinear energy blueshift has been previously observed for inter-layer excitons and recognized as a fingerprint of emergent excitonic correlations42,43. Specifically, when the power is below the critical value, where the exciton density remains low, the observed blueshift primarily arises from dipolar interactions between inter-layer excitons20,44. However, beyond this critical power, high-density inter-layer excitons start to correlate with each other, rearranging their spatial distribution to minimize the Coulomb interaction energy. Upon forming this correlated state, the system reaches a new equilibrium, where the further increase of exciton density no longer significantly affects the interaction energy. In this case, the energy blueshift with the contribution from correlation interactions turns to saturate (see the details in Supplementary Notes 9, 10, and 13), resulting in the nonlinear energy blueshift as observed experimentally (Supplementary Fig. 12d–f)19,43. Similar nonlinear energy blueshifts observed for CLL trions further suggest the emergence of correlation behavior between CLL trions as well (Supplementary Notes 10 and 13), highlighting that the trilayer system as a promising platform for exploring fascinating many-body correlations. These results also echo the above findings where the CLL trions and inter-layer excitons correlate with each other to maintain a fixed distribution ratio (60:40) over a wide power range (see the details in Supplementary Note 9).

Note that two side peaks are also observed in the inter-layer exciton band at higher powers, as revealed by multi-peak fitting analysis (Fig. 3a). These side components are associated with excitonic complexes related to inter-layer excitons. The higher-energy side peak (in dark blue) has been identified as an inter-layer bi-exciton (IXX)44. This assignment was supported by the super-linear relationship between excitation power (P) and integrated intensity \((I,I\propto {P}^{\alpha })\), where the power-exponent \((\alpha \approx 1.2)\) for the inter-layer bi-exciton is twice that of the inter-layer excitons \((\alpha \approx 0.6)\) (Supplementary Fig. 14, Supplementary Note 11), confirming the assignment of inter-layer bi-exciton, with its higher energy resulting from on-site repulsive dipole-dipole interaction20,44. Polarization-resolved measurements further validated the existence of this bi-excitonic state (Supplementary Fig. 15 and Supplementary Note 11), where the valley polarization at the bi-exciton peak was found to be zero, aligning with theoretical calculations and previous studies19,45. On the other hand, the lower energy side peak (in yellow) was previously reported as the charged counterpart of inter-layer excitons (IX+)39,46,47, formed by binding interactions between neutral excitons and extra carriers. In our case, we can tentatively attribute the lower energy side peak (IX+) to the charged counterpart of inter-layer excitons as well. Since the transition from CLL trions to inter-layer excitons is accompanied by the generation of holes in the third layer due to the conservation of charge numbers, these dissociated holes likely interact with inter-layer excitons or CLL trions, forming their charged counterparts at lower energies (IX+ in yellow and CLL trion+ in light pink in Fig. 3a). The difference is that the charged inter-layer exciton (IX+) formed here was considered consisting of an inter-layer exciton in the WSe2/WS2 bilayer and an extra hole in the other WSe2 layer of the hetero-trilayer, forming a structure similar to a loosely bound CLL trion. In other words, IX+ behaves as an intermediate species between the inter-layer exciton and CLL trion, with its PL energy located between them (Fig. 3a).

Electric-field-tunable charge-layer-locked trions

Taking advantage of the unique charge-layer-locked internal structures of IX+ and CLL trion, the Coulomb attractive forces between the inter-layer excitons and holes in these quasiparticles are expected to be broken down by applying an out-of-plane electric field, which can facilitate the above-mentioned transition from CLL trions to inter-layer excitons while suppressing the formation of IX+ as well. Based on this scenario, we conducted PL measurements on the WSe2/WS2/WSe2 hetero-trilayer under different electric fields, corresponding to an applied voltage (VTG-VBG) of 0 V, 2 V and 4 V. Under these conditions, we observed a more efficient transition from CLL trions to inter-layer excitons, as well as the suppression of IX+ formation. As shown in Fig. 3a–c, with the applied voltage increased from 0 to 2 V, the PL spectrum, initially dominated by the CLL trion band in the low power region ( < 1 μW), turns to be dominated by the inter-layer exciton band, and when further increasing the voltage to 4 V, the inter-layer bi-exciton emerges at the higher energy side of the inter-layer exciton band. Notably, this electric-field-induced transition is nearly complete at high powers ( > 500 μW), with emission from inter-layer bi-excitons becoming dominant in the PL spectra under 2 V and 4 V. As expected, the IX+ component nearly vanished in PL spectra under electric fields (see Supplementary Fig. 20 for the comparison of PL spectra under different electric fields at different powers). A schematic diagram for the transitions among these excitonic complexes can be summarized in Fig. 3e. Such transitions demonstrate that CLL trions can be manipulated by both optical and electric fields, dissociating into other quasiparticles with distinct natures. As stated above, these phenomena principally benefit from the charge-layer-locked internal structure of the CLL trion, where its three constituent charges are layer-separated and thus respond sensitively to external fields, especially the out-of-plane electric field.

It is worth noting that the transition from CLL trions to inter-layer excitons is less efficient under negative voltages (Supplementary Note 12), which is probably due to the asymmetric binding forces between the middle electron and outer two holes of the CLL trion. For the hetero-trilayer studied here, the top inter-layer excitons exhibit stronger PL intensity than the bottom inter-layer excitons (Supplementary Fig. 6b), which can be attributed to the different stacking and twist angles between layers37 (\({\theta }_{{top}}=59.88\pm 0.15^\circ\), \({\theta }_{{bottom}}=0.38\pm 0.33^\circ\), Supplementary Fig. 3f). This difference in PL intensity suggests the stronger electron-hole coupling in the top bilayer. Therefore, for the CLL trion formed in the trilayer region, the Coulomb attraction between its electron and hole in the top bilayer could be stronger than that in the bottom bilayer. This results in the more efficient transition from CLL trions to inter-layer excitons when a positive electric field is applied from the top to the bottom layer.

Correlated states of the tunable charge-layer-locked trions

Following the observation of the CLL trion to inter-layer exciton transition induced by optical and electric fields, we investigated the dynamic evolution of the correlated states of these excitonic quasiparticles in the trilayer system by combining the optical excitation and electric field tuning methods. It should be pointed out that the dissociation of CLL trions under these external fields generates both inter-layer excitons (bosons) and holes (fermions). These dissociated fermions and bosons can serve as sources for charge and exciton fillings within the crystal lattice, facilitating the formation of correlated states. Unlike conventional lattice filling methods that rely on external doping, here the CLL trions themselves function as a reservoir, providing quasiparticle sources for charge and exciton fillings into the lattice. This offers an alternative strategy to manipulate the many-body correlation in trilayer excitonic systems.

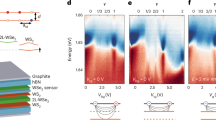
Based on this strategy, we explored and analyzed the correlated states of CLL trions and inter-layer excitons as well as their dynamic evolution, by examining their electric field-dependent PL emission at various excitation powers. As shown in Fig. 4a–d, the PL emissions of both CLL trion and inter-layer exciton are significantly modified as tuning the electric field at different powers (1.2 μW, 8.8 μW, 62 μW and 271 μW). Two important features can be revealed from these data. First, with increased electric field, the PL intensity ratio of the CLL trion band decreases while that of the inter-layer exciton band increases at each excitation power (Fig. 4e–h). This confirms the former observation that an electric field induces the dissociation of CLL trions into inter-layer excitons and holes. These dissociated particles then participate in exciton and charge fillings within the lattice, leading to the formation of correlated states as identified below. Second, sharp jumps in the PL intensity (indicated by white arrows in Fig. 4a–d) were observed as tuning the electric field, and these PL intensity jumps become increasingly pronounced at higher excitation powers. Note that such PL intensity jumps have been widely recognized as an indicator of forming correlated states in previous studies8,11,19,48, in which the transition between correlated states was accompanied by a sudden change of the quasiparticle density, leading to a sudden jump of the PL intensity. Therefore, the observed PL intensity jumps in our case suggest the emergence of correlated states associated with CLL trions or inter-layer excitons or both in our hetero-trilayer, as tuning the electric field at different powers.

Fig. 4: Correlated states of CLL trions, inter-layer excitons and their mixtures.
figure 4

a–d Electric field-dependent photoluminescence (PL) emission at the excitation power of ~ 1.2 μW (a), 8.8 μW (b), 62 μW (c), and 271 μW (d) from Device 2. White arrows indicate the locations of PL intensity jumps in the charge-layer-locked trion (CLL trion) band and inter-layer exciton (IX) band. e–h Corresponding PL integrated intensity ratios of CLL trions (red dots) and inter-layer excitons (blue dots) as functions of the electric field under the excitation power of ~ 1.2 μW (e), 8.8 μW (f), 62 μW (g), and 271 μW (h). Shaded regions in the PL ratio plot highlight step-like features associated with CLL trions (red) and inter-layer excitons (blue). i, j Schematic illustration of the correlated states associated with the CLL trions and inter-layer excitons (correlated CLL trion-IX state) (i) and the correlated inter-layer exciton state (correlated IX state) (j).

Full size image

Specifically, taking the case at 62 μW as an example (Fig. 4c), a number of clear PL intensity jumps could be observed in both the CLL trion and inter-layer exciton bands. For the CLL trion band, as the voltage varying from 0 to 4 V, its intensity ratio varies within the range from ~ 60% to ~ 40% (Fig. 4g). Notably, this intensity ratio decreases with the voltage in an unusually stepwise pattern, where the position of each step appearing in Fig. 4g corresponds exactly to the position of each intensity jump occurring in Fig. 4c. Such PL intensity jumps and ratio steps strongly support the formation of a series of correlated states11,39 associated with CLL trions as tuning the lattice filling by the electric field. However, unlike previous reports where the charge filling for realizing correlated states was achieved through electrostatic doping, here the filling is driven solely by the holes or inter-layer excitons dissociated from CLL trions. Similarly, PL intensity jumps also appear in the inter-layer exciton band (Fig. 4c, Supplementary Fig. 18) because exciton and hole fillings occur simultaneously during the dissociation of CLL trions. Accordingly, the intensity ratio of the inter-layer exciton band increases with the voltage in a similar stepwise pattern, where a one-to-one correspondence between steps and intensity jumps could be observed as well (Fig. 4g). This indicates that correlated states associated with inter-layer excitons were also present in this case. Therefore, as tuning the voltage from 0 to 4 V at 62 μW, the correlated states associated with both CLL trions and inter-layer excitons can emerge simultaneously in the hetero-trilayer, signifying the formation of a fermionic-bosonic mixed state in the system (Fig. 4i, see the details in Supplementary Note 14).

Notably, once the voltage exceeds 4 V, an abrupt energy jump—a hallmark of the formation of the Mott correlated state16,19,20,39—appears in the inter-layer exciton band (Fig. 4c). The energy value at which this jump occurs well coincides with that of the inter-layer bi-excitons, suggesting that this correlated state is likely a bosonic insulator. That is, all the available sites in this ordered state are filled by inter-layer excitons, and adding an extra inter-layer exciton requires an additional energy cost due to the on-site exciton-exciton repulsive interaction (Fig. 4j, see the details in Supplementary Notes 14 and 15). Obviously, such an exciton filling can only arise from the dissociation of CLL trions at a fixed excitation power, as evidenced by the sharply weakened intensity of CLL trions in this case (Fig. 4c, g).

For the cases at lower excitation powers (1.2 μW, 8.8 μW), the initial background quasiparticles are dominated by CLL trions (Fig. 4e, f). Here, the PL intensity jumps and ratio steps were observed in the CLL trion bands (Fig. 4a, b, e, f), indicating the formation of fermionic correlated states associated with CLL trions (Supplementary Note 14). While for the case at the higher excitation power (271 μW), the initial background quasiparticles are dominated by inter-layer excitons. In this case, a number of PL intensity jumps and ratio steps were observed in the inter-layer exciton band (Fig. 4d, h). However, the discrete intensity and energy jumps that observed in the lower power cases turn to vary more continuously with the electric field in this higher power case. This is probably due to the melting of the correlated orders13,28 by extra filling of the bosonic state.

These results reveal an unexpected correlated state transition from fermionic to bosonic nature via controllable tuning of both excitation power and electric field. The corresponding Hubbard Hamiltonians to describe these correlated states were detailed in Supplementary Note 14. The charge-layer-locked internal structure of CLL trions plays a crucial role in realizing such a correlated state transition. As discussed, this unique internal structure enables CLL trions to dissociable under both optical and electric fields, thus making CLL trions function as a reservoir for both charge and exciton fillings to realize those fermionic and bosonic correlated states and their dynamic evolution. While van der Waals bilayers have been demonstrated as a powerful platform to individually realize the fermionic and bosonic correlated states4,6,7,8,10,11,16,17,19,39, the interplay between fermions and bosons as well as their dynamical evolution with correlated behaviors on a single system remain largely unexplored20,26,28. Therefore, our findings provide an attractive perspective for investigating correlated states with the interacting quasiparticles ranging from fermions, fermionic-bosonic mixtures to bosons on a single trilayer system.

Discussion

In summary, we demonstrate the existence of an unconventional trion with a charge-layer-locked internal structure in the twisted trilayer heterostructures. This spatially-indirect trion can evolve into a bosonic inter-layer exciton and an extra charge by an applied optical or electric field, thereby acting as a reservoir for lattice fillings to facilitate the emergence of correlated states. The fingerprint of a correlated insulating state evolving from fermionic, fermionic-bosonic, to bosonic nature is spotted on this trilayer system. Specifically, in contrast to the commonly reported charge orders, a distinct fermionic correlated state associated with these spatially indirect trions interacting with the decomposed charges is observed. Notably, a hybrid fermionic-bosonic correlated state is realized via the interplay between the fermionic trions and bosonic inter-layer excitons. Our studies establish the trilayer system as a prosperous platform for generating unconventional quasiparticles, and a tunable playground for engineering both fermionic and bosonic correlated states especially for the fermionic-bosonic hybrid many-body effects, stepping towards a comprehensive understanding of quasiparticle-quasiparticle interactions.

Methods

Sandwiched heterostructure and Device fabrication

We used a layer-by-layer dry transfer method to fabricate the hetero-trilayers and dual-gate devices. The main steps are illustrated in the following. (1) First, we fabricated the WSe2, WS2 monolayers, hexagonal boron nitride (hBN) capping layers and few-layer graphite (Gr) via mechanical exfoliation onto a polydimethylsiloxane sheet (PDMS) substrate. During this process, we only chose the exploited TMD flakes with cleavage edges along the zigzag and armchair directions of the monolayers spanning either 60° or 120° angle, and hBN flakes with the same thicknesses. The crystal axes of TMD flakes were further confirmed by angle-resolved second harmonic generation (SHG) as discussed below, and the thickness of hBN flakes was confirmed by atomic force microscope (AFM). (2) Then, we transferred few-layer-graphite back gate, the bottom hBN flakes, the WSe2, WS2 and WSe2 monolayers, the few-layer graphite contact, the top hBN flakes and few-layer graphite top gate in sequence on doped silicon substrates covered with silicon oxide 280 nm thick, and the dual-gate configuration was shown in Fig. 2a. (3) Further, during the heterostructure fabrication process, these monolayer TMDs were vertically stacked according to optical alignment of the flake well-defined edges. The final constructed device was annealed under ultrahigh vacuum (around 10-6 mbar) at 200 °C for 6 hours. Finally, all contacts to the few-layer graphene were formed by Ni/Au (10 nm/70 nm) using standard photolithography system and electron-beam evaporation. The top and bottom gate voltages were applied by using Keithley 2400 source meters.

Low temperature photoluminescence measurements

We used a Horiba LabRAM system equipped with a confocal microscope for PL measurements. The hetero-trilayer was loaded into a closed-cycle cryostat with electrical connection for low temperature measurement, the temperature was kept at 10 K (Cryocooler G2B-LT) unless specified otherwise, and a piezoelectric controller was used to position the hetero-trilayer. A 488 nm Ar-ion continuous laser served as the excitation source and was focused on the hetero-trilayer via a 50\(\times\) objective lens (numerical aperture, 0.55), and the PL signal was collected using a high-resolution spectrometer with a diffraction grating of 150 grooves per millimeter. A charge-coupled device (CCD) was used as a detector (detection range between 400 nm and 1,000 nm).

Angle-resolved second harmonic generation measurements

Angle-resolved second harmonic generation (SHG) measurements were conducted to determine the stacking configuration and twist angles between the TMD layers in the hetero-trilayers. The SHG setup was illustrated in Supplementary Fig. 2. A mode-locked Ti: sapphire laser (Spectra Physics, Tsunami) with a photon energy of 1.55 eV, repetition rate of 80 MHz, and pulse duration of 100 fs was used as the excitation source. The beam was focused onto the sample through a 100× objective lens (numerical aperture: 0.55). The second-harmonic signal was collected in reflection geometry using the same objective and directed through an analyzer into a spectrometer equipped with a liquid-nitrogen-cooled charge-coupled device (CCD) camera. A 400 nm band-pass filter was placed in the detection path to block the fundamental excitation. A half-wave plate (λ/2 plate) was used to control the polarization of the incident beam with respect to the sample orientation, while an analyzer set parallel to the excitation polarization was used to resolve the polarization of the SHG signal. The sample was placed on a rotation stage to measure the SHG intensity as a function of the azimuthal angle, allowing for precise determination of the twist angle between adjacent TMD layers.

Electrical tuning measurements

We used a dual-gate configuration to achieve a neutral electric field. From the device structure depicted in Fig. 2a, VTG and VBG denote the top- and back-gates, and an additional graphite was directly connected with the middle WS2 served as a grounded-gate. The electric field was calculated by \({E}_{z}=\frac{{V}_{{{\rm{TG}}}}-{V}_{{{\rm{BG}}}}}{{d}_{{{\rm{total}}}}}\bullet \frac{{\varepsilon }_{{{\rm{hBN}}}}}{{\varepsilon }_{{{\rm{HET}}}}}\), here, VTG and VBG were applied together with a voltage ratio \(\alpha\) (\(\alpha=\frac{{d}_{{{\rm{top}}}}^{{{\rm{hBN}}}}}{{d}_{{{\rm{bot}}}}^{{{\rm{hBN}}}}}\approx 1\) in our study), \({d}_{{{\rm{total}}}}\) is the total hBN thickness, and \({\varepsilon }_{{{\rm{hBN}}}}=3.5\)49 and \({\varepsilon }_{{{\rm{HET}}}}=7.4\)44 are the hBN and heterostructure permittivity, respectively. Due to this voltage relation of \({V}_{{{\rm{BG}}}}=-\alpha {V}_{{{\rm{TG}}}}\), the electrons and holes with equal amounts will simultaneously be injected to the middle WS2, effectively eliminating charge doping. The low temperature measurement was achieved in a closed-cycle cryostat. Additional configuration details were provided in Supplementary Note 7, but all procedures and parameters required for reproducibility are fully described here.