Introduction

Magnetic topological insulator has emerged as a novel platform that has attracted significant attention in this decade. The intrinsic magnetization breaks time-reversal symmetry and opens an exchange gap, while the nontrivial band topology leads to the formation of a chiral edge state (CES) within the exchange gap. This CES enables dissipationless edge transport and gives rise to the quantum anomalous Hall (QAH) effect, making the system a QAH insulator1,2. From an application standpoint, the QAH effect is superior to the conventional quantum Hall effect because it eliminates the need for an external magnetic field. Several promising prospects have emerged for the development of QAH insulators. For instance, they are predicted to support chiral Majorana edge modes when coupled with superconductors, making them ideal candidates for topological quantum computation3. The dissipationless nature of CES also motivates the development of chiral interconnects and the integration of QAHE into electronic circuits to reduce power consumption4. Additionally, recent research has demonstrated that the chirality of CES can be electrically modulated, paving the way for persistent chiral memory, a key concept in spintronic devices5. The interest in QAHE insulators is driven by their potential applications, which further drives the ongoing research into materials exhibiting QAH effect. The first demonstration of the QAHE was achieved in a magnetic-doped topological insulator system, specifically in Cr-doped (Bi, Sb)2Te36. While the CES in this system has been thoroughly studied, the disorder induced by magnetic doping limits sample quality and restricts QAHE to ultra-low temperatures7. A significant breakthrough came with the discovery of MnBi₂Te₄ (MBT), an intrinsic magnetic topological insulator. MBT is an A-type antiferromagnetic van der Waals material composed of Te-Bi-Te-Mn-Te-Bi-Te septuple layers (SL). The adjacent SL are connected by weak van der Waals bonds and demonstrate antiparallel magnetization orientations. This unique combination of topology and magnetic order has attracted intense research interest8,9,10,11,12,13,14. Notably, due to its layer-dependent magnetization, MBT is predicted to hold different topological phases based on the number of layers. For even-layer MBT, axion insulator state was predicted and realized9,15. For odd-layer, the nonzero net magnetization makes it a QAH insulator, and has been successfully realized in experiment16. Unlike magnetically doped topological insulators, MBT offers a more ideal platform for QAHE since the magnetic moment is ordered in the lattice structure. While QAHE has been observed in 5-SL MBT, attempts to observe zero-field CES in MBT by electrical transport is not realized17,18.

Here, we systematically identify and investigated the CES using electrical transport in a well quantized 5SL-MBT sample at zero magnetic field. Four-terminal Hall and longitudinal resistance measurements reveal a well quantized QAH state at zero field. Three-terminal non-local measurements provide further evidence for the existence of CES. Finally, nonreciprocal resistance confirms the dominance of CES at charge neutrality point (CNP) and the gate dependent measurement reveals its interplay with trivial edge states and bulk states.

Results

Four-terminal electrical measurements at zero magnetic field

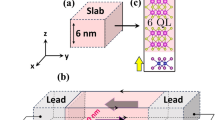
First, we performed four-terminal electrical transport measurements to investigate our device. The structure of device is illustrated in Fig. 1a. We use the Al2O3-assisted exfoliation method to fabricate a 5SL-MnBi2Te4 device16. The device has a dual-gate configuration, with Al2O3 and Si/SiO2 serving as its back gate while graphite and hBN used as top gate. The electrical transport measurements were performed at 1.6 K. By applying gate voltage to both top and bottom gates, we can tune the electric field and carrier density of our MBT device independently. To minimize thermal effect, a small AC current of 10 nA was applied through the device. Figure 1b shows the measurement configurations. Figure 1c shows the longitudinal and transverse resistance of the device as a function of carrier density. The carrier density at which the maximum of Hall resistance (Ryx) occurs, coincides with that of longitudinal resistance (Rxx) minimum, indicating the Fermi level of the device reaches CNP. Field-dependent measurements were subsequently conducted at the CNP with the magnetic field applied perpendicular to the sample plane. Figure 1d, e show the longitudinal and transverse resistance as a function of magnetic field. From the transverse resistance, we observed a nearly quantized value of 24.2 kΩ (0.936 h/e2) at zero field, accompanied by a longitudinal resistance of 801 Ω (0.0310 h/e2). The zero-field transverse resistance remains up to 0.810 h/e2 at 6 K, as shown in Supplementary Fig. 2. With the temperature dependent longitudinal resistance (Shown in Supplementary Fig. 1), we are able to estimate the activation energy gap of our sample. At zero field, the energy gap is estimated to be 0.524 meV. The gap size is slightly smaller with a value of 0.483 meV at coercivity field (0.5 T) and reached 0.879 meV in the ferromagnetic phase (7 T). The zero-field energy gap is comparable to the previously reported value obtained by transport measurement, showing the relative high quality of our sample16. However, this value is significantly smaller than the gap size of MBT measured by Angle-resolved photoemission spectroscopy19 (70 meV) and Scanning tunnelling spectroscopy20 (175 meV). This substantial discrepancy may primarily attribute to surface band broadening caused by defects16.

Fig. 1: Four-terminal measurements of 5-SL MBT device.
figure 1

a Schematic structure of the MnBi2Te4 device. b The electrode configuration of the device. Gray boxes represent electrodes and the number within denotes the serial number of each electrode. c Rxx and Ryx as functions of carrier density with back gate voltage fixed at 19.82 V. AC current with RMS amplitude of 10 nA is added through electrode 1 and 5. Vxx and Vxy are measured with electrode 2–3 and 2–8, respectively. The blue shaded area denotes the charge neutrality region. d Magnetic field dependent Rxx at CNP. Red and blue curve represents the up and down sweep of magnetic field. e Magnetic field dependent Ryx at CNP. Rxx and Ryx curves are symmetrized and antisymmetrized to eliminate components from other direction. f Arrhenius plots of Rxx at different magnetic fields. The x axis is the reciprocal of temperature while the y axis being ln Rxx, lines are linear fitting of data points.

Full size image

To verify the reproducibility of the high quantization of Hall resistance, we repeated the same fabrication process and achieved 70% quantization at zero-field in a second 5SL-MBT device (Device #2). Moreover, we also fabricated another 5-SL MBT sample (Device #3), with a few nanometers of AlOx capped on its top surface as prompted by recent research21. This new device exhibits improved quantization (92%). The corresponding data are provided in the Supplementary Notes 8 and 9.

Landauer-Büttiker Formalism verification by three-terminal measurements

In ideal case, for QAH insulator, the bulk is insulating, and the current will only transport via the chiral edge channel. The electrical transport behaviour of CES can be described by Landauer- Büttiker Formalism22. The current flows out of each electrode can be expressed in terms of the voltage and transmission probability between them:

$${I}_{i}={\sum}_{i\ne j}\frac{{e}^{2}}{h}{T}_{{ji}}({V}_{i}-{V}_{j})$$
(1)

where Ii is the current leaving the ith electrode, Vi,is the voltage at the ith electrode and Tji is the transmission probability from the jth to the ith electrode. For the CES, the edge current flows in one direction without backscattering. Applying the formula to our sample, considering the case where M < 0 with a couterclockwise propagating edge mode, we have

$${T}_{{{{\rm{ji}}}}}={\delta }_{i,j+1}$$
(2)

where i,j being the serial number of electrode denoted in schematic in Fig. 2a. Specially, \({T}_{81}=1.\,\)Under these conditions, injecting current from electrode 1 to electrode 5 produces two equipotential edges: V1 = V2 = V3 = V4 along one edge and V5 = V6 = V7 = V8 along the opposite edge. When current \({i}_{0}\) is injected from electrode 1 and the drain electrode potential is referenced to ground (0 V), the potential at right edge voltage is \({i}_{0}h/{e}^{2}\) and left edge potential is 0 V.

Fig. 2: Three-terminal measurements.
figure 2

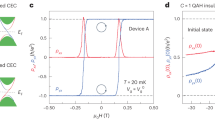
a Schematic illustration of electrode configuration and chiral edge state distribution. Blue arrowed lines indicate the transport route of chiral edge current when M < 0 whereas the red ones are chiral edge current when M > 0. b three-terminal resistance as functions of magnetic field. The red and blue curves represent resistances for up and down sweep of magnetic field, respectively.

Full size image

To verify the aforementioned theoretical arguments in experiments, we conduct three-terminal resistance measurement. We denote \({R}_{{ij},{ik}}\) as the resistance measured when current flows from electrode i to j while the voltage drop is measured between electrode i and k. For the ideal case discussed above, three-terminal resistances along the right edge are, \({R}_{{{\mathrm{15,1}}}k}=0\) (k = 2,3,4). Along the left edge, \({R}_{{{\mathrm{15,1}}}{k}^{{\prime} }}=h/{e}^{2}\,({k}^{{\prime} }={{\mathrm{6,7,8}}})\). Reversing the sample’s magnetization flips the chirality of the edge mode, thereby exchanging the voltages of the left edge with those of the right edge. Consequently, sweeping magnetic field back and forth will create a hysteresis loop of three-terminal resistance that alternates between h/e2 and zero. As shown in Fig. 2b, our measurements exhibit two distinct resistance states at zero field: one near zero and one close to h/e2. The largest difference of the two resistance states at zero field is 0.919 h/e2 (R15,17), which agrees with our four-terminal Hall resistance measurement result. Furthermore, the three-terminal resistance loops for the left and right edges are approximately symmetric under magnetization reversal, consistent with the predictions of the Landauer–Büttiker framework. It is noteworthy that the three-terminal resistances slightly exceed h/e2 when magnetic field sweeps to near 4 T or −4 T. This is possible when the sample slightly deviates from QAH state and bulk channel with dissipation coexists with the CES (details are explained in Supplementary Note 3). Such deviation is due to the spin-flop transition of MBT, which causes the weakening of surface magnetization. This behavior is consistent with recent MBT research23.

To reinforce the conclusion that transport proceeds primarily through the CES, we also measure the nonlocal three-terminal resistance (Supplementary Fig. 3), injecting current from electrode 1 to electrodes 3 or 7 and monitoring the voltage drop between electrode 1 and a remote electrode. The nonlocal measurements yield results similar to the local ones, reinforcing that the current is carried by the CES rather than by bulk states. At a higher magnetic field of 7 T, where all spins align in the same direction, the quantization becomes even more pronounced, with the high-resistance state exceeding 0.97 h/e2 and low-resistance falling below 0.01 h/e2. We will discuss the small discrepancies between the zero-field and high-field data in a later section.

Nonreciprocal resistance measurements

We further investigated the CES in MBT at zero magnetic field using nonreciprocal resistance measurements. Nonreciprocal resistance has been observed in lots of systems such as semiconductors24,25,26,27, superconductors28,29 and magnets30,31,32,33,34, and it can arise from several different origins. In QAH systems, the nonreciprocal resistance may originate from the interplay between chiral edge channel and additional nonchiral conduction channel35,36. When the Fermi level slightly deviates from the CNP, either bulk conduction channels or non-chiral edge channels become available. As illustrated in Fig. 3a, b, the transport direction of the CES (orange arrows) depends solely on the orientation of the bulk magnetization, whereas the other channels lack such chirality. Asymmetric scattering between the chiral edge channel and trivial channels then causes a difference in resistance when the current is reversed. In our experiments, we demonstrate this nonreciprocity by applying an AC current and measuring second-harmonic voltage (See Supplementary Note 4). The nonreciprocal resistance is defined as \({R}_{{xx}}^{2\omega }={V}_{{xx}}^{2\omega }/{I}_{{xx}}^{\omega }\), where \({V}_{{xx}}^{2\omega }\) is the second harmonic voltage and \({I}_{{xx}}^{\omega }\) is magnitude of the AC current applied.

Fig. 3: Magnetic field dependent nonreciprocal resistance measurements.
figure 3

a, b Schematic illustration of different edge state chirality with up and down magnetization. The orange arrows indicate the transport direction of chiral edge state, yellow arrows show the bulk current direction. Pink arrow with red sphere is a representation of the bulk magnetization direction. The chiral edge current direction is associated with the bulk magnetization whereas the bulk current direction is not affected. c Nonreciprocal resistance of left edge as a function of magnetic field at CNP. Red and blue lines are resistance for up and down sweep of magnetic field. The resistance is deduced from voltage signal obtained by electrode 8 and 6. d, e Nonreciprocal resistances of left, right edge as functions of magnetic field at various carrier densities. The back gate is fixed at 40 V. Left edge second harmonic voltages are taken with electrode 8 and 6, right edge is taken with electrode 2 and 4. The insets are illustrations of the band structure of MnBi2Te4 and the position of Fermi level.

Full size image

We inject a 4 μA (rms) AC current through electrode 1 and 5 and simultaneously measure the first- and second-harmonic voltage drops at the left and right edge of the sample. We denote the corresponding longitudinal resistance and nonreciprocal resistance on the left edge by RL and \({R}_{L}^{2\omega }\), respectively, and on the rifht edge by RR and \({R}_{R}^{2\omega }\). Initially, we tune the Fermi level to the CNP. As shown in Fig. 3c, the nonreciprocal resistance vanishes at zero field, in stark contrast to a previous, non-quantized MBT sample that exhibited a pronounced nonreciprocal signal at the CNP36. We then tune the Fermi level away from the CNP to examine the resulting nonreciprocal behavior. Figure 3d, e depict the carrier-density-dependent hysteresis loops of the nonreciprocal resistance measured at the left and right edges. The signal switches sign when the Fermi level moves from the hole-doped to electron-doped regime, and at a fixed Fermi level, it flips sign from edge to edge. These observations align with prior studies of edge-current-induced nonreciprocal resistance35,36. We also consider other scenario which can induce nonreciprocal resistance and exclude them (See supplementary Note 5 and 6). Figure 4a, b present a summary of both longitudinal and nonreciprocal resistances on the left and right edges at various carrier densities. At both edges, the nonreciprocal resistance is minimal at the CNP—where the longitudinal resistance also reaches its lowest value—and increases to a maximum at the band edges before diminishing again as the Fermi level shifts further away from the CNP. This behavior can be explained by the band structure of MBT. Ideally, within the band gap, the only active conduction channel is the CES, so without any bulk conduction, there is no interplay to produce a nonreciprocal signal. When the Fermi level approaches the band edges, bulk channels start to appear, leading to increased scattering between these channels and the CES, which enhances the nonreciprocal resistance. As further doping, the bulk channels dominate, and scattering with the CES decreases, reducing the nonreciprocal signal. Thus, the marked contrast between large nonreciprocal resistance at the band edges and its near absence at the CNP supports the existence of a CES and its dominant role at the CNP. To estimate the strength of the nonreciprocal resistance, we adopt the phenomenological formula36,

$${V}_{{xx}}=i{R}_{{xx}}=i{R}_{0}+\gamma {i}^{2}\left(\hat{M}\times \hat{P}\right)\cdot \hat{i}$$
(3)

where R0 represents the invariant part of the resistance, \(\hat{M},\,\hat{P},\,\hat{i}\) are the unit vector corresponding to magnetization, electric polarization on the edge, and current direction, respectively. The constant \(\gamma\) indicates the strength of the nonreciprocal resistance. At the band edge, we estimated \(\gamma=4178\,{A}^{-1}\) at zero field, and \(8013\,{A}^{-1}\) at 7 T (details shown in Supplementary Note 4). These values exceed those from previous work on MnBi₂Te₄ by roughly a factor of three at zero field and a factor of 1.8 at 7 T. They also surpass the value of 1700 A−1 reported for the Cr-doped (Bi,Sb)₂Te₃ system at 7 T, making them among the largest in most known systems (see Supplementary table 1 for further comparison). Such a sizable nonreciprocal response at zero magnetic field renders MBT a compelling candidate for applications such as high-frequency rectification37.

Fig. 4: Summary on nonreciprocal resistances for varying carrier density and temperature.
figure 4

a, b Carrier density dependent nonreciprocal resistance and longitudinal resistance of left edge and right edge of the sample. Red circle and curve show the nonreciprocal resistance, blue ones are for the longitudinal resistance, namely first order harmonic resistance. The green arrows indicate the carrier densities shown in Fig. 3d, e Measurements were taken with back gate fixed at 40 V. c Temperature dependent nonreciprocal resistance. Measurement was conducted with carrier density fixed at \(2.0\times {10}^{12}c{m}^{-2}\) at 0 T.

Full size image

Finally, we conducted temperature-dependent measurements of the nonreciprocal resistance. As shown in Fig. 4c, with a fixed Fermi level near the band edge and a carrier density of 2.0 × 1012 cm−2, the nonreciprocal resistance remains significant over a wide temperature range. The resistance initially increases with rising temperature until reaching a maximum value, after which it begins to decrease. This behavior aligns well with observations reported in the Cr-doped (Bi,Sb)2Te3 system35. The phenomenon can be attributed to shifts in the relative contributions of CES and bulk conduction channels. As temperature rises, QAH state and CES are gradually undermined. Meanwhile thermal activation of bulk channels becomes more pronounced, contributing increasingly to the total conductance. The interplay between CES and bulk channels reaches its maximum when the two channels have comparable contributions, resulting in peak nonreciprocal resistance. Above the Néel temperature (TN ≈ 22 K), the exchange gap closes and CES diminishes, causing the nonreciprocal resistance to drop sharply to near zero.

To further validate our findings on temperature-dependent nonreciprocal resistance, we conducted additional measurements on Device #3 (results are presented in Supplementary Note 10). We maintained the Fermi level near the band edge while continuously sweeping the temperature from 1.8 K to 30 K. The magnitude of temperature-dependent nonreciprocal resistance, shown in Supplementary Fig. 10, exhibits a trend consistent with our observations from Device #1.

Discussion

Our transport measurements provide solid proof for the presence of CES in the MBT sample. In our four-terminal measurements, over 93% quantized Hall resistance at zero field is a hallmark for the QAH effect. The longitudinal resistance also shows a minimal value of 0.031 h/e2. Though this value is already smaller than previous study of MBT, the dissipation still exists. The origin of such dissipation can be complex38,39,40. Recent studies have investigated the magnetic texture of MBE-grown MBT samples using magnetic force microscopy, and found that even in samples achieving zero-field QAHE, magnetic nonuniformities exist41. These samples consist of multiple QAH puddles, and the dissipation is attributed to tunneling between these puddles. A similar phenomenon may be occurring in our exfoliated samples, contributing to the observed dissipation. However, the significantly lower longitudinal resistance in our sample compared to earlier studies suggests that the dissipation and magnetic disorder are substantially reduced. Additionally, the relatively high measurement temperature of 1.6 K facilitates to thermal activation of bulk channels, further contributing to dissipation. Consequently, the transmission probabilities between electrodes deviate from the ideal case, and both longitudinal resistance and three-terminal resistances persists with a nonzero value. In the presence of magnetic field, the sample undergoes spin-flop transition, during which the QAH state is undermined, and dissipation increases, eventually enters ferromagnetic phase with magnetic field higher than 4 T, characterized by unidirectional spin alignment across all van der Waals layers. In this scenario, exchange gap is enlarged and a more robust QAH state is realized15. This leads to a reduction of Rxx and better quantization of Ryx value at high fields.

In summary, we have successfully achieved QAH state in 5-SL MBT devices and demonstrated the chiral edge transport at zero magnetic field. Our comprehensive study elucidates the transport characteristics of chiral edge states in the MBT system and establishes a foundation for future device applications of this promising material.

Methods

Device fabrication

5-SL MnBi2Te4 flake is exfoliated from high-quality bulk crystal grown by flux method. Al2O3 assisted exfoliation is adopted16. Aluminum was thermally evaporated and oxidized with an O2 pressure of 2 × 10−4 hPa in a thermal evaporator. The oxidized Al2O3 is deposited onto the surface of freshly cleaved bulk MBT. Thermal release tapes are then adhered to the Al2O3 covered MBT bulks and MBT thin flakes/Al2O3 are exfoliated onto the thermal release tapes at room temperature. The MBT thin flakes/Al2O3 stacks are then transferred onto polydimethylsiloxane (PDMS) at the release temperature of the tape. The time of transfer is controlled to be under 10 s. The thickness of the flake is verified by optical contrast. Then, the exfoliated flake is transferred onto Si/SiO2 substrate. Cr/Au electrodes are subsequently deposited onto the MBT flake using thermal evaporator, and the shape of the electrodes is defined by a stencil mask. hBN flake obtained by mechanical exfoliation is then dry transferred onto MBT by PDMS stamp. The hBN flake serves as encapsulation layer to protect MBT from oxidation, which is also functioned as dielectric layer for top gate. Finally, graphite flake is transferred onto the device as top gate electrode. The whole process is conducted in a glovebox filled with N2 atmosphere to avoid degradation of MBT.

For Device #3, we integrate our fabrication process with the AlOx capping method introduced in recent research21. After Al2O3 assisted exfoliation process, 5-SL MBT flake is selected and transferred onto Si/SiO2 substrate. Then, 3 nm AlOx is evaporated onto the top surface of the MBT flake. The flake is cut into regular shape by a needle and Cr/Au electrodes are directly deposited onto AlOx-capped MBT using thermal evaporation with stencil mask. No extra encapsulation layer is used. The excellent quantization observed in Device #3 suggests that AlOx capping plays a crucial role in achieving a robust QAH state. Aside from acting as encapsulation layer like hBN, it might have more effects on the sample, for instance, earlier TEM studies have pointed to structural collapse at the MnBi2Te4 surface42, which may be mitigated by this protective capping layers. Additionally, several fabrication optimizations are implemented throughout the fabrication, including shortening exposure time in the glovebox, reducing thermal release time, and minimizing temperature during metal electrode evaporation by lowering the evaporation rate. Compared to our previous devices, which were fabricated using the same crystal but typically exhibited less than 50% zero-field quantization, the results of this study mark a significant advancement, underscoring the importance of these fabrication improvements.

Electrical transport measurements

AC transport measurements are carried out in a Cryomagnetic cryostat. Gate voltages are applied with a Keithley 2636B dual-channel source meter. The AC measurements are conducted with Zurich MFLI lock-in amplifiers. All measurements are performed at 1.6 K unless otherwise specified.