Introduction

Dielectrics have widespread applications in electronic fields as fundamental components of electrostatic capacitors1,2. The developing trend of device miniaturization has put forward higher requirements for dielectrics with colossal permittivity (>104), low dielectric loss, and excellent temperature stability. However, these key factors are strongly correlated in dielectric materials. For example, in BaTiO3-based dielectrics, the strong polarization contributes to a high permittivity (>104) near the Curie temperature, yet a large loss and severe temperature dependence due to the ferroelectric phase transition3. Besides, CaCu3Ti4O12 ceramics show a colossal permittivity (CP) while maintaining satisfying temperature stability owing to a frustrated phase transition, yet the high dielectric loss (>0.1) limits its broader application4. On the other hand, paraelectric SrTiO3 (STO) ceramics possess low dielectric loss (<0.01) and are almost temperature-independent, but suffer from an inferior permittivity (~300)5. As such, simultaneously achieving colossal permittivity, low dielectric loss, and temperature-stable performance in dielectrics has been a big challenge and a common objective in this field.

The dielectric properties have been recognized to be directly correlated with the polarization process, including interfacial polarization and dipole polarization6,7,8, suggesting possible ways of regulating the overall performance of dielectrics. Accordingly, various efforts have been made over the years to develop preferable dielectric materials based on the principle of polarization improvement. On the one hand, CP can be achieved in ACu3Ti4O12 (A = Ca, Bi2/3, La2/3, Y2/3, etc.)- and NiO-based ceramics by constructing a core-shell structure consisting of semiconducting grains and insulating grain boundaries, which originates from the enhanced interfacial polarization. For example, by forming abundant subgrains and the consequent polarized interfaces, the Y2/3Cu3Ti4O12 ceramics can achieve a giant permittivity of 4.49 × 105, but is accompanied by an unexpectedly high loss (0.51)9. On the other hand, significantly improved permittivity can also be realized in materials such as TiO2 and STO ceramics. For instance, in Nb + In co-doped TiO2 ceramics, CP (~6 × 104) and low dielectric loss (~0.05) can be obtained due to the defects induced by donor-acceptor co-doping8. In STO ceramic, CP (~2.8 × 104) and low dielectric loss (~0.007) can be realized due to the promoted production of \({{{\rm{V}}}}_{{{\rm{O}}}}^{\cdot \cdot }\)10. However, a further increase in permittivity depends on high-concentration doping, leading to an inevitable increase in dielectric loss, which limits further performance improvements.

Recently, the high-entropy design strategy has been reported to be effective in achieving a higher concentration of defects in some high-entropy systems, e.g., (La0.6Sr0.4)(Co0.2[FeMnNiMg]0.8)O311, which is mainly ascribed to the atomic disorder and lattice distortion12,13,14. Inspired by these findings, we believe that this high-entropy approach is highly desirable for the design of CP materials, taking advantage of its probable defect-generating effects and expanded solid solubility. In this work, CaTiO3 (CTO) was determined as the matrix material, considering its similar crystal structure to the reported defect-dependent CP ceramics. By the entropy design on its A-site, our results demonstrate a CP of 2.37 × 105 and an ultralow loss of 0.005 obtained in the high-entropy CTO ceramic. This high-entropy design approach is expected to provide a feasible method for the development of high-performance dielectrics.

Results and discussion

High-entropy design on CTO-based dielectric ceramics

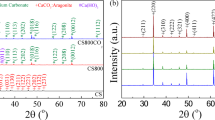
Nb, Er co-doped CTO was determined to be the starting material based on previous experimental experience, and additional Sr, Na, and Sm were equimolarly incorporated into Ca sites. Ceramic samples with compositions of Ca(Ti0.97Nb0.015Er0.015)O3 (CT), (Ca0.5Sr0.5)(Ti0.97Nb0.015Er0.015)O3 (CST), (Na0.33Sm0.33Ca0.33)(Ti0.97Nb0.015Er0.015)O3 (NSCT), and (Na0.25Sm0.25Ca0.25Sr0.25)(Ti0.97Nb0.015Er0.015)O3 (NSCST) were synthesized using the conventional solid-state reaction method (Table S1). The quantitative chemical compositions of the synthesized ceramics were confirmed by the XRF test results (Table S2). Figure 1a depicts the schematic diagram of the high-entropy design on the A-site of CT. Based on calculations and Rietveld refinements, the structures show an increasing atomic disorder and lattice distortion as more elements were introduced (Table S3).

Fig. 1: Evolution of phase and structure as a function of configurational entropy.
figure 1

a Schematic diagram depicting the progression of atomic disorder and lattice distortion as configurational entropy increases. b XRD patterns of the entropy-regulated ceramics. c SEM images of the cross-sectional area with element mapping of the NSCST ceramic. d Atomic size disorder level as a function of configurational entropy.

Full size image

The configurational entropy (Sconfig) is used to quantify the overall compositional inhomogeneity, defined as \({S}_{{{{\rm{config}}}}}=-R[{({\sum }_{i=1}^{N}{x}_{i}\, {{{\rm{ln}}}}\, {x}_{i})}_{{{{\rm{cation}}}}-{{{\rm{site}}}}}+{({\sum }_{j=1}^{M}{x}_{j}\, {{{\rm{ln}}}}\, {x}_{j})}_{{{{\rm{anion}}}}-{{{\rm{site}}}}}]\), where \(R\), \(N\)(\(M\)), \({x}_{i}\)(\({x}_{j}\)) represent the ideal gas constant, number of elements at the cation (anion) sites, and the molar ratio of the elements, respectively15. As more foreign elements randomly occupy equivalent A-site in CT, Sconfig gradually increases from 0.16 R (CT) to 1.54 R (NSCST), transitioning accordingly from low entropy (Sconfig < 1 R) through medium entropy (1 R ≤ Sconfig < 1.5 R) to high entropy (Sconfig ≥ 1.5 R), and give rise to atomic size disorder (\(\Delta {\delta }_{{\mbox{size}}}^{*}\)) (Fig. 1d). The XRD results confirm that all samples possess a pure orthorhombic phase, and the slight peak position shift is consistent with the ionic size changes of the introduced A-site elements, verifying the sufficiency of the solid solution (Fig. 1b). EDS mapping of the NSCST sample shows a uniform and homogeneous dispersion of the constituent elements, demonstrating successful preparation of the high-entropy ceramic sample (Fig. 1c). Rietveld refinement of the XRD patterns further proves that all CTO-based ceramics have a pure Pbnm structure. The merging or disappearance of some peaks or groups of peaks is the consequence of A-site compositional fluctuation, which affected lattice parameters and diffraction patterns rather than phase transition16,17 (Figs. S1 and S2). Based on the refined lattice parameter data, the relative densities were calculated, revealing the compact structures obtained in all samples (Table S4), which is also supported by the cross-sectional SEM images (Fig. S3). The average grain size (AG) gradually increases as Sconfig increases. Based on compositional and electrical test results shown below, we propose that this facilitated grain growth in the high-entropy ceramics is due to the elevated concentration of oxygen vacancies, which promotes the mass transportation process during sintering18,19. The above results together confirm the feasibility of applying the high-entropy strategy to construct CTO-based ceramics and provide more tunability for subsequent performance optimization.

Promoted defect generation by high-entropy design

To validate the feasibility of the high-entropy design in inducing more lattice defects, we conducted defect-related electrical measurements and valence state analysis. The complex impedance spectra of the CTO-based ceramics were measured at 500 °C and were fitted according to the equivalent circuit20,21, which reflects the electrical response from grains and grain boundaries, respectively (Fig. 2a). The spectra for all samples consist of one obvious arc attributed to the grain boundary response, while that of grains is indistinguishable due to their relatively small resistance. The arc diameter gradually decreased as more elements were introduced into the A-site of CTO, indicating a reducing trend of grain boundary resistance, which can be attributed to larger amounts of defects aggregated at the grain boundaries (Fig. S4). Meanwhile, the diameter of the arcs decreases with increasing temperature (Fig. S5), indicating a thermally activated process that follows the Arrhenius law: \({\sigma }_{{{{\rm{gb}}}}}={\sigma }_{0}\exp \left(-{E}_{{{{\rm{gb}}}}}/{k}_{B}T\right)\), where \({\sigma }_{{{{\rm{gb}}}}}\) is the grain boundary conductivity, \({\sigma }_{0}\) is the pre-exponential factor, \({E}_{{{{\rm{gb}}}}}\) is the activation energy of the grain boundary, and \({k}_{B}\) is the Boltzmann constant. The experimental data were fitted accordingly (Fig. 2b), showing a decreasing trend of the activation energies as the entropy increases. Although the activation energy value varies slightly between samples, the grain boundary resistance is obviously minimal for NSCST, indicating the existence of a larger number of defects in the high-entropy ceramic. Moreover, the average value of the fitted grain boundary activation energies for all samples is around 1.7 eV, higher than that of most STO-based CP systems10,22,23, which is beneficial for the suppression of the dielectric loss.

Fig. 2: Electrical response and defect generation modified by the varying configurational entropy.
figure 2

a The complex impedance spectra of CTO-based ceramics measured at 500 °C. Inset: the equivalent circuit model, consisting of two sets of parallel combinations of a resistor and a constant phase element (CPE), representing grain (Rg, CPEg) and grain boundary (Rgb, CPEgb) response. b Fitting results of the grain (Eg) and grain boundary (Egb) activation energies of CTO-based ceramics. c TSDC curves of CTO-based ceramics tested under a polarization voltage (Ep) of 100 V/mm and a polarization temperature (Tp) of 200 °C. Inset: detailed variation in the low depolarization current density region. d TSDC curves of the NSCST ceramic (Tp = 200 °C, Ep = 100–200 V/mm). Inset: magnified view of Peak 1. e The imaginary part of the electric modulus (M″) as a function of frequency for the NSCST ceramic. Inset: fitted activation energy (U) of the detected relaxation peaks circled by the dashed line. f TGA results of CT, CST, and NSCST, indicating the difference in weight loss degree (Δ) between CT and NSCST. g The Ti K-edge XANES spectra of CT, CST, and NSCST. Inset: enlarged view showing the absorption-edge position variation. h, i XPS O 1s spectra of CT (h) and NSCST (i).

Full size image

Furthermore, TSDC tests were performed to determine the defect characteristics in entropy-regulated ceramics (Fig. 2c). Two groups of peaks can be seen in all four sets of data, where the one located at a higher temperature range shows an obvious increase in intensity as the entropy increases. To better understand the defect mechanism, TSDC curves of the NSCST ceramic tested under different polarization voltage (Ep) and temperature (Tp) were analyzed in detail (Fig. 2d). It has been reported that three types of defects, including trap charges, defect dipoles, and space charges (mainly referring to oxygen vacancies) can be distinguished from the positions at the TSDC relaxation curves24,25,26. In our case, three peaks can be identified, distinguished by different peak temperatures (Tm) and denoted as Peak 1 (50 °C < Tm < 55 °C), Peak 2 (205 °C < Tm < 210 °C), and Peak 3 (266 °C < Tm < 286 °C), respectively (Fig. S6). Among these three peaks, Peak 1 and Peak 3 shift towards a higher temperature as Ep increases, which fits the characteristic of \({{{\rm{V}}}}_{{{\rm{O}}}}^{\cdot\cdot }\)27. The position of Peak 2 remains still, and its maximum depolarization current density (Jm) increases linearly with Ep, corresponding to a defect dipole-related relaxation process26,28. To further determine the exact defect types, an initial rise method29 was used to calculate the activation energies: \({{\mathrm{ln}}}\left[{J}_{{{{\rm{D}}}}}\left(T\right)\right]\cong {\mbox{const}}.\,\left(-{E}_{a}/{k}_{B}T\right)\), where \({J}_{{{{\rm{D}}}}}\) is the depolarization current density. Three activation energy values were calculated to be 0.238–0.242 eV (Peak 1), 0.578–0.715 eV (Peak 2), and 1.264–1.513 eV (Peak 3), corresponding to in-grain \({{{{\rm{V}}}}}_{{{{\rm{O}}}}}^{\cdot \cdot }\), defect dipoles, and across-grain-boundary \({{{{\rm{V}}}}}_{{{{\rm{O}}}}}^{\cdot \cdot }\) respectively30,31,32 (Fig. S7). Considering the valence variability and relative content of the involved elements, \({{{{\rm{V}}}}}_{{{{\rm{O}}}}}^{\cdot \cdot }\) and \({{{{\rm{Ti}}}}}_{{{{\rm{Ti}}}}}^{{\prime} }\) should be the dominant lattice defects, which can be shown as: \({{{{\rm{Ti}}}}}_{{{{\rm{Ti}}}}}^{\times }+{{{\rm{e}}}}^{\prime} \to {{{{\rm{Ti}}}}}_{{{{\rm{Ti}}}}}^{{\prime} }\), \({{{{\rm{O}}}}}_{{{{\rm{O}}}}}^{\times }\to {{{{\rm{V}}}}}_{{{{\rm{O}}}}}^{\cdot \cdot }+2{{{\rm{e}}}}^{\prime}+\frac{1}{2}{{{{\rm{O}}}}}_{2}\uparrow\). Therefore, \({{{{\rm{Ti}}}}}_{{{{\rm{Ti}}}}}^{{\prime} }{-{{{\rm{V}}}}}_{{{{\rm{O}}}}}^{\cdot \cdot }{-{{{\rm{Ti}}}}}_{{{{\rm{Ti}}}}}^{{\prime} }\) would be the most likely existing form of the defect dipoles developed during sintering, which is supported by the similar activation energy value reported in the previous work30. According to the mathematical definition of the dipole polarization intensity (Pe), the dipole concentration (Nd) can be evaluated by integrating the area under the corresponding peak24. Results show a larger Peak 2 area for NSCST (Fig. S8), pointing to the highest dipole concentration in the high-entropy ceramic, consistent with the above discussions.

Generally, the defect characteristics can also be analyzed through relaxation behaviors that appear in the dielectric property-frequency diagram33,34. The imaginary part of the electrical modulus M″ is used here to magnify potential defect signals of the NSCST ceramic in the finite frequency test range (Fig. 2e). M″ was calculated as follows: \({M}^{{\prime} {\prime} }={\varepsilon }^{{\prime} {\prime} }/\left({\varepsilon }^{{\prime} 2}+{\varepsilon }^{{\prime} {\prime} 2}\right)\), where \({\varepsilon }^{{\prime} }\) and \({\varepsilon }^{{\prime} {\prime} }\) are the real and imaginary parts of the complex relative permittivity. A group of relaxation peaks appears in the frequency range of 10–103 Hz and shifts towards a higher frequency with increasing temperature, suggesting a faster polarization process35: \({f}_{{{{\rm{peak}}}}}={f}_{0}\exp \left(-U/{k}_{B}T\right)\), where \({f}_{{{{\rm{peak}}}}}\) is the peak frequency and f0 is a constant. U was calculated to be 0.925 eV, suggesting the existence of oxygen vacancies at the grain boundaries, as confirmed by other reported experimental results of similar material systems35,36,37,38. TGA test results can further verify the existence of oxygen vacancies (Fig. 2f). The evaporation effect of the physically adsorbed H2O has already been excluded. The CT ceramics presented a drastic weight loss with the increase of temperature, while that of the NSCST ceramics is relatively gentle, indicating that a larger amount of oxygen vacancies exists in NSCST ceramics and mitigates the weight loss due to the compensating effect of the backfilled oxygen atoms39,40. The Ti K-edge XANES spectra were collected to validate the generation of \({{{{\rm{Ti}}}}}_{{{{\rm{Ti}}}}}^{{\prime} }\) (Fig. 2g). The edge position showed a shift towards lower photon energy as the entropy increases, demonstrating a reduced average Ti valence and more \({{{{\rm{Ti}}}}}_{{{{\rm{Ti}}}}}^{{\prime} }\) in the high-entropy NSCST ceramics.

To directly visualize the variation of oxygen vacancy concentration after entropy regulation, XPS tests were conducted focusing on O 1s valence state changes (Fig. 2h, i, Fig. S9). Three peaks with binding energies of around 532 eV, 530.8 eV, and 529.7 eV were observed, attributed to the response of absorbed H2O, oxygen vacancies, and lattice oxygen, respectively8,41,42. The spectra vary obviously between samples, and the main difference comes from the intensity change of Peak 2, corresponding to the oxygen vacancy concentration. Compared to CT, Peak 2 shows a prominent enhancement in NSCST, indicating a promoted production of oxygen vacancies after entropy regulation. From the results and analysis above, it is proven that the high-entropy strategy is an effective approach for stimulating the production of defects, as expected.

To gain further insight into the nature of this high-entropy-induced defect generation, DFT calculations were performed on regulated CT supercells to visualize the structural evolution as a function of configurational entropy. Multiple O atoms were removed from the CT, CST, and NSCST ceramics to obtain structural information considering various defect quantities. Electron localization function (ELF) mappings from different views of CT, CST, and NSCST were simulated (Fig. 3a–d, Fig. S10 and 11), which reflect the localization extent of the reference electron. The ELF value ranges from 0 to 1, where 0 represents no electrons, and 1 corresponds to perfect localization43. Along \([51\bar{2}]\), local atom size disorder resulted in a certain degree of lattice distortion in NSCST (Fig. 3a, c). With Na, Sm, and Sr elements entering A-sites in CT, regions around O atoms appear to be darker, demonstrating a notably reduced covalency of the A/B–O bonds44 as a result of the entropy modulation. These changes in the electron distribution are attributed to the diversity between different A-site atoms, which leads to changes in chemical bonding characteristics within the lattice. Further analysis focusing on unit bond strengths in entropy-regulated systems helps to quantify these bonding property differences with distinct intensity variations (Fig. 3e, f). The A–O bond shows a monotonically weakening bond strength as the entropy increases, regardless of the retracted amount of O atoms. Meanwhile, the high-entropy NSCST ceramic also presents the weakest B–O bond under equivalent circumstances, providing beneficial conditions for the A/B–O bond dissociation and the escape of O atoms45. In addition, the defect formation energy \((\Delta {E}_{{{{\rm{defect}}}}})\) was calculated correspondingly as a descriptor for defect formation difficulty (Fig. 3g)). Horizontally viewing, it would cost less energy to generate lattice defects in the high-entropy NSCST system. ELF simulations, each with 6 absent O atoms, were taken as comparative examples (Fig. 3b, d), visualizing lattice distortions and Ti–O bonding changes from the direction of [001]. Since the defect formation energy for CT exceeds zero, this structure with more absent O atoms can only stably exist in high-entropy NSCST ceramics. In other words, the weakened chemical bonding of NSCST ceramics is conducive to generating larger amounts of lattice defects, which explains our previous defect-related experimental results. The dipole moment (\(\Delta p\)) was also evaluated as a quantitative indicator pointing to overall dielectric performance (Fig. 3h). The NSCST ceramics exhibit a maximum dipole moment value, which is directly associated with enhanced polarization, validating the effectiveness of this high-entropy strategy. Additional DFT calculations are shown in Figs. S12 and S13, demonstrating a lower ICOBI value, a narrowed band gap, and a reduced effective mass of charge carriers with the increase of entropy, pointing to a more semiconductive characteristic in the high-entropy NSCST ceramic, which is in agreement with the tested activation energies and other experimental results.

Fig. 3: Simulations of local structure and defect formation evolutions with increasing entropy.
figure 3

a–d ELF mappings of CT (a, b) and NSCST (c, d) along different directions. e, f The integrated crystal orbital Hamilton populations (ICOHP) value in a unit bond length (L) of A–O (e) and B–O (f) for CT, CST, and NSCST ceramics, indicating the bond strength changes as the entropy increased. g, h Comparison of defect formation energy (ΔEdefect) (g) and the electric dipole moment (Δp) (h) between CT, CST, and NSCST ceramics.

Full size image

Significantly improved dielectric performance in the high-entropy NSCST ceramics

Dielectric performance from all aspects was evaluated to further confirm the feasibility of achieving CP through the high-entropy strategy. The frequency dependence of dielectric properties, including permittivity and dielectric loss (tanδ), was measured at room temperature (RT) for CTO-based ceramics (Fig. 4a). All samples show frequency-independent characteristics in the low-frequency range, and undergo a slight degradation beyond 100 kHz. No obvious interfacial relaxation behaviors were detected in the low-frequency range, excluding major contributions from interface polarizations7. The permittivity also remained stable when applied with various DC bias voltages, confirming no electrode effect was involved in the achieved CP performance46,47 (Fig. S14). Specifically, in the low-entropy CT ceramic, both colossal permittivity (7.02 × 104) and low tanδ (0.019) were obtained simultaneously, demonstrating that CP can also be achieved in the CTO matrix. As more substitutional elements were introduced into the A-site, the permittivity monotonically increased and reached an exceptional level of 2.37 × 105 in the high-entropy NSCST ceramic, while effectively maintaining an ultralow tanδ of 0.005 (Fig. 4a, e). This remarkable evolution trend of permittivity reveals a close association between dielectric properties and configurational entropy and confirms the effectiveness of this strategy in achieving permittivity improvement. Thermal stability is also evaluated for CTO-based ceramics (Figs. 4b, S15). Each of them shows a good temperature-stable capacitance in the test temperature range (−50 to 250 °C). The detected loss increase at higher temperatures should be attributed to the migration of thermally activated carriers48. Notably, the calculated temperature coefficient (ΔC/C25 °C) value at 1 kHz for the high-entropy NSCST is within ±15% (Fig. 4c), sufficient to satisfy the temperature stability requirements of X9R capacitors (ΔC/C25 °C ≤ ± 15%, −50 to 200 °C).

Fig. 4: Dielectric responses of entropy-modulated CTO-based ceramics.
figure 4

a Frequency-dependent permittivity and dielectric loss (tanδ) of CTO-based ceramics measured at room temperature (RT). b Temperature-dependent permittivity and dielectric loss (tanδ) of CTO-based ceramics measured at 1 kHz. c Temperature dependence of dielectric properties at various frequencies (100 Hz, 1 kHz, 10 kHz, 100 kHz) for the NSCST ceramic, indicating a small capacitance temperature coefficient (ΔC/C25°C) and an excellent thermal stability. d Variation in the chemical bonding property (ICOHP/L) and semiquantitative oxygen vacancy (Vo) concentration after entropy modulation. e Evolution of dielectric performance (RT, 1 kHz) as a function of configurational entropy. f Comparison between this work with other representative CP materials8,9,34,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75.

Full size image

The intrinsic correlation between configurational entropy and dielectric performance needs to be further discussed and concluded. As a directly affected parameter of compositional change, the bond strengths of A–O and B–O show a distinct entropy-dependent performance (Fig. 4d). The enhancement of entropy leads to an increase in atomic size disorder and the change in electron distribution within the lattice49. These effects are manifested as weakened bonding in the high-entropy NSCST, benefiting the bond dissociation process and the escape of oxygen atoms. The semiquantitative concentrations of oxygen vacancies in CT, CST, and NSCST were estimated based on XPS fitting results (Fig. 4d). Considering the requirements of charge conservation, corresponding amounts of electronegative defects would be generated for compensation, most likely Ti3+ in these titanium-based systems50. With efficiently produced defects, including \({{{{\rm{V}}}}}_{{{{\rm{O}}}}}^{\cdot \cdot }\) and \({{{{\rm{Ti}}}}}_{{{{\rm{Ti}}}}}^{{\prime} }\), the dipole polarization of CTO-based ceramics was significantly enhanced, eventually obtaining an exceptional dielectric performance in the high-entropy NSCST (Fig. 4e). A colossal permittivity of 2.37 × 105, an ultralow tanδ of 0.005, and a favorable frequency/temperature stability were simultaneously achieved, outperforming other CP ceramic materials8,9,34,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75 (Fig. 4f).

Our results prove that CP behavior can be achieved in CTO-based ceramics. By regulating the configurational entropy with proper substitutional elements and modulating chemical bonding properties, an increasing amount of lattice defects can be generated in CTO-based ceramics. The intentionally induced defects further interact to form defect dipoles and clusters, giving rise to dipole polarization while contributing to the localization of carriers, thus achieving an overall optimization of the dielectric performance. This strategy could be used in dielectric ceramics with similar structures to simultaneously obtain colossal permittivity and ultralow dielectric loss. This study offers an additional option for CP matrix determination and provides a feasible solution for the design of other defect-dependent functional materials.

Methods

Sample preparation

The CTO-based ceramics with the compositions of Ca(Ti0.97Nb0.015Er0.015)O3, (Ca0.5Sr0.5)(Ti0.97Nb0.015Er0.015)O3, (Na0.33Sm0.33Ca0.33)(Ti0.97Nb0.015Er0.015)O3, and (Na0.25Sm0.25Ca0.25Sr0.25)(Ti0.97Nb0.015Er0.015)O3 were fabricated by conventional solid-state reaction method. High-purity powders of CaCO3 (99.5%, Aladdin, China), SrCO3 (99.5%, Aladdin, China), Na2CO3 (99.99% Aladdin, China), Sm2O3 (99.9% Aladdin, China), TiO2 (99% Aladdin, China), Nb2O5 (99.99% Aladdin, China), and Er2O3 (99.99% Aladdin, China) were used as raw materials and were weighed stoichiometrically (Na2CO3 5% excess). The powders were mixed thoroughly through ball-milling with ethanol for 24 h and were calcined in the air at 1100–1150 °C for 3 h before being ball-milled for the second time. The resulting powders were then mixed with 5 wt% PVA as a binder and pressed into pellets with a 12 mm diameter under axial pressure. The as-prepared cylindrical pellets were then heated at 600 °C for 3 h to eliminate the binder. Finally, the samples were sintered at 1400–1500 °C for 3 h in a 5% H2/N2 atmosphere. A group of pellets was sintered in air separately at corresponding temperatures for TSDC tests. Both sides of the samples were polished, coated with silver paste, and heated at 600 °C to obtain electrodes for electrical measurements.

Structure characterizations

X-ray diffraction (XRD, Bruker D8 Advance, Germany) with Cu Kα X-ray source was used to identify the phase structure of the ceramic samples. To further confirm the structural parameters, Rietveld refinement was performed using the GSAS (General Structure Analysis System) software. The cross-sectional morphology of the microstructure and the elemental distribution were analyzed using scanning electron microscopy (SEM, Zeiss Merlin Compact, Germany), and the grain size distribution was calculated using the software “Nano Measurer”. The relative density of the samples was calculated according to the measured density and the theoretical density. X-ray photoelectron spectroscopy (XPS, Thermo Fisher Scientific ESCALAB 250Xi, the U. S.) was used to investigate the valence states of the elements and thus determine the possibly existing lattice defects. Thermogravimetry analysis (TGA, NETZSCH Scientific Instruments Trading Ltd X70, Germany) was used to visualize the oxygen refill process and quantify the bulk defect concentration. X-ray absorption near edge structure (XANES) of Ti K-edge was performed at BL14W1 beamlines at the Shanghai Synchrotron Radiation Facility (SSRF, Shanghai, China) in a transmission mode to evaluate the valence change. The absorption-edge position was defined as the photon energy of the peak in the first derivative spectrum. All test results were calibrated by aligning the absorption-edge energy shift of a Ti metal foil at 4966 eV. X-ray fluorescence (XRF, Thermo Fisher Scientific ARL PERFORM’X, the U.S.) analysis was conducted to provide quantitative elemental compositions of the synthesized ceramics.

Electrical and dielectric measurements

The dielectric properties were measured by a broadband dielectric/impedance spectrometer (Novocontrol Technologies GmbH& Co. KG, Germany), which was equipped with a liquid nitrogen cooling system to provide precise test results over a broad temperature and frequency range (−50 to 300 °C, 100 Hz–100 kHz). The thermally stimulated depolarization current (TSDC) measurements were performed using an electrometer/high resistance meter (B2985A, Keysight, the U. S.), equipped with the same quatro-temperature controller mentioned above. The pellets were first polarized under a DC electric field (Ep) at a certain temperature (Tp) for 10 min (100 V/mm ≤ Ep ≤ 200 V/mm; Tp = 200 °C), then rapidly cooled to −50 °C to freeze the oriented defects, and gradually heated up to 300 °C to gather the depolarization current. The complex impedance spectra (IS) were tested by an impedance/gain-phase analyzer (Solartron SI 1260) at various temperatures (450–550 °C) in the frequency range of 1 Hz to 1 MHz.

Calculations

The atomic size disorder

The atomic size disorder (\(\Delta {\delta }_{{\mbox{size}}}^{*}\)) of the ceramics can be calculated as follows:

$${\Delta {{{\rm{\delta }}}}}_{{{{\rm{size}}}}}^{*}=\sqrt{\mathop{\sum }_{i=1}^{n}{c}_{i}{\left(1-\frac{{r}_{i}}{{\sum }_{i=1}^{n}{c}_{i}{r}_{i}}\right)}^{2}}$$
(1)

where \(n\), \({c}_{i}\), and \({r}_{i}\) represent the number of elements, the atomic fraction of the ith element, and the radii of the ith element, respectively. In our case, the perovskite structure has A and B two cation sites, thus its \(\Delta {\delta }_{{\mbox{size}}}^{*}\) can be modified as76:

$${\Delta {{{\rm{\delta }}}}}_{{{{\rm{size}}}}}^{*}=\sqrt{\Delta {\delta }_{{\mbox{size}}({\mbox{A}})}^{2}+\Delta {\delta }_{{\mbox{size}}({\mbox{B}})}^{2}}$$
(2)

here, the ionic radii for the involved elements are 1.34 Å (Ca2+), 1.44 Å (Sr2+), 1.39 Å (Na+), 1.24 Å (Sm3+), 0.605 Å (Ti4+), 0.64 Å (Nb5+), and 0.89 Å (Er3+)77.

The distortion index

The parameter of distortion index (D) was applied to quantify the distortion extent within the octahedron, which is defined as78,79:

$$D=\frac{1}{6}\mathop{\sum }_{i=1}^{6}\frac{\left|{l}_{i}-{l}_{{av}}\right|}{{l}_{{av}}}$$
(3)

where \({l}_{i}\) and \({l}_{{av}}\) represent individual and average Ti–O bond lengths, respectively. The D values were calculated according to bond length data, which were obtained from Rietveld refinement results, as shown in Table S3.

DFT

All first-principles calculations were performed using the Vienna Ab Initio Simulation Package (VASP)80,81 based on density functional theory (DFT). The exchange-correlation function was performed using the generalized gradient approximation (GGA) of Perdew–Burke–Ernzerhof (PBE)82. Considering the strong correlation between localized Sm 4f and Ti 3d electrons, the DFT + U approximation was used for correction, with the effective U parameter taken to be 8 eV (Sm 4f), and 5.8 eV (Ti 3d)83. The cut-off energy was set to 450 eV for the plane-wave based on the maximum energy of the atoms in the potential. The Brillouin zone of the reciprocal space was set to 1 × 5 × 3. The force components for each atom were all less than 0.005 eV/Å, and the total energy difference was less than 10−6 eV. All structures were fully relaxed before property calculations. The bonding information was obtained from the LOBSTER software84, and the electron localization function was visualized by VESTA software85.

Based on pristine CaTiO3 (0 R), a 5 × 2 × 2 supercell (100 atoms) was used to obtain entropy-modified structures. The structures of CST and NSCST were obtained by substituting 50% of Ca with Sr, and equally substituting 75% of Ca with Sr, Na, and Sm, respectively. Oxygen vacancies were obtained by removing 2 (3.33%), 4 (6.67%), and 6 (10%) O atoms from each entropy-modified structure. The bond strength was evaluated by the integrated crystal orbital Hamilton populations (ICOHP) value in a unit bond length (L). The integrated crystal orbital bond index (ICOBI) of A–O and B–O bonds, the band structure, and the corresponding density of states (DOS) were acquired for CT (0Vo), CST (2Vo), and NSCST (4Vo) systems.