Reinforcement learning increasingly relates to memory specificity from childhood to adulthood

Abstract

In some contexts, abstract stimulus representations can effectively promote reward pursuit, whereas in others, detailed representations are needed to guide choice. Here, we ask how, across development, the reward statistics of the environment influence the specificity of both value-guided learning computations and recognition memory. Across two experiments (N = 224), we show that participants ages 8 − 25 years adaptively up- and down-weight detailed versus broader stimulus representations and that these learning computations relate to mnemonic specificity. When participants place greater weight on granular representations during learning, they better remember stimulus details, whereas when they place greater weight on broader representations, they show enhanced memory only for categorical information. Moreover, the strength of the coupling between learning and memory specificity increases with age. We demonstrate that from early in life, reward shapes the granularity with which the world is partitioned, and increasingly across development, the specificity with which experiences are remembered.

Introduction

Experiences can be represented at multiple, nested levels of abstraction. Last Friday, you may have eaten pasta at a restaurant and then gone to a movie—but you may have also eaten carbonara at an Italian bistro and seen Barbie in IMAX at the newly renovated cinema by your apartment. The specificity with which you represent your experiences has functional consequences for future behavior— representing your meal as pasta may help you decide whether to eat an unfamiliar pasta dish, but may prove unhelpful in the future if you face a choice between carbonara and alfredo. More abstract representations may facilitate the acquisition of generalizable knowledge, whereas more specific representations can be leveraged to guide decisions that require finer-grained distinctions between similar entities¹. While choices about eating pasta may be relatively unimportant, the specificity of our representations influences how we learn from the outcomes of our actions^2,3,4,5, form lasting memories that underpin our mental models of the environment^1,6,7,8,9, and ultimately, harness our past experiences to guide our future behavior.

The generality or specificity with which experiences are represented may be particularly consequential early in life. Children, who are equipped with more capacity-limited learning and memory systems^10,11, must navigate a world of less familiar structure. Recent developmental studies of value-based learning and of episodic memory have suggested that there may be systematic increases in the specificity with which experiences are represented from childhood to adulthood. Younger children show broader generalization of threat responses to novel stimuli^12,13,14, provide reports of autobiographical memories that lack rich detail^15,16,17, and perform poorly on lab-based tasks of mnemonic discrimination^18,19,20,21. Theoretical proposals have suggested that representing information with less specificity early in life may be adaptive—a bias toward more general representations may promote the recognition of shared features across diverse experiences, which may be particularly useful for children as they build semantic knowledge of the world^22,23,24.

Several recent findings, however, suggest that developmental change in the specificity of learning and memory representations may not follow a simple, context-invariant trajectory. While some studies of value-based learning have indeed seen broader generalization in younger participants^12,13, others have found that generalization increases with age²⁵. Studies of developmental changes in episodic memory have similarly revealed mixed findings, particularly in later childhood and adolescence. While some work has suggested that mnemonic specificity increases through late childhood²⁰, other research has not found evidence for significant age-related change in the granularity with which information is remembered²⁶. Even at younger ages, mnemonic specificity is not static; it can be enhanced if information is made more salient²⁷. Moreover, while theoretical proposals posit advantages for reduced mnemonic specificity, it is unclear whether the formation of less granular memories promotes adaptive generalization. The extent to which specificity and generality trade off may also change with age; detailed and more abstracted representations can compete for expression during learning²⁸, but detailed memories can also support generalization²⁹, perhaps to a greater extent in adults than in children³⁰.

These varied developmental trajectories of the specificity of value associations and episodic memory may reflect emerging adaptivity in the representations used for learning. The relative costs and benefits of representing experiences more abstractly versus more specifically do not just vary across the lifespan —they vary across the multiple, diverse learning environments that children, adolescents, and adults experience every day. In some contexts, more general representations can guide adaptive choice, and in others, more specific representations are needed. At the dog park, for example, walkers should represent the individuating features of each dog so they can learn to approach those that are friendly and avoid those that bite; in the woods, however, hikers can ignore the specific features of wolves and represent them more generally because they should avoid all of them—attempting to individuate each one may needlessly tax cognitive resources and prevent effective generalization. Adaptive value-guided learning thus requires the flexibility to adjust the specificity of value associations to the reward statistics of the environment^2,31,32,33. Some research suggests that the ability to dynamically tune value-learning computations to the optimal settings for particular environments improves from childhood to adulthood^34,35. Other work, however, suggests that adults may approach new learning problems with stronger prior beliefs about the information most relevant for guiding behavior and show less flexibility in updating them in the face of new information^36,37. Developmental changes in the specificity of value-learning computations may be driven by changes in the extent to which learning representations are dynamically shaped by the statistics of varied learning environments.

The specificity with which information is represented during learning may, in turn, influence the specificity with which information is encoded in memory, such that detailed information is preserved when it is useful for guiding behavior. A growing body of work has revealed a tight coupling between value learning and episodic encoding^38,39—across development, the statistics of the environment (e.g., surprise, reward) govern both how value associations are learned as well as what information is attended and prioritized in memory^{27,40,41,42,43,44,45,46,47,48}. Further, individual and developmental differences in how people learn value associations relate to the information that they subsequently remember^41,49. Despite research that indicates a strong influence of learning computations on what information is prioritized in memory, it is unclear both how value-learning influences the adaptive specificity of memory representations, and how individual and developmental differences in the specificity of value-learning computations are reflected in subsequent memory.

Thus, our goals in this study were twofold. First, we sought to characterize how children, adolescents, and adults flexibly adapt the specificity with which they represent information during value-guided learning. We hypothesized that participants would rely on more general representations when such representations could support adaptive choice, and represent more specific information when doing so was necessary for making good decisions. We further expected the adaptive modulation of the specificity of learning representations to increase with age. Second, we asked how the specificity of the information used during value-based choice influences the specificity with which information is represented in memory. We hypothesized that across age, participants would demonstrate more specific memory for information encountered in the context in which detailed information was needed to guide choice. Further, we hypothesized that individual and developmental differences in the specificity of learning computations would be reflected in subsequent memory, such that people who placed more weight on detailed information during learning would show corresponding enhancements in memory specificity.

We tested these questions across two reinforcement-learning experiments in which stimuli comprised unique exemplars drawn from broader categories. While many prior studies of category learning have examined how people learn to cluster novel stimuli, here we used stimuli from familiar conceptual categories to ask how people learn to effectively arbitrate between representations at different levels of abstraction. We manipulated the reward structure of the learning task across blocks, such that in some contexts, reward contingencies were determined by unique exemplars, whereas in others, they were governed by the broader categories. In both experiments, we found that participants across age flexibly adapted their use of exemplar-level and categorical information to make effective choices across contexts. In line with our hypothesis, individual differences in learning were reflected in subsequent memory, such that the specificity of memory was shaped by the specificity of value-guided learning. Further, we found that the influence of learning on memory strengthened across development, such that adults demonstrated a tighter coupling between the specificity of their learning computations and subsequent memory representations. Our findings reveal that the specificity of learning and memory does not follow a single developmental trajectory; instead, the structure of the environment shapes the specificity of the representations that children, adolescents, and adults use to guide choice, which are in turn, increasingly reflected in memory across development.

Results

Experiment 1 design

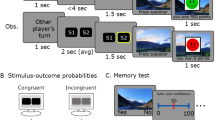
In our first experiment, 151 participants between the ages of 8 and 25 years completed a six-block “approach/avoid” reinforcement-learning task across which the specificity of the representations that could best guide choice varied (see Methods). Within each block of the learning task, participants completed 51 trials in which they had to decide whether to approach or avoid one of 15 unique stimuli, drawn from three broader categories, to earn the most points (Fig. 1). The order of stimulus presentation was randomized, and within each broader category, two images repeated six times, one image repeated three times, and two images were only shown once during learning, which meant that novel images were introduced throughout each learning block. Critically, in half of the task blocks (category-predictive blocks), the three broader stimulus categories determined the average gains and losses associated with approaching each stimulus. In category-predictive blocks, stimulus values were sampled anew from Gaussian distributions on every trial, where the mean of the distribution was determined by stimulus category. One category was randomly determined to be “good” such that the mean of its reward distribution was between 3 and 6; one category was “neutral” such that the mean of its reward distribution was zero (though zero was never actually presented as an outcome); and one category was “bad” such that the mean of its reward distribution was between −6 and −3. In the other half of the task blocks (exemplar-predictive blocks), each unique exemplar was assigned a deterministic positive or negative point value between −9 and 9, distributed such that the broader stimulus categories could not be used to guide effective approach/avoid decision making (Fig. 1B). The order of the blocks was randomized for each participant, with the constraint that the first two blocks were always of different conditions.

Fig. 1: Experiment 1 task design.

A Each block of the reinforcement-learning task included 15 unique stimuli (shown in the gray box), which comprised five exemplars each drawn from three broader categories. For each stimulus set, three additional novel exemplars per sampled category and an additional category with eight novel stimuli were used in a test of subsequent memory (see panel D). B In the category-predictive condition, rewards on every trial were sampled from normal distributions centered on means determined by the stimulus categories. In the exemplar-predictive condition, rewards on every trial were determined by the individual exemplars. C On every trial of the reinforcement-learning task, participants chose whether to approach or avoid a stimulus. Participants won or lost points if they chose to approach the stimulus. While they did not win or lose any points if they chose to avoid, they saw counterfactual feedback showing how many points they would have won or lost had they approached. D Approximately 1 week after completing the reinforcement-learning task, participants completed a test of recognition memory in which they had to decide whether stimuli were old or new on a four-point confidence scale. The images in the figure are illustrative; actual task stimuli differed slightly. Image credit: iStock/GlobalP (https://www.istockphoto.com/portfolio/GlobalP), Life on White (https://www.lifeonwhite.com/).

Learning to approach and avoid

We first analyzed whether participants across age learned to approach stimuli with positive values and avoid those with negative values, via a logistic mixed-effects model with continuous age, within-block trial, block condition, within-condition block number, and their interactions as predictors. Participants increasingly made correct responses across trials within each block, χ²(1) = 279.4, p < 0.001, odds ratio (OR) = 1.66, 95% Confidence Interval (CI) = [1.60, 1.72] (Fig. 2A). Older participants made more correct responses than younger participants, χ²(1) = 33.4, p < 0.001, OR = 1.25, 95% CI =  [1.17, 1.35], increasingly so across trials (age x trial interaction: χ²(1) = 27.4, p < 0.001, OR = 1.11, 95% CI = [1.07, 1.16]). Across age, performance was better in category-predictive relative to exemplar-predictive blocks, χ²(1) = 185.2, p < 0.001, OR = 1.62, 95% CI = [1.54, 1.71], suggesting that participants leveraged categorical information to guide their choices. Further, the effect of block condition varied by age — older participants demonstrated stronger benefits from the ability to exploit categorical information, χ²(1) = 6.8, p = 0.009, OR = 1.07, 95% CI = [1.02, 1.13]. Performance also improved across blocks of the task, χ²(1) = 57.2, p < 0.001, OR = 1.26, 95% CI = [1.19, 1.33] (see Supplementary Note 1 for full details). Taken together, these findings suggest that participants learned effectively across block conditions, such that they could learn both from individual exemplars as well as from the broader categories from which they were drawn.

Fig. 2: Participants across age flexibly adjusted the specificity of information used for learning.

A–C Depict participant responses in the learning task, while (D), (E) show parameter estimates derived from the best-fitting computational model of reinforcement learning. A Over the course of each block, participants learned to make more optimal responses to stimuli in both the category-predictive and exemplar-predictive conditions, though performance was better in category-predictive relative to exemplar-predictive blocks. B In the category-predictive condition, participants increasingly generalized learned category responses to respond optimally to novel stimuli. C Category win-stay lose-shift behavior increased across trials in category-predictive blocks and decreased across trials in exemplar-predictive blocks, increasingly so with age. D In the category-predictive block condition, participants with higher category-level choice weights and higher exemplar-level choice weights earned more points. In the exemplar-predictive block condition, participants with higher exemplar-level choice weights earned more points. E Participants across age demonstrated higher category-level choice weights in category-predictive blocks, indicating that they increased the weight they placed on category-level information during decision-making when doing so was useful. In panels (A–C), (E), horizontal lines show individual participant means. The points and error bars show age group mean values ± SEM. In panel (D), points show individual participants’ total points summed across the three blocks within each condition; lines show the best-fitting linear regressions through the points, with the shaded region depicting 95% confidence intervals. In panels (D), (E), choice-weight magnitude values reflect normally distributed parameter estimates, which were exponentiated within each model. Negative values reflect low, positive choice weights. All panels show data from 151 participants (n = 50 children, 50 adolescents, and 51 adults). Statistical analyses were conducted using mixed-effects models that assessed effects within participants while accounting for variation across them.

Generalization of learned category values to novel stimuli

Throughout each block of the learning task, participants encountered novel stimuli that they had never seen before. In exemplar-predictive blocks, the value of each stimulus was determined independently, meaning participants could not infer the value of unseen stimuli based on their previous experiences. In category-predictive blocks, however, participants could respond optimally to completely novel stimuli by generalizing learned category values. Indeed, in category-predictive blocks, participants responded correctly to novel stimuli at well-above-chance levels (Fig. 2B), indicating successful generalization. Participants made more correct responses to novel stimuli in category- relative to exemplar-predictive blocks, χ²(1) = 211.9, p < 0.001, OR = 1.72, 95% CI = [1.63, 1.81], an effect that grew increasingly strong as participants encountered more stimuli from each category (block condition x category repetition interaction: χ²(1) = 156.3, p < 0.001, OR = 1.32, 95% CI = [1.26, 1.38]). In addition, the effect of block condition on correct responses grew stronger with increasing age, χ²(1) = 6.6, p = 0.010, OR = 1.07, 95% CI = [1.02, 1.13], indicating more effective generalization in category-predictive blocks in older participants. Generalization also strengthened across blocks of the task (block condition x block number interaction: χ²(1) = 16.0, p < 0.001, OR = 1.10, 95% CI = [1.05, 1.14]; see Supplementary Note 1 for full details).

Though successful generalization was not possible in the exemplar-predictive condition, participants may have nonetheless attempted to generalize learned stimulus values to other, within-category exemplars, particularly within the first few trials of each block. For example, if participants approached a dog and were rewarded, then they may approach the next dog they encounter, even if its specific features differ. Likewise, if they approached a dog and lost points, they may avoid the next dog they encounter. To test whether participants attempted to generalize learned category values, we coded learning trials as “category win-stay” if participants repeated winning responses (i.e., gaining points or avoiding point losses) and as “category lose-shift” if participants avoided repeating losing responses (i.e., losing points or avoiding point gains) that they made to the last, previously encountered within-category stimulus, excluding trials in which this stimulus was also the same exemplar. Thus, trials in which participants demonstrated this signature of category generalization were coded as 1, and those in which they did not were coded as 0. We then examined how this behavior changed over trials within the two block conditions. We expected that participants would show stronger category win-stay lose-shift (WSLS) behavior in category-predictive blocks, where it was adaptive, relative to exemplar-predictive blocks.

At the beginning of blocks across both conditions, participants demonstrated this WSLS behavior, such that they tended to repeat rewarded “approach/avoid” responses and switch unrewarded responses upon their subsequent encounter with a different stimulus from the same broader category. On average, in the first ten trials within each block, participants made category WSLS responses in both category-predictive and exemplar-predictive blocks (mean proportion WSLS: category: 0.67 (SE = 0.01), exemplar: 0.59 (SE = 0.01); Fig. 2C), indicating that they began each block with a propensity to use categorical information to guide choice. But across trials, WSLS behavior increased in category-predictive blocks, where it was an effective choice strategy, and decreased in exemplar-predictive blocks, where it was maladaptive (trial x block condition effect: χ²(1) = 175.8, p < 0.001, OR = 1.17, 95% CI = [1.14, 1.20]). WSLS behavior also diverged across block conditions more strongly in later blocks of the task (block condition x block number interaction: χ²(1) = 39.4, p < 0.001, OR = 1.08, 95% CI = [1.05, 1.10]; see Supplementary Note 1 for full details).

Finally, we conducted an additional regression analysis in which we examined how prior within-category rewards and prior same-exemplar rewards influenced participants’ approach decisions (see Supplementary Note 1 for full details). In accordance with our WSLS analysis, we found that participants began each block with a tendency to rely on both within-category rewards and same-exemplar rewards to guide their choices. In exemplar-predictive blocks, the influence of within-category rewards was attenuated across trials, indicating that participants learned through experience to stop over-generalizing.

Flexibility in the specificity of learning representations

Taken together, our learning data suggest that participants across age could use both categorical and exemplar-level information to learn to respond optimally to each stimulus. To what extent did participants flexibly shift the extent to which they weighted categorical versus exemplar-level information when making decisions across block conditions? To address this central question, we fit our data with variants of a reinforcement-learning model that differentially weighted information across levels of abstraction during choice (see Methods). Briefly, all model variants assumed that participants tracked the value of approaching each stimulus at both the categorical and exemplar level, such that on every trial, they incrementally updated one of three categorical value estimates and one of fifteen exemplar-level value estimates based on the reward feedback they received. At choice, these value estimates were converted to choice probabilities via a softmax function with inverse temperature parameters (which we will refer to as ‘choice weights’) that determined the extent to which decisions were guided by categorical and exemplar-level value estimates. We fit variants of the model with a single choice weight (in which equal weight was placed on categorical and exemplar-level value estimates), two choice weights (in which the weights placed on categorical and exemplar-level value estimates differed) and four choice weights (in which the weights placed on categorical and exemplar-level value estimates differed and varied across block conditions). We used a Bayesian model-fitting and selection procedure (see Methods) to determine the best-fitting model at the group level. Relative to models with one and two choice weights, the four choice-weight model had an exceedance probability of 1, indicating that it was the most frequent, best-fitting model across participants.

Choice weights derived from the best-fitting, four choice-weight model related to task performance. Participants with higher category choice weights earned significantly more points in category-predictive blocks, t(149) = 8.0, p < 0.001, b = 38.8, 95% CI = [29.2, 48.3], but not exemplar-predictive blocks, t(149) = −1.0, p = 0.339, b = −6.6, 95% CI = [−20.3, 7.0] (Fig. 2D). Participants with higher exemplar choice weights earned more points in both exemplar-predictive (t(149) = 8.5, p < 0.001, b = 58.9, 95% CI = [45.3, 72.6]) and category-predictive blocks (t(149) = 2.5, p = 0.014, b = 10.8, 95% CI = [2.2, 19.5]; Fig. 2D; see Supplementary Note 1 for additional analyses that show that participants considered exemplar-level information in category-predictive blocks).

Participants’ category and exemplar choice weights varied across block conditions, indicating that they shifted the specificity of the representations used to guide choice in accordance with the reward structure of the learning environment (block condition x specificity interaction effect, F(1, 447) = 76.5, p < 0.001, β = 0.32, 95% CI = [0.25, 0.40]; Fig. 2E). Post-hoc analyses in which we separately examined category and exemplar choice weights indicated that participants had higher category choice weights in category- versus exemplar-predictive choice blocks (F(1, 150) = 125.1, p < 0.001, β = 0.57, 95% CI = [0.47, 0.67]), indicating that they down-weighted categorical information when more granular information was needed to effectively guide choice. Exemplar choice weights, however, did not significantly vary across block conditions (F(1, 150) = 3.6, p = 0.061, β = −0.08, 95% CI = [−0.16, 0.003]). This indicates that participants continued to use exemplar-level information even in category-predictive blocks. This may reflect the fact that exemplar-level information could be used to effectively gain reward across both block conditions (Fig. 2D), but may also reflect participants’ initial uncertainty about whether tracking individuating details would be useful, or the difficulty of suppressing attention to previously relevant types of information. In additional analyses (see Supplementary Note 3), we further demonstrated that category and exemplar choice weights did not significantly trade off—we did not observe evidence that increases in category choice weights correspond to decreases in exemplar choice weights.

Though we had hypothesized that the flexible weighting of representations at different levels of abstraction would increase across development, we did not observe evidence for an age-varying block condition by choice weight interaction effect (age x block condition x specificity: F(1, 447) = 2.33, p = 0.127, β = 0.06, 95% CI = [−0.02, 0.13]); participants across age effectively reduced the weight they placed on more general, categorical representations in accordance with the reward structure of the environment (Fig. 2E). We did find that older participants demonstrated higher values of choice weights overall, F(1, 447) = 13.1, p < 0.001, β = 0.18, 95% CI = [0.08, 0.28], in line with prior findings suggesting an age-related decrease in choice stochasticity³⁵.

An influence of the learning context on memory

Our learning data indicate that the reward statistics of the task environment influenced the specificity of the representations used for value-based choice. Did environmental reward statistics similarly influence memory? To address this question, we analyzed data from a test of incidental memory, which was administered online 1 week after the initial reinforcement-learning task session. Overall, participants correctly categorized old and new images on 72.8% of trials (SE = 0.6%; Children: 71.2% (SE = 1.1%), Adolescents: 72.9% (SE = 1.0%; Adults: 74.1% (SE = 1.1%)).

Importantly, our memory test was designed to allow us to measure mnemonic specificity. The test included novel exemplar foils, which were drawn from the categories participants saw during learning (e.g., novel cows, horses, and goats; Fig. 1A) and novel category foils, which were drawn from categories from each stimulus set that were not presented (e.g., sheep; Fig. 1A). From these two classes of foil images, we constructed categorical and exemplar-level receiver operating characteristic (ROC) curves for each participant by examining their hit rates (i.e., responses to old images) and their false alarm rates (i.e., responses to foils) at each memory response level (1–4, “definitely new”, “maybe new”, “maybe old”, “definitely old”; Fig. 1D). We then computed the area under each of these curves (AUC)⁵⁰, to derive two measures of memory: category memory, which reflected the discrimination of old images from novel category foils, and exemplar memory, which reflected the discrimination of old images from novel exemplars drawn from the same categories they had seen during learning. An AUC value of 1 indicates perfect discrimination of old images from new foils, while an AUC value of 0.5 reflects chance-level performance. Participants’ average category and exemplar-level AUCs were 0.83 (SE = 0.006) and 0.71 (SE = 0.006), indicating above-chance discrimination of old and new items at both levels of specificity.

We further analyzed memory separately for the images (and foils) from category-predictive and exemplar-predictive blocks of the task, to derive measures of category and exemplar memory performance for each participant in each block condition. We originally hypothesized that the block condition in which the stimuli were encountered would influence memory 1 week later. We expected that in exemplar-predictive blocks, participants’ greater attention to the individuating features of each stimulus would enhance memory for those details, whereas in category-predictive blocks, we expected that participants’ attention to the shared features of stimuli would impede encoding of the individual exemplars. Thus, we expected to observe both a main effect of block condition and a block condition × specificity interaction effect on memory, such that participants would demonstrate better memory, particularly at the exemplar-level, for stimuli encountered in exemplar-predictive blocks.

Across task blocks, participants demonstrated better category versus exemplar memory, reflecting the increased difficulty of discriminating old items from novel, within-category exemplars, F(1, 451.2) = 605.5, p < 0.001, β = 0.060, 95% CI = [0.055, 0.065] (Fig. 3A). In line with our hypothesis, we observed a main effect of block condition on memory, such that participants were better able to distinguish old and new stimuli from exemplar-predictive versus category-predictive blocks, F(1, 451.2) = 12.0, p < 0.001, β = −0.008, 95% CI = [−0.013, −0.004] (Fig. 3A). In contrast to our second prediction, however, we did not observe a significant block condition x specificity interaction effect, F(1, 451.2) = 0.3, p = 0.602, β = 0.001, 95% CI = [−0.004, 0.006]. Participants demonstrated a similar enhancement of exemplar and category memory for stimuli encountered in exemplar-predictive blocks —the reward statistics of the learning environment shaped overall memory, but we did not observe evidence that they shaped memory specificity per se (see Supplementary Note 2 for additional analyses demonstrating that the effect of reward experienced during learning also differentially shaped memory across block conditions.) Finally, we additionally observed that overall memory performance improved with age, F(1, 149.3) = 5.3, p = 0.023, β = 0.016, 95% CI = [0.002, 0.029], though the influence of block condition on memory did not significantly vary across development (F(1, 451.2) = 3.0, p = 0.085, β = −0.004, 95% CI = [−0.009, 0.001]).

Fig. 3: The learning context influenced memory across age.

A Participants demonstrated better memory for category-level versus exemplar-level information, as well as for stimuli from the exemplar-predictive versus category-predictive blocks of the task. Memory at both levels of specificity also improved with increasing age. B Participants who earned the most points in the exemplar-predictive blocks also demonstrated better memory for exemplar-level information encountered in those blocks. Participants are binned into equal-sized performance groups based on the number of points earned in each block condition for visualization purposes only. In panels (A), (B), thin colored lines show individual participants’ category (top row) and exemplar (bottom row) memory performance, as indexed by AUC, within each block condition. The black points and error bars indicate age group mean values ± 1 SEM. C Participants who weighted exemplar-level information most strongly demonstrated the best exemplar memory. This effect was stronger in the exemplar-predictive relative to the category-predictive condition, and increased with age. Participants who weighted category-level information most strongly demonstrated better category memory but worse exemplar memory. The plots depict marginal effects from linear-mixed-effects models examining the effects of age, block condition, specificity (exemplar and category), choice weight magnitude (exemplar or category), and their interactions on memory performance, as indexed by AUC. Age was analyzed continuously; the lines show the predicted performance of participants at three different ages (the mean age of the sample, ±1 SD), with the shaded regions depicting 95% confidence intervals. All panels show data from 151 participants (n = 50 children, 50 adolescents, and 51 adults). Statistical analyses were conducted using mixed-effects models that assessed effects within participants while accounting for variation across them.

Individual differences in learning influence how reward shapes mnemonic specificity

While our preceding memory analyses take into account the specificity of the representations that were useful for learning, they do not take into account the extent to which representations were actually used to guide choice. We expected the environment to influence memory via its effects on value-guided learning, meaning that we expected to see the largest influence of block condition on mnemonic specificity for participants who effectively learned the task’s reward statistics, as evidenced by their performance on the learning task. To test this prediction, we re-ran our memory accuracy model, but included participants’ total number of points earned within each block condition as an interacting fixed effect. Here, we found that participants who earned the most points during learning demonstrated better memory across levels of specificity, F(1, 579.2) = 4.2, p = 0.040, β = 0.009, 95% CI = [0.000, 0.018]. Critically, however, this benefit was particularly pronounced for exemplar-level information encountered in exemplar-predictive blocks, as evidenced by a points × block condition × specificity interaction, F(1, 437.9) = 5.6, p = 0.018, β = 0.007, 95% CI = [0.001, 0.013] (Fig. 3B). In line with our hypothesis, these results suggest that the participants who most effectively upregulated their attention to and learning from the individuating features of the stimuli in exemplar-predictive blocks showed the greatest specificity in their memory for these stimuli. In other words, participants who were most sensitive to the reward statistics of the learning context also demonstrated the greatest influence of the learning context on subsequent memory specificity. The relation between learning performance and memory did not significantly vary with age (ps > 0.080).

The relation between reinforcement-learning computations and memory increased with age

Next, we asked how individual differences in the representations used for choice related to the effects of the learning environment on mnemonic specificity. Our analysis of model-derived choice weights revealed heterogeneity in the extent to which participants weighted exemplar-level information. This heterogeneity may be reflected in subsequent memory specificity, with participants who relied on more specific representations during learning showing enhanced exemplar memory and participants who relied on more general representations during learning showing enhanced category memory.

We first examined how exemplar-level choice weights in each block condition related to memory by adding them as an interacting fixed effect in our memory model (Supplementary Table 1). We observed a strong effect of choice weight magnitude on memory, with participants with higher exemplar choice weights exhibiting better memory performance at both levels of specificity, F(1, 577.2) = 14.6, p < 0.001, β = 0.018, 95% CI = [0.009, 0.027] (Fig. 3C). This indicates that participants’ whose choices were more driven by learning from individual exemplars also demonstrated a stronger ability to discriminate those learned exemplars from both novel category and novel exemplar foils. We also observed a choice weight magnitude x block condition interaction effect, F(1, 497.1) = 9.6, p = 0.002, β = −0.010, 95% CI = [−0.016, −0.004], such that the relation between exemplar-level choice weights on memory was greater in exemplar-predictive blocks. In other words, participants who placed more weight on exemplar-level information during learning showed particularly enhanced exemplar-level memory when using that granular information was necessary for effective learning.

Moreover, the relation between learning and memory varied with age, as evidenced by a choice weight magnitude x age interaction effect, F(1, 534.7) = 8.3, p = 0.004, β = 0.016, 95% CI = [0.005, 0.027], and a choice weight magnitude × age × block condition interaction, F(1, 500.2) = 5.1, p = 0.025, β = −0.008, 95% CI = [−0.014, −0.001]. Older participants demonstrated a stronger effect of exemplar choice weight magnitude on memory, particularly in the exemplar-predictive blocks (Fig. 3C). Interestingly, though children, adolescents, and adults similarly relied on exemplar-level information during learning, older participants’ weighting of the exemplars more strongly related to how well they remembered them 1 week later.

We observed a different pattern of results when we examined how category choice weights related to memory (Supplementary Table 2 and Fig. 3C). Here, we found that participants who weighted category-level information most strongly demonstrated better category memory but worse exemplar memory (choice weight magnitude × specificity interaction effect: F(1, 443.1) = 5.9, p = 0.015, β = 0.007, 95% CI = [0.001, 0.013]; Fig. 3C). No other choice weight effects or interactions reached significance (ps > 0.053).

Together, these results support our hypothesis that the statistics of the learning environment influenced memory through their effects on the representations that were used to guide value-based choice. Participants who used exemplar-level representations to the greatest extent during learning also demonstrated the best memory for the exemplars they encountered, particularly in the environment in which specific representations were most useful. Critically, it was not the case that participants who were ‘better’ at learning were also better at memory across the board—in category-predictive blocks, higher category choice weights led to better learning performance but worse memory for exemplars. The strength of the relation between learning and memory varied across development; the extent to which older participants weighted exemplar-level information during choice more strongly related to their subsequent category and exemplar memory 1 week later.

Experiment 2 design

In Experiment 1, we found that people across age adapted the extent to which they weighted exemplar-level versus categorical representations when learning to make good choices, and that individual differences in the specificity of the representations used to guide choice were reflected in subsequent memory. Somewhat unexpectedly, we also found that the strength of the relation between the specificity of the representations used for value-based choice and memory increased with age. In Experiment 2, we aimed to replicate and extend these findings.

Experiment 2 followed the same general structure as Experiment 1, but the reinforcement-learning task differed in several ways (Fig. 4). Our Experiment 1 design did not penalize the use of exemplar-level information in category-predictive blocks—the reward statistics of the task meant that in category-predictive blocks, exemplar-level information could still be used to guide optimal decision-making. This may explain why we did not observe shifts in exemplar-level choices weights across conditions, and why we observed global memory enhancements, rather than specificity enhancements, for stimuli encountered in exemplar-predictive blocks. Unlike in Experiment 1, in real-world environments, one advantage to using more abstract representations to guide choice is that they are more robust to stochasticity or noise—a single aberrant experience will shift value representations of broader categories to a lesser degree, and for a shorter period of time, because one will more rapidly accrue additional experiences with other category members. Further, using more abstract representations is less computationally demanding and requires learning a much smaller set of stimulus-action values. In our Experiment 1 task, exemplar-level reward distributions were not very noisy, and the computational demands of tracking individual exemplars may not have been sufficiently costly for participants to ignore or downweight exemplar-level representations during decision making. Thus, in Experiment 2, we changed the reinforcement-learning task to (a) induce more noise in reward distributions by making outcomes binary and (b) make tracking exemplar-level information more computationally demanding by having participants select between three actions on every trial (Fig. 5C). In addition, because the age effects we observed in Experiment 1 were monotonic, we included only children (n = 34; ages 8–12 years) and adults (n = 39; ages 18–25 years), between whom we expected to see the largest performance differences.

Fig. 4: Experiment 2 task design.

A Each block of the reinforcement-learning task included nine unique stimuli, which comprised three exemplars each drawn from three broader categories. Each stimulus set also included an additional stimulus category with five novel stimuli, as well as two additional novel exemplars per sampled category. B In the category-predictive condition, rewards on every trial were sampled from Bernoulli distributions with win probabilities determined by the stimulus categories. In the exemplar-predictive condition, rewards on every trial were sampled from Bernoulli distributions with win probabilities determined by the individual exemplars. The optimal action (depicted by the shaded color) resulted in wins on 90% of trials and losses on 10% of trials. The two other actions resulted in wins on 10% of trials and losses on 90% of trials. C On every trial of the reinforcement-learning task, participants saw a stimulus and three choice options. After selecting an option, they viewed the outcome of their choice: either a win (+1 point) or a loss (−1 point). The images in the figure are illustrative; actual task stimuli differed slightly. Image credit: iStock/GlobalP (https://www.istockphoto.com/portfolio/GlobalP), Life on White (https://www.lifeonwhite.com/).

Fig. 5: Results from Experiment 2 replicated key findings from Experiment 1.

A Over the course of each block, participants (n = 34 children; n = 39 adults) learned to make more optimal responses to stimuli in both the category-predictive and exemplar-predictive conditions, though performance was better in category-predictive relative to exemplar-predictive blocks. B In the category-predictive condition, participants increasingly generalized learned category responses to respond optimally to novel stimuli. C Participants across age groups demonstrated higher category-level choice weights in category-predictive blocks. Choice-weight magnitudes reflect normally distributed parameter estimates, which were exponentiated within each model. Thus, negative values reflect low, positive choice weights. D Participants demonstrated better memory for stimuli from the exemplar-predictive versus category-predictive blocks of the task. E Participants who earned the most points in the exemplar-predictive blocks also demonstrated better memory for exemplar-level information encountered in those blocks. Participants are binned into equal-sized performance groups based on the number of points earned in each block condition for visualization purposes only. In panels (A–E), horizontal lines reflect individual participant means. The points and error bars indicate group means ± 1 SEM. Statistical analyses were conducted using mixed-effects models that assessed effects within participants while accounting for variation across them. F Participants who weighted exemplar-level information most strongly during learning also demonstrated better category and better exemplar memory. The strength of this relation between learning and memory increased with increasing age. Participants who weighted category-level information most strongly demonstrated better category memory but not better exemplar memory. The plots depict marginal effects from linear-mixed-effects models examining the effects of age group, block condition, specificity (exemplar and category), choice weight magnitude (exemplar or category), and their interactions on memory performance, as indexed by AUC. The shaded regions depict 95% confidence intervals.

Replication of Experiment 1 learning results

As in Experiment 1, participants made increasingly correct responses across trials (ps < 0.001; Fig. 5A), with increasing age (p = 0.001), and in the category-predictive relative to the exemplar-predictive condition (p < 0.001). Older participants continued to demonstrate larger benefits from being able to use categorical information to guide choice, χ²(1) = 4.0, p = 0.045, OR = 0.89, 95% CI = [0.79, 1.0].

Increasingly with age, participants used category values to guide their responses to novel stimuli, demonstrating generalization of correct responses to novel stimuli from previously encountered categories in the category-predictive block (Main effect of category repetition: χ²(1) = 10.0, p = 0.002, OR = 1.12, 95% CI = [1.04, 1.20]; category repetition x block condition interaction: χ²(1) = 43.0, p < 0.001, OR = 1.26, 95% CI = [1.17, 1.35]; age group x block condition interaction: χ²(1) = 6.8, p = 0.009, OR = 0.89, 95% CI = [0.81, 0.97]; Fig. 5B). As in Experiment 1, participants also demonstrated increasing category win-stay lose-shift (WSLS) behavior in the category-predictive blocks and decreasing category WSLS behavior in the exemplar-predictive blocks (trial × block condition interaction effect: χ²(1) = 49.0, p < 0.001, OR = 1.14, 95% CI = [1.11, 1.18]), an effect that was stronger in adults than children (block condition × age group interaction: χ²(1) = 10.0, p = 0.002, OR = 0.9, 95% CI = [0.84, 0.96]).

When we fit reinforcement-learning models to the Experiment 2 choice data, the best-fitting model again included four choice weights, reflecting differences in the weighting of categorical and exemplar-level representations across block conditions. As in Experiment 1, choice weights related to task performance: Category choice weights positively related to the number of points participants earned in category-predictive blocks (t(71) = 8.5, p < 0.001, b = 39.8, 95% CI = [30.5, 49.2]) but not exemplar-predictive blocks (t(71) = −1.8, p = 0.069, b = −6.8., 95% CI = [−14.1, 0.54]). Exemplar choice weights positively related to the number of points participants earned in both exemplar-predictive (t(71) = 7.5, p < 0.001, b = 19.2, 95% = [14.1, 24.4]) and category-predictive blocks (t(71) = 2.6, p = 0.012, b = 16.5, 95% CI = [3.8, 29.2]).

Participants flexibly adapted the extent to which they weighted categorical versus exemplar-level representations across conditions (block condition × abstraction interaction effect: F(1, 213) = 6.14, p = 0.014, β = 0.14, 95% CI = [0.03, 0.24]; Fig. 5C). Here, we expected that by making exemplar-level information less useful in category-predictive blocks, we might observe changes in both category and exemplar choice weights across block conditions. We found, however, that as in Experiment 1, changes in the weighting of representations across blocks were still largely driven by changes in the extent to which participants weighted categorical representations (F(1, 72) = 7.8, p = 0.007, β = 0.18, 95% CI = [0.05, 0.31]) rather than the extent to which they weighted exemplar-level representations (F(1, 72) = 2.6, p = 0.112, β = −0.09, 95% CI = −0.22, 0.02]). Participants continued to use exemplar-level information to guide choices, even in category-predictive blocks, where they could have fully relied on broader stimulus categories.

Replication of Experiment 1 memory results

One week after learning, participants correctly categorized 75.8% (SE = 1.3%) of images presented during the memory test as old or new. Replicating the results of Experiment 1, participants demonstrated better memory for stimuli encountered in exemplar-predictive relative to category-predictive learning blocks, F(1, 213) = 20.0, p < 0.001, β = −0.018, 95% CI = [−0.026, −0.010], (Fig. 5D). While we initially hypothesized that exemplar memory would be specifically enhanced in exemplar-predictive blocks, we did not observe a significant block condition x abstraction level interaction effect: F(1, 213) = 3.74, p = 0.054, β = 0.008, 95% CI = [−0.000, 0.016]. (Fig. 6B). When we added participants’ total number of points earned within each block condition as an interacting fixed effect, we found that participants who earned the most points demonstrated the best memory, F(1, 254.5) = 14.9, p < 0.001, β = 0.040, 95% CI = [0.020, 0.061], and that as in Experiment 1, this effect was strongest for exemplar-level memory for stimuli encountered in exemplar-predictive blocks, F(1, 192.4) = 4.1, p = 0.043, β = 0.014, 95% CI = [0.000, 0.027] (Fig. 5E).

Individual differences in the extent to which participants weighted exemplar-level representations during learning, as indexed by exemplar choice weights, also robustly related to memory, F(1, 265.4) = 19.1, p < 0.001, β = 0.035, 95% CI = [0.019, 0.050] (Fig. 5F and Supplementary Table 3). As in Experiment 1, the relation between learning and memory strengthened with age (choice weight magnitude x age group interaction effect: F(1, 265.4) = 4.1, p = 0.045, β = −0.016, 95% CI =  [−0.032, −0.000]; see Supplementary Note 2 for analyses with continuous age). In other words, adults who weighted exemplar-level information to the greatest degree during learning also demonstrated the best memory for those exemplars, but children did not show this effect. While this effect was strongest in exemplar-predictive blocks in Experiment 1, here, we did not observe a significant choice weight magnitude × age group × block condition interaction (p = 0.181); older participants demonstrated a stronger effect of exemplar choice weight magnitude on memory across conditions.

Replicating our Experiment 1 findings, we did not observe a main effect of category choice weight on memory (p = 0.264; Supplementary Table 4), but rather a choice weight magnitude × specificity interaction (F(1, 202.7) = 7.8, p = 0.006, β = 0.011, 95% CI = [0.003, 0.019]; Fig. 5F), indicating that participants who weighted category-level representations most strongly demonstrated better category memory, but not better exemplar memory. Here, we additionally observed an age group × choice weight magnitude × block condition interaction effect, F(1, 212.9) = 6.5, p = 0.012, β = .012, 95% CI = [0.003, 0.020] (Fig. 5F), such that children demonstrated a more positive influence of category choice weight magnitude on memory in the category-predictive blocks. As in Experiment 1, while higher weights on exemplar-level representations during learning related to enhanced memory across levels of specificity, higher weights on categorical representations during learning only related to better category memory.

In Experiment 2, we made learning the optimal responses to individual exemplars in the reinforcement-learning task more costly by making reward values binary and presenting three choice options on every trial. Despite these differences from the task used in Experiment 1, we continued to observe adaptive flexibility in participants’ weighting of representations at different levels of abstraction, as well as reflections of learning weights in subsequent memory specificity. Critically, we also replicated our finding that the coupling between reinforcement learning and mnemonic specificity increased with age: Individual differences in the extent to which people weighted exemplar-level representations during learning were more tightly linked to individual differences in memory in adults versus children.

Discussion

Across two developmental studies, we examined how the specificity of the representations used for value-guided learning and memory are shaped by the statistics of the environment. We found that from childhood to early adulthood, participants adapted their learning representations to match the level of abstraction most useful for guiding behavior across environments. Originally, we hypothesized that more specific information would be preserved in memory only when it was useful for adaptive choice. We found, however, that specific information was remembered not when it was useful, but rather when it was used: The use of specific representations to guide reward learning related to better memory for both category and exemplar-level information. The use of broader, categorical representations for learning related to better category memory only, and in some cases, related to impaired exemplar memory. Moreover, the strength of the relation between learning and memory increased with age, such that relative to children, adults demonstrated a stronger relation between the specificity of their reinforcement-learning representations on subsequent memory. These findings suggest that the environment shapes memory specificity through its influence on reward learning, with the strength of the coupling between learning and memory increasing across development.

Our experiments revealed early-emerging flexibility in the specificity of value-guided learning. One challenge for learning within complex environments is determining which stimulus dimensions are relevant for choice⁵¹. In our learning task, there were no explicit cues that signaled whether idiosyncratic exemplar features or more general stimulus categories determined reward contingencies; instead, participants had to learn through experience the specificity of the representations that could most effectively guide choice. We expected that over the course of each block, reciprocal interactions between attention and reinforcement learning would increasingly cause participants to attend to either the shared or individuating features of stimuli within a category^52,53,54. We found that participants across age demonstrated adaptive up- and down-weighting of categorical information based on the environment’s reward structure. Our work builds on prior research demonstrating that adults can learn reward contingencies across multiple levels of abstraction^55,56; here, we extend these findings and show that across development, in accordance with the predictions of theoretical models³¹, individuals can flexibly arbitrate between more specific and more general representations to guide behavior.

In our learning task, participants began each block with a tendency to use categorical representations; as they accumulated more experience within each environment, they up- or down-weighted these categorical representations based on whether they were useful in obtaining the reward. This bias toward more abstract representations likely emerged due to the nature of our task stimuli; in our experiments, stimulus categories were at the ‘basic-level’⁵⁷, meaning they reflected a middle level of abstraction and grouped items with a high degree of similarity. In our task, stimuli within each task category shared greater perceptual similarity with one another than with stimuli in other categories. However, participants’ baseline bias toward categorical representations and their better performance in category-predictive blocks was likely facilitated not just by increased perceptual similarity, but also by the natural category groupings that they had learned through extensive experience with them prior to the task. While we specifically chose stimuli from categories that would be highly familiar to participants across our age range (e.g., chairs, apples, dogs), future work could use more abstract stimuli to separate the influence of perceptual similarity from prior experience. Future work could also manipulate different features of the task stimuli to better elucidate how learning from reward statistics in real-world environments across development constrains or facilitates the flexibility of value-learning representations in new contexts. For example, the granular features of different stimuli may become particularly salient or ecologically relevant at different developmental timepoints—adolescents may be particularly attuned to socially relevant stimuli like clothing brands or iPhone variants. Importantly, our findings suggest that while people may initially be guided by prior experience and knowledge of useful ways of carving up the world, their learning is remarkably flexible. Children as young as 8 years old could learn to overcome the tendency to generalize across category members.

Though participants across age flexibly modulated their use of categorical information to guide choice, in both experiments, they also relied on exemplar-level information even in category-predictive blocks. Participants continued to attend to, consider, and encode details of individual exemplars, in environments with reward statistics determined solely by their more abstract category membership. There are multiple reasons why this may be the case. First, as with categorical information, participants may have learned through real-world experience that drawing on specific past experiences is useful for reward-guided choice, such that they began each task with a strong prior to attend to the individual exemplars. Though general representations are useful for guiding behavior in novel situations, in familiar situations, the most similar, past experiences are often the best guide for how to behave³⁸. In addition, it may be the case that general representations depend on specific, exemplar-level representations^{30,58,59,60,61}, though we did not observe significant relations between exemplar and category choice weights in category-predictive blocks. Still, while our model posited separate, non-interacting representations for category and exemplar value estimates, in reality, participants may derive category-level value estimates from their representations of individual exemplars. Specific features of our task design may have also promoted the continued reliance on exemplar-level information. The costs of individuation were low— perceptual discrimination of the individual exemplars was relatively easy, and, even in category-predictive blocks, using exemplar-level information to guide choice did not impede reward gain. Further, when we increased the difficulty of tracking individual exemplar values by increasing the number of choices in Experiment 2, we also increased the difficulty of tracking category values, perhaps attenuating the difference in cognitive costs each strategy imposed. In addition, at the beginning of each block participants were not aware of whether categories or exemplars determined optimal actions, requiring some initial tracking of exemplar-level information to discern the environment’s structure. By further manipulating the cognitive difficulty and explicit reward costs of individuation, future studies can test age-related change in both the extent to which general value representations depend on exemplar-level representations, as well as the conditions under which the use of exemplar-level information can be flexibly modulated.

Though younger participants made fewer optimal responses in the learning task, our modeling results revealed that age-related improvements in learning were not driven by changes in a bias toward generality or specificity, or by reduced flexibility in learning across levels of abstraction. Instead, we found that younger participants had overall lower choice weight magnitudes, indicating that their poorer learning performance was driven by greater choice stochasticity^35,62,63. The potential sources and adaptive benefits of stochasticity or noise has been a longstanding puzzle in cognitive science⁶⁴, and our observation of greater noise at younger ages aligns with many developmental reinforcement-learning studies³⁵. Though greater choice stochasticity is often interpreted as heightened exploration^35,65, we likely attenuated exploratory motivations in Experiment 1 by providing full information about reward outcomes on every trial. Choice stochasticity may also reflect a mismatch between the model’s proposed value-learning algorithm and participants’ true value-learning algorithm—which here, may have been greatest at younger ages. Additional cognitive processes, like working memory or sustained attention, which our learning algorithm does not account for, could, in theory, differentially influence reinforcement learning across age. However prior work⁶⁶, suggests that developmental changes in working memory likely do not account for age-related changes in reinforcement learning⁶⁷ and further, given the limited capacity of working memory, we would expect its contribution to modulate the use of the small number of category-level value estimates but not the large number of exemplar-level value estimates⁶⁶, leading to greater age-related differences in category relative to exemplar choice weights. In addition, while it is possible that children had a harder time remaining engaged in the task, we found that across our age range, performance improved across blocks in the experiment. Thus, while developmental improvements in sustained attention may have contributed to better task performance at older ages⁶⁸, we did not observe evidence that attention over the course of the study differentially waned across age.

Here we also extended past work showing that reward learning relates to memory^{41,42,45,49,69}, demonstrating that memory reflects the level of abstraction of reward-learning computations. When participants used specific representations for choice, they preserved more detailed information in memory, whereas when they used more abstract representations, they demonstrated better generalization but poorer memory for individual exemplars. This tight link between between learning and mnemonic specificity aligns with the predictions of models of categorization; exemplar-based models^70,71,72 posit that memories for individual exemplars facilitate inferences about novel instances, whereas prototype models^57,73 suggest that individuals store and use more abstracted features to represent meaningful groupings of the world. More recent category-learning models posit adaptive flexibility in representations, such that individuating features are represented only when needed for successful classification and inference². A key property of all these models is that the way in which the world is parsed directly influences the specificity of the representations that are stored in memory over time. Merging multiple conceptual frameworks that propose mechanistic links between learning computations and memory^39,74, our work demonstrates that across development, reward shapes the granularity with which the world is partitioned, and in turn, the specificity of the information preserved in memory.

Moreover, we found that the strength of the relation between learning and memory specificity increased across development, which may be due to age-related increases in the influence of goals on feature-based selective attention at older ages^75,76. Adults may have learned through experience to attend to the information most useful for guiding choice, such that their exemplar choice weight magnitudes reflected the extent to which they both used and attended to exemplar-level information. Children, however, may have still attended to individuating features of stimuli even after learning that such features were irrelevant for decision-making. Indeed, prior research has suggested that category learning recruits different attentional mechanisms at different developmental timepoints: The ability to focus on relevant features may emerge earlier than the “filtering” of, or suppression of attention to, irrelevant information^77,78. Across multiple domains of learning, children demonstrate broader patterns of attention relative to adults, such that they attend to and learn about information that is irrelevant for the task at hand^{79,80,81,82,83,84}. This greater breadth of attention also influences memory, with children demonstrating better subsequent memory for information that they were not cued to attend to during learning^79,83,84. While much of this prior work has focused on younger, preschool-aged children, the executive control systems thought to underlie selection-based category-learning systems continue to change across adolescence^78,85. Thus, in our task, children may have shown a greater dissociation between the representations used for choice and their allocation of selective attention during learning. Their learning representations may therefore relate less strongly to the specificity of their subsequent memory. Future work can more directly test hypotheses about age-related change in attention during learning by using stimuli with spatially segregated features (e.g., ref. ⁵²) and measuring how differences in patterns of visual gaze during learning relate to subsequent memory specificity.

In our task, participants completed the memory test after a 1-week delay. Prior research has suggested that both the influence of reward statistics on memory^86,87,88 and individual differences in memory specificity²⁶, may strengthen as the delay between encoding and retrieval increases. The strengthening of these effects over time suggests that post-encoding consolidation processes play an important role in mnemonic specificity. Models of systems consolidation suggest that over time, memories may increasingly reflect generalized knowledge extracted from commonalities across multiple reactivated episodes^89,90. In our experiments, it may be the case that age differences in the influence of reinforcement learning on memory were partially driven by age-related changes in consolidation in the week between the learning and memory tasks^26,91. It may be the case that in adults, useful information is more strongly prioritized during consolidation, such that representations used to guide decision making are “replayed” or reactivated^88,92,93,94 to a greater extent than in children. Because all participants in our experiments completed the memory task after a week-long delay, we cannot determine how encoding versus consolidation mechanisms may have differentially contributed to memory for specific versus more general information across age. Future studies can test memory at different delay periods to examine the influence of consolidation time on the development of adaptive mnemonic specificity.

The ability to flexibly adjust the specificity of value learning and episodic memory is critical for building adaptive mental models of the environment across the lifespan. Here, we demonstrate that children, adolescents, and adults can dynamically adapt the relative weight they place on more specific versus more general information during reward learning. Further, we show that across development, the specificity of memory increasingly reflects the specificity of learning computations. The coupling of early-emerging flexibility in learning and a more protracted developmental timecourse of the influence of learning on memory may be adaptive^95,96. Memory that is less constrained by beliefs about the usefulness of information may promote the acquisition of broad knowledge of the world, while protecting against adverse consequences of learning representations at ineffective levels of abstraction. Across development, individuals’ adaptive parsing of the world’s structure may increasingly shape memory, and these lasting traces may guide adaptive behavior over increasingly long timescales.

Methods

All study procedures were approved by New York University’s Institutional Review Board (IRB-FY2021-5654).

Experiment 1

Participants

A priori, we determined a target sample size of 150 participants based on our prior studies of learning across age-continuous samples of children, adolescents, and adults^97,98. One hundred and fifty-one participants aged 8–25 years completed the two-part online study and were included in all analyses. An additional 24 participants (n = 5 children, n = 9 adolescents, n = 10 adults) completed both parts of the study but were excluded from all analyses for: (a) interacting with their browser window (minimized, maximized, or clicked outside the window) more than 20 times throughout either the learning or memory task (n = 15), (b) failing to respond on more than 10% of the 306 learning trials (>30 trials) or 10% of the 192 memory trials (>20 trials) (n = 7), or (c) responding in less than 100 ms on more than 10% of learning or memory trials (n = 2). In addition, one additional participant was excluded due to a glitch that prevented data from being saved. Participants were compensated with a $20 Amazon gift card for completing both parts of the study. They also received a bonus that ranged from $0 to $5 depending on their performance in the learning task. Adult participants and parents of minors provided informed consent; participants under 18 years assented to participate.

The 151 participants included in the final sample comprised n = 50 children (8.0–13.0 years; Mean age = 10.4 years, n = 24 females), n = 50 adolescents (13.1–17.8 years; Mean age = 15.4 years, n = 28 females), and n = 51 adults (18.2–25.9 years, Mean age = 21.8 years, n = 31 females). Gender was determined by self-report; we aimed to recruit a roughly equal distribution of male and female participants, but did not include gender as a covariate in our analyses due to no a priori hypotheses about effects of gender on our constructs of interest. All participants reported normal or corrected-to-normal vision and no diagnosed psychiatric or learning disorders. 57.6% of participants were White, 22.5% were Asian, 10.6% were Black, and 9.3% were of two or more races. In addition, 10.6% of participants were Hispanic. We include a more detailed description of participant demographics in the Supplementary Methods.

As with our previous online studies^34,99, participants were primarily recruited from ads on Facebook and Instagram, as well as via word-of-mouth, science fairs, events, and fliers distributed around New York University. Prior to entering our participant database and being eligible to complete the online study, all potential participants completed a 5-min zoom call with a researcher. During this zoom call, all participants (and a parent or guardian, if the participant was under 18 years of age) were required to be on camera and confirm the full name and date of birth they provided when they signed up for our database. Adult participants and parents of child and adolescent participants were further required to show photo identification.

Experimental procedure

Participants completed three experimental tasks across two sessions. All tasks were coded in jsPsych version 6.3.1¹⁰⁰ and hosted on Pavlovia. In the first session, participants completed a reinforcement-learning task, which took ~40 min. In the second session, participants completed a test of recognition memory, which took ~15 min. Participants who completed the learning task during the first session were invited to complete the second session six days later and had five days to complete it (e.g., if a participant completed the first session on a Wednesday, they would be invited to participate in the second session on Tuesday, and would have until the following Saturday to complete it). On average, participants completed the second session 7.1 days after completing the second session.

To examine how participants used categorical and exemplar-level representations to guide learning, we developed a value-based learning task in which participants had to choose whether to approach or avoid a stimulus on every trial. If participants chose to “approach” the stimulus, they would win or lose points depending on its value. If they chose to “avoid” the stimulus, they would not win or lose any points, but they were provided with full counterfactual information, meaning they would see how many points they would have won or lost had they chosen to approach the stimulus.

The task comprised six blocks, each with its own stimulus set (Table 1). The stimulus set assigned to each of the six blocks was randomized for each participant. The six stimulus sets included 32 unique images, divided into four broader categories (Fig. 1A). The broader categories were selected to be familiar to children as young as 8 years old (Fig. 1E). All stimulus images were taken from Google images and edited such that they showed a single item on a white, square, uniformly sized background. The instructions for each task block followed the same format but varied depending on the stimulus set. For example, in the “Pets” block, participants were instructed that petting animals would sometimes make them happy, causing them to win points, and sometimes make them angry, causing them to lose points, whereas in the ‘Vehicles’ block, participants were instructed that taking their friend for a ride in some vehicles would make them thrilled and other vehicles would make them upset.

Table 1 Stimulus sets used across blocks

In each block of the reinforcement-learning task, participants saw 15 unique images. For each participant, five images were randomly selected from three of the four categories in each block to serve as learning stimuli. Within each category, two images repeated six times, one image repeated three times, and two images were only shown once during learning. The order of image presentation was randomized within each block for each participant.

Critically, participants completed three blocks in the category-predictive condition and three blocks in the exemplar-predictive condition. In the category-predictive condition, stimulus values were sampled from Gaussian distributions (SD = 1.5) on every trial, where the mean of the distribution was determined by stimulus category. One category was randomly determined to be good such that the mean of its reward distribution was between 3 and 6; one category was randomly determined to be neutral such that the mean of its reward distribution was zero (though zero was never actually presented as an outcome); and one category was randomly determined to be bad such that the mean of its reward distribution was between −6 and −3. Values were rounded to the nearest non-zero integer. Values were sampled from these distributions anew on every trial, meaning the reward associated with approaching the same stimulus might differ across repetitions.

In the exemplar-predictive condition, each stimulus was pseudo-randomly assigned a deterministic reward value between −9 and 9. To ensure that categorical information could not be used to effectively guide choice, one stimulus within each category was assigned a value between −9 and −6, one was assigned a value between −5 and −3, one was assigned a value between −2 and 2, one was assigned a value between 3 and 5, and one was assigned a value between 6 and 9. In addition, within each block, no two stimuli were assigned the same value, and no stimulus was assigned a value of zero. This meant that all broader categories included two or three stimuli that should be avoided, and two or three stimuli that should be approached.

The condition of the first block was counterbalanced across participants within each age group, such that roughly half of the children, adolescents, and adults experienced a category-predictive block first, and the other half experienced an exemplar-predictive block first. For each participant, the first two blocks of the task were always different conditions. The latter four blocks included two additional exemplar-predictive blocks and two additional category-predictive blocks, in a random order.

To ensure participants had equal exposure to all stimuli, all trials lasted 3 seconds, regardless of how quickly participants made their response. Within the 3-s time limit, participants made their approach or avoid selection by pressing 1 or 0 on a standard keyboard, respectively. After making their selection, participants saw their choice highlighted for 500 ms, and then the outcome of their choice for the remainder of the trial (Fig. 1B). For “approach” decisions, winning outcomes were displayed in green text and losses were displayed in red text. For “avoid” decisions, the points that the participant would have won or lost were always displayed in gray text, inside a red or green box. The colors of the boxes corresponded to whether they made an optimal or suboptimal choice on that trial. Missed wins were displayed in red boxes and avoided losses were displayed in green boxes—this color cue was intended to help participants across age with counterfactual learning. In addition, the choice screen displayed coins in each of its corners, which were animated depending on the choice outcome: The coins would bounce for wins, fall off the screen for losses, and become grayed out for avoid decisions. Trials were separated by a 500 ms inter-trial interval in which no stimuli appeared on the screen. Participants lost five points each time they failed to respond within the 3-s time limit.

Prior to completing the real trials of the learning task, participants completed an extensive tutorial, which included child-friendly instructions that were both written on the screen and read aloud via audio recordings. Participants were unable to advance past each instruction page until the audio recording finished playing. The tutorial also included a short practice block in which participants had to approach or avoid different pieces of sports equipment. Participants completed twelve practice trials. Stimuli on each trial were sampled (with replacement) from eight images across two categories (balls and rackets), and their values were randomly sampled on each trial from −9 to 9, with replacement. In this way, the reward structure of the practice block did not align with either the category-predictive or exemplar-predictive condition, but still allowed participants to learn the mechanics of the learning task. After the tutorial, participants answered three True/False comprehension questions about the task. If they answered a question incorrectly, they would see (and hear) the correct answer with an explanation, and have to try to answer the same question again. On average, participants answered all three comprehension questions correctly in 3.05 attempts (Mean number of attempts: Children: 3.06; Adolescents: 3.08; Adults: 3.00). There was not a significant effect of age on the number of question attempts required (b = −0.005, SE = 0.003, p = 0.15).

In the second experimental session, which took place between 6 and 10 days after the first (Mean delay = 7.1 days, SD = 1.3 days) participants completed a test of recognition memory (see Supplementary Note 2 for an analysis of the effects of delay duration on memory). On each trial, participants saw an image and had to determine whether it was Definitely New, Maybe New, Maybe Old, or Definitely Old, by pressing the 1, 2, 3, and 4 keys on their keyboard, respectively (Fig. 1D). Participants had 10 s to make each response. They did not receive any feedback.

The memory test comprised 192 trials, which included all 32 images from each of the six stimulus sets. This meant that for each of the six stimulus sets, participants saw the 15 old images used during the learning task, nine new exemplars from the three presented categories, and eight new images from a fourth category that was not presented during learning. All images from all six stimulus sets were intermixed and presented in a random order at the test. As with the learning task, participants completed a child-friendly tutorial and several practice trials prior to beginning the real memory test.

Analysis approach

To examine participant performance during the learning task, we coded a correct response variable as 1 if participants chose to approach stimuli with positive values and avoid stimuli with negative values, and 0 if they chose to avoid stimuli with positive values and approach stimuli with negative values. For analyses of correct responses, we excluded trials involving stimuli from the neutral category in the category-predictive condition.

To examine memory performance, we used participants’ memory confidence ratings to construct receiver operating characteristic curves for each participant by computing the proportion of old and new images that they responded to at or below each confidence level (ranging from 1, definitely new, to 4, definitely old). We constructed four separate curves for each participant: one for each block condition (category-predictive, exemplar-predictive) at each level of stimulus abstraction (category, exemplar). We analyzed levels of stimulus abstraction separately to probe the specificity of memory representations— we aimed to examine, for example, whether participants remembered that they had seen images from broader categories (e.g., cows) or whether they had seen specific exemplars (e.g., a specific black-and-white cow). The same sets of “old” images were included in the analyses across both levels of abstraction, but the novel foils that were included in the computation varied: Novel category foils were used to construct the category ROC curves and novel exemplar foils were used to construct the exemplar ROC curves (Table 2). In this way, we could examine whether participants could distinguish old from new categories (e.g., cows vs. sheep) separately from whether they could distinguish old from new exemplars (e.g., an old black-and-white cow from a new brown cow). We then used the ‘pROC’ R package¹⁰¹ to compute the area under each of these curves (AUC), as our measure of memory performance. AUC is a theory-neutral metric of memory performance that avoids the incorrect all-or-none (i.e., remembered or forgotten) assumptions that are inherent to measures like corrected recognition, and is instead sensitive to graded confidence levels⁵⁰. AUC values of 1 indicate perfect memory, while values of 0.5 indicate chance-level performance.

Table 2 Stimuli used in memory analyses

In addition to the memory analyses described in the results, we also examined how memory varied as a function of the delay (in days) between the learning and memory tasks, and as a function of the number of times each stimulus was repeated during the learning task. While we observed effects of both delay (i.e., worse memory with increasing delays) and stimulus repetition (i.e., better memory with increasing repetitions), these effects did not interact with any of our predictors of interest. As such, for simplicity, we collapsed across these variables in the models described in the main text, and report delay and repetition analyses in Supplementary Note 1.

We used the ‘afex’ package (version 1.3-1)¹⁰² for R (version 4.3.1) to fit mixed-effects models to our data. All continuous variables were z-scored prior to their inclusion in the models. Dependent variables were not standardized. Models included random intercepts for each participant and random slopes across fixed effects and their interactions for each participant. When models failed to converge, we pruned interactions between random slopes and then random slopes themselves¹⁰³. We analyzed continuous dependent variables with linear models and binary dependent variables with logistic models; we confirmed via visual inspection that continuous variables were roughly normally distributed but did not formally test for normality or equal variances. For logistic mixed-effects models, we assessed the significance of fixed effects with likelihood ratio tests. For linear-mixed-effects models, we assessed the significance of fixed effects with F tests using the Satterthwaite approximation to estimate the degrees of freedom. All reported statistical tests are two-sided.

To test how participants learned and used categorical and exemplar-level information to choose whether to approach or avoid each stimulus, we fit our data with variants of a temporal difference reinforcement learning model¹⁰⁴. Due to the number of model variants we considered, we performed model comparison and selection in stages, which we describe below. Model-fitting and comparison were conducted using the computational and behavioral modeling (cbm) package¹⁰⁵ within Matlab 2020b¹⁰⁶. Because the cbm package relies on normally distributed parameters, within each model, we exponentiated choice weight parameters to ensure they were positive, and transformed learning rate parameters to be between 0 and 1, using sigmoidal functions. We first fit all models to each participant’s choice data individually. For first-level fitting, we used common, relatively uninformative priors for all model parameters: Normal(mean =  0, variance = 6.25). We also scaled all reward outcomes to be between −1 and 1 by dividing by the maximum absolute reward value that participants experienced (11). We similarly scaled initial Q values within each model by dividing them by 10.

These first-level fits were then fed into a second-level fitting and model comparison algorithm. The second-level fitting procedure performs simultaneous hierarchical parameter estimation and Bayesian model comparison, in which each participant is treated as a random effect (i.e., different participants may be best fit by different models). We determined the best-fitting model at the group level by examining exceedance probabilities (XP), which reflect the probability that a given model is the most frequent best-fitting model for a group of participants¹⁰⁷.

The baseline model assumed that participants tracked the overall value of each category of stimuli (three value estimates per block) as well as the value of each individual exemplar (15 value estimates per block). On every trial, the probability that a participant would approach the stimulus was determined via a softmax function with choice weight parameters (inverse temperatures; ${\beta }_{c},\,{\beta }_{e}$) that scaled the category- and exemplar-level value estimates $(Q\left(c\right),{Q}\left(e\right))$.

$$p\left({approach} | s\right)=\frac{{e}^{{\beta }_{c}*Q\left(c\right)+{\beta }_{e}*Q(e)}}{{e}^{{\beta }_{c}*Q\left(c\right)+{\beta }_{e}*Q(e)}+{e}^{0}}$$

(1)

The choice weights thus govern the extent to which category-level and exemplar-level information influence choices, with higher weights indicating choices that are more driven by the category- and exemplar-level value estimates.

After choosing to approach or avoid each stimulus, participants update their category-level and exemplar-level value estimates such that:

$$Q{\left(c\right)}_{t+1}=Q{\left(c\right)}_{t}+\alpha*(r-Q{\left(c\right)}_{t})$$

(2)

$$Q{\left(e\right)}_{t+1}=Q{\left(e\right)}_{t}+\alpha*(r-Q{\left(e\right)}_{t})$$

(3)

where $r$ is the reward for approaching the stimulus on that trial, and $\alpha$ is a participant-specific learning rate, governing the extent to which recent rewards influence value estimates.

We tested variants of this model with one choice weight, two, and four choice weights, (allowing them to vary across levels of abstraction and allowing them to vary across both levels of abstraction and block conditions, respectively). At the group level, the best-fitting model included four choice weights (i.e., “fourB”, model frequency = 0.78; exceedance probability (XP) = 1). In Supplementary Note 3, we include additional comparisons with models in which learning rates also varied across levels of abstraction and block conditions; we continued to observe that the model with four choice weights and a single learning rate best captured participant behavior.

Next, we assessed whether model fit could be further improved by allowing initial stimulus value estimates to vary (rather than being fixed at 0). We tested three variants of the fourB model that allowed for 0, 1, or 2 initial Q values (across levels of abstraction). At the group-level, the best-fitting model included a single free parameter for initial Q values (i.e., “fourB_oneQ”, model frequency = 0.70, XP = 1).

Finally, we assessed whether participants updated value estimates equivalently after approach and avoid decisions. We tested three variants of the fourB_oneQ model: the winning model from our prior comparisons, which included full counterfactual learning, as well as a model that allowed for separate learning rates after approach versus avoid decisions, and a model with no counterfactual learning, in which value estimates were not updated on “avoid” trials. At the group-level, the best-fitting model included full counterfactual learning (fourB_oneQ, model frequency = 0.76, XP = 1; see Supplementary Note 3 for age group analyses).

To ensure that models within each comparison set were distinguishable from one another, we conducted recoverability analyses in which we generated 100 simulated datasets of 151 simulated agents. Parameters for each simulated agent were drawn randomly from uniform distributions with minima and maxima determined by the minimum and maximum fitted values from the empirical data. In addition, for the model with two initial q values, we constrained their non-transformed values to be at least 1 apart. For the model with a separate counterfactual learning rate, we constrained the non-transformed values of the counterfactual learning rates to be greater than −2 (so that its transformed value would be distinguishable from 0) and to be at least 1 apart from the choice learning rate. We then fit each simulated dataset with all three models in each model comparison set, and fed these first-level fits through the same second-level fitting and model comparison algorithm that we used with our empirical data. We then examined the proportion of the 100 simulated experiments for which the model with the highest exceedance probability matched the true, generating model.

The model with four choice weights was highly distinguishable from the models with one or two choice weights (Fig. 6A). Similarly, the model with full counterfactual learning was highly distinguishable from the model with a separate counterfactual learning rate and the model without counterfactual learning (Fig. 6C). However, while distinguishable from the model that initialized value estimates at 0, the model with one initial q value was not distinguishable from the model with two initial q values (Fig. 6B), indicating that with our experimental design, we could not measure whether participants initialized categorical stimulus values differently from exemplar stimulus values.

Fig. 6: Experiment 1 model recoverability.

For each model within each stage of model comparison, 100 simulated “experiments” were conducted in which choice data were simulated from 151 agents, with parameters sampled from uniform distributions with ranges determined by the empirical fits. Data from each simulated experiment were then fit with each model within the comparison set. The top panels show confusion matrices, where the values within each tile represent the proportion of experiments for which each fitted model had the highest exceedance probability (top panels). The bottom panels show inversion matrices, where the values within each tile represent the proportion of experiments for which the fitted model had the highest exceedance probability that were generated by each of the models. Black lines outline the model that best fits the empirical data within each comparison stage. A Models with different numbers of choice weights were highly distinguishable from one another. B Models in which exemplar and category values were initialized with either one or two free parameters were distinguishable from a model in which exemplar and category values were both initialized at 0. However, models with one or two initial values were not distinguishable from one another. C The winning model, in which participants learned equivalently from experienced and counterfactual outcomes, was highly distinguishable from a model in which participants learned with separate learning rates for experienced and counterfactual outcomes, as well as a model in which participants did not learn from counterfactual outcomes.

We extracted parameter estimates from our best-fitting model (fourB_oneQ) to examine their relation with other variables of interest (e.g., age, memory performance). Because we were interested in individual differences in parameter estimates, we examined estimates from the first level of model-fitting, in which models were fit to individual participants’ data using common, uninformative priors.

To ensure that parameter values were recoverable¹⁰⁸, we simulated data from 15,100 participants (e.g., 100 simulations of 151-participant “experiments”). For each simulated participant, we randomly sampled a task stimulus and reward sequence from one of our participants. We sampled parameter values from uniform distributions with minima and maxima determined by the minimum and maximum parameter estimates from fitted participant data. We then performed first-level model-fitting on these simulated datasets, and examined the correlation between simulated and recovered parameter values. Across all parameters, recoverability was high, with correlations ranging from 0.73 to 0.91 (Fig. 7A). When exemplar choice weights were high (e.g., >1), exemplar values dictated participants’ choices and category choice weights were pulled toward the mean of the prior (0), such that they demonstrated poorer recoverability (Fig. 7B).

Fig. 7: Experiment 1 parameter recovery for the fourB_oneQ model.

A Correlations between simulated and recovered parameter values for the fourB_oneQ model ranged from 0.73 to 0.91. Choice data were simulated for 15,100 agents, with parameter values sampled from uniform distributions with minima and maxima determined by the minimum and maximum parameter estimates from the fitted data. B Exemplar choice weight values influenced category choice weight recoverability, such that category choice weights could be better recovered when exemplar choice weights were lower.

Finally, we also examined the extent to which model simulations recapitulated key aspects of our behavioral results. We describe these posterior predictive checks in the Supplementary Methods, but note here that simulations from our winning model can successfully reproduce important signatures of participant task performance.

Experiment 2

Participants

Seventy-three participants completed the two-part online study and were included in all analyses. An additional 13 participants (n = 9 children; n = 4 adults) completed both parts of the study but were excluded from all analyses for: (a) interacting with their browser window (minimized, maximized, or clicked outside the window) more than 20 times throughout either the learning or memory task (n = 8), (b) failing to respond on more than 10% of learning or memory trials (n = 1), or (c) responding in less than 100 ms on more than 10% of learning or memory trials (n = 4). In addition, three additional participants were excluded due to a glitch that prevented data from being saved. Participants were recruited, tested, and compensated as in Experiment 1, though base payment was increased to $23 because the learning task was slightly longer. All study procedures were approved by New York University’s Institutional Review Board. Adult participants and parents of minors provided informed consent; participants under 18 years assented to participate.

The 73 participants included in the final sample comprised n = 34 children (8.1–12.9 years; Mean age = 10.9 years, n = 17 females) and n = 39 adults (18.4–25.8 years, Mean age = 21.9 years, n = 27 females). 52% of participants were White, 32% were Asian, 2.7% were Black, 12% were two or more races, and 1.3% were Pacific Islander or Native Hawaiian. In addition, 9.3% of participants were Hispanic (see Supplementary Methods for more demographic details).

Experimental procedure

The reinforcement-learning task used in Experiment 2 was similar to that used in Experiment 1, but participants had to select from three choice options on every trial (Fig. 6C). Each stimulus was associated with an optimal choice that would usually cause the participant to win a point, and two suboptimal choices that would usually cause the participant to lose a point. As in Experiment 1, the task comprised six blocks, each with its own stimulus set. We used the same six stimulus sets as in Experiment 1, though they were modified to include fewer images. Here, the six stimulus sets each included 20 unique images, divided into four broader categories (Fig. 4A). Three stimuli from three broader categories were used during each block of the learning task. The two unused stimuli from each of the three broader categories, and all five stimuli from the remaining, fourth category were used as novel exemplar and category images, respectively, in the subsequent test of recognition memory.

As in Experiment 1, the instructions for each task block varied slightly depending on the stimulus set. For example, in the Farm Animals block, participants were instructed that they had to return animals to the barns where they lived. Returning animals to the correct barn would usually make them happy, causing participants to win a point, and returning animals to the incorrect barn would usually make them sad, causing participants to lose a point.

Participants completed three category-predictive blocks and three exemplar-predictive blocks, in a pseudorandom order (as in Experiment 1). In category-predictive blocks, the broader stimulus categories determined the stimulus-action reward probabilities, such that all members of a broader category were associated with the same optimal choice (Fig. 4B). In exemplar-predictive blocks, one exemplar from each broader category was randomly paired with each of the three choice options, such that within a broader category, the optimal choices for all three exemplars differed. Selecting the optimal choice for a stimulus resulted in winning one point on 90% of trials and losing one point on 10% of trials; selecting either of the two other choices resulted in winning one point on 10% of trials and losing one point on 90% of trials. All stimuli were repeated eight times within each block, in a random order, such that each block comprised 72 trials. Block order was pseudorandomized for each participant as in Experiment 1.

All trials lasted 4 s, regardless of how quickly participants made their response. Within the 4-s time limit, participants made their choice selection by pressing 1, 2, or 3 on a standard keyboard. After making their selection, participants saw their choice highlighted for 500 ms, and then the outcome of their choice for the remainder of the trial (Fig. 4C). Participants saw green checkmarks with a bouncing animation and “+1” if they won a point, and red X’s with a swinging animation and “−1” if they lost a point. Trials were separated by a 500 ms inter-trial interval in which no stimuli appeared on the screen. The positions of the choice images were randomized on every trial.

As in Experiment 1, participants completed an extensive, child-friendly tutorial prior to beginning the reinforcement-learning task. After the tutorial, participants answered three True/False comprehension questions about the task. If they answered a question incorrectly, they would see (and hear) the correct answer with an explanation. On average, participants answered 2.7 comprehension questions correctly (Age group means: Children: 2.68; Adults: 2.71). There was no significant effect of age group on the number of questions answered correctly (p = 0.71).

The memory test was identical to that used in Experiment 1. Participants completed the memory test between 6 and 9 days after they completed the reinforcement-learning task (except for one adult who completed the memory test on day 5, and one child who completed it on day 10; Mean delay = 7.1 days; SD = 1.1 days; See Supplementary Note 2 for an analysis of the effects of delay duration on memory).

Analysis approach

Our analysis approach largely aligned with our approach in Experiment 1. Here, however, because we did not collect data from adolescents, rather than analyzing age as a continuous variable, we treated age group (children and adults) as a categorical variable.

We fit the same computational models to our data, with several modifications to take into account the different reward structure of the task. First, rather than tracking three category values and 15 exemplar values, here, the models track 9 (3 categories × 3 choices) category-action values and 27 (9 exemplars × 3 choices) exemplar-action values. We re-coded the binary rewards as 0 and 1, and constrained initial Q values to fall in this range. In addition, in Experiment 1, counterfactual feedback was presented explicitly to participants on “avoid” trials in which they did not experience gains or losses. Here, no counterfactual feedback was presented. Instead, our counterfactual learning models assumed that participants might infer that the unselected choice options would have yielded gains when the selected choice option yielded a loss and vice versa.

We followed the same model-fitting and stage-wise selection approach as in Experiment 1, and found that the best-fitting model also included four choice weights and one initial Q value. Here, rather than exhibiting equivalent learning from experienced and counterfactual outcomes, we found that participants’ choices were best fit by a model (fourB_oneQ_CF) that included separate learning rates for experienced outcomes from selected options and inferred outcomes from unselected choice options. Models (Fig. 8) and parameter values from the winning model (Fig. 9) both showed good recoverability, with correlations between simulated and fitted parameters ranging from 0.65 to 0.91. In addition, model simulations recapitulated key features of participant choice behavior (see posterior predictive checks in the Supplementary Methods).

Fig. 8: Experiment 2 model recoverability.

For each model within each stage of model comparison, 100 simulated experiments were conducted in which choice data were simulated from 73 agents, with parameters sampled from uniform distributions with ranges determined by the empirical fits. Data from each simulated experiment were then fit with each model within the comparison set. The top panels show confusion matrices, where the values within each tile represent the proportion of experiments for which each fitted model had the highest exceedance probability (top panels). The bottom panels show inversion matrices, where the values within each tile represent the proportion of experiments for which the fitted model had the highest exceedance probability that were generated by each of the models. Black lines outline the model that best fit the empirical data within each comparison stage. A Models with different numbers of choice weights were highly distinguishable from one another. B Models in which exemplar and category values were initialized with either one or two free parameters were moderately distinguishable from one another. C Models with a single learning rate, separate learning rates for experienced and inferred counterfactual outcomes, and no counterfactual learning were highly distinguishable from one another.

Fig. 9: Experiment 2 parameter recoverability for the fourB_oneQ model.

Correlations between simulated and recovered parameter values for the fourB_oneQ model ranged from 0.65 to 0.91. Choice data were simulated for 10,000 agents, with parameter values sampled from uniform distributions with minima and maxima determined by the minimum and maximum parameter estimates from the fitted data.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.