Introduction

Artificial intelligence (AI) has gained widespread attention due to its remarkable performance in diverse applications, such as data processing, image recognition, and classification1. The advancement of AI involves more than just enhancing algorithms; it also entails creating increasingly complex and deeper neural networks. This necessitates the use of additional computing parameters, which strains conventional hardware. Consequently, there is a rising demand for energy-efficient AI accelerators capable of efficiently handling the growing volume of data.

Additionally, there has been a significant surge of interest in implementing AI on edge devices, often referred to as edge AI2. This technology provides unique advantages in AI utilization; edge AI enables the use of AI in environments where networks are not connected or in situations with security concerns regarding network usage. Furthermore, edge AI can conduct initial computations of cloud-based deep neural networks, simplifying the large volumes of data generated at the input stage before transmitting them to cloud AI. This helps alleviate data bottleneck issues between the input source and cloud AI. However, edge devices must be more energy-efficient, considering the inherent energy constraints in edge environments. Additionally, they should be wearable or attachable to ensure effective utilization in edge environments3.

In this regard, traditional CMOS transistor-based digital hardware faces limitations, and new hardware alternatives are needed4,5. One of the most notable technologies is the memristive dot product engine (MDPE), which performs large-scale vector-matrix multiplication (VMM) operations using a memristive crossbar array6,7,8,9,10,11,12,13. The MDPE is fundamentally very energy-efficient, as it performs VMM operations based on physics principles (i.e., Kirchhoff’s law and Ohm’s law). Additionally, flexible crossbar arrays have been actively investigated recently, and they have potential in diverse edge applications, including image recognition14, classifying input data measured from sensors15,16,17, and diagnosing biosignals such as ECGs18,19. These studies demonstrate the potential of MDPE for edge AI, and it is crucial to validate and demonstrate these capabilities using reliably fabricated MDPE.

In MDPE fabrication, selecting a memristor is crucial, and we suggest that a charge trap memristor is the best choice based on its various proven advantages20,21,22,23,24,25,26. It has a low current analog operation capability and electroforming-free characteristics, allowing high reliability and uniformity. Furthermore, the self-rectifying characteristics of the device enable large-array operation without complex transistor or selector processes, and the device is highly compatible with the conventional CMOS process. In addition, the fabrication of charge trap memristor-based MDPE on flexible substrates should proceed at a low temperature because a high thermal budget destroys the substrate, which has not been demonstrated.

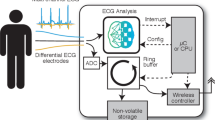
Furthermore, once the MDPE is ready, it is crucial to explore detailed methodologies for systematically utilizing this hardware in appropriate applications. Given that AI technology offers significant advantages in analyzing signal patterns, its application in electrocardiogram (ECG) diagnosis is particularly well suited27,28. Typical ECG diagnosis primarily relies on the experience and judgment of medical professionals. However, ECG diagnosis requires long-term monitoring of intermittently occurring abnormal signals, imposing a significant burden in terms of both accuracy and efficiency29. Therefore, recent efforts have been made to address this issue with the help of AI. However, AI-based analysis often relies on data collected over short periods or requires remote processing, posing certain limitations. For a more comprehensive diagnosis, ECG signal collection and analysis must be carried out continuously and in real time, making this an optimal application for edge AI. Figure 1a shows the real-time ECG diagnosis system, where the edge AI device collects ECG data and detects arrhythmia heartbeats in real time.

Fig. 1: Overview of a flexible memristive dot product engine (f-MDPE) embodying a self-rectifying charge-trap memristor for ECG diagnosis.
figure 1

a Illustration of the real-time ECG monitoring system with the f-MDPE. b Key advantages of the f-MDPE for edge AI applications.

Full size image

In this study, we introduce the charge trap memristor-embodying flexible MDPE (f-MDPE) and propose its utilization in an edge AI system for ECG diagnosis. We fabricated a 32 × 32 crossbar array on a polyimide (PI) substrate containing a low-temperature (<180 °C) processed charge trap memristor as the f-MDPE. Figure 1b highlights the key advantageous features of the f-MDPE for edge AI accelerators. The device exhibits highly self-rectifying behavior in a simple capacitor structure, enabling easy, selector-less passive crossbar array integration and allowing accurate programming and reading operations. Additionally, the electroforming-free nature of these materials ensures high device-to-device and cycle-to-cycle uniformity. The f-MDPE can be integrated in a conventional fab environment at low temperatures, compatible with the PI substrate, demonstrating its scalability with CMOS processing. Moreover, the f-MDPE shows high electrical and mechanical stability even under 5 mm bending conditions, highlighting its suitability for wearable applications. Last, its low current operation enables inference with very minimal energy. To demonstrate these advantages of the f-MDPE, we conducted a real-time ECG diagnosis. Here, we devised an algorithmic approach during the training process that accommodates hardware specifications such as non-Ohmic I-V characteristics and quantized weight properties. We built and trained a single-layer perceptron (SLP) using the MIT-BIH ECG database on software and mapped it onto the f-MDPE hardware. Then, we conducted laboratory-scale real-time ECG diagnosis using the f-MDPE, demonstrating its potential for in situ ECG inference, as it consumes only 0.3% of the energy compared to digital approaches with a classification accuracy of 93.5%, highlighting its potential for edge AI hardware.

Results

Electrical characteristics, reliabilities, and bending durability of an f-MDPE array

Figure 2a shows optical images of the f-MDPE array. The layered structure of the charge trap memristor (Ti/Pt/Ti/Al2O3/NbOx/Ta2O5/Pt, from bottom to top) was integrated on a flexible PI substrate. We have previously proposed this structure, but it was on a SiO2/Si substrate22, so the device itself may not be novel. However, to implement this structure on a flexible substrate and overcome the slow operation speed of conventional devices, we introduced three key modifications in this study. First, since the PI substrate is vulnerable to high temperatures, we developed and applied low-temperature processes below 180 °C for all layers. Second, we replaced the oxidant for the Al2O3 tunneling layer from H2O to O3 to reduce the H-passivated traps30,31,32,33, thereby improving the programming speed (see Supplementary Fig. 1 in the supplementary information (SI) for a detailed discussion on the changes in the Al2O3 deposition process and their impact on the programming speed). Third, we inserted a 30-nm-thick Pt layer in the middle of the Ti layer (i.e., Ti/Pt/Ti) to enhance the flexibility of the bottom electrode (BE), as Ti alone is mechanically brittle. More details on the device fabrication process can be found in the Method section. The cross-sectional transmission electron microscopy (TEM) image in Fig. 2b confirms the thicknesses of the oxide layers: 7 nm for Al2O3, 25 nm for NbOx, and 6 nm for Ta2O5. The NbOx layer is non-stoichiometric and amorphous, which is a key factor that acts as a charge trap layer22. The Al2O3 and Ta2O5 layers act as tunneling and blocking oxides, respectively, stabilizing the trapped electrons.

Fig. 2: Electrical characteristics of the f-MDPE.
figure 2

a Optical images of the f-MDPE on a polyimide (PI) substrate. b Cross-sectional transmission electron microscopy (TEM) image of the device. A single representative TEM image is measured. c I–V curves of the device with various compliance currents (ICC). The inset shows the nonlinearity and on/off ratio at 10 µA of ICC. d I–V curves of 160 cells in the array under 1 µA of ICC. e Repeated potentiation and depression cycles of the device. f Retention characteristics of 8 conductance states at 85 °C. g Long-term retention characteristics at various temperatures. h Endurance performance for LRS (red) and HRS (blue) up to 105 cycles at room temperature.

Full size image

The device exhibited analog set switching characteristics, with its conductance being tunable by a compliance current (ICC), as shown in Fig. 2c, with a maximum on/off ratio of ~104 at 3 V, as shown in the inset. The analog switching characteristics are attributed to the Schottky barrier height modulation accompanied by electron trapping and detrapping in the NbOx layer22. Additionally, the device showed a rectifying ratio of ~103 at a read voltage of ±3 V, as shown in the inset. Owing to its self-rectifying characteristics, the device may operate accurately even in a 1k × 1k array without sneak path disturbance34,35 (see Supplementary Fig. 2 in the SI for a discussion on the available array size and read margin of the f-MDPE array). To further evaluate the impact of voltage drop caused by wire resistance in a scaled-up device, we conducted cell voltage distribution simulations (see Supplementary Fig. 3). In the simulation, the conductance of each cell was randomly assigned a value between 1 nS and 15 nS, while the wire resistance between cells was assumed to be 10 Ω36. A read voltage of 3 V was applied, and the voltage drop was analyzed across array sizes ranging from 32 × 32 to 1024 × 1024. The results indicate that the wire resistance has little impact on f-MDPE operation, suggesting its highly reliable performance even in large-scale arrays.

Figure 2d shows I–V curves of 160 cells (32 × 5) in the array at an ICC of 10−6 A, confirming a 100% yield and high array-level uniformity (see Supplementary Fig. 4 in the SI for the 160 raw I–V curves). Figure 2e shows 70 cycles of potentiation and depression (P/DP) curves from a representative cell. To obtain the P/DP characteristics, 100 µs of +12 V, 100 µs of −10 V, and 500 µs of +3 V were used as the programming, erasing, and reading voltages, respectively, as shown in the inset. The results demonstrate the high feasibility and uniformity of these devices when they are suitable for analog devices.

The retention characteristics of eight different conductance states were confirmed at 85 °C, as shown in Fig. 2f. All conductance states were stable up to 104 s without significant changes. This gives an operating conductance window from 0.1 nS to 15 nS at 3 V. Figure 2g shows the retention characteristics of the high resistance state (HRS) and low resistance state (LRS) for 104 s at different temperatures (RT, 85 °C, and 125 °C). The Arrhenius plot suggested that both the HRS and LRS could be maintained for more than 3 years (see Supplementary Fig. 5 in the SI for the Arrhenius plot with the failure time at 20% conductance change). Additionally, Fig. 2h shows the endurance of the device for up to 105 cycles, using 5 ms of +12 V pulse for programming and 5 ms of −10 V pulse for erasing, respectively. Here, the on/off ratio was smaller than in Fig. 2g, where a DC sweep was used, due to the shorter pulse duration. Although this is not the full on/off ratio, we still achieve an on/off ratio of approximately 70, which we believe is sufficient for verifying the endurance characteristic. These results confirm the practical feasibility of the f-MDPE approach.

We also examined the bending durability of the f-MDPE for wearable applications. Figure 3a shows the memory windows of ten randomly selected cells at various bending radii. The results showed that the cells operated well down to a curvature radius (r) of 5 mm but deteriorated to less than 5 mm. This is likely due to an increase in electrode resistance under bending conditions, which results in the inability to apply voltage to the cell. Nevertheless, considering that the curvatures of the human body are greater than 5 mm (insets, r = 15 mm at a wrist and r = 5 mm at a finger), the stability at r = 5 mm is practically meaningful. In addition, retention characteristics were examined at r = 5 mm, revealing that the bending stress did not negatively affect the stability over 3 years, as shown in Fig. 3b. Figure 3c shows the high stability of multiple conductance states while changing curvatures from flat to r = 5 mm for 200 s at each curvature (total 103 s). For this measurement, we first programmed the device into specific conductance states and measured the retention for 200 s at each bending radius while gradually decreasing the radius to 15 mm, 10 mm, 7.5 mm, and 5 mm. We repeated this measurement for 8 different conductance states.

Fig. 3: Bending stability of the f-MDPE.
figure 3

a Memory window for various curvature radii. b Long-term retention characteristics under a 5 mm curvature radius. c Retention characteristics of 8 conductance states and d potentiation and depression under various curvature radii from flat to r = 5 mm. e Potentiation and depression after repeated bending cycles under a 5 mm radius. f–h I–V curves after repeated bending cycles under various curvature radii.

Full size image

Furthermore, the device exhibited reliable synaptic characteristics under bending conditions. Figure 3d shows the P/DP characteristics under various bending conditions (i.e., flat, 16.5, 10, 7.5, and 5 mm bending radii). Figure 3e confirms the high bending durability of the synaptic characteristics over bending cycles (100, 500, 1000, and 2000 cycles) at r = 5 mm.

Next, the bending cycle endurance for the electrical characteristics was investigated. Figure 2f–h shows the I–V characteristics during 103 bending cycles with various bending radii. The device operated well under r = 10 mm (Fig. 3f) and r = 5 mm (Fig. 3g) while maintaining a wide memory window. However, significant degradation was observed at r = 2 mm (Fig. 3h); the LRS degraded gradually after up to 500 cycles and eventually collapsed to the HRS after 1000 cycles. This was also associated with the fatality of the electrode, which is consistent with the previous results in Fig. 3a. In conclusion, the device exhibited sufficient electrical and mechanical stability.

Hardware-aware training for addressing non-Ohmic conduction behavior

Neural networks execute the multiplication of an input vector and a weight matrix, known as the VMM. The operations can be efficiently conducted in the MDPE through Kirchhoff’s law and Ohm’s law, which can be given by \({I}_{j}={\sum }_{i=1}^{n}{g}_{{ij}}\cdot {V}_{i}\), where I is the output current, g is the conductance, V is the input voltage, i and j are row and column indices, respectively, and n is the number of inputs. In conventional MDPEs, the conductance (\({g}_{{ij}}\)) is assumed to be constant regardless of the input voltage (i.e., Ohmic conduction), so multiple input voltages can be easily applied7,37.

However, the proposed f-MDPE exhibited a nonlinear current response to input voltages stemming from non-Ohmic conduction. This is not a specific problem in our device but is an inherent challenge in low-current devices, where the conduction mechanism is non-Ohmic38,39. Therefore, the effective conductance varies depending on the input voltage, as depicted in Fig. 4a. In this case, the trained weight using the conventional method cannot be directly mapped to g. Instead, training and inference must be performed considering that the weight is a function of the input voltage corresponding to the non-Ohmic behavior of devices40. However, it necessitates additional partial derivative operations of the weight matrix during backpropagation, significantly increasing the computational complexity and thus presenting a highly intricate dilemma.

Fig. 4: Hardware-aware training for addressing non-Ohmic conduction behavior.
figure 4

a Output currents of multiple states as a function of the input voltages of non-Ohmic devices following Schottky conduction (Isch). b Output currents represented by the transformed voltage, V′. g′ remains constant over the input voltages. c Crossbar array after linear transformation (V to V′ and g to g′), enabling a formal VMM operation in the f-MDPE. d Crossbar array with non-Ohmic cells. In this case, the conductance changes according to the input voltage. e Four bits (i.e., 16 levels) of multilevel conductance states at the reference voltage, 3 V, with 15 cells. Note that box plots are defined by the minimum, 25th percentile (Q1), median, 75th percentile (Q3), and maximum values, with the box indicating the interquartile range (IQR) and the whiskers representing the full data range. f I–V curves at the read voltage region at each analog state. g g′ obtained by extracting values for each analog state using a compensation constant k = 7.

Full size image

Here, we introduce a hardware-aware training approach to address this non-Ohmic behavior issue. This process involves converting the nonlinear weight function into a linear function during training mathematically, allowing for effective network training. Then, the trained weights, reflecting the nonlinear characteristics, are converted to conductance, which can be directly mapped onto f-MDPE, enabling inference.

The first step of this process is to determine the non-Ohmic function. The f-MDPE device followed Schottky conduction (see Supplementary Fig. 6 in the SI for the detailed conduction mechanism fitting results). Therefore, the I–V characteristics of the device can be expressed by the following Schottky equation

$$I=I_{sch}={{AT}}^{2}\exp \left[\frac{-q({\varPhi }_{{{\rm{b}}}} - \sqrt{-{qE}/4{{\rm{\pi }}}{\varepsilon }_{r}{\varepsilon }_{0}})}{{kT}}\right]$$
(1)

where A is a constant, \(q{\varPhi }_{b}\) is the Schottky barrier height, T is the temperature, q is the electronic charge, E is the electric field, \({\varepsilon }_{0}\) is the permittivity in vacuum, \({\varepsilon }_{r}\) is the optical dielectric constant, and k is the Boltzmann constant. Equation (1) can be simplified to the form of \(I=\exp \left(a+b\sqrt{V-c}\right)\), where a is the variable that depends on the conductance state related to Φ, and b and c are constants, assuming a constant T. Thus, the nonlinear current can be defined as a function of a and V:

$$I\left(a,V\right)=\exp (a)\cdot \exp (b\sqrt{{{V}}-{{c}}})$$
(2)

Here, we put a compensation constant k that scales the value of each exponential term accordingly, addressing potential issues with scale consistency and ensuring that the neural network operates within a stable and efficient regime (see Supplementary Table 1 for scale between \(g^{\prime}\) and \(V{^\prime}\) with constant k).

$$I\left(a,V\right)=\exp ({{a}}+{{k}})\cdot \exp \left(-{{k}}+{{b}}\sqrt{{{V}}-{{c}}}\right)$$
(3)

Then, by defining \(g^{\prime}=\exp (a+k)\) and \({V}^{\prime}=\exp (-k+b\sqrt{V-c})\), Eq. (3) can be reformulated as a linear multiplication function:

$$I={g}^{\prime} \cdot V^{\prime}$$
(4)

Consequently, the output currents can be expressed as a linear function of \(V^{\prime}\) with a slope of \(g^{\prime}\), a function of the device state a, as depicted in Fig. 4b. Then, the current output at the jth neuron during VMM can be given by the simple dot product between \(g^{\prime}\) and \(V^{\prime}\) matrices:

$${I}_{j}={\sum }_{i=1}^{n}{{g}^{\prime} }_{{ij}}\cdot {V}_{i}^{{\prime} }$$
(5)

Equation (5) indicates that the f-MDPE can perform the VMM by substituting g with \(g^{\prime}\) and V with \(V^{\prime}\) for neural network training. Consequently, non-Ohmic I–V curves can be converted to Ohmic I–\(V^{\prime}\) curves (see Supplementary Fig. 7 for transformed I–\(V^{\prime}\) curves), where the slope represents \(g^{\prime}\). By transforming linear VMM, unnecessary additional partial derivatives of Schottky functions during backpropagation in the training process are avoided, enabling energy-efficient neural network learning (see Supplementary Table 2 for the comparison of the network model, output form, and weight gradient function between three cases: ideal software case, hardware using Ohmic memristor case, and hardware using Schottky memristor case). Here, V were transformed to \(V^{\prime}\) using the hardware parameters, retaining the features of the original signal (see Supplementary Fig. 8 for an example of the transformation from \(V\) to \(V^{\prime}\)). Note that both V and \(V^{\prime}\) are directly generated by receiving external signals through a controller unit. Therefore, the conversion from V to \(V^{\prime}\) does not impose any additional circuit burden.

After hardware-aware training, one can obtain \({g}^{\prime}_{ij}\) matrix, as depicted in Fig. 4c. The next step is converting \({g}^{\prime}_{ij}\) to \({g}_{ij}\) and mapping \({g}_{{ij}}\) onto f-MDPE for inference, as depicted in Fig. 4d. To achieve this, the relationship between \(g^{\prime}\) and \(g\) must be defined, which can be obtained through the following process.

To consider the variation in analog conductance states, we defined 16 quantized conductance states as available weights, whose conductance at 3 V (gref) ranged from 0.1 nS to 15 nS with a 1 nS interval, as shown in Fig. 4e. The distinct gref were observed without overlap between states, indicating their suitability for the quantized weights of the neural network. Figure 4f shows the read currents for the 16 quantized states at various input voltages (square dots) alongside the Schottky fitting curves (solid lines) (see Supplementary Fig. 9 in the SI for the I–V curves of 16 states obtained by 20 devices demonstrating the stability of each state, and see Supplementary Fig. 10 and Supplementary Table 1 for the Schottky fitting results). For hardware-aware training, hardware parameters for each state are extracted from the fitting curves, and \(g^{\prime}\) values are obtained from the hardware parameters. Figure 4g shows \(g^{\prime}\)–gref plot, which is used for converting the trained \(g^{\prime}\) to gref to map the gref onto f-MDPE.

In summary, after obtaining the trained \(g^{\prime}\) matrix, the corresponding gref map can be transferred to the f-MDPE, and by using \(V\) as input, the f-MDPE can perform the VMM. This hardware-aware approach can generally be applied to all memristors exhibiting non-Ohmic conduction behavior; furthermore, it can address any hardware nonideality issues41.

ECG dataset classification using the f-MDPE array

Here, we aim to demonstrate the feasibility of using f-MDPE as edge AI hardware by utilizing it for real-time ECG diagnosis. Previous studies have used AI for ECG signal analysis and proven its effectiveness, demonstrating that its implementation in real-time edge environments is novel in this work42,43,44,45,46. Figure 5a illustrates the proposed ECG diagnosis process involving (i) ECG signal sensing, (ii) signal preprocessing, (iii) f-MDPE inference, and (iv) ECG diagnosis using the trained f-MDPE array. For training, we adopted the ECG dataset from the MIT-BIH arrhythmia database, which classifies the ECG signals into five categories47: normal (N), supraventricular ectopic beat (S), ventricular ectopic beat (V), unknown beat (Q), and fusion beat (F). Among these categories, only N represents normal signals, which are observed most frequently, while the others denote intermittent abnormal signals. The MIT-BIH database contains raw data from continuous ECG signals. To utilize these data as input data for the f-MDPE, it is necessary to preprocess them into the ECG dataset and adjust them appropriately to fit the f-MDPE. Therefore, we extracted individual ECG signals and resized them into 32-time frames to align them with the number of input terminals of the 32 × 32 f-MDPE. Additionally, we adjusted the amplitude corresponding to the input voltages from 2.0 to 3.5 V (see Supplementary Table 3 for details on the data preprocessing procedure). Subsequently, we utilized this ECG dataset to train a single-layer perceptron (SLP) with a size of 32 × 5 on software, enabling it to distinguish between 5 categories of ECG patterns using an input size of 32. During training, we also implemented hardware-aware training methodologies reflecting non-Ohmic conduction behavior and quantized conductance characteristics, as described in the previous section (Fig. 4). The trained weight matrix contains both positive and negative values, which cannot be directly mapped as conductance, allowing only positive values. In such cases, a common approach is to represent one weight using a pair of columns, each representing positive or negative weight values8,48,49. Thus, the 32 × 5 weight matrix was reconstructed to a 32 × 10 matrix. Figure 5b shows the weight matrix trained by the SLP with a size of 32 × 10, where the weight values include both positive (red) and negative (blue) values, each having 16 quantized levels. The zeroth state (Level 0) denotes an unprogrammed conductance state (i.e., initial state, whose conductance was 1.6 pS, which is much smaller than the 0.1 nS of Level 1). Figure 5c shows the conversion of these conductance values into target current values at 3 V for actual mapping onto the f-MDPE. Here, Levels 1–16 are converted from 0.3 nA to 45 nA at 3 V.

Fig. 5: The f-MDPE-based hardware system for ECG heartbeat diagnosis.
figure 5

a Schematics of in-situ inference with a pretrained f-MDPE array for ECG diagnosis. b Pretrained weight matrix of a 32 × 5 sized network, using positive and negative weights separately. c Target current at 3 V of the transferred weight matrix in (b). d Measured current at 3 V of the pretrained f-MDPE array. e Error distribution between the target and measured currents at each single point. f Summed output currents for the given input heartbeats from the MIT-BIH heartbeat dataset represented as N, S, V, Q, and F. The neuron indicating each heartbeat has the highest output current, indicating a correct classification. g, h Confusion matrices of the network for 5-category classification (g) and normal/abnormal classification (h).

Full size image

Next, we programmed the f-MDPE with the prepared weight matrix in Fig. 5b and examined its programmed accuracy. For this weight mapping, we used ISPP (incremental step pulse programming)-type programming and verification scheme to accurately programming the cells50. Figure 5d shows the measured currents of the programmed f-MDPE read at 3 V. Figure 5e compares the target current (Itarget) of Fig. 5c with the measured read current (Imeasured) of Fig. 5d for the entire 320 weight cells. The correlation coefficient between Itarget and Imeasured was 0.998, confirming the accurate programming of the trained weight matrix onto the f-MDPE array (see Supplementary Fig. 11 for more detailed statistics of the target and measured current difference).

Before we used the f-MDPE model for real-time diagnosis, we tested its ability to perform an inference test on the ECG dataset. Figure 5f shows five examples of outputs selected from different categories. Note that the total output current is the difference between the currents from the positive and negative weights. In these examples, the highest output corresponding to the correct category indicates that the inputs are accurately distinguished.

The estimated performance of the f-MDPE method for inferring signals from the ECG dataset was investigated. Figure 5g shows a confusion map of the inference results for the 4255 test dataset. The F1-macro score was 0.774, while the F1-micro score was 0.815 (see Supplementary Note for the details on the F1 score definition). This score represents the recognition rate for all the data. However, in ECG diagnosis, abnormal signals can be misidentified among abnormal signals, so the ECG pattern can be categorized as normal or abnormal, where abnormal includes S, V, Q, or F. Figure 5h shows the reconstructed confusion map, which gives an F1-macro score of 0.804 and an F1-micro score of 0.847. Furthermore, considering that classifying abnormalities is the most crucial aspect of diagnosis, when focusing on abnormal signal detection, the accuracy of the abnormal dataset was 0.873, which is an attractive number considering that such abnormal ECG patterns may occur several times per day or hour51. In summary, although the f-MDPE is a prototype hardware with only a 32×32 size capable of driving the SLP, it can efficiently diagnose the ECG.

A real-time ECG diagnosis demonstration

Figure 6a shows a photograph of a laboratory-scale real-time ECG diagnosis system comprising a control PC, an f-MDPE controller, an f-MDPE, and an ECG sensor, where the ECG sensor and the f-MDPE are attached to a human wrist (see Supplementary Fig. 12 for the detailed electrical connection scheme between the f-MDPE and the controller). The f-MDPE was programmed to perform only inference operations based on the weight matrix trained ex-situ through software. The control PC receives the ECG signals from the ECG sensor, preprocesses them to the input voltage signal for f-MDPE inference, and sends instructions to the f-MDPE controller. The f-MDPE controller sends the input voltages to the f-MDPE, receives the output currents, and returns them to the PC. Then, the PC determines the category of the ECG signals (see Supplementary Fig. 13 for the flowchart of the real-time ECG diagnosis system).

Fig. 6: Experimental demonstration and scalability of f-MDPE for ECG diagnosis.
figure 6

a Photograph of the integrated system: ECG sensor, f-MDPE, and f-MDPE controller integrated on a control PC. ECG diagnosis of N pulses from the b MIT-BIH dataset and c personal signals acquired from the ECG sensor. d Schematics of the scaled-up 1D convolutional neural network (1D CNN). e Recognition rates of ECG diagnosis for the proposed 1D CNN architectures. The recognition rate is saturated in the 2k model. f Energy consumption comparisons of the f-MDPE algorithm and conventional processors (CPU and GPU) for inferring a single heartbeat signal from the 2k model. g Energy consumption per bit and area per cell comparisons of the f-MDPE and flexible or stretchable memristive arrays. The green squares represent flexible arrays, and the blue rectangles represent stretchable arrays.

Full size image

We attempted two real-time tests in this system: (1) using the MIT-BIH ECG dataset for reference (w/o the ECG sensor part) and (2) using the preprocessed ECG data collected in real-time from ECG sensors. The preprocessing of the real-time ECG data was performed via software (Python) and included signal denoising, resizing, and peak detection to ensure accurate dataset generation (see Supplementary Video for the real-time ECG diagnosis demonstration). Figure 6b shows an example of four consecutive N signals from the MIT-BIH dataset (left panel) and the f-MDPE’s output currents for each signal (right panel), confirming that the system effectively categorized the input signals. Figure 6c shows the preprocessed real-time ECG signals collected from the ECG sensor (left panel) and the collected output currents (right panel). The results show that the system can accurately distinguish N pulses from a regular person. Note that the purpose of this testing is not to conduct actual diagnoses but to demonstrate the operation of the entire system. Therefore, we tested this approach with a regular person and observed N pulses.

A scale-up feasibility demonstration via virtual f-MDPE hardware

We adopted a small network size of 32 × 5 and a simple network structure of SLP to fit the f-MDPE. As a result, we achieved an F1 macro score of 0.774, indicating the potential of the ECG diagnosis system. However, there is also a need to achieve better performance at larger sizes. Therefore, we simulated a large-scale neural network using virtual f-MDPE hardware built into software and evaluated the behavior of the f-MDPE. Additionally, we adopted a method of partitioning a single piece of hardware to operate a multilayer perceptron. Here, we employed a one-dimensional convolutional neural network (1D CNN), whose network structure is shown in Fig. 6d, as it is known to be the best for pattern recognition tasks52. We built three 1D CNN network models, namely, 1k, 2k, and 4k, referring to the available number of weights in 32 × 32 (1k), 64 × 32 (2k), and 64 × 64 (4k) arrays of the virtual f-MDPE, respectively (details of 1D CNN architectures across varying network sizes are described in Supplementary Table 4). Although the 2k and 4k arrays were not physically fabricated, they were simulated assuming that the 1k-sized f-MDPE array was directly scaled up. This virtual scaling approach is widely applied in other studies as well13,53, as it provides valuable insights into large-scale performance with high reliability in advance. Figure 6e shows the F1-macro score and F1-micro score for the proposed 1D CNN models. The table also includes the experimental SLP scores for reference. The results suggested that the recognition rate was saturated in the 2k model, with 0.99 for the F1-micro score and 0.94 for the F1-macro score. Supplementary Fig. 14 shows the confusion matrix obtained by the 2k model, revealing its high performance. The hardware-aware training method is also applicable to 2D CNNs, indicating its broad applicability across various applications (see Supplementary Fig. 15 for more details of hardware-aware training models).

Figure 6f shows the estimated energy consumption for ECG inference on various computing platforms when the 2k model is used. Note that this comparison focuses on the energy consumption of running neural networks, excluding other sources of energy consumption, such as ECG sensors. The energy consumption per inference by the conventional CPU and GPU approaches was 168 µJ and 41 µJ, respectively13,54. However, the f-MDPE with a 5-µm-line width required only 120 nJ, far below that of conventional computing approaches. This energy consumption can be further reduced by scaling the array with a 100-nm-line width55,56. We anticipate that the energy consumption can reach 2.64 nJ, outperforming GPU-based inference by more than four orders of magnitude (detailed energy consumption and latency are described in Supplementary Figs. 16–18 and Tables 5 and 6). Furthermore, compared with other flexible or stretchable memristive arrays, the f-MDPE offers advantages in terms of energy efficiency and size (Fig. 6g)15,16,18,57,58,59,60,61,62.

Discussion

In summary, we reported energy-efficient neuromorphic applications utilizing the f-MDPE, characterized by its highly nonlinear and self-rectifying characteristics with a low-current operation, suitable for energy-efficient and reliable vector-matrix multiplication operations. Also, the device exhibited mechanical durability up to a 5-mm bending curvature, making it suitable for wearable applications. We successfully demonstrated the use of f-MDPE for in situ ECG classification by applying a hardware-aware training method that overcomes hardware characteristics such as non-Ohmic conduction and weight quantization. Furthermore, we simulated the proposed method using scaled-up 1D CNNs, confirming its feasibility for real-time ECG diagnosis with high diagnostic accuracy.

In edge computing, utilizing edge hardware plays a dominant role in reducing overall energy consumption. For example, in real-time ECG diagnosis, the overall process can be summarized as follows: (1) ECG signal acquisition, (2) preprocessing, (3) inferencing, and optionally, (4) wireless transmission (e.g., via Bluetooth). A single ECG pulse acquisition (assuming a 1-s acquisition) consumes around 6.1–17.4 µJ63,64,65. The preprocessing stage requires negligible energy, around tens of nJ66. Inferencing using a GPU requires 42 µJ, but this energy consumption can be reduced to 120 nJ by using f-MDPE, significantly alleviating this energy burden. Furthermore, edge computing processes data locally, minimizing external signal transmission. This drastically reduces the high energy consumption required for wireless transmission (real-time Bluetooth transmission typically consumes 22.7 mW67). As such, the f-MDPE aligns well with future analog signal processing at edge devices, providing energy-efficient artificial intelligence solutions.

While the f-MDPE shows promise for real-time and long-term signal monitoring due to its energy efficiency and portability, several challenges remain to be addressed for further advancements. First, for its use as a fully neuromorphic processor, its functionality should be expanded beyond inference to training. To achieve this, a control unit must be integrated, which would require advancements in wearable electronics. Even in this scenario, the low programming energy of f-MDPE would remain a significant advantage. Second, improving the higher operating voltage and slower switching speed of f-MDPE through the development of materials and process optimizations could further enhance its usability. If these aspects can be enhanced in the future, it would significantly broaden the applicability of f-MDPE across a wider range of applications.

Methods

Device fabrication

For an f-MDPE array, the integrated device consisted of Pt/Ta2O5/NbOx/Al2O3/Ti/Pt/Ti on a polyimide (PI) substrate. Polydimethylsiloxane (PDMS) was spin-coated on a 1-mm-thick glass substrate, and a 50-µm-thick PI film was attached to it. Next, the f-MDPE device was integrated by the following steps: First, an adhesive of 4-nm-thick Ti followed by a 30-nm-thick Pt insertion and a 10-nm-thick Ti bottom electrode were deposited by e-beam evaporation (KVE-E2000) without breaking the vacuum on a bottom electrode pattern formed by a mask aligner (Midas MDA-600S). These layers were then patterned by a lift-off process. Next, a 7-nm-thick Al2O3 layer was deposited by thermal atomic layer deposition (ALD) at 180 °C using trimethylaluminum and O3 as the Al precursor and oxygen source, respectively. The NbOx layer was deposited by reactive sputtering (Daeki Hitech cosputtering system) at 170 °C in an Ar and O2 mixed gas ambient environment using an Nb target. Next, the Ta2O5 layer was deposited using plasma-enhanced ALD at 180 °C using Tris(diethylamido)(tert-butylimido)tantalum(V) and O2 plasma for the Ta precursor and the oxidant, respectively. Then, a 60-nm-thick Pt top electrode was deposited by e-beam evaporation and patterned by a lift-off process. Finally, the f-MDPE was detached from the glass substrate. The line width for the active area in the array was 5 µm.

Electrical measurements

Electrical characterization was performed using a Keithley 4200A-SCS and an ArcOne f-MDPE controller. The pulse measurements were obtained by a Keithley 4200A-SCS and an ArcOne. During the measurement, the TE was biased, and the BE was grounded.

Measurement of personal ECG signals

This study received an exemption confirmation from the Institutional Review Board of Korea Advanced Institute of Science and Technology (KAIST IRB) (No. 2025-03-1-460). The personal ECG signals of the main authors, Y. Lee and G. Kim, were obtained by utilizing a commercial ECG sensor. Written consent was obtained from all participants prior to data collection. The purpose of this experiment was solely to collect data for hardware validation. No biometric data were stored, trained, or reused, and the study is entirely unrelated to any medical procedures. In selecting participants for the experiment, factors such as the number of volunteers, sex, and age were not considered.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.