Introduction

Optically active chiral materials with left-/right-circularly polarization abilities, which exhibit circular dichroism (CD), present great advantages in the potential applications of 3D display1, chiral synthesis2, and information storage3,4. Especially, the CD response located in near-infrared (NIR) region makes them attractive for bio-related applications5,6,7. For such advanced applications, the chiral materials must yield strong intensity of the chiroptical signal with high optical asymmetry (g-factor). To achieve this, various chiroptical active materials have been explored, including biomaterials8,9, cholesteric liquid crystals10, helical structures11, and inorganic chiral nanomaterials12,13. Specifically, plasmonic chiral structures have attracted great interest due to their strong light-matter interactions and plasmonic coupling14,15,16.

Plasmonic chiral nanomaterials can be fabricated through top-down17,18 and bottom-up approaches19,20, including direct laser writing, photolithography, glancing angle deposition, and template-assisted colloidal assembly of nanoparticles. However, these methods are associated with either high cost and complicated processing, or need liquid crystals21, DNA22,23, chiral fibers24, and micro-origami25 as templates. In comparison, the template-based “bottom-up” approaches have more versatility for dynamically tuning of the chiroptical signals26,27, in which, the change of nanoparticle spatial arrangements facilitated by reconfigurable templates can result in programmable CD response28,29,30. However, the optical asymmetry, g-factor, is usually far below the theoretical limit of ±219.

Recently, planar metasurface, composed of 2D rationally designed nanostructures as building blocks, has been explored to improve the chiroptical response by precisely controlling light-matter interactions31,32. Amongst the strategies of phase change materials, electrical biasing, thermal stimuli, and mechanical twisting are used to achieve tunability in planar structure for advanced optic applications33,34,35. For instance, chiral films with break mirror-symmetrical configuration have been obtained by twisted stacking of plasmonic nanostructures36,37,38. By tuning the twisting angle, layer number, and interlayer spacing, the chiroptical signals can be tuned. Even so, in most reported work, the CD signal is well below 20°, and the g-factor remains low, in the range of 10−3 –10−139. In comparison, chiroptical materials fabricated by pairing a linear dichroism (LD) and a linear birefringence (LB) active materials usually can generate much strong “apparent” CD and simplified the fabrication process12, in which, the unpolarized light is transferred to linear polarized state after passing through the LD plate, then turned into circularly polarized light through a phase retardance induced by LB active materials. Their high interaction strength and asymmetry relative to the light propagation direction offer exciting prospects for engineering transduction schemes between photonic spin states and matter-based chiral excitations40. However, the thickness and orientation for LD/LB plates are usually optimized for specific wavelength, lacking of dynamical tunability of CD properties.

Herein, a facile approach to construct chiral plasmonic nanostructures in the vis-NIR spectral region is established by assembling gold nanoparticle chains onto a pre-stretched elastomeric substrate (Fig. 1). These plasmonic nanomaterials show high chiroptical performance with a CD signal up to 40° and a record g-factor of 1.71 at 880 nm wavelength. The linearly assembled plasmonic chains and the stretched substrate play as complementary contributions with high LD and LB, respectively. Furthermore, the CD magnitude, handedness, and frequency are readily modulated by controlling the orientation of plasmonic chains and pre-stretching of polymer substrates. This tunable design principle is universally applicable to diverse elastomeric polymers which can be combined with plasmonic nanoparticle arrays, to provide high and tunable chiroptical responses.

Fig. 1: Chiroptical film with strong and tunable circular dichroism.
figure 1

General schematics of plasmonic chiroptical films composed of unidirectional periodic plasmonic nanoparticle chains on the stretched elastomeric substrate, generating strong chiroptical signal, high g-factor, and switchable handedness.

Full size image

Results

Chiral plasmonic films

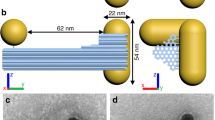
The chiroptical film is fabricated by assembling monodispersed AuNSs (an average diameter of 63 ± 2 nm, Supplementary Fig. 1a, b) as linearly periodic nanoparticle arrays onto a stretched elastomeric polydimethylsiloxane (PDMS) film via template-assisted assembly (Fig. 2a)41. PDMS slabs with unidirectional surface wrinkle are utilized as a template for plasmonic chain assembly42 (Supplementary Fig. 1c, d). Highly ordered, parallel linear chains of closely packed AuNSs are achieved on the other flat PDMS substrate within a pre-stretching state, uniformly covering the entire centimeter-size area (Fig. 2b, Supplementary Fig. 2). A strong and consistent iridescence across the whole region is observed, arising from the grating effect (Supplementary Fig. 3), further confirming the highly ordered plasmonic array over macroscopic region41. These large-scale and uniform plasmonic nanoparticle arrays are critical to ensure tunable and strong chiroptically active nanomaterials. Moreover, the closely packed plasmonic nanoparticles with gap of 1–2 nm along the linear chains facilitate strong plasmonic coupling, resulting in a collective plasmonic resonance shifted to the NIR region, centered at 880 nm (longitudinal plasmonic resonance, LSPR) (Supplementary Fig. 4)25,41. A relative weaker transversal plasmonic resonance mode (TSPR) is also observed at 530 nm.

Fig. 2: Chiroptical properties of the plasmonic flexible film.
figure 2

a Template-assisted assembly of AuNSs on a stretched PDMS (thickness: 2.5 mm). b SEM image of the linear assembly of AuNSs. c The CD spectra under varied strains of substrates ranged from 0.1 to 0.6. d Circularly polarized light dependent transmission spectra of the plasmonic film (substrate strain: 0.4). e The g-factor at the wavelength with the maximum CD intensity as a function of strains. f Strain-dependent intensity of CD mode 1 (CD1) and mode 2 (CD2). g Comparison of the CD intensity reported in current work with plasmonic-based chiral systems reported previously (The detailed references and values are presented in Supplementary Table 1). Source data are provided as a Source Data file.

Full size image

The pre-stretched PDMS film covered with uniformly oriented plasmonic nanoparticle chains exhibits strong chiroptical response (Fig. 2c). Two distinct CD modes are observed: one negative peak with an intensity of ≈−2° at 530 nm (CD1), and the other mode (CD2) located at NIR region (wavelength 880 ± 10 nm) with a high ellipticity, up to 40°. These two modes are associated with the TSPR and LSPR modes43. Correspondingly, the structure indicates circular-polarization dependent transmittance, in which, a significant extinction of left-circularly polarized light (LCP) at the wavelength of LSPR is observed, meanwhile, an extinction of right-circularly polarized light (RCP) at the wavelength of TSRP is presented (Fig. 2d).

The varied pre-stretching ratios of PDMS substrates, defined as strain (ε, the ratio of elongation to the original length of PDMS), modulate CD signals, showing an enhanced intensity by increasing the strain (Fig. 2c). The CD2 mode is significantly boosted by more than 5 times, to the maximum value of 39.8°, when the strain increases from 0.1 to 0.5. Accordingly, the g-factor reaches the maximum value of 1.71 at the strain of 0.4, which well exceeds reported values and is close to the theoretical limit of 239. A similar trend is observed for the CD1 mode, reaching the maximum intensity of −2.1° at ε = 0.4 (Fig. 2e, f). In comparison, there is no CD signal for the linear AuNSs chains assembled on non-stretched PDMS film (Supplementary Fig. 5). Additionally, the CD spectra collected from different samples with the same stain or different positions on one sample both demonstrate the high repeatability and uniformity (Supplementary Fig. 6). Such a strong CD signal and broad-range response frequency exceed most of the plasmonic-based ones by orders of magnitude, especially in the NIR regime (Fig. 2g)44.

Mechano-induced linear birefringence

To understand the origin of the enhanced chiroptical performance, the optical properties of the elastomeric substrate and the linearly assembled plasmonic chains are explored separately. For the bare elastomeric polymer substrate, linearly polarized light-dependent transmission spectra are collected by placing it between a set of orthogonal linear polarizer and analyzer with the stretching orientation of 45° in relative to the polarizer (Fig. 3a).

Fig. 3: Stretching induced linear birefringence of the elastic polymer substrate and the modulated CD spectra.
figure 3

a Experimental setup for measuring the transmission spectra of the stretching-state polymer film without AuNSs by placing it between a pair of orthogonal linear polarizers and analyzer. b The transmission spectra of linearly polarized light propagating through stretched films with different strain ratios. The stretching direction was set to 45° in relative to both the polarizer and analyzer. c Corresponding polarized optical microscope images of the stretched film, showing interference colors at varied strains. d–f Phase retardance of the stretched films with different strains (d), phase retardance at 880 nm (e), and birefringence (f), respectively. g–h Thickness modulated phase retardance (g) of the stretched films (with fixed strain of 0.2), and corresponding phase retardance at 880 nm (h). i Tunable CD spectra as a function of film thickness in the presence of plasmonic nanoparticle chains (with fixed substrate strain of 0.2, and chain assembly angle of 45°). Source data are provided as a Source Data file.

Full size image

Under this set of orthogonal linear polarizers, no transmission signal and optical images are detected at the non-stretched state (Fig. 3b, c). In contrast, distinct transmission spectra are obtained as the strain (ε) increased from 0.1 to 0.6 (Fig. 3b). The stretching is accompanied by a vivid interference color change from violet to yellow, red, and blue, as observed under polarized optical microscope (Fig. 3c, Supplementary Fig. 7). This appearance suggests that the stretched PDMS film exhibits LB (Δn), ascribing to the linear alignment of the polymer chains induced by stretching45. Furthermore, the maximum transmitted peak redshifts from the UV to visible regions, and the sequence of interference color changes aligned with the Michel-Levy color chart, indicating a progressive increase in birefringence level46. No light is transmitted to the orthogonal linear polarizers at ε = 0, indicating no birefringence, which is ascribed to the isotropic amorphous organization in the non-stretched PDMS film.

As known, when placing a birefringent material that has an optical axis between a pair of orthogonal linear polarizer and analyzer, the transmitted intensity of linearly polarized light (I⊥) depends on the angle (θ) between the optical axis and polarizers according to the equation: \({I}_{\perp }=\sin (2\theta ){\sin }^{2}(\frac{{{\rm{\pi }}}d\Delta n}{\lambda })\), where d stands for film thickness, λ for wavelength, and Δn for birefringence47,48. Birefringence can be induced by stretching due to the preferred orientation of macromolecular segments. Thus, the linearly polarized light can be transmitted only as the PDMS film is under stretching state. Moreover, according to the equation, for a stretching-state PDMS substrate with a fixed strain, the transmittance reached maximum intensity as the stretching direction is set to 45° in relative to both the polarizer and analyzer (Supplementary Fig. 8). The phenomenon is in good agreement with the theoretical analysis mentioned above48.

Next, the birefringent properties are quantitatively analyzed using spectroscopic ellipsometry in terms of the phase retardation (δ) and birefringence (Δn, defined as the difference between the extraordinary refractive index (ne) and the ordinary refractive index (no))48. As observed, the phase retardance increases gradually in the range of 0–180° across visible to NIR region in response to the applied strain (Fig. 3d). Taking the value at the wavelength of 880 nm (CD2 mode), a linear increment in phase retardation from ≈13° to ≈102° is detected as increasing the strain from 0.1 to 0.6 (Fig. 3e). Correspondingly, the calculated birefringence, Δn = δ*λ/(2πd) (where δ is the phase retardation, λ is the wavelength, and d is the thickness of the sample)48, is in the order of 10−5–10−4 (Fig. 3f), which is comparable to previously reported work for this polymer49. And the birefringence is positively correlated with the strain. It is worth mentioning that the phase retardance is consistent over the whole stretched PDMS film (Supplementary Fig. 9a, b), and is fully reversible even after multiple stretching/releasing cycles (Supplementary Fig. 9c).

As discussed above, the maximum CD signal at 880 nm is achieved by stretching the PDMS substrate to a strain of 0.5 (Fig. 2f). Under this strain, the phase retardance of the PDMS approaches 90° (Fig. 3e). Further increasing the strain causes the phase retardance to deviate from 90°, leading to a reduction of CD signal. This is ascribed to that the intensity of CD generated based on the LD/LB configuration is determined by the values of LB, LD, and the tilting angle (\(\alpha\)) between them, as \({{\rm{CD}}}\propto {{\rm{LB}}}\cdot {{\rm{LD}}}\cdot \cos (2\alpha -90^\circ )\), according to the Müller calculus12. For α fixed at 45°, CD signal reaches the maximum value by retarding a linearly polarized light with a phase shift of 90°.

Similarly, the phase retardance increases linearly from 14° to 70° for the PDMS thickness increasing from 1 mm to 5 mm (with a fixed strain ratio of 0.2) (Fig. 3g, h), a common trend for linear birefringent film50. Correspondingly, the intensity of CD signal increased significantly for a thicker PDMS substrate, by about five times, which can be attributed to the retardance approaching 90° (Fig. 3i). Thus, the controllable LB of polymeric substrate enables tunable phase retardance, facilitating the conversion of linearly polarized light into circularly polarized light in a programmable way by changing the film thickness and applied strain.

Linear dichroism of the plasmonic nanoparticle chains

Next, the optical response of plasmonic nanoparticle arrays on an unstretched PDMS film is explored (Fig. 4). The transmission spectra demonstrate distinct features under parallel (P) and perpendicular (S) light polarization with respect to the orientation of plasmonic nanoparticle chains (Fig. 4a). Notably, in the NIR region, a dominated extinction dip at ≈920 nm is observed only in the P- state, while two subtle peaks around 600 nm and 530 nm are presented in both P- and S- states (Fig. 4b). This characteristic optical anisotropy suggests that the uniform parallel aligned AuNSs chains endows a LD, exhibiting a very high dichroic ratio (DR) up to 0.73 at 920 nm and a relative lower DR of −0.08 at 530 nm. This difference is contributed by the polarization-dependent extinction of the longitudinal and transversal plasmonic modes.

Fig. 4: Linear dichroism of the linearly assembled plasmonic nanoparticles and tunable chiroptical properties as a function of plasmonic chain orientation.
figure 4

Scheme of experimental set-up (a) and the corresponding transmission spectra (b) when the incident light is parallel (P) and vertical (S) to the orientation of nanoparticle chains. In (a, b), the plasmonic chains are assembled on a non-stretched substrate. c CD spectra of the chiral plasmonic films as a function of varied assembly angles in respect to the substrate stretching direction (with a fixed strain of 0.2). Experimental (d) and calculated (e) CD Intensity as a function of assembly angles. f–g Simulation of chiroptical response: calculated transmission spectra (f) and electric field enhancement (g) of plasmonic chains under P- and S-polarized light. The color scale is linear. h The simulated CD spectra as a function of the plasmonic chain orientation in relative to the linear phase retarder (with fixed phase retardance of 10.8° at 800 nm). Source data are provided as a Source Data file.

Full size image

Thus, combining the birefringence of the aforementioned PDMS film, the generation of chiroptical signal in current configuration follows the principle of applying a different phase shift to S- and P- polarized light through a phase-retardant waveplate. Here, the linearly assembled AuNSs array produces linearly polarized light at the plasmonic resonance frequency, and the stretched polymer substrate facilitates a LB to contribute phase retardance.

The chiroptical response can be further tuned continuously by varying the assembly tilting angle (α) of the plasmonic chains with respect to the film stretching direction (defined the clockwise rotated angle as positive, vice versa). The highest ellipticity of the circular polarized light is obtained as the 45° angle between linear polarizer and phase-retardant waveplate. Deviating from 45° to either lower (30°, 15°) or high values (60°, 75°), results in significant decrease of all CD modes (Fig. 4c, d). Finally, CD signal completely vanishes as the angle reaches 0 and 90°.

To further understand the CD intensity, theoretical analysis is carried out. It is assumed that the left- and right-circularly polarized light propagate through the ideal LB and LD materials in sequence. In which, the LB material is virtually a quarter-wave plate, so the circularly polarized light is completely converted to linearly polarized light without loss of light intensity. Meanwhile, the ideal LD material possesses the LD ratio of 1. According to Malus’ law51, the transmitted intensity exhibits a clear cos2 dependence on the tilting angle. So,

$${{{\rm{CD}}}}_{{{\rm{cal}}}}= \left(\frac{{\mathrm{ln}}10}{4}\right)\left(\frac{180^\circ }{{{\rm{\pi }}}}\right)\left({A}_{{{\rm{L}}}}-{A}_{{{\rm{R}}}}\right)=32.98^\circ \left(-\log \frac{{I}_{{{\rm{L}}}}}{{I}_{0}}+\log \frac{{I}_{{{\rm{R}}}}}{{I}_{0}}\right) \\ = 32.98^\circ \left[\log {\cos }^{2}\left(\alpha -45^\circ \right)-\log {\cos }^{2}\left(\alpha+45^\circ \right)\right]$$
(1)

where AL and AR are absorbance of left- and right-circularly polarized light, respectively. The IL and IR stand for the transmitted intensity of left- and right-circularly polarized light, respectively, and α is the tilted angle between the LD and LB materials (see “Methods”).

The stretched PDSM substrate works as LB component to provide phase retardance, which is depended on the stretching ratio and the thickness (Fig. 2d, g). Thus, a phase retardance of 90° at the wavelength of longitudinal plasmonic resonance is achievable. Meanwhile, the linear assembly of plasmonic nanoparticles plays the role of LD component. Ascribing to the strong light-matter interaction of the plasmonic nanoparticle and plasmonic coupling25, it exhibits a high DR up to 0.73 at the wavelength of the longitude plasmonic resonance. Moreover, the tilted angle can be controlled to ±45°. Thus, according to the above mathematic analysis, this configuration could facilitate strong CD signals and a high g-factor. Moreover, the calculated CD intensity as a function of the tilted angle (α) based on the mathematical expression is consistent with the experimental results (Fig. 4d, e).

Next, to confirm the origin of the LD and tunability of strong chiroptical activities, FDTD simulations are carried out for the assembled plasmonic chains (Fig. 4f–h) (see “Methods”)52,53,54. The simulations with periodic boundary conditions recreate an infinite array with perfect linearly dimer AuNSs chains. Differential transmission is observed depending on the light polarization with a pronounced longitudinal peak around 800 nm observed under P-polarization (Fig. 4f). Correspondingly, the calculated electric field enhancement at this wavelength concentrates in the gaps along the long axis of plasmonic chains (Fig. 4g, P-polarized light), confirming its origin of longitudinal mode. Meanwhile, a weaker peak centered at 520 nm appears under S-polarized light, which can be assigned to the transversal plasmonic mode. The respective electrical field is mainly enforced between the chains along transversal direction of the assembly (Fig. 4g, S-polarized light). And the peak centered at 610 nm is attributed to the coupling between the dimers as supported by simulations (Supplementary Fig. 10)41. Indeed, simulations for singlet and triplet chains also show the differential transmission depended on the light polarization (Supplementary Fig. 12). Overall, LSPR peak shows red-shift from 741 to 812 nm as increasing the chain width from singlet to triplet assembly.

Furthermore, an anisotropic (n, k) plate is added before the plasmonic nanoparticle chains, working as a phase retarder to investigate the chiroptical properties (Supplementary Fig. 11a). As the light propagating through the phase retarder, its ellipticity is controlled by the phase retardance, with linear-polarization occurring at a retardance of 90° (the quarter-wave plate condition). Then, the polarized light is selectively absorbed depending on its vibration direction in relative to the orientation of plasmonic nanoparticle chains.

The orientation angle of the optical axes of the phase retarder is critical in light propagation. The simulations show that the strongest CD signal is achieved under chain orientation of ±45°, and the CD spectra are mirror-symmetrical for clockwise and anticlockwise orientations (Fig. 4h). On the other hand, the intensity of CD signal at 780 nm is significantly enhanced with increased retardance, reaching the highest magnitude at the retardance of 90° (Supplementary Fig. 11b). Overall, the simulated modeling confirms that the interaction of the LD of plasmonic chains and the LB of the stretched polymer substrate results in potentially tunable chiroptical activity.

Reversible dynamical modulation of the chiroptical response

Furthermore, the optical configuration explored here facilitates the feasibility of dynamic tuning of the chiroptical signal through a re-stacking approach (Fig. 5). Indeed, the linear polarizing block of oriented plasmonic chains and the phase-retardant block of pre-stretched birefringent substrates can be prepared separately, then stacking together to generate CD property. Here, no minimum distance is required, which is different from the chiral configuration-based CD response39.

Fig. 5: Dynamic tuning of chiroptical properties.
figure 5

a Schematic illustration of how the plasmonic structure obtains circularly polarized light. The linearly assembled AuNSs chains (assembled on an unstretched elastic PDMS substrate) function as linear polarizer, and the stretched PDMS films without AuNSs working as a phase retarder, and the assembly angle of the plasmonic chains with respect to the stretching direction of film determines the chirality: clockwise resulted in right-circularly polarized light, RCP, vice versa. b CD intensity at 880 nm after ten cyclic treatments of reversible stretching/releasing (strain: 0–20%). c In-situ dynamic modulation CD spectra by varying the tilted angles (α) with respect to the substrate stretching direction (ε = 0.2). d In-situ dynamic modulation of CD spectra as a function of the substrate stretching ratio (ε = 0–0.4) with a fixed assembly angle of 45°. e Normalized CD spectra by changing the plasmonic chain length. f Normalized CD spectra as changing chain width from singlet to triplet AuNSs chains. g Modulation of CD spectra as a function of AuNSs size. Source data are provided as a Source Data file.

Full size image

The cross-overlay of these two blocks permits dynamic modulation of the CD properties including magnitude, handedness, and frequency via changing the tilting angle and the substrate strain ratio (Fig. 5a). For instance, fully reversible “on-off” switching of CD signal is obtained by stretching/releasing treatment, which is preserved even after multiple cyclic treatments (Fig. 5b). Re-stacking the two blocks at angle of ±α yields mirror-symmetrical CD spectra with handedness inversion (Fig. 5c). And a dynamically continuous enhancement in CD intensity is achieved by in-situ increasing the strain of the elastomeric layer from 0.1 to 0.4, with the tilting angle of plasmonic chains fixed at 45° (Fig. 5d).

Moreover, the frequency of CD response exhibits dynamical tunability along with the “break-down” of plasmonic chains via post-stretching (see “Methods”, and Supplementary Fig. 14a). The longitude plasmonic resonance blue-shifts as the chain length reduced (Supplementary Figs. 14b and 15). Correspondingly, the wavelength of CD2 mode shifts gradually to from 880 nm to 726 nm (Fig. 5e, Supplementary Fig. 14c).

Meanwhile, the CD frequency can be further controlled by the nanoparticle chain width and size. Indeed, triplet chains induce a high red-shifting of CD2 mode by 170 nm compared to the usually explored singlet-dimer mixed chains (Fig. 5f, Supplementary Fig. 16). The chain width affects the wavelength of the chiroptical signal, is well agreed with the simulation results (Supplementary Fig. 12d). While the smaller particle results in a blue-shifted wavelength of CD2 mode, as well as a decreased CD intensity (Fig. 5g, Supplementary Fig. 17).

Overall, fine-tuning over all the CD characteristics, including handedness, magnitude and wavelength can efficiently facilitate in current configuration. Such high freedom of dynamic modulation, while maintaining strong CD intensity and high g-factor are rarely reported39. Even so, the CD intensity in our system is lower than that of commercial polarizers. While this plasmonic film designed here endows the chiral response in a broad wavelength range from visible to NIR region, and is capable of dynamic tunability and predictable programmability in comparison with the commercialized circular polarizer (Supplementary Fig. 18) and gold stripe-based chiroptical materials55,56.

Universal strategy for constructing chiroptical structures

To verify the universality of current twisted birefringent-retardance stacking design of chiral materials, diverse substrates from commercially available polymer films, including polyethylene (PE), polyethylene terephthalate (PET), and polyvinyl chloride (PVC), have been explored as the phase retardance substrates (Fig. 6). As expected, these partially crystalline polymer films have preferential orientation of polymer chains and crystalline lamellae induced during the manufacture processing, which can generate birefringence and phase retardance (Supplementary Fig. 19).

Fig. 6: The extension of designing principle to chiroptical structures by assembling plasmonic chains on diverse birefringent polymer films.
figure 6

a Phase retardance of the commercially available polyethylene (PE) sheet with oriented polymer chains. Each regime marked with horizontal dashed lines presents the increment of phase retardant of 180°. b CD spectra of the PE sheets with linearly assembled AuNSs (k is an integer). c CD handedness switch based on phase over one π (180°) at the wavelength of 716 nm and 575 nm in (b). Phase retardance of the PET (d) and PVC (f) films. CD spectra of plasmonic structures on the PET (e) and PVC (g) films. Source data are provided as a Source Data file.

Full size image

When the plasmonic chains are assembled onto these polymer substrates, pronounced CD modes are observed in the vicinity of the plasmonic resonances (Fig. 6b, e, g). And, multiple peak-valley features are obtained, indicating alternating handedness of the CD signal. As the linearly polarized light propagates through a phase retardance plate, a positive/negative phase switch is generated over every π (180°), which causes multiple inversions of the chiroptical signal57. Therefore, the commercial birefringent polymer films have much higher phase retardance than that of stretched PDMS films over the wavelength 400–1600 nm (Fig. 6a, d, f), the phase changes over multiple π values, yielding the multiple reversed CD peaks.

For instance, the PE film generates a phase retardance (δ) of 842°–215° at the wavelength range from 400 to 1600 nm (Fig. 6a). Two CD modes appear, in which, one positive peak at λ1 = 716 nm related to δ1 = 470° of PE film (red point in Fig. 6a, b), and negative peak located at λ2 = 575 nm corresponds to δ2 = 580° (blue point in Fig. 6a, b). There is a phase retardance difference over one π (180°) between the two wavelengths, specifically, changed from 470° (2 × 180° + 110°, in turn, 2π + n) at λ1 to 580° (3 × 180° + 40°, in turn, 3π + n) at λ2. Correspondingly, the CD signal switches from negative (−0.75°) to positive (1.14°) as the phase changes over one π period (Fig. 6b, c). Therefore, this design strategy suggested here is universally applicable for generating strong CD signals and tailoring the handedness for a wide variety of polymer substrates.

It is worth noting that the phase retardance of PE-plasmonic film reaches (k + 1/2)π (k is an integer) at the wavelength of 1260 nm and 748 nm (with a phase retardance of 270° and 450°, respectively). However, the wavelengths largely deviate from the longitudinal plasmonic resonance peak of AuNSs chains (at the wavelength of 920 nm), which has the largest LD. According to the Müller calculus12, \({{\rm{CD}}}\propto {{\rm{LB}}}\cdot {{\rm{LD}}}\cdot \cos (2\alpha -90^\circ )\), as mentioned above, the CD intensity is not only determined by the phase retardance of LB, but also the LD value. Thus, the CD intensity of PE-plasmonic film obtains the maximum value at the wavelength of 716 nm and 585 nm due to the interplay of LD and LB. Moreover, the CD intensity of commercial polymer-based plasmonic films is much lower than that of PDMS-based ones. This is ascribed to two reasons: first, the phase retardance at the wavelength of CD modes deviates from (k + 1/2)π (e.g., 90°, 270°, where k is an integer)58. Second, the AuNSs assembly on commercial films is less uniform as compared to that on the smooth PDMS surface (Supplementary Fig. 19) due to the excessive surface roughness (Supplementary Fig. 20), which results in weaker LD contribution and thus a reduced CD signal.

Discussion

In conclusion, plasmonic nanoparticle-based flexible chiroptical films are constructed by assembling arrays of oriented plasmonic nanoparticle chains onto a pre-stretched elastomeric substrate. This plasmonic nanomaterial configuration exhibits an exceptional strong CD signal up to 40° and an asymmetry with a g-factor of 1.71 within the visible to NIR region of 880 nm. In contrast to the current reports, the chiroptical properties of these materials originate from interplay of the LD of oriented plasmonic nanoparticle chains and the LB provided by the stretched elastomeric substrate, acting as phase retarder. Such a tunable configuration offers facile modulation over all the CD characteristics, including amplitude, handedness, and wavelength, by tuning the orientation angle of AuNSs chains, the length and width of the nanoparticle chains, and the strain and thickness of the polymer substrate.

These findings exhibit circular polarization magnitude tunability in plasmonic chiral nanostructures and establish a design strategy of flexible and tunable chiroptical materials. The approach can be universally applicable to fabricate stackable flexible structures composed of ordered plasmonic nanostructures and diverse birefringent commercial polymer substrates frequently utilized in optical devices. Universality of this design broadens the potential scope of prospective photonic applications in diverse fields, including optical devices, biosensors, optical communication, and chiral synthesis.

Methods

Materials

Hydrogen tetrachloroaurate (HAuCl4, >99.9%), ascorbic acid (AA, C6H8O6, >99%), hexadecyltrimethylammonium bromide (CtaB, >99%), cetyltrimethylammonium (CtaC, 25 wt% in water), sodium borohydride (NaBH4, 99.99%) were purchased from Sigma-Aldrich. Poly(ethyleneglycol) methyletherthiol (CH3O-(CH2CH2O)n-CH2CH2-SH, >95%, average Mn 5000 g mol−1, mPEG-5k-SH) was obtained from MeloPEG. Sylgard 184 PDMS elastomer was purchased from Dow Corning. All the above chemicals and solvents were used without further treatment. Purified water was obtained by Milli-Q-grade, 15.0 Ω cm−1 at 25 °C. The polyethylene film (PE, thickness: 0.1 mm) was from Dow Chemical. And the polyvinyl chloride film (PVC, thickness: 0.1 mm), the polyethylene terephthalate film (PET, thickness: 0.1 mm) were bought from Dongguan Jubang Plastic Materials Co., Ltd, China.

Gold nanospheres (AuNSs) synthesis

The AuNSs were synthesized in the known seed-mediated two-step growth process59, and the ligand was exchanged to mPEG-5k-SH. Typically, HAuCl4 (0.25 mM) and CtaB (100 mM) were mixed under continuous stirring. A fresh NaBH4 solution (10 mM, 0.6 mL) was rapidly added into the mixture at 750 rpm for 30 s, then the stirring was kept at 250 rpm for 25 min to obtain 2–3 nm Wulff seed. Aqueous solutions of CtaC (200 mM, 20 mL), AA (100 mM, 1.5 mL), and Wulff seed (0.5 mL) was mixed in a 250-mL glass bottle. An aqueous HAuCl4 solution (0.5 mM) was quickly poured into the mixture and stirred at 600 rpm for 15 min to carry out the first growth step for obtain AuNSs with a diameter around 10 nm. The AuNSs were concentrated by centrifugation at 15,000 × g for 1 h and then washed with Milli-Q water to reduce the residual reducing agent for three times.

Next, the AuNSs (average diameter of 10 ± 1 nm) obtained from the first growth step were dispersed in 1 mL aqueous CtaC solution (10 mM) and used as a seed for the second growth step. In detail, a solution consisting of CtaC (50 mM, 10 mL), AA (1 M, 39 μL), and the 10 ± 1 nm AuNSs (0.57 mg mL−1, 15 μL) was prepared under stirring of 350 rpm at 45 °C. Then, a 20-mL aqueous solution including HAuCl4 (1.5 mM) and CtaC (55 mM) was mixed and added dropwise into to the solution with the AuNSs utilizing a pump system at 0.5 mL min−1 to prepare AuNSs with the targeted diameter around 63 nm. The finally synthesized AuNSs were collected by centrifuging at 350 × g for 20 min and washed with CtaC solution (1.5 mM) for three times.

For ligand exchange, 0.75 mL suspension of the AuNSs with a diameter of 63 ± 2 nm (Supplementary Fig. 1b) was added into aqueous solution of mPEG-5k-SH (2 mg mL−1, 0.75 mL), and the mixture was treated by ultrasound for 10 min. Then the ligand exchange was taken overnight under vigorous stirring. The final AuNS colloidal solution was washed with CtaC solution (0.3 mM) for three times and concentrated up to 25 mM for following assembly.

PDMS wrinkled template preparation

A mixture (25 g) of Sylgard-184 A and Sylgard-184 B (mass ratio = 10:1, Dow Corning) precursors was added into a container (100 mL) and was thoroughly stirring with a planetary centrifugal mixer (AR-100, Thinky Corporation, Japan) for two steps, mixing mode (800/2200 rpm) and de-foaming mode (2200 rpm, 2 min)41. Then the mixture was poured into a Petri dish (10 × 10 cm2) and vacuumed for 30 min to remove the air. The PDMS was placed on a leveled stage overnight at room temperature and cured at 80 °C for 5 h. The obtained PDMS film was cut into strips (45 × 10 × 2.5 mm3).

Template-assisted capillary assembly

The assembly of AuNSs was obtained by template-assisted capillary assembly. A flat PDMS film (with certain stain) was used as the substrate. And a unidirectional wrinkled PDMS with a wavelength of 324 ± 27 nm and an amplitude of 75 ± 2 nm was utilized as the assembly template. In detail, the wrinkled PDMS was fabricated by oxygen plasma treatment (0.3 mbar, 3 min, 21 W, and 40% strain ratio) on a pre-stretched PDMS slab, followed by releasing the strain, surface wrinkles generated41. Then the wrinkled PDMS slab was cut into 10 × 10 × 2.5 mm3, to be used as templates. For the flat PDMS substrate, an oxygen plasma treatment (0.3 mbar, 5 min, 21 W) was carried right before the assembly to facilitate hydrophilicity. Then, a droplet of AuNSs@mPEG-5k-SH suspension (3 μL) was placed onto the flat PDMS substrate, followed by covering the wrinkled PDMS template onto the AuNSs suspension. An oriented AuNSs array was obtained by peeling off the PDMS template after dried overnight at room temperature. During the assembly and chiroptical properties measurements, the PDMS substrates remained in a stretching state with varied strains for providing phase retardance, unless mentioned otherwise.

To obtain AuNSs chains with increased chain-width, PDMS templates with higher amplitude and wavelength were fabricated. The PDMS template with 589 ± 17 nm wavelength and 128 ± 6 nm amplitude was prepared by oxygen plasma treatment (0.3 mbar, 3 min, 120 W, and 40% pre-strain ratio).

Stretching-induced fragmentation of the assembled AuNSs chains

If the AuNSs chains were assembled on a PDMS substrate which was pre-treated by plasma (even slightly treatment for hydrophilicity), wrinkles could be formed as applying a post-assembly stretching. This would cause the twisting of the nanoparticle chains. To avoid this behavior, the assembled AuNSs chains were transferred onto a non-plasma-treated PDMS film with the help of polyethylenimine (PEI) as an adhesion layer. In detail, the PDMS substrate was incubated with a PEI solution (10 mg/mL) for 3 h, then washed with DI water, and dried under nitrogen gas, obtaining the PEI-PDMS substrate. Then, the linearly assembled AuNSs array was pressed onto the PEI-PDMS substrate, leaving the AuNSs chains on the PEI-PDMS. For the obtained AuNS chains with different lengths, a post-stretching treatment with varied strains was applied to this sample. The morphology of the plasmonic chains was in situ characterized by AFM under different strains.

For exploring the effect of chain length on CD properties, another stretching-state PDMS film without AuNSs chains was prepared for CD measurements. The specific light path of CD measurements was set as shown in Supplementary Fig. 14a.

Scanning electron microscopy (SEM)

SEM images were taken with a JSM-7800F scanning electron microscope at 5 kV with 8 mm working distance. The samples were all sputter with Au layer with a thickness around 6 nm by using a gold spraying instrument (JEC-3000FC, JEOL) before capturing the images.

Atomic force microscopy (AFM)

Atomic force microscopy height images were measured using a Dimension Fastscan (Bruker) operated in tapping mode in air with stiff cantilevers (40 N m−1, 300 kHz, RTESPA-300, Nanoworld). The NanoScope Analysis software was used for data analysis.

Spectroscopic ellipsometry

The chiroptical properties were analyzed with spectroscopic ellipsometry in transmission mode using J. A. Woollam RC2. The polarization response of an optical device or system can be described by a Müller matrix M, which acts with input polarization states \(\vec{{{{\bf{S}}}}_{{{\bf{in}}}}}=\left({S}_{0},{S}_{1},{S}_{2},{S}_{3}\right)\), and results in the output polarization states \(\vec{{{{\bf{S}}}}_{{{\bf{out}}}}}=\left({S}_{0}^{{\prime} },{S}_{1}^{{\prime} },{S}_{2}^{{\prime} },{S}_{3}^{{\prime} }\right)\). And it can be written in the form of Stokes parameters60:

$${\left[\begin{array}{c}{S}_{0}^{{\prime} }\\ {S}_{1}^{{\prime} }\\ {S}_{2}^{{\prime} }\\ {S}_{3}^{{\prime} }\end{array}\right]}_{{{\rm{out}}}}=\left[\begin{array}{cccc}{M}_{11} & {M}_{12} & {M}_{13} & {M}_{14}\\ {M}_{21} & {M}_{22} & {M}_{23} & {M}_{24}\\ {M}_{31} & {M}_{32} & {M}_{33} & {M}_{34}\\ {M}_{41} & {M}_{42} & {M}_{43} & {M}_{44}\end{array}\right]{\left[\begin{array}{c}{S}_{0}\\ {S}_{1}\\ {S}_{2}\\ {S}_{3}\end{array}\right]}_{{{\rm{in}}}}$$
(2)

The Stokes parameter describes light transmission for different polarizations as:

$${{\bf{S}}}=\left[\begin{array}{c}{S}_{0}\\ {S}_{1}\\ {S}_{2}\\ {S}_{3}\end{array}\right]=\left[\begin{array}{c}{I}_{x}+{I}_{y}\\ {I}_{x}-{I}_{y}\\ {I}_{{+45}^{{{\rm{o}}}}-}{I}_{{-45}^{{{\rm{o}}}}}\\ {I}_{{{\rm{R}}}}-{I}_{{{\rm{L}}}}\end{array}\right]$$
(3)

where \({I}_{x}\), \({I}_{y}\), \({I}_{{+45}^{{{\rm{o}}}}}\) and \({I}_{{-45}^{{{\rm{o}}}}}\) are the intensities of linearly polarized light oriented along the x, y, +45°, and −45° directions, respectively; and IR and IL are the intensities of right and left circular polarizations, respectively.

Normalized Stokes vectors \(\hat{{{\bf{S}}}}\) and Muller matrix \(\hat{{{\bf{M}}}}\) were obtained by dividing \({S}_{0},{S}_{1},{S}_{2}\) and \({S}_{3}\) by \({S}_{0}\) and \({M}_{{xy}}\) by \({M}_{11}\)

$$\hat{{{\bf{S}}}}=\frac{1}{{S}_{0}}*\left[\begin{array}{c}{S}_{0}\\ {S}_{1}\\ {S}_{2}\\ {S}_{3}\end{array}\right]=\left[\begin{array}{c}1\\ {\hat{S}}_{1}\\ {\hat{S}}_{2}\\ {\hat{S}}_{3}\end{array}\right]$$
(4)
$$\hat{{{\bf{M}}}}=\frac{1}{{M}_{11}}*\left[\begin{array}{cccc}{M}_{11} & {M}_{12} & {M}_{13} & {M}_{14}\\ {M}_{21} & {M}_{22} & {M}_{23} & {M}_{24}\\ {M}_{31} & {M}_{32} & {M}_{33} & {M}_{34}\\ {M}_{41} & {M}_{42} & {M}_{43} & {M}_{44}\end{array}\right]=\left[\begin{array}{cccc}1 & {m}_{12} & {m}_{13} & {m}_{14}\\ {m}_{21} & {m}_{22} & {m}_{23} & {m}_{24}\\ {m}_{31} & {m}_{32} & {m}_{33} & {m}_{34}\\ {m}_{41} & {m}_{42} & {m}_{43} & {m}_{44}\end{array}\right]$$
(5)

Because we normalize to the total intensity, the remaining Stokes parameters are restricted between ±1. According to Eq. (3), LCP/RCP/unpolarized excitation corresponds to \(\left[\begin{array}{c}1\\ 0\\ 0\\ -1\end{array}\right]/\left[\begin{array}{c}1\\ 0\\ 0\\ 1\end{array}\right]/\left[\begin{array}{c}1\\ 0\\ 0\\ 0\end{array}\right]\).

As \({S}_{0}^{{\prime} }\) refer to the output intensity,

$${S}_{0}^{{\prime} }=\left[\begin{array}{cccc}{M}_{11} & {M}_{12} & {M}_{13} & {M}_{41}\end{array}\right]\left[\begin{array}{c}{S}_{0}\\ {S}_{1}\\ {S}_{2}\\ {S}_{3}\end{array}\right]={M}_{11}{S}_{0}\left[\begin{array}{cccc}1 & {m}_{12} & {m}_{13} & {m}_{41}\end{array}\right]\left[\begin{array}{c}1\\ {\hat{S}}_{1}\\ {\hat{S}}_{2}\\ {\hat{S}}_{3}\end{array}\right]$$
(6)

the transmission (\({S}_{0}^{{\prime} }/{S}_{0}\)) at unpolarized input light \(\left(\left[\begin{array}{c}1\\ 0\\ 0\\ 0\end{array}\right]\right)\) can be written as:

$${{\rm{trans}}}={M}_{11}$$
(7)

And the CD can be described as the extinction difference between LCP and RCP \(\Delta {{{\rm{Ext}}}}_{{{\rm{LCP}}}/{{\rm{RCP}}}}=-\log \left(\frac{{M}_{11}-{M}_{14}}{{M}_{11}+{M}_{14}}\right)\) or as CD in degrees:

$${{\rm{CD}}}=\left(\frac{{\mathrm{ln}}10}{4}\right)\left(\frac{180^\circ }{{{\rm{\pi }}}}\right)\Delta {{{\rm{Ext}}}}_{{{\rm{LCP}}}/{{\rm{RCP}}}}$$
(8)

Moreover, the dissymmetry factor can be calculated by Eq. (7) and Eq. (8),

$$g=2\frac{{A}_{{{\rm{L}}}}-{A}_{{{\rm{R}}}}}{{A}_{{{\rm{L}}}}+{A}_{{{\rm{R}}}}}= -2\frac{\log ({M}_{11}-{M}_{14})-\log ({M}_{11}+{M}_{14})}{\log ({M}_{11}-{M}_{14})+\log ({M}_{11}+{M}_{14})} \\= -2\frac{\log \left(\frac{{M}_{11}-{M}_{14}}{{M}_{11}+{M}_{14}}\right)}{\log \left({M}_{11}-{M}_{14}\right)\left({M}_{11}+{M}_{14}\right)}$$
(9)

The linear DR was calculated as follows:

$${{\rm{DR}}}=\frac{{E}_{{{\rm{p}}}}-{E}_{{{\rm{s}}}}}{{E}_{{{\rm{p}}}}+{E}_{{{\rm{s}}}}}$$
(10)

where Ep and Es represent the extinction measured for linear polarization of the incident light parallelly and perpendicularly to the AuNSs chain, respectively.

Theoretical calculation of circular polarization

For simplification, it was assumed that the LB material was considered as an ideal quarter-wave plate, and there was no intensity lost as light passed through. And the LD ratio of LD material was assumed to be 1. The left-handed circularly polarized light was converted to linearly polarized light at the intensity of I0, which vibrated in a direction of 45o with respect to the fast axis of stretched substrate. Meanwhile, the right circularly polarized light was converted to linearly polarized light, which vibrated in the direction of −45°. Next, when the linearly polarized light entered the LD materials, the component vibrating parallel to the axis of LD material was absorbed, while the perpendicular one was passed, and collected by the detector. According to Malus’ law, the transmitted intensity exhibited a clear cos2 dependence on the polarizer angle, which was typical for dipolar plasmonic modes51.

$${I}_{{{\rm{L}}}}={I}_{0}{\cos }^{2}(\alpha+45^\circ )$$
(11)
$${I}_{{{\rm{R}}}}={I}_{0}{\cos }^{2}(\alpha -45^\circ )$$
(12)

Where IL and IR stood for the transmitted intensity of left- and right-circularly polarized light, respectively, when light passed the sample.

CD can be calculated according to Eq. (13):

$${{{\rm{CD}}}}_{{{\rm{cal}}}}=\left(\frac{{\mathrm{ln}}10}{4}\right)\left(\frac{180^\circ }{{{\rm{\pi }}}}\right)\left({A}_{{{\rm{L}}}}-{A}_{{{\rm{R}}}}\right)=32.98^\circ \left({A}_{{{\rm{L}}}}-{A}_{{{\rm{R}}}}\right)$$
(13)

Where AL and AR were absorbance of left and right circular polarized light, respectively61. As A = −log(I/I0), where I0 was the incident light intensity, Eq. (13) could be expressed as Eq. (14).

$${{{\rm{CD}}}}_{{{\rm{cal}}}}=32.98^\circ \left(-\log \frac{{I}_{{{\rm{L}}}}}{{I}_{0}}+\log \frac{{I}_{{{\rm{R}}}}}{{I}_{0}}\right)=32.98^\circ \\ \left[\log {\cos }^{2}\left(\alpha -45^\circ \right)-\log {\cos }^{2}\left({{\rm{\alpha }}}+45^\circ \right)\right]$$
(14)

The chiroptical activity could be quantified by g-factor:

$$g=2\frac{{A}_{L}-{A}_{R}}{{A}_{L}+{A}_{R}}$$
(15)

Furthermore, the g-factor could be expressed as:

$$g=2\frac{{A}_{L}-{A}_{R}}{{A}_{L}+{A}_{R}}=-2\frac{{lg}{\cos }^{2}\left(\alpha -45^\circ \right)-{lg}{\cos }^{2}\left(\alpha+45^\circ \right)}{{lg}{\cos }^{2}\left(\alpha -45^\circ \right)+{lg}{\cos }^{2}\left(\alpha+45^\circ \right)}$$
(16)

According to Eq. (16), CDcal was calculated and exhibited the same trend with experimental CD values (Fig. 4d, e). CD signal had the highest value when α = ± 45°, then reduced gradually to 0° as decreasing the tilted angle to 90° or 0°. Theoretically, the maximum value of g-factor is ±2 at a tilted angle α = ±45°. It was noticeable that the CD and g value obtained in the experiments were much smaller than the calculated ones. There are three main factors that resulted in the difference: one is that the transmission of experimental polymer substrate was not 100%, another one is that the retardance of the experimental polymer substrate deviates from 90° under ε = 0.2. Moreover, the LD ratio of AuNSs assemblies is below 1 in experiments.

Finite-difference time-domain (FDTD) simulations

A commercial electromagnetic software (Ansys Lumerical FDTD 3D, 2023 R2.1) was used to model and simulate the transmittance of linearly and circularly polarized light3. The AuNSs array was modeled with gold spheres with a diameter of 63 nm and a NPs gap of 2 nm62. Periodic boundary conditions were imposed on the unit cell which contained one sphere total with a x-axis distance 65 nm and a y-axis distance 500 nm. A mesh override with 2 nm mesh step was imposed on the sphere regions to ensure sufficient accuracy. The periodic conditions ensure the simulation over an infinite array of nanospheres with ideally linear mono-, di-, and trimer chains spaced 500 nm in the y-axis direction.

The array was illuminated by a plane-wave source in the range 400–1700 nm with 0° and 90° polarization corresponding to the experimental P- and S-polarizations, respectively. The transmittance and electric field values were collected by a “Frequency-domain field and power monitor” over 500 data points spanning the simulated range. For the circularly polarized light source, a combination of 0° and 90° polarizations each with amplitude of 1 was used. For the right-handed light the 90°-polarized plane-wave source was set with a +90° phase shift, and for the left-handed source the phase was set to −90°. For the FDTD region, the minimum mesh step was set to 0.25 nm in the mesh settings window and override of 2 nm mesh for the nanospheres. The staircase meshing algorithm was applied with 10 points per wavelength.

First, simulations on the array only were performed with S and P-polarized light to investigate the LD. Then, an anisotropic (n, k) material was added before the nanosphere array and the plane-wave source to investigate the CD. The (n, k) material was modeled with thickness d = 800 nm, extinction coefficient k = 0.003, refractive indices nx = nz = 1.39 and ny = 1.42 to achieve retardance δ = 10.80° for wavelength λ = 800 nm defined by Eq. (17)48.

$$\delta=\frac{2{{\rm{\pi }}}\left({n}_{{{\rm{e}}}}-{n}_{{{\rm{o}}}}\right)d}{\lambda }$$
(17)

Permittivity rotation of 0°, ±15°, ±30°, ±45°, ±60°, and ±75° was applied for the CD simulations. The simulation was performed with left-handed circular polarized light (LH-CPL) and right-handed circular polarized light (RH-CPL), and CD was obtained by subtracting the absorbances, where the absorbance A was defined as Eq. (18).

$$A=-\log \left({T}_{{{\rm{CPL}}}}\right)$$
(18)

The final value of CD was obtained by multiplying the absorbance difference by a constant for a result in decimal degrees:

$${{\rm{CD}}}=\left({A}_{{{\rm{LH}}}-{{\rm{CPL}}}}-{A}_{{{\rm{RH}}}-{{\rm{CPL}}}}\right)\frac{{\mathrm{ln}}\left(10\right)}{4}\frac{180^\circ }{{{\rm{\pi }}}}$$
(19)

Next, anisotropic (n, k) material with different retardance δ from 30° to 110° was applied with 45° relative to AuNSs chains for the CD simulation. The mesh resolution was increased through the auto-meshing functions as demonstrated in the simulated results in Supplementary Fig. 11b.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.