Assessing and improving reliability of neighbor embedding methods: a map-continuity perspective

Abstract

Visualizing high-dimensional data is essential for understanding biomedical data and deep learning models. Neighbor embedding methods, such as t-SNE and UMAP, are widely used but can introduce misleading visual artifacts. We find that the manifold learning interpretations from many prior works are inaccurate and that the misuse stems from a lack of data-independent notions of embedding maps, which project high-dimensional data into a lower-dimensional space. Leveraging the leave-one-out principle, we introduce LOO-map, a framework that extends embedding maps beyond discrete points to the entire input space. We identify two forms of map discontinuity that distort visualizations: one exaggerates cluster separation and the other creates spurious local structures. As a remedy, we develop two types of point-wise diagnostic scores to detect unreliable embedding points and improve hyperparameter selection, which are validated on datasets from computer vision and single-cell omics.

Introduction

Data visualization plays a crucial role in modern data science, as it offers essential and intuitive insights into high-dimensional datasets by providing low-dimensional embeddings of the data. For visualizing high-dimensional data, the last two decades have witnessed the rising popularity of t-SNE¹ and UMAP², which are extensively used in, e.g., single-cell analysis^3,4,5 and feature interpretations for deep learning models^6,7.

The neighbor embedding methods^8,9 are a family of visualization methods, which include t-SNE, UMAP, and LargeVis¹⁰ as popular examples, that determine embedding points directly by solving a complicated optimization algorithm to minimize the discrepancy between similarities of input points and those of the corresponding low-dimensional points. Given input data x₁, …, x_n, a neighbor embedding algorithm ${{\mathcal{A}}}$ computes the points $({{{\bf{y}}}}_{1},\ldots,{{{\bf{y}}}}_{n})={{\mathcal{A}}}({{{\bf{x}}}}_{1},\ldots,{{{\bf{x}}}}_{n})$ in the 2D plane, aiming to preserve the essential structures of x₁, …, x_n. Due to algorithmic complexity, ${{\mathcal{A}}}$ is often used as a black-box visualization tool.

These visualization methods are often interpreted as manifold learning algorithms, which extract and represent latent low-dimensional manifolds in 2D and 3D spaces^11,12,13. However, unlike classical dimension reduction methods such as PCA¹⁴, where a parametric mapping f_θ is determined and any input point x is embedded through y = f_θ(x), there is no globally defined embedding map for neighbor embedding methods as the “embedding points” y₁, …, y_n are determined in a discrete manner.

A key conceptual difficulty is the lack of sample-independent notion of embedding maps, since the embedding points y₁, …, y_n depend on n input points x₁, …, x_n collectively, which makes it challenging to understand the correspondence between an input point x_i and an embedding point y_i. Thus, it is unclear what structures the embedding points inherit from the input points, even in ideal settings where inputs are drawn from known distributions or simple manifolds. The lack of continuous-space embedding maps leads to recent recognition that neighbor embedding methods often produce misleading results by creating severe distortion through the embedding maps and introducing spurious clusters in low-dimensional visualization^15,16. Moreover, neighbor embedding methods are sensitive to the choice of optimization algorithms¹⁷, initialization schemes¹⁸, and hyperparameters^18,19, leading to inconsistent interpretations^20,21.

Some progress has been made to improve the reliability of these visualization methods, including insights on embedding stages^19,22,23, force-based interpretations²⁴, visualization quality^22,23,25, initialization schemes, and hyperparameter selection^{3,16,26,27,28}. To enhance the faithfulness of neighbor embedding methods, multiple diagnostic approaches have been proposed^{3,16,26,27,29,30,31}. However, most existing diagnostic methods offer only partial solutions and rely on ad hoc fixes, sometimes even introducing new artifacts.

In this work, we show that the manifold learning interpretation, which implicitly assumes a continuous mapping, is inaccurate. Our analyses reveal intrinsic discontinuity points in the embeddings that result in severe distortions. Our results imply that t-SNE and UMAP—which can induce topological changes to visualization—are fundamentally different from PCA and other parametric embedding methods.

We address the conceptual difficulty by proposing a notion of embedding map—which we call LOO-map—induced by a given neighbor embedding method ${{\mathcal{A}}}$. LOO-map is a mapping in the classical sense and approximates the properties of ${{\mathcal{A}}}$ around each embedding point. It is based on a well-established strategy from statistics known as the leave-one-out (LOO) method, which posits that adding, deleting, or changing a single input point has negligible effects on the overall inferential results. Using LOO, we can decouple the pairwise interaction in the algorithm ${{\mathcal{A}}}$: we add a new input point x to x₁, …, x_n and freeze y₁, …, y_n in the optimization problem, allowing only one free variable y. We call the resulting minimizer f(x) the LOO-map, which satisfies the approximation $({{{\bf{y}}}}_{1},\ldots,{{{\bf{y}}}}_{n},{{\bf{f}}}({{\bf{x}}}))\approx {{\mathcal{A}}}({{{\bf{x}}}}_{1},\ldots,{{{\bf{x}}}}_{n},{{\bf{x}}})$. By design, the LOO-map f not only satisfies f(x_i) ≈ y_i for all i’s, but also reveals the embedding point f(x) of a potential new input point x. As such, LOO-map extends the mapping defined over the discrete input set {x₁, …, x_n} to the entire input space.

LOO-map offers a unified framework for understanding known issues like distance distortion^16,32, low stability³⁰, and poor neighborhood preservation^16,33, while also revealing new insights into embedding discontinuity. In our view, discontinuities of f(x) represent an extreme form of distortion that accompanies topological changes in the embedding space, e.g., connected clusters become separated and a uniform shape is fractured into pieces. In contrast, classical dimension reduction methods such as PCA do not suffer from map discontinuity since a continuous parametric map f_θ(x) is constructed explicitly. In this regard, embedding discontinuity is an innate issue of the family of neighbor embedding methods.

Using LOO-map, we identify two types of observed distortion patterns, one affecting global properties of the embedding map and the other affecting local relationships. Both types of distortion are a consequence of discontinuities in f(x) and can cause topological changes in the embedding structures.

• Overconfidence-inducing (OI) discontinuity. Overlapping clusters or data mixtures in the input space are embedded into well-separated clusters, which creates a misleading visual impression of over-confidence that there is less uncertainty in the datasets. This biased perception of uncertainty can, in turn, lead to overly confident scientific conclusions.

• Fracture-inducing (FI) discontinuity. Small spurious and artificial clusters form in the embedding space, even for non-clustered data. Unlike OI discontinuity, such spurious clusters are small, localized, and formed in arbitrary locations.

We propose two types of point-wise diagnostic scores, namely perturbation scores and singularity scores, to quantify the severity of the two types of map discontinuity at each embedding point. Our approach is flexible and works as a wrapper around many neighbor embedding algorithms (Supplementary File Section 1) without any label information.

In this work, we demonstrate the utility of our method through two use cases: detecting out-of-distribution data (or distribution shifts) in computer vision using the perturbation score, and selecting hyperparameters in single-cell data analysis using the singularity score. We evaluate our method on multiple simulated and real-world datasets (Supplementary Table 1, “Methods”). Comparisons with existing approaches show that our method achieves superior performance in detecting topological changes in embedding and hyperparameter selection. The R package implementing our method, along with a tutorial, is publicly available on GitHub: https://github.com/zhexuandliu/MapContinuity-NE-Reliability.

Results

Overview of methods

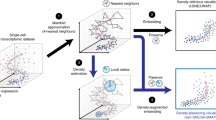
We provide an overview of LOO-map and demonstrate the proposed two diagnostic scores (Fig. 1).

Fig. 1: Overview: assessment of embeddings generated by neighbor embedding methods, illustrated with image data.

a We use a standard pre-trained convolutional neural network (CNN) to obtain features of image samples from the CIFAR10 dataset, and then visualize the features using a neighbor embedding method, specifically t-SNE. b Basic ideas of singularity scores and perturbation scores. c t-SNE tends to embed image features into separated clusters even for images with ambiguous semantic meanings (as quantified by higher entropies of predicted class probabilities by the CNN). Perturbation scores identify the embedding points that have ambiguous class membership but less visual uncertainty. d An incorrect choice of perplexity leads to visual fractures (FI discontinuity), which is more severe with a smaller perplexity. We recommend choosing the perplexity no smaller than the elbow point. Source data are provided as a Source Data file.

First, we introduce a general strategy to discern and analyze discontinuities in neighbor embedding methods (e.g., t-SNE, UMAP). Given input points x₁, …, x_n in a potentially high-dimensional space, e.g., attribute vectors or feature vectors, an embedding algorithm ${{\mathcal{A}}}$ maps them to 2D points y₁, …, y_n by solving an optimization problem involving O(n²) pairwise interaction terms. The LOO strategy assumes no dominant interaction term so that perturbing any single input point has negligible effects on the overall embedding. We extensively verify this assumption on simulated and real datasets (Table 1, Supplementary Table 2, Methods). By adding a new input x and optimizing its corresponding y while freezing ${({{{\bf{y}}}}_{j})}_{j\le n}$, LOO-map reduces the optimization problem to only O(n) effective interaction terms. We identify the discontinuity points of f(x) as the source of the observed distortions and artifacts.

Table 1 Empirical validation of LOO on both simulated and real datasets

Then, we devise two label-free point-wise diagnostic scores to quantitatively assess embedding quality (Fig. 1a). The first quantity, namely the perturbation score, quantifies how much an embedding point y_i moves when the input x_i is moderately perturbed, which helps to probe the discontinuity of f(x) from the input space. The second quantity, namely the singularity score, measures how sensitive an embedding point is to an infinitesimal input perturbation, thus providing insights into f(x) at each specific location x = x_i. The two scores, as we will show below, are motivated by different considerations and reveal qualitatively distinct features of the visualizations (Fig. 1b–d).

Finally, we demonstrate how our scores can improve the reliability of neighbor embedding methods. Following the workflow in Fig. 1a, we extract high-dimensional features of image data using a deep learning model (e.g., ResNet-18³⁴) and apply t-SNE for the 2D embedding. We observe that some inputs with ambiguous (mixed) class membership are misleadingly embedded into well-separated clusters (Fig. 1c), creating overconfidence in the cluster structure. Ground-truth labels and label-informed entropy scores confirm that the visualization under-represents the uncertainty for mixed points, making them appear more distinct than they should be (Fig. 1c). Further examination of image examples confirms such an artifact of reduced uncertainty in the embedding space. As a diagnosis, we find that embedding points with high perturbation scores correlate well with such observed (OI) discontinuity.

Our second diagnostic score can help with hyperparameter selection. A practical challenge of interpreting t-SNE embeddings is that the results may be sensitive to tuning parameters. In fact, we find that a small perplexity tends to induce small spurious structures similar to fractures, visually speaking, suggesting the presence of local (FI) discontinuity in the LOO-map f (Fig. 1d). Our singularity score captures such FI discontinuity as more high-scoring points emerge under smaller perplexities. With this diagnosis, we recommend choosing a perplexity no smaller than the elbow point of the FI discontinuity curve.

Leave-one-out as a general diagnosis technique

We start with a generic setup for neighbor embedding methods that encompasses SNE³⁵, t-SNE¹, UMAP², LargeVis¹⁰, PaCMAP¹⁵, among others. First, we introduce basic mathematical concepts and their interpretations.

• Input data matrix ${{\bf{X}}}={[{{{\bf{x}}}}_{1},\ldots,{{{\bf{x}}}}_{n}]}^{\top }\in {{\mathbb{R}}}^{n\times d}$: the input data to be visualized. Dimension d may be large (e.g., thousands).

• Embedding matrix ${{\bf{Y}}}={[{{{\bf{y}}}}_{1},\ldots,{{{\bf{y}}}}_{n}]}^{\top }\in {{\mathbb{R}}}^{n\times p}$: the embedding points we aim to determine for visualization, where p can be 2 or 3.

• (Pairwise) similarity scores ${({v}_{i,j})}_{i < j}$: a measure of how close two input points are in the input space, often calculated based on a Gaussian kernel.

• (Pairwise) embedding similarity scores ${({w}_{i,j})}_{i < j}$: a measure of how close two embedding points are, which takes the form of a heavy-tailed kernel (e.g., t-distribution). The computation often requires a normalization step.

• (Pairwise) loss function ${{\mathcal{L}}}$: a measure of discrepancy between v_i,j and w_i, j. An NE method minimizes this loss function over embedding points to preserve local neighborhood structures. The algorithms of NE methods aim to find the embedding Y by minimizing the total loss composed of the sum of the divergences between v_i,j and w_i,j of all pairs of points and a normalization factor Z(Y).

For convenience, we introduce a generic optimization problem that neighbor embedding methods aim to solve as follows:

$${\min}_{{{\mathbf{y}}}_1,\ldots,{{\mathbf{y}}}_n \in {\mathbb{R}}^2} \,{\sum}_{1\le i < j\le n} \underbrace{{{{\mathcal{L}}}}(w({{\mathbf{y}}}_i,{{\mathbf{y}}}_j); v_{i,j}({{\mathbf{X}}}))}_{{{{\rm{unnormalized}}}\, {{\rm{pair}}}\,{{\rm{wise}}}\, {{\rm{loss}}}}}+\underbrace{Z({{\mathbf{Y}}})}_{{{{\rm{normalization}}}\, {{\rm{factor}}}}}.$$

(1)

Particularly, in the t-SNE algorithm (see Supplementary Methods 2 for other algorithms), we have,

$$\begin{array}{rc}&{{\mathcal{L}}}({w}_{i,j};{v}_{i,j})=-2{v}_{i,j}\log ({w}_{i,j}),\\ &{w}_{i,j}=w({{{\bf{y}}}}_{i},{{{\bf{y}}}}_{j})={(1+\parallel {{{\bf{y}}}}_{i}-{{{\bf{y}}}}_{j}{\parallel }^{2})}^{-1},\quad Z({{\bf{Y}}})=\log \left({\sum}_{k\ne l}w({{{\bf{y}}}}_{k},{{{\bf{y}}}}_{l})\right).\end{array}$$

(2)

A fundamental challenge of assessing the embeddings is that we only know how discrete points—not the input space—are mapped since the optimization problem is solved numerically by a complicated algorithm. Consequently, it is unclear if underlying structures (e.g., clusters, low-dimensional manifolds) in the input space are faithfully preserved in the embedding space.

Consider adding a new point x to existing data points. We may wish to fix x₁, …, x_n and analyze how embedding points ${{\mathcal{A}}}({{{\bf{x}}}}_{1},\ldots,{{{\bf{x}}}}_{n},{{\bf{x}}})$ change as we vary x, thereby quantifying the mapping of x under ${{\mathcal{A}}}$. However, the embedding points would depend on all n + 1 input points, and require re-running the neighbor embedding algorithm for each new x.

To address this, we use a generic decoupling technique known as leave-one-out (LOO), which enables us to isolate the changes of one embedding point versus the others^{36,37,38,39,40,41}. We introduce the LOO assumption, the LOO loss function, and LOO-map as follows.

• LOO assumption: adding (or deleting/modifying) a single input point does not change embedding points significantly (Fig. 2a).

• LOO loss function L(y; x): it consists of n pairwise loss terms relevant to the newly added point x. We aim to determine the embedding y for x (Fig. 2b).

• LOO-map f: it is defined as ${{\bf{f}}}:{{\bf{x}}}\, \mapsto \,{{{\rm{argmin}}}}_{{{\bf{y}}}}L({{\bf{y}}};{{\bf{x}}})$ for all possible input x (Fig. 2b). This definition allows us to examine the map property in the entire region.

Fig. 2: Diagrams showing the idea of Leave-one-out (LOO) and LOO-map.

a Idea of LOO. Adding one input point does not significantly change the overall positions of embedding points. The assumption allows us to analyze the properties of the embedding map over the entire input space via an approximated loss which we call LOO loss. b We introduce a global embedding map (LOO-map) ${{\bf{f}}}({{\bf{x}}})={{{\rm{argmin}}}}_{{{\bf{y}}}}L({{\bf{y}}};{{\bf{x}}})$ defined in the entire input space as an approximation to the neighbor embedding method ${{\mathcal{A}}}$.

Rooted in the stability idea^42,43,44, LOO assumes that adding (or deleting/modifying) a single input point does not change embedding points significantly (Fig. 2a). This assumption allows us to study the map ${{\bf{x}}}\, \mapsto \,{{\mathcal{A}}}({{{\bf{x}}}}_{1},\ldots,{{{\bf{x}}}}_{n},{{\bf{x}}})$ approximately. Consider the optimization problem in Equation (1) with n + 1 input points x₁, …, x_n, x. Under the LOO assumption, when adding the new (n + 1)-th input point x, we can freeze the embedding matrix ${{\bf{Y}}}={[{{{\bf{y}}}}_{1},\ldots,{{{\bf{y}}}}_{n}]}^{\top }$ and allow only one free variable y in the optimization problem. More precisely, the mathematical formulation of LOO loss function is given by

$$L({{\bf{y}}};{{\bf{x}}})={\sum}_{1\le i\le n}{{\mathcal{L}}}\left(w({{{\bf{y}}}}_{i},{{\bf{y}}});{v}_{i,n+1}\left(\left[\begin{array}{c}{{\bf{X}}}\\ {{{\bf{x}}}}^{\top }\end{array}\right]\right)\right)+Z\left(\left[\begin{array}{c}{{\bf{Y}}}\\ {{{\bf{y}}}}^{\top }\end{array}\right]\right)\ .$$

(3)

The LOO loss is motivated by the following observation: suppose $[\begin{array}{c}\widetilde{{{\bf{Y}}}}\\ {\widetilde{{{\bf{y}}}}}^{\top }\end{array}]$ is the embedding of ${{{\bf{X}}}}_{+}=[\begin{array}{c}{{\bf{X}}}\\ {{{\bf{x}}}}^{\top }\end{array}]$, i.e., it reaches the minimum of the original loss, then ${{\bf{y}}}=\widetilde{{{\bf{y}}}}$ is necessarily the minimizer of a partial loss involving the embedding point of the point x:

$$\widetilde{{{\bf{y}}}} ={{{\rm{argmin}}}}_{{{\bf{y}}}\in {{\mathbb{R}}}^{2}}{\sum}_{1\le i\le n}{{\mathcal{L}}}\left(w({\widetilde{{{\bf{y}}}}}_{i},{{\bf{y}}});{v}_{i,n+1}\left(\left[\begin{array}{c}{{\bf{X}}}\\ {{{\bf{x}}}}^{\top }\end{array}\right]\right)\right)+Z\left(\left[\begin{array}{c}\widetilde{{{\bf{Y}}}}\\ {{{\bf{y}}}}^{\top }\end{array}\right]\right)\\ \approx {{{\rm{argmin}}}}_{{{\bf{y}}}\in {{\mathbb{R}}}^{2}}{\sum}_{1\le i\le n}{{\mathcal{L}}}\left(w({{{\bf{y}}}}_{i},{{\bf{y}}});{v}_{i,n+1}\left(\left[\begin{array}{c}{{\bf{X}}}\\ {{{\bf{x}}}}^{\top }\end{array}\right]\right)\right)+Z\left(\left[\begin{array}{c}{{\bf{Y}}}\\ {{{\bf{y}}}}^{\top }\end{array}\right]\right)$$

where the approximation is based on the LOO assumption $\widetilde{{{\bf{Y}}}}\approx {{\bf{Y}}}$. This approximation allows us to decouple the dependence of ${\widetilde{{{\bf{y}}}}}_{i}$ on x. We then define the LOO-map as ${{\bf{f}}}:{{\bf{x}}}\, \mapsto \,{{{\rm{argmin}}}}_{{{\bf{y}}}}L({{\bf{y}}};{{\bf{x}}})$.

We empirically validate the LOO assumption by demonstrating that Y and $\widetilde{{{\bf{Y}}}}$ are very close for a large sample size n. Define the normalized error between embeddings before and after deleting a data point by

$${\epsilon }_{n}=\frac{1}{\parallel {{\bf{Y}}}{\parallel }_{F}}\parallel {{\bf{Y}}}-\widetilde{{{\bf{Y}}}}{\parallel }_{F},$$

(4)

where ∥ ⋅ ∥_F means the Frobenius norm of a matrix. A sufficiently small ϵ_n will support the approximation in our derivation of the LOO-map.

We calculate this error extensively on both simulated and real datasets (“Methods”). The results support our LOO assumption (Table 1, Supplementary Table 2). We observe that the approximation errors are small and generally decreasing in n, which validates our LOO assumption.

LOO-map reveals intrinsic map discontinuities

By analyzing the LOO loss, we identify the two observed discontinuity patterns as a result of the map discontinuities of f(x). We use t-SNE as an example to illustrate the main results.

We generate mixture data by sampling 500 points from two overlapping 2D Gaussian distributions and run t-SNE with two representative choices of perplexity, 5 and 50. The resulting visualizations confirm the two discontinuity patterns (Fig. 3a). OI discontinuity pushes mixed points to cluster boundaries, creating overly tight structures, while FI discontinuity fragments embeddings into small pieces, leading to many sub-clusters. Similar discontinuity patterns are also common among other neighbor embedding methods (Supplementary Fig. 1).

Fig. 3: LOO loss landscape reveals the origins of two distortion patterns.

a We illustrate two discontinuity patterns on simulated Gaussian mixture data. OI discontinuity: t-SNE embeds points into well-separated clusters and creates visual overconfidence. FI discontinuity: t-SNE with an inappropriate perplexity creates many artificial fractures. b Origin of OI discontinuity: LOO loss contour plot shows distantly separated minima. We add a new input point x at one of the 4 interpolated locations x = tc₁ + (1 − t)c₂ where t ∈ {0, 0.47, 0.48, 1} and then visualize the landscape of the LOO loss L(y; x) using contour plots in the space of y. The middle two plots exhibit two well-separated minima (orange triangle), which cause a huge jump of the embedding point (as the minimizer of the LOO loss) under a small perturbation of x. c Origin of FI discontinuity: We show LOO loss contour plots with interpolation coefficient t ∈ {0.2, 0.4, 0.6, 0.8}. The plots show many local minima and irregular jumps. Under an inappropriate perplexity, the loss landscape is consistently fractured. Numerous local minima cause an uneven trajectory of embedding points (dashed line) when adding x at evenly interpolated locations. Source data are provided as a Source Data file.

We trace the origins of the observed discontinuity patterns by the LOO loss function. To this end, we add a single point x at varying locations to the input data and track how x is mapped. By visualizing the landscape of the LOO loss L(y; x) at four different inputs x, we provide snapshots of the LOO-map ${{\bf{x}}}\, \mapsto \, {{{\rm{argmin}}}}_{{{\bf{y}}}}L({{\bf{y}}};{{\bf{x}}})$. More specifically, we choose the centers c₁, c₂ of the two Gaussian distributions and consider the interpolated input x(t) = tc₁ + (1 − t)c₂, t ∈ [0, 1]. Since x(t) is mapped to the LOO loss minimizer, tracking the loss minima reveals the trajectory of the corresponding embedding point y(t) under varying t.

We find that the observed OI discontinuity is caused by a discontinuity point of f(x) in the midpoint of two mixtures. To demonstrate this, we visualize the LOO loss landscape and the embedding of the added point x(t) at four interpolated locations where t ∈ {0, 0.47, 0.48, 1}. There are two clearly well-separated minima in the LOO loss landscape when t ≈ 0.5 (Fig. 3b). As a result, the embedding point y(t) jumps abruptly between local minima with a slight change in t. A further gradient field analysis shows a hyperbolic geometry around the discontinuity point of f(x) (see below).

We also find that the FI discontinuity is caused by numerous irregular local minima of L(y; x) under an inappropriate choice of perplexity. This conclusion is supported by the observation that the loss landscape of L(y; x) is consistently irregular and contains many local valleys under a small perplexity (Fig. 3c). Moreover, varying the interpolation coefficient t from 0 to 1 at a constant speed results in an uneven trajectory of the embedding point y(t). Because of many irregularities, the embedding points tend to get stuck at these local minima, thus forming spurious sub-clusters. In addition, we find that larger perplexity typically lessens FI discontinuity (Supplementary Figs. 2, 3).

LOO-map motivates diagnostic scores for capturing topological changes

OI discontinuity and FI discontinuity reflect the properties of f(x) at different levels: OI discontinuity is relatively global, while FI discontinuity is relatively local. To quantify their severity respectively, we introduce two point-wise scores (Methods): (i) perturbation scores for OI discontinuity and (ii) singularity scores for FI discontinuity. For computational efficiency, both scores are based on modifying individual input points instead of adding a new point so that we maintain n data points in total. This approach is justified by the LOO assumption, allowing using the partial loss as LOO loss.

Briefly speaking, we define the perturbation score as the amount of change of an embedding point y_i under the perturbation of an input point x_i of a moderate length. As the data distribution is not known a priori, we search the perturbation directions using the top principal directions of the data (Methods).

We define the singularity score as the inverse of the smallest eigenvalue of a Hessian matrix that represents the sensitivity of the embedding point y_i under infinitesimal perturbations. Our derivation (Supplementary Methods 1) reveals that small eigenvalues can produce substantial local discontinuities, whereas a singular Hessian matrix leads to the most severe discontinuity. We find that infinitesimal perturbations are particularly effective for capturing the local characteristics of FI discontinuities. Detailed expressions for the singularity scores of t-SNE, UMAP and LargeVis are provided in Supplementary Methods 2.

Generally, we recommend using the perturbation score to diagnose the trustworthiness of cluster structures, and the singular score to detect spurious local structures.

Simulation studies

We implement our proposed point-wise scores for t-SNE as an example. We evaluate our diagnostic scores on two types of simulated datasets (Methods): (i) 2D Gaussian mixture data with 5 centers (unequal mixture probabilities, n = 700) and 8 centers (equal probabilities, n = 800), and (ii) Swiss roll data, where n = 800 points are sampled from a 3D Swiss-roll manifold.

We apply perturbation scores to the 5-component Gaussian mixture data, where t-SNE creates misleadingly distinct cluster boundaries (Fig. 4a left). Without label information, our scores identify unreliable points with deceptively low uncertainty (Fig. 4a, right). Meanwhile, the entropy differences use the ground-truth labels to calculate the reduced class entropies (Methods) in the embedding space, thus providing an objective evaluation of the degree of confidence (Fig. 4a middle). Our perturbation scores are closely aligned with the entropy differences.

Fig. 4: Simulation studies demonstrate the effectiveness of proposed scores.

a Perturbation scores identify unreliable embedding points that have reduced uncertainty. Input points from 5-component Gaussian mixture data form separated clusters in the embedding space. t-SNE reduces perceived uncertainty for input points in the overlapping region (left), as captured by the label-dependent measurements, namely the entropy difference (middle). Our perturbation scores can identify the same unreliable embedding points without label information (right). Singularity scores reveal spurious sub-clusters on Gaussian mixture data (b) and Swiss roll data (c). At a low perplexity, t-SNE creates many spurious sub-clusters. Embedding points receiving high singular scores at random locations is an indication of such spurious structures. Source data are provided as a Source Data file.

Next, we apply singularity scores to the 8-component Gaussian mixture and Swiss roll data under two perplexity settings (Fig. 4b–c). Each embedding is colored by ground-truth labels, singularity scores, and dichotomized singularity scores (binary thresholding). The embeddings differ visually: a low perplexity creates spurious sub-clusters, while a high perplexity preserves cluster and manifold structures. Additionally, the distributions of dichotomized scores vary: a low perplexity results in more high scores at randomly scattered locations, whereas a high perplexity yields fewer high-scoring points.

Moreover, we quantitatively assess the clustering quality for the 8-component Gaussian mixture data using three indices: DB index⁴⁵, within-cluster distance ratio (Methods), and Wilks’ Λ⁴⁶. All three indices (small values are better) indicate that t-SNE visualizations with less severe FI discontinuity, i.e., lower singularity scores, achieve better clustering quality, with the DB index dropping from 0.5982 to 0.3038, the within-cluster distance ratio from 0.0480 to 0.0024, and Wilks’ Λ from 0.0028 to 9.0 × 10⁻⁶. To further study the change in clustering quality, we generate 6 simulated datasets with varying cluster structures and dimensions. Across all datasets, tuning perplexity using singularity scores consistently improves clustering quality, reducing the DB index by approximately 50%, the within-cluster distance ratio by 65–91%, and Wilks’ Λ by 57–99% (Supplementary Table 3).

Use case 1: detecting out-of-distribution image data

One common practical issue for statistical methods or machine learning algorithms is the distribution shift, where the training dataset and test dataset have different distributions, often because they are collected at different sources^47,48,49. These test data are called out-of-distribution (OOD) data.

In this case study, we identify one rarely recognized pitfall of t-SNE visualization: OOD data may become harder to discern in t-SNE embeddings because they tend to be absorbed into other clusters. Our perturbation score is able to identify the misplaced OOD embedding points.

We use a standard ResNet-18 model³⁴ trained on the CIFAR-10 dataset⁵⁰ to extract features of its test dataset and an OOD dataset known as DTD (describable textures dataset)⁵¹. Ideally, visualization of the features of test images and OOD images would reveal the distribution shift. However, the t-SNE embedding shows that a fraction of OOD features are absorbed into compact, well-defined CIFAR-10 clusters (Fig. 5a). Without the label information, one may mistakenly assume that the misplaced OOD embedding points belong to the regular and well-separated classes in CIFAR-10. We find that the embedding misplacement results from OI discontinuity. Our inspection of the original feature space shows that the misplaced OOD data points appear to have mixed membership, resembling both CIFAR-10 and OOD data—thus their cluster membership is, in fact, less certain than what t-SNE suggests.

Fig. 5: Perturbation scores detect out-of-distribution (OOD) image data.

a We use a pretrained ResNet-18 model to extract features of CIFAR-10 images and, as out-of-distribution data, of DTD texture images. Then we visualize the features using t-SNE with perplexity 100. A fraction of OOD embedding points are absorbed into clusters that represent CIFAR-10 image categories such as deer, truck, and automobile. b–d Perturbation scores can effectively identify misplaced out-of-distribution data points. The ROC curves show the proportion of OOD points correctly identified by the perturbation scores. Source data are provided as a Source Data file.

Our perturbation scores can successfully identify most of these misplaced OOD embedding points (Fig. 5b–d). The areas under the ROC curves (AUROC) are on average 0.75 for the three selected clusters. Compared with other methods aiming for OOD detection, our perturbation score demonstrates superior performance, with kernel PCA⁵² achieving an average AUROC of 0.698 and the one-class support vector machine⁵³ achieving an average AUROC of 0.410 (Supplementary Fig. 4, Methods). Additionally, we use the prediction probabilities given by the neural network to calculate the entropy of each point and find that the entropies significantly correlate with the perturbation scores; specifically, the correlations are 0.49, 0.58, and 0.64 for the selected clusters. These findings suggest that perturbation scores are effective in detecting OOD data and can help safeguard against misinterpretation of t-SNE visualizations.

Use case 2: enhancing interpretation of single-cell data

Our second example concerns the application of singularity scores in single-cell data. In this case study, we investigate how incorrect choices of perplexity induce spurious sub-clusters. We also provide a guide of choosing perplexity based on singularity scores, thereby reducing such spurious sub-clusters.

The first dataset we examined is single-cell RNA-seq data from 421 mouse embryonic stem cells (mESCs) collected at 5 sampling time points during differentiation⁵⁴. The second dataset is another single-cell RNA-seq data from 25,806 mouse mammary epithelial cells across 4 developmental stages⁵⁵. We also include our analysis on a mid-sized mouse brain chromatin accessibility data in the Supplementary File (Supplementary Fig. 5, Supplementary Table 4). Through analysis of the datasets, we find that a small perplexity tends to create spurious sub-clusters (Fig. 6a, c, Supplementary Fig. 5a). Our singularity scores can provide informative insights into the spurious clusters even without the ground-truth labels, as summarized below.

• (Distribution difference) Embedding points with large singularity scores tend to appear in random and scattered locations if the perplexity is too small. In contrast, under an appropriate perplexity, embedding points with large singular scores are mostly in the periphery of clusters.

• (Elbow point) As the perplexity increases, the magnitude of large singular scores (calculated as the average of the top 5%) rapidly decreases until the perplexity reaches a threshold.

Fig. 6: Singularity scores inform the selection of the perplexity parameter.

Comparative t-SNE embeddings and the corresponding singularity scores at two different perplexities in mouse embryonic cell differentiation data (a) and in mouse mammary epithelial cell data (c). The perplexity as a tuning parameter has a large impact on t-SNE visualization qualitatively. At a small perplexity, there are many spurious sub-clusters. Embeddings with high singular scores appear in random locations, which indicates the presence of such spurious structures and severe FI discontinuity. Plots of the degree of FI discontinuity and neighborhood preservation versus perplexity are shown for mouse embryonic cell differentiation data (b) and for mouse mammary epithelial cell data (d). We recommend choosing a perplexity no smaller than the elbow point, as this ensures that randomly positioned points with high singularity scores largely disappear, remaining only at cluster peripheries. Consequently, the neighborhoods of most points are embedded more faithfully, resulting in better neighborhood preservation score. Source data are provided as a Source Data file.

The distribution of large singular values indicates spurious sub-clusters, reflecting the irregular LOO loss landscape (Supplementary Fig. 3a, c). We extensively validated the distribution difference between small and large perplexities through statistical tests, including Spearman’s correlation test between singularity scores and cluster center distances, F-tests, and permutation tests for local regression models (singularity scores regressed against locations). At low perplexities, Spearman’s correlation tests showed non-significant results for all five mESCs clusters and five mammary epithelial cell clusters (average p-values: 0.36 for mESCs clusters at perplexity 4 and 0.29 for mammary epithelial cell clusters at perplexity 5, Supplementary Tables 4, 6). Increasing perplexities to the singularity score elbow points (Fig. 6b, d) yielded significant correlations in four of five mESCs clusters and five of eight mammary epithelial cell classes. Similarly, F-tests and permutation tests showed p-values dropping from  ~0.3 to  < 0.001 (mESCs) and  <10⁻¹³ (mammary epithelial cells), confirming the dependence of singularity scores on location at higher perplexities. This transition aligns with LOO loss geometry: low perplexities create scattered local minima, forming spurious sub-clusters (Supplementary Fig. 3a, c), whereas higher perplexities smooth the loss landscape (Supplementary Fig. 3b, d), reducing artifacts.

We also observe that the degree of FI discontinuity, as indicated by the magnitude of the singularity scores, decreases rapidly until the perplexity reaches the elbow point (Fig. 6b, d). Beyond the elbow point, the spurious sub-clusters largely disappear, aligning with the improvement of neighborhood preservation (Fig. 6b, d), as measured by the nearest-neighbor distance correlation between the input and embedding spaces (Methods). However, we would not suggest increasing perplexity excessively, as it may merge clusters²⁶, result in the loss of certain microscopic structures³, and often lead to longer computational running time²⁷. Therefore, we suggest choosing a perplexity around the elbow point.

Computational cost of perturbation score

Theoretically, the computational complexity for solving the LOO loss optimization takes O(n) flops, instead of O(n²) flops of the original loss which involves every pairwise interaction term. Practically, our R package has the following running time.

• For exact perturbation scores, it takes 35.2 s to compute the score per point for the CIFAR-10 images in Fig. 1 on a MacBook Air (Apple M2 chip).

• Leveraging pre-computed quantities, we also provide an approximation method to reduce the running time per point to 7.1 s, while preserving high accuracy relative to the exact score (Supplementary Fig. 8).

• In addition to the approximation, we introduce a pre-screening step to increase the computational efficiency by 14X for the same dataset. This pre-screening step identifies a subset of embedding points most likely to yield high scores, and thus significantly reduces computational cost while still providing a comparable assessment of OI discontinuity locations (Supplementary Fig. 7). Combining the approximation method and the pre-screening step results in an average of 0.47 s.

Computational cost of singularity score

Theoretically, the computational complexity for calculating the singularity scores for the entire dataset is O(n²) flops, primarily due to matrix operations when calculating Hessian matrices. Practically, the running time for computing singularity scores for CIFAR-10 is 15.9 s for all 5000 points on a MacBook Air (Apple M2 chip).

Comparison with other assessment metrics

There are multiple recent papers on assessing and improving the reliability of neighbor embedding methods. None of these papers view the observed artifacts as an intrinsic map discontinuity and as a result, cannot reliably identify topological changes in their proposed diagnosis. For illustration, we compare our method with EMBEDR²⁹, scDEED²⁸, and DynamicViz³⁰.

• EMBEDR identifies dubious embedding points by using statistical significance estimates as point-wise reliability scores. This process begins by computing point-wise KL divergences between the kernels in the input and embedding spaces, followed by a permutation test to determine whether the neighborhood preservation is significantly better than random chance. Lower p-values from the test indicate higher embedding reliability. EMBEDR selects the perplexity by minimizing the median p-values.

• scDEED calculates point-wise p-values by conducting a similar permutation test on the correlations of nearest-neighbor distances. Similarly, lower p-values indicate higher embedding reliability. ScDEED provides two approaches for parameter selection based on dubious embedding points: the first locates the elbow point, and the second selects the perplexity to minimize the number of dubious points.

• DynamicViz employs a bootstrap approach to assess the stability of embeddings. Point-wise variance scores are constructed based on resampling, defined as the average variance of distances to the neighbors. Embedding points with lower variance scores are considered more reliable. DynamicViz selects the perplexity by minimizing the median variance score.

Compared with existing methods, our perturbation score offers the following advantages in detecting distortions of global structure. First, perturbation scores are better at locating the topological changes of global structures by pinpointing the exact points. By design, they capture embedding points close to the intrinsic discontinuity of the embedding map. In a simulated Swiss roll dataset, t-SNE erroneously splits the smooth manifold into two disconnected pieces (Fig. 7a), which is a severe visualization artifact caused by OI discontinuity. Our perturbation scores accurately highlight unreliable points exactly at the disconnection location (Fig. 7b). In contrast, EMBEDR and scDEED label most points as unreliable, failing to pinpoint the discontinuity (Fig. 7c, d), as they emphasize neighborhood preservation rather than topological changes. DynamicViz identifies the general region but lacks precision (Fig. 7e).

Fig. 7: Comparing perturbation scores with three diagnostic scores for the t-SNE embedding on the simulated Swiss roll dataset.

a The t-SNE embedding of n = 1000 simulated points from the Swiss roll manifold under perplexity 150. The colors correspond to the ground-truth spiral angles of the points. t-SNE algorithm erroneously breaks the smooth manifold into two disconnected parts, which indicates OI discontinuity. b Perturbation scores clearly mark the unreliable embedding points where disconnection (discontinuity) occurs. c EMBEDR uses the p-values from one-sided permutation tests to identify unreliable embedding points. It suggests that most embedding points are unreliable (lower p-values are more reliable). But it does not identify the discontinuity location. d ScDEED evaluates most embedding points as dubious, but similar to EMBEDR, it does not identify the discontinuity location. e DynamicViz marks both the discontinuity location and the areas at both ends of the Swiss roll as unstable, making it difficult to distinguish the actual discontinuity locations. Furthermore, while it can roughly identify the discontinuity location, it still fails to pinpoint the exact points where the split occurs. Source data are provided as a Source Data file.

Second, perturbation scores are also robust to low-density regions. In the simulated Gaussian mixture dataset (Supplementary Fig. 9a), DynamicViz fails to accurately characterize discontinuity locations in areas with a lower point density, as these areas are prone to insufficient sampling (Supplementary Fig. 9c). In contrast, our perturbation scores are more robust to the low-density regions (Supplementary Fig. 9b).

Compared with existing methods, our singularity score consistently selects a perplexity that is neither too small nor too large, thereby reducing sub-clusters while preserving fine-grained structures. We illustrate the advantage of this consistency in aiding hyperparameter selection using three datasets (Supplementary Table 7).

For the mouse embryonic cell differentiation data (Fig. 6a), scDEED recommends two approaches for perplexity selection; the first is based on the elbow point and yields 3, and the second is based on minimizing the number of dubious points and does not produce a unique value (Supplementary Fig. 10a). EMBEDR fails to suggest a valid hyperparameter because we encountered errors potentially due to a small dataset size. DynamicViz and singular scores select moderate perplexity (20 and 25), reducing spurious sub-clusters compared to perplexity of 3 (Supplementary Fig. 10b) and achieving the higher neighborhood preservation score (0.5594 (singularity score, highest), 0.4955 (scDEED), 0.5524 (DynamicViz)).

For the mouse brain chromatin accessibility data (Supplementary Fig. 5a), scDEED selects 10 (elbow point) and 145 (minimizing dubious points). EMBEDR chooses perplexity of 145, showing a tendency of favoring larger perplexity that is also observed by Xia et al.²⁸. DynamicViz selects perplexity of 10. Our singularity score selects perplexity of 95 (Supplementary Fig. 11a). By visual inspection, perplexity of 10 is inappropriately small because visualization exhibits numerous spurious sub-clusters. In contrast, perplexities of 95 and 145 avoid spurious sub-clusters while maintaining fine-grained structures (Supplementary Fig. 11b). Quantitatively, the perplexities suggested by singular scores, scDEED, and EMBEDR lead to similar neighborhood preservation scores (0.4108, 0.4223, 0.4223).

In the mouse mammary epithelial cell dataset, similar phenomena are observed: our singularity score selects a balanced perplexity while scDEED and EMBEDR select perplexities that are either too small or too large, and DynamicViz lacks scalability for large datasets due to its bootstrap-based approach, which requires repeated execution of visualization algorithms (Supplementary Fig. 12). Overall, the singularity score offers robust guardrail perplexities that significantly reduce spurious sub-clusters while producing informative visualization.

Theoretical insights: landscape of LOO loss

By analyzing the LOO loss function in Equation (3) under a simple setting, we will show that OI discontinuity is caused by a hyperbolic saddle point in the LOO loss function, thereby theoretically justifying Fig. 3b.

Suppose that n input points x₁, …, x_n are generated from a data mixture with two well-separated and balanced groups, where the first group is represented by the index set ${{{\mathcal{I}}}}_{+}\subset \{1,2,\ldots,n\}$ with $| {{{\mathcal{I}}}}_{+}|=n/2$ and the second group represented by ${{{\mathcal{I}}}}_{-}=\{1,2,\ldots,n\}\setminus {{{\mathcal{I}}}}_{+}$. Without loss of generality, we assume that the mean vectors of ${({{{\bf{y}}}}_{i})}_{i\in {{{\mathcal{I}}}}_{+}}$ and ${({{{\bf{y}}}}_{i})}_{i\in {{{\mathcal{I}}}}_{-}}$ are θ and  −θ, respectively, since embeddings are invariant to global shifts and rotations. Equivalently, we write

$${{{\bf{y}}}}_{i}=\left\{\begin{array}{ll}{{\mathbf{\theta }}}+{{{\mathbf{\delta }}}}_{i}&i\in {{{\mathcal{I}}}}_{+}\\ -{{\mathbf{\theta }}}+{{{\mathbf{\delta }}}}_{i} &i\in {{{\mathcal{I}}}}_{-}\end{array}\right.$$

where ${\sum }_{i\in {{{\mathcal{I}}}}_{+}}{{{\mathbf{\delta }}}}_{i}={\sum }_{i\in {{{\mathcal{I}}}}_{-}}{{{\mathbf{\delta }}}}_{i}={{\bf{0}}}$. To simplify the loss function, we make an asymptotic assumption: consider (implicitly) a sequence of problems where input data have increasing distances between the two groups, so we expect an increasing separation of clusters in the embedding space:

$$\parallel {{\mathbf{\theta }}}\parallel \to \infty,\quad {\max }_{i\le n}\parallel {{{\mathbf{\delta }}}}_{i}\parallel=O(1)\,.$$

Now consider adding an input point (‘mixed’ point) to a location close to the midpoint of the two groups. We assume that its similarity to the other inputs is

$${v}_{i,n+1}=\left\{\begin{array}{l}{p}_{0}+\varepsilon+o(\varepsilon )\quad \\ {p}_{0}-\varepsilon+o(\varepsilon )\quad \end{array}\right.$$

for 1 ≤ i ≤ n, where p₀ > 0 and ε is a small perturbation parameter. This assumption is reasonable because the similarity of the added point x ≔ x^ε has roughly equal similarities to existing inputs up to a small perturbation. We make the asymptotic assumption ∥θ∥⁻¹ ≍ ε, namely ε∥θ∥ = O(1) and [ε∥θ∥]⁻¹ = O(1).

Theorem 1

Consider the LOO loss function for t-SNE given in Eqs. (2) and (3). Under the assumptions stated above, the negative gradient of the loss is

$$-\nabla_{{{\mathbf{y}}}} L({{\mathbf{y}}}; {{\mathbf{x}}}^{\varepsilon})=(1+o(1)) \left( \underbrace{\frac{{{\mathbf{y}}}_{//} - {{\mathbf{y}}}_{\bot}}{\| {{\mathbf{\theta}}}\|^2}}_{{{{\rm{hyperbolic}}}\, {{\rm{term}}}}}+\underbrace{\frac{{\varepsilon} {{\mathbf{\theta}}}}{\| {{\mathbf{\theta}}}\|^2}}_{{{{\rm{perturbation}}}\, {{\rm{term}}}}} \right)$$

where y_// = θθ^⊤y/∥θ∥² is projection of y in the direction of θ, and y_⊥ = y − y_//.

This result explains how the hyperbolic geometry creates OI discontinuity.

• The hyperbolic term indicates the unstable saddle point of the loss at y = 0. Indeed, it is exactly the tangent vector of a hyperbola, so in the embedding force (negative gradient) field there is a pull force towards the x-axis and a push force away from the y-axis (Fig. 8).

• The perturbation term reflects the effects of input point x^ε. It tilts the negative gradients slightly in the direction of θ if ε > 0 or  − θ if ε < 0, which causes the algorithm to jump between widely separated local minima of L(y; x) under small perturbations.

Fig. 8: Negative gradient fields of the real/theoretical LOO loss.

a We draw the negative gradient fields (force fields) − ∇_yL(y; x^ε) based on the LOO loss under the same setting as in Fig. 3b. b We draw a similar field plot based on the hyperbolic term $\frac{{{{\bf{y}}}}_{\parallel }-{{{\bf{y}}}}_{\perp }}{\parallel {{\mathbf{\theta }}}{\parallel }^{2}}$ from Theorem 1, where we take θ = (c₁ − c₂)/2 and c₁, c₂ are the centers of two clusters in the embedding. In addition, we add loss contours to both plots, which show hyperbolic paraboloids around the origin. We observe a strong alignment between the negative gradient field of the LOO loss and that of the theoretical analysis. Both field plots show a pull force towards the x-axis and a push force away from the y-axis. Source data are provided as a Source Data file.

Discussion

We developed a framework to interpret distortions in neighbor embedding methods as map discontinuities by leveraging the LOO strategy. Based on our LOO-map, we introduce two diagnostic scores to identify OI and FI discontinuities. While being generally effective, our method may not capture all distortion patterns, as factors like initialization, iterative algorithms, and other hyperparameters can introduce different types of distortions. We also recognize the absence of a formal mathematical framework for rigorously characterizing the LOO-map.

In future research, we aim to explore links between classical parametric and implicit embedding maps to fully address topological issues and improve interpretability. We also aim to enhance the scalability of our methods through efficient optimization, sparsity, tree-based approximations, and parallel computation.

Methods

Verify leave-one-out assumption empirically

Our LOO approach assumes that adding (or deleting/modifying) a single input point does not change the embeddings of other points on average significantly. To verify the LOO assumption, we conduct the following experiment.

Let ${{\bf{X}}}={[{{{\bf{x}}}}_{1},\ldots,{{{\bf{x}}}}_{n}]}^{\top }$ be the input data matrix, and ${{\bf{Y}}}={[{{{\bf{y}}}}_{1},\ldots,{{{\bf{y}}}}_{n}]}^{\top }$ be the matrix of embedding points. We then add one point x to X to have the new input data ${{{\bf{X}}}}_{+}={[{{{\bf{x}}}}_{1},\ldots,{{{\bf{x}}}}_{n},{{\bf{x}}}]}^{\top }$. We then run the t-SNE algorithm to obtain the embedding of X₊ as ${[{\widetilde{{{\bf{y}}}}}_{1},\ldots,{\widetilde{{{\bf{y}}}}}_{n},\widetilde{{{\bf{y}}}}]}^{\top }$. Denoted $[{\widetilde{{{\bf{y}}}}}_{1},\ldots,{\widetilde{{{\bf{y}}}}}_{n}]$ as $\widetilde{{{\bf{Y}}}}$. To verify LOO empirically, we keep track of the difference between Y and $\widetilde{{{\bf{Y}}}}$:

$${\epsilon }_{n}=\frac{1}{\parallel {{\bf{Y}}}{\parallel }_{F}}\parallel {{\bf{Y}}}-\widetilde{{{\bf{Y}}}}{\parallel }_{F}$$

and expect ϵ_n to be small.

We initialize the t-SNE algorithm in the second run by the embedding points we obtain from the first run: when calculating the embedding of X₊, we use Y as the initialization for the first n points. This initialization scheme aims to address two issues: (i) the loss function in a neighbor embedding method is invariant to a global rotation and a global shift of all embedding points, so it is reasonable to choose embedding points with an appropriate initialization. (ii) There are potentially multiple local minima of the loss function due to non-convexity. We verify the LOO assumption at a given local minimum (namely Y) obtained from the first run.

The experiment is conducted with different sample sizes n and with different types of datasets (simulated cluster data, simulated manifold data, real single-cell data, deep learning feature data). The comprehensive results showing the values of ϵ_n under different settings are presented in Supplementary Table 2. We observe that the approximation errors ϵ_n are small and generally decreasing in n, which supports our LOO assumption.

Perturbation score

For implementation convenience, our calculation of the perturbation score and the singularity score is based on modifying an input point instead of adding a new input point. According to the LOO assumption, the difference is negligible.

Given an input data matrix ${{\bf{X}}}={[{{{\bf{x}}}}_{1},\ldots,{{{\bf{x}}}}_{n}]}^{\top }$ and its embedding matrix ${{\bf{Y}}}={[{{{\bf{y}}}}_{1},\ldots,{{{\bf{y}}}}_{n}]}^{\top }$, we view y_i as the mapping of x_i by the partial LOO-map f_i:

$$\begin{array}{rcl}&&{{{\bf{f}}}}_{i}({{\bf{x}}})={{{\rm{argmin}}}}_{{{\bf{y}}}\in {{\mathbb{R}}}^{2}}{L}_{i}({{\bf{y}}};{{\bf{x}}}),\quad \,{\mbox{where}}\,\\ &&{L}_{i}({{\bf{y}}};{{\bf{x}}})={\sum}_{k\ne i}{{\mathcal{L}}}\left(w({{{\bf{y}}}}_{k},{{\bf{y}}});{v}_{i,k}(\bar{{{\bf{X}}}})\right)+Z(\bar{{{\bf{Y}}}}),\end{array}$$

(5)

where $\bar{{{\bf{X}}}}={[{{{\bf{x}}}}_{1},\ldots,{{{\bf{x}}}}_{i-1},{{\bf{x}}},{{{\bf{x}}}}_{i+1},\ldots,{{{\bf{x}}}}_{n}]}^{\top }$ differs from X only at the i-th input point, and $\bar{{{\bf{Y}}}}={[{{{\bf{y}}}}_{1},\ldots,{{{\bf{y}}}}_{i-1},{{\bf{y}}},{{{\bf{y}}}}_{i+1},\ldots,{{{\bf{y}}}}_{n}]}^{\top }$ has frozen embedding points except for the i-th point which is the decision variable in the optimization problem. This partial LOO-map f_i is based on perturbing (or modifying) a single input point rather than adding a new point, thus maintaining n points in total. According to the LOO assumption, f_i ≈ f, so we calculate the perturbation score for the i-th point based on f_i.

To assess the susceptibility of y_i under moderate perturbations in x_i, we apply a perturbation of length λ in the direction of e to x_i and measure the resulting change in the embedding map determined by the partial LOO-map f_i. In our implementation, we search the perturbation directions among the first 3 principal directions of the data {e₁, e₂, e₃} and their opposites { −e₁, −e₂, −e₃}, and the perturbation length λ is specified by the user. In this way, we can define the perturbation score of the i-th data point as

$${\max }_{{{\bf{e}}}\in \{\pm {{{\bf{e}}}}_{1},\pm {{{\bf{e}}}}_{2},\pm {{{\bf{e}}}}_{3}\}}\parallel {{{\bf{f}}}}_{i}({{{\bf{x}}}}_{i}+\lambda {{\bf{e}}})-{{{\bf{y}}}}_{i}{\parallel }_{2}.$$

(6)

In general, perturbation scores are not sensitive to perturbation lengths. Supplementary Fig. 6 illustrates the perturbation scores of the CIFAR10 deep learning feature data for three perturbation lengths (λ ∈ {1, 2, 3}). Points with high perturbation scores remain consistent across different perturbation lengths. In practice, we recommend that users run perturbation scores on a subset of data points and test with a few different perturbation lengths. Conceptually, the perturbation score detects points that fall within a radius of λ around the location of the OI discontinuity.

Moreover, we provide two approximation algorithms to accelerate the calculation of the perturbation score for t-SNE along with a strategy for users to pre-screen points for which the perturbation score should be computed.

Approximation method 1

For high-dimensional input data, often PCA as a pre-processing step is implemented before calculating the similarity scores. As similarity scores are recalculated for each perturbation we consider, PCA is repeated numerous times, leading to a significant increase in computation. Since PCA is robust to perturbing a single input point, we reuse the pre-processed input points after one PCA calculation based on the original input data. This approximation avoids multiple calculations of PCA. We find that this approximation is sufficiently accurate, as the differences between perturbation scores by approximation method 1 and the exact perturbation scores are empirically negligible (Supplementary Fig. 8a).

Approximation method 2

Besides reducing PCA computations, we can further accelerate the calculation of perturbation scores by approximating the similarity scores.

Given the input data matrix ${{\bf{X}}}={[{{{\bf{x}}}}_{1},\ldots,{{{\bf{x}}}}_{n}]}^{\top }$ and perplexity ${{\mathcal{P}}}$, the computation of (exact) similarity scores ${({v}_{i,j}({{\bf{X}}}))}_{i < j}$ in the t-SNE algorithm follows the steps below.

• Calculate the pairwise distance d_ij = ∥x_i − x_j∥₂ for i, j = 1, …, n.

• Find σ_i, i = 1, …, n that satisfies

  $$-{\sum}_{j\ne i}\frac{\exp (-{d}_{ij}^{2}/2{\sigma }_{i}^{2})}{{\sum}_{k\ne i}\exp (-{d}_{ik}^{2}/2{\sigma }_{i}^{2})}{\log }_{2}\left(\frac{\exp (-{d}_{ij}^{2}/2{\sigma }_{i}^{2})}{{\sum}_{k\ne i}\exp (-{d}_{ik}^{2}/2{\sigma }_{i}^{2})}\right)={\log }_{2}({{\mathcal{P}}}).$$

  (7)

• Calculate ${p}_{j| i}=\frac{\exp (-{d}_{ij}^{2}/2{\sigma }_{i}^{2})}{{\sum}_{k\ne i}\exp (-{d}_{ik}^{2}/2{\sigma }_{i}^{2})}$, i, j = 1, …, n. And

  $${v}_{i,j}({{\bf{X}}})=\frac{{p}_{j| i}+{p}_{i| j}}{2n}.$$

The main computational bottleneck is at step 2, where we conduct a binary search algorithm for n times to solve ${({\sigma }_{i})}_{1\le i\le n}$.

To provide an approximation method, we note that when perturbing the k-th point, for i ≠ k, Equation (7) still approximately holds for the original standard deviation σ_i since only one of the terms has been changed. Therefore, we can set ${\widetilde{\sigma }}_{i}\approx {\sigma }_{i}$ for i ≠ k as an approximation to ${({\widetilde{\sigma }}_{i})}_{1\le i\le n}$, the standard deviations after perturbation. In this way, we only need to conduct the binary search once to solve ${\widetilde{\sigma }}_{k}$, which significantly speeds up the calculation of the similarity scores after perturbation.

In terms of computational performance, approximation method 2 leads to a reduction of running time by nearly 80% for a dataset of size 5000. We also find that approximation method 2 is highly accurate. As shown in Supplementary Fig. 8b, perturbation scores based on approximation method 2 are approximately equal to the exact perturbation scores for most of the points.

Pre-screening of points

To further speed up the computation, we use the heuristic that embedding points receiving high perturbation scores are often found at the peripheries of clusters. This heuristic motivates us to calculate the perturbation scores only for the peripheral points in the embedding space, as these points are most likely to be unreliable. We find that applying this pre-screening step tends to find most of the unreliable points (Supplementary Fig. 7) with significantly increased computational speed.

We use the function dbscan in the R package dbscan (version 1.2-0) to identify embeddings on the periphery of clusters.

Singularity score

Given an input data matrix ${{\bf{X}}}={[{{{\bf{x}}}}_{1},\ldots,{{{\bf{x}}}}_{n}]}^{\top }$ and its embedding matrix ${{\bf{Y}}}={[{{{\bf{y}}}}_{1},\ldots,{{{\bf{y}}}}_{n}]}^{\top }$, we describe our derivation of singularity scores. If we add an infinitesimal perturbation ϵe to x_i, then by the Taylor expansion of the partial LOO-map f_i, the resulting change in the i-th embedding point is expressed as

$${{{\bf{f}}}}_{i}({{{\bf{x}}}}_{i}+\epsilon {{\bf{e}}})-{{{\bf{y}}}}_{i}=-\!\epsilon {{{\bf{H}}}}_{i}^{-1}{\sum}_{k:k\ne i}\frac{{\partial }^{2}{{\mathcal{L}}}(w({{{\bf{y}}}}_{i},{{{\bf{y}}}}_{k});{v}_{i,k}({{\bf{X}}}))}{\partial {{{\bf{y}}}}_{i}\partial {{{\bf{x}}}}_{k}^{\top }}{{\bf{e}}}+o(\epsilon ),$$

(8)

where H_i denotes the Hessian matrix of the partial LOO loss L_i(y; x_i) with respect to y at y = y_i. Notably, when ϵ = 0 (no perturbation), we have f_i(x_i) = y_i. Denote the total loss as

$${\mathfrak{L}}({{{\bf{y}}}}_{1},\ldots,{{{\bf{y}}}}_{n};{{\bf{X}}})={\sum}_{1\le i < j\le n}{{\mathcal{L}}}(w({{{\bf{y}}}}_{i},{{{\bf{y}}}}_{j});{v}_{i,j}({{\bf{X}}}))+Z({{\bf{Y}}}).$$

Then, H_i can be written as

$${{{\bf{H}}}}_{i}={\left.\frac{{\partial }^{2}{L}_{i}({{\bf{y}}};{{{\bf{x}}}}_{i})}{\partial {{\bf{y}}}\partial {{{\bf{y}}}}^{\top }}\right\vert }_{{{\bf{y}}}={{{\bf{y}}}}_{i}}=\frac{{\partial }^{2}{\mathfrak{L}}({{{\bf{y}}}}_{1},\ldots,{{{\bf{y}}}}_{n};{{\bf{X}}})}{\partial {{{\bf{y}}}}_{i}\partial {{{\bf{y}}}}_{i}^{\top }},$$

i.e., H_i is also equal to the Hessian matrix of the total loss ${\mathfrak{L}}$ with respect to the i-th variable taking value at y_i.

Importantly, H_i is independent of the perturbation direction e. The more singular H_i is, the more sensitive the embedding point of x_i becomes to infinitesimal perturbations. Thus, we define the singularity score of the i-th data point as the inverse of the smallest eigenvalue of the Hessian matrix of ${\mathfrak{L}}$, that is ${\lambda }_{\min }^{-1}({{{\bf{H}}}}_{i})$. Supplementary Methods 1 provides detailed derivations of Eq. (8), and Supplementary Methods 2 provides expressions of singularity scores for t-SNE, UMAP, and LargeVis.

Scoring metrics and statistical tests

Entropy of class probabilities

For a classification task, a statistical or machine learning algorithm outputs predicted class probabilities for a test data point. For example, in neural networks, the probabilities are typically obtained through a softmax operation in the final layer. Often, the model predicts a class with the largest probability among all classes. The entropy of the probabilities can quantify how confident the model is in its prediction.

For a classification task of k classes, if we denote the output class probabilities for one data point x as p = (p₁, …, p_k), then we define the entropy as $E({{\bf{p}}})=-{\sum }_{j=1}^{k}{p}_{j}\log ({p}_{j})$. This quantity is widely used for measuring class uncertainty.

Entropy difference

We will describe an uncertainty measurement given access to the labels of input points. For a dataset ${({{{\bf{x}}}}_{i})}_{i\le n}$ with clustering structures, we posit the following k-component Gaussian mixture model (GMM) from which each x_i is sampled. Consider a uniform prior on the k clusters, i.e., $p({A}_{j})=\frac{1}{k}$, j = 1, 2, …, k. Given cluster membership A_j, we define the conditional probability density function

$$p({{\bf{x}}}| {A}_{j})=g({{\bf{x}}}| {{{\mathbf{\mu }}}}_{j},{{{\mathbf{\Sigma }}}}_{j}),$$

where μ_j, Σ_j are the mean and covariance matrix in the j-th component, and g(x∣μ_j, Σ_i), j = 1, 2, …, k are the Gaussian density functions with mean μ_j and covariance matrix Σ_j. We then have the posterior probability of A_j given an observation x as

$$p({A}_{j}| {{\bf{x}}})=\frac{p({{\bf{x}}}| {A}_{j})}{\mathop{\sum }_{j=1}^{k}p({{\bf{x}}}| {A}_{j})}.$$

(9)

In the analysis of neighbor embedding methods, we will use the posterior probabilities as an uncertainty measurement. Given the ground-truth labels of the data points, we can fit two GMMs, one in the input space and the other in the embedding space, yielding estimated parameters ${({{{\mathbf{\mu }}}}_{j},{{{\mathbf{\Sigma }}}}_{j})}_{j\le k}$ for each fitted GMM. Then we can calculate the posterior probabilities of each data point belonging to the k components by Equation (9) with fitted parameters, in both the input space and the embedding space. For any data point, denote the posterior probabilities in input space as p = (p₁, p₂, …, p_k) and in embedding space as q = (q₁, q₂, …, q_k). Finally, we define the entropy difference for each point as the difference between the entropy of p and the entropy of q, i.e., $E({{\bf{p}}})-E({{\bf{q}}})=-\mathop{\sum }_{j=1}^{k}{p}_{j}\log ({p}_{j})+\mathop{\sum }_{j=1}^{k}{q}_{j}\log ({q}_{j})$.

The entropy difference measures the amount of decreased uncertainty of cluster membership. A positive entropy difference means E(q) < E(p), so the associated data point appears to be less ambiguous in cluster membership after embedding. Vice versa, a negative entropy difference means increased uncertainty after embedding.

Since calculating entropy differences is based on ground-truth labels and fitting a clear statistical model, we believe that entropy differences are a relatively objective evaluation of visual uncertainty. If a diagnostic score without label information is aligned with the entropy difference, then the diagnostic score is likely to be reliable.

Evaluation score of neighborhood preservation

We calculate point-wise neighborhood preservation scores to evaluate how well the local structures are preserved by an embedding algorithm. Given the input matrix X and the embedding matrix Y, to calculate the neighborhood preservation score for the i-th point, we first identify its k-nearest neighbors in the input space, with their indices denoted as ${{{\mathcal{N}}}}_{i}=\{{i}_{1},{i}_{2},\ldots,{i}_{k}\}$. Then, we compute the distances from the i-th point to its neighbors in both the input and embedding spaces:

$${{{\bf{d}}}}_{i}^{\,{\mbox{input}}\,} ={[d({{{\bf{x}}}}_{i},{{{\bf{x}}}}_{{i}_{1}}),\ldots,d({{{\bf{x}}}}_{i},{{{\bf{x}}}}_{{i}_{k}})]}^{\top }\\ {{{\bf{d}}}}_{i}^{\,{\mbox{embedding}}\,} ={[d({{{\bf{y}}}}_{i},{{{\bf{y}}}}_{{i}_{1}}),\ldots,d({{{\bf{y}}}}_{i},{{{\bf{y}}}}_{{i}_{k}})]}^{\top }.$$

The neighborhood preservation score for the i-th point is defined as the correlation between ${{{\bf{d}}}}_{i}^{\,{\mbox{input}}\,}$ and ${{{\bf{d}}}}_{i}^{\,{\mbox{embedding}}\,}$. A higher correlation indicates better preservation of the neighborhood structure.

We use the median neighborhood preservation score across all points in the dataset to assess the overall neighborhood preservation of the embedding. For hyperparameters, we choose k = [n/5] and use the Euclidean distance as the metric d in implementation.

Davies-Bouldin index

We calculate the DB index⁴⁵ using the R function index.DB in the R package clusterSim (version 0.51-3) with p = q = 2, i.e., using the Euclidean distance.

Within-cluster distance ratio

Consider m clusters and in each cluster i, there are n_i data points, denoted as ${\{{{{\bf{x}}}}_{ij}\}}_{1\le j\le {n}_{i}}$. The centroid for each cluster is denoted as ${{{\bf{x}}}}_{i\cdot }=\frac{1}{{n}_{i}}\mathop{\sum }_{j=1}^{{n}_{i}}{{{\bf{x}}}}_{ij}$ and the mean of all data points is denoted as ${{{\bf{x}}}}_{\cdot \cdot }=\frac{1}{n}\mathop{\sum }_{i=1}^{m}\mathop{\sum }_{j=1}^{{n}_{i}}{{{\bf{x}}}}_{ij}$.

Denote the total sum of squares (TSS) and the within-cluster sum of squares (WSS) by

$$\,{\mbox{TSS}}\,=\mathop{\sum }_{i=1}^{m}{\sum }_{j=1}^{{n}_{i}}\parallel {{{\bf{x}}}}_{ij}-{{{\bf{x}}}}_{\cdot \cdot }{\parallel }_{2}^{2},\quad \,{\mbox{WSS}}\,={\sum }_{i=1}^{m}{\sum }_{j=1}^{{n}_{i}}\parallel {{{\bf{x}}}}_{ij}-{{{\bf{x}}}}_{i\cdot }{\parallel }_{2}^{2}.$$

The within-cluster distance ratio is defined as $\,{\mbox{WCDR}}=\frac{{\mbox{WSS}}}{{\mbox{TSS}}\,}$. A smaller within-cluster distance ratio WCDR indicates a more pronounced clustering effect.

Wilks’ Λ

We compute Wilks’ Λ statistic⁴⁶ by performing a multivariate analysis of variance using the manova function from the R package stats (version 4.2.1), followed by a statistical test.

Statistical tests for distribution difference of singularity scores

We have claimed that embedding points with large singularity scores tend to appear in random locations under small perplexities but appear in the periphery of clusters under large perplexities. To quantitatively verify such distinction, we conduct several statistical tests and find that the results of the tests support our claim about the distribution difference (Supplementary Tables 4–6). We provide the details of the tests as follows.

We first conducted Spearman’s rank correlation tests. Given the embedding ${{\bf{Y}}}={[{{{\bf{y}}}}_{1},\ldots,{{{\bf{y}}}}_{n}]}^{\top }$ and the cluster label of each point as well as their singularity scores ${{\bf{s}}}={[{s}_{1},\ldots,{s}_{n}]}^{\top }$, we can first calculate the distance of each point to its cluster center. The distance vector is denoted as ${{\bf{d}}}={[{d}_{1},\ldots,{d}_{n}]}^{\top }$. We then conduct the Spearman’s rank correlation test⁵⁶ on the singularity scores s and the distances to cluster center d. The tests show that there is no significant correlation under low perplexity but a significant correlation under larger perplexity.

We use the function cor.test in the R package stat (version 4.2.1) to perform Spearman’s rank correlation tests.

We then conducted tests for the local regression models. To test for distribution differences, we first fit a local regression model⁵⁷ using the singularity scores as the response variables and the coordinates of embedding points as predictors. Next, we fit a null model with the singularity scores as the response and only the intercept as the predictor. An F-test is then conducted to determine whether the magnitude of the singularity scores is associated with the locations of the embedding points.

We also perform permutation tests by shuffling the singularity scores and fitting a local regression model for each shuffle to approximate a null distribution for the residual sum of squares. Empirical p-values are then computed to assess whether the singularity scores are distributed randomly. Lower p-values suggest rejecting the null hypothesis of random distribution.

We use the loess function from the R package stat (version 4.2.1) to fit the local regression models.

Benchmark methods for OOD detection

Kernel PCA

We implemented the state-of-the-art kernel PCA method for out-of-distribution detection⁵² to benchmark against the perturbation score. Since our perturbation score does not require separate training and testing steps and was directly applied to the dataset, kernel PCA was trained on the dataset and then evaluated on the same dataset to ensure a fair comparison. Additionally, to maintain consistency with the default PCA preprocessing step in the t-SNE algorithm, we applied PCA before training, retaining the first 50 principal components.

One-class support vector machine

We implemented the one-class support vector machine (SVM)⁵³ using the OneClassSVM function from the Python package scikit-learn (version 1.2.0), employing a polynomial kernel for optimal performance. Since our perturbation score does not require separate training and testing steps and was directly applied to the dataset, one-class SVM was also trained on the dataset and then evaluated on the same dataset to ensure a fair comparison. To align with the preprocessing step in t-SNE, we first applied PCA, reducing the data to its top 50 principal components before training.

Datasets

Gaussian mixture data

A Gaussian mixture model with k components is a linear combination of k-component Gaussian densities. The probability density function of the random variable x generated by Gaussian mixture model⁵⁸ is

$$p({{\bf{x}}})={\sum }_{i=1}^{k}{\pi }_{i}g({{\bf{x}}}| {{{\mathbf{\mu }}}}_{i},{{{\mathbf{\Sigma }}}}_{i}),$$

where μ_i, Σ_i are the mean and covariance matrix in the i-th component, the scalars π_i, i = 1, 2, …, k are the mixture weights satisfying $\mathop{\sum }_{i=1}^{k}{\pi }_{i}=1$, and g(x∣μ_i, Σ_i), i = 1, 2, …, n are the probability density functions of the Gaussian distribution family with mean μ_i and covariance matrix Σ_i.

We randomly generated Gaussian mixture datasets with various numbers of components and mixture weights using the function rGMM in the R package MGMM (version 1.0.1.1).

Swiss roll data

The Swiss roll data is a classical manifold data. Usually, the dataset consists of three-dimensional i.i.d. data points, denoted as ${(x,y,z)}^{\top }\in {{\mathbb{R}}}^{3}$, where

$$x=t\cos (t),\,y=t\sin (t),z=z.$$

Here, t is the parameter controlling the spiral angle and is uniformly distributed in a chosen range [a, b]. And z is the height parameter and is also uniformly distributed in the chosen span of heights [c, d].

We randomly generated Swiss roll datasets and used the function Rtsne in the R package Rtsne (version 0.17) to obtain the t-SNE embeddings of the datasets. We computed the perturbation scores with perturbation length 1 in Fig. 7b.

Deep learning feature data

We used the pretrained ResNet-18 model to perform a forward pass on the CIFAR-10 dataset to extract features of dimension 512. We also performed the forward pass using the same pre-trained model on the Describable Textures Dataset (DTD) dataset⁵¹ as our out-of-distribution data in Fig. 5. We also randomly subsampled both datasets to reduce computational load. Specifically, in Fig. 1, we sampled 5000 images from the CIFAR-10 test dataset as our deep learning feature data and obtained the t-SNE embedding under perplexity 125. We then computed the perturbation scores with perturbation length 2. In Fig. 5, we sampled 2000 CIFAR-10 images and 1000 DTD images, combining them into a dataset that includes OOD data points. We obtained the t-SNE embedding under perplexity 100 and computed the perturbation scores with perturbation length 2.

Mouse brain single-cell ATAC-seq data

The ATAC-seq dataset was created to capture the gene activity of mouse brain cells. The dataset has been preprocessed by Luecken et al.⁵⁹. We applied the R functions CreateSeuratObject, FindVariableFeatures and NormalizeData in R package Seurat to identify 1000 most variable genes for 3618 cells. The dataset was subsampled when being used to verify the LOO assumption.

Mouse embryonic stem cell differentiation data

The single-cell RNA-seq dataset was constructed to investigate the dynamics of gene expression of mouse embryonic stem cells (mESCs) undergoing differentiation⁵⁴. The dataset was preprocessed, normalized, and scaled by following the standard procedures by R package Seurat using functions CreateSeuratObject, NormalizeData and ScaleData. We also used R function FindVariableFeatures to identify the 2000 most variable genes for all 421 cells.

Human pancreatic tissue single-cell RNA-seq data

The single-cell RNA-seq data generated from human pancreatic tissues⁶⁰ provides a comprehensive view of gene expression across 8 different cell types in pancreatic tissue. The dataset was preprocessed, normalized, and scaled by following the standard procedures described above. We also used R function FindVariableFeatures to identify the 2000 most variable genes for all 2364 cells. The dataset was subsampled when being used to verify the LOO assumption.

Single-cell RNA-seq data of PBMCs with treatment of interferon-beta

This single-cell RNA-seq dataset profiles gene expression in peripheral blood mononuclear cells (PBMCs) following interferon-β (IFNB) treatment, capturing cellular responses to immune stimulation⁶¹. The dataset was preprocessed, normalized, and scaled by following the standard procedures described above. We used R function FindVariableFeatures to identify the 2000 most variable genes for all 6,548 cells. The dataset was subsampled when being used to verify the LOO assumption.

Mouse mammary epithelial single-cell data

This dataset contains the gene expression profile of mammary epithelial cells across from two mice at four developmental stages: nulliparous, mid-gestation, lactation, and post-involution⁵⁵. The dataset was preprocessed, normalized, and scaled by following the standard procedures described above. We used R function FindVariableFeatures to identify the 2000 most variable genes for all 25,806 cells.

Implementation of t-SNE

We used the function Rtsne in the R package Rtsne (version 0.17) to perform the t-SNE algorithm. We choose theta = 0 to perform exact t-SNE. We also adjusted the code in Rtsne to access the similarity scores ${({v}_{i,j}({{\bf{X}}}))}_{i < j}$. The adjusted function Rtsne can be found in https://github.com/zhexuandliu/MapContinuity-NE-Reliability.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.