Introduction

Prior to the introduction of the Omicron variant in Hong Kong, one primary case infected with the ancestral Wuhan-like strain of SARS-CoV-2 might infect on average two or three secondary cases when the surrounding population is completely susceptible, according to the estimates of the basic reproduction number1,2 i.e. R0 = 2-3. However, it has been commonly observed that the offspring distribution of SARS-CoV-2 infected individuals is highly heterogenous or “heavy-tailed”, whereby 20% of cases may be responsible for 80% of all new infections3,4. Transmission heterogeneity can be measured directly by the dispersion parameter k of a negative-binomial distribution5,6 when fitted to a count distribution of individual offspring, that is, the number of secondary cases directly infected by any one case, including zero. When looking into individual offspring, superspreading event is observed when a few cases infected many others than the rest of the cases. Extending to a general form, superspreading event is observed when a few transmission clusters involved far more cases and resulted in large outbreaks than the rest of the transmission clusters which only involved a few cases. Given such, the dispersion parameter k can also be indirectly estimated from distributions of final cluster sizes or transmission chain sizes when modelled as a stochastic branching process7. This approach can be particularly useful in public health because contact tracing data detailing infector-infectee relationships is rarely feasible except for minor outbreaks. Importantly, smaller values of k correspond to greater degrees of overdispersion. Consequently, when k decreases (holding the mean of offspring or final cluster size constant), the expected probability of observing large explosive clusters, i.e. superspreading events, increases, which poses unique challenges for outbreak control compared to outbreaks with less heterogenous transmission (when k is higher). Past studies estimating overall transmission heterogeneity for SARS-CoV-2 found k ranged between 0.2 and 0.64,8,9,10, which indicate considerable superspreading potential, assuming a threshold value for superspreading of k = 1. However, these estimates largely reflect overall transmission heterogeneity at the population level4,8, though some studies have examined transmission heterogeneity in a single setting10, or stratified by the age of infectors9.

From an outbreak control perspective, it is important to consider how transmission dynamics may be different across settings. At least one previous study on COVID-19 found substantial differences between estimates of the reproduction number by setting11, emphasizing the need for setting-specific control measures. Moreover, previous studies have found that public health and social measures (PHSMs) could shorten the realized generation interval12,13 by truncating the infectious period. But these results only represent shortening of the generation interval at the population level, again, with rare studies examining whether realized generation intervals could differ by setting14. As such, investigation of setting-specific superspreading potential and generation interval could be used to understand the effectiveness of PHSMs, and the need for setting-specific interventions to better prepare for future outbreaks.

In this work, we use detailed clustering data on COVID-19 cases in Hong Kong provided by the Centre for Health and Protection (CHP) from 2020 to 2021, to characterize eight distinct transmission settings, and investigate the superspreading potential in a general form based on observed final cluster size distribution stratified by transmission settings. We compare the estimated mean (\({C}_{Z}\)) and degree of overdispersion (k) of the number of new infections (secondary cases generated by the index case plus any further subsequent infections) per transmission cluster under each setting, and additionally estimate the realized mean generation interval under each setting.

Results

Cluster identification and observed cluster size distribution

From data on 8647 confirmed COVID-19 cases in Hong Kong during the study period (23 January 2020 to 15 December 2021), we identified 2228 local transmission clusters involved at least two cases that fell under eight transmission settings of interest (households; restaurants; close-social indoor activities; retail and leisure activities; office work; manual labour work; nosocomial setting; and residential care homes), and 1582 single index cases regarded as clusters of size n = 1, resulting in a total of 3810 clusters. Household setting involved the majority of all discrete clusters identified (87.1%, 3318/3810), with the rest of the other settings involved substantially fewer clusters: 365 clusters were identified as office-work clusters, followed by 282 restaurant clusters, 253 manual labour work clusters, 108 retail and leisure activity clusters, 80 nosocomial clusters, 61 close-social indoor clusters and 59 care home clusters. Figure 1 visualized the contact tracing process and how cases were denoted as cluster members and entered into CHP’s line list. When defining single index cases, we in principal identified these cases as those who were initially denoted by CHP as local cases (no recent travel history reported) with unknown source of infection (so that could not be linked to any other reported case or cluster), but provided valid information in at least one of the following: (i) residence address; (ii) occupation; (iii) workplace; so that can be classified into the transmission settings of our interest. Exceptions were made for care home setting, that among the 1582 single index cases identified, there were 12 cases who were not initially denoted as local cases with unknown source of infection by CHP, but were household cluster members. However, we included these cases as single index cases under care home setting due to their occupation/workplace were related with care homes, meaning they had been stayed in care homes but did not spread infections in their related care homes. There were 716 out of 1582 single index cases classified into two transmission settings, household and either of the remaining seven settings, due to having valid information in residence plus workplace and/or occupation. Additional details can be found in method section, supplementary methods 1.1 and supplementary table 1. Moreover, among all the 8647 cases, 1934 were asymptomatic cases (22.37%), while the asymptomatic proportion by transmission setting ranged from 12% to 39% (Supplementary Table 1).

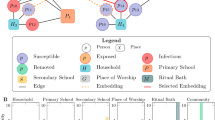
Fig. 1: Visualization of contact tracing and returned line list data when an outbreak happened in a specific venue in Hong Kong.
figure 1

The figure describes an outbreak was first occurred in a bar, with cases A to E (as indicated by pink dots) identified, then contact tracing found subsequent household infectees (cases F to H, indicated by green dots) generated by case E, and subsequent infectees (cases I and J, indicated by orange dots) generated by case C in a restaurant. The table at right side showed how these cases were entered into the line list with transmission cluster information presented.

Full size image

Figure 2a, b showed the empirical distribution of cluster sizes and the relative proportion of cluster sizes under different transmission settings. For all settings, the median cluster size did not exceed two, but the maximum cluster size differed substantially. Specific examples included a large outbreak with n = 395 cases originating from a close-social indoor activity. In contrast, care homes, manual labour work, and retail & leisure settings, had a maximum observed cluster size around 50, while office work setting did not have any cluster with more than 10 cases.

Fig. 2: Empirical transmission cluster size distribution and cluster category frequency during COVID−19 pandemic in Hong Kong from 23 January 2020 and 15 December 2021.
figure 2

a Boxplots of cluster size distribution overall and stratified by transmission setting, single index case was counted as size of 1 in each setting. Box showed the inter-quartile range (IQR), bold line within box showed the median, whisker showed upper quartile plus 1.5 times IQR, dots showed the empirical values. The y-axis shows the cluster size, the numbers under the labels of x-axis indicate number of clusters identified in each transmission setting. Number of clusters involved at least 2 cases in each setting sum together equals to 2228 as in all clusters, while number of single index cases in each setting sum together equals to 2298, but number of single index cases in all clusters is 1582, due to single index cases could belong to more than one setting. b Histogram of empirical cluster size distribution in each setting. Colors in green, grey, orange, blue, teal, purple, pink and brown represent all clusters, households, office work, restaurants, manual labour work, retail & leisure, nosocomial, close-social indoor and care homes respectively.

Full size image

Setting-specific transmission heterogeneity and mean cluster size

Our cluster size model assuming an underlying negative binomial distribution estimated an overall dispersion parameter k was 0.56 (95% CI (Confidence Interval): 0.51, 0.61) with mean \({C}_{Z}\) (number of new infections generated per cluster) of 1.29 (1.21, 1.37), based on observed size distribution of all clusters. This means that an average of 1.29 new infections were expected per transmission cluster at the population level, but its variance is over three times larger than the mean, due to a relatively small value of k, such that large outbreaks were possible to occur in the population. Household setting had the lowest degree of overdispersion (k = 1.11, 95% CI: 0.94, 1.28) in number of new infections per cluster, while retail and leisure setting had highest degree of overdispersion (k = 0.05, 95% CI: 0.01, 0.09). Estimates of k for other settings ranged between 0.1 and 0.5. Estimates of \({C}_{Z}\) also varied between settings: office work setting had the lowest \({C}_{Z}\) = 0.38 (0.26, 0.50), followed by retail and leisure setting with an estimated \({C}_{Z}\) of 0.58 (0, 1.17). The point-estimates of \({C}_{Z}\) for manual labour work, nosocomial and restaurant settings ranged between 1.0 and 1.5 (Fig. 3a), while for care homes and close-social indoor settings, \({C}_{Z}\) was estimated to be more than 6 with wide confidence intervals. Combining estimates of \({C}_{Z}\) and k, the upper 26% of clusters ranked by size in descending order were responsible for 80% of all new infections happened at the population level. However, we calculated that outbreaks within retail and leisure setting had the highest transmission heterogeneity, whereby the upper 5% clusters were responsible for 80% of the total number of cases infected within this setting. In other words, the great majority of retail and leisure setting’s clusters (95%) were responsible for only 20% of newly infected cases within this setting. For manual labour, care homes and close-social indoor settings, the ratio of upper clusters ranked by size responsible for 80% of all new infections within each setting was around 10%:80%, followed by office and nosocomial settings with a ratio fell within the range of 15–20%:80%; while restaurants and household settings were less heterogenous with a ratio around 25%:80% and 30%:80%, respectively (Fig. 3b, Table 1).

Fig. 3: Jointly estimated dispersion parameter k and mean cluster size \(1+{C}_{Z}\) in all clusters and in each transmission setting, and visualization of transmission heterogeneity.
figure 3

a 95% confidence ellipse of jointly estimated k and 1 + \({C}_{Z}\) and the central estimates (as shown by points), for all clusters and in each specific setting; b Proportion of top clusters ranked by size in descending order that accounted for 80% of all new infections identified in each specific setting based on the central estimates of k and 1 + \({C}_{Z}\) (as shown by points), colors in red from light to dark represent proportion in descending order. Note both the x and y-axis are on a logarithmic scale. Lower values of the dispersion parameter k indicate a more heterogeneous distribution of number of new infections per cluster. Colors in green, grey, orange, blue, teal, purple, pink and brown represent all clusters, households, office work, restaurants, manual labour work, retail & leisure, nosocomial, close-social indoor and care homes respectively.

Full size image
Table 1 Estimation results of k, \({C}_{Z}\) and proportion of upper clusters ranked by size responsible for 80% of all new infections based on cluster ascertainment model
Full size table

Note that the cluster size model estimated \({C}_{Z}\) and k based on given values of the probability of a case being reported (\({q}_{1}\)) and the probability of a reported case being classified to cluster events by contact tracing (\({q}_{2}\)). For the main analyses we assumed all COVID-19 cases were being detected and appeared in the line list during the study period in Hong Kong (such that \({q}_{1}\) = 1), but they had a probability of \({q}_{2}\) to be successfully linked to their related transmission clusters (cluster ascertainment), otherwise they would be missed from the identified clusters in the line list. Based on Hong Kong’s COVID-19 surveillance archive15, we assumed \({q}_{2}\) varied between 0.5 and 0.9 in different settings, with close-social indoor setting having the lowest \({q}_{2}\) (0.5) and household setting the highest (0.9), because of differences in contact tracing efficiency. Table 1 shows the exact values proposed for \({q}_{2}\) in each setting. While in sensitivity analyses we tested the other two types of ascertainments, (a) the individual ascertainment, assuming all detected cases were linked to their related clusters successfully (such that \({q}_{2}\) = 1), but cases had a probability of \({q}_{1}\) to be detected and reported; and (b) the double ascertainment, assuming that cases first had a probability of \({q}_{1}\) to be detected and reported, followed by another probability of \({q}_{2}\) to be successfully traced to their related clusters. See supplementary methods 1.2 for more details, and the results of these two alternative ascertainment models can be found in supplementary table 2. We also tested combinations of different \({q}_{1}\) and \({q}_{2}\), and found the estimated degree of overdispersion decreased (i.e. k increased) as either cases being more likely to be reported (\({q}_{1}\) increased) or cases being more likely to be successfully traced to their corresponding clusters (\({q}_{2}\) increased, see Supplementary Fig. 1). In contrast, we observed \({C}_{Z}\) increased as \({q}_{2}\) increased, but decreased when \({q}_{1}\) increased (Supplementary Fig. 2).

Setting-specific infection-to-report delay and generation intervals

To infer the setting-specific generation intervals, we first inferred the setting-specific delay distribution from infection to report (as during the process of imputing infection times for each case, see method section for more details). We found differences in the average delay interval between settings. Specifically, care home setting had the shortest mean delay interval of 9.1 days with standard deviation (SD) of 3.2 days, while retail and leisure setting had the longest mean delay interval of 12.5 days with SD of 3.8 days. For all other settings the mean delay intervals were within 10–12 days (Supplementary Table 3, Supplementary Fig. 3).

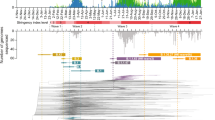
Upon obtaining each case’s infection times, we used a Gamma mixture model to estimate the generation interval (GI) distribution considering four possible paths underlying the infection time intervals between earliest case and the rest of the cases in a cluster (Supplementary Fig. 4). Setting-specific estimates of the generation interval were similar overall with overlapping confidence intervals in mean and standard deviation (Table 2, Fig. 4). In terms of pooled mean GI estimates, restaurants, close-social indoor and retail & leisure settings had similar mean GIs around 5.5 days, while the mean GI for manual labour setting was about one day longer. The longest mean GIs were found in care home and nosocomial settings, both with a pooled mean around 7 days, while office work setting had the shortest GI with pooled mean around 4.4 days. We also visualized the density of different transmission paths estimated from first to successive cases under each transmission setting in Supplementary Fig. 5. Additional sensitivity analyses of the GI distributions by setting found little differences compared with the main results, when applying an alternative delay interval distribution based on Pei et al.16 (Supplementary Methods 1.3, Supplementary Table 4, Supplementary Fig. 3). More technical details can be found in Supplementary Methods 1.4.

Fig. 4: Estimated generation interval distribution in each transmission setting.
figure 4

a Estimated mean generation interval (as shown in points, which is the pooled mean of point-estimated mean generation interval over 100 sample sets of each cluster’s index-case-to-case infection intervals in each setting) with 95% bootstrap confidence interval (as shown in error bars, which is the 2.5% to 97.5% quantile of estimated mean generation interval over 100\(\times\)100 bootstrap resampled data) in each transmission setting, horizontal dashed line indicate pooled mean generation interval of all clusters; b Estimated standard deviation of the generation interval (as shown in points, which is the pooled mean of point-estimated standard deviation of the generation interval over 100 sample sets of each cluster’s index-case-to-case infection intervals in each setting) with 95% bootstrap confidence interval (as shown in error bars, which is the 2.5% to 97.5% quantile of estimated standard deviation of the generation interval over 100\(\times\)100 bootstrap resampled data) in each transmission setting, horizontal dashed line indicate pooled standard deviation of all clusters; c, Probability density of inferred generation interval distribution based on central estimates in each transmission setting, density plotted by dashed line indicate inferred distribution based on pooled mean and standard deviation of all clusters. Colors in green, grey, orange, blue, teal, purple, pink and brown represent all clusters, households, office work, restaurants, manual labour work, retail & leisure, nosocomial, close-social indoor and care homes respectively.

Full size image
Table 2 Inferred mean and standard deviation of generation interval in each setting
Full size table

Sensitivity result on individual-level mean offspring size and overdispersion by setting

To further explore individual level transmissibility and transmission heterogeneity, and to check whether that should be consistent with cluster level findings under specified settings, we divided the total cluster size into offspring size in each transmission generation relative to the cluster index case, assuming up to quaternary transmission was possible, based on the setting-specific GI estimates. We then fitted the same negative binomial model on these offspring sizes, thus to directly obtain the mean and dispersion parameter of the setting-specific offspring distribution, where the mean offspring size by setting equals to the setting-specific reproduction number (denoted as \({R}_{C}\)). Methodology details were presented in method section and supplementary methods 1.5. Based on the main model (as in cluster ascertainment), we estimated the setting-specific reproduction number varied from 0.34 (in office setting) to 5.32 (in close-social indoor setting), and the dispersion parameter varied from 0.1 (most heterogeneous, in retail and leisure setting) to above 100 (least heterogeneous, in household setting) (Table 3). Further on these estimates, the proportion of infectors that were responsible for 80% of the infectees under each setting varied from 8.20% (as in retail and leisure setting) to 39.23% (as in household setting). The estimates remained consistent when considering both individual ascertainment and double ascertainment scenarios for the negative binomial model (Supplementary Table 5).

Table 3 Estimation results of setting-specific mean and dispersion parameter of individual level offspring distribution and proportion of infectors responsible for 80% of all offspring cases based on cluster ascertainment model
Full size table

Association between realized generation interval and cluster size based on simulation

We found that more truncation on the realized generation interval (as in lower threshold of a maximum length of the generation interval that an infectious contact could have) would result in smaller maximum offspring size an infector could generate, holding initial settings of dispersion parameter k and mean number of infectious contact constant. Such impact was more obvious when the initial setting for the number of infectious contacts was more heterogeneous: Given same truncation threshold on realized generation interval, simulated epidemics with smaller k in the initial setting for the number of infectious contacts would have more reduced maximum offspring size than simulated epidemics with larger k in the initial setting. Details can be found in Supplementary Methods 1.6, Supplementary Fig. 6.

Discussion

Using detailed clustering data from Hong Kong, this study quantified and compared the transmission heterogeneity of SARS-CoV-2 across eight distinct transmission settings and inferred the generation interval distributions within these settings. At the population level, the estimated dispersion parameter (k = 0.56) and mean (\({C}_{Z}\) = 1.29) for the number of new infections per cluster over all transmission settings (Fig. 3a) indicated a moderate degree of transmission heterogeneity, as we estimated 26% of upper clusters ranked by size in descending order were responsible for 80% of all new infections (Fig. 3b), which was consistent with previous study of overall transmission heterogeneity reported in Hong Kong4.

When specified by setting, substantial transmission heterogeneity was observed in three particular settings: (i) retail and leisure setting such as shopping malls and supermarkets; (ii) care homes for elders and disabled persons; and (iii) close-social indoor setting such as bars and clubs; where less than 10% of the upper clusters were responsible for 80% of all new infections within these settings. However, there was large difference in point-estimates of \({C}_{Z}\) between these settings, with care home and close-social indoor settings had \({C}_{Z}\) above 6, while retail setting had \({C}_{Z}\) less than 1. Looking into k and \({C}_{Z}\) together, controlling SARS-CoV-2 outbreaks in close-social indoor setting and care homes should be prioritized than retail and leisure setting, because although they all had very small value of k (≤0.1) indicating high degree of overdispersion, much larger \({C}_{Z}\) in care homes and close-social indoor settings suggested transmission events were much more sustainable than retail and leisure setting if without effective interventions. While for retail and leisure setting, although it had the smallest k (0.05) over all settings, a \({C}_{Z}\) lower than 1 suggested on average the outbreaks within this setting were unsustainable despite occasional superspreading events. As the variance of the number of new infections per cluster is dependent on both k and \({C}_{Z}\), it explains that although manual labour setting had slightly less transmission heterogeneity than retail setting (\({k}^{{retail}}\) = 0.05 <\({k}^{{manual\; labour}}\) = 0.13), we observed similar maximum cluster size in these two settings due to the fact that manual labour setting had \({C}_{Z}\) higher than retail setting \(({C}_{Z}^{{manual\; labour}}=1.04 > {C}_{Z}^{{retail}}=0.58)\). Restaurant, nosocomial, manual labour, and household settings had similar point-estimates of \({C}_{Z}\) within the range of 1 – 1.5, but k for households was a unique outlier (k > 1). This phenomenon could be explained by the physical constraints of households, where clusters were limited by household size. In Hong Kong, the average household size is 2.7 persons (statistics from year 202317), which is smaller than the capacity of most of the other settings investigated in this study, which naturally limits superspreading potential within households. In all, these results were consistent with early observational studies on COVID-19, showing some particular settings such as care homes, social and manual labour settings had considerable superspreading potential4,8,9,18. Note that traditional epidemiological studies usually focus on the effective reproduction number over time at population level, but rare studies provided detailed investigation by setting10 as shown in this study.

In Hong Kong, routine testing and active surveillance were implemented in care homes. Despite these efforts, we found care homes had both strong superspreading potential and larger than average cluster sizes, and also had the longest pooled mean GI (7.0 days), suggesting difficulties in outbreak control were experienced. However, it should be noted that given the small number of care home clusters reported, confidence intervals were relatively wide in care home setting’s estimated parameters (3.7–10.3 days for mean GI, 0–20.81 for \({C}_{Z}^{{care\; home}}\), 0.03 – 0.16 for \({k}^{{care\; home}}\)). Taken together, the small number of care home clusters observed in our study may also indicate the specific effectiveness of interventions preventing infection introductions into care homes, compared to interventions designed to control transmission within care homes, meaning outbreaks were large, but infrequent. Although we inferred that care homes had the shortest average delay interval from infection to report than other settings (Supplementary Table 3) (likely due to proactive routine testing), it was insufficient to prevent widespread within-setting transmission.

The overall pooled mean generation interval (GI) across all settings was 5.5 days, which was similar to many population-level estimates of the generation interval14. When specified by settings, office work setting had the shortest pooled mean GI of 4.4 days, while care home setting had the longest pooled mean GI at 7.0 days. Despite differences in age and underlying conditions between office work cases and care home cases that could contribute to different GIs19, a 2.6-day shorter mean GI in office setting might also suggest forward transmissions in offices were more likely to be prevented than that in care homes, thus resulted in much smaller cluster size (in both mean and maximum numbers) in office setting than in care home setting.

The sensitivity results of setting-specific mean and overdispersion of offspring distribution were generally in line with the main results based on total cluster sizes (Tables 1 and 3). The values of estimated k in offspring distribution were larger than that in main results (i.e. less overdispersion), which was expected as dividing total cluster size into offspring sizes reduced the extreme values. Note that at individual offspring level, household and retail settings still represent the least and most heterogenous transmission setting respectively. The estimates of mean offspring size \({R}_{C}\) were slightly smaller than the estimates of \({C}_{Z}\) in general for each setting, suggesting transmissions within clusters identified in this study were mainly primary to secondary transmissions, despite the differences between offspring size and cluster size by definition. Social setting had the largest \({R}_{C}\) while office setting had the smallest, and the descending order of estimated \({R}_{C}\) by setting was the same as based on main estimates of \({C}_{Z}\). Yet, \({R}_{C}\) for care home setting was much smaller than \({C}_{Z}^{{care\; home}}\) (2.64 v.s. 6.17), indicating more sustainable transmissions, which could possibly be primary to tertiary or quaternary transmissions, were more likely to occur in care homes than other settings. Although this sensitivity analyses relied on the assumptions of underlying transmission paths, and there could be some bias in these estimates (details in Supplementary Notes 2.4), the results showed the consistency of the model outcome and provided a feasible approach to assess individual level transmission heterogeneity based on cluster level data.

Our simulation study showed that truncation on infectious period led to shorter realized generation intervals and fewer offspring. This effect was especially pronounced when k was small (Supplementary Notes 2.5, Supplementary Fig. 6), like with our estimates of k in office work setting. Relating observational and simulation results together, the shorter generation interval and smaller cluster size found in office work setting could be explained by the strict control measures implemented in this setting during the study period in Hong Kong. Interventions in offices included mask wearing, temperature screening and mandatory symptom monitoring in periods outside of work from home policies; self-isolation and contact tracing would be quickly implemented when a test positive case was reported in the office. Thus, potential outbreaks within offices might have been controlled more easily compared with other settings. For outbreaks within retail and leisure setting, close-social indoor venues, and manual labour setting, logistic delays in contact tracing might explain the slightly longer mean GIs (as in pooled mean estimates) and therefore larger maximum cluster sizes observed.

This study is a unique extension of previous studies on superspreading events and generation interval estimation4,20, at both data level and methodology level, although limitations should be noted. First, categorization of the transmission clusters in this study was specific to the observed outbreaks in Hong Kong and may therefore not be generalizable to other locations. Second, small sample sizes for some settings have reduced the precision of setting-specific estimates of k, \({C}_{Z}\) and the generation interval. Third, our cluster size model relied on given information of the success rates in case detection and cluster identification. Our results would be biased if detection rates were inconsistent across cluster members or identification rates were inconsistent across clusters. Although we did test multiple realistic ascertainment scenarios in our sensitivity analysis, and found sensitivity results did not differ significantly from main results. Fourth, the infection times were imputed based on fixed delay distributions, while detailed exposure time data would allow us to conduct more accurate inference of the infection times in a temporal manner13,21, if available. Fifth, our analyses strongly relied on contact tracing data, but potential bias in data collection in different settings and at different times during the epidemic might have influenced the primary data source in unknown ways. Moreover, although our line list data recorded symptoms for each case if applicable, these symptom records contained recall bias and were not limited to typical respiratory symptoms, thus could not be used to infer the underreporting rate as the study conducted by Poletti et al.22, otherwise could be helpful to improve our model inference. Lastly, our data was limited to the ancestral SARS-CoV-2 (Wuhan) strain, as no variants of concern sustained circulation in Hong Kong during the study period. Future studies could investigate whether setting-specific transmission heterogeneities in k, \({C}_{Z}\) and the generation interval differ by variants if data allows.

In conclusion, we conducted a unique analysis of setting-specific transmission characteristics of COVID-19 in terms of superspreading potential and generation interval, and explored the relationship between the generation interval and the maximum cluster size a transmission event could achieve, in the context of targeted interventions and varying superspreading potential within different settings. Tailored intervention strategies should consider three aspects to control setting-specific outbreaks: (1) reducing superspreading potential (e.g. limiting the number of exposures), (2) reducing average transmission potential (e.g. physical distancing, masking, and ventilation), and (3) reducing the average infectious period (e.g. rapid case detection and isolation).

Methods

Our study received ethical approval from the Institutional Review Board of the University of Hong Kong (HKU/HA HKW IRB Ref. No.: UW 20-341).

Data collection and event setting categorization

We compiled a line list of all SARS-CoV-2 infected individuals confirmed in Hong Kong by polymerase chain reaction (PCR) between 23 January 2020 and 15 December 2021 using data provided by the Centre for Health Protection (CHP), Department of Health of Hong Kong. The initial contact tracing information are available from CHP’s press release archive23, previous studies also used such data to conduct updated analyses of COVID-19 transmission dynamics in Hong Kong4,24,25,26. Note that before the Omicron wave, Hong Kong implemented strict containment measures and managed to keep the local transmission of SARS-CoV-2 at very low level27,28, thus the public health officers were able to conduct detailed and intense contact tracing. The contact tracing findings resulted in a line list data that recorded demographics of age, sex, address, workplace and occupation where available, and complete dates of symptom onset (if symptomatic and reported), confirmation, and admission to hospital and discharge (or death), for each SARS-CoV-2 infected individual confirmed by CHP. These individuals were treated as the COVID-19 cases by the CHP and were sent to designated hospitals or healthcare institutes to complete at least 14-day quarantine and/or treatment until PCR negative, regardless of symptom status29. All cases were classified as either locally infected or infected overseas if reported onset dates overlapped a recent history of overseas travel given a maximum 14-day incubation period. All cases reported during the study period occurred before the importation and spread of the Omicron subvariant in Hong Kong. A previous study had used this line list data to explore the unique time-varying pattern of the serial interval distribution in Hong Kong24, while based on the same data, this study focused on the local transmission clusters instead of one-to-one local transmission pairs.

Suspected local transmission clusters were initially identified by the CHP if at least two cases were found to have common source of exposure in time and space, e.g. recent patronage at a restaurant; or had a clear epidemiological linkage, e.g. living in the same household; and at least one case in the cluster was identified as being locally infected. In this way, these discrete clusters consist of index case and all subsequent infections/generations directly involved within each cluster, e.g. secondary cases, as well as potential tertiary and quaternary cases. Figure 1 illustrated an example of the cluster sourcing and contact tracing conducted by CHP. Furthermore, this study focused on local transmission clusters only, therefore clusters of cases solely comprising imported cases were excluded from the analysis; however, clusters where the primary case was infected overseas but linked to local transmission, i.e., an introduction event, were included. Moreover, we further checked the cluster size that each identified transmission cluster involved, clusters that were complete subsets of larger clusters were removed from the analyses; cluster size would be subtracted if a cluster had more than one case with exposure history to another cluster that was linked to an earlier transmission event; cluster size would also be reduced if there was more than one imported case involved. Details can be found in Supplementary Methods 1.1.

Clusters were classified into eight aggregate and distinct event settings: (i) households, (ii) restaurants, (iii) close-social indoor activities, (iv) retail and leisure activities, (v) office work, (vi) manual labour work, (vii) nosocomial, and (viii) residential care homes. Close-social indoor setting other than restaurants included cases related to bars, gyms, clubs, beauty salons, or similar indoor venues unrelated to primary food service; while retail and leisure activities included cases related to malls, supermarkets, or other similar venues unrelated to primary food service. Manual labour setting included workplaces at construction sites, container terminals, slaughterhouses; or work types as cleaning works and other similar work types unrelated to office work or food service (who were included in restaurants). In the line list, there were some cases identified by the CHP as local cases due to no overseas travel history, but were denoted as with unknown source of infection as they could not be linked to any known transmission cluster or any other detected case by CHP’s manual contact tracing. We therefore defined these cases as single index cases and classified them into settings using available residence address, occupation, and workplace information. For example, a single index case who reported his/her occupation as ‘cleaner’ but could not be linked to any known clusters through contact tracing would be identified as a cluster with only one infected individual under the manual labour setting, and this case would also be regarded as a single index case in household setting if residence address was also available and no other reported cases had the same residence address. Also note that a cluster member in a particular setting could also be an index case in another setting (i.e. an infectee in a bar cluster could be an infector in a household cluster), thus this case would be counted in each of the setting involved. Complete details of cluster setting classification and the composition of clusters under each specified transmission setting can be found in Supplementary Table 1.

Joint estimation of k and \({C}_{Z}\) based on cluster size distribution

Using a Negative Binomial cluster size model that considered the ascertainments of case detection and cluster identification as proposed by Tupper et al.10, we jointly estimated the mean (\({C}_{Z}\)) and dispersion parameter (k) of total number of new infections per infection cluster under each transmission setting. We first denote n as the total size of each cluster and assumed one index case per cluster, and denote Z as number of secondary cases as well as any subsequent infections linked to the index whereby Z = n–1. As such, under a specified setting, the average of Z is the setting-specific \({C}_{Z}\). Based on that, \({C}_{Z}\) is not directly comparable to setting-specific estimates of the reproduction number (denote as \({R}_{C}\))11, which represents the mean offspring size for each infected individual under a particular transmission setting. Furthermore, it follows that any setting-specific \({R}_{C}\) can be no larger than \({C}_{Z}\), and these two properties can only be equal when all cases of Z are secondary infections of the index case in each discrete cluster within a setting category.

Assuming Z is a random variable following Poisson distribution with a rate \(\nu\) following Gamma distribution with parameters k and \(\theta\) standing for shape and scale respectively, Z actually follows the Negative-Binomial distribution as Z ~ NB (r, p), where r = k and \(p=1/\left(1+\theta \right)\), so that mean of Z can be expressed as CZ = k·θ, and variance of Z can be expressed as \({\sigma }_{Z}^{2}={C}_{Z}+{C}_{Z}^{2}/k\). Denote parameter set \({{\mathbf{\Theta }}}=\left(k,\theta \right)\), the probability mass function of Z is expressed as follows:

$$\begin{array}{c}{V}_{{{\mathbf{\Theta }}}}\left(j\right)=P\left(Z=j\right)=\frac{\varGamma \left(j+r\right)}{j!\varGamma \left(r\right)}{p}^{r}{\left(1-p\right)}\,^{j}=\frac{\varGamma \left(j+k\right)}{j!\varGamma \left(k\right)}\frac{1}{{\left(1+\theta \right)}^{k}}\frac{{\theta }\,^{j}}{{\left(1+\theta \right)}\,^{j}}\\=\frac{\varGamma \left(j+k\right)}{j!\varGamma \left(k\right)}\frac{{\theta }\,^{j}}{{\left(1+\theta \right)}^{k+j}}\end{array}$$
(1)

We then considered two types of ascertainment. If each SARS-CoV-2 infected individual had a probability of \({q}_{1}\) to be detected and appeared in the line list, this is the individual ascertainment and thus observing number of X cases follows a binomial distribution \(X\sim {{\rm{Bin}}}({{\rm{size}}}=Z+1,{{\rm{prob}}}={q}_{1})\), note \(Z\) itself has the probability mass function described above. Further, suppose upon being detected, each case had a probability of \({q}_{2}\) to be correctly traced to this case’s related cluster, given valid information of residence address, occupation and workplace. Otherwise there was a probability of 1 - \({q}_{2}\) that a case only appeared in the line list but could not be linked to any known cluster or classified into a single index case under any of the transmission setting of our research interest, this is the cluster ascertainment and thus observing a cluster with m cases is \(1-{\left(1-{q}_{2}\right)}^{m}\). Therefore, the resulting probability that m cases were observed in an identified transmission cluster is given as:

$${W}_{{{\mathbf{\Theta }}},{q}_{1},{q}_{2}}\left(m\right)={\sum }_{j=0}^{\infty }\left(\begin{array}{c}{j+1} \\ {m}\end{array}\right){V}_{{{\mathbf{\Theta }}}}\left(j\right){q}_{1}^{m}{\left(1-{q}_{1}\right)}^{j+1-m}\left[1-{\left(1-{q}_{2}\right)}^{m}\right]$$
(2)

Where \({V}_{{{\mathbf{\Theta }}}}\left(j\right)\) represents the probability of the identified cluster generated j number of subsequent infections given parameter set \({{\mathbf{\Theta }}}=(k,\theta )\). But the “true” value of j is unknown, observing m cases linked to this cluster is therefore a subset of the underlying “true” cluster size \((m\le j+1)\), where \(\left({j+1}{m}\right){q}_{1}^{m}{\left(1-{q}_{1}\right)}^{j+1-m}\) is the probability from the binomial distribution that represents individual ascertainment, and \([1-{(1-{q}_{2})}^{m}]\) is the probability that represents cluster ascertainment. Since j is unknown, this probability function sums over the possible values of j from 0 to infinity. But note for m = 0, 1, …. we cannot observe a cluster of size 0, thus the above expressed probability should be further modified into

$$P\left(X=m\right)={U}_{{{\mathbf{\Theta }}},{q}_{1},{q}_{2}}^{-1}{W}_{{{\mathbf{\Theta }}},{q}_{1},{q}_{2}}\left(m\right),{for\; m}=1,2,\ldots,$$
(3)

Where X represent the observed cluster size, \({U}_{\varTheta,{q}_{1},{q}_{2}}^{-1}\) is the denominator to adjust for probability \({W}_{{{\mathbf{\Theta }}},{q}_{1},{q}_{2}}\left(m\right)\) that \({U}_{{{\mathbf{\Theta }}},{q}_{1},{q}_{2}}={\sum }_{m=1}^{\infty }{W}_{{{\mathbf{\Theta }}},{q}_{1},{q}_{2}}(m)\).

For a vector X that consists of the observed total size numbers of n clusters, the final log-likelihood function for parameter set \({{\mathbf{\Theta }}}\) is:

$${\sum }_{i=1}^{n}\log \left[{U}_{{{\mathbf{\Theta }}},{q}_{1},{q}_{2}}^{-1}{W}_{{{\mathbf{\Theta }}},{q}_{1},{q}_{2}}\left({X}_{i}\right)\right]$$
(4)

Note if \({q}_{1}=1\) and \({q}_{2} < 1\), the model only considers cluster ascertainment, which means it is assumed all cases have been detected but not all cases have been successfully linked to their related clusters; if \({q}_{1} < 1\) and \({q}_{2}=1\), the model only considers individual ascertainment, which means it is assumed not all cases have been detected but all detected cases have been successfully linked to their related clusters; if \({q}_{1} < 1\) and \({q}_{2} < 1\), the model considers double ascertainment.

For our main analyses, we adopted the cluster ascertainment model (set \({q}_{1}=1\)), because Hong Kong implemented strict containment measures and active case surveillance including community-wide testing schemes during the COVID-19 pandemic before the Omicron wave, it can be assumed that almost every infected individual had been detected. But due to the limitation of manual contact tracing, not all detected cases had been correctly linked to their clusters. While for sensitivity analyses, we tested the individual ascertainment model (set \({q}_{2}=1\)) and double ascertainment model given different combinations of \({q}_{1}\) and \({q}_{2}\), with more details of the sensitivity analyses described in Supplementary Methods 1.2.

Furthermore, given the estimates of k and \({C}_{Z}\), we calculated the proportion of top clusters ranked by size in descending order that accounted for 80% of all new infections identified in each specific setting, which was generalized from Adam et al.4:

$$1-{{\rm{P}}}80{{\rm{\%}}}=\int _{0}^{Z}{{\rm{N}}}{{\rm{B}}}(\lfloor z\rfloor ;k,\frac{k}{{C}_{Z}+k})dz$$
(5)

Where Z (the number of new infections per cluster) satisfies

$$1-0.8=\frac{1}{{C}_{Z}}\int _{0}^{Z}\lfloor z\rfloor {{\rm{N}}}{{\rm{B}}}\left(\lfloor z\rfloor ;k,\frac{k}{{C}_{Z}+k}\right)\,dz$$
(6)

And

$$\frac{1}{{C}_{Z}}\int _{0}^{Z}\lfloor z\rfloor {{\rm{N}}}{{\rm{B}}}\left(\lfloor z\rfloor ;k,\frac{k}{{C}_{Z}+k}\right)\,dz=\int _{0}^{Z-1}\lfloor z\rfloor {{\rm{N}}}{{\rm{B}}}\left(\lfloor z\rfloor ;k+1,\frac{k}{{C}_{Z}+k}\right)\,dz$$
(7)

Inferring infection times for all cases

We inferred infection times for symptomatic and asymptomatic cases in each cluster setting based on their symptom onset dates and report dates respectively. First, we inferred the infection times for symptomatic cases by using their symptom onset dates minus random draws from an assumed Gamma distributed incubation period with mean of 6.5 days and standard deviation (SD) of 2.6 days. Upon obtaining the infection times of the symptomatic cases, we then fitted the resulting infection-to-report delay interval distribution of symptomatic cases. We further assumed that under Hong Kong’s active case surveillance and effective contact tracing, the asymptomatic cases followed the same infection-to-report distribution as the symptomatic cases, thus we inferred the infection times for asymptomatic cases using their report dates minus random draws from the infection-to-report distribution fitted in previous step. This procedure was repeated 100 times so that each case would have 100 samples of the inferred infection times. See Supplementary Methods 1.3 for more details in the sampling procedure for inferring the infection times.

Estimating the generation interval by mixture model

Based on the inferred infection dates, we constructed index case-to-case (ICC) infection intervals for each cluster as the difference between the date of infection of the earliest infected case and each successive case. Extending upon previous work by Vink et al.30, we assumed the ICC infection interval distribution within each cluster is a mixture of the corresponding generation interval distribution given various potential transmission paths and the underlying chain of infection. We modeled this distribution as a Gamma mixture model with four components corresponding to four paths: (i) co-primary; (ii) primary to secondary (the natural generation interval); (iii) primary to tertiary, and (iv) primary to quaternary. We considered up to quaternary transmission as in line with Vink et al.30, because more intermediate paths would bring more complicity in the model and also more burden on computing efficiency. Visualization and interpretation of the assumed paths is shown in Supplementary Fig. 4. Therefore, we could estimate the mean and standard deviation of the generation interval given the ICC infection interval from the density function of the mixture model formulated as:

$$f\left(x | \mu,{\sigma }^{2}\right)={\sum }_{i=1}^{4}{w}_{i}{f}_{i}\left(x | \mu,{\sigma }^{2}\right)$$
(8)

Where \({f}_{i}(x)\) is the component density of the i’th transmission path, and \({w}_{i}\) is this path’s corresponding weight. Note that for the first transmission path (co-primary infection), infection intervals were assumed to follow a folded Gamma distance distribution31,32, while infection intervals in latter paths were assumed to each follow a Gamma distribution with mean \((i-1)\mu\) and variance \((i-1){\sigma }^{2}\), for i = 2, 3, 4. Due to limited number of transmission paths assumed, we set constraints on number of cases to be sampled in large clusters, details can be found in Supplementary Methods 1.4.

As we obtained 100 samples of infection times for each case, we therefore could obtain 100 sample sets of the ICC infection intervals for each cluster under each setting. We then fitted our generation interval mixture model to each sample set of the ICC infection intervals specified by setting, and estimated the mean and SD by cluster setting by the expectation-maximization algorithm30. Uncertainty around each of the 100 estimates of the mean and SD was determined by non-parametric bootstrap resampling of the ICC infection intervals (n = 100 times). Final point-estimates of the mean and SD of the generation interval were calculated as the pooled mean over 100 estimates based on each ICC infection interval sample set, while confidence intervals were calculated as the 2.5% and 97.5% quantiles of all bootstrap estimates (\({n}_{{bootstrap}}=100\times 100=10000\)) under each setting. Further details of the Gamma mixture model estimation procedure can be found in the Supplementary Methods 1.4.

Sensitivity analyses on individual-level mean offspring size and overdispersion by setting

To assess the transmission heterogeneity at the individual level, rather than at the cluster level, we refined our method to divide total cluster size that might contained multiple transmission generations into offspring sizes in each assumed transmission generation. For a given cluster member’s ICC infection interval, the likelihood of this case belonging to each assumed transmission path from the index case could be calculated based on the fitted generation interval distribution. Thus, each cluster member was categorized into a specified transmission generation counting from the index case, as in one of the four assumed transmission paths (co-primary, primary-secondary, primary-tertiary, primary-quaternary) in particular, based on the highest likelihood assignment. We then re-defined clusters corresponding to offspring cases assigned to each transmission generation plus one assumed index case, and applied the cluster size model on these clusters. This allowed us to estimate the individual-level mean and dispersion parameter of the offspring distribution, and the mean would be equal to the reproduction number specified by setting (\({R}_{C}\)). Results based on cluster ascertainment model were presented as the main result, while those based on individual and double ascertainment models were included in Supplementary Table 5. Details of carrying out this algorithm was described in Supplementary Methods 1.5.

Simulation study on exploring the relationship between realized generation intervals and maximum observed cluster size

We would like to know if there was potential association between realized generation interval and maximum cluster size a transmission cluster could have, as we assumed the impact of behavioural changes and intense non-pharmaceutical control measures would shorten the realized generation interval12,13, thus prevented further transmissions and resulted in fewer subsequent infections. We tested this assumption through a stochastic individual-based SIR (Susceptible-Infectious-Recovered) simulation which has been used in previous studies13,21, we checked how that would have impact on the resulting maximum cluster size observed. For simplicity we defined each transmission cluster in the simulated transmission as each infector plus the direct secondary cases generated by this infector, and thus the cluster size is one plus the offspring size.

We set the initial condition as a closed population with 1000 people, 10 infectors at the beginning, each infector would generate random contact with infectees following a negative binomial distribution with dispersion parameter k and mean R (in such case the mean can be regarded as a proxy of the basic reproduction number by assuming 100% probability of infection through contact), and each random contact was accompanied with a generation interval value following a given generation interval distribution. Therefore, we set different threshold of maximum generation interval that an infector could generate during the simulated epidemic process, and thus contacts with generation intervals beyond the threshold were removed. We then recorded under such condition, the maximum offspring size that one simulated epidemic could achieve, and repeated for 1000 times. We also tested different combinations of given initial settings in the negative binomial distribution for the number of contacts and different choices of the generation interval threshold. Details can be found in Supplementary Methods 1.5.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.