Introduction

With the rapid development of quantum information, its intersection with condensed matter physics has been attracting increasing attention in recent decades1,2. One important topic is to probe the intrinsic physics of many-body systems using the entanglement entropy (EE)3,4,5,6,7. For example, among its many intriguing features, it offers a direct connection to the conformal field theory (CFT) and provides a categorical description of the problem under consideration8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27. Using EE to identify novel phases and critical phenomena represents a cutting-edge area in the field of quantum many-body numerics. A particularly recent issue is the dispute at the deconfined quantum critical point (DQCP)28,29,30. The EE at the DQCP, e.g., in the J-Q model31,32, exhibits markedly different behaviors compared with those in normal criticality within the Landau-Ginzburg-Wilson paradigm21,33,34,35,36,37. According to the prediction from the unitary CFT38,39, the EE with a cornered cutting at the criticality should follow the behaviors s = al − blnl + c, where s is the EE and l is the length of the entangled boundary, in which the coefficient b cannot be negative. However, some recent quantum Monte Carlo (QMC) studies show that b is negative, which seemingly suggests that the DQCP in the J-Q model is not a unitary CFT, possibly indicating a weakly first-order phase transition23,35,36. In contrast, another recent work indicates that the sign of b depends on the cutting form of the entangled region. For a tilted cutting, b is positive and consistent with the emergent SO(5) symmetry at the DQCP34. All in all, the relationship between the EE and condensed matter physics has been growing increasingly closer in recent years.

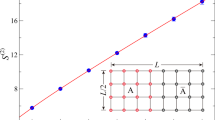
However, obtaining high-precision EE via QMC40,41,42,43,44,45,46,47,48,49,50 with reduced computational cost and a low technical barrier remains a significant challenge in large-scale quantum many-body computations. Although many algorithms have been developed to extract the EE7,51,52,53,54,55,56,57,58,59, some of which can achieve high precision, the details of these algorithms have become increasingly complex. Specifically, the nth order Rényi entropy is defined as \({S}^{(n)}=\frac{1}{1-n}{{\rm{ln}}}{R}_{A}^{(n)}\). The key point in extracting the Rényi ratio \({R}_{A}^{(n)}={Z}_{A}^{(n)}/{Z}^{n}\) is to calculate the ratio of two partition functions within different space-time manifolds \({Z}_{A}^{(n)}\) and Zn directly51,55. In common studies, people usually fix the Rényi order n = 2 as shown in Fig. 1a, b. Due to the area law of EE, \({R}_{A}^{(2)}\propto {e}^{-al}\) decays to zero rapidly in large systems, where l is the perimeter of the entangled region. Once the ratio \({R}_{A}^{(2)}\to 0\), obtaining high-precision \({R}_{A}^{(2)}\) values by QMC based on sampling becomes extremely difficult. To overcome this difficulty, the incremental method of the entangled region was introduced51,52. Its main spirit is one by one adding the lattice sites to increase the entangled region and multiply the ratio of all these intermediate processes to obtain the final ratio. It can be written as: \({R}_{A}^{(2)}={Z}_{A}^{(2)}/{Z}^{2}={\prod }_{i=0}^{{N}_{A}-1}{Z}_{{A}_{i+1}}^{(2)}/{Z}_{{A}_{i}}^{(2)}\), where the i denotes the number of lattice sites in the entangled region, i.e., \({Z}_{{A}_{0}}^{(2)}={Z}^{2}\) and \({Z}_{{A}_{{N}_{A}}}^{(2)}={Z}_{A}^{(2)}\). In this way, a super small value has been divided into a product of several larger values. By calculating each intermediate ratio \({Z}_{{A}_{i+1}}^{(2)}/{Z}_{{A}_{i}}^{(2)}\), high-precision \({R}_{A}^{(2)}\) can be extracted. The shortcoming of this method is that the number of lattice sites must be an integer, which means the process must be split into a finite number of steps, and some ratios \({Z}_{{A}_{i+1}}^{(2)}/{Z}_{{A}_{i}}^{(2)}\) may still be close to zero even after splitting. Moreover, we must note that the replica manifold changes during the calculation due to the intermediate processes in this scheme, which increases the technical barrier of QMC.

Fig. 1: A geometrical presentation of two partition functions within different space-time manifolds.
figure 1

a \({Z}_{A}^{(2)}={{\rm{Tr}}}{[{{{\rm{Tr}}}}_{B}{e}^{-\beta H}]}^{2}\) and b \({Z}^{2}={[{{\rm{Tr}}}({e}^{-\beta H})]}^{2}\), where H is the Hamiltonian of the system. a The entangling regions A of two replicas are glued together along the imaginary time direction and the environment regions B of replicas are not connected each other. While the glued region is zero, it becomes back to Z2 as shown in (b). c Reweighting a distribution: the sampled distribution (black, before reweighting) is used to reweight another distribution (blue, after reweighting), which is reasonable if these two distributions are close to each other, as the importance sampling can be approximately kept.

Full size image

To address the finite splitting problem mentioned above, a continuously incremental algorithm of QMC has been developed7,54. This algorithm involves a virtual process described by a general function \({\tilde{Z}}_{A}^{(2)}(\lambda)\), where \({\tilde{Z}}_{A}^{(2)}(\lambda=1)={Z}_{A}^{(2)}\) and \({\tilde{Z}}_{A}^{(2)}(\lambda=0)={Z}^{2}\). The problem then becomes calculating the ratio \({\tilde{Z}}_{A}^{(2)}(\lambda=1)/{\tilde{Z}}_{A}^{(2)}(\lambda=0)\), which can be expressed as \({\prod }_{{\lambda }_{i}}{\tilde{Z}}_{A}^{(2)}({\lambda }_{i+1})/{\tilde{Z}}_{A}^{(2)}({\lambda }_{i})\). Here λ is a continuous parameter ranging from 0 to 1; thus, the interval [0,1] can be divided into any number of segments {λi} according to the computational requirements. This method improves the calculation of EE to unprecedented accuracy and enables the study of systems of unprecedented size. However, the introduction of additional detailed balance (where the entangled region needs to be varied during the simulation in this method) imposes specific technical requirements on the code implementation. Moreover, due to the virtually non-physical intermediate processes, the results of these intermediate processes \({\tilde{Z}}_{A}^{(2)}(\lambda \ne 1,0)\) cannot be effectively utilized, leading to waste.

In this paper, we propose a simple method that does not alter the space-time manifold during simulation, and the intermediate process values are physically meaningful and valuable. High-precision EE can now be obtained with lower computational cost and a low technical barrier. Moreover, an efficient scheme for extracting the derivative of EE is proposed for the first time to probe phase transition points.

Results

Method

The EE of a subsystem A coupled with an environment B is defined by the reduced density matrix \({\rho }_{A}={{{\rm{Tr}}}}_{B}\rho \), where ρ = e−βH/Z and \(Z={{\rm{Tr}}}{e}^{-\beta H}\) (H is the Hamiltonian). As mentioned in the introduction, the nth order Rényi entropy is defined as \({S}^{(n)}=\frac{1}{1-n}{{\rm{ln}}}[{{\rm{Tr}}}({\rho }_{A}^{n})]=\frac{1}{1-n}{{\rm{ln}}}{R}_{A}^{(n)}\), where \({R}_{A}^{(n)}={Z}_{A}^{(n)}/{Z}^{n}\). The different space-time manifolds of the two partition functions \({Z}_{A}^{(2)}\) and Z2 (considering n = 2) are shown in Fig. 1. From the above equations, we know that \({Z}_{A}^{(n)}\propto {{\rm{Tr}}}({\rho }_{A}^{n})\) while Zn is the proportional factor. The normalization factor Zn is sometimes not important, for example, when we are only concerned with the dynamical information of the entanglement Hamiltonian (e.g., the entanglement spectrum)27,60,61,62,63,64. In these cases, only the manifold of \({Z}_{A}^{(n)}\) needs to be simulated. However, when we consider the calculation of the EE, the factor becomes non-negligible for obtaining the detailed value. In fact, the hardest difficulty of calculating EE comes from the ratio \({R}_{A}^{(n)}={Z}_{A}^{(n)}/{Z}^{n}\). This is why the EE algorithms often have to change the manifold between \({Z}_{A}^{(n)}\) and Zn.

Unlike the traditional method that directly calculates the ratio \({R}_{A}^{(n)}\), we calculate \({Z}_{A}^{(n)}\) and Zn respectively to avoid the hardness. Let us introduce why we do not need to change the manifold during the simulation. Given a distribution function \({Z}_{A}^{(n)}(J)\) (where \({Z}_{A}^{(1)}\equiv Z\) without losing generality), and J is a general parameter (e.g., temperature, coupling constants in the Hamiltonian, etc.), the ratio of \({Z}_{A}^{(n)}({J}^{{\prime} })\) and \({Z}_{A}^{(n)}(J)\) can be simulated via QMC sampling:

$$\frac{{Z}_{A}^{(n)}({J}^{{\prime} })}{{Z}_{A}^{(n)}(J)}={\left\langle \frac{W({J}^{{\prime} })}{W(J)}\right\rangle }_{{Z}_{A}^{(n)}(J)}$$
(1)

where the notation \({\langle ...\rangle }_{{Z}_{A}^{(n)}(J)}\) indicates that the QMC samplings have been performed under the manifold \({Z}_{A}^{(n)}\) at parameter J. The weights \(W({J}^{{\prime} })\) and W(J) represent the corresponding weights for the same configuration sampled by QMC, but with different parameters \({J}^{{\prime} }\) and J, respectively. This means that we simulate the system at parameter J to obtain a set of configurations with weight W(J). Simultaneously, we estimate the corresponding weight \(W({J}^{{\prime} })\) by treating the parameter as \({J}^{{\prime} }\) for the same configuration. The ratio of \(W({J}^{{\prime} })/W(J)\) can be calculated for each QMC sample to determine the final average, as given in Eq.(1).

In principle, the ratio \({Z}_{A}^{(n)}({J}^{{\prime} })/{Z}_{A}^{(n)}(J)\) for any \({J}^{{\prime} }\) and J can be solved using the method described above. However, we need to consider how to maintain the importance sampling in our QMC simulation. Clearly, if \({J}^{{\prime} }\) and J are sufficiently close, the weight ratio \(W({J}^{{\prime} })/W(J)\) is close to 1, making it easier to estimate by sampling. The QMC simulation would be inefficient when the ratio becomes too small or too large. As shown in Fig. 1c, if we want to use a known distribution \({Z}_{A}^{(n)}(J)=\sum W(J)\) to calculate another distribution \({Z}_{A}^{(n)}({J}^{{\prime} })=\sum W({J}^{{\prime} })\) by resetting the weights of the samplings, the weights before and after resetting for the same configuration should be close to each other. In this sense, it remains an importance sampling when \({J}^{{\prime} }\) and J are sufficiently close65,66,67,68. Therefore, we introduce the continuously incremental trick to address the issue:

$$\frac{{Z}_{A}^{(n)}({J}^{{\prime} })}{{Z}_{A}^{(n)}(J)}=\mathop{\prod }_{i=0}^{N-1}\frac{{Z}_{A}^{(n)}({J}_{i+1})}{{Z}_{A}^{(n)}({J}_{i})}$$
(2)

where J0 = J and \({J}_{N}={J}^{{\prime} }\), with other Ji values incrementally between the two. Thus, QMC can maintain importance sampling through this reweight-annealing approach66,68.

In this way, we are able to obtain any ratio \({Z}_{A}^{(n)}({J}^{{\prime} })/{Z}_{A}^{(n)}(J)\) in realistic simulations even when the \({J}^{{\prime} }\) and J are far away. However, it still cannot yet give a solution of \({Z}_{A}^{(n)}({J}^{{\prime} })/{Z}^{n}({J}^{{\prime} })\). The antidote comes from some well-known points. Considering that we have calculated the values of \({Z}_{A}^{(n)}({J}^{{\prime} })/{Z}_{A}^{(n)}(J)\) and \(Z({J}^{{\prime} })/Z(J)\) from the method above, the problem \([{Z}_{A}^{(n)}({J}^{{\prime} })/{Z}^{n}({J}^{{\prime} })=?]\) can be addressed through a known reference point \({Z}_{A}^{(n)}(J)/{Z}^{n}(J)\). A simple reference point is that \({Z}_{A}^{(n)}(J)/{Z}^{n}(J)=1\) when the ground state is a product state \(\left\vert A\right\rangle \otimes \left\vert B\right\rangle \). A product state is easy to achieve, for example, by adding an external field in a spin Hamiltonian to polarize all the spins. Of course, other known reference points are also acceptable, such as the state at infinite temperature or a point obtained through other numerical methods.

One might be concerned about how to deal with a Hamiltonian without a product state in its limit of parameters. An easy approach is to reduce the coupling between A and B to 0, allowing the ground state to become a product state \(\left\vert A\right\rangle \otimes \left\vert B\right\rangle \) (in this case, the EE reduces to the thermal Rényi entropy of isolated A, as discussed in Supplementary Note 5). In fact, the method of connecting to a reference point is varied. For example, one can anneal the couplings between separated parts solved by exact diagonalization or hand-weaving from zero to the target value, then the problem has also been addressed. In the Supplementary Note 5, we presented an example where the EE is calculated by annealing the system size starting from the EE of a small system that can be exactly diagonalized.

Now the parameter of the incremental process is continuously tunable, different from the non-equilibrium method7,54, the incremental path of our method becomes physical and meaningful. It can be set as the real parameter path of a concerned Hamiltonian. In other words, under similar computational cost, the previous method obtains a single point of EE, while ours gains a curve of EEs. A lot of EEs can be obtained in a single simulation, as the number of iterations in the incremental process scales as  ~ βLd (d is the space dimension, details are in the Supplementary Notes 2 and 3). We will demonstrate that the method is useful for determining the critical points and critical exponents by scanning the EE (see the following section) (It is worth noting that if the goal is to capture unknown phase transitions by scanning the EE without requiring the exact value, the number of iterations can be significantly reduced according to your needs.)

Additionally, we derived a formula to calculate the derivative of the EE (see Eq.(5) in the following section), which does not require numerical differentiation from the dense data of EEs and is as simple as computing the fluctuation of energies in different space-time manifolds. The scheme introduced above does not rely on specific, detailed QMC methods and many-body models. To further understand and test its performance, we will use the spin-1/2 dimerized antiferromagnetic (AFM) Heisenberg model69,70 as an example in the following. We will use the stochastic series expansion (SSE) QMC method, which we are familiar with, to analyze the model40,41,42,43,44,71.

Dimerized Heisenberg model

We simulate a spin-1/2 dimerized AFM Heisenberg model on a two-dimensional (2D) square lattice as an example to obtain its EE. The Hamiltonian is given by

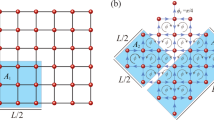
$$H={J}_{1}{\sum}_{\langle ij\rangle }{S}_{i}{S}_{j}+{J}_{2}{\sum}_{\langle ij\rangle }{S}_{i}{S}_{j}$$
(3)

where 〈ij〉 denotes the nearest-neighbor bonds; J1 and J2 are the coupling strengths of the thin and thick bonds, respectively, as shown in Fig. 2. Its ground-state phase diagram (Fig. 2c) has been accurately determined by previous QMC studies69,70 where the inverse temperature β = 2L is sufficient to achieve the desired data quality with high efficiency. In the following simulations, we fix J2 = 1 and tune J1 from 0+ to 1. It is worth noting that the ground state is a dimer product state when J1 → 0, where the \({Z}_{A}^{(n)}/{Z}^{n}=1\) if the dimers are not cut by the entangled edge.

Fig. 2: Spin-1/2 dimerized AFM Heisenberg model on 2D lattices.
figure 2

The strong bonds J2 > 0 are indicated by thick lines. The weak bonds J1 > 0 are indicated by thin lines. a The entanglement region A is considered as a L × L cylinder on the 2L × L torus with smooth boundaries and with the length of the entangling region l = 2L. b The entanglement region A is chosen to be a \(\frac{L}{2}\times \frac{L}{2}\) square with four corners and boundary length is l = 2L. c The diagram of the model setting strong bonds J2 = 1 in which quantum critical point (QCP) is J1 = Jc = 0.52337(3)69.

Full size image

In the SSE framework, the Eq.(1) becomes72

$$\frac{{Z}_{A}^{(n)}({J}_{{1}^{{\prime} }})}{{Z}_{A}^{(n)}({J}_{1})}={\left\langle {\left(\frac{{J}_{{1}^{{\prime} }}}{{J}_{1}}\right)}^{{n}_{{J}_{1}}}\right\rangle }_{{Z}_{A}^{(n)}({J}_{1})}$$
(4)

where \({n}_{{J}_{1}}\) is the number of J1 operators in the SSE sampling, regardless of whether the space-time manifold \({Z}_{A}^{(n)}\) or \({Z}_{A}^{(1)}\equiv Z\) being simulated66. The details of this equation can be found in Supplementary Note 2.

In the realistic simulation, we need to calculate \({Z}_{A}^{(2)}({J}_{{1}^{{\prime} }})/{Z}_{A}^{(2)}({J}_{1}={0}_{+})\) and \(Z({J}_{{1}^{{\prime} }})/Z({J}_{1}={0}_{+})\) respectively. We then obtain the final ratio \([{Z}_{A}^{(2)}({J}_{{1}^{{\prime} }})/{Z}^{2}({J}_{{1}^{{\prime} }})]\) based on \([{Z}_{A}^{(2)}({0}_{+})/{Z}^{2}({0}_{+})]=1\).

Cornerless cutting

Firstly, we calculate the EE with cornerless cutting as shown in Fig. 2a. According to previous works21,23,24, only the entangled edge without cutting dimers (thick bonds) gives correct results consistent with CFT predictions. In Fig. 3a, we present several curves of EE data for different values of J1. The fitting data based on area law are shown in Table 1. According to theoretical prediction73,  −b = NG/2 = 1 in the Néel phase of the spin-1/2 dimerized Heisenberg model, where NG means the number of Goldstone modes. Our calculations provide consistent results, as shown in Table 1 with  −b ~ 1 at J1 = 1.0, 0.9, 0.8, 0.6. In addition, the theoretical calculation74 points out that the  −b = 0 at the Wilson-Fisher O(N) quantum criticality of d ≥ 2 systems. Our result at Jc in the table also supports this prediction. We further provide a graph of  −b as a function of J1 with some discussions in the Supplementary Note 6. We note that recent works75 have found that the finite size effect in the spin-1/2 AFM Heisenberg model is strong, which notably affects the fitting of the parameter  −b = 1, and a good fitting needs some more corrections considering the finite size effect. However, we find that the simple fitting is not bad in our results. The reason may be that the total system we chose is a rectangle, while the region A is a square, whereas they chose a square total system and a rectangular region A. Other QMC works with similar cutting choice as ours also obtains  −b~1 using the non-equilibrium algorithm, but in larger sizes7,23. Our temperature setting β = 2L may coincidentally help us approach the correct number of Goldstone modes even in smaller sizes.

Fig. 3: 2nd Rényi entanglement entropy S(2) of the spin-1/2 dimerized Heisenberg model.
figure 3

The entanglement region A is either cornerless [(a), (b), (c) and (d)] or cornered [(e), (f), (g) and (h)]. The cornerless/cornered cutting is shown in Fig. 2a/b. a The relation between S(2) and entangled perimeter l under different couplings J1. The fitting results are listed in Table 1. e S(2) versus l at the QCP J1 = Jc = 0.52337. The fitting result is S(2)(l) = 0.083(1)l−0.08(1)lnl + 0.19(2) with R/P–χ2 are 0.85/0.56. b, f Scanning S(2) along couplings J1 of different l to identify the critical point. c, g The derivative of S(2), dS(2)/dJ1 goes with the coupling J1 in different l. The peaks of dS(2)/dJ1 appear at the QCP Jc. d, h Area-law prefactor a versus J1. The red curve is the fitting of ∣a(J)−a(Jc)∣~∣J−Jc∣ν.

Full size image
Table 1 Fitting results for the data in Fig. 3a with S(2)(l) = al−blnl + c
Full size table

Another advantage of our method is the natural ability to obtain the EE for different parameter values, as shown in Fig. 3b. This allows QMC to probe phase transitions by scanning the EE in 2D and higher-dimensional systems, similar to how the density matrix renormalization group does in 1D76,77,78,79,80. In Fig. 3b, the convexity of the function changes at the critical point, which is more clearly seen in the derivative of the EE (Fig. 3c). In the following section, we will introduce a much simpler method to calculate the derivative of the EE without an incremental process and show that the peak of the derivative is located at the QCP. It is worth noting that sometimes the original EE function directly probes the phase transition, while other times the derivative does, which will be carefully discussed in our upcoming work81.

Cornered cutting

For the cornered cutting case, the value b~0.08 at the (2+1)D O(3) quantum criticality is also known according to previous theoretical and numerical works21,23,82,83,84. In Fig. 3e, the fitting yields a consistent result of b = 0.08(1) at Jc. Similar to the cornerless case, the EE for J1 also displays a change in the convexity at the QCP, as shown in Fig. 3f. Combined with the data of EE’s derivative and the fitting of critical exponent presented in the next sections, we will find that the shape of the entangled region has little effect on extracting the critical point and critical exponent of the system.

EE derivative

It has been proved in the Supplementary Note 1 that the derivative of the nth Rényi EE can be measured in the form:

$$\frac{d{S}^{(n)}}{dJ}=\frac{1}{1-n}\left[-n\beta {\left\langle \frac{dH}{dJ}\right\rangle }_{{Z}_{A}^{(n)}}+n\beta {\left\langle \frac{dH}{dJ}\right\rangle }_{Z}\right]$$
(5)

where J is a general parameter, n is the Rényi index, the first average is simulated on the manifold of \({Z}_{A}^{(n)}\) and the second is based on Z. Taking the spin-1/2 dimerized Heisenberg model as an example, with fixed J2 = 1 and n = 2, and adjustable parameter J1, the Eq.(5) becomes: \(d{S}^{(2)}/d{J}_{1}=2\beta {\langle {H}_{{J}_{1}}/{J}_{1}\rangle }_{{Z}_{A}^{(2)}}-2\beta {\langle {H}_{{J}_{1}}/{J}_{1}\rangle }_{Z}\) where \({H}_{{J}_{1}}\) denotes the J1 term of the H. Since H is a linear function of J1, this transformation is straightforward. In the SSE framework, this measurement is similar to measuring energy, which is very simple. The details can be found in the Supplementary Note 1.

This conclusion inspires us that we do not need to calculate dense data of EE to obtain the derivative numerically. Instead, simulating the average, \(2\beta {\langle {H}_{{J}_{1}}/{J}_{1}\rangle }_{{Z}_{A}^{(2)}}-2\beta {\langle {H}_{{J}_{1}}/{J}_{1}\rangle }_{Z}\), at the J1 value we concerned is sufficient. We found a similar approach has been used in calculating the derivative of Rényi negativity with respect to the inverse temperature85. Using this method, we have calculated how the derivative of EE goes with J1 in Fig. 3c, g, the peaks of EE derivative locate at the QCP.

In fact, this measurement of EE’s derivative also points out another way to calculate the EE through an integral:

$${S}^{(n)}({J}^{{\prime} })=\int_{{J}_{0}}^{{J}^{{\prime} }}\frac{d{S}^{(n)}}{dJ}dJ+{S}^{(n)}({J}_{0})$$
(6)

where dS(n)/dJ can be obtained from Eq. (5), and the EE S(n)(J0) at the reference point should be known. We demonstrate the equivalence of the two methods (Eq. (4) and Eq. (6)) by taking the spin-1/2 dimerized Heisenberg model as an example, as shown in Fig. 4, both in the cornerless and cornered cases.

Fig. 4: 2nd Rényi entanglement entropy S(2) of the spin-1/2 dimerized Heisenberg model as a function of the coupling J1 are calculated by Reweighting method (Re) and integral method (Int) either in cornerless or cornered entanglement region A with l = 16.
figure 4

The results are consistent within error bar for both methods.

Full size image

We note that Jarzynski’s equality86 can also be used in our methods, similar to the previous non-equilibrium algorithms7,54. However, we found that there is almost no acceleration effect for the non-equilibrium version compared with the equilibrium QMC (Zhe Wang, Zhiyan Wang, Yi-Ming Ding, Zheng Yan, et al. In preparation).

EE and critical behaviors

Most previous works have focused on studying the scaling behavior of EE at a known QCP. In this section, we aim to use EE to probe the QCP and extract the critical exponent ν of a system. We first consider using the parameter position corresponding to the peak of the EE’s derivative to determine the QCP of the system. As shown in Fig. 3, it is evident that the peaks of the EE’s derivative gradually approach the QCP as the system size increases. We try to obtain the value of the QCP by extrapolating it (see Supplementary Note 7). We find Jc = 0.521(2) for cornerless cutting (dashed line in Fig. 3c) and Jc = 0.521(3) for cornered cutting (dashed line in Fig. 3g), which are consistent with the previous result Jc = 0.52337(3) within the error bar69. Performing a fitting of s = al − blnl + c, we extract in particular the leading area-law coefficient a, which is shown in Fig. 3d, h as a function of J1 for both cornered and cornerless cutting. The figures show that a exhibits a non-monotonic behavior as a function of J1 and develops a local maximum at the phase transition point. Similar behavior has been observed in the pioneering work84, but in which the normal QMC algorithm costs much more computational resources. The behavior of a in the vicinity of Jc follows an algebraic scaling (considering a (2 + 1)D O(N) QCP): ∣a(J) − a(Jc)∣ ~ ∣J − Jc∣ν, where ν is the correlation length exponent74,84. We are now using this algebraic scaling to extract the critical exponent.

Let us first consider the case without corners. Setting Jc and ν as free fitting parameters, we found that Jc = 0.53(1) and ν = 0.88(9). The value 0.53(1) is consistent with 0.52337(3), while ν = 0.88(9) is slightly larger than the (2 + 1)D O(3) universality class ν = 0.710(2)69. We then fix Jc = 0.521 obtained from the EE’s derivative above and found ν = 0.708(31), which is consistent with ν = 0.710(2). For the cornered case, we found Jc = 0.526(2) and ν = 0.701(16) when setting Jc and ν as free fitting parameters, which are consistent with Jc = 0.52337(3) and ν = 0.710(2) within error bars. Note that the above fits are all based on the data smaller than the QCP (J1 < Jc), because the data larger than the QCP are non-monotonic and difficultly give meaningful results through fitting. Using the known QCP and critical exponent, previous work has already validated ∣a(J) − a(Jc)∣ ~ ∣J − Jc∣ν84. Our method, which naturally generates dense data, can be used to effectively extract the QCP and critical exponent.

Discussion

Overall, we develop a practical and unbiased scheme with low technical barrier to extract the high-precision EE and its derivative from the QMC simulations. The space-time manifold does not need to be changed during the simulation, and the measurement is a simple diagonal observable. The quantities obtained from intermediate measurements are physical, which makes it possible for QMC to probe novel phases and phase transitions by scanning the EE over large-scale systems in a wide parameter region.

Taking the spin-1/2 dimerized Heisenberg model as an example and scanning along the path from the dimerized phase to the Néel order, we found that a peak of EE’s derivative instead of EE itself arises at the phase transition point. We have successfully extracted the universal coefficient of the sub-leading term of EE both at O(3) criticality and in the continuous-symmetry-breaking phase. Our results demonstrate that EE and its derivative are useful information-theoretic measures of quantum phases and criticalities. In addition, our method is not limited to boson QMC, but can also be applied to other QMC approaches, such as the fermion QMC for highly entangled quantum matters87.

Methods

We have developed the bipartite reweight-annealing algorithm of QMC in this work. Details have been explained in the main text.