Introduction

Proton transfer (PT) in the ground electronic state is a pivotal process in various domains of chemistry and biology1,2,3,4, and its dynamics have been under investigation since the early days of fast chemical kinetics5. These initial observations indicated that PT often occurs at an exceedingly rapid rate. In his Nobel Prize lectures, Manfred Eigen referenced Eucken’s textbook on chemical kinetics, stating that the rate of true neutralization reactions has proven to be immeasurably fast5. Utilizing relaxation techniques, Eigen elegantly demonstrated that the PT process frequently operates as a diffusion-limited process, exhibiting measurable rates on a microsecond timescale6.

The advent of laser technology enabled the direct tracking of PT dynamics. Water upon valence ionization emerged as a natural candidate for investigating PT dynamics7. The PT times, as determined from ab initio calculations conducted at various levels of sophistication, consistently indicated a PT time less than 100 fs8,9,10,11,12. However, femtosecond pump-probe technology, offering a time resolution of hundreds or thousands of femtoseconds, only suggested that PT in liquid water occurs well below 100 fs12. It was only recently, with the broader availability of X-ray free-electron lasers, direct spectroscopy observation of PT in liquid water13 and in a water dimer9 became possible. Both studies confirmed a nearly identical lifetime of approximately 50-60 fs, highlighting the relevance of dimer studies to understanding condensed-phase dynamics for hydrogen-bonded systems, which is also confirmed by the studies of PT in urea solution14 and in a urea dimer15. Additionally, an ultrafast electron diffraction study hinted at OH(H3O+) radical-cation pair formation within 140 fs16. Notably, this conclusion does not contradict previous timescales, as the ultrafast electron diffraction technique solely detects the position of the heavy atoms, that relax only after the completion of the PT. Even faster PT reactions in water following inner valence ionization17 or core level ionization18 can be indirectly inferred using the core-hole internal clock.

The comprehensive understanding of PT in water stands in stark contrast to the limited exploration of PT following the ionization of hydrated biomolecules. The significance of these processes lies in their potential role in radiation damage and DNA mutations, necessitating a thorough understanding of the underlying mechanisms at the molecular level19,20,21,22. In this context, excited-state PT in biomolecular clusters has been investigated14,23.

Upon ionization, water or solute molecular cations can transfer a proton to a neighboring molecule, resulting in the formation of a protonated ion and a deprotonated group. However, the reaction pathways of PT between ionized water and solute molecules, or between ionized biomolecules and water, remain poorly understood. The directionality of these processes is particularly unclear. Protons can be transferred barrierlessly from ionized water molecules to solute molecules along a water chain through the Grotthuss-type mechanism24. The transmission of protons along a water chain occurs exceedingly rapidly. As mentioned above, the elementary PT process takes place within 50 fs9,13,16. Ionization-induced PT between nucleobases can also be impeded by the hydrogen-bonded network of the DNA-water environment; instead, protonated nucleobases are generated through PT from an ionized water molecule25. In the two different directions of PT processes induced by outer-valence ionization, PT from water to solute, such as biomolecules, is barrierless when accessing an ionized state localized in water25. However, when the charge is localized on the biomolecule, PT from the biomolecule to the water molecule encounters a large barrier, obstructing the PT pathway in this direction25. These findings have piqued our interest: is PT unidirectional in ionized hydrated biomolecules? Is there a means to open up the PT pathway from biomolecules to water molecules, and what will be the timescale?

An attractive approach for investigating PT dynamics is the double ionization of biomolecules26. Double ionization can provide a unique environment where proton transfer is more readily facilitated due to the localized charge separation, which is not present in neutral molecules. These dicationic states can be readily accessed through high-energy ionizing radiation via Auger processes, which, however, leave the system in a mixture of states. Alternatively, direct double ionization is possible either via photons or electron collision. Doubly ionized biomolecules may also be produced within radiolysis, as a large number of secondary electrons with a mean energy of roughly 60 eV are generated during radiolysis processes27,28. This serves as an important ionization source in the medium, producing also molecular dications. When two charges are localized on one molecule, the system’s energy is generally higher than that of a state with dispersed charges due to the former’s higher Coulomb potential. This could facilitate a barrierless PT pathway from biomolecules to water molecules. However, localized double ionization of a molecule also introduces a new challenge: doubly ionized molecules are typically unstable and may undergo dissociation. Consequently, PT must precede dissociation, necessitating a faster PT. Despite numerous efforts, elucidating the PT mechanism from ionized biomolecules to water molecules remains elusive.

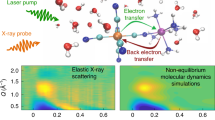
In this study, we generated hydrated pyrrole dications (C4H5N2+-H2O) with two charges localized on the pyrrole unit through electron-impact (see Fig. 1a). We also used the strong-field femtosecond laser as an alternative way to the doubly ionized state formation. The choice of the hydrated pyrrole complex as our experimental model for biological proton-relay systems stems from pyrrole’s well-established reputation as a biologically active scaffold with diverse activities29,30. The electron-density donating position of water in the vicinity of pyrrole (i.e., water donates electron-density to pyrrole through intermolecular H-bonding) leads to an energy reduction of the localized double ionization state (C4H5N2+-H2O), which lies below the delocalized double ionization state (C4H5N+-H2O+)31. This indicates that C4H5N2+-H2O is the ground state of the dication, thus the system tends to favor this charge localized dicationic state during the ionization process. We anticipate a facile PT from the doubly ionized biomolecule to a water molecule, supported by the experimentally observed high-yield PT channel. Further dynamical insights into PT in hydrated pyrrole dications are revealed through adiabatic and non-adiabatic ab initio molecular dynamics (AIMD) simulations.

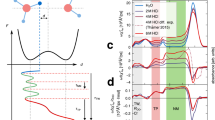
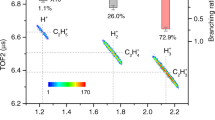
Fig. 1: Schematic of COLTRIMS reaction microscope upon electron-impact and proton transfer pathway of H3O+ + C4H4N+ and measured TOF correlation spectrum.
figure 1

a The local double ionization of C4H5N-H2O complex upon electron-impact. The dots between water and pyrrole denote intermolecular H-bond; b Proton transfer from doubly ionized C4H5N2+ to H2O molecule; Atomic colors: C (gray), H (white), N (blue). c Schematic diagram of the COLTRIMS setup. Purple, red, blue and turquoise lines respectively represent UV laser, ions, electrons and gas jet. The black arrows represent the directions of electric and magnetic fields. d Measured TOF correlation map between the first and the second cations. The cyan and green arrows represent the direct dissociation H2O++C4H5N+ and the proton transfer H3O++C4H4N+ channels, respectively. The vertical and horizontal lines are from false coincidence. The count intensity is color-coded on a linear scale. Source data are provided as a Source Data file.

Full size image

In our investigation, we employ two complementary approaches to unravel the PT dynamics. We trace the dynamics indirectly by scrutinizing the energetics of the outgoing fragments measured in coincidence, a method applicable to cluster systems. Alternatively, we directly probe the dynamics through pump-probe-type experiments. The combination of electron-impact and photon-driven processes yields additional insights into the nature of the formed dicationic state.

Results

Two-body breakup pathways of (C4H5N-H2O)2+ dications

Let us start with a brief discussion of the structure and electronic configuration of the pyrrole-water complex. In the pyrrole-water complex, the pyrrole molecule forms a hydrogen bond with the water molecule, characterized by a N–O distance of 3.02 Å as evaluated at the CCSD/aug-cc-pVDZ level of theory (see Supplementary Tables 1 and 2). The first ionization potential is measured at 8.21 eV, with the electron being ionized from the highest occupied molecular orbital (HOMO) corresponding to the π orbital of the pyrrole unit32. Intriguingly, the three lowest doubly ionized states of the pyrrole-water system exhibit two charges localized on the pyrrole unit (23.26 eV (T0), 23.41 eV (S1), and 23.90 eV (S2) above the ground state minimum), see Table 1 and Supplementary Tables 3–6. The localized dicationic states are somewhat stabilized by the hydration31. The S3, T1, and higher excited states of the doubly ionized cluster feature a charge delocalization between the pyrrole and water units.

Table 1 Double-ionization potentials (DIP), relative DIP of pyrrole-water complex and molecular orbitals (MOs) mostly involved in ionization for both singlet and triplet manifolds
Full size table

In our experiments, as shown in Fig. 1a, the localized dicationic state of the pyrrole-water complex can be populated via electron-impact ionization, followed by ultrafast PT from C4H5N2+ to H2O molecule (see Fig. 1b). The fragment ions resulting from the double ionization of C4H5N-H2O complexes are detected in coincidence with a COLTRIMS reaction microscope33,34 (see Fig. 1c and Methods). By measuring the time-of-flight (TOF) and position of particles hitting on the time- and position-sensitive detector, six momentum parameters (three for each fragment ion) are determined for a single explosion event. The direct dissociation C4H5N++H2O+ and proton transfer C4H4N++H3O+ channels are clearly defined by the TOF correlation map between two fragments ions, which is shown in Fig. 1d. The PT channel exhibits a significantly higher yield, approximately 2.5 times that of the direct dissociation channel, which is mainly because the PT originates from the electronic ground state of the dicationic complex, i.e. the charge localized C4H5N2+-H2O state.

Measurements of the initial ionization states

In the current electron collision experiment, the PT channel can be accessed by local double ionization of the hydrated pyrrole complexes, which can be determined by the measured projectile energy loss spectrum associated with the ion pair (C4H4N++H3O+). Here, the projectile energy loss is defined as the energy difference between the incident electron (E0) and the scattered electron (E1), i.e., Eloss = E0 - E1. The energy loss spectrum is calibrated by the single ionization of helium (Eloss[He+] = 24.6 eV). As shown in Fig. 2a, the onset of the Eloss associated with the PT channel is determined as about 23.5 eV, which indicates that the PT channel is initiated by the charge-localized C4H5N2+-H2O state (two charges localized on pyrrole), corresponding to the T0, S1, S2 states presented in Table 1. This C4H5N2+-H2O precursors can be formed by direct double ionization or Auger process in the electron collision processes. The electron-density donating position of water reduces the double ionization threshold of pyrrole, allowing Auger decay of the lowest C 2s−1 state, which is forbidden in isolated pyrrole molecules. The higher-lying O 2s−1 states of water molecule can also decay to the C4H5N2+-H2O states by electron transfer mediated decay (ETMD)35. In the ETMD, the pyrrole transfers an electron to the O 2s vacancy, and the released energy results in the ionization of another electron in pyrrole. However, due to the large intermolecular distance between pyrrole and water, the overlap of the inner-valence orbital with the outer-valence orbital on the same site is much better than with the outer-valence orbital on the neighboring water center35,36,37. As a result, the O 2s−1 states tend to decay through the intermolecular Coulombic decay (ICD)38 process over ETMD forming C4H5N++H2O+ ions pairs, and the contribution of the ETMD channel to the localized double ionization states is arguably small. This is also confirmed by the measured Eloss of the PT channel, which is much smaller than the ionization threshold of O 2s−1 band.

Fig. 2: Projectile energy loss and KER spectra.
figure 2

a Projectile energy loss spectrum for the proton transfer channel H3O+ + C4H4N+. The vertical dashed line represents the double-ionization threshold of the hydrated pyrrole complex. b, c Measured and (d, e) calculated KER for the proton transfer channel H3O+ + C4H4N+. The solid (b) and hollow dots (c), as well as solid (d) and hollow (e) bars, represent the results of electron-impact and laser experiments, AIMD and CASPT2 theoretical calculations43, respectively. Error bars in (a–c) represent statistical standard deviation (s.d.), and were calculated by the square root of the true coincidence counts. Source data are provided as a Source Data file.

Full size image

Kinetic energy release (KER) spectra

In the single pulse laser experiment, two electrons can be removed sequentially via strong field tunneling ionization, and the probability of such sequential double ionization exponentially relies on the ionization potential for each ionization step39. Thus the population of the ground state of the dication (i.e., localized double ionization of pyrrole) is dominant and the same PT channel is initiated as in the electron-impact experiment. The measured KER spectra of the PT channels in both electron-impact and fs laser experiments are presented in Fig. 2b, c, which show a single peak at about 2.6 eV. The measured KER spectra for the PT channel show good agreement between two experiments, which indicates that both results correspond to the same initial electronic state and structure of the system. The measured KER spectra show obvious discrepancy with the Coulomb explosion model ( ~ 3.5 eV) calculated with two point charges at the center of mass (COM) of the two molecules40. This is mainly because the potential energy surface (PES) of the PT channel can be different from 1/R, and the polarization forces between water and pyrrole can also contribute to the non-Coulombic effect9,41.

Molecular dynamics calculations

To reveal the dynamical details of PT, we performed molecular dynamics simulations using two different approaches: we use either Born-Oppenheimer dynamics with density functional theory and quasiclassical initial conditions or non-adiabatic simulations based on correlated multi-reference PES with initial conditions sampled by molecular dynamics. We show that these two very distinct approaches provide us with very similar results, demonstrating the robustness of the PT process.

In the first approach, the optimized hydrated pyrrole complex was sampled at a finite temperature (30 K in our supersonic gas jets) and were stripped two outermost electrons from pyrrole (see Methods). The KER of every trajectory is obtained by summing the kinetic energies of the simulated molecular cations at t = 500 fs and the remaining Coulomb potential energy considering the COM distance. The calculated KER is presented in Fig. 2d, which matches very well the experimental results. As in previous studies on PT dynamics in water clusters16, intermolecular PT is not a simple one-dimensional motion of a hydrogen nucleus along a hydrogen bond. Here, our AIMD calculations indicate that it also involves significant rearrangement of the other heavy atoms. As illustrated in Fig. 3, the distance between N and O atoms rO−N (Fig. 3b, e), as well as H connecting to N and O atoms rO−H (Fig. 3c, f) are plotted as a function of propagation time. Upon ionization, the intermolecular distance rO−N undergoes a rapid decrease within 50 fs due to the increasing attractive interactions upon removing two electrons from the closed-shell pyrrole, transitioning from approximately 3.02 Å to 2.44 Å. After a brief pause in the intermediate state (N-H ⋅ ⋅ ⋅ O), the C4H4N+ and H3O+ ions start to separate due to Coulomb repulsion, leading to a fast increase in rO−N after 75 fs. Simultaneously with the contraction of rO−N, the proton initially attached to the N atom transfers to a neighboring water molecule. At t ~ 50 fs, the initial N-H ⋅ ⋅ ⋅ O hydrogen bond breaks, and the proton transfers to a water molecule. These results indicate that despite the nearly linear hydrogen bonding between pyrrole and water molecules (∠N-H ⋅ ⋅ ⋅ O ~ 178°) and the short distance between the proton-accepting (O) and proton-donating (N) atoms (3.02 Å), the PT reaction coordinate is not a simple proton motion along the hydrogen bond, but also involves the motion of the heavy atoms. The initial contraction of intermolecular distance between C4H5N2+ and H2O could be an important prerequisite for intermolecular PT, which is also adhered to the pattern of hydrogen-to-covalent bond conversion42.

Fig. 3: Molecular dynamics simulation diagrams.
figure 3

a The rigid two-dimensional potential energy surface scan in triplet ground state, calculated with the CCSD/aug-cc-pVDZ method. A white curve with arrows describes the minimum-energy path toward proton transfer and subsequent Coulomb explosion. b, c Evolution of interatomic distances analyzed from AIMD simulation in triplet ground state using the B3LYP/cc-pVDZ method. Distances between O and N atoms (rO−N) (b) and distances between O atom and H atom on pyrrole molecule (rO−H) (c) as functions of time. d Reaction channel evolution for surface hopping starting from state T0 with the localized charge on pyrrole molecule. The channel analysis focused on the dissociation of water molecules, and PT followed by dissociation. Other channels, such as dissociation of the hydrogen atom, were not observed. Channel ratio refers to the proportion of the dissociation events of the ground state hydrated pyrrole dication that occur via different channels. e, f Evolution of interatomic distances analyzed from the surface hopping simulation in triplet ground state for rO−N (e) and rO−H (f) as functions of time. The black solid curves in (b, c) and (e, f) represent the average data of all the trajectories. Source data are provided as a Source Data file.

Full size image

The system is likely prepared in the ground electronic state of the dication, as indicated by the measured electron energy loss spectrum. The Born-Oppenheimer molecular dynamics simulations might thus seem adequate, especially considering the good match with the experiment (as shown in Fig. 2b and d). The molecular dynamics simulations in the ground adiabatic electronic state neglect the possible interaction between the electronic states. As discussed above, the delocalized state of the dication (S3) is positioned only 1 eV above the electronic ground state (T0) with localized charge and this energy distance can even shrink within the dynamics. Furthermore, the first excited state of the dication is only 0.5 eV above the ground state. The non-adiabatic processes potentially play a role. We have, therefore, extended the non-adiabatic simulations and modeled the PT process with the non-adiabatic surface hopping molecular dynamics, utilizing the multi-reference wavefunction.

The details of the simulations are described in the Methods section. We considered five different initial states, T0 and T4 with two charges localized on the pyrrole unit and T1, T2, and T3 states with two charges dispersed across the water and pyrrole molecules (see Table 1, Supplementary Table 6, and Supplementary Fig. 1). The electronic structure was calculated with the CASPT2 electronic structure method43, including thus both dynamical and static correlation. The active space comprised of 6 electrons in 6 MOs. Due to the computational demands, we made a larger number of calculations only for the T0 and S1 (localized charge) states. As shown in Fig. 3d and Supplementary Fig. 2, the PT dominated for simulations starting with a charge localized on pyrrole, the total yield for the PT channel amounted to around 98%. The reaction channel yields were considered at the end of the evaluation, which was set to 500 fs. The non-adiabatic simulations also provided very similar distributions of the KER spectra (see Fig. 2e and Supplementary Fig. 3) and we also confirm the structural changes during the simulations (Fig. 3e, f).

In hydrated biomolecular clusters, PT from outer-valence ionized biomolecule to water molecule is typically inhibited due to the high barrier along the PT path25. The reverse PT observed in the doubly ionized hydrated biomolecules implies a transformation in the potential energy landscape between reactants and products. As can be seen from the structure of the C4H5N-H2O complex (shown in Fig. 1a), pyrrole and water molecules form a linear N-H ⋅ ⋅ ⋅ O hydrogen bond with ∠NHO  ~178° and relatively short (3.02 Å) distance between the proton-accepting (O) and proton-donating (N) atoms as evaluated at the CCSD/aug-cc-pVDZ level of theory. However, as shown by the molecular dynamics simulations described above the proton transfer coordinate is not a simple smooth proton movement from nitrogen to oxygen and turns out to involve the motion of both molecules. This statement can be further illustrated by the two-dimensional PES scan performed for the ground state of the hydrated pyrrole dication (see Fig. 3a and Supplementary Fig. 4), where the potential energy of the complex is plotted as the function of the N-O and O-H distances. The white arrows represent the preferred proton transfer path from C4H5N2+-H2O to C4H4N+-H3O+ system which is barrierless. It is clearly seen that in the course of the continuous shortening of the O-H bond due to the proton migration, the N-O distance also decreases, while after the formation of a delocalized dicationic system C4H4N+-H3O+, the N-O distance continuously increases, corresponding to the Coulombic repulsion of the positively charged fragments C4H4N+ and H3O+. This picture is consistent with our molecular dynamics simulations and implies that after the double ionization of the hydrated pyrrole, the C4H5N2+ dication can rapidly transfer a proton to the neighboring water molecule along this pathway. It has been shown that in the pyrrole-water system, the water acts as an electron-density donor to the pyrrole molecule, this effect reduces the electronic density of water and makes it more costly to remove an electron from it. On the other hand, the electronic density of the pyrrole is increased which lowers the energy required to ionize an additional electron. The preferential occupation of localized dication states due to reduced double ionization energy, along with the absence of the PT barrier contributes to the higher yield of the PT channel compared to the direct dissociation channel (C4H5N+ + H2O+) as observed in our experiments.

In our calculations, we further determine the PT time using the distance of rO−H as a function of the propagation time. As shown in Fig. 3c and f, the rO−H becomes smaller than 1.25 Å when the hydronium cation H3O+ is formed, i.e. the PT is complete. In Fig. 4a, we obtain the time-dependent PT channel yield by selecting rO−H  < 1.25 Å in Fig. 3c. We analyze the PT channel yield using the growth function \(Y(t)=A(1-{{{{\rm{e}}}}}^{-(t-{t}_{0})/\tau })\), where A and t0 are the amplitude and the time offset, and τ represents the PT time. These calculations determine the PT time τ = 52.8  ± 0.5 fs.

Fig. 4: Femtosecond tracking of proton transfer dynamics.
figure 4

a Calculated time-dependent yield of the PT channel. The yield is fitted with a growth function (pink dashed line), giving a PT time constant of τ = 52.8  ± 0.5 fs. b Schematic of the laser pump-probe experiment. Black, red, and purple arrows represent the 800 nm pump, 800 nm probe, and 400 nm probe, respectively. Black, blue, red and purple shadows represent wave packets on the PECs of C4H5N-H2O, C4H5N2+-H2O, C4H5N+-H2O+, and C4H4N+-H3O+. Red shadows at 3.1 eV and 3.9 eV delineated by black dotted lines represent the expected KER of the 800 nm pump - 800 nm probe and 800 nm pump - 400 nm probe schemes, respectively. c H2O+ + C4H5N+ yields versus pump-probe time delay, which are smoothed with a moving average. The PT times τ1 = 34  ± 5 fs and τ2 = 31  ± 6 fs are determined by fitting with decay functions (pink/purple dashed lines). The orange line shows the instrument response function (IRF). d Time delay-dependent KER distribution. Dashed box highlights the 3.9 eV transient. e Time-dependent yield curve for the direct dissociation channel at KER  ~ 3.9 eV in the case of 800 nm pump - 400 nm probe. The PT time τ = 55  ± 24 fs is determined by fitting with decay functions. Error bars represent statistical s.d., and were calculated by the square root of the true coincidence counts. The PECs (blue, red, and purple solid curves) in (b) are calculated using constrained DFT with Configurational Interaction approach and the B3LYP/aug-cc-PVTZ method. Source data are provided as a Source Data file.

Full size image

Time-resolved measurements

Finally, we quantify the timescale of PT with the femtosecond pump-probe experiments, wherein a linearly polarized laser functioned as the pump pulse and a temporally delayed elliptically polarized laser served as the probe pulse. As shown in Fig. 4b, the pump pulse initiates PT by inducing local double ionization in the hydrated pyrrole complex. The pump pulse ionizes two electrons sequentially via strong-field tunneling ionization. Since the tunneling ionization exponentially relies on the ionization potential, the sequential ejection of two electrons from the pyrrole unit dominates and thus leads to the population of the double ionization ground state of hydrated pyrrole, which is supported by the fact that the measured KERs are identical in both laser and electron-impact experiments (Fig. 2b, c). This result also indicates that the motion between pyrrole and water during sequential ionization can be negligible. The probe pulse acts as a disruptive pulse, converting the intermediate C4H5N2+-H2O to C4H5N+-H2O+ states through single-photon absorption.

As illustrated in Fig. 4b, following the localized double ionization of hydrated pyrrole complexes, the C4H5N2+ dication and H2O molecule approach each other due to the attractive potential between them. Since the energy gap of the local and nonlocal doubly ionized states can roughly match the photon energy of 800 nm laser pulse, the evolving wavepacket on C4H5N2+-H2O state prepared by the pump pulse can be projected to the C4H5N+-H2O+ state via single-photon absorption from the probe pulse. This leads to a direct dissociation of C4H5N+-H2O+ into C4H5N+ + H2O+ via Coulomb explosion with a KER of about 3.1 eV (see Supplementary Fig. 5). As the delay time increases, the wavepacket on the PES of the C4H5N2+-H2O intermediate state culminates in PT, such that the system can no longer be excited to the C4H5N+-H2O+ state by the probe pulse due to the strong Coulomb repulsion between H3O+ and C4H4N+ (see Fig. 4b), which greatly hinders the probability of hydrogen transfer from H3O+ back to C4H4N+. As a result, the yield of the direct dissociation channel decays as increasing the time delay, which reflects the time scale of PT. Fig. 4c shows the time-resolved ion yields of the direct dissociation channel ranging from -150 to 200 fs. The positive time delay indicates that the pump pulse arrives earlier than the probe pulse. The yield curve of the direct dissociation channel including both positive and negative regimes can be well fitted with two mono-exponential decay functions convoluted with the same instrument response function (see Methods). Through the fit, we extracted the decay time τ1 = 34  ± 5 fs and τ2 = 31  ± 6 fs. In this scheme, the obtained decay time is possibly influenced by the reduced probe efficiency in the intersection region ( ~ 2.5 Å) where the energy gap between C4H5N2+-H2O and C4H5N+-H2O+states becomes larger compared to the vertical transition position as shown in Fig. 4b.

To overcome this issue, we implemented a second two-color measurement in which the 400 nm pulse is used as a probe to drive the transition from C4H5N2+-H2O to C4H5N+-H2O+ states. According to the calculated potential energy curves shown in Fig. 4b, the transition in the intersection region will lead to a featured KER distribution centered at around 3.9 eV. Since the PT will prohibit the transition from C4H5N2+-H2O to C4H5N+-H2O+ states, the temporal dynamics at KER  ~ 3.9 eV can provide a direct measure of the PT time. The measured time-dependent KER distribution of C4H5N+ + H2O+ channel is presented in Fig. 4d, where the positive and negative time delays stand for the 800 nm pump - 400 nm probe and 400 nm pump - 800 nm probe, respectively. We further select the KER region of 3.8  ~ 4.1 eV (dashed box in Fig. 4d) and show the time-dependent yield distributions in Fig. 4e for the 400 nm probe result. By fitting the yield curve with a mono-exponential decay function (see Methods), we extracted the decay time 55  ± 24 fs, which verifies our molecular dynamics calculations of the PT time. It is noted here that we have run this measurement for more than 400 scans within 60 days beam-time, the low statistics is mainly caused by the dilute nature of the pyrrole-water complex and the weak signal of the pump-probe experiment. However, the clear difference between 400 nm and 800 nm probes in Fig. 4e and the background-free feature of this transient at KER  ~ 3.9 eV can verify our observations (see Supplementary Figs. 9 and 10).

Discussion

We demonstrated unambiguously an ultrafast PT in the doubly ionized hydrated biomolecular complexes. The complete picture of the structural and dynamical properties of PT in pyrrole-water complex is revealed by the simultaneous investigation of the PT by electron-impact double ionization, femtosecond laser pump-probe experiments following the strong-field ionization, and ab initio calculations. The doubly ionized states are populated by electron-impact and strong-field laser experiments, which are two independent ways to initiate the ultrafast PT process. The electron-impact experiments reveal directly the initial states and dynamical information, by inspecting the kinetic energy distributions of the outgoing fragments and scattered electrons. The strong-field laser experiments allowed for a direct tracing the real-time evolution of the PT dynamics and the ab initio calculations have revealed the dynamical details.

The overall picture of the process is as follows. The PT is initiated by a localized double ionization with two charges residing on the pyrrole unit. The kinetic energy distributions agree well between electron-impact and strong-field ionization experiments, indicating that the lowest dicationic state is predominantly formed in both experiments. In the electron-impact experiment, the energy loss spectrum is measured in coincidence with the fragment ions to resolve the initial ionization state. The simulated KERs are in very close agreement with these experiments both for Born-Oppenheimer molecular dynamics (assuming adiabatic dynamics on a single surface) and the non-adiabatic dynamics with fewest switches surface hopping method, even though a non-negligible fraction of the wavepacket undergoes a transition between adiabatic states. Molecular dynamics simulations reveal an intrinsic PT time τ  ~ 52.8  ± 0.5 fs.

The PT in hydrated pyrrole complexes involves a complicated collective motion rather than just the one-dimensional movement of the proton along hydrogen bonds. During this process, a contraction of the intermolecular distance between C4H5N2+ and H2O is observed in our calculations. This is supported by the two-dimensional PES scan, which indicates that the PT is barrierless but not a direct process. It contains also the nuclear motions of N and O in which the N-O distance first shrinks and then elongates. This indirect character of the PT is typically for the process in the electronic ground state8 or low-lying ionized state while the PT following the inner valence or core ionization are direct processes involving mainly the movements of proton17,18.

The charge localization on the pyrrole unit is due to the electron-donor role of water in hydrated pyrrole complexes. The localization of the two charges forms the C4H5N2+-H2O structure which corresponds to the ground state of the dication, and thus leads to a higher yield of the PT channel than the direct dissociation channel. The latter process is found to originate from the electronically excited state of the dication (see Table 1). Utilizing the fs laser pump-probe technology, we measure a PT time τ = 55  ± 24 fs. This demonstrates the ultrafast character of PT between doubly ionized biomolecules and water molecules. The measured data are in agreement with the theory, supporting again the mechanistic picture outlined above. This study is expected to provide a fundamental insight into the mechanism and dynamics of PT in more complex systems, such as larger clusters and liquid solutions, particularly for the lifetime.

Finally, we briefly discuss the potential relevance of PT to radiation damage. In biological systems, solvation shuts down PT between the bases induced by single ionization25. Exposed to high-energy radiations, dications can readily be formed through direct double ionization or Auger-type autoionization. The PT channel from doubly ionized nucleobases to surrounding water molecules is opened, which could contribute to the tautomerization of DNA base pairs causing point mutations and inappropriate pairing between bases19,20,21,22. The currently observed PT similarly offers a way for highly excited biomolecules to be shielded from ring-opening dissociation following localized decay by transferring a proton to neighboring water molecules. This ultrafast PT needs to be considered in investigations and models on high-energy radiation damage in a real-life scenario.

Methods

Multi-particle coincidence momentum spectroscopy

The experiment was performed using a COLTRIMS reaction microscope spectrometer33,34,44,45. The hydrated pyrrole complexes are generated by helium carrier gas passing through sample vapors containing water and pyrrole, followed by supersonic expansion. As shown in Fig. 1c, the electron beam is generated using a photoemission electron gun, in which a tantalum photocathode is irradiated by a pulsed 266-nm ultraviolet laser. The pulsed electron beam (E0 = 200 eV, ΔT  ~ 0.5 ns) collides orthogonally with the supersonic molecular jet and causes ionization processes. The resultant electrons and ions are guided by homogeneous electric and magnetic fields to time- and position-sensitive multi-hit detectors. A low electric field (1.5 V cm−1) and magnetic field (7.8 G) are utilized to extract and detect the outgoing electrons, after 500 ns when the electrons have reached the detector, the electric field is raised up to 25 V cm−1 to extract efficiently the fragment ions with high kinetic energies. The effective detection areas of the electron and ion detectors are circular planes with diameters of 80 mm and 100 mm, respectively. The unscattered electron beam is directed through a hole in the electron detector without generating a signal. During off-line analysis, the three-dimensional momentum vector of each detected particle is reconstructed from the measured TOF and position. In our experiments, we perform the electron-ion-ion triple coincidence measurements. The detected electrons include both ejected and scattered electrons that are typically differentiated by the measured slow and fast electrons, which enable us to determine the projectile energy loss and further elucidate the initial ionization mechanisms44,45. As shown in Fig. 1d, the specific dissociation channel is defined by the TOF correlation spectrum of ions. The x and y coordinates correspond to the TOFs of the first and second ions of the coincidence pairs. In the TOF correlation map, the two-body fragmentation channel displays a diagonal structure with a slope of -1, due to the back-to-back emission of two fragments with equal momentum magnitude. The PT channel C4H4N++H3O+ is located to the lower right of the direct dissociation channel C4H5N++H2O+, which is attributed to the fact that the TOF of ion is positively correlated to its momentum and mass-to-charge ratio.

The time-resolved pump-probe technique in combination with Coulomb explosion imaging is employed to track PT dynamics. A linearly polarized laser pulse with a central wavelength of 800 nm and a pulse width of 35 fs was split into two beams. One beam served as the pump pulse, which ionized hydrated pyrrole complexes to the ground state of dication and prepared a wavepacket, and the other beam served as the probe pulse, which further projected the wavepacket to the excited state of the dication through single-photon absorption process. Linearly and elliptically polarized laser pulses are used for pump and probe, respectively, and their peak intensities are estimated to be 120 TW cm−2 and 170 TW cm−2. The single-pulse experiments were conducted using independent linearly and elliptical polarization laser with pulse durations of 35 fs and intensities of 120 TW cm−2 and 170 TW cm−2, respectively, which show identical KER spectra. The major axis of the elliptically polarized pulse is aligned to the linearly polarized pulse. In the strong-field experiment, non-sequential double ionization occurs as a result of the laser-induced electron re-collision process, leading to the double ionization of pyrrole-water complex and Coulomb explosion. Relative to sequential double ionization, non-sequential double ionization is strongly suppressed when driven by the elliptical laser pulse, which rules out the electron re-collision because of the large electron drift momentum. Ellipticity-dependent relative yields of direct dissociation and proton transfer channels are provided in Supplementary Fig. 6, which reveals that the yields for both channels exhibit weak dependence on the ellipticity of the driving laser pulse. Thus, we infer that the sequential double ionization mechanism is dominant in the present experimental condition. The instrument response function is 45  ± 1 fs obtained by fitting the experimental time-dependent ionization yield of He atom, which also served as a reference to calibrate the time-zero between two pulses. A translation stage was used to control the time delay between the pump and probe pulses, with a step size of 6.6 fs, and data were integrated for 20 seconds at each delay point. To extract the decay time, the time-dependent yield curve is fitted using two mono-exponential decay functions46, each convoluted with the same instrument response function, as follows:

$$S(t)=\left({A}_{1}\cdot {e}^{-\frac{t}{{\tau }_{1}}}(t > 0)+{A}_{2}\cdot {e}^{\frac{t}{{\tau }_{2}}}(t < 0)\right)\otimes G(t)+k$$
(1)

where A1 and A2 represent the amplitudes of the positive and negative signals, respectively. τ1 and τ2 are the decay time constants of the exponential component corresponding to the elliptical laser pulse probe (positive time) and linear laser pulse probe (negative time). k denotes the baseline and G(t) is the Gaussian instrument response function with a fixed full width at half maximum (FWHM) of 45 fs. The fitting results of the unsmoothed data are shown in Supplementary Fig. 7 and the fit with a Gaussian distribution without exponential decay function is also shown in Supplementary Fig. 8 for comparison.

In addition, we applied a two-color pump-probe measurement to directly obtain the PT time. A linearly polarized 800 nm laser pulse is used as a pump, and a linearly polarized 400 nm pulse is used as a probe. The 400 nm pulse is produced as the 800 nm passing through a BBO crystal. The polarizations of two pulses are parallel. The peak intensity for 800 nm is estimated to be 120 TW cm−2, and the peak intensity for 400 nm is estimated to be 100 TW cm−2. The instrument response function is 50  ± 1 fs. The PT time is extracted by fitting the time-dependent yield curve with an exponential decay function46, as follows:

$$S(t)={A}_{1}\cdot {e}^{-\frac{t}{\tau }}\otimes G(t)+G(t)+k$$
(2)

where A1 represents the amplitudes of the positive signal. τ is the decay time constants of the exponential component. k denotes the baseline and G(t) is the Gaussian instrument response function with a fixed full width at half maximum.

Molecular dynamics simulations

The Born-Oppenheimer ab initio molecular dynamics simulations were performed using the Gaussian 16 package47. The initial conditions, i.e. geometries of hydrated pyrrole complexes were sampled by the quasi-classical fixed normal-mode sampling method under the temperature of the supersonic gas jet (30 K). The populations of the initial vibrational states of the complexes were determined by Boltzmann distributions. The molecular dynamics simulations were performed under the extended Lagrangian molecular dynamics scheme, adopting the so-called atom-centered density matrix propagation (ADMP) method48,49,50 using the density-functional theory (DFT) method at B3LYP/cc-pVDZ level. All atoms were characterized by their three-dimensional momentum vectors. Propagation was performed for a total simulation duration of 500 fs with a time step of 0.5 fs. The total KER can be calculated by adding the kinetic energies of the simulated two molecular cations together with the remaining Coulomb potential energy considering the center-of-mass distance at this instant under the assumption that the potential can be approximated by 1/R51,52. We notice here that after 500 fs the Coulomb potential can be estimated accurately, because the distance between two ions is larger than  ~ 14 Å, i.e. the ions can be safely considered as point charges, see e.g.41,44,45,52.

Nonadiabatic molecular dynamics simulations

Nonadiabatic dynamics calculations were performed with the surface hopping scheme in its fewest switches version53. The equations of motion were integrated with the velocity Verlet integrator with a timestep of 4 a.u., with a total simulation duration of 500 fs in the ABIN package54. The electronic structure was described with the extended multi-state complete active space second-order perturbation theory (XMS-CASPT2)43. We used the cc-pVDZ basis set. The energies, gradients, and non-adiabatic couplings were computed in the BAGEL electronic structure package, version 1.2.055. The active space was set to 6 electrons in 6 MOs and in total 5 electronic states were included. The initial conditions for the surface hopping simulations were generated with the molecular dynamics in a neutral state using Path Integral MD combined with the quantum thermostat based on the generalized Langevin equation56,57,58 (PI+GLE). The temperature was set at 300 K. As the PI+GLE approach does not provide physically relevant velocities, these were sampled using Boltzmann distribution probabilities. The ωB97x functional with 6-31++g** basis set was used for the sampling simulations together with the D3 dispersion correction. The electronic structure was described using the TERACHEM59 package and the ABIN package was used to integrate the equation of motion with the time step of 20 a.u. and the total length of simulations equal to 29 ps. KER was calculated as a sum of kinetic energies, using the COM momenta of individual fragments, and Coulombic energy using the Mulliken charges on individual atoms.

Potential energy calculations

The rigid two-dimensional scan of the PES shown in Fig. 3a was calculated using the CCSD/aug-cc-pVDZ method with the computational package QCHEM version 6.160. As the initial structure, we used a geometry optimized using the B3LYP/aug-cc-pVTZ method in a doubly-ionized triplet ground state with the distance constraint for N-O distance being 3.02 Å. Particular geometries were created by changing the N-O and N-H distances with a step of 0.05 Å. The H2O+ + C4H5N+, H3O+ + C4H4N+ and H2O + C4H5N2+ curves in the one-dimensional PES scan shown in Fig. 4a were calculated using constrained DFT with Configurational Interaction (CDFT-CI) approach and the B3LYP/aug-cc-PVTZ method. In addition, we also calculated the two-dimensional PES for the proton transfer channel using the relaxed PES scan method, which is presented in Supplementary Fig. 4. The scan is performed by fixing the intermolecular N-O and O-H distances at each point, all other coordinates were optimized at the CCSD/cc-pVDZ level at each step, the step size is 0.1 Å.