Abstract
Studying the interplay of electron correlation and topology is crucial for discovering new quantum states, such as the fractional quantum spin Hall effect and topological superconductors. Unlike linear transport, nonlinear electrical responses, which encode both symmetry and topological features remain largely unexplored in systems with electron correlation and topology. Here we report that nonlinear Hall measurements reveal the emergence of a correlated state in few-layer topological semimetal TaIrTe₄ below a critical temperature and bias current. This state, exhibiting ultra large nonlinear conductivity, is attributed to the formation of a charge density wave in TaIrTe4 that leads to substantial Berry curvature redistribution. This origin is further supported by the observation of a Raman amplitude mode associated with the charge density wave, enhanced second harmonic generation, and first-principles calculations. Our findings demonstrate that nonlinear electrical probes can access rich phase diagrams in topological materials and highlight the potential of correlated topological systems for developing nonlinear electronics.
Similar content being viewed by others
Introduction
Topological semimetals are materials characterized by gapless electronic excitations and unique band crossings in their electronic structure, leading to exotic phenomena such as the chiral anomaly and Fermi arcs1,2,3,4. Many of these intriguing quantum phenomena are closely related to their topological properties, including chiral Weyl nodes and sizable Berry curvature in the momentum space1,2,4,5. Probing how these topological properties evolve in different quantum orderings and quantum transitions is crucial for advancing the understanding of topological semimetals and paving the way for high-performance topological electronics. The recently discovered nonlinear Hall effect (NLHE) has been utilized as a Berry curvature probe to characterize the asymmetric distribution of positive and negative Berry curvature, namely the Berry curvature dipole (BCD), in the momentum space of topological semimetals with broken inversion symmetry6,7,8. In a material with a nonzero BCD, an electric field, E, induces a second-order transverse current, whose magnitude quantitatively reveals the BCD near the Fermi level. The response of this nonlinear transport is also sensitive to ordering symmetry6,7,8,9, making it a useful tool for probing order parameters of broken symmetry states and their impact on topological properties.
Beyond non-interacting electronic structure studies, there is a growing interest in exploring strong correlations in topological semimetals to discover new quantum states of matter. This approach promotes quantum fluctuations and induces rich correlated states, such as topological superconductors, axion charge density waves (CDW), and fractional quantum spin Hall3,10,11,12,13,14. Given the fact that strong correlations lead to instability and reconstruction of electronic bands near the Fermi surface, along with the change in topology, the associated Berry curvature redistribution makes NLHE a potential tool for exploring rich correlated phase transitions in topological semimetals, which remains largely unexplored.
TaIrTe4, as a type-II Weyl semimetal15, has attracted a lot of interest recently due to its remarkable topological properties in both bulk and monolayer forms, such as Berry curvature enhanced photoresponse and the quantum spin Hall effect16,17,18. NLHE has been studied in bulk TaIrTe4, in which a sizable BCD is observed as a result of substantial Berry curvature near Weyl points and broken inversion symmetry19, but has remained unexplored in the atomically thin limit due to the centrosymmetric structure of monolayer TaIrTe4, which diminishes any intrinsic BCD. The recent work of the dual quantum spin Hall effect in monolayer TaIrTe4 indicates the formation of a strongly correlated state, which could be a CDW, yet the direct experimental evidence is missing18. Therefore, few-layer topological semimetal TaIrTe4 becomes a favorable candidate to study the interplay of strongly correlated states and topological features by NLHE.
In this work, we use NLHE to reveal an electronic phase diagram in layered topological semimetal TaIrTe4 (from two layers to ten layers). Our findings reveal a two-orders-of-magnitude enhancement in NLHE below the critical temperature and current, indicative of the emergence of a correlated state. Transition to this state can exhibit temperature- and current-dependent hysteresis in NLHE, respectively. Through temperature-dependent low-frequency Raman spectroscopy and symmetry information extracted from angle-dependent NLHE and nonlinear optical measurements, we identify this state as a one-dimensional (1D) CDW along the Ta atom chain. Density functional theory (DFT) calculations further confirm the formation of this 1D CDW state arises from a strong electronic instability in few-layer TaIrTe₄, and results in the enhancement of BCD and NLHE.
Results and discussion
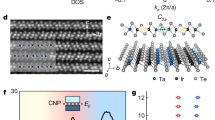
The lattice structure of a few-layer TaIrTe4 is shown in Fig. 1a with a mirror plane \({M}_{\hat{{{{\rm{a}}}}}}\). As restricted by symmetry, NLHE is nonzero along the \(\hat{{{{\rm{b}}}}}\)-axis in response to a perpendicular driving current, \({I}^{\omega }={I}_{0}\sin (\omega t)\), with frequency \({{{\rm{\omega }}}}\) along the \(\hat{{{{\rm{a}}}}}\)-axis, while NLHE is expected to be negligible along the \(\hat{{{{\rm{a}}}}}\)-axis19 (See Supplementary Note 1). To accurately determine the crystal orientation of anisotropic two-dimensional (2D) flakes, polarized Raman spectroscopy is employed in a parallel configuration20 (see “Methods”). Figure 1b displays the Raman spectrum for two representative polarization directions with respect to the crystal \(\hat{{{{\rm{a}}}}}\)-axis. The intensity of several modes depends strongly on the polarization direction, especially the modes at 77 \({{{\rm{c}}}}{{{{\rm{m}}}}}^{-1}\), 103 \({{{\rm{c}}}}{{{{\rm{m}}}}}^{-1}\), and 160 \({{{\rm{c}}}}{{{{\rm{m}}}}}^{-1}\), which correspond to the A1 modes of Td-TaIrTe418. Specifically, the polarization direction corresponding to the maximum of the 103 \({{{\rm{c}}}}{{{{\rm{m}}}}}^{-1}\) mode and the minimum of 77 \({{{\rm{c}}}}{{{{\rm{m}}}}}^{-1}\) and 160 \({{{\rm{c}}}}{{{{\rm{m}}}}}^{-1}\) modes is along the \(\hat{{{{\rm{a}}}}}\)-axis of the crystal20, which helps to identify the \(\hat{{{{\rm{a}}}}}\)-axis for Hall bar-shaped devices. Accordingly, high-quality TaIrTe4 Hall bar devices are fabricated with source-drain electrodes along the \(\hat{{{{\rm{a}}}}}\)-axis and encapsulated by hexagonal boron nitride (hBN) (Fig. 1c, see “Methods” for more details). To quantify NLHE, transverse voltage along the \(\hat{{{{\rm{b}}}}}\)-axis \({V}_{{{{\rm{ab}}}}}^{2\omega }\) is measured with the input AC along the \(\hat{{{{\rm{a}}}}}\)-axis \({I}_{{{{\rm{aa}}}}}^{\omega }\).
a The lattice structure of TaIrTe4 from the top view (left) and side view (right). The crystalline directions are noted. b Angle-resolved Raman spectra intensity for the hBN-covered few-layer TaIrTe4 measured in a parallel-polarized configuration at stage rotation angles of 0° and 90°, the polarization is parallel with the crystalline \(\hat{{{{\rm{a}}}}}\)-axis and \(\hat{{{{\rm{b}}}}}\)-axis, respectively. c Schematic and optical image of the Hall bar-shaped device to measure NLHE. The second harmonic Hall voltage is maximized along the \(\hat{{{{\rm{b}}}}}\)-axis with alternating driving current along the \(\hat{{{{\rm{a}}}}}\)-axis. Scale bar, 10 µm. d The typical NLH response \({V}_{{{{\rm{ab}}}}}^{2\omega }\) at temperatures of \(T=2\) \({{{\rm{K}}}}\) and \(T=300\) \({{{\rm{K}}}}\). Dashed curves represent quadratic fits to the V–I characteristics.
Unconventional nonlinear conductivity enhancement
Figure 1d shows the nonlinear Hall (NLH) measurements in a six-layer sample at \(T=2\) \({{{\rm{K}}}}\) and \(T=300\) \({{{\rm{K}}}}\). In both cases, \({V}_{{{{\rm{ab}}}}}^{2\omega }\) exhibits a clear quadratic dependence on \({I}_{{{{\rm{aa}}}}}^{\omega }\), but with a striking difference in magnitude. At \(2\) \({{{\rm{K}}}}\), the NLH response is 350 times larger than at room temperature. We quantify this enhancement by extracting the second-order nonlinear conductivity \({\chi }_{\alpha \beta \beta }\) from the nonlinear I-V curves using the relation \({j}_{\beta \alpha }^{2\omega }={\chi }_{\alpha \beta \beta }{E}_{\beta }{E}_{\beta }\), where \({j}_{\beta \alpha }^{2\omega }\) is the second-order current density in the \(\alpha\) direction, driven by the electric field, \({E}_{\beta }\), in the \(\beta\) direction6\(.\) Such observation distinctly differs from the temperature-dependent NLHE in bulk TaIrTe4, where both the nonlinear conductivity and BCD show no significant enhancement at low temperature, other than minor changes due to Fermi level shifts19. Additionally, in the few-layer limit, the absolute value of \({\chi }_{{{{\rm{baa}}}}}\) (\(\sim \! 20\) \({{{\rm{\mu }}}}{{{\rm{m}}}}{{{{\rm{V}}}}}^{-1}{\Omega }^{-1}\)) is significantly boosted by more than five orders of magnitude compared to previous studies on bulk19, suggesting an enhancement mechanism unique to ultrathin TaIrTe₄.
Phase diagram probed by NLHE
To understand the physics of the enhanced NLHE in few-layer TaIrTe4 at low temperature, we conduct systematic temperature-dependent NLH measurements on a 6-layer TaIrTe4, across a wide range of injected current, \({I}_{{{{\rm{aa}}}}}^{\omega }\), as shown in Fig. 2. In particular, \({V}_{{{{\rm{ab}}}}}^{2\omega }\) (Fig. 2a) and the corresponding phase \({\theta }_{{{{\rm{ab}}}}}^{2\omega }\) (Fig. 2b) are probed. \({\theta }_{{{{\rm{ab}}}}}^{2\omega }\) is expected to be \(\pm\)90°, depending on the direction of BCD, based on the expression of the second-order NLH voltage7: \({V}_{{{{\rm{ab}}}}}^{2\omega }={V}_{0}\sin (2\omega t+{\theta }_{{{{\rm{ab}}}}}^{2\omega })\propto {{\pm \left({I}_{{{{\rm{aa}}}}}^{\omega }\right)}^{2}|}_{{{{\rm{AC}}}}}=\frac{1}{2}{I}_{0}^{2}\sin (2\omega t\pm \frac{{{{\rm{\pi }}}}}{2})\). Interestingly, with varying \({I}_{{{{\rm{aa}}}}}^{\omega }\) and temperature, we find two distinct states (marked as state I and state II, respectively) with clear NLH voltage and phase boundaries, separated by a critical temperature, \({T}_{{{{\rm{C}}}}}\) \(\sim 60\) \({{{\rm{K}}}}\) and critical driving current, \({I}_{{{{\rm{C}}}}}\le 20\) \({{{\rm{\mu A}}}}\). Within the dome enclosed by these thresholds (state II), relative to the outer region (state I), \({V}_{{{{\rm{ab}}}}}^{2\omega }\) exhibits two orders’ enhancement and a sign reversal with a 180° phase shift from −90° to 90°.
a The 2D map of the NLH voltage \({V}_{{{{\rm{ab}}}}}^{2\omega }\) as a function of temperature and input current. b Corresponding map of the NLH phase \({\theta }_{{{{\rm{ab}}}}}^{2\omega }\). Both maps indicate the onset of state II below 60 K and low driving current below 20 \({{{\rm{\mu }}}}{{{\rm{A}}}}\). Crosscuts of \({V}_{{{{\rm{ab}}}}}^{2\omega }\) and \({\theta }_{{{{\rm{ab}}}}}^{2\omega }\) for state I and state II are shown in c and d respectively. In both panel, dashed lines represent linear fits to the \({V}_{{{{\rm{ab}}}}}^{2\omega }\) data and the solid lines are guides to the \({\theta }_{{{{\rm{ab}}}}}^{2\omega }\) data. Phase transition between state I and state II with hysteresis window, driven by current and temperature independently, are shown in e, f, respectively. In e the dashed curves represent quadratic fits to the V–I characteristics. In f error bars represent the standard error of \({\eta }_{{{{\rm{ab}}}}}\) from quadratic fitting and the dashed line marks \({\eta }_{{{{\rm{ab}}}}}=0\) as a reference for the direction of the NLHE.
In the following, we will take a closer look at each of state and the transition between them. From 300 K to 70 K, TaIrTe4 shows a standard NLH response as the temperature changes. As shown in Fig. 2c, line cuts of \({I}_{{{{\rm{aa}}}}}^{\omega }\) versus \({V}_{{{{\rm{ab}}}}}^{2\omega }\) for 6 different isotherms all show a second-harmonic transverse voltage which scales quadratically with the applied longitudinal current (\({V}_{{{{\rm{ab}}}}}^{2\omega }\propto ({{I}_{{{{\rm{aa}}}}}^{\omega }})^{2}\)), maintaining a −90° phase across the whole current range. The value of the NLH generation efficiency21,22, \({\eta }_{{{{\rm{ab}}}}}=\frac{{V}_{{{{\rm{ab}}}}}^{2\omega }}{{\left({V}_{{{{\rm{aa}}}}}^{\omega }\right)}^{2}}\), shows a gradual shifting from 0.5 to 1 \({{{{\rm{V}}}}}^{-1}\) in this region, which is attributed to the shifting of the chemical potential with temperature. The value of \({\eta }_{{{{\rm{ab}}}}}\) of our few-layer sample in state I is already four orders of magnitude higher than its bulk counterpart, since only the surface of the bulk contributes to NLHE19.
Below 60 K, TaIrTe4 exhibits a distinctly different NLHE, suggesting the formation of state II in the critical region (\(T < {T}_{{{{\rm{C}}}}}\) and \({I}_{{{{\rm{aa}}}}}^{\omega } < {I}_{{{{\rm{C}}}}}\)). By taking line cuts within this critical region (Fig. 2d), we find that \({V}_{{{{\rm{ab}}}}}^{2\omega }\) maintains a quadratic relationship below 5 µA and is enhanced by two orders of magnitude with respect to room temperature, with a relative shift of \({{{\rm{\pi }}}}\) for \({\theta }_{{{{\rm{ab}}}}}^{2\omega }\) as compared to state I. When \({I}_{{{{\rm{aa}}}}}^{\omega }\) is above 5 µA, the quadratic behavior diverges, suggesting that the large current can destroy state II. This effect is highlighted in Fig. 2e, where \({V}_{{{{\rm{ab}}}}}^{2\omega }\) is measured at 10 K by sweeping \({I}_{{{{\rm{aa}}}}}^{\omega }\). As shown, continuing to increase the \({I}_{{{{\rm{aa}}}}}^{\omega }\) above 20 µA restores the NLH response, where \({V}_{{{{\rm{ab}}}}}^{2\omega }\) scales quadratically with \({I}_{{{{\rm{aa}}}}}^{\omega }\) with \({\theta }_{{{{\rm{ab}}}}}^{2\omega }\) flipping back to −90°, the same as state I. This observation implies that the transition between state I and state II can be driven by current. We also show the very slight change of \({{V}_{{{{\rm{ab}}}}}^{2\omega }/\left({I}_{{{{\rm{aa}}}}}^{\omega }\right)}^{2}\) above \({I}_{{{{\rm{C}}}}}\) over the whole temperature region from 300 K to 2 K (See Supplementary Note 2) and the linear resistance behavior across the entire temperature range, which is consistent with Fermi-liquid theory for currents exceeding \({I}_{{{{\rm{C}}}}}\) (See Supplementary Note 3). Both observations consolidate that TaIrTe4 has fully transitioned to state I above \({I}_{{{{\rm{C}}}}}\) and there is a uniform state—state I—outside the critical region, where TaIrTe4 displays normal NLH behavior with moderate strength, as corroborated in other studies7,8,19. The 2D maps of the NLHE also suggest that the transition between state I and state II can be driven by either temperature or incident current, where the Joule heating effect induced by current has been excluded (See Supplementary Note 4). A possible mechanism for this current-induced phase transition could be the depinning of charge order induced by current as discussed in Supplementary Note 5.
First-order phase transition driven by current and temperature
Moreover, we observe a hysteresis of NLHE when sweeping either the current or temperature. In Fig. 2e, NLH response is measured at 10 K by sweeping \({I}_{{{{\rm{aa}}}}}^{\omega }\). During the transition between the two states, hysteresis windows between 7 µA and 20 µA are observed in both the NLH voltage \({V}_{{{{\rm{ab}}}}}^{2\omega }\) and phase \({\theta }_{{{{\rm{ab}}}}}^{2\omega }\), plotted in black and red respectively. Similarly, in Fig. 2f, a thermal hysteresis window, approximately 5 K wide, is also observed in \({\eta }_{{{{\rm{ab}}}}}\) during the temperature sweeps across state I and state II, when measured at small driving currents (<5 µA). This hysteresis behavior has been reproduced in multiple devices, with an example of a bilayer device shown in Supplementary Note 6, suggesting that the formation of state II undergoes a first-order transition.
To further elucidate the NLH response across the transition, we compare the behavior of \({\eta }_{{{{\rm{ab}}}}}\) under different current amplitudes. Under large driving currents (>20 µA), \({\eta }_{{{{\rm{ab}}}}}\) evolves smoothly from 100 K to 2 K, without a clear turning point (black line in Fig. 2f), indicating a gradual change contributed to the chemical potential shift. In contrast, at small driving currents, \({\eta }_{{{{\rm{ab}}}}}\) dramatically increases from approximately 0.7 \({{{{\rm{V}}}}}^{-1}\) at 100 K to about 50 \({{{{\rm{V}}}}}^{-1}\) below 10 K, with a distinct turning point near 60 K. This is about a 2-orders-of-magnitude enhancement of NLHE, primarily arising from a BCD increase induced by the phase transition, as confirmed by the scaling law analysis (See Supplementary Note 7). The corresponding nonlinear conductivity at low temperature is enhanced to 20 \({{{\rm{\mu }}}}{{{\rm{m}}}}\) \({{{{\rm{V}}}}}^{-1}{\Omega }^{-1}\), which is the highest value reported among existing 2D material systems22,23,24 (See Supplementary Note 8).
Optical features of correlated state II
To investigate the characteristic of state II in few-layer TaIrTe₄, we employ temperature-dependent Raman spectroscopy, a sensitive technique for revealing lattice dynamics and possible collective excitations during phase transitions25,26,27,28. Figure 3a summarizes the temperature-dependent Raman spectra of a typical TaIrTe4 thin film, captured from 55 cm−¹ to 115 cm−¹ between 2 K and 200 K. Above the critical temperature \({T}_{{{{\rm{C}}}}}\), the spectra exhibit one A2 mode near 68 cm−¹ and three A1 modes around 79, 86, and 105 cm−¹, consistent with both room-temperature data and the previous report18. As the temperature drops below \({T}_{{{{\rm{C}}}}}\), a new peak emerges around 83 cm−¹, corresponding to an energy of 10.3 meV, in addition to the existing modes at higher temperatures. The peak position and intensity of this new peak are determined using Voigt fitting, with examples at 5 K, 40 K, and 100 K shown in Fig. 3b. Control fittings using only two peaks for the spectra below \({T}_{{{{\rm{C}}}}}\) exhibit significant deviations from the experimental data, ruling out the possibility that the increase in intensity around 83 cm−¹ is due to the broadening of nearby Raman modes (see Supplementary Fig. 9). To quantify the evolution of this new peak at 83 cm−¹, we plot its integrated intensity as a function of temperature in Fig. 3c, which increases sharply below \({T}_{{{{\rm{C}}}}}\). The temperature dependence of this new peak’s intensity is well-fitted by the mean-field theory (detailed in Supplementary Note 9), as characteristic behavior of amplitude modes in CDW systems, which suggests the state II below 60 K is CDW phase29,30,31. And the energy peak’s energy (~10.3 meV), which is a typical energy for the amplitude mode of a CDW, further supports this interpretation31,32,33,34. The fitting reveals a transition temperature of 60 K, which is consistent with the critical temperature \({T}_{{{{\rm{C}}}}}\) observed in NLHE.
a The Raman spectra of TaIrTe₄ from 55 cm−¹ to 115 cm−¹ at temperatures between 2 K and 200 K. The rising of a new peak at ~83 cm−¹ emerging below 60 K indicates the excitation of the amplitude mode in the CDW phase. b Raman spectra at 5 K, 40 K, and 100 K, with Voigt fitting between 75 and 90 cm−¹. The new peaks at 40 K and 5 K are shown in the green dashed line and highlighted by the green arrow. c The temperature dependence of the new peak’s integrated intensity \({I}_{{{{\rm{A}}}}}\), with the solid line representing the mean-field theory fit, suggests the phase transition temperature at 60 K. Error bars represent the standard error of Raman peak intensities obtained from Voigt fitting. d Polarized SHG patterns of TaIrTe4 at 100 K and 1.7 K with normalized maximum. With normalized peak intensity along the \(\hat{{{{\rm{b}}}}}\)-axis, the intensity along the \(\hat{{{{\rm{a}}}}}\)-axis is greatly enhanced at 1.7 K. e Temperature dependence of the SHG intensity. A significant enhancement of SHG intensity also emerges below 60 K. Error bars represent the standard error of the mean of SHG intensities at each temperature point. f NLH generation efficiency \({\eta }_{\alpha \beta }\) as a function of T from 300 K to 2 K for current applied along the \(\hat{{{{\rm{a}}}}}\)-axis and \(\hat{{{{\rm{b}}}}}\)-axis, respectively (the \(\hat{{{{\rm{b}}}}}\)-axis data are multiplied by 100 times). Inset: two measurement configurations.
To further reveal the symmetry of state II, identified as CDW in Raman measurements, we employ second harmonic generation (SHG) microscopy and angle-resolved transport measurements, both of which are sensitive to the crystal structure’s symmetry35,36,37. We conduct SHG microscopy across different temperatures and compare the SHG polarization pattern of our few-layer TaIrTe4 sample at 100 K (state I) and 1.7 K (state II) (see “Methods” for more details). As shown in Fig. 3d, both SHG patterns show four lobes and two-fold rotation symmetry, which belongs to the Pm space group. However, at 1.7 K, a stronger anisotropy in SHG intensity is observed along the crystalline \(\hat{{{{\rm{a}}}}}\)-axis, which is the Ta atom chain. By fitting both SHG patterns with the nonlinear susceptibility matrix in the Pm space group, we find a significant enhancement of ~25% in the nonlinear optical susceptibility element d11 from state I to state II, while the other elements, such as d12, remain nearly unchanged (See Supplementary Note 10). This suggests that the formation of the CDW state enhances the in-plane anisotropy of the orthorhombic TaIrTe₄ crystal without altering the space group symmetry. Moreover, temperature-dependent SHG intensity shows a notable increase below 60 K, consistent with the onset temperature identified in our NLHE measurements (Fig. 3e). Given the substantially enhanced pattern elongation and nonlinear susceptibility value along the \(\hat{{{{\rm{a}}}}}\)-axis without further symmetry breaking, the CDW state is likely to exhibit a 1D electronic density modulation along the crystalline \(\hat{{{{\rm{a}}}}}\)-axis38,39,40.
The 1D electronic density modulation along the \(\hat{{{{\rm{a}}}}}\)-axis is further supported in the angle-dependent NLHE. We compare temperature-dependent NLH measurements with the current (below 20 \({{{\rm{\mu }}}}{{{\rm{A}}}}\)) along the \(\hat{{{{\rm{a}}}}}\)-axis and the \(\hat{{{{\rm{b}}}}}\)-axis, respectively, in the Hall bar-shaped device, as shown in the inset of Fig. 3f. The strength of the NLHE along the \(\hat{{{{\rm{a}}}}}\)-axis, \({\eta }_{{{{\rm{ab}}}}}\), exhibits a two order of magnitude enhancement from room temperature to 2 K (red plot in Fig. 3f), in contrast to \({\eta }_{{{{\rm{ba}}}}}\) along the \(\hat{{{{\rm{b}}}}}\)-axis, which remains near zero (black plot in Fig. 3f). This enhanced anisotropy in state II is consistent with the result shown in the SHG polarization pattern, underscoring the transition’s 1D character, where electronic ordering occurs predominantly along the \(\hat{{{{\rm{a}}}}}\)-axis, supporting a 1D CDW.
To explain the microscopic origin of the CDW phase and its relationship with BCD and the associated NLHE, we conduct first-principles calculations to model the phase instability and quantify the BCD. (“Methods” and Supplementary Note 11). Firstly, the electronic susceptibility of conduction bands has been calculated, whose value reflects the tendency of electronic instability. Indeed, we find a local electronic susceptibility maximum at a nesting vector of \({\bf {Q}}^{*}=\)(\({0.11,0}\)) \({{{\text{\AA }}}}^{-1}\), suggesting a strong tendency to form a CDW state at low temperature (see Fig. 4a top). In real space, such electronic ordering corresponds to an electron density modulation along the 1D Ta chain (\({\hat{{\rm{a}}}}\)-axis), with a relatively large period of about 15 atomic unit cells (Fig. 4a bottom). This 1D CDW phase scenario as the microscopic origin for state II can well explain the observed anisotropic SHG and angle-resolved transport signatures: the proposed 1D CDW phase does not further break the mirror symmetry (\({M}_{\hat{{{{\rm{a}}}}}}\)) of pristine few-layer TaIrTe4 crystal in the Pm space group but results in larger SHG anisotropy and NLH transport anisotropy with the formation of additional charge ordering along the crystalline \(\hat{{{{\rm{a}}}}}\)-axis. As for the SHG intensity boost, this can be understood by considering the electronic density of state increment for related optical transitions due to the periodic CDW-induced band folding39,40. Taken together, the observed changes in both SHG polarization pattern and intensity are consistent with the formation of a 1D CDW state emerging in few-layer TaIrTe4.
a Calculated electronic susceptibility of the conduction band based on first-principles calculations (top). The white arrow highlights a local maximum of the electronic susceptibility at a wavevector \({\bf {Q}}^{*}\). It corresponds to a superlattice of about 15 unit cells along the one-dimensional Ta chain direction (bottom). Band structures with Berry curvature (\(\varOmega\)) under an electrical field of 0.1 V/nm, b without, and c with superlattice potential with a periodicity of 15 unit cells, show an enhanced Berry curvature near the CDW gap around 0.2 eV. d, e Corresponding momentum-resolved Berry curvature dipole (\({D}_{{{{\rm{ac}}}}}\)) at the energy level of 0.16 eV. Blue and red colors present positive and negative BCD amplitudes indicating that the BCD magnitude in these hotspots increases from \(2\times {10}^{3}\) in state I to \(4\times {10}^{4}\) in state II, representing a 20-fold enhancement.
Given that the 1D CDW phase preserving mirror symmetry \({M}_{\hat{{{{\rm{a}}}}}}\) is highly possible as the origin of state II, we further analyze how this electronic modulation can result in large BCD and corresponding enhanced nonlinear responses. By introducing the 1D superlattice potential into the system, we have calculated both band structure changes and the evolution of the BCD using an 8-band tight-binding model. Comparing Fig. 4b, c, the CDW potential opens a gap between the two lowest conduction bands. In the real case of our multilayer TaIrTe4 device, this band gap is shrunk but still exists. As shown in the color scale, a large Berry curvature, \(\varOmega\), appears near the edges of the band gap. For the BCD distribution calculations, a 0.1 V/nm electric field is employed to break the inversion symmetry and mimic the inversion symmetry breaking in thin-film TaIrTe4. It is noted that in TaIrTe4 films, only the component of BCD, \({D}_{{{{\rm{ac}}}}}\), is nonzero due to the absence of the mirror plane \({M}_{\hat{{{{\rm{b}}}}}}\). Next, we show the momentum resolved BCD maps in Fig. 4d (state I) and 4e (state II) at a chemical potential of 0.16 eV, which corresponds to the experimentally determined Fermi level at \({T}_{{{{\rm{C}}}}}\) extracted from the Hall measurement. As illustrated in two maps, the \({D}_{{{{\rm{ac}}}}}\) hotspots are significantly enhanced by a factor of 20 near the CDW gap and exhibit opposite signs between state I and state II. Both the magnitude enhancement and the sign reversal match our observation in the experimental NLH response. A more comprehensive analysis of the BCD as a function of chemical potential near the band gap, and its relevance to the NLHE enhancement, is provided in Supplementary Note 12.
In summary, our results show that the NLHE can be used as a sensitive probe for detecting correlated phases and constructing rich phase diagrams in topological semimetals. The combination of nonlinear transport and optical measurements points out the formation of a 1D CDW in the few-layer topological semimetal TaIrTe4, which provides a unique material platform to explore the interplay of strongly correlated states and topological properties. Moreover, its recorded-high nonlinear susceptibility at both cryogenic and room temperature also makes it competitive for nonlinear device development, such as energy harvesters and infrared detectors.
Methods
TaIrTe4 growth
Single crystals of TaIrTe4 were synthesized via a self-flux method. Ta powder (99.98%), Ir powder (99.99%), and Te chunks (99.9999%) were loaded in a 1:1:20 ratio (Ta:Ir:Te) into an alumina Canfield crucible and sealed in a quartz ampoule under vacuum (10−6 Torr). The sealed ampoule was then heated to 1100 °C over 24 h and dwelled for 5 days, before cooling to 600 °C at 1 °C/hr. The ampoule was then quickly cooled to 525 °C and centrifuged to remove excess Te. To remove any residual Te on the surface, the resulting crystals were sealed in another evacuated ampoule and placed in a tube furnace with a 200 °C temperature gradient and the crystals were placed at the hot end (425 °C) for 2 days.
Raman measurement
The angle-resolved Raman spectra are obtained using a Horiba/AIST-NT LabRAM system. A linearly polarized laser beam with the wavelength of 633 nm is directed and focused onto the samples using a 100× objective lens with a numerical aperture of 0.9. The same lens captures the scattered Raman signals and directs them back to the spectrometer. During the measurements, the sample is rotated on a stage in 6° increments while keeping other experimental conditions consistent. Another low-frequency Raman measurement system with three band notch filters designed for 5 cm−1 band stop of excitation bandwidth is used for the temperature-dependent Raman spectra. Raman spectra are obtained using the 1800 lines per mm grating in an Andor Shamrock 500i Spectrometer. A linearly polarized laser beam with 633 nm wavelength is directed and focused into the Quantum Design OptiCool Cryostat on the samples using a 50× long working distance objective lens with a numerical aperture of 0.6.
Device fabrication
Multi- and few-layer TaIrTe4 exhibit high air sensitivity. Therefore, all device fabrication processes were conducted within a nitrogen-filled glove box. Initially, a layer of pre-patterned metal (2/10 nm Ti/Au) was deposited onto the Si/SiO2 chip using e-beam lithography and subsequent e-beam evaporation. The metal contacts underwent a cleaning step using a limited amount of O2 plasma for 25 min before introduction into the glove box. TaIrTe4 flakes were mechanically exfoliated onto a polydimethylsiloxane stamp and then transferred onto Si/SiO2 substrates. The specific layers (2–15 layers) were then identified based on optical contrast observed on the Si/SiO2 substrates and further confirmed by measuring step heights with an atomic force microscope. Subsequently, hBN (20–40 nm thickness) was picked up using a dry stacking method41. This hBN layer was then utilized to pick up the targeted TaIrTe4 flake, and the whole hBN/TaIrTe4 stack was placed onto the pre-patterned metal contacts situated on the Si/SiO2 chip.
Transport measurement
Transport measurements were conducted within cryogenic systems (Physical Property Measurement System or the OptiCool system by Quantum Design), which provide temperature control from 1.7 K to 300 K and magnetic fields up to 14 Tesla. An AC excitation \({I}_{{{{\rm{aa}}}}}^{\omega }={I}_{0}\sin (\omega t)\), whose frequency \(\omega\) ranges from 17.7 to 1007.7 Hz was sourced using a lock-in amplifier (OE1022D by Sine Scientific Instruments), yielding consistent NLHE (See Supplementary Note 13). Both fundamental and second-harmonic frequencies of longitudinal and transverse voltages were captured by two dual-channel lock-in amplifiers (OE1022D by Sine Scientific Instruments).
Nonlinear optical measurement
The measurements were performed based on an optical second harmonic detection setup coupled with a cryogenic system (OptiCool by Quantum Design) with a temperature range from 1.7 K to 300 K. In particular, the excitation light at 1040 nm was extracted using a tunable femtosecond laser (Discover NX by Coherent). The excitation laser was linearly polarized by a polarizing beamsplitter. The laser was focused by a 50× NIR objective on the sample with a spot size of around 3 μm. The SHG signal was detected in the backscattering configuration and finally collected by photon-counting PMT modules. In the SHG polarization pattern study, we used a half-wave plate to control the incident light polarization, while the emitted by the sample was examined by a polarizer.
DFT and model calculations
We use the Vienna ab initio simulation package to determine the most stable structure and analyze the electronic properties of TaIrTe4. The electronic susceptibility was calculated by the Lindhard function. The parameters of DFT calculations and CDW susceptibility can be found in the Supplementary Note 11.
To simulate the superlattice band structure under a periodic modulation of CDW potential, we use the Frohlich-Peierls method to introduce an additional term in the Hamiltonian.
Where \(V\) is the amplitude of the CDW potential and \({{{\bf{Q}}}}\) is the wave vector corresponding to the periodicity of the CDW, \(r\) is the position vector, and \(\phi\) is the phase shift. The intrinsic part of the NLH conductivity \({\chi }_{\alpha \beta \beta }\) can be described by the BCD, which can be calculated from first principle method42 as follows:
Where \({D}_{\beta \gamma }\) is the BCD, \({f}_{n}^{0}({{{\bf{k}}}})\) is the equilibrium Fermi-Dirac distribution, \(\tau\) is the relaxation time, \({\epsilon }_{\alpha \beta \gamma }\) is the third rank Levi-Civita symbol, \(\alpha,\beta={{{\rm{a}}}},{{{\rm{b}}}}\) and \(\gamma={{{\rm{c}}}}\) in 2D. The Berry curvature \({\varOmega }_{c}\) in the 2D system can be calculated by,
Where \({\epsilon }_{n}\) and \({|n}\rangle\) are eigenvalues and eigenvectors, respectively. In 2D, the BCD is in a unit of length. Due to the \({M}_{\hat{{{{\rm{a}}}}}}\) reflection, only \(\frac{\partial {\varOmega }_{{{{\rm{c}}}}}}{{\partial k}_{{{{\rm{a}}}}}}\) is finite, and the \({\chi }_{{{{\rm{baa}}}}}\) is nonzero.
Data availability
The source data underlying all main manuscript figures are provided with this paper. All other data that support the findings of this study are available from the corresponding authors upon request. Source data are provided with this paper.
Code availability
The codes used for the calculations are available from the corresponding authors on request.
References
Armitage, N. P., Mele, E. J. & Vishwanath, A. Weyl and Dirac semimetals in three-dimensional solids. Rev. Mod. Phys. 90, 015001 (2018).
Burkov, A. A. Topological semimetals. Nat. Mater. 15, 1145–1148 (2016).
Yan, B. & Felser, C. Topological materials: Weyl semimetals. Annu. Rev. Condens. Matter Phys. 8, 337–354 (2017).
Xu, S.-Y. et al. Discovery of a Weyl fermion semimetal and topological Fermi arcs. Science 349, 613–617 (2015).
Chang, G. et al. Topological quantum properties of chiral crystals. Nat. Mater. 17, 978–985 (2018).
Sodemann, I. & Fu, L. Quantum nonlinear Hall effect induced by Berry curvature dipole in time-reversal invariant materials. Phys. Rev. Lett. 115, 216806 (2015).
Ma, Q. et al. Observation of the nonlinear Hall effect under time-reversal-symmetric conditions. Nature 565, 337–342 (2019).
Kang, K., Li, T., Sohn, E., Shan, J. & Mak, K. F. Nonlinear anomalous Hall effect in few-layer WTe2. Nat. Mater. 18, 324–328 (2019).
Du, Z. Z., Wang, C. M., Li, S., Lu, H.-Z. & Xie, X. C. Disorder-induced nonlinear Hall effect with time-reversal symmetry. Nat. Commun. 10, 3047 (2019).
Gooth, J. et al. Axionic charge-density wave in the Weyl semimetal (TaSe4)2I. Nature 575, 315–319 (2019).
Paschen, S. & Si, Q. Quantum phases driven by strong correlations. Nat. Rev. Phys. 3, 9–26 (2021).
Chen, L. et al. Topological semimetal driven by strong correlations and crystalline symmetry. Nat. Phys. 18, 1341–1346 (2022).
Qi, X.-L., Hughes, T. L. & Zhang, S.-C. Fractional charge and quantized current in the quantum spin Hall state. Nat. Phys. 4, 273–276 (2008).
Trang, C. X. et al. Conversion of a conventional superconductor into a topological superconductor by topological proximity effect. Nat. Commun. 11, 159 (2020).
Koepernik, K. et al. TaIrTe4: a ternary type-II Weyl semimetal. Phys. Rev. B 93, 201101 (2016).
Ma, J. et al. Nonlinear photoresponse of type-II Weyl semimetals. Nat. Mater. 18, 476–481 (2019).
Belopolski, I. et al. Signatures of a time-reversal symmetric Weyl semimetal with only four Weyl points. Nat. Commun. 8, 942 (2017).
Tang, J. et al. Dual quantum spin Hall insulator by density-tuned correlations in TaIrTe4. Nature 628, 515–521 (2024).
Kumar, D. et al. Room-temperature nonlinear Hall effect and wireless radiofrequency rectification in Weyl semimetal TaIrTe4. Nat. Nanotechnol. 16, 421–425 (2021).
Liu, Y. et al. Raman signatures of broken inversion symmetry and in-plane anisotropy in type-II Weyl semimetal candidate TaIrTe4. Adv. Mater. 30, 1706402 (2018).
Wang, S. et al. Nonlinear Hall effect and scaling law in Sb-doped topological insulator MnBi4Te7. Appl. Phys. Lett. 124, 153102 (2024).
Huang, M. et al. Giant nonlinear Hall effect in twisted bilayer WSe2. Natl Sci. Rev. 10, nwac232 (2023).
He, P. et al. Graphene moiré superlattices with giant quantum nonlinearity of chiral Bloch electrons. Nat. Nanotechnol. 17, 378–383 (2022).
Duan, J. et al. Giant second-order nonlinear Hall effect in twisted bilayer graphene. Phys. Rev. Lett. 129, 186801 (2022).
Wang, Y. et al. Structural phase transition in monolayer MoTe2 driven by electrostatic doping. Nature 550, 487–491 (2017).
Wall, S. et al. Ultrafast changes in lattice symmetry probed by coherent phonons. Nat. Commun. 3, 721 (2012).
Cong, X., Liu, X.-L., Lin, M.-L. & Tan, P.-H. Application of Raman spectroscopy to probe fundamental properties of two-dimensional materials. NPJ 2D Mater. Appl. 4, 1–12 (2020).
Rodin, A., Trushin, M., Carvalho, A. & Castro Neto, A. H. Collective excitations in 2D materials. Nat. Rev. Phys. 2, 524–537 (2020).
Xi, X. et al. Strongly enhanced charge-density-wave order in monolayer NbSe2. Nat. Nanotechnol. 10, 765–769 (2015).
Liu, G. et al. Observation of anomalous amplitude modes in the kagome metal CsV3Sb5. Nat. Commun. 13, 3461 (2022).
Tsang, J. C., Smith, J. E. & Shafer, M. W. Raman spectroscopy of soft modes at the charge-density-wave phase transition in 2H−NbSe2. Phys. Rev. Lett. 37, 1407–1410 (1976).
Chen, R. Y., Zhang, S. J., Zhang, M. Y., Dong, T. & Wang, N. L. Revealing extremely low energy amplitude modes in the charge-density-wave compound LaAgSb2. Phys. Rev. Lett. 118, 107402 (2017).
Yusupov, R. V., Mertelj, T., Chu, J.-H., Fisher, I. R. & Mihailovic, D. Single-particle and collective mode couplings associated with 1- and 2-directional electronic ordering in metallic RTe3. Phys. Rev. Lett. 101, 246402 (2008).
Demsar, J., Forró, L., Berger, H. & Mihailovic, D. Femtosecond snapshots of gap-forming charge-density-wave correlations in quasi-two-dimensional dichalcogenides 1T−TaS2 and 2H−TaSe2. Phys. Rev. B 66, 041101 (2002).
Zhao, Y. et al. Spectroscopic visualization and phase manipulation of chiral charge density waves in 1T-TaS2. Nat. Commun. 14, 2223 (2023).
Kumar, N. et al. Second harmonic microscopy of monolayer MoS2. Phys. Rev. B 87, 161403 (2013).
Wang, Y., Xiao, J., Yang, S., Wang, Y. & Zhang, X. Second harmonic generation spectroscopy on two-dimensional materials [Invited]. Opt. Mater. Express 9, 1136–1149 (2019).
Mennel, L. et al. Optical imaging of strain in two-dimensional crystals. Nat. Commun. 9, 516 (2018).
Lu, B. et al. Second-harmonic generation in the topological multifold semimetal RhSi. Phys. Rev. Res. 4, L022022 (2022).
Janisch, C. et al. Extraordinary second harmonic generation in tungsten disulfide monolayers. Sci. Rep. 4, 5530 (2014).
Wang, L. et al. One-dimensional electrical contact to a two-dimensional material. Science 342, 614–617 (2013).
Zhang, Y., Sun, Y. & Yan, B. Berry curvature dipole in Weyl semimetal materials: an ab initio study. Phys. Rev. B 97, 041101 (2018).
Acknowledgments
H.J., H.M., and Y.W. acknowledge support from the Department of Energy Office of Basic Energy Sciences through grant DE-SC0024176 (Device fabrication, transport, optical measurement). T.X. and J.X. acknowledge support from the Office of Naval Research through contract No. N00014-24−1−2068 (Optical measurement). J.L. was primarily supported by the National Science Foundation Materials Research Science and Engineering Center program through the UT Knoxville Center for Advanced Materials and Manufacturing under grant DMR-2309083 (theory modeling). Y.Z. was supported by the start-up fund at University of Tennessee. D.R., Y.H., and Y.M. are supported by National Science Foundation through the University of Wisconsin Materials Research Science and Engineering Center under grant No. DMR-2309000 (Growth of TaIrTe4 crystal and device fabrication). K.W. and T.T. acknowledge support from the JSPS KAKENHI (grant No. 21H05233 and 23H02052), the CREST (JPMJCR24A5), JST and World Premier International Research Center Initiative (WPI), MEXT, Japan (Growth of BN crystal).
Author information
Authors and Affiliations
Contributions
H.J. and Y.W. initiated and conceived the project; H.J. fabricated the devices, carried out the transport measurements, and analyzed all the data supervised by Y.W.; T.X. carried out the SHG measurement and analyzed optical results with H.J., Y.W., and J.X.; J.L. carried out the first-principles calculations of the single-particle band and the CDW band structures under the guidance of Y.Z.; Y.H. grew the TaIrTe4 bulk crystals under the guidance of D.R.; H.M. carried out the low-frequency Raman measurement under the guidance of H.J. and Y.W.; K.W. and T.T. grew the BN bulk crystals. All authors jointly wrote or commented on the manuscript, with a main contribution from H.J., Y.M., J.X., and Y.W.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Flavio Giorgianni, Dushyant Kumar, and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Source data
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Jiang, H., Xi, T., Li, J. et al. Probing interplay of topological properties and electron correlation in TaIrTe4 via nonlinear Hall effect. Nat Commun 16, 6351 (2025). https://doi.org/10.1038/s41467-025-61347-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-025-61347-3