Introduction

The performance of modern radio systems is intricately tied to a host of essential factors like transmitting power, antenna characteristics, and receiver sensitivity. The propagation environment of electromagnetic (EM) waves also exerts a determining influence on the system efficacy. For instance, in open spaces such as deserts or plains, it is easy for wireless signals to travel over long distances with relatively small attenuation. However, in complex environments such as urban areas with densely packed high-rise buildings and moving vehicles, the spread of EM waves will encounter various physical processes, including multiple reflections, refraction, and scattering, leading to severe signal fading and distortions that significantly degrade the system quality. The unpredictability of wave propagation introduces some variability in signal quality and reliability across various applications such as communication and radar, posing significant challenges to the overall effectiveness of the radio systems1,2,3. Consequently, substantial efforts have been made to acquire sufficient information about the propagation environment to mitigate the risk of system failures and ensure reliable operation4,5,6,7. For instance, to improve wireless communication quality, people are actively striving to acquire channel state information (CSI) through diverse methods8,9, making it possible to alter the transmission parameters and error correction methods dynamically for reliable and efficient data conveyance.

Recent advances of programmable metasurface and reconfigurable intelligent surface (RIS) furnish a fresh approach to freely manipulate the wireless propagation environment10,11,12,13,14,15,16,17. By describing various reflection/transmission states of the element with binary coding, the programmable metasurface exhibits prominent capabilities over the control of EM wave properties (e.g., magnitude, phase, and polarization) in a digital way, allowing for a plenty of applications like beam shaping, spectral modulation, polarization conversion and vortex wave generation based on different space-time coding strategies18,19,20,21,22,23. More importantly, the programmable metasurface can be reconfigured in real time and switched among various functionalities, which renders an excellent hardware platform to confront various scenarios for wireless applications in complicated propagation environments24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41.

Despite a formidable performance in wave manipulations, the programmable metasurface still lacks effective sensing means to secure wireless channel information in order to supply a ground for efficient control strategies for EM waves. Thus, it is hard to reshape the wireless propagation environment effectively and raise the system’s performance to the greatest extent. To tackle this challenge, more and more attempts have been made to endow the programmable metasurface with the power of sensing, spurring the generation of an adaptively programmable metasurface (APM). One route to realize APM is that the metasurface reflects most of the impinging signals, while a small fraction is coupled into sensing chains embedded within each element5,6,42,43,44,45,46,47. Another involves incorporating active modules (such as antennas) into certain elements to enable the direct reception of incident signals for sensing7. An additional option is to rest on external sensors to present auxiliary sensing information to the traditional metamaterials48.

Nevertheless, the existing solutions still encounter numerous bottleneck issues. Firstly, most reported adaptive metasurfaces can only acquire the magnitude of the incident signal without phase information. Secondly, the phase quantization bit of the adaptive metasurfaces is limited to 1 bit or 2 bits, and will produce a slight influence on the precision of the scattering beam pointing. Thirdly, the existing adaptive metasurfaces are deficient in the sensing and regulation capabilities in the element level, which will dramatically lower the flexibility of the metasurfaces for efficient wave controls.

Confronted with the aforementioned challenges, here we propose an intelligent APM with enhanced capabilities. The proposed APM can simultaneously acquire both magnitudes and phases of the surrounding EM waves. This considerably improves the sensing power of APM, making it possible to acquire the information from a broader perspective and swiftly modify its own scattering features to adapt to the complex propagation environment. The metasurface also confers the ability of continuous phase alteration with full phase range, while maintaining the reflection magnitude higher than 0.84. This is especially valued to promote the accuracy of scattering beam control. Furthermore, the proposed design employs a reception-reflection scheme that facilitates element-by-element sensing and manipulating. To demonstrate the powerful capability of the proposed APM, three representative integrated sensing and communication (ISAC) scenarios are investigated, and the performance of APM is experimentally validated. The results display good application vistas of APMs in boosting the performance of the current and future wireless systems.

Results

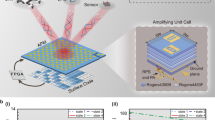
Figure 1 illustrates the schematic diagram of wireless environment regulation empowered by the proposed APM and a closed-loop working paradigm involving wave manipulation, sensing, and analysis. APM can sense the incident field element-by-element across its entire surface and obtain extensive wireless environmental information. After obtaining the environmental information, analysis is carried out to obtain the reflection matrix Φ of the elements by an optimization algorithm, which is employed to characterize the element phases in order to obtain the desired EM field distributions on the surface. The microcontroller unit (MCU) then generates DC control signals to adjust the working states of all APM elements corresponding to the matrix Φ.

Fig. 1: Adaptively programmable metasurface (APM) for intelligent wireless environment regulation and analysis by sensing the incident fields.
figure 1

APM can sense the complex electromagnetic field distributions around and dynamically manipulate the waves and signals in real time under the guidance of the sensed information.

Full size image

To illustrate the working principle of APM, Fig. 2a portrays a typical scenario of wireless environment regulation, where the sources, scatterers, and metasurface exist simultaneously. J(r) and M(r) are equivalent electric and magnetic currents at the position r = [rx, ry, rz], as the EM radiators; while ε(r), μ(r) and σ(r) stand for the permittivity, permeability, and conductivity at different locations in space, respectively, which can describe the material properties of various complex scatterers in the environment. APM has M × N elements that respond to the incident EM waves dynamically. The propagation and manipulation processes can be described by the following equation (see Supplementary Information for more details):

$$\begin{array}{c}{{\bf{E}}}({{\bf{r}}})={{{\bf{E}}}}_{{{\rm{in}}}}({{\bf{r}}})+\mathop{\sum }\limits_{m=1}^{M}\mathop{\sum }\limits_{n=1}^{N}\left(-j\omega {\mu }_{0}\right)[1+\frac{1}{{k}^{2}}\nabla \nabla ]\,{{{\bf{J}}}}^{{{\bf{s}}}}({{{\bf{r}}}}_{{m},\,{n}})\cdot G({{\bf{r}}},\,{{{\bf{r}}}}_{{m},\,{n}})\\={{{\bf{E}}}}_{{{\rm{in}}}}({{\bf{r}}})+\mathop{\sum }\limits_{m=1}^{M}\mathop{\sum }\limits_{n=1}^{N}\left(-j\omega {\mu }_{0}\right)\left[1+\frac{1}{{k}^{2}}\nabla \nabla \right]\cdot {\Gamma }_{m,\,n}\cdot {{{\bf{Z}}}}^{{H}}\cdot {{{\bf{E}}}}_{{{\rm{in}}}}({{{\bf{r}}}}_{{m},\,{n}})\cdot G({{\bf{r}}},\,{{{\bf{r}}}}_{{m},\,{n}})\end{array}$$
(1)

where E(r) and Ein(r) denote the total and incident electric fields evaluated at the point r, respectively; rm,n and \({\Gamma }_{m,\,n}={A}_{m,\,n}{{{\rm{e}}}}^{{{\rm{j}}}{\phi }_{m,\,n}}\) are the location and complex reflection coefficient of the APM element (m, n); and G(r, rm,n) is the Green’s function of the scalar Helmholtz equation, which is closely related to the wireless environment. The Green’s function can be expressed as G(r, r′) = − e−jk|r−r′|/4π|r−r′| in free space. However, in the complex EM circumstance populated with irregular scatterers, it is extremely tough to predict or portray the Green’s function analytically.

Fig. 2: Wireless environment regulations in different conditions and the structure of the proposed design.
figure 2

a The wireless environment regulation with the aid of a traditional metasurface, including various sources and scatterers. b The communication scenario in the regulated wireless environment based on the proposed APM, in which f and g are matrices describing the channel state information, while Φ is the reflection matrix of APM. c The structure of the APM element. d Details of the sensing and manipulating circuit. Geometric details of the element can be found in the Supplementary Information.

Full size image

For the conventional metasurface, it is possible to change the reflection matrix Φ for wave manipulation with the help of optimization methods29,30,31,32,33,34:

$$\varPhi=\left[\begin{array}{cccc}{\Gamma }_{1,1} & {\Gamma }_{1,2} & \cdots & {\Gamma }_{1,N}\\ {\Gamma }_{2,1} & {\Gamma }_{2,2} & \cdots & {\Gamma }_{2,N}\\ \vdots & \vdots & \ddots & \vdots \\ {\Gamma }_{M,1} & {\Gamma }_{M,2} & \cdots & {\Gamma }_{M,N}\end{array}\right]\in {{\mathbb{C}}}^{M\times N}.$$

However, in complex wireless environments, the Green’s function in Eq. (1) is unknown and unpredictable. As a result, the matrix Φ cannot always be guaranteed as the most optimal and may not be the best fit for the channel. An improved way is to get the channel information directly as the basis for adjusting the reflection matrix. But this requires the addition of extra sensors or antennas. These devices will share the aperture with the metasurface elements, which not only increases the cost and complexity but also has a non-negligible influence on the EM performance of the metasurface. Therefore, if the metasurface can directly access information from the incident waves in an element-by-element way, it would significantly enhance the sensing accuracy and real-time performance, and minimize the cost.

To handle the aforementioned issue, we present a new design of APM, in which each element is able to directly acquire information from the environment, thus establishing a new closed-loop working paradigm for sensing, analyzing, and manipulating the EM waves. APM combines autonomous analysis and decision-making without relying on pre-predicted information from external sensors, which can greatly improve the flexibility of the metasurface for EM manipulation, minimize the impact on the overall reflection performance due to the enhanced sensing ability, and increase the real-time response speed of the system.

APM element design

The detailed design of the proposed APM is shown in Fig. 2c. The element has a size of 40 × 40 mm2 (0.47 × 0.47 square wavelengths at 3.50 GHz), and is composed of three layers. The top layer consists of an F4BTM substrate sandwiched by two metallic patches with different sizes. The middle layer is made of a Rogers 4003 C substrate, whose front side has a metallic ground etched with an H-shaped slot, while the reverse has microstrip functional circuits for sensing and manipulation. The bottom layer is a full metallic ground. We remark that the two patches and the H-shaped slot can be amalgamated to form an antenna, which is cooperated with the microstrip circuit to couple a portion of the incident EM energy. The bottom metallic ground is used to enhance the reflection efficiency of APM. See Supplementary Information for more details.

Below, we summarize the conceptual principles of APM’s manipulating and sensing abilities. Initially, the incident wave is received by the slot antenna and subsequently coupled to the sensing and manipulating circuits (refer to Fig. 2d). Then, the received signal passes through a phase shifter. The programmable phase shift is achieved using different equivalent capacitances CVAR of the internal varactor diodes by applying the external DC voltage VDC. After the phase shifter, the signal reaches a weakly parallel-coupled line, in which a small fraction of the signal energy is coupled to the parallel microstrip line for sensing, while the majority continues to propagate forward until being reflected by the open-circuited load. Finally, the reflected signal follows its original path to go back. It is adjusted by the phase shifter again and sent to free space by the same slot antenna. Meanwhile, the signal coupled into the parallel microstrip line enters the sensing chain and helps in generating the reflection matrix Φ for APM.

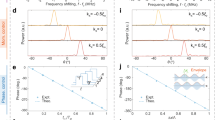
The manipulating and sensing capabilities of the APM elements are first evaluated by full-wave simulations. To evaluate the manipulating performance, the reflection coefficient of the APM element is defined as the ratio Γ = Eout/Ein, in which Eout and Ein represent the complex amplitudes of the reflected and incident fields, respectively. The relation between Γ and CVAR is depicted in Fig. 3a, b. As CVAR varies from 0.140 pF to 0.710 pF, the phase of Γ continuously varies in the range from 0° to 360°, demonstrating the large phase tuning range of the proposed APM element. To assess the EM sensing performance, the coupling coefficient of the APM element is defined as the ratio α = Ecou/Ein, in which Ecou represents the complex amplitude of the signal coupled into the chain. The dependence of α on CVAR is depicted in Fig. 3g, h. It can be observed that the presented APM element can provide a stable and moderate coupling at the desired frequency for EM sensing. It is worth noting that the absolute value of α is not crucial, because the primary concern often lies in the relative magnitude or phase values of the environmental parameters in wireless systems.

Fig. 3: The performance of the APM element.
figure 3

a, b The dependence of simulated reflection magnitude and phase spectra on CVAR. c, d The dependence of measured reflection magnitude and phase spectra on VDC. e, f The measured reflection magnitude and phase spectra at 3.50 GHz as VDC varies from 0 to 15 V. g, h The dependence of simulated coupling magnitude and phase spectra on CVAR.

Full size image

Experimental validation

A prototype of the proposed APM comprising 6 × 6 identical elements is fabricated to verify the APM’s capabilities of EM manipulating and sensing. There are 36 individual DC voltages supplied by the MCU to control the elements independently, as shown in Fig. 4. The relationship between the reflection coefficient Γ and the biasing voltage VDC for each element is extracted and depicted in Fig. 3c, f. As VDC is gradually raised from 0 to 7 V, the reflection phase of Γ can be continuously tuned in the range from 0° to 360°, while its magnitude remains above 0.84 (− 1.45 dB). The relationship between CVAR in the simulation and VDC in the experiment can be found in the phase shifter section in the Supplementary Information.

Fig. 4: Prototype of APM comprising 6 × 6 elements.
figure 4

a The oblique view of the prototype. b, c The back view of the prototype with and without the bottom metallic ground. The circular holes on the ground serve as the interfaces to the sensing chains.

Full size image

Firstly, we experimentally confirm the APM’s ability to achieve dynamic beam scanning in a programmable fashion, with the traditional beamforming algorithm given in Equation (S3) (in Supplementary Information). The measurement setup is shown in Fig. 5a. The APM prototype is placed on a turntable in an anechoic chamber. A horn antenna serves as the source, with the incident wave directions at θ = 0° and − 20° respectively in the plane of φ = 0°. In the far-field region, another receiving horn antenna is employed to record the scattering pattern. The measurement results, depicted in Fig. 6a, b, indicate that the scattering beam can be scanned in the range of ± 60°. It is clear that there are slight beam distortions near 0° and − 20° stemming from the obstruction of the antenna in front of the metasurface.

Fig. 5: Measurement configurations for experimental validation.
figure 5

a The measurement configuration of the dynamic beamforming. b–d Measurement configurations of three ISAC scenarios. In Scenario #1, the signal is transmitted non-line-of-sight (NLoS) between the transmitter and the receiver through the metasurface, while the propagation path is blocked by a triangular metallic obstacle. The surrounding absorbing materials are used to eliminate the multipath effect. In Scenario #2, the signal is transmitted between the transmitter and the receiver in an open corridor environment with distinct multipath effects. In Scenario #3, the signal is transmitted line-of-sight (LoS) between the transmitter and the receiver through the metasurface without any obstacle in the propagation path.

Full size image
Fig. 6: Measurement results validating the APM array’s performance in dynamic beamforming and incident-field perception.
figure 6

a, b The measurement scattering patterns for dynamic beamforming when the feed horn antenna is placed at θ = 0° and − 20°, respectively. c, e The calculated magnitudes and phases of the received signals by the 6 × 6 sensing elements with Equation (S1). d, f The measured magnitudes and phases by the 6 × 6 sensing elements. Here, m and n denote the indices of the column and row. g The relationship between the actual angle and estimated angle in the direction of arrival (DOA) estimation experiment.

Full size image

Then we proceed to assess the sensing capability of APM. We remark that all APM elements are furnished with the sensing chains, thereby endowing each element with the capability to capture both magnitude and phase information of the incident wave. In the experiment, a source is positioned in the far-field zone, and the emitted EM waves are incident upon APM obliquely. The received magnitudes and phases by the 6 × 6 sensing elements are respectively presented in Fig. 6d, f. In the meanwhile, the theoretical field distributions on APM in free space are obtained from Equation (S1) in Supplementary Information, as shown in Fig. 6c, e. Given that the propagation environment in the microwave chamber is close to free space, the experimental results are in good accordance with the theoretical predictions. Taking the magnitude and phase information collected by all elements as a reference, the proposed APM can easily complete the DOA estimation task (see more details in the Supplementary Information). From Fig. 6g, the measured results demonstrate a small estimation error below 1° when the incident angle is within ± 60°. Before the experiment, the 6 × 6 sensing chains are connected to an RF switch matrix. During the measurements, the switch matrix is electronically controlled to quickly toggle among selected links, allowing for rapid information acquisition from all 36 signal paths. Further details on the RF switch matrix can be found in the Supplementary Information.

Finally, we conduct an inspection of the joint sensing and beam-regulation capabilities of the metasurface to determine whether they can operate independently and concurrently for the ISAC applications. Figure 2b illustrates a typical ISAC scenario, which consists of an APM, the base station, the user ends (transmitter and receiver), and unknown scatterers. The APM can separately obtain all CSI (see more details in Supplementary Information):

$${{\boldsymbol{f}}}=\left[\begin{array}{cccc}{f}_{1,1} & {f}_{1,2} & \cdots & {f}_{1,N}\\ {f}_{2,1} & {f}_{2,2} & \cdots & {f}_{2,N}\\ \vdots & \vdots & \ddots & \vdots \\ {f}_{M,1} & {f}_{M,2} & \cdots & {f}_{M,N}\end{array}\right]\in {{\mathbb{C}}}^{M\times N}\,{{\rm{and}}}\,{{\bf{g}}}=\left[\begin{array}{cccc}{g}_{1,1} & {g}_{1,2} & \cdots & {g}_{1,N}\\ {g}_{2,1} & {g}_{2,2} & \cdots & {g}_{2,N}\\ \vdots & \vdots & \ddots & \vdots \\ {g}_{M,1} & {g}_{M,2} & \cdots & {g}_{M,N}\end{array}\right]\in {{\mathbb{C}}}^{M\times N},$$

in which fm,n and gm,n represent the transmission coefficients between the (m, n)th element and the transmitter and the receiver, respectively. APM then adjusts the reflection matrix Φ using the adaptive algorithm to optimize the communication quality between the transmitter and the receiver (for both simple and complex propagation environments, see more details in Supplementary Information). For experimental validations, three typical ISAC scenarios are considered as illustrated in Fig. 5b–d.

In the first scenario (Fig. 5b), the signal is transmitted non-line-of-sight between the transmitter and the receiver through the metasurface, while the propagation path is blocked by a triangular metallic obstacle. The surrounding absorbing materials are used to eliminate the multipath effect. Without loss of generality, the transmitter and the receiver are positioned at angles of θ = 40° and − 20°, respectively, in the plane of φ = 0°. The phase information of all components in f and g matrices are measured and depicted in Fig. 7a, b. Based on the adaptive algorithm (Equation (S8) in Supplementary Information), the optimal reflection matrix Φ is generated, as shown in Fig. 7c. The transmitter then transmits a QPSK-modulated signal, and the received constellation diagram and signal spectrum at the receiver are given in Fig. 8a. For comparison, a metallic board of the same size as APM is placed in the same position, and the corresponding received constellation diagram and the signal spectrum are shown in Fig. 8b. In addition, in the same scenario, APM is loaded with Φ calculated by the traditional beamforming algorithm, and the measurement is repeated, as shown in Fig. 8c. Note that it is necessary to provide the positions of the transmitter and receiver to APM in advance (i.e., θ = 40° and − 20°), which reveals one of the drawbacks of the traditional beamforming algorithm. In contrast, the proposed APM with the adaptive algorithm does not require any prior input of external environmental information.

Fig. 7: The environmental information sensed by APM and its corresponding reflection matrix in integrated sensing and communication (ISAC) scenarios.
figure 7

a, b Phases of f and g measured in Scenario #1. c The phase of the optimal reflection matrix Φ in Scenario #1. d, e Phases of f and g measured in Scenario #2. f The phase of the optimal reflection matrix Φ in Scenario #2. Here, m and n denote the indices of the column and row.

Full size image
Fig. 8: The received constellation diagram and signal spectrum at the receiver under different scenarios.
figure 8

a, d Measurement results when the adaptive algorithm is applied. b, e Measurement results when an equally sized metallic board is placed. c, f Measurement results when the traditional beamforming algorithm is applied.

Full size image

In contrast to the static metallic board, APM can provide an additional channel gain of approximately 19 dB, as shown in Fig. 8a, b. This gain enhancement indicates a substantial improvement of the wireless communication quality provided by the proposed APM. In complex wireless situations, from Fig. 8a, c, it is seen that APM exhibits a notable enhancement in adaptability compared to the traditional methods, even without prior location information on the transmitter and receiver. The performance degradation of the traditional beamforming algorithm stems from its reliance on the assumption of an ideal free-space propagation environment, which may fail in NLoS scenarios such as Scenario #1. In this case, it does take the inhomogeneity of the incoming wave into account, leading to the non-coherent superposition of the scattered waves from the APM elements toward the receiver. (see more details in Supplementary Information).

The second scenario (Fig. 5c) takes into account an open corridor environment, in which the signals from the transmitter to the receiver undergo distinct multiple effects. The phases of f and g matrices are measured and depicted in Fig. 7d, e, respectively, which display obvious interference to the previous cases due to multipath effects and the scattering from obstacles. The transmitter also transmits a QPSK-modulated signal. The adaptive algorithm is applied to APM to generate the required matrix Φ, as shown in Fig. 7f. The traditional beamforming algorithm is then applied to APM for comparison. In addition, a metallic board of the same size as APM is used to replace APM to observe the change of the received signal quality. The constellation diagram and the signal spectrum received by the receiver under these conditions are shown in Fig. 8d–f.

Clearly, APM outfitted with the adaptive algorithm can supply an 8 dB gain boost in the cascaded channel. However, using the traditional beamforming algorithm, the performance of APM is significantly degraded, which is only comparable to the metallic board. Similar to Scenario #1, the near failure of the traditional beamforming algorithm is because of the NLoS propagation environment.

Besides the above two complex situations, the third scenario is established in Fig. 5d, where the signal is transmitted line-of-sight between the transmitter and receiver through the metasurface without any obstacle in the propagation path. In this case, APM can enhance the communication quality with the traditional beamforming algorithms, similar to conventional metasurfaces, while simultaneously performing DOA estimation to identify the directions of the transmitter and receiver. The measured results in this scenario are provided in the Supplementary Information.

In summary, assessing APM’s performance in these scenarios highlights its advantages over the conventional metasurface. Firstly, APM exhibits superior adaptability to complex environments owing to its universal strategy of CSI sensing. Secondly, by taking advantage of its closed-loop working mode of sensing, analysis, and control, APM can be independently operated without extra information on the channel in advance. Meanwhile, the performances of the conventional metasurfaces and algorithms are likely to degrade significantly in complex environments. The measured results demonstrate the significant advantages of APM in intelligent sensing and wave manipulation.

Discussion

An APM with simultaneous wave manipulating and sensing capabilities is proposed. The working principle and prototype implementation are demonstrated, and its performances are validated by experiments. The measured results show that APM can manipulate the phases of EM waves over a range from 0 to 360 degrees while maintain the reflection loss of no more than 1.45 dB. More importantly, APM can simultaneously sense the complex amplitude of the incident signals element by element. Three APM-assisted ISAC scenarios are constructed and measured. The results show that the proposed APM can significantly enhance communication quality in complex propagation environments intelligently and provide more powerful capabilities for the in-depth applications of metasurfaces in wireless systems in the future.