Introduction

High-performance bulk metallic materials with ultrahigh σy and excellent εu are highly desirable for developing reliable, energy-efficient, and light-weight components across automotive, aircraft, and airspace industries. For most metallic materials, however, an increase in strength often comes at the expense of ductility, displaying the strength-ductility trade-off1,2. Hence, in traditional simple alloy systems, only a few martensite-based steels could occasionally accomplish the goal3,4. Unfortunately, such ultrahigh-strength steels usually lose most of their toughness and ductility when the temperature falls below the ductile-brittle transition temperature, limiting their further applications at cryogenic temperatures5.

The recent emergence of high- or medium-entropy alloys (H/MEAs), employing multiple-principal-element systems, opens a new avenue to break through the strength-ductility paradox6,7. Unlike simple metals, these alloys exhibit appreciable concentration inhomogeneity8, local chemical order9,10, and severe lattice distortion11, which can result in unusual dislocation behaviors and unprecedented mechanical properties9,10,11. Superior strength and ductility, high strain hardening, and exceptional damage tolerance have been realized in some single-phase face-centered cubic (fcc) alloys6,7,11. Nonetheless, these fcc H/MEAs, have a relatively low σy7, limiting their potential usability.

An effective approach for enhancing σy is the introduction of ordered intermetallic compounds (IMCs) into the matrix, known as the second phase strengthening12. However, most IMCs with atomically ordered structure are intrinsically brittle, causing local stress concentration and triggering premature fracture12. To date, only a few simple ductile IMCs with high-symmetry cubic crystal structure, such as B2 and L12-type ordered phases, have been successfully introduced into multicomponent fcc solid-solutions to improve mechanical properties13,14,15,16. These multiple-phase H/MEAs usually evolve from several ternary or quaternary derivatives of the Cantor alloy6 via further alloying with elements like Ti and Al, leading to rather limited freedom for compositional adjustments. Additionally, certain B2-type IMCs-strengthened H/MEAs suffer from reduced ductility at cryogenic temperatures17,18,19. Consequently, the development of effective IMCs for second-phase strengthening in fcc H/MEAs has encountered a bottleneck, and other structurally simple IMCs need to be further exploited to enhance the strength-ductility synergy.

Traditionally, the D019 phase (e.g., Ti3Al, Co3W, and Ni3Sn), one of the simplest ordered hexagonal close-packed (hcp) superlattices, is considered to be a highly favorable strengthening phase20,21,22. For example, α2-Ti3Al with a D019 superlattice structure is a significant constituent phase in the TiAl-based alloys20. However, polycrystalline aggregates of D019-type IMCs exhibit limited ductility and toughness at room temperature and below due to the difficulty in activating pyramidal slip of dislocations with a Burgers vector of <2c + a > , which is required to accommodate strain along the c-axis of the D019 unit cell23,24. The difficulty in generating these non-basal dislocations lies primarily in their high critical activating stresses24.

Here, we address this dilemma by demonstrating that non-basal slip activated in a material strengthened by a D019 IMC precipitate can provide both strength and ductility. We illustrate this in a NiCoCr0.5V0.5 MEA using tensile tests over a wide temperature range spanning from room temperature to liquid-helium temperature. We have observed the unexpected non-basal slip of D019 IMCs during the deformation of a duplex phase UFG structure. This dual-phase UFG architecture comprises a fully recrystallized fcc UFG matrix and D019 nano-lamellae. The combination of grain-boundary strengthening from the fcc UFG matrix and solid solution strengthening from the multi-principal elements in the fcc matrix, generates sufficiently high matrix stress levels to overcome the stress barrier for pyramidal slip of D019 nano-lamellae. This approach demonstrates that by achieving sufficiently high matrix stress levels, brittle D019 nano-precipitates can be transformed into a ductile strengthening phase without initiating damage at the heterointerfaces. Coupled with the formation of dynamically refined nanosized dislocation and stacking fault (SF) substructures in the fcc UFG matrix, our duplex phase UFG alloy exhibits promising mechanical properties over a broad temperature range, particularly achieving a σy of ~2100 MPa and a εu of ~15% at cryogenic temperatures.

Results and discussion

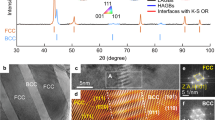
The as-cast alloy underwent homogenization at 1150 °C, followed by hot forging, and was then cold-rolled to 1.5 mm-thick sheets with 96% total thickness reduction (CR state). X-ray diffraction (XRD) results confirmed that the CR sample remains in a single fcc phase (Supplementary Fig. 1a). Transmission electron microscopy (TEM) observations verified that the cold deformed microstructure consists of extremely refined nanosized grains with a high density of dislocations and SFs, without elemental segregation (Supplementary Fig. 2). An annealing treatment was then performed at 750 °C for 15 min (hereinafter referred to as CR750) to obtain the fcc/D019 duplex phase UFG architecture (Supplementary Fig. 1). After annealing, a uniformly recrystallized microstructure developed featuring nano-scale D019 lamellae embedded in the fcc UFG matrix. The fcc UFG matrix (mean grain size: 409 nm; 75.8 vol%) exhibited an equiaxed grain morphology with abundant annealing twins, as illustrated by transmission Kikuchi diffraction (TKD) results (Fig. 1a–c). The nanoscale D019 lamellae (mean thickness: 120 nm; aspect ratio: 3.5; 24.2 vol%) frequently intersected to form interconnected colonies that spanned the entire fcc grain (Fig.1a, b, d, e). TEM characterization further revealed that the D019 superlattice structure is perfectly coherent with the fcc matrix (Fig. 2). Scanning TEM bright-field (STEM-BF) images near the [11\(\bar{2}\)0] zone axis and the STEM high-angle annular dark-field (STEM-HAADF) atomic lattice image showed that the D019 phase contains smaller substructures, decorated with massive SFs (Fig. 2c, d, f). Specific crystallographic orientation relationships were also observed between the fcc matrix and the D019 lamellae: \({\{1\bar{1}1\}}_{{\rm{fcc}}}\) // \({\{0002\}}_{{{\rm{D}}0}_{19}}\) and \({ < 110 > }_{{\rm{fcc}}}\)// \({ < 11\bar{2}0 > }_{{{\rm{D}}0}_{19}}\); \({\{220\}}_{{\rm{fcc}}}\) // \({\{\bar{2}4\bar{2}0\}}_{{{\rm{D}}0}_{19}}\) and \({ < \bar{1}12 > }_{{\rm{fcc}}}\) // \({ < 10\bar{1}0 > }_{{{\rm{D}}0}_{19}}\); \({\{13\bar{1}\}}_{{\rm{fcc}}}\) // \({\{\bar{2}4\bar{2}\bar{2}\}}_{{{\rm{D}}0}_{19}}\) and \({ < \bar{1}12 > }_{{\rm{fcc}}}\) // \({ < 10\bar{1}0 > }_{{{\rm{D}}0}_{19}}\) (Fig. 2c–e). An obvious elemental partitioning between the duplex phases existed with V atoms segregating into D019 lamellae and Cr atoms enriching in fcc matrix (Fig. 2g). Neutron diffraction (ND) measurements further confirmed that the lattice parameter at 298 K a = 0.3578 nm for the fcc matrix, and a = 0.5051 nm and c = 0.4112 nm for the D019 lamellae (Supplementary Fig. 1b).

Fig. 1: Transmission Kikuchi diffraction (TKD) characterization for the CR750 alloy, showing a fully-recrystallized fcc/D019 (fcc/D019) dual-phase ultrafine-grained (UFG) architecture.
figure 1

a TKD phase map. b TKD inverse pole figure. c–e Statistical size distribution of (c) grain size of the fcc UFG matrix, (d) D019 lamellar thickness, and (e) D019 lamellar length. ‘HAGB’ and ‘TB’ denote high-angle grain boundary and twin boundary, respectively. TKD measurements were repeated three times on three distinct samples to enable statistical size analysis. The combined dataset was used for size distribution analysis and fitted with Gaussian functions (solid lines), revealing approximately normal distributions. Source data for (c–e) are provided as a Source data file.

Full size image
Fig. 2: Scanning transmission electron microscopy (STEM) characterization for the CR750 alloy.
figure 2

a, c STEM-BF images viewed from different directions. b Corresponding selected area electron diffraction (SAED) pattern from the cyan circle in (a). d, e Corresponding SAED patterns from the blue circle in (c). Red and cyan circles represent diffraction signals from the fcc matrix and the D019 phase, respectively. f Atomic-scale STEM high angle annular dark-field (STEM-HAADF) image of the fcc/D019 dual-phase region, showing D019 lamellae decorated with a high density of stacking faults. g Corresponding STEM energy-dispersive X-ray spectroscopy (STEM-EDS) mapping from the green square in (c), showing elemental partitioning in the two phases.

Full size image

We performed three-dimensional atom probe tomography (3D-APT) to offer a quantitative compositional analysis for the CR750 alloy at the atomic scale. The 3D-APT results revealed a clear elemental partitioning between the fcc and D019 duplex phases, with V-rich regions corresponding to the D019 lamellae and Cr atoms segregating into the fcc matrix (Fig. 3a), in excellent accordance with the STEM-EDS mapping result (Fig. 2g). A one-dimensional compositional profile shows the quantitative elemental partitioning of each element (Fig. 3b), with the chemical composition of Ni31.99Co34.47Cr18.52V15.02 (at.%) in the fcc matrix and Ni34.67Co35.08Cr11.50V18.75 (at.%) in the D019 lamellae. We identified the D019 IMC as the Ni3Sn-type ordered superlattice22, with Ni, Co, and Cr atoms occupying the ‘Ni’ sites, and V atoms substituting for the ‘Sn’ sublattice. The atomic arrangements of the superlattice are schematically shown in Fig. 3c, d. We evaluated the energetics of several competing models, including disordered-hcp, D019-ordered, and D0a-ordered structures based on density-functional theory (DFT) calculations (Supplementary Table 1). The D019 configuration exhibited the lowest formation energy (–5.354 eV atom−1), confirming its thermodynamic stability as an ordered superlattice. Furthermore, single-crystal electron diffraction simulations, based on the established D019-ordered superlattice (Supplementary Fig. 3), particularly the extra weak spots due to the superlattices, showed good agreement with our TEM analyses (Fig. 2b, d, e), verifying the existence of the D019 phase. Detailed crystallographic information of this D019 structure is provided in Supplementary Table 2. Our subsequent molecular dynamics (MD) simulations of the mechanical properties of the D019 phase were based on the as-constructed atomistic model.

Fig. 3: Three-dimensional compositional distributions of the dual-phase fcc/D019 UFG architecture in the CR750 alloy.
figure 3

a Three-dimensional reconstruction map of a typical atom probe tomography tip showing the distribution of each element. The fcc/D019 interface is highlighted using iso-composition surfaces containing 18 at.% V and 18 at.% Cr. b one-dimensional compositional profiles computed along the white arrow in (a), showing the compositional changes across the interface. Error bars refer to the standard deviations of the counting statistics in each bin of the profiles. Standard error s is calculated as: \({{\mbox{s}}}=\sqrt{\frac{{{c}}_{{i}}\left(1\,- \, {{c}}_{{i}}\right)}{{{n}}_{{t}}}}\) in which nt is the total number of ions in the sample, and ci is the concentration in atomic fraction of solute i in the sample, which is calculated as: \({{\mbox{c}}}_{i}=\frac{{{\mbox{n}}}_{{\mbox{i}}}}{{{\mbox{n}}}_{{\mbox{t}}}}\) in which ni is the number of ions of solute i in the sample. c Ordered crystallographic structure and site occupancies of the D019 phase viewed along the c-axis direction by density functional theory calculations. d Atomic arrangement in the (0001) planes of the D019 phase with a (Ni, Co, Cr)3V stoichiometry. Large circles represent atoms in the A-layer, the plane of the paper, and small circles represent atoms in the B-layer, immediately below the A-layer. Source data for (b) are provided as a Source data file.

Full size image

The CR750 alloy exhibits impressive tensile properties, combining an ultrahigh σy of 1575 MPa and a large εu of 10.1% at ambient temperature (298 K) (Fig. 4a, Supplementary Fig. 4 and Supplementary Table 3). As the temperature decreases, both the strength and ductility further enhance simultaneously. Specifically, σy and εu rise to 2095 MPa and 15.0% at liquid-nitrogen temperature (77 K), and 2146 MPa and 15.5 % at liquid-helium temperature (4.2 K), respectively. Repeated tests of different samples exhibited highly consistent results (Supplementary Fig. 4a). This is a remarkable outcome for ultrahigh-strength bulk alloys, demonstrating superb strength-ductility synergy over a wide temperature range. The strength-ductility combinations can even compete with those of some ultrahigh-strength steels, which typically suffer from inhomogeneous plastic flow3,4 and ductile-to-brittle transition5. Interestingly, even at such an ultrahigh σy in the post-yield region, the present alloy shows exceptional strain-hardening rates, which increase as the temperature decreases (Fig. 4b). This contributes to delaying plastic instability while maintaining excellent εu. We compared the tensile properties of the CR750 alloy with other high-performance bulk alloys15,17,19,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61 (Fig. 4c, d, Supplementary Fig. 4b and Supplementary Table 4). Our alloy stands out in terms of σy vs εu, over a wide temperature range from 298 K to 4.2 K.

Fig. 4: Tensile properties of the CR750 alloy and comparison with other high-performance alloys.
figure 4

a Engineering stress-strain curve tested at 298 K (black line), 77 K (red line), and 4.2 K (blue lines), respectively. b Corresponding strain-hardening rate (dotted lines) and true stress (solid lines) vs true strain curves. Due to the strong serrations observed in the 4.2 K tensile tests, we performed polynomial fitting on the engineering stress-strain curve to determine the strain-hardening rate. c, d Comparison of the CR750 against other state-of-the-art alloys in terms of their σy vs εu at 77 K (c) and 4.2–20 K (d), respectively. The data on the mechanical properties of these reported materials are also listed in Supplementary Table 4. This work has a superior combination of σy and εu compared with other alloys, including fcc H/MEAs25,26,27,28,29,30,31,32,33,34,35,36, body-centered cubic (bcc) H/MEAs37, TRIP H/MEAs38,39,40,41,42, fcc + B2 H/MEAs17,19,43,44, fcc + L12 H/MEAs15,45,46,47, steels29,48,49,50,51,52,53, H/MEAs26,27,29,30,32,34,35,36,54, and Ti alloys55,56,57,58,59,60,61. ‘H/MEAs’ and ‘TRIP’ denote high/medium entropy alloys and transformation-induced plasticity. Source data are provided as a Source data file.

Full size image

The ultrahigh σy of the CR750 alloy primarily derives from grain boundary strengthening, lattice friction stress from the fcc UFG matrix, and second-phase strengthening from the D019 lamellae. In the CR750 alloy, the ordered D019 lamellae are stronger than the disordered fcc UFG matrix, as demonstrated by our nano-indentation tests (Supplementary Fig. 5). Consequently, the fcc/D019 phase boundaries act as effective barriers against dislocation motion. Based on Hall-Petch relation modeling of the fcc matrix and the rule of mixtures62, we quantified the strengthening contributions of the fcc grain boundaries (787 MPa at 298 K and 1069 MPa at 77 K), the lattice friction (167 MPa at 298 K and 315 MPa at 77 K), and the D019 lamellae (621 MPa at 298 K and 711 MPa at 77 K) (Supplementary Fig. 6).

To uncover the origin of the high strain-hardening capability of the CR750 alloy at ultrahigh stress levels, we performed TKD experiments for the tension-fractured samples at 298 K, 77 K, and 4.2 K, respectively. Our observation revealed that as the deformation temperature decreases, the CR750 alloy deforms more homogeneously (Supplementary Fig. 7), indicating an increasingly significant role played by the D019 lamellae in carrying plasticity at low temperatures. Inhomogeneous plastic deformation features at phase interfaces, grain boundaries, twinning boundaries, and within grain interiors of the fcc UFG matrix are clearly visible at 298 K, significantly reduced at 77 K, and become almost undiscernible at 4.2 K (Supplementary Fig. 7). Neither mechanical twins nor deformation induced transformation were detected during straining at any temperatures (Supplementary Fig. 7).

To elucidate the underlying deformation mechanism, detailed TEM analyses were conducted on the CR750 alloy samples strained at various temperatures. At 298 K, dislocation planar slip dominates in the fcc UFG matrix across the entire strain range, forming a directionally nanosized dislocation substructure with increasing strain (spacing ≈ 66 nm) (Supplementary Fig. 8a, d, g). Additionally, the D019 lamellae demonstrate a significant capability to accommodate deformation. At low-to-medium strains, <a >-type dislocations of the D019 superlattice were observed and their quantities increased with increasing strain (Supplementary Fig. 8b, c, e, f). It is worth noting that prolific non-basal < 2c + a >-type dislocations (pyramidal slip) appeared at the late stage of deformation after tensile fracture (Supplementary Fig. 8h, i).

At 77 K, at a strain of ~2% (Fig. 5a), dislocation slip is activated on the {111} planes in the fcc UFG matrix, accompanied by the appearance of a few SFs, indicating the early stage of planar dislocation glide. As the strain increases to ~5% (Fig. 5d), a much higher density of SFs is generated, and intersecting SFs commence. Upon reaching fracture strain (Fig. 5g), hierarchical SF networks with nanoscale spacing (~34 nm) become activated, accompanied by the formation of Lomer–Cottrell (LC) locks (Fig. 6a). Highlighting the deformation responses of the D019 lamellae, we show that, unlike at 298 K, <c> and <2c + a >-type dislocations are successively activated at 77 K even at small strains and persist through the entire strain range. The number of various types of dislocations stored in the D019 lamellae is significantly higher than those at 298 K (Fig. 5b, c, e, f, h, i). Additionally, some <2c + a> dislocations, e.g., dislocation 1 and 2 in Fig. 5e, h, exhibit step-shaped configurations, indicating that the <2c + a> dislocations may undergo double cross-slips between the first-order (pyramidal I) and the second-order (pyramidal II) pyramidal slip systems, further enabling a compatible and continuous deformation63.

Fig. 5: Deformation mechanism of the CR750 alloy at 77 K.
figure 5

a STEM-BF image of the 2% strain, showing the early stage of planar slip, accompanied by the occurrence of a small number of stacking faults (SFs) in the fcc UFG matrix; the inset shows the corresponding SAED pattern from the region outlined by the red circle. b, c Two-beam STEM-BF images of the D019 phase after 2% strain, with the viewing direction of [10\(\bar{1}\)0] under g = [000\(\bar{2}\)] (b) and g = [\(\bar{2}\)4\(\bar{2}\)0] (c), respectively. d STEM-BF image of the 5% strain, showing the formation of a high density of SFs in the fcc UFG matrix; the inset shows the corresponding SAED pattern from the region outlined by the red circle. e, f Two-beam STEM-BF images of the D019 phase after 5% strain, with the viewing direction of [10\(\bar{1}\)0] under g = [0002] (e) and g = [\({\bar{2}}\)4\(\bar{2}\)0] (f), respectively. g STEM-BF image of the fracture sample that shows the formation of nano-spaced hierarchical SF networks in the fcc UFG matrix; the inset shows the corresponding SAED pattern from the region outlined by the red circle. h, i Two-beam STEM-BF images of the D019 phase after fracture, with the viewing direction of [10\(\bar{1}\)0] under g = [0002] (h) and g = [2\(\bar{4}\)20] (i), respectively.

Full size image
Fig. 6: Crystal defect evolutions during straining in the CR750 alloy measured by in-situ neutron diffraction.
figure 6

a SF probability (SFP) vs engineering strain in the fcc UFG matrix at 77 K (red solid circles), with the result at 298 K (black solid squares) plotted together for comparison. The inset shows a high-resolution TEM image of the intersected SF networks with the LC locks in the fcc UFG matrix after fracture. The error bars are conveyed from errors of peak fit of neutron diffraction profiles, since the SFP is calculated from peak center variations. b Dislocation density vs engineering strain in the fcc UFG matrix at 77 K (red solid circles), with the result at 298 K (black solid squares) plotted together for comparison. Source data are provided as a Source data file.

Full size image

The deformation characteristics of the CR750 alloy after tensile fracture at 4.2 K shows similar deformation substructures to those at 77 K (Supplementary Fig. 9). The notable differences include a much denser SF network (with a spacing of ≈10 nm) in the fcc UFG matrix and a much higher dislocation density in the D019 lamellae. These deformation features indicate that the role of the D019 lamellae in accommodating deformation is further enhanced by the easier generation of non-basal dislocations. The abundance of SFs coupled with the formation of LC locks after cryogenic deformation at 4.2 K is likely responsible for the observed serrated flow at ultralow temperatures27,64. In addition, we observed that certain dislocations can transmit across the phase boundaries from the fcc matrix into the D019 lamellae during straining (Fig. 5 and Supplementary Figs. 8 and 9).

To gain insights into the evolution of crystal defects in real-time, we conducted in situ ND measurements on the CR750 alloy at 298 K and 77 K. During tensile deformation, the diffraction peaks of the fcc/D019 duplex phases show progressive broadening and shifts with increasing strain, indicating the continuous accumulation of defects such as dislocations and SFs (Supplementary Fig. 10a, b). Also, the CR750 maintained a fcc/D019 dual-phase state throughout tensile straining, with no phase transformation observed (Supplementary Fig. 10c). The derived SF probability (SFP) at 77 K was much higher than at 298 K (Fig. 6a), consistent with our TEM results (Fig. 5 and Supplementary Fig. 8). Convolutional multiple whole profile (CMWP) analysis of the ND data also revealed a significantly higher density of dislocation at 77 K, compared to 298 K (Fig. 6b). While quantitative analysis of crystal defects in the D019 lamellae during tensile deformation would be of great interest, the low diffraction peak intensity renders such analysis intractable.

Based on the observations outlined above, we explore the physical origin of the excellent tensile ductility of the CR750 alloy. Typically, the deformation mechanism of the fcc-based metals is governed by the SF energy (SFE), which dictates the deformation mode: single dislocation glide for SFE above 45 mJ/m2, mechanical twinning for SFE between 15 and 45 mJ/m2, and deformation-induced phase transformation for SFE below 15 mJ/m2 (ref[. 65.). We have quantified the SFEs of the fcc matrix through weak-beam dark-field STEM analysis (Supplementary Figs. 11 and 12), finding values of 24 ± 4 mJ/m2 at 298 K and 18 ± 2 mJ/m2 at 77 K, respectively, which aligns satisfactorily with our theoretical calculations of the SFE without considering the temperature effect (Supplementary Table 5). Given that the SFE values fall within the range of 15–45 mJ/m2, mechanical twins are therefore expected to be the underlying deformation mechanisms. However, the fcc UFG matrix and coherently nanosized D019 lamellae significantly impede the initiation of mechanical twins15,16,66. As a result, dynamically refined SFs are preferred during the plastic deformation due to their relatively low critical stress15,16. Therefore, planar-slip predominates in the plastic deformation of the fcc UFG matrix at 298 K due to relatively low flow stress, while SFs become the dominant mechanism at cryogenic temperatures, facilitated by further enhanced flow stress and reduced SFE.

The compositionally disordered fcc matrix maintains a coherent interface with the structurally ordered D019 phase, allowing transmission of dislocations across heterointerfaces with minimal resistance67. Specifically, the activation of these <c>-component dislocations (i.e., either <c> or <2c + a >-type dislocations) enhances transmission of edge dislocations in fcc UFG matrix across phase boundaries68, avoiding dislocation jam and relieving stress concentration. Nevertheless, as these non-basal dislocations are activated relatively late at 298 K, their contribution to plasticity is limited. Consequently, the notable strain hardening rate at 298 K is primarily due to the dynamic slip-band refinement in the fcc UFG matrix. The accumulation of massive dislocations within the slip bands significantly reduces the mean free path of the mobile dislocations, which increasingly hinders their movement as the strain increases and the slip-band spacing narrows. Moreover, pronounced slip planarity curtails dynamic recovery and promotes dislocation storage11, leading to a high and sustained strain-hardening rate and extensive uniform elongation at 298 K.

At cryogenic temperatures, the substantially increased stress enables the early generation of non-basal dislocations after yielding, thus greatly improving the deformability of the D019 lamellae. The deformation behavior helps mitigate stress concentration at the phase boundaries, prevents premature crack initiation, and leads to uniform macroscopic plastic deformation. Furthermore, the hierarchical SF networks dynamically subdivide the fcc UFG matrix into even finer nano-domains during straining, reducing their mean free path of dislocations and increasing the strain-hardening capability through a dynamic Hall-Petch effect15,16. Besides, the formation of the numerous immobile LC locks not only acts as a strong obstacle to pin the dislocation motion, but also promotes the dislocation multiplication by serving as Frank-Read dislocation sources, thereby facilitating consistent and progressive strain-hardening rates15,16. As such, the synergies of the dual-phase UFG architecture with the coherent boundaries, dynamically refined SF networks, high-density immobile LC locks, and extensive activation of the non-basal dislocations in D019 lamellae collectively enhance the plastic deformation stability and strain-hardening capability of the CR750 alloy at cryogenic temperatures, resulting in the superior tensile ductility at an ultrahigh-strength level.

We now elucidate the possibility of non-basal slips within the D019 lamellae. The likelihood of activating non-basal dislocations (e.g., pyramidal dislocations) in the D019 phase is intrinsically linked to the critical resolved stress (CRSS) of their slip systems, Schmid factors, and the external loads. To reveal the dislocation plasticity, we computed the generalized stacking fault energies (GSFEs) that govern dislocation activation and pathways, along with the CRSS of the corresponding slip systems at 298 K (Fig. 7, Supplementary Figs. 13 and 14, and Supplementary Tables 5 and 6), combining both large-scale MD and DFT. These computations reveal that, as a result of superdislocation activation, the CRSS for pyramidal I slip systems reaches up to 800 MPa, and for pyramidal II, it escalates to 875 MPa at 298 K, which is roughly one order of magnitude higher than that of the bulk fcc matrix phase (105 MPa).

Fig. 7: Generalized SF energies of the {2\(\bar{2}\)01} plane and {11\(\bar{2}1\)} plane in the D019 phase, and corresponding critical resolved shear stress (CRSS) calculation of their slip systems.
figure 7

a, d Atomic arrangements and slip directions in the pyramidal I (a), and pyramidal II (d) slip systems. b, e γ Surfaces of pyramidal I plane (b), and pyramidal II plane (e). The atomic packing scheme on each slip plane is overlaid on top of the γ surface. Note that the minimum energy path (MEP) for planar slip in the pyramid I slip system (b) is along the short arrows (cyan), rather than the long Burger’s vector. c, f Illustration of slip systems in the D019 unit cell of pyramidal I plane (c), and pyramidal II plane (f) (not all atoms are shown). g, h MEPs of pyramidal I plane (g), and pyramidal II plane (h) calculated by embedded atom method (EAM) and density functional theory (DFT). The slip paths are indicated by short arrows in (b) and (e), respectively. i CRSS calculation for pyramidal I slip system by molecular dynamics (MD). The <2c + a> superdislocation dissociates into superpartials and is separated by an antiphase boundary (APB) area, consistent with the MEP calculations and similar to ref. 89. Source data for (g) are provided as a Source data file. MD trajectory data and script for (h) are provided in the Supplementary Data.

Full size image

The corresponding Schmid factors for these pyramidal systems in our experiments are provided in Supplementary Fig. 15, with pyramidal I exhibiting the largest Schmid factors with a mean value of 0.437, closely followed by pyramidal II at 0.392. Considering the CRSS values and Schmid factors, we estimated the corresponding average normal stress (NS) for the activation of these slip systems at 298 K (Supplementary Fig. 16). Specifically, the NS values of two pyramidal slip systems (1831 MPa for pyramidal I and 2232 MPa for pyramidal II) are larger than the flow stress at the onset of yielding, indicating that the activation of the <2c + a> dislocations is difficult during the initial deformation stage at 298 K, aligning well with our experimental observations. As strains increase, strain hardening from the dynamically refined slip bands in the fcc matrix and <a> dislocation slips within D019 lamellae enable the resolved shear stress (RSS) acting on the pyramidal slip systems with high Schmid factors to surpass the CRSS at higher strains, signaling the engagement of <2c + a> dislocations during the later stages of deformation, moderately extending its plasticity.

In contrast, as temperatures drop to 77 K and below, the flow stress values increase rapidly to reach ~2100 MPa at yielding (Fig. 4). This increase enables <2c + a> dislocations to activate at the early stages of deformation. Meanwhile, the enhanced defect proliferation efficiency at cryogenic temperatures boosts the flow stress, further augmenting the non-basal slipping capability of the D019 lamellae. The facilitation of non-basal slip essentially results from an extremely high dislocation glide stress in the fcc matrix caused by the UFG and the high solution friction stress (Supplementary Figs. 6 and 13 and Supplementary Table 6). As deformation progresses and flow stress increases, more <2c + a> dislocations are sequentially activated with the RSS surpassing the CRSS required for the non-basal slipping. Consequently, such non-basal slip in the D019 lamellae, together with the multiple strain hardening mechanisms within the fcc UFG matrix, imparts unparalleled strength and ductility to this alloy at cryogenic temperatures.

The dual-phase UFG architecture of our NiCoCr0.5V0.5 MEA, featuring high-density D019-type nano-scale lamellae within the complex alloy system, confers attractive ductility and ultrahigh strength at ambient and cryogenic temperatures. Beyond the dynamically refined nano-sized dislocation or SF substructures, the CR750 alloy utilizes the deformability of the D019 superlattice through the sufficient activation of non-basal dislocations, substantially enhancing the alloy’s overall ductility. We anticipate that the microstructural design concept holds promise for broad applications across various other alloy systems, including TiAl-based alloys, superalloys, and H/MEAs, potentially delivering exceptional properties for critical applications.

Methods

Materials preparation

Bulk NiCoCr1–χVχ (χ = 0.4, 0.5, 0.6, at.%) MEA ingots were prepared by magnetic levitation melting of high-purity constituent metals (>99.9 wt%) under a high-purity argon atmosphere. The as-cast ingots (60 mm in height × 90 mm in diameter) were homogenized at 1150 °C for 2 h under argon, followed by hot forging into billets (240 mm (length) × 40 mm (width) × 40 mm (height)). Subsequent thermo-mechanical processing included cold rolling to 1.5 mm thickness (96% reduction) and annealing at 700–850 °C for 10–15 min with water quenching.

To determine the Hall-Petch relationship and SFE of the fcc matrix, bulk ingots with composition Ni31.99Co34.47Cr18.52V15.02 (at.%)—matching the fcc UFG matrix in the CR750 alloy as identified by 3D-APT—were prepared via vacuum induction melting under argon atmosphere. The ingots were subjected to sequential thermo-mechanical processing: (i) homogenization at 1150 °C for 2 h, (ii) hot forging at 1150 °C, (iii) cold rolling with 85% thickness reduction, and (iv) recrystallization annealing at 850–1200 °C for varying durations under argon, followed by water quenching.

Mechanical properties at room temperature

Uniaxial quasi-static tensile tests were performed at room temperature (298 K) using an Instron 5980 testing machine at a constant strain rate of 1 × 10–3 s–1. Dog-bone-shaped flat tensile specimens with gauge dimensions of 15 × 3 × 1.5 mm3 (length × width × thickness) were prepared by electrical discharge machining. Three repeat tests were conducted for statistical reliability, and strain measurements were acquired via a non-contact optical extensometer. Nanoindentation measurements were performed on the CR750 alloy using a Hysitron triboindenter equipped with a diamond Berkovich tip. A maximum load of 2000 μN was applied to characterize the hardness-depth profiles across different microstructural zones. To ensure statistical reliability, a 4 × 10 indentation matrix was implemented with 5 μm spacing between test points. Prior to testing, the sample was prepared by electrochemical polishing to achieve optimal surface conditions.

Tensile tests at cryogenic temperatures

Uniaxial tensile tests were performed on an Instron 5980 testing system at cryogenic temperatures of 77 K (liquid nitrogen) and 4.2 K (liquid helium), employing a constant strain rate of 1 × 10–3 s–1. Specimens with dog-bone geometry were fabricated by electrical discharge machining, featuring gauge dimensions of 10 × 2.5 × 1.5 mm³ for 77 K tests and 27 × 4 × 1.5 mm³ for 4.2 K experiments. For cryogenic testing, specimens and fixtures were fully immersed in liquid nitrogen or liquid helium using two dedicated cryostats mounted on the testing machine’s crosshead. To ensure statistical significance, four replicates were performed at 77 K and two at 4.2 K. Strain measurements were acquired using customized extensometers: an Epsilon 3442-010M-LT for 77 K measurements and an Epsilon 3542-025M-050-LT for 4.2 K characterization. In particular, the 4.2 K experiments utilized a vacuum-insulated cryogenic Dewar tank to minimize helium evaporation and maintain thermal stability. A rhodium-iron thermometer was installed in the cryogenic setup, positioned above the specimen to ensure accurate temperature monitoring at liquid helium levels.

SEM characterizations

The phase type, grain size, grain orientation, distribution, and phase fraction were characterized using the TKD technique performed with TESCAN CLARA plus Field Emission Gun SEM operating at 30 kV, equipped with the Oxford Instrument Channel 5 EBSD system and a Nordlys-S EBSD detector. The step size used for data collection was 10 nm. The TKD samples were prepared via electropolishing (Struers TenuPol-5 Twin Jet Electropolisher) in an electrolyte solution containing 10% perchloric acid and 90% alcohol at a temperature of –20 °C. TKD tests were repeated three times on three individual samples in order to perform a statistical size analysis, which involved counting 785 fcc grains and 619 D019 lamellae.

TEM characterizations

The microstructure of the recrystallized and pre-strained specimens was characterized by TEM, HRTEM, and STEM with a TALOS F200X G2 operating at 200 kV. An aberration-corrected Thermo Fisher Scientific Spectra300 was used to analyze the atomic-level STEM-HAADF image at an accelerating voltage of 300 kV. The observed specimens were first mechanically ground to 30 μm thickness and then twin-jet electropolished using 10% perchloric acid + 90% alcohol solution at a temperature of –20 °C.

To conduct the g·b analyses to determine the dislocation types activated in the D019 lamellae, we chose g = [0002] (or [000\(\bar{2}\)]) and g = [2\(\bar{4}\)20] (or [\(\bar{2}4\bar{2}\)0]) beams under the viewing direction of [10\(\bar{1}\)0] for STEM-BF imaging in the present work. b is the Burgers vector of the dislocation. Based on the g·b invisibility criterion, <2c + a> is simultaneously visible in the STEM-BF images obtained with g = [0002] (or [000\(\bar{2}\)]) and g = [2\(\bar{4}\)20] (or [\(\bar{2}4\bar{2}\)0]). <a> dislocation is invisible when g = [0002] (or [000\(\bar{2}\)]), and <c> dislocation is invisible when g = [2\(\bar{4}\)20] (or [\(\bar{2}4\bar{2}\)0]).

To quantitatively evaluate the SFEs of the fcc matrix in the CR750 alloy, TEM dislocation analysis was conducted on the recrystallized coarse-grained samples (composition: Ni31.99Co34.47Cr18.52V15.02) after 3% tensile deformation at 298 K (mean grain size: 26.3 μm) and 77 K (mean grain size: 44.3 μm), respectively. The separation behavior of partial dislocations was acquired by a g(3g) weak-beam dark-field STEM imaging method on a TALOS F200X G2 microscope. The g·b analysis of the partial dislocations (g = [02\(\bar{2}\)], g = [20\(\bar{2}\)], and g = [2\(\bar{2}\)0], respectively) was performed to identify the Burgers vectors, where the contrast from a dislocation is eliminated when g·b = 0. The actual partial dislocation separation was further obtained by calibrating the observed values, as proposed by Cockayne69,70. Then, the SFEs were estimated according to the following equation69:

$${SFE}=\frac{G{b}_{p}^{2}}{{8\pi d}_{{act}}}\left(\frac{2-{{\nu }}}{1-{{\nu }}}\right)1-\left(\frac{2{{\nu }}\cos (2\beta )}{2-{{\nu }}}\right)$$
(1)

where G is the shear modulus of the fcc UFG matrix (85 GPa), bp is the magnitude of the Burgers vector of partial dislocations (0.14612 nm at 298 K and 0.14588 nm at 77 K, respectively, derived from the measured lattice parameters based on ND patterns in Supplementary Figs. 1 and 10), dact is the separation width of partial dislocations, υ is the Poisson ratio of the fcc UFG matrix (0.313), and β is the angle between the Burgers vector of perfect dislocation and the dislocation line. Note that the composition of the fcc UFG matrix is very close to that of V0.4Cr0.6CoNi alloy, the values of G and υ are therefore adopted from this alloy71.

APT characterizations

Needle-shaped APT specimens were prepared using Helios G4 UX dual-beam focused ion beam (FIB) tools with standard FIB lift-out procedures. APT experiments were performed using a local electrode atom probe (LEAP 4000× Si) with a specimen temperature of 40 K, a laser pulse repetition rate of 200 kHz, a laser pulse energy of 40 pJ, and a target evaporation of 0.8%. APT data analysis was performed using the CAMECA Visualization and Analysis Software (IVAS 3.8.6).

In situ ND measurements

To obtain the evolution of the planar defects probability and dislocation density during deformation, the samples before and after the tensile tests were characterized using a time-of-flight neutron diffractor at BL19 “TAKUMI” in the Materials and Life Science Facility (MLF) at the Japan Proton Accelerator Research Complex (J-PARC). The loading axis of the sample was oriented +45° to the incident neutron beam, and the width and height of the incident beam were set as 3 mm and 5 mm. The sample was mounted inside the cryogenic cell chamber, which was sealed and evacuated to <10–3 kPa before the cooling was started. A Gifford–McMahon (GM) cooler having a stage of 77 K was installed in the cryogenic load frame to cool the grips and the specimen. The sample was cooled down and held for 1 h at a stable temperature of 77 K (vacuum ~ 10–5 kPa) before the loading was commenced. Details of the instrument and measurement procedures for the ND have been reported in previous studies72,73. Continuous ND data were collected by two detector banks positioned at ±90° relative to the incident beam after an exposure time of 20 min, which corresponds to the loading and transverse directions of the specimen, respectively. The data at room temperature was also obtained in a similar manner. The collected diffraction profiles were analyzed using the Z-Rietveld code to calculate the lattice parameters, phase volume fraction, and {hkl}-dependent d-spacing of the individual phases74,75.

The SFP was estimated from the difference in peak shifts between crystallographically equivalent orientations74,75, i.e., {111}–{222} and {200}–-{400} pairs, with the scattering vector parallel to the loading direction. The CMWP method, a modified Williamson-Hall method, was used to calculate the dislocation density74,75,76. The instrumental profile was acquired by measuring a LaB6 standard powder sample under the same conditions for CMWP analysis. The experimental error margin was calculated by the fitting error.

The relative amounts of phases were calculated based on {200} γ-fcc and {20\(\bar{2}\)1} D019-hcp peaks using Sage and Guillaud’s method described by Sage and Guillaud77:

$${f}_{{{{{\rm{D}}}0}}_{19}}=\frac{{{{I}}}^{20\bar{2}1}_{{{{\rm{D}}}0}_{19}}}{{{{I}}}_{{{{\rm{D}}}0}_{19}}^{20\bar{2}1}+1.5\times {{{I}}}_{{{\rm{fcc}}}}^{200}}$$
(2)

where \({f}_{{\rm{D}}{0}_{19}}\) is the fraction of D019 phase, and I is the integrated intensity of the corresponding ND peaks.

Ab initio calculations

All ab initio calculations were performed using the DFT-based Vienna Ab-initio Simulation Package (VASP). The projector augmented-wave (PAW) method78,79 was used to describe the electron-ion interactions, and the generalized gradient approximation (GGA) was employed for exchange-correlation functionals. The valence electrons of Ni, Co, Cr, and V were specified as 3d84s2, 3d74s2, 3d54s2, and 3d34s2, respectively. The spin-polarization effect was not considered. For high-precision ab initio total-energy calculations, a K-spacing of 0.3 Å–1 was typically used. To calculate the formation energies of competing phases, the supercell method10 was used with more than 300 atoms for each model. The formation energies were averaged over 20 configurations after geometric optimization.

Empirical interatomic potential development

An empirical potential for Ni–Co–Cr–V alloy system has been developed using the embedded atom method (EAM)80,81,82, by matching a large ab initio database established for the quaternary system without explicit consideration of spin polarization. The ab initio database includes a comprehensive set of atomic configurations (see below) with corresponding cohesive energies, atomic forces, and stress tensors. A similar force-matching method has previously been employed to develop highly optimized potentials for the ZrCuAl82 and NiCoCr10 systems. In this work, special attention was given to the energetics of various SFs and the ordering of Ni–Co–Cr–V solid solutions. To accurately model the Ni–Co–Cr–V system across its full compositional range, we increased the previous database established for the development of the Ni–Co–Cr potential. More than 7500 atomic configurations were selected to form a new ab initio database from non-spin-polarized DFT calculations. These atomic configurations encompass all reported IMCs in the Ni–Co–Cr–V system and include liquid/glass structures, various types of defects, transition pathways, and more, within a large pressure-temperature phase space. The revised Potfit code81 was used for potential fitting. The potential was improved through an iterative process and further refined to match experimental data, including cohesive energies, lattice parameters, elastic constants, and phonon frequencies of the constituent elements. The as-developed EAM potential enables us to investigate the dislocation plasticity via large-scale MD.

Structural ordering in the MEA

The structural ordering and formation of the D019 phase from the Ni–Co–Cr–V MEA were investigated using hybrid MD/Monte Carlo (MC) simulations employing the EAM potential. First, we calculated the chemical potential of Co, Cr, V with respect to Ni employing hybrid MD and MC simulations under the semi-grand canonical ensemble at 1500 K, similar to ref. 10. The following chemical potentials were obtained for the Ni0.333Co0.333Cr0.167V0.167 composition: ΔμNi–Cr =  –0.20 eV, ΔμNi–Co  =  –0.13 eV, and ΔμNi–V  =  –1.57 eV. Subsequently, hybrid MD and MC simulations, with the variance-constrained semi-grand-canonical ensemble83, were carried out to obtain the equilibrium configurations at different annealing temperatures Ta. The variance parameter κ used in our simulations is 103. The initial configuration consisted of 144,000 atomic sites with the x, y, and z directions aligned along the [11\(\bar{2}\)], [111], and [1\(\bar{1}\)0] crystal directions, respectively. Periodic boundary conditions were applied in all directions. The final ordered structure was further refined by adjusting the composition to form the D019 superlattice structure, as shown in Fig. 3 of the main text. All simulations were carried out using the LAMMPS package84 (version lammps-2Aug2023), and the atomic configurations were visualized with the Ovito package85.

SFE calculation

GSFEs, or γ surfaces, were evaluated using the EAM potential, which involved over 100,000 atoms for each calculation. During the GSFE calculations, half of the crystal was displaced by a designated vector, and the structure was allowed to relax in the direction perpendicular to the SF planes.

Formation energies of certain SFs (i.e., SFEs) in the fcc and D019 phases (see, e.g., Supplementary Table 5) were further accurately evaluated following ab initio methods. To this end, various types of SFs were created for the fcc and D019 phases. For instance, the SFs on the basal plane of the D019 phase are illustrated in Supplementary Fig. 13. We used a slab method for the SFE calculation, typically involving more than 300 atoms per configuration. Energy minimization was carried out to obtain structurally relaxed configurations in all directions. Due to the random occupancies of some atoms in both structures, we typically averaged over 20 configurations for each type of SF in our DFT treatment.

Minimum energy path (MEP) calculation

Atomic plane slip occurs along an MEP, revealing the energy barriers and slip directions. In this work, the MEP for a given slip system was determined using the nudged elastic band (NEB) method86 with both DFT and EAM treatments. In MEP calculations, the slip direction is often referred to as the reaction coordinate. The initial configuration represents a perfect crystal, while the final configuration corresponds to a crystal with one-half shifted by a Burgers vector. For instance, in the case of pyramidal I slip, it occurs along the <11\(\bar{2}\)6> direction on the {2\(\bar{2}\)01} plane. The initial configuration typically consists of more than 300 atoms, arranged so that the slip plane is perpendicular to the z direction. The configuration was structured in a slab mode with periodic boundary conditions applied to the x and y directions only. In our NEB calculations, the bottom two layers of atoms in the z direction were kept fixed to prevent motion of the bottom part. We typically used 16 images along the slip direction for the NEB calculations. For systems involving a very large Burgers vector, such as <11\(\bar{2}\)6 >/3 in the pyramidal I slip (which is roughly 9.8 Å in length), the NEB calculation was performed in two steps due to the extensive computational requirements of the DFT treatment. The first NEB run solved for the MEP toward the intermediate antiphase boundary (APB) configuration, located in the middle of the large Burgers vector, and the second step solved for the MEP from the APB configuration to the final configuration.

CRSS calculation

For each slip system, the CRSS was determined as the minimum stress that activates the motion of the dislocation on the slip system, using classical MD. We considered the motion of edge dislocations in five different slip systems for the fcc and D019 phases of Ni–Co–Cr–V (as listed in Supplementary Table 6). Edge dislocations for each slip system were created by superposing two half-crystals, followed by structural relaxations87. This method is found to be more effective than alternative approaches88 in creating stable superdislocations due to the large Burgers vector involved. The dimensions and the number of atoms in the simulation system are provided in Supplementary Table 6.

For dislocation activation simulations, the slip plane was placed on the xy-plane, perpendicular to the z direction, as shown in Fig. 7 and Supplementary Figs. 13 and 14. During our MD simulations, periodic boundary conditions were applied in the x and y directions only, with surfaces along the z direction. Stress was applied to the crystal by adding unilateral forces to the atoms on the outer layers (with a thickness of 1 nm) parallel to the slip plane (i.e., along the x direction). The total momentum was zeroed out during the simulation. We used a bisection method to determine the minimum stress that drives the (super)dislocation to sweep through the crystal within 500 ps. Our MD simulations were carried out in NVT ensembles, with a timestep of 2 fs at 298 K. The MD trajectories and scripts for calculating the CRSS are provided in the Supplementary Data.

Statistics and reproducibility

All experiments were repeated independently with similar results multiple times. To elucidate the microstructural characteristics of the fcc/D019 dual-phase UFG architecture in the CR750 alloy, SAED patterns were systematically acquired along multiple zone axes, including [0001], [11\(\bar{2}\)0], and [10\(\bar{1}\)0]. These diffraction analyses were complemented by corresponding low-magnification STEM-BF images and atomic-resolution STEM-HAADF imaging to provide comprehensive structural characterization at different length scales. For comprehensive microstructural characterization, multiple low-magnification STEM-BF images (>10 images per observation direction) were systematically acquired. Additionally, an extensive set of atomic-resolution STEM-HAADF images (>20 images) was obtained along the [11\(\bar{2}\)0] zone axis to reveal detailed atomic arrangements.