Introduction

In nonmagnetic materials with strong spin-orbital coupling, the passage of charge current can generate pure spin currents via the spin Hall effect (SHE)1,2,3 as well as nonequilibrium spin accumulation from both the SHE and Rashba-Edelstein effect (REE)4,5,6. These charge-to-spin conversion (CSC) mechanisms can be harnessed for the electrical generation and manipulation of spins in spintronic devices7,8,9,10, such as in spin-orbit torque (SOT) magnetic memory and oscillators, while their inverse effects can be further used for electrical spin sensing11,12. In conventional CSC materials, the charge current, spin current, and spin polarization directions are constrained by the crystal symmetry to be mutually orthogonal13,14, which limits the configuration of magnetic moments that can be created or detected. Recently, low-symmetry two-dimensional (2D) topological materials like MoTe2 and WTe2 have been reported to host unconventional (nonorthogonal) CSC, making them particularly appealing for next-generation spintronic applications15,16,17,18,19,20,21. At the same time, strong nonlinear anomalous Hall transport have been uncovered in these compounds22,23,24,25, which results from the current-induced magnetization and can be directly exploited for high-frequency wave rectification26,27,28. There is thus diverse need to fully elucidate the underlying CSC mechanisms and their relationship with the crystal symmetries. While there have been important studies on the SOTs15,18,19,20 and spin currents/polarizations in such systems29,30,31,32,33,34,35,36, unresolved issues persist due to several challenges. First, as both the SHE and REE can yield the same torque and spin components, these effects can be extremely difficult to disentangle. Second, spin currents are hard to sense directly, and so their directions are often inferred from the device geometry. Third, it is unsettled what symmetries remain in the ultrathin limit and which/why certain unconventional CSC components are allowed.

In this work, we set out to directly detect the local current-induced spin accumulation (and associated in-plane spin polarization directions) in MoTe2 flakes across a range of thicknesses. While magneto-optical techniques can be applied to directly image the spin accumulation in semiconductors37, the signal is much weaker in metallic systems and is sensitive only to out-of-plane polarization38. We instead electrically probe the spin-dependent electrochemical potential39,40 using a combination of ferromagnetic and nonmagnetic electrodes in contact at various positions on the sample and in-plane field control of the ferromagnetic spin orientation. Since the REE produces a uniform bulk magnetization while the SHE generates opposite spin polarizations at the sample boundary (perpendicular to the spin current), we can clearly distinguish between these two effects. By measuring from ~20 nm-thick flakes down to four atomic layers, we observe spin accumulation throughout the sample bulk from a conventional SHE and unconventional REE that persists for all thicknesses as well as distinct edge spin accumulation from unconventional SHEs that appear as thickness is lowered. By comparison with ab-initio calculations, the observed behavior can be explained by considering symmetry-breaking from a combination of reduced dimensionality and interlayer stacking shifts in thin flakes, the latter property being recently uncovered in cross-sectional electron microscopy41. Our study maps out the full thickness evolution of the spatially dependent nonequilibrium spin accumulation in MoTe2 and elucidates the underlying crystal-symmetry-coupled CSC mechanisms that can be exploited for future electronic and spintronic applications.

The layered topological semimetals MoTe2 and WTe2 with octahedral coordination are both prime candidates for CSC and nonlinear transport phenomena, although we focus on the former in this study. Below ~250 K, thick MoTe2 exists in the noncentrosymmetric Td phase42,43 (see Fig. 1a, left panel), which contains mirror and glide plane symmetries normal to the a-axis and b-axis, respectively, and a screw axis along the c-axis24,31. The corresponding Pmn21 space group allows for both a REE of the form: \({S}_{i}={\alpha }_{{ij}}{E}_{j}\) with nonzero matrix elements \({\alpha }_{{ab}}\) and \({\alpha }_{{ba}}\), and a SHE of the form: \({j}_{i}^{k}={\sigma }_{{ij}}^{k}{E}_{j}\) with nonzero spin Hall conductivity elements \({\sigma }_{{bc}}^{a},\) \({\sigma }_{{ac}}^{b},{\sigma }_{{ab}}^{c},{\sigma }_{{cb}}^{a},\) \({\sigma }_{{ca}}^{b},{\sigma }_{{ba}}^{c}\)44. Here, \(\left({E}_{a},{E}_{b},{E}_{c}\right)\) is the applied electric field along the \(a\), \(b\), and \(c\) axes, respectively, \({S}_{i}\) is the induced polarization component, and \({j}_{i}^{k}\) is the spin current density with direction \({i}\) and spin polarization along \(k\). As the charge current, spin current, and spin polarization directions are always mutually orthogonal, the thick crystal structure can only yield conventional CSC, in principle. For thin (or surface) layers, the glide plane and screw axis symmetries are nominally broken, and so additional unconventional elements may become available13,31. In reality, the structure of MoTe2 flakes is more complex. Previous Raman studies have reported both the presence and absence of the Td phase at room temperature in few-layer samples18,41,45,46, while a recent transmission electron microscopy study has shown substantial interlayer stacking rearrangements along the b-axis even for thicknesses of tens of nm41, which would also break the glide plane and screw axis symmetries. The same microscopy study also may observe slight shifts along the a-axis, thus subtly breaking the last remaining mirror symmetry. The CSC mechanisms and components are hence intimately tied to the detailed microscopic structure.

Fig. 1: Concept and demonstration of spin accumulation measurements on MoTe2 flakes.
figure 1

a Left panel: crystal structure of Td-MoTe2. Middle panel: schematic of the device and measurement setup. Purple and cyan flakes represent MoTe2 and blocking h-BN, respectively. Gray and gold electrodes represent Ni and Au, respectively. The charge current is applied along the MoTe2 a-axis and the magnetic field can be applied along any direction within the ab-plane to polarize the Ni. The voltage measured between the Ni and Au Hall leads senses the spin-dependent electrochemical potential locally in MoTe2 at the Ni contact position. A difference is detected for current-induced spin polarization aligned or anti-aligned with the Ni polarization. Right panel: optical image of example MoTe2 device with Ni contact to the MoTe2 “bulk”. The MoTe2 flake and blocking h-BN are outlined by purple and cyan dashed line. The Ni electrode is colorized with gray for convenience. b Representative spin accumulation results taken at 2 K for Device 1 (20 nm). Left panel: background-subtracted spin-dependent electrochemical potential V as a function of magnetic field B (\(\theta=-{22}^{\circ }\)) for various positive currents (I = 0.3, 0.6, 1 mA). A “positive” hysteresis loop is seen due to the change of the magnetization state of the Ni relative to the local MoTe2 spin polarization. The height of the hysteresis scales with current. The upper left inset shows the extracted hysteresis voltage ΔV (defined in the main panel) vs. current, indicating a linear relationship. Right panel: V vs. B for negative current flow (I = −1 mA) exhibits a “negative” hysteresis loop.

Full size image

Results

The middle panel of Fig. 1a shows the principle of our device geometry consisting of nonmagnetic Au current leads as well as ferromagnetic Ni and Au voltage leads in a Hall configuration and MoTe2 crystals of varying thickness transferred on top (see Methods for fabrication details). We aligned our devices to pass current along the MoTe2 a-axis, which was confirmed by magnetoresistance and/or optical second harmonic generation measurements (see Methods, Fig. S8, and Supplementary Section 1). The Ni serves as a local spin sensor, whose magnetization direction can be polarized in any direction within the ab-plane via a small magnetic field. By measuring the potential difference between the Ni and Au voltage leads, we can determine the spin-dependent electrochemical potential at the Ni position39,40. The Ni can either be contacted near the MoTe2 edge to sense the edge spin accumulation or be extended deeper into the sample with the edge blocked by insulating hexagonal boron nitride (h-BN) to sense only the bulk spin accumulation at the electrode tip, as is the case shown in the schematic. A representative optical image for a bulk Ni contact device (Device 1, see Supplementary Table 1 for a list and description of all devices measured) is shown in the right panel of Fig. 1a.

Figure 1b demonstrates our measurement scheme on Device 1. As shown in the left panel, for positive current along the a-axis (defined by a common convention with respect to the electrode orientation), sweeping the magnetic field at 2 K generally traces out hysteretic behavior for the Ni-Au voltage (see Fig. S9 for background subtraction procedure), which can be understood from the inset markings. The accumulated spin polarization in MoTe2 is determined by the current direction, while the Ni polarization can be oriented and switched by the magnetic field. When the two are parallel (antiparallel), a positive (negative) voltage is detected after background subtraction39. The switching occurs for field values that are consistent with the coercive fields for the Ni film (see Fig. S10 and Methods). While the height of the hysteresis (difference between the two saturated voltage levels at positive and negative field) increases with the current magnitude, the sense of the hysteresis changes with the current direction (see Fig. 1b, right panel). The left inset of Fig. 1b further shows that the hysteretic voltage change \(\Delta V\) follows a linear relationship with current, thus indicating our measurement is a direct probe of the linear-response spin accumulation in MoTe2 at the Ni contact induced by current flow. We note that we have carefully ruled out the possibility of anomalous Hall effects in Ni as the origin of the hysteresis (see discussion in Supplementary Section 2). We have also performed the field sweeps at higher temperatures and find that \(\Delta V\) decreases monotonically (see Fig. S11). This effect is qualitatively similar to that seen in previous potentiometric measurements of spin accumulation40, and so we maintain 2 K to maximize the signal in our experiment.

By selective placement of the Ni tip(s) at different locations on the sample, we can determine the local spin polarization and further distinguish between the REE and SHE mechanisms for nonequilibrium spin accumulation. Figure 2a shows a device schematic for Device 2 (19 nm) where four Ni electrodes contact the left/right bulk and left/right edges of the sample (see Fig. S12 for optical image of device). There is a corresponding Au electrode for each Ni to allow for separate and balanced Hall voltage measurements. The field sweeps for each Ni contact with positive a-axis current flow and field orientation along the b-axis are plotted in the upper panels in Fig. 2b. We have normalized the voltage signal by current density for easy comparison across devices. For the left and right bulk contacts, we observe hysteresis loops of the same sense (labeled negative according to our definition in Fig. 1b), which indicates a sizeable spin population with polarization component along the negative b-axis (Sb) present in the sample interior. However, no hysteresis is observed for both edge contacts, thus indicating insignificant spin accumulation there within our measurement resolution.

Fig. 2: Position-dependent spin accumulation measurements of thicker MoTe2.
figure 2

a Device schematic for local bulk and edge spin accumulation detection at left and right sides of a single sample. Separate Ni-Au electrode pairs allow for balanced Hall measurements. b Top panels: spin accumulation measurements for each Ni contact on Device 2 (19 nm) with B || b to detect for b-axis spin polarization (Sb). Negative hysteresis loops are observed for both bulk Ni contacts, but negligible hysteresis is seen for edges. Bottom panels: same for Device 3 (23 nm) with B || a to detect for a-axis spin polarization (Sa). Positive hysteresis loops are observed for both bulk Ni contacts, but negligible hysteresis is seen for edges. Each voltage signal is normalized to current density j. c Spin accumulation signal \(\Delta V/{j}\) for each measurement in b as a function of the Ni contact position along the sample b-axis. Both Sb and Sa data appear relatively symmetric with respect to the sample center. The grey dashed lines indicate the position of the sample boundaries. d Schematics of the two CSC mechanisms determined for thicker MoTe2. The observed Sb and Sa spin polarizations in the sample bulk are assigned to conventional SHE \({\sigma }_{{ca}}^{b}\) and unconventional REE \({\alpha }_{{aa}}\), respectively, while the sample edges remain unpolarized. The unconventional CSC element is outlined by the red dashed lines. e Magnetic field angle dependence of \(\Delta V\) for bulk Ni contact taken on Device 1 (20 nm). Solid line is fit to \(\propto \cos \left(\theta+{22}^{\circ }\right)\), indicating the polarization axis for spins accumulated on the interior of the bottom surface.

Full size image

We have performed similar measurements on Device 3 (23 nm) (see Fig. S12 for optical image) for field sweeps along the a-axis and the results are shown in the lower panels in Fig. 2b. While the edges again show immeasurable spin accumulation, positive hysteresis loops are now observed for both bulk contacts, thus indicating the spins in the sample interior have a substantial spin component along the positive a-axis (Sa) as well. As this direction is parallel to the charge current flow, this already points to an unconventional CSC mechanism. In Fig. 2c, we have plotted the height of the hysteresis for each measurement (normalized to current density) as a function of the position of the Ni contact along the b-axis relative to the sample center. For both Sb and Sa, this value is similar for the opposing bulk contacts, suggesting that a relatively strong and symmetric spin accumulation develops in the interior, which then rapidly falls to zero at the flake boundaries.

Both the REE element \({\alpha }_{{ba}}\) and SHE element \({\sigma }_{{ca}}^{b}\) can give rise to the observed b-axis spin polarization (see Fig. S3). As discussed in Supplementary Section 3, symmetry dictates that the former would always exhibit the same spin polarization direction when probing the bottom surface of the sample (for fixed current and field orientations), while the latter can show opposite spin directions depending on how the flake is “flipped”. Our consistent results obtained across many devices allow us to conclude that \({\sigma }_{{ca}}^{b}\) is responsible for Sb, which is a conventional SHE process allowed by the symmetry of the bulk crystal. Similarly, while both the REE element \({\alpha }_{{aa}}\) and SHE element \({\sigma }_{{ca}}^{a}\) can give rise to the unconventional a-axis spin polarization (see Fig. S3), we attribute Sa to \({\alpha }_{{aa}}\) using the same symmetry arguments. Schematics of these two assigned processes are shown in Fig. 2d for the sample interior (where we place our bulk Ni contacts), while the edges remain unpolarized. Broken translational symmetry at the sample boundaries can possibly reduce the local \({\sigma }_{{ca}}^{b}\) and \({\alpha }_{{aa}}\) contributions, leading to undetectable edge spin accumulation.

When both Sa and Sb are finite, the spin axis within the ab-plane can also be directly measured. In Fig. 2e, we show the hysteretic voltage change \(\Delta V\) for a bulk Ni contact as a function of the applied magnetic field angle \(\theta\) relative to the a-axis for Device 1 (see Fig. S13 for complete field sweeps at various angles). We have fit the data to a cosine dependence and the maximum \(\Delta V\) is extracted for \(\theta=-{22}^{\circ }\), which indicates the orientation of the spins on the interior of the bottom sample surface. We then expect that the corresponding spins polarization on the top surface to be pointed along \(\theta={22}^{\circ }\). Note that the spin axis varies across different samples (see Supplementary Table 2).

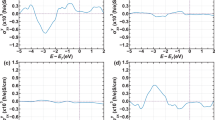
The observation of unconventional spin components as well as contrasting bulk and edge effects in even relatively thick samples motivates further measurements down to lower thicknesses. We have probed the local spin accumulation in MoTe2 down to 2.8 nm, or four layers, the lowest thickness (highest sample resistivity) for which the hysteresis loops can still be clearly distinguished above the noise level by our technique. Due to the smaller areas of 2.8 nm flakes, we have fabricated separate devices for bulk and edge Ni contacts (Devices 5–8). Figure 3a shows device schematics for various such contact configurations, while optical images are shown in Fig. S12. For each Ni position, the b- and a-axis field sweeps (probing for Sb and Sa, respectively) are plotted in Fig. 3b. While the left and right bulk contacts both show negative hysteresis like that for the thicker sample (Device 2), the two edges now exhibit finite and opposite hysteresis—positive (negative) hysteresis is seen for the left (right) edge. For \(a\)-axis field sweeps, positive hysteresis is observed for both left and right bulk contacts (similar to Device 3), but again the edges show opposite hysteresis loops—negative (positive) for the left (right) edge. These results indicate that ultrathin layers not only inherit the CSC elements \({\sigma }_{{ca}}^{b}\) and \({\alpha }_{{aa}}\) from their thicker counterparts that give rise to the same spin polarization in the sample interior but further possess additional contributions that yield finite spin accumulation at the edges. When the edge spin polarizations are opposite, it indicates a SHE with spin current along the b-axis is the underlying mechanism. We thus attribute the edge \({S}_{b}\) and \({S}_{a}\) spin components in ultrathin MoTe2 to the unconventional SHE elements \({\sigma }_{{ba}}^{b}\) and \({\sigma }_{{ba}}^{a}\). In contrast to \({\sigma }_{{ca}}^{b}\) and \({\alpha }_{{aa}}\), for these two processes the spins accumulated at the edges originate from separation that occurs throughout the width of the sample (and not just locally near the edges themselves). We thus expect the accumulation to be less sensitive to the precise atomic structure at the flake boundaries. All the CSC processes detected from 2.8 nm MoTe2 are illustrated in Fig. 3c.

Fig. 3: Distinct bulk and edge spin polarization in 2.8 nm (four-layer) MoTe2.
figure 3

a Device schematics for left edge, left bulk, right bulk, and right edge Ni contacts on 2.8 nm MoTe2 samples. Gold and gray circles indicate Au and Ni contacts, respectively. b Spin accumulation measurements normalized to current density for each Ni contact with B || b to detect for Sb (top panels) and B || a to detect for Sa (bottom panels). The left and right bulk measurements are consistent with those seen for thicker flakes; however, left and right edges now exhibit finite and opposite hysteresis in both Sb and Sa configurations. c Schematics of the four CSC mechanisms determined for 2.8 nm MoTe2. As in thicker flakes, SHE \({\sigma }_{{ca}}^{b}\) and REE \({\alpha }_{{aa}}\) account for the bulk spin polarizations Sb and Sa, respectively, while additional Sb and Sa edge polarizations are attributed to SHE elements \({\sigma }_{{ba}}^{b}\) and \({\sigma }_{{ba}}^{a}\), respectively. The unconventional CSC elements are grouped and outlined by the red dashed lines.

Full size image

Discussion

Our remaining discussion will be focused on a unified understanding of all the experimentally observed SHE and REE components with changing MoTe2 thickness. To show this dependence explicitly, we have plotted the all the spin accumulation \(\Delta V\) (for Sb and Sa, bulk and edge) normalized to the current density as a function of thickness in Fig. 4a. When a finite signal is observed across all thicknesses, as in the case of the bulk measurements, the values decrease with increasing thickness, which can be understood from the expected scaling with sample resistivity (see discussion in Supplementary Section 4). Although the b-axis glide mirror plane \(\bar{{M}_{b}}\) and c-screw-axis \(\vec{{S}_{c}}\) symmetries present in thick MoTe2 are nominally broken in thin samples, a recent transmission electron microscopy study has reported changes in the interlayer stacking along the b-axis for MoTe2 flakes with tens of nm thickness41, the same thickness range where we observe the unconventional component \({\alpha }_{{aa}}\) in our experiment. This leads to a mixed phase between the pure 1 T’ or Td stacking configurations, thereby breaking both \(\bar{{M}_{b}}\) and \(\vec{{S}_{c}}\) symmetries explicitly. The same microscopy study also may have observed slight shifts along the a-axis. Although the magnitude of the a-axis shifts is much smaller than those for the b-axis, it would lead to subtle breaking of the last remaining mirror plane \({M}_{a}\) symmetry as well.

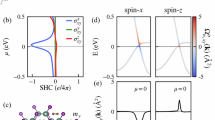
Fig. 4: Thickness dependence of various spin polarization signals and DFT calculations of the CSC components.
figure 4

a Bulk and edge, Sb and Sa spin polarization signals normalized to current density vs. MoTe2 thickness. The responsible CSC element for each is indicated in parentheses. b Left panel: the relevant SHE and REE components vs. Fermi energy calculated for pristine 2.8 nm and thick Td-MoTe2. Middle panel: same calculations for a mixed-phase 2.8 nm MoTe2 with layer shift along b-axis. Right panel: same calculations for a 2.8 nm MoTe2 with layer shift along a-axis. Schematics of the structures are shown in the insets above. The unconventional CSC elements are outlined in red in both a and b.

Full size image

We have modeled the effects of reduced thickness and interlayer shifts using ab-initio density functional theory (DFT) calculations on pristine thick and 2.8 nm MoTe2 with various stacking configurations that reflect the microscopy results of ref. 41 (see Methods and Supplementary Section 5). In the left column of Fig. 4b, we consider a particular 2.8 nm structure with ideal Td stacking. This is captured by the alternating shifts of the Te atoms shown in the inset above. In the panels below, we have plotted all the relevant SHE and REE tensor components as function of the Fermi level calculated for this structure in solid lines. For comparison, we also show the corresponding plots for a thick crystal in the pure Td phase using dashed lines.

We see that reducing thickness alone does not lead to qualitative differences in the conventional component \({\sigma }_{{ca}}^{b}\) that gives rise to bulk \({S}_{b}\), as the relevant symmetries are already broken for the thick crystal structure. On the other hand, the unconventional component \({\sigma }_{{ba}}^{b}\) giving rise to edge \({S}_{b}\) is allowed for the 2.8 nm system only, while \({\sigma }_{{ba}}^{a}\) and \({\alpha }_{{aa}}\) are forbidden in both structures. These results indicate that the appearance of edge \({S}_{b}\) in our 2.8 nm devices can already be explained even without the inclusion of interlayer stacking changes, yet bulk and edge \({S}_{a}\) seen in 2.8 nm MoTe2 cannot be accounted for from the pristine structure.

To include the effects of the interlayer stacking, we have repeated the calculations in the middle panels of Fig. 4b for a particular low-energy mixed-phase 1 T’ / Td structure with b-axis shifts. Calculations performed for related structures as well as pure 1 T’ four-layer are shown Fig. S6. In the right panels of Fig. 4b, we show the calculated components for a plausible structure with a-axis shifts that gives the stack a slight tilt starting from the pristine Td four-layer. Taken together, these results indicate that the effects of stacking changes are relatively small for elements that are already nonzero in the pristine four-layer (\({\sigma }_{{ca}}^{b}\) and \({\sigma }_{{ba}}^{b}\)). However, components \({\sigma }_{{ba}}^{a}\) and \({\alpha }_{{aa}}\) that give rise to edge and bulk \({S}_{a}\), respectively, can only be explained with the inclusion of a-axis shifts that break the last remaining \({M}_{a}\) symmetry. We have additionally tried other structures with a-axis shifts and find that \({\sigma }_{{ba}}^{a}\) and \({\alpha }_{{aa}}\) will generally be nonzero independent of the details of the shift since \({M}_{a}\) is always broken. This analysis thus captures the totality of our experimental results from a microscopic point of view.

Our direct measurements of spatially and thickness dependent nonequilibrium spin accumulation in MoTe2 and supporting theoretical calculations put the CSC mechanisms on firm footing. While various current-induced spin polarizations have been previously deduced in this material using the inverse spin Hall effect29,30,31,32,36, the indirect nature of these measurements together with multiple charge and/or spin current directions possible at the contacts and interfaces make definitive assignment of the SHE or REE components difficult. Our results also shed new light on earlier SOT experiments in MoTe2. Specifically, it has been shown that b-axis spin polarization (for charge current along the a-axis) leads to efficient switching of nearby ferromagnets with in-plane anisotropy20; however, it was unclear whether this was generated by the SHE component \({\sigma }_{{ca}}^{b}\) or REE component \({\alpha }_{{ba}}\). This work indicates that \({\sigma }_{{ca}}^{b}\) is the predominant contributor. Additionally, SOT ferromagnetic resonance measurements have possibly detected small torque components generated by a-axis spin polarization18. If these torques are indeed finite, it most likely originates from \({\alpha }_{{aa}}\) caused by \({M}_{a}\)-symmetry-breaking. Finally, an extremely large c-axis nonlinear anomalous Hall effect has been reported in both thin and thick MoTe224. As the anomalous Hall voltage develops as a consequence of the current-induced magnetization, it is also consistent with our direct observation of REE \({\alpha }_{{aa}}\) in even relatively thick samples.

By use of a local spin accumulation sensor, we have uncovered a plethora of unconventional spin polarizations in the low-symmetry topological material MoTe2 that develop nonuniformly across the sample and can be tuned with thickness. Our work paves the way for the deliberate design of spatially dependent SOT or inverse SHE/REE device geometries that can fully take advantage of the distinct bulk and edge spin accumulation and/or thickness-dependent CSC processes in 2D MoTe2 to realize more exotic functionalities in the future.

Methods

Crystal Synthesis

1 T’-MoTe2 single crystals were grown by the flux method using Te as a solvent. Mo (Alfa Aesar, 99.9%), Te (Alfa Aesar, 99.99%) powders were ground and placed into alumina crucibles in a ratio of 1:25 and sealed in a quartz ampoule. After the quartz ampoule was heated to 1050 °C and held for 2 days, the ampoule was slowly cooled to 900 °C and centrifuged. Shiny and plate-like crystals with lateral dimensions up to several millimeters were obtained.

Device fabrication

Au (35 nm)/Ti (5 nm) and Ni (35 nm)/Ti (5 nm) electrodes in a Hall-bar geometry were pre-patterned on Si wafers with 285 nm-thick SiO2 using conventional photolithography and electron-beam deposition. h-BN (HQ graphene) and MoTe2 flakes were exfoliated onto blank SiO2/Si wafers. The thickness of the MoTe2 was determined by optical reflection contrast and atomic force microscopy (see Fig. S14). We have maintained the orientation of the bulk crystal during the exfoliation process and aligned the rectangular MoTe2 flakes with the electrode pattern. This allows for current injection along a-axis, which can be confirmed by measuring the magnetoresistance or optical second harmonic generation, as we have done in our previous work24. After the desired flakes were identified, a polymer stamp coated with polycarbonate was used to sequentially pick up the entire h-BN/ MoTe2/ h-BN heterostructure to avoid contamination between the layers. Prior to heterostructure transfer, the chip with electrodes was immersed in ammonia for five minutes to remove excess surface nickel oxide and then ultrasonicated in acetone and isopropanol. The heterostructure was then aligned and transferred onto the pre-patterned electrodes. The exfoliation, pick-up, and transfer processes were performed within a nitrogen-filled glovebox to avoid degradation of MoTe2 in air.

Optical second harmonic generation measurements

The rotational anisotropy second harmonic generation (RA-SHG) measurements were performed to determine the crystal axes of the MoTe2. The samples were cooled to 80 K inside an optical cryostat. A 1200 nm pulsed laser with a repetition rate of 200 kHz was focused onto the MoTe2-containing devices with a 20× objective lens at normal incidence. The reflected 600 nm light was collected by the same objective lens. To isolate the SHG signal, the 1200 nm fundamental light was filtered out using optical shortpass filters, allowing only 600 nm SHG light to be detected by an electron-multiplying charge-coupled device. The incident light polarization was rotated using a half-wave plate, and the reflected light was selected to keep either parallel or crossed relative to the incident light polarization. The RA-SHG results are provided in Supplementary Section 1.

Magnetotransport measurements

The spin accumulation measurements were carried out in a superconducting magnet Helium-4 cryostat. The devices were mounted on a rotator stage. An AC current with frequency 17 Hz was passed along the a-axis of the MoTe2 flake, and AC voltages were measured using an SR860/865 lock-in amplifier. For thicker samples (~20 nm), we generally applied a current of 1 mA, and the current density ranges between 1.5–2.0 × 109A/m2 depending on the flake geometry. For four-layer samples, we applied a current between 0.1–0.2 mA, and the current density ranges between 3–8 × 109A/m2. Except for the temperature-dependent measurements presented in Fig. S11, all measurements were performed at 2 K.

Magnetization measurements

The magnetic properties of the Ni film were measured using a vibrating sample magnetometer (Lake Shore 8607). A DC magnetic field was applied by an electromagnet. The sample was attached to a sample rod made of fluorocarbon-based polymer using GE Varnish. The background signal was removed by performing the same measurement with the bare rod and GE Varnish.

Ab-initio calculations

We performed ab-initio density functional theory (DFT) calculation to estimate the spin Hall conductivity and Rashba-Edelstein coefficients. The DFT calculation was performed with the Vienna ab-initio simulation package (VASP) with a projector augmented wave (PAW) potential47,48. The exchange-correlation function was considered in the generalized gradient approximation (GGA) level with Perdew-Burke-Ernzerhof (PBE) functional49. The cut-off energy for the plane wave expansion is considered 350 eV. The lattice constants for the thick samples were taken to be a = 3.477 Å, b = 6.335 Å, and c = 13.883 Å43. The thin films have been realized as 4-layer slabs. For the thick samples and slabs, \(12\times 8\times 4\) and \(12\times 8\times 1\) k-grid was considered, respectively. To calculate different physical properties, a tight-binding model was constructed using the maximally localized Wannier functions using the VASP2WANNIER90 codes50,which was further symmetrized using the WannierTools 42. For the Wannier fitting, we considered the p orbitals of Te and d orbitals of Mo atoms. The spin Hall conductivities and the Rashba-Edelstein coefficients were calculated using in-house codes. The details of the calculations are provided in Supplementary Section 5.