A collective intelligence model for swarm robotics applications

Abstract

Swarm intelligence models represent a powerful tool to address complex tasks by multi-agent systems, although they are rarely used in practical applications as decentralized cooperation logic. Modern challenges include the improvement of model reliability with small swarm sizes and enhancing performance with minimal number of free parameters. Available techniques are generally tuned for computational optimization, at the expense of the applicability to real-world scenarios. Merging concepts from meta-heuristic methods and consensus theory we propose a swarm cooperation model which can act both as virtual optimizer and vehicle controller. The model shows a higher or equal success rate with respect to benchmark methods on 22 out of 33 landscapes when dealing with less equal 16 agents and low dimensional problems. Beyond multimodal optimization, a computational proof of concept shows that the method can successfully drive the contaminant localization in a complex marine environment by controlling a group of autonomous underwater vehicles.

Introduction

Swarm intelligence embraces all the emergent behaviors of groups of social living beings, such as bird flocks, fish schools, ant colonies and human groups^1,2,3, which outperform the single individuals in a variety of tasks of common concern. These comprise escape from predators, foraging, migration and any joint decision-making processes. Any intelligent collective behavior arises from the reaction of individuals to a cognitive and a social stimulus⁴. The balance between these two types of information drives the actions of the individual, and potentially leads the group to the accomplishment of tasks that are beyond the reach of any component operating alone^5,6.

This paradigm has inspired several meta-heuristic methods to address pure optimization problems, as well as to control multi-agent robotic systems. Any search process, domain exploration or classification procedure can be accomplished by a swarm of virtual or physical agents with the appropriate design of the individual perception method and the group communication protocol^7,8.

The most widespread algorithms encapsulating the key ingredients of swarm intelligence are the Particle Swarm Optimization (PSO), the Artificial Bee Colony (ABC), and the Differential Evolution Method (DEM)^9,10,11. They are often chosen to handle computationally demanding problems with few or no assumptions about the landscape function. Similar algorithms, usually formulated as a sequence of discrete updates, optimize a problem by iteratively improving a candidate solution with respect to a given quality measure across multiple search rounds. As counterpart of their algorithmic simplicity, meta-heuristics methods do not guarantee that the optimal solution is ever found. Furthermore, their success and convergence rate strongly depends on empirical coefficients¹². The automatic adaptation of these tuning coefficients to a specific case-study has collected extensive efforts in the scientific computing community, resulting in hybrid strategies involving multi-swarm approaches¹³, evolutionary state estimation¹⁴, swarm size adaptation and re-initialization¹⁵, just to name a few. Nevertheless, the majority of the algorithmic sophistication is typically accompanied by a broader array of coefficients or thresholds that must be empirically determined.

Beyond computational optimization problems, swarm intelligence has found rare applications to robotics¹⁶. Although groups of robots are widely employed in industry, they still rely on centralized control strategies rather than swarm intelligence principles. This is mainly attributed to the predictability of results and to the limits of current communication architectures, which often do not sustain the required information load¹⁷. When dealing with physical agents, many of the algorithmic enhancements are not applicable, because the swarm size is fixed and the agent motion is subjected to its own body dynamics. The swarm size itself might represent a bottleneck for applying meta-heuristic methods to physical agents, as the minimum size required to ensure an high success rate can easily exceed the number of available agents or result in unsustainable communication loads. Empirical studies on a variety of multimodal test functions showed that an acceptable compromise between success rate and function evaluations can be achieved with 50 ÷ 7; 100 particles for the PSO¹⁸ and 20 ÷ 7; 50 for the ABC¹⁹.

Successful examples of decentralized robot control rely on consensus-driven methods²⁰. These forms of swarm intelligence lead multi-vehicle operations where a group of agents responds to unexpected situations or environmental changes when approaching a sufficiently shared value about certain “coordination data”²¹. Consensus based methods have been applied for formation stabilization and maneuvering, rendezvous, payload transport,²². Although applications of consensus based methods are now widespread (for instance to unmanned air vehicles and satellites), they are limited to simple environments and neighbor-constrained communications, whereas exploration of multi-modal landscape and non-convex search problems are considered out of range for this coordination technology²². The recently developed Consensus Based Optimization (CBO)²³ exploits the principles of the consensus theory to raise a novel optimizer, but it has been mainly developed in the mean-field limit, which still move its applicability away from robotics.

Merging concepts from swarm intelligence approaches and consensus-seeking methods, we introduce a Swarm Cooperation Model (SCM) to address bounded multi-modal optimization problems for both virtual agents and physical vehicle groups. The SCM exploits a time-continuous formulation, valid for both static and dynamic N-dimensional landscape functions. The key novelties of this work include:

• A self-regulating stochastic forcing governed by the swarm consensus, allowing agents to explore any steady or unsteady landscape with no prior topological information other than an estimate of the characteristic domain size.

• A success rate higher or equal to that guaranteed by the benchmark methods on 22 out of 33 test cases for limited swarm sizes (16 agents or less) on different two- and three-dimensional landscapes. This ranks the SCM as an appealing option for controlling a broad class of autonomous vehicles. Benchmark methods include the Particle Swarm Optimization on behalf of meta-heuristic approaches and the Multistart Interior Points Algorithm (MIPA) as a gradient-based technique.

• The integration with a vehicle control scheme to run a search problem by means of an agent fleet. We computationally prove the effectiveness of the swarm cooperation model simulating the localization of a contaminant in a realistic marine environment, by means of a swarm of Autonomous Underwater Vehicles (AUVs).

Swarm cooperation model

Assume an ensemble of M agents searching for the location of the absolute maximum of a scalar landscape function ψ(x¹, x², . . . , x^N, t), with generic unit [φ], over an N-dimensional domain. Agents can share at any time only their position in space ${x}_{k}^{i}(t)$, with i = 1, . . . , N and k = 1, . . . , M, the perceived fitness about the landscape function, V_k, i.e., an estimate about the landscape function, and its gradient. Information exchange involves the full agent network. Agent interactions take place as a result of their level of disagreement about the mutual location, without any memory of their evolution. In absence of other stimuli, the social push induces the rendezvous of the swarm, with no control about the meeting point.

The swarm cooperation process is assisted by a stochastic forcing. Thus, the time-continuous process driving the emergence of a collective behavior can be formulated, for the k-th agent, as an overdamped Langevin equation. The characteristic domain length L [m], the social interaction strength J [s⁻¹] and the perceived fitness weight ρ [s⁻¹ φ⁻¹] can be used to make the problem dimensionless, such that the governing equation reads:

$$\frac{\partial {x}_{k}^{i}(t)}{\partial t}=-\frac{2}{\pi }\frac{\partial {E}_{k}^{i}}{\partial {x}_{k}^{i}}+\xi \frac{4}{{\pi }^{2}}\frac{\partial {V}_{k}}{\partial {x}_{k}^{i}}+\frac{2}{\pi }{\mu }_{k}(t){\eta }_{k}^{i}(t).$$

(1)

A complete derivation of Eq. (1) is provided in section 1 of Supplementary Information (SI) for a generic decision variable.

The evolution of the agent position is thus governed by: i) the gradient of the social interaction energy ${E}_{k}^{i}$, ii) the gradient of the perceived landscape fitness, interpreted as a potential energy, and iii) a standard Wiener process, W_k, such that ${\eta }_{k}^{i}(t)=d{W}_{k}^{i}(t)/dt$. The stochastic velocity fluctuations are needed to allow the agents to escape local maxima when exploring non-convex landscapes. The first term denotes a force proportional to the level of conflict of the k-th agent with the full network about its i-th coordinate:

$$\frac{\partial {E}_{k}^{i}}{\partial {x}_{k}^{i}}=\frac{1}{M-1}\sum _{h=1}^{M}\left(1-{\delta }_{hk}\right)\sin \left(\frac{2}{\pi }\left({x}_{k}^{i}(t)-{x}_{h}^{i}(t)\right)\right),$$

(2)

with δ_hk being the Kronecker delta. The coefficient ξ = ρϕ/J balances the contribution of perceived fitness and social interaction energy, i.e., cognitive stimulus and social interactions. Here ϕ denotes the scale value of the landscape function. Since ϕ is unknown, the coefficient ξ is chosen as the inverse of the swarm-averaged L₂ norm of the fitness gradient (see section 2 in SI for further details), such that both the social gradient and the fitness gradient are of order 1. Low-order finite difference formulas can be used to approximate the landscape gradient when its analytical expression is unknown.

The intensity of the stochastic forcing inherently represents a key parameter in the search process. Hence, the robustness and the effectiveness of the model strongly depend on the ability of the swarm to self-regulate the noise intensity. In this connection, we consider the base random fluctuation ${\eta }_{k}^{i}(t)$ to be modulated by an adaptive factor μ_k(t). ${\eta }_{k}^{i}(t)$ is drawn from a Gaussian distribution with null mean value, $\langle {\eta }_{k}^{i}(t)\rangle=0$, unitary variance, Var$\left[{\eta }_{k}^{i}(t)\right]=1$, and time-independent increment 〈η_k(t₁)η_k(t₂)〉 = δ(t₁ − t₂)²⁴, with δ the Dirac delta. The factor μ_k(t) is the product of a global variable σ(t) and an agent dependent parameter λ_k: μ_k(t) = σ(t) λ_k(t). Both are assumed to depend on the global swarm consensus C:

$$C=1-\frac{2}{M}\sum _{k=1}^{M}{d}_{k},$$

(3)

which measures the mean level of agreement among agents. Since the success of the search process is inherently related to the agent clustering, the global consensus C is built out of the distance d_k, denoting the distance of the k-th agent from the swarm centroid, ${x}_{c}^{i}$. This is intended as the fitness-weighted average location:

$${d}_{k}=\sqrt{\sum _{i=1}^{N}{\left({x}_{k}^{i}-{x}_{c}^{i}\right)}^{2}},\quad {x}_{c}^{i}=\frac{{\sum }_{k=1}^{M}\,{x}_{k}^{i}\,\left({V}_{k}-\mathop{\min }_{k}({V}_{k})\right)}{{\sum }_{k=1}^{M}\,\left({V}_{k}-\mathop{\min }_{k}({V}_{k})\right)}.$$

(4)

The agent-dependent parameter λ_k simply yields:

$${\lambda }_{k}(t)=\frac{{d}_{k}}{{d}_{\max }}{C}^{-1},$$

(5)

with d_max being the maximum reciprocal distance among agents. According to this definition, the noise magnitude on the k-th agent velocity is expected to increase if it is sensing a low relative fitness, in a region far from the largest agent clusters.

The global noise coefficient σ(t) instead evolves by discrete increments, according to the following differential equation:

$$\frac{{{\rm{d}}}\sigma (t)}{{{\rm{d}}}t}=\omega \,\frac{\min \{I(C,\tau ),0\}}{I(C,\tau )}\,\delta \left(t-\tau \lfloor t/\tau \rfloor \right),$$

(6)

where ω is a coefficient denoting the increment magnitude, τ denotes the minimum time interval for the σ(t) update. An incremental approach is preferred to grant the agents enough time to exploit the fluctuations to jump out of local optima or simply advance the search process. The term I(C, τ) provides an integral measure of the consensus trend:

$$I(C,\tau )=\int_{t-\tau /2}^{t}C(t)dt-\int_{t-\tau }^{t-\tau /2}C(t)dt.$$

(7)

This formulation allows the global noise factor σ(t) to be increased in case the swarm manifests a nearly steady consensus in the past τ time window, meaning that the agents are not able to escape local minima with the current noise magnitude.

Although σ(t) grows monotonically, the amplitude of the associated fluctuations do not have a negative impact of the agents with the highest consensus C_k, because their social condition generate reduced λ_k values, which counterbalance the increase in σ(t). The robustness of this approach is enhanced by setting a limiter on σ(t), ${\sigma }_{\max }$, beyond which it is restarted to the initial value σ₀. In all simulations, the used value is ${\sigma }_{\max }=0.3$.

The hyper-parameters ω and τ might affect the convergence rate of the search process. Larger ω values, or smaller τ, accelerate the noise adaptation procedure, but increase the noise overshoot risk. The sensitivity of the model to these hyper-parameters is investigated in section 3 of the SI, showing clear trends which provide a rationale for a robust choice. However, the self-regulation mechanism for the stochastic forcing will be proved to be robust enough to guarantee the research success with the same value of ω and τ on a variety of static landscape functions.

Results

Optimization on static landscape functions

In first instance, the swarm model has been tested as optimization tool against 6 landscape functions typically used as benchmark cases for optimization algorithms. These feature dominant global maxima (Ackley function), nearly-optimal local maxima (the global maxima of the Rastrigin and Griewank functions take values 4.5% and 2% larger than the adjacent local maxima, respectively), non isotropic spatial modes (Griewank function) and a fractal pattern. Function expressions and reference are provided in section 4 of SI. The locations of the global optimum are displaced in diverse regions of the exploration domain. All cases are computed with a global noise increment ω = 0.2, initial global noise σ₀ = 0.05 and time interval τ = 60Δt in light of the outcomes of the sensitivity analyses reported in section 3 of SI. The search process is marked as successful whether the swarm holds a nearly unitary consensus within the τ period, i.e., if $\int_{t-\tau }^{t}C(t)\,dt > \gamma (M)\,\tau$, with $\gamma (M)=\left[1-\tanh \left(M/100\right)\right]/20+0.9$ being a threshold function which allows to relax the target consensus for large swarms. When increasing the swarm size, M, the achievement of a unitary consensus becomes increasingly difficult even though the swarm centroid holds a stable position. Therefore, the termination threshold is formulated as a function of M which tends asymptotically to 0.9 τ. Once the threshold is achieved, the majority of the agents has gathered around estimated global optimum. Numerical experiments will successively show that this occurrence corresponds to an high success rate.

A pseudo-code for the SCM implementation is provided in section 5 of SI.

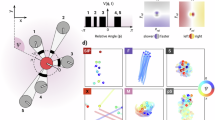
To elucidate the model operation, we illustrate (see Fig. 1) the evolution of the search process on the Rastrigin landscape with a few agents, i.e., M = 5. The agent initial position is picked from an uniform random distribution (the reader is referred to the black dots in panel d of Fig. 1). After a fast transient, the agents settle to the closest local maxima. From then on, they share a nearly steady consensus, as neither the social interaction term, nor the stochastic forcing allow them to escape the local optima. After a τ period without significant consensus variations, the σ(t) Eq. (6) triggers two successive increments of the global noise factor, until the stochastic fluctuations allow the agent 3 to join the agent 5 and the agent 2 to join the agent 4. In the formation shown on panel b, agents 3 and 5 exert a larger social attraction force with respect to agents 2 and 4 because they detect a larger fitness, thus they shift the swarm centroid towards them. Therefore, the former receive the smaller individual noise factor λ_k, whereas the latter receive λ_k > 1. In this condition, agents 2 and 4 are more likely to jump out of their local optima than agents 3 and 5 to change location. Figure 1f shows how the convergence processes can successfully take place even in presence of very similar fitness values. An animated version of the search process with 5 agents is available, on all tested landscape functions, in Supplementary movies 1–6.

Fig. 1: Example of swarm cooperation process.

Localization of the global maximum on the two-dimensional Rastrigin function with a 5 agents swarm. Consecutive snapshots of the agent position over the landscape function (a–c); the red star symbol denotes the location of the global maximum. Pointwise agent trajectory through the search process; the color is associated to time instants (d). Black dots denote the initial agent positions. Time-traces of the global consensus C and the global noise modulation factor σ (e), and of the perceived fitness value (f) for each agent. For an animated version of this figure, see Supplementary movie 3.

Performance comparison

The performance of the swarm model are now compared on different test functions with increasing dimensionality. For a fair comparison the initial agent position is chosen solving the “circle packing in a square” problem²⁵ extended to an arbitrary dimensionality. This guarantees the most uniform mutual separation among the agents, which in turn provides the higher exploration potential ab initio. Results are compared with those obtained with the PSO²⁶ and the MIPA²⁷, whose setups are listed in the Methods section. The benchmark methods were chosen as well-established representatives of meta-heuristic, gradient-free approaches and deterministic, gradient-based approaches, respectively. The comparison, carried out in terms of success rate, SR, and mean number of function evaluations 〈FE〉, offers the full picture about the optimization performance. An ideal approach would have a 100% success rate, with a minimum number of function evaluations. In a swarm robotics scenario, a minimal 〈FE〉 does not represent a necessary requirement to run the optimization, since the evaluation of the landscape corresponds to a sensor sampling, unless the 〈FE〉 entails an optimization duration which is not compatible with the robot range. The sampling of the landscape function is performed sporadically during the robot locomotion (further details are provided in the following paragraph), so neither the sampling frequency nor the amount of samples affect the SCM convergence. On the contrary, an high SR entails an increase of the reliability, which has long hindered the growth of applied swarm robotics¹⁷. The SR and the 〈FE〉 are computed out of 100 replications, using 100 different Wiener processes ${\eta }_{k}^{i}(t)$ for both SCM and PSO. The success rate of all methods is obtained by counting the number of replications in which the distance of the swarm centroid from the true global optimum is lower than 0.05L. The stop criterion, described at the beginning of the preceding paragraph, finalizes the search only when the majority of the agents converge to the swarm centroid. In case it does not match the global optimum, the case is marked as unsuccessful. All SCM simulations have been run with dimensionless time step-size J Δt = 0.1.

The comparisons are presented by means of the histogram matrices in Fig. 2a, b. Each row corresponds to a landscape function, whereas each column refers to a dimension N. The fractal landscape has been tested in two dimensions only because it is hardly generalizable to an arbitrary dimension while holding topological similarity. The box plots in Fig. 2b indicate mean value and standard deviation of 〈FE〉. The corresponding data are provided in Supplementary Dataset 1–3.

Fig. 2: Performance benchmark.

Histogram matrices of success rate SR (a) and mean number of function evaluations 〈FE〉 (b). Each row corresponds to a landscape function (the reader is referred to section 4 of SI for landscape formulas), whereas each column corresponds to a dimension, N. The single histogram compares SR or 〈FE〉 of three methods, Particle Swarm Optimization (PSO), Multistart Interior-Point Algorithm (MIPA) and Swarm Cooperation Model (SCM), for different swarm sizes, M. The box plots about 〈FE〉 indicates the mean value and the corresponding standard deviation.

Figure 2a shows that a clear ranking among the three methods cannot be established regardless of the features of the landscape function or its dimensionality. However, it is worth pointing out that, when considering M ≤ 16 on two and three dimensions, the SCM outperforms or matches the SR of other methods on 22 out of 33 cases. This subset identifies the cases of interest in swarm robotics, where the decision variables correspond to the spatial coordinates in a two- or three-dimensional search domain. A substantial difference in the SR can be observed in the dependency on the number of agents, M. Both PSO and MIPA show a monotonic increase with M, whereas the SCM does not in a few cases. The benchmark methods comply with the “best-known” criterion by which they hold in memory the best-known position during the search process. The SCM agents do not hold any global information apart from the swarm consensus, C(t), instead. This makes the probability of finding the global optimum less sensitive to the swarm size. It is worth mentioning that this also enables the SCM to work on unsteady landscape functions without algorithmic complications, as shown in the following paragraph.

The most favorable comparison occurs on the Griewank landscape, where many nearly optimal stationary points surround the global optimum (the reader is referred to Fig. 3 in the SI for a visual interpretation), whereas the worst scenario occurs on the Schwefel function, featuring a diverging envelope (the global maximum is surrounded by the smallest local minima). On the latter, the SCM requires the agent to receive significant fluctuations to counteract the gradient-related force and jump over the local minima towards the target. On similar landscapes, the PSO, which does not exploit landscape gradients, is inherently advantaged in the convergence process. A 100 % SR is guaranteed in any dimension on the Ackley function, where the global maximum dominates over 35 local maxima. On this landscape, as soon as an agent passes by the global optimum, the fitness-weighted centroid will be highly displaced, stimulating the migration of other agents. The replications on the fractal landscape foster the SCM in terms of SR, proving that the numerical approximation of the landscape gradient by finite differences does not undermine the method advantage with few agents. The fractal landscape is numerically generated as a randomly rough surface with fractal dimension 1.8, tile wavelength 0.1 m and null roll-off wavelength over 512 pixels per side.

Fig. 3: Schematic of the AUV-integrated swarm model.

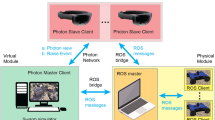
Satellite view of the region of interest, image courtesy of the U.S. Geological Survey (a). Snapshot of the simulated marine current over the search area (b). Agent of the swarm illustrated as AUV (c). Flowchart illustrating the logical sequence of AUV dynamics and swarm cooperation step (d). Here the blue window delimits the operational steps involved in the swarm intelligence procedure (SCM), which take place at discrete time intervals once all agents have achieved the assigned target location. The superscripts n and m indicate the time advancement levels of the AUV dynamics model and the swarm cooperation model, respectively. The parameter ${q}_{k}^{n}$ denotes a coordinate of the center of mass of the k-th AUV at the m-th time step. The coordinate ${x}_{k}^{T}$ represents the navigation target for the AUV set by the swarm model at the n-th time step.

The SCM performance degrades with problems of high dimensions on a peer swarm size basis, likewise any optimization algorithm. PSO has been documented to reduce its SR with problems of high dimensionality²⁸. Furthermore, it has been shown that increasing the swarm size might not be a sufficient solution, depending on the landscape itself²⁸. In our numerical experiments, scalability issues occur in all analytical landscapes except the Ackley and the Griewank functions.

The 〈FE〉 comparison in Fig. 2b, shows a monotonically increasing trend with the number of agents, M. Such a dependence is approximately shifted towards higher values when increasing the problem dimensionality. A clear ranking is shown in all cases beside the Ackley function: the PSO offers the least 〈FE〉 and the SCM the largest. The SCM generally presents a larger standard deviation on the 〈FE〉 due to the coexistence of a gradient descent term and a stochastic forcing. Furthermore, it is worth noting that the 〈FE〉, as well as the mean run time, 〈t_f J〉, can be further reduced by initializing the simulations with a case-specific global noise value σ(0).

Numerical experiments have shown that the SCM can provide a larger or equal SR with respect to PSO and MIPA when considering a cohort of cases with reduced swarm size (M ≤ 16) and two- or three-dimensional landscapes. However, the SR benefit comes at the cost of nearly ten times more function evaluations. On the same case cohort, the 〈FE〉 is significantly higher on 24 out of 33 landscapes. The 〈FE〉 comparison turns out to be unfavorable for SCM, and this shortcoming should be considered when selecting on optimization tool. A larger 〈FE〉 is the result of the SCM not holding the best-known optimum in the agent memory. This feature disadvantages the SCM on static landscapes with respect to benchmark methods, but it allows the model to work effectively on dynamic landscapes, where the topology of the objective function evolve in time. A computational demonstration is provided in the following paragraph. The SCM can be considered as a competitive option for optimization problems where (i) each function evaluation has a minimal or negligible cost, (ii) the amount of available agents is constrained to M ≤ 16 and the problem has three optimization variables at most, (iii) the optimization framework must work on both steady and unsteady landscapes. All of these conditions make the SCM theoretically compatible with swarm robotics scenarios.

Application to a simulated marine environment

To verify the theoretical applicability of the SCM to a real multi-vehicle system, we simulate the localization of the maximum concentration spot of a diffusive contaminant, within a convection-dominated marine environment. The search process is performed over a 6 km square area by a swarm of communicating AUVs. In this context, the simulated marine current transports the contaminant as a passive scalar field (see the Method section for details), which herein plays the role of a dynamic landscape function, and contextually imposes the hydrodynamics disturbances to the AUV navigation. The involved vehicles, endowed with a contaminant sensor, can measure their fitness and navigate seeking for the highest concentration. This problem is proposed as a computational proof-of-concept for the application of the swarm cooperation model to a real-world scenario.

Each AUV corresponds to an agent of the swarm, and the output of the swarm model leads the swarm dynamics by means of the AUV control system. At the n-th iteration of the swarm intelligence model, each AUV receives an individual target point, which indicates the spatial coordinates the agent must reach to measure the landscape value and its gradient. The target information is used to compute the rudder error in the AUV proportional-derivative control system. Once the AUV, subjected to its own dynamics, hits the target point and performs the measurements, it can fulfill the necessary network communications and thus advance the swarm model to set the successive target location. This sequence is visually described by the sketch and the flowchart in Fig. 3. The AUV dynamics relies on a well-established model^29,30, typically used to design control schemes and assess mission performance; related details are provided in the section 6 of SI.

The hydrodynamic environment is obtained from high-fidelity numerical simulations performed with the high-resolution coastal modeling system of the Taranto Gulf³¹, developed by the Euro-Mediterranean Center on Climate Change (CMCC) Foundation.

We select, as search domain, a 6 km square box in the Gallipoli bay (approximate coordinates ${40}^{\circ} \,0{6}^{\prime} \,$N, ${17}^{\circ} \,8{9}^{\prime} \,$E), in the southern Italian coastal area, where currents ranging from 0.05 to 0.2 m/s acts at 4–6 meter depth. Additional information about the hydrodynamic simulation are provided in the “Methods” section 2. The hydrostatic approximation for the fluid motion generates vertically stratified flow fields at the kilometer scale, meaning that the momentum transport in the vertical direction is much limited with respect to the other spatial directions. Owing to this condition, both the contaminant transport and AUV dynamics are simulated on a two-dimensional domain at 4-6 meter below the mean sea surface level. The size of the search domain is chosen to allow for acoustic communications with commercial hydro-acoustic telemetry, currently denoted as the best option for AUVs^32,33.

Figure 4 provides an overview of the application, including the initial contaminant concentration (panel e), five snapshots with the evolution of the marine current and the advected phase, as well as the time traces of the global consensus and perceived fitness. An animated version of the figure is available at the Supplementary movie 7.

Fig. 4: Synopsis of the contaminant search test by an AUV swarm.

Marine current magnitude and direction (a–d) at four consecutive instants. Contour plots of contaminant distribution ψ, alias for a dynamic landscape function, with corresponding agent location (e–h) on red triangles. Triangle size is magnified 30 times with respect to the actual AUV size ($\tilde{3}0$ m). Instantaneous configurations in panels (a–h) refer to the physical time t^*, expressed in hours:minutes. The red lines in panels (e–h) intersect at the instantaneous global ψ maxima for reference. Panel (i) shows the full history of consensus C and global noise coefficient σ as a function of the swarm dimensionless time, whereas panel (j) shows the perceived fitness per agent. Eventually, panel (k) displays the full agent trajectory with colors corresponding to the legend in panel (j). For an animated version of this figure, see Supplementary movie 7.

The test case shows how a successful search can be performed over a broad area in a reasonable time (about 16.6 hours) over a landscape with changing topology and peak values due to the advective and diffusive process (this can be observed on the decreasing perceived fitness in Fig. 4j. The same test, entailing a 5 AUV swarm initialized with the circle packing method, has been replicated 100 times by sampling different ${\eta }_{k}^{i}(t)$ distributions to assess the SCM performance. The parameter τ was set to 30Δt to get faster noise increments, such that the search can be finalized before the contaminant is advected outside the search domain. This setting guaranteed a 86% success rate with mean search time equal to 20.8 ± 3.82 h, and mean traveled distance equal to 93.8 ± 17.3 km per agent. We emphasize that the swarm model requires the agents communicate only their location, the perceived fitness value and its gradient at each SCM iteration.

Discussion

We have shown how swarm intelligence can be used to systematically address demanding optimization problems on bounded spaces or to drive the cooperation of a multi-vehicle system in a search process. The proposed Swarm Cooperation Model (SCM), formulated as an overdamped Langevin equation, leverages the features of meta-heuristic optimization and consensus information theory to operate indistinctly on steady and unsteady landscapes. It is shown to outperform the success rate of the Particle Swarm Optimization (PSO) and the Multistart Interior Points Algorithm (MIPA) on 22 out of 33 cases when dealing with a fairly limited swarm size (less equal to 16 agents) in two- and three-dimensional problems, while avoiding algorithmic techniques that would compromise the applicability to real-world scenarios. This advantage comes at the cost of about 1 order of magnitude more function evaluations with repect to the benchmark methods, which does not represent an issue in applied robotics, where a function evaluation corresponds to a sensor measurement.

The model is endowed with a self-adapting stochastic forcing able to settle the noise magnitude on the most suitable level for any landscape function. Differently from existing approaches, the SCM, in its dimensionless form, operates on both steady and unsteady landscape function and requires the choice of hyper-parameters which have minor effects on the success rate.

The SCM has been applied, as a computational proof-of-concept, to control a swarm of Autonomous Underwater Vehicles (AUV) in the search of a generic contaminant transported by the sea current in a coastal area. This scenario entails an unsolved applied problem, where the contaminant concentration potentially represents liquid pollutants, micro-plastics, harmful algae, or anything whose detection is not accessible to satellite measurements. In the proposed setting the search process is further complicated by the advection/diffusion of contaminant operated by sea current, which alters the landscape topology during the research. The SCM still showed an high success rate with a reasonable search time.

The SCM can be possibly enhanced testing the effect of stochastic fluctuations picked from a “thick-tailed" distribution, such as the Levy distribution or the Cauchy distribution, rather than the Gaussian one. Well-established meta-heuristic optimizers, such as the PSO³⁴ and the ABC³⁵, have been randomized with these distributions, showing superior convergence rates³⁶.

Within an applied robotic scenario the Langevin Eq. (1) can possibly be mapped to the vehicle angular position rather than the center of mass coordinates. This requires a re-formulation of the conflict energy for the agents to be directed towards successive target locations. However, the effectiveness of this alternative deserves to be investigated.

Beyond modeling aspects, key agent communication factors must be addressed in view of a practical implementation, especially when considering the applied test case of AUV swarm. Location precision can be achieved with an accuracy of 0.5% of the traveled distance when using a dead reckoning navigation system³³. Agent communication still poses relevant challenges, instead. While commercial high-frequency radio devices and radars can be used for communications among ground agents, hydroacustic telemetry appears to be the only acceptable option for underwater swarms at the kilometer scale³³. Acoustic waves travel long distances without significant attenuation, they can transmit at a Baud rate up to 62 kbps at 150 kHz, but they reflect on hard surfaces, increasing the amount of noise in the communications³². The former does not represent a limit indeed, since the agents must communicate only position, fitness value and fitness gradient, whereas the latter needs to be addressed by designing a dedicated noise filter.

The general counterpart of the SCM, derived in the section 1 of SI for an unspecified decision variable, can be easily applied to optimize other life-science applications of arbitrary dimensionality, such as wireless networks, power supplies, risk assessment, software development, training of artificial neural networks and any process which can be formulated as a bounded optimization problem with a measurable fitness function. The simplicity of the model and its effectiveness with a small swarm size paves the way for the application of the swarm intelligence paradigm to the control of multi-agent robotic systems.

Methods

Numerical integration of the Langevin model

The governing Eq. (1) contains a nonlinearity in the social energy term, thus explicit time-marching schemes are the most suitable options, considering that integration period is a case-dependent quantity. In this connection, the numerical integration is carried out by means of the Euler-Maruyama scheme.

In the infinitesimal time step limit, the differential of a Wiener process associated to the k-th agent takes the form³⁷:

$$d{W}_{k}\approx {W}_{k}(t+\gamma \,\Delta t)-{W}_{k}(t)=\sqrt{\gamma \,\Delta t}\,{{{\mathcal{N}}}}_{k}(0,1),$$

(8)

where ${{{\mathcal{N}}}}_{k}(0,1)$ is a normal distribution with null mean value and unitary variance and γ is the time fraction depending on the chosen time scheme. The agent coordinate is discretized at the time tⁿ = nΔt, with Δt being the time step size. Once dropped the decision superscript for the sake of readability, the discrete counterpart of Eq. (1), at the time level n + 1 reads:

$${x}_{k}^{n+1}={x}_{k}^{n}+\Delta tf\left({x}_{k}^{n},{x}_{h}^{n}\right)+{\mu }_{k}^{n}\,\sqrt{\Delta t}\,{{{\mathcal{N}}}}_{k}^{n+1}(0,1),$$

(9)

where

$$f\left({x}_{k}^{n},{x}_{h}^{n}\right)=-\frac{2}{\pi (M-1)}\sum _{h=1}^{M}\left(1-{\delta }_{hk}\right)\,\sin \left(\frac{\pi }{2}\left({x}_{k}^{n}-{x}_{h}^{n}\right)\right)+\xi \frac{4}{{\pi }^{2}}\frac{\partial {V}_{k}^{n}}{\partial {x}_{k}^{n}}.$$

(10)

Although more accurate schemes are available, such as the Milstein method or stochastic Runge-Kutta methods³⁸, most of them require additional evaluations of the state function $f\left({x}_{k}^{\alpha },{x}_{h}^{\alpha }\right)$. In a swarm model where any landscape evaluation needs the agent to physically reach the evaluation point, accurate methods would bring additional time and energy consumption for each agent. Therefore, the search process would not benefit from an increased time accuracy in real-world search scenarios.

Benchmark methods

The performance of the SCM have been compared with two well-established optimizers: the Particle Swarm Optimization (PSO)²⁶ on behalf of gradient-free, meta-heuristic optimizers and the Multistart Interior Point Algorithm (MIPA)²⁷ of behalf of gradient-based, deterministic approaches.

The comparison with the PSO (see Fig. 2 and related discussion) has been carried out by means of the built-in function particleswarm available in Matlab³⁹. This function runs an optimization process based on the original algorithm proposed by²⁶, with the modifications suggested by⁴⁰. This represents an acknowledged compromise between algorithm performance and versatility. The (steady) inertia coefficient is set to 0.4, whereas the self-weight coefficient is set to 2.4 ans the social-weight coefficient to 1.3⁴⁰. The particles are initialized with the same circle packing method used for the SCM, whereas the convergence conditions are determined by a relative optimality tolerance equal to 10⁻⁴ over a 60 iterations span, consistently with the τ = 6 and J Δt = 0.1 values used to integrate the SCM.

The other benchmark method was chosen among gradient-based optimizers due to its effectiveness and reliability on unconstrained problems over bounded search spaces. MIPA optimization has been performed with the MultiStart function available in Matlab³⁹. This function provides parallel calls to the local solver Interior-Points, each associated with a starting point, then it compares the fitness of each point to estimate the location of the global optimum. The MIPA attempts a solution of the linearized problem via Newton iterations, thus relying on a second-order gradient descent method²⁷. The termination tolerance for the first-order optimality (the so called KKT residual) is set to 10⁻⁴. Gradients are estimated via forward differences with a fixed step size of 10⁻⁸, as it was found to be the asymptotical convergence value for the success rate over all tested landscapes. The MIPA has a deterministic nature, thus, it must be initialized multiple times with different starting point locations to optimize a multimodal landscape. In the present comparison, each replication was performed by picking the initial locations from a uniform random distribution. The success rate of both benchmark methods relies on the same definition used for the SCM, introduced in section 2.

Simulated marine environment

In order to recreate a realistic hydrodynamic environment we resort to high-fidelity sea current models. The most widespread coastal ocean circulation models are fully-baroclinic and rely on the hydrostatic and Boussinesq approximations⁴¹. The circulation field has been simulated across the entire Taranto Gulf. It is forced by well-established, high-fidelity, data-assimilative modeling products, specifically by atmospheric data from the ECMWF-IFS analysis⁴² (https://www.ecmwf.int/en/forecasts/datasets/set-i#I-i-a) at the surface and by reanalysis data from the Mediterranean Sea provided by the Copernicus Marine Service⁴³ (https://data.marine.copernicus.eu/product/MEDSEA_MULTIYEAR_PHY_006_004) at the open-ocean boundary. The Taranto Gulf modeling system is also set in operational forecasting mode, and a glimpse of the forecasts over the area can be observed at the website https://taranto.cmcc.it/. The core model is SHYFEM (System for HYdrodynamic Finite Element Modules)^44,45, an unstructured-grid finite-element model based on a layer-integrated approach to the primitive equations, where the fluid is discretized into vertical layers of specific thickness in which the variables are considered to be constant (e.g., 2m thickness at layer depths between 4 and 6 meters, where the AUV dynamics are simulated). Turbulence is modeled by means of the Smagorinsky’s approach⁴⁶, in conjunction with the GOTM k − ω model⁴⁷ for the parameterization of the horizontal and vertical eddy viscosity. Details on the hydrodynamic formulation, as well as the discretization, can be found in^48,49,50, whereas the software is publicly available at⁵¹https://zenodo.org/records/5596734. An animated version of the simulated current used for the coupled swarm-AUV test is available in Supplementary movie 8.

We recall that the scope of hydrodynamic simulation is to provide a realistic transport scenario for an initial landscape function and compute the drag force on the swimmer with space and time variability. We collect current fields in the 4–6 m depth layer with hourly frequency for 5 days. Thus, we model the transport of a passive scalar function ψ, which plays the role of a dynamic landscape function in the swarm scenario, by solving on the chosen depth layer the two-dimensional transport equation:

$$\frac{\partial \psi }{\partial t}+{{\bf{u}}}\cdot \nabla \psi={k}_{H}{\nabla }^{2}\psi,$$

(11)

with homogeneous Neumann boundary conditions, i.e., n ⋅ ∇ ψ `= 0. In Eq. (11) the vector u denotes the local current, whereas k_H is the horizontal eddy diffusivity.

The planar transport hypothesis holds due to the stratified solution obtained for regional sea currents, which typically entails a vertical momentum exchange orders of magnitude lower than the horizontal one. Given the domain scale, we neglect the molecular diffusivity of the mean while relying on the gradient diffusion hypothesis (with constant coefficients) to describe the turbulent diffusion process⁴¹. The eddy horizontal diffusivity takes value k_H = 0.2 m²/s, according to experimental measurements^52,53 in coastal areas with low wave orbital velocity.