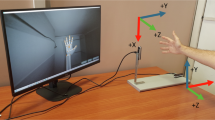
Abstract
The anthropomorphic hand plays a crucial role in human-machine interaction tasks. However, there are very few hands that realize multimodal perception with high degrees of freedom (DOF) in a low-cost way. Here, we present a dexterous hand that achieves multimodal sensing solely through a camera. The hand has 18 DOF but does not require any position or force sensors, making it cost-effective and easy to manufacture. We develop an integrated forearm for the hand that provides both actuation and multimodal sensing information simultaneously. This includes the 18 joint angles, 5 fingertip positions and contact forces, and information on object softness and contour. The core principle of perception is that the camera can track the displacement and tension of all tendons simultaneously. The multimodal perception model is developed by characterizing tendon properties and coupling them with the hand dynamics. Experiments indicate that our hand has potential in multimodal sensing and dexterity.
Similar content being viewed by others
Introduction
The uncertainty of unstructured environments presents a significant challenge for robots1. To enable versatile and precise manipulation in complex environments, numerous anthropomorphic hands have been developed for applications2,3, such as human-robot interaction4,5,6,7, as well as in industrial8,9,10,11,12 and medical prosthetics13,14,15. Among these, the Shadow Hand16,17, widely used by researchers, provides unprecedented accuracy and dexterity due to its ultra-high degrees of freedom (DOF) and numerous sensors for position, pressure, torque, and temperature18.
However, the increasing DOF in robotic systems proportionally amplify the demand for force and position sensors. This growth introduces three key challenges19: integration complexity (e.g., sensor mounting constraints, wires, and communication protocols); changes in finger dynamics; and higher costs. Therefore, achieving low-cost, human-like sensory capabilities remains a significant challenge for robotic hands. The human hand perceives information from the surrounding environment through three primary sources: sensory receptors in the skin, proprioceptive inputs from muscles and joints, and centrally-originating signals20. To reduce dependency on the number and variety of sensors, an effective approach is to use multimodal sensors that integrate proprioception and tactile sensing.
With advancements in neuroscience, information science, and new materials and sensors21, numerous sensor mechanisms have been developed to simultaneously measure proprioception (such as strain and bending) and tactile information (such as contact force). Examples include those based on conductive textile22, e-skin23,24,25, triboelectric nanogenerators (TENGs)26, liquid metal27, ionic liquid28, ionogel (printed)29, nanocomposite30,31,32, smart braid33,34,35, waveguide36,37 and heterogeneous sensing38. Among these, sensors based on optical waveguides have been integrated into soft prosthetic hands36 to perceive curvature, elongation, and tactile information. Although tactile sensing is limited to single-point pressure at the fingertips and relies on complex circuitry and wiring, it has already demonstrated the potential for multimodal perception.
Another category of multimodal sensing approaches involves vision-based tactile sensors. These sensors primarily utilize cameras to capture images of contacted objects, and subsequently leverage image recognition techniques to extract tactile information, which serves as feedback for robotic manipulation39,40,41,42,43. Representative sensors include GelForce44,45, Gelsight46, TacTip47, GelSlim48,49, which can achieve texture recognition50, grasping forces51, and temperature sensing52. However, the perceptual information from these sensors is typically limited to the fingertips and constrained by manufacturing processes and size, potentially interfering with the dynamics at the fingertips.
Integrating the drive components with multimodal sensing components could be a promising solution53,54, as this would reduce the impact (such as wiring, size, mechanism dynamics, and maintainability) of sensors on the robot’s body. The drive components of DLR hand include 38 flexible antagonistic spring element (FAS) sensors used to obtain tendon tension55. Another tendon-based robotic hand56 utilizes motor rotary encoders to indirectly measure tendon length and tension. However, this approach requires the installation of sensors for each drive component, which increases the size and complexity of the drive components.
The integration of visual systems with drive components may address this challenge57,58. The vision camera offering the high resolution and low cost, can also observe all drive components in the field of view at the same time. It can therefore reduce the number of sensors on the drive components. A passive soft hand without drive components is proposed, utilizing cameras to simultaneously track markers on each tendon to obtain tendon length and tension59, which are used to estimate hand posture and external forces. In previous work60, we explored the potential of visual integration in a fully actuated finger, achieving proprioception (joint angles) and external sensing (joint torques).
In this work, we propose a low-cost, high-DOF and vision-based multimodal sensing hand (VMS Hand). It consists of an actuation-perception forearm and modular fingers that do not require any sensor installation (Fig. 1a), facilitating easy manufacturing and maintenance. The actuation-perception forearm utilizes a monocular camera to achieve multimodal sensing (Fig. 1b) for the dexterous hand manipulation (Fig. 1c), capturing the 18 joints angles (Fig. 1d), external torques (Fig. 1e), positions and contact forces at 5 fingertips (Fig. 1f), as well as the softness and contour of contacted objects. We conducted various experiments on position and force to evaluate its sensing capabilities and dexterity. The vision-based approach eliminates the need for traditional position/force sensors on the fingers, significantly reducing sensing complexity and cost compared to traditional robotic hands (see Supplementary Tables 1, 2).
a The vision-based multimodal sensing (VMS) hand mechanism design. Left: Comparison between our VMS hand and the human hand (reproduced with permission from Alamy Stock Photo). The VMS hand uses a motor-tendon system to mimic the muscle (red) and tendon (white) mechanism. The VMS hand captures information with a camera and sends image to the controller, while human hand sensory signals are transmitted to the brain via nerves (yellow). Right: the VMS hand prototype, fitted with a 3D printed enclosure. The exposed fingers indicates that there are no sensors attached to the fingers. b Principle of multimodal perception. During hand movement, a camera continuously tracks the reflective markers at both ends of each tendon-connected spring, capturing changes in tendon length and tension. This data is then integrated into a multimodal model to provide information on position, force, and object properties. c Demonstration of hand grasping capabilities: precise grasp (ball) and power grasp (bottle). d Demonstration of hand perception capabilities. While performing a manipulation task (e.g., grasping a bottle), the multimodal perception model provides real-time feedback on joint angles (left), external torque (center), and fingertip contact force (right).
Results
Integrated actuation-perception hand design
The VMS Hand mimics the human hand’s structure, comprising a forearm, palm, five fingers, and a 3D-printed enclosure, as shown in Fig. 1a. The forearm integrates a motor-tendon actuation system that replicates the muscle-tendon transmission mechanism of the human hand61. Compliant force transmission is achieved via springs62, mimicking the connective tissue membranes in biological muscle-tendon systems. Inspired by neural tactile signal transmission in humans, the VMS Hand embeds a monocular camera in the forearm assembly. This camera captures real-time tendon motion images (see Fig. 1b and Supplementary Movie 1), which are processed by perception algorithms to extract multimodal information (e.g., contact forces, joint angles).
The VMS Hand comprises 18 DOF, with its forearm controlling hand movements through 13 active tendons (Fig. 2a). The layout of the active tendons is shown in Fig. 2b. The forearm integrates 13 modular actuation units and a camera to achieve actuation and perception (Fig. 2c). Each actuation unit’s core component is a tension spring that serves dual functions: mechanically transmitting motor power to the tendon system while simultaneously reflecting tendon tension information through its own deformation. To enable a monocular camera to observe all spring deformations, the 13 actuation units are arranged in a circular pattern. Each actuation unit is equipped with a planar mirror angled at 45 degrees relative to the spring plane (Fig. 2d), allowing the camera to capture virtual images of all springs through mirror reflections.
a Overview of the VMS hand in which the forearm integrating 13 actuation units controls 5 fingers via 13 active tendons. The palm is connected to the forearm by four connecting rods. Motion-coupling tendons on the fingers enable synergistic movement between the proximal interphalangeal (PIP) and distal interphalangeal (DIP) joints. b Layout of the 13 active tendons in the palm. c The workflow diagram of the actuation-perception forearm mechanism. d The Schematic of an actuation unit. Motor rotation induces spring deformation \(\delta x\). Since the tendon origin is fixed to Slider-A, \(\delta m\) represents the tendon displacement. A brown arrow indicates the initial distance between Slider-A and slider-b. The plane mirror redirects markers into camera view (\({{\rm{m}}}{'}\) and \({{\rm{M}}}{'}\)). e The abduction (top) and flexion (middle) of the metacarpophalangeal (MCP) joint are controlled by 2 active tendons, and the PIP joint is controlled by 1 active tendon (bottom). f Kinematic parameters (palmar view) and reset structures (dorsal view) of the primary fingers. g The structure of the secondary fingers, which differs from the primary finger in that the MCP joint has no degrees of freedom (DOF) for abduction.
Two sliders (slider-A and slider-B) are mounted at each end of the spring, with limited movement along linear guides (see Supplementary Fig. 1a). To rapidly track positional changes at the spring ends, reflective markers are installed on the slider surfaces. Due to the spring’s initial length, slider-B’s movement would exceed the planar mirror’s effective reflection area during motion. Therefore, an additional slider-b is added to the linear guide rails and connected to slider-B via a rigid rod. Consequently, the spring’s deformation \(\delta x=\delta M-\delta m\) can be calculated as the displacement difference between slider-A and slider-b (Fig. 2d). Since the tendon origin is fixed to Slider-A, the tendon length changes are represented by the displacement \(\delta m\) of slider-A. Thus, during the dexterous hand’s motion, a monocular camera tracks in real time the displacements of the markers \({m}_{i},{M}_{i}(i=1,2,\cdots 13)\) at both ends of the springs in the 13 actuation units. These measurements are fed into the multimodal perception model, enabling real-time estimation of the hand’s position and force feedback.
Modular fingers design
The five fingers are modular, each containing three joints: metacarpophalangeal (MCP), proximal interphalangeal (PIP) and distal interphalangeal (DIP). This reduces manufacturing complexity and facilitates post-maintenance. The MCP joints of the thumb, index, and middle fingers feature two DOF enabling abduction and flexion (Fig. 2e), controlled by two active tendons with dual restoring springs on the dorsal palm for joint reset. The kinematic parameters of each finger are shown in Fig. 2f. Although sharing the same mechanical configuration, the MCP joints of the ring and little fingers are actuated by a single tendon, retaining only flexion DOF due to their auxiliary role in grasping and spatial constraints in forearm integration10,63,64 (Fig. 2g).
Based on the differences in the DOF of the MCP joints, the thumb, index finger, and middle finger are described as primary fingers, while the ring finger and little finger are referred to as secondary fingers. Considering the kinematic coupling characteristics of the PIP and DIP joints of the human hand64, the DIP joint was designed as a passive joint that moves in synchronization with the PIP via a pair of parallel tendons. This pair of parallel tendons is referred to as motion-coupled tendons, similar to the function of four-bar linkage. The PIP joint is actuated by an active tendon (Fig. 2f). Tension springs on the backs of the fingers provide the resetting function for the PIP and DIP joints.
Characterizations of the tendon elongation
There is a clear geometric relationship between the joint angles \({{\bf{q}}}\) of the dexterous hand and the ideal tendon lengths \({{\bf{l}}}\), as shown in Eq. (1). For a single tendon, since it undergoes elastic deformation when subjected to tension (Fig. 3a), the ideal tendon length \(l\) can be expressed as \(l=\delta m-\delta l\). \(\delta m\) represents the displacement of marker m (equivalent to the tendon input displacement), obtained by real-time tracking of the internal vision (see Supplementary Movie 2). \(\delta l\) denotes the elongation of the tendon itself. \(\delta l\) is related to the physical properties and tension of the tendon itself, and can thus be expressed as \(\delta l=f(\delta x)\), where \(\delta x=\delta M-\delta m\) represents the spring’s deformation.
a The relationship between tendon input displacement \(\delta m\) and output ideal length \(l\) during motion. b The relationship between joint angle and tendon displacement and velocity; the arrows indicate the trend of joint angle changes. c The relationship between \(\delta M\) and \(\delta m\) under different joint angles and contact conditions. d The results of visual recognition, where the yellow and white fonts represent the identifiers for the markers m and M on each actuation unit, respectively. The yellow line indicates the distance (\(\delta m\)) between marker m and the origin. e Tension variation along the tendon transmission path; f Visual recognition results during the pressing of the force sensor by the fingertip of the ring finger. The data within the red box indicates the length change \(\delta m\) of one tendon controlling the ring finger, and the deformation \(\delta x\) of the series-connected spring. g Fitting results of external torque \({{{\boldsymbol{\tau }}}}_{ext}\) and increment of spring deformation \(\delta {x}_{c}\) under different joint configurations.
An angle calibration platform (see Supplementary Fig. 2a) has been built to evaluate the tendon elongation. However, since the spring does not exhibit a significant change in length until the initial tension is exceeded (see Supplementary Fig. 2b, c), it becomes challenging to determine the elongation \(\delta l\) by solving the \(f(\delta x)\). Figure 3a shows that the mapping relationship between \(\delta m\) and \(l\) differs during the phases of increasing and decreasing tendon displacement. To estimate joint angle from tendon displacement \(\delta m\), tendon velocity \(\delta \dot{m}\) is used to distinguish the direction of tendon movement. The responses of joint angle relative to tendon displacement and tendon velocity are shown in Fig. 3b. Based on Eq. (1), the ideal tendon length \(l\) is geometrically related to the joint angle. Therefore, \(l\) can be expressed as:
By performing polynomial fitting on the ideal tendon length \(l\) and \((\delta m,\delta \dot{m})\), we obtained fitting function \(\varGamma (\cdot )\). Substituting Eq. (2) into Eq. (1) yields the relationship between the finger joint angles \({{\bf{q}}}\) and \((\delta {{\bf{m}}},\delta \dot{{{\bf{m}}}})\), as shown in Eq. (3). The fingertip position can be obtained from the forward kinematics model of the finger.
Characterizations of the tendon contact detection
Another additional exploration focused on the impact of finger-environment contact on tendon characteristics, as this would help the dexterous hand rely solely on internal vision to determine contact. Typically, the tendon tension will differ when the finger reaches the same joint configuration under non-contact and external force conditions, meaning that the same \(\delta m\) corresponds to different spring deformations \(\delta x\). However, when the deformation of the spring is within the dead zone (Supplementary Fig. 2b), the system cannot accurately determine contact. Fortunately, we found that the displacement \(\delta M\) of the marker at the slider-b of the spring consistently showed significant movement. Therefore, \(\delta x\) can be replaced by \(\delta M\) and apply the same approach to detect contact, can be expressed as:
where \(F(\cdot )\) represents the mapping function from \(\delta m\) to \(\delta M\) in a non-contact state. \(\delta \hat{M}\) is the predicted displacement of the marker M in the non-contact state based on \(\delta m\). Figure 3c illustrates the relationship between \(\delta M\) and \(\delta m\) at different joint configurations and contact conditions. The straight segments in the figure represent the mapping relationship between \(\delta M\) and \(\delta m\) in the non-contact state, while the three inflection points indicate instances of contact. Since the displacements of all markers (m and M) can be output by vision in real time (Fig. 3d), the contact states of the different fingers can be obtained according to Eq. (4).
Characterizations of the tendon transmission
In an ideal scenario, the relationship between fingertip force, joint torque, and tendon tension in the dexterous hand can be analyzed using classical robotic dynamics. Since the tendon is in series with the stretching spring, the input tension of the tendon can be indirectly measured through the spring deformation. However, frictional losses are inevitably present in the tendon transmission path, necessitating a quantitative analysis of these losses to determine the output tension at the tendon end.
For a joint controlled by an active tendon, the analysis of the tension transmission process is shown in Fig. 3e. When the fingertip makes contact with the environment, the torque \({\tau }_{l}^{i}\) exerted by the i-th active tendon to resist the external torque can be expressed as Eq. (5). Detailed derivation can be found in Supplementary Method 1.
Where \({t}_{c}\) represents the moment at the instant of contact; \(\delta x(t)\) represents the i-th spring deformation, derived indirectly via visual tracking of markers displacement(see Fig. 3f and Supplementary Movie 3); \(\delta {x}_{c}^{i}\) represents the deformation increment of the i-th spring after contact; \({K}_{i}=\psi (q,\mu )\) is the equivalent stiffness coefficient of the i-th series tendon spring, which is related to the joint angle \(q\) and friction coefficient \(\mu\) at the moment of contact.
Based on Eq. (5) and the finger dynamics, the external torque \({{{\boldsymbol{\tau }}}}_{ext}\) at each finger joint can be obtained, as shown in Eq. (6). Figure 3g illustrates the variation of external torque \({{{\boldsymbol{\tau }}}}_{ext}\) with increment of spring deformation \(\delta {x}_{c}\) under varying joint angle. The fingertip contact force \({{{\bf{F}}}}_{ext}={({{{\bf{J}}}}^{T})}^{{{\boldsymbol{+}}}}{{{\boldsymbol{\tau }}}}_{ext}\), where \({({{{\bf{J}}}}^{T})}^{{{\boldsymbol{+}}}}\) is the generalized inverse of the Jacobian matrix transpose.
Position perception experiment
The finger joint angles can be calculated from the marker displacement \(\delta m\) measured by the forearm-mounted camera using Eq. (3). We define the joint numbering as \({q}_{ij}\), where \(i=1,2,\ldots 5\) sequentially represents the thumb, index, middle, ring, and little finger; For primary fingers (e.g., thumb), \(j=1,2,3,4\) corresponds to the MCP abduction joint, flexion joint, PIP joint, and DIP joint respectively; For secondary fingers, \(j=1,2,3\) represents the MCP flexion joint, PIP joint, and DIP joint.
The accuracy of position perception was evaluated by 12 repetitive joint motion experiments. The camera-estimated angles \(\hat{{{\bf{q}}}}\) and encoder-measured ground truth \({{\bf{q}}}\) were synchronously recorded (see Fig. 4a and Supplementary Fig. 3). Results showed mean absolute errors of 1.14°, 1.04°, and 0.95° for the MCP abduction joint, flexion joint and PIP joint, respectively. Since the MCP abductor joint is actuated differentially by two tendons, small variations in the differential tendon lengths are amplified into larger angular deviations. Consequently, the prediction errors are further magnified. Variations in accuracy among the different joints may arise from factors such as mechanical dimensional tolerances incurred during manufacturing and calibration inaccuracies.
a Comparison of the internal perception joint angles \(\hat{{{\bf{q}}}}\) and the actual joint angles \({{\bf{q}}}\) of the VMS Hand. b Joint angle tracking response under multi-step reference signal input. c Anti-disturbance experiment during finger motion, with orange arrows indicating external disturbance directions. d The visual recognition results during the tennis ball grasping. e The time-varying joint angle profiles during the grasping task. f The three-dimensional trajectories of five fingertips throughout the grasping process. g The grasp taxonomy with all 33 standard modes.
The dexterous hand achieves closed-loop position control by real-time acquisition of joint angle feedback signals integrated with position control algorithms. As the MCP abduction and flexion joints are actuated by two coordinated tendons, the desired joint angles \({{{\bf{q}}}}_{d}\) must be converted into corresponding tendon length variation \({{{\bf{l}}}}_{d}\) to establish a decoupled joint control model. For a given set of desired joint angles \({{{\bf{q}}}}_{d}(t)\), the corresponding desired tendon length \({{{\bf{l}}}}_{d}(t)\) change can be computed using Eq. (1). Subsequently, a delay-compensated control input \({{\bf{u}}}(t)\) is constructed, as shown in Eq. (7).
where \({{{\bf{K}}}}_{f}\) is the feedforward position gain, \({{{\bf{K}}}}_{p}\) and \({{{\bf{K}}}}_{d}\) are the feedback position gain and derivative gain, respectively. \(\varsigma\) represents the system time delay calibrated via frequency response analysis or step response experiments (see Supplementary Fig. 4)
To validate the tracking performance and robustness of the proposed control system, we conducted stepped reference trajectory tracking experiments and external disturbance tests (see Supplementary Movie 4). The reference trajectory was designed as a multi-step signal with 5° increments at 1-second intervals. The angle tracking performance is shown in Fig. 4b; with the addition of the feedforward term, the tracking error decreased by 34.3% compared to the case without feedforward control (see Supplementary Fig. 5). To evaluate the anti-interference capability of system, six external force perturbations (three downward/three upward) were applied during fingertip motion (Fig. 4c). The experimental results demonstrated that the perception system could detect the position changes caused by the external disturbances. The controller promptly adjusted and restored motion to the preset target position after force removal, demonstrating the robustness and stability of the adopted control scheme.
To assess the dexterous hand’s ability to synergistically perceive angle and position, we conducted experiments with grasping a tennis ball. During the experiment, a camera on the forearm tracked the displacement of all markers in real time (Fig. 4d), enabling simultaneous monitoring of the joint angles (Fig. 4e) and the five fingertips positions (Fig. 4f). The dexterity of the VMS hand was evaluated in the standardized Feix GRASP taxonomy65 test (see Supplementary Movie 5). The VMS hand successfully implemented 33 grasping modes (Fig. 4g), including precise grasping operations requiring fingertip coordination, such as pen holding, egg pinching, and chopstick manipulation. All grasping tasks were stably executed via feedforward-feedback closed-loop control based on predefined joint angle configurations. Experimental results demonstrating the system’s adaptability in multi-scenario grasping applications.
External force perception experiment
Relying only on the information provided by the internal vision of the forearm, the VMS hand can detect contact and also provide real-time feedback on the external torques at the joints and external forces at the fingertips. To evaluate the external perception capabilities of the hand, we conducted three parts of experiments: contact detection, contact force evaluation, and object rotation experiments.
The plate was positioned above a six-dimensional force sensor, enabling the sensor to reflect changes in force during fingertip contact with the plate. Simultaneously, the actuation-perception forearm transmits \(\delta M\) and \(\delta m\) in real time to the tendon contact model (see Eq. (4)) to detect contact occurrence (Fig. 5a). This data can be compared with the force sensor measurements to validate the effectiveness of contact detection.
a Experimental results of contact detection for the ring finger; b Experimental results of contact detection for the four fingers and comparison with force sensor measurements; c External force test experimental platform (top), and visual recognition images during little finger pressure sensor measurement (bottom). d Comparison of the internal perception external torques \({\hat{{{\boldsymbol{\tau }}}}}_{ext}\) and the actual external torques \({{{\boldsymbol{\tau }}}}_{ext}\) of the little finger; e Comparison of the internal perception external forces \({\hat{{{\bf{F}}}}}_{ext}\) and the actual external forces \({{{\bf{F}}}}_{ext}\) of the little finger; f Visual tracking images during object manipulation. g Fingertip contact force variations during in-hand object rotation. h External torque variations across joints during object manipulation.
The fingertips of the index, middle, ring, and little fingers were sequentially controlled to press the plate and then return to their initial positions (see Supplementary Movie 6). The detection results and the force sensor’s response curve are shown in Fig. 5b. The results indicate that the normal force from the sensor gradually increased upon fingertip contact with the tray and decreased as the fingertips returned to the initial position. During this process, our measurement system also detected fingertip contact in real time, consistent with the trends observed in the force sensor data.
In the characterization of tendon transmission, we calibrated the friction coefficient \(\mu\) and \({K}_{1}\) for each tendon during the transmission process. In this experiment, we controlled the little finger to press the six-dimensional force sensor under different joint configurations to evaluate the measurement capabilities of external torques and contact forces (see Supplementary Movie 7). The experimental setup was shown in Fig. 5c. During the experiment, the six-dimensional force sensor provided real-time outputs of the external force \({{{\bf{F}}}}_{ext}^{6{{\rm{x}}}1}\) applied by the fingertip. The \(\delta m\) output from the actuation-perception forearm was used to measure the joint configuration \({{\bf{q}}}\) and calculate the Jacobian matrix \({{\bf{J}}}\), while \(\delta x\) was substituted into Eq. (6) to measure the joint external torque \({\hat{{{\boldsymbol{\tau }}}}}_{ext}\) and the fingertip contact force \({\hat{{{\bf{F}}}}}_{ext}={({{{\bf{J}}}}^{T})}^{-1}{\hat{{{\boldsymbol{\tau }}}}}_{ext}\). The actual external torque is given by \({{{\boldsymbol{\tau }}}}_{ext}={{{\bf{J}}}}^{T}{{{\bf{F}}}}_{ext}\).
The relationship between external torque and fingertip contact force with the increment of spring deformation after contact for different joint configurations is shown in Fig. 5d and Fig. 5e, respectively. Experimental results indicate that our measurement model effectively characterizes the transmission properties of tendons at various contact angles. The maximum error in the normal contact force during the experiment reached 0.49 N. The errors in contact force may arise from angle inaccuracies, internal visual recognition errors, and calibration errors in the friction coefficient. The actuation-perception base can output not only the normal force \({F}_{z}\) but also the tangential force \({F}_{x}\), which aids in slip detection during grasping tasks.
The position sensing capability of the dexterous hand during grasping ((Fig. 4e, f) and its flexibility (Fig. 4g) have been demonstrated. To further showcase the hand’s external force sensing ability, an in-hand object rotation experiment was designed (see Supplementary Movie 8). First, a stable grasp of the object is achieved using a preset grasping configuration. Then the tension of the ring and little finger tendons were increased to enhance fingertip contact pressure and induce object rotation. Figure 5f illustrates the visual-tracked spring deformation variations during object manipulation. The dynamic profiles of fingertip output forces and joint external torque for the ring and little fingers are shown in Fig. 5g and Fig. 5h, respectively. Experimental results demonstrate that the vision-based multimodal perception scheme can achieve real-time monitoring of joint torque and fingertip contact force changes. With this information, the hand has the potential to perform various complex tasks, including object manipulation, in-hand repositioning, multi-finger coordination, force control, haptic feedback integration, adaptive grasping, and tool use.
Active tactile perception
Tactile feedback allows robotic hands to assess the physical properties of objects, including softness and surface texture, facilitating the adjustment of grasping force and posture to optimize manipulation task performance. To validate the active tactile sensing capability of the VMS hand, experiments for softness detection and contour recognition were designed.
The robotic hand quantifies object softness by measuring differences in compression displacement. Its principle is that when the fingertip applies the same force to surfaces of varying softness, the surfaces produce different compression displacements due to differences in material compliance. When a fingertip is controlled by a single tendon, the time point of contact detection is defined as \({t}_{c}\). We define the force applied by the fingertip as positively correlated with the deformation of the spring after contact, represented as \(\delta {x}_{c}=\delta x-\delta x({t}_{c})\). Additionally, the compression displacement of the fingertip is positively correlated with the displacement of the tendon after contact, denoted as \(\delta {m}_{c}=\delta m-\delta m({t}_{c})\). Thus, the softness of the object can be defined as \({K}_{obj}=\delta {x}_{c}/\delta {m}_{c}\).
A validation experiment was conducted using three representative materials (wood, foam, and sponge) to evaluate tactile softness perception (see Supplementary Movie 9). During the experiment, pressure was applied to the materials by independently adjusting the tendon tension of the middle finger PIP joint, while maintaining the same pressing speed for all materials. The states of the middle finger pressing the surfaces of the wood block, foam block, and sponge block are shown in Fig. 6a. The vision system within the actuation-perception forearm continuously provides real-time feedback on \(\delta x\) and \(\delta m\), with the recognition results shown in Fig. 6b. Based on \(\delta m\), \(\delta x\) and the contact moment \({t}_{c}\), the relationship between \(\delta {x}_{c}\) and \(\delta {m}_{c}\) can be obtained, as shown in Fig. 6c. The slope of this curve reflects the softness \({K}_{obj}\). As expected, the experimental data indicate a decreasing order of softness: wood block, foam block, and sponge block. It is noteworthy that since the fingertip shell itself deforms under pressure, employing shell materials with higher Shore hardness may improve softness detection performance (see Supplementary Fig. 6).
a The fingertip of the middle finger presses against the states of wood, foam, and sponge; b The visual recognition images and output displacement information (\(\delta x\) and \(\delta m\)), when the fingertip presses against different objects; c The curves of \(\delta {x}_{c}\) and \(\delta {m}_{c}\) during the pressing of different objects, where the slope reflects the softness of the target; d Detection of the contours of objects at different heights (above) and the scanning results (below); e Detection of the contour of a stapler (above) and the scanning results (below); f Detection of the contour of a mouse (above) and the scanning results (below).
When external visual and laser radar devices reconstruct the shape of objects, they may encounter occlusions. Using tactile devices to touch occluded surfaces could address this challenge. Here, since the actuation-perception forearm can provide contact force detection and fingertip position information, we utilize the fingertips as tactile sensors to identify the object contours. The coordinate systems of the robotic arm and hand are unified into the world coordinate system (Fig. 6d). This ensures that when the robotic arm moves horizontally (along the negative z-axis) to scan the object surface, the fingertip position is referenced to the world coordinate system rather than the hand base.
The object surface was positioned directly beneath the palm to ensure contact detection during finger flexion (see Supplementary Movie 10). Initial contact triggers spatial registration between fingertip coordinates and surface contact points. Upon contact detection, the 3D position was recorded, followed by controlled negative z-axis arm motion for continuous contour mapping. Using this approach, we tested the fingers’ ability to recognize surface contours of step heights (Fig. 6d). The VMS hand could also distinguish the shapes of irregular objects, such as stapler (Fig. 6e) and computer mouse (Fig. 6f). While the accuracy and sensitivity of the VMS hand remain inferior to human hand capabilities, it has already demonstrated potential in shape reconstruction.
Discussion
In this paper, we propose the VMS hand that offers low cost, multimodal perception, and dexterity. The fingers are modular and do not require the installation of any position sensors or expensive force sensors. Therefore, they are easy to manufacture and maintain, making them suitable for harsh environments (such as tasks involving high electromagnetic interference or grasping sharp objects). Due to the hand’s cost-effectiveness (see Supplementary Table 1), we believe it will have a wide range of applications, such as in industrial humanoid robots and prosthetic hands.
The proposed vision-based multimodal sensing scheme has been validated through a series of positional, external force, and tactile experiments. It demonstrates two core advantages: First, the sensing cost is cost effective, accounting for only 6% of the total system cost (see Supplementary Table 2). The cost advantage becomes more pronounced as the number of DOF increases. Second, it simplifies manufacturing and maintenance processes. Compared to flexible electronic sensing requiring sophisticated fabrication techniques, the core components of this vision-based solution are easily accessible and assembled using common materials such as springs, tendons, planar mirrors, and a camera. Moreover, the vision-based sensing scheme can be adapted to other mechanisms, including tendon-driven robotic arms and cranes.
While the VMS hand demonstrates significant potential in terms of cost and sensing capabilities, there remain areas that require further enhancement. First, the flexibility could be enhanced by increasing the DOF of the wrist. The actuation and sensing components for the wrist could be integrated into the existing forearm, requiring only adjustments to size and camera field of view. Second, the selection of camera and actuator has a significant impact on forearm size. Parameters including the lens’s minimum working distance, camera resolution, and frame rate influence forearm size and weight. Meanwhile, the current servo motors’ bulky size leads to excessive actuator layout space consumption. Adopting smaller brushless DC motors could improve forearm compactness.
The spatial separation between actuators and sensors introduces non-collocation challenges. While the feedforward control law mitigates this issue for predefined trajectory tracking tasks, advanced control strategies (e.g., adaptive control66) should be explored to enable dexterous manipulation in complex scenarios. Furthermore, the current sensing accuracy remains inferior to specialized sensors. Integrating precise physical models with machine learning techniques or enhancing calibration methods (e.g., self-calibration67) could further improve perception accuracy.
Methods
Objectives and design of the study
Our objective is to develop a dexterous hand system that combines multimodal perception with low cost, demonstrating the feasibility of a vision-based integrated actuation-perception approach. Due to the high resolution and wide field of view of the vision camera, the advantages of the integrated actuation-perception scheme become more pronounced as the robot’s DOF increase. We designed an actuation unit composed of commonly used materials such as motor, springs, reflective markers, and planar mirrors, making it easy to manufacture and maintain. Thirteen actuation units are arranged in a circular array, with a low-cost industrial camera mounted on the base of the actuation units to capture the deformation of the springs across all units. The dexterous hand is designed to be tendon-driven, allowing for high flexibility and intrinsic compliance controlled by the actuation units. Thorough exploration of the spring deformation data helps us gather valuable information about the dexterous hand, such as joint angles and fingertip forces.
Fabrication of actuation units
The actuation unit of the finger is designed to be modular, consisting of a planar mirror bracket, planar mirror, linear guides, bearing carriage, springs, tendons, wire spools (radius = 10 mm), servo motor, and mounting plate, as shown in Supplementary Fig. 1a. To minimize the weight of the module, we adopted a hollow design for the mounting plate, retaining only the necessary components to secure the servo motor, linear guides, and planar mirror bracket. Two linear guides are fixed to the mounting plate by a guide rod support, allowing the springs to stretch axially. The servo motor drives the rotation of the wire spools, which in turn stretches the tendons and the springs. The ends of the springs are secured to two sliders, with reflective circular markers mounted on their surfaces for camera recognition. The planar mirror is mounted on a bracket that is inclined at a 45-degree angle to the mounting plate, ensuring that the virtual image of the reflective markers in the mirror forms a 90-degree angle with the mounting plate.
Fabrication of actuation-perception forearm
To reduce the overall size of the forearm part, we arranged the 14 actuation units in a circular pattern and fixed them to a circular base (Supplementary Fig. 1b). The 14th actuation unit is reserved for potential future use to add DOF. It will serve as a backup for future enhancements in DOF. We designed a circular PCB that facilitates 16-channel PWM output and manages the power supply for the entire system. A mini-industrial camera (201 fps at 1280 × 1024 Mono 8, 1.5 W at 5 VDC) is positioned at the center of the circular circuit board to track the reflective markers on the actuation units. The parameters of the camera and lens are shown in Supplementary Table 3. A circular LED light source is fixed to the mounting plate for illumination.
The circular PCB is secured to the mounting plate of the actuation units using screws. A cooling fan is mounted on the upper circular base to dissipate heat from the camera and circuit board. To prevent interference from external light fluctuations during recognition, a 3D-printed circular enclosure is installed on the forearm, with ventilation holes designed to ensure heat dissipation.
Fabrication of finger
Each finger is modular, featuring identical structural designs as illustrated in Fig. 2b. After assembling the fingers, one end of the tendon is anchored to the joint, then routed through the pulley system on the palm to connect with the forearm. The material properties of the tendon are shown in Supplementary Table 4. To minimize losses during the tendon transmission process, ball bearings are installed on each pulley. To avoid coupling between the MCP and PIP joints, the tendon controlling the motion of the PIP joint is routed through the axis of the MCP joint and ultimately connected to the actuation unit. Except for the restoring spring in the MCP joint of the thumb, the restoring springs for all other joints are mounted on the dorsal side of the palm and fingers. The bottom of the restoring springs is secured to the palm with a rectangular base, which has two screws to adjust the pre-tension of the return springs. The palm of the dexterous hand is fixed to the upper surface of the arm using four aluminum alloy rods. Both the palm and finger components are machined from aluminum alloy to ensure structural durability, while the enclosures of the forearm and finger adopt 3D-printed components (black resin) for cost efficiency and weight reduction.
Visual recognition
The basic principle of camera recognition for circular reflective markers is contour detection. This is achieved by detecting changes in the gradient of image grayscale values to extract variations in the center pixel. We utilized OpenCV to implement this fundamental function. The real challenge lies in quickly tracking the pixel changes of 26 reflective markers, which is crucial for real-time control. To address this, we adopted an image segmentation and multithreaded concurrent processing approach, dividing the camera image into four rectangular regions and performing contour detection in each of the four threads. Finally, the pixel coordinates of all the markers are output in sequence to the controller.
Camera calibration
Typically, a monocular camera can only output two-dimensional pixel coordinates and pixel distances. To obtain physical distances, we place all detected targets on the same plane, allowing us to calibrate the scaling factor between pixel distance and actual distance. First, before mounting the camera to the forearm, we perform intrinsic calibration using Zhang’s checkerboard method to correct image distortion.
Subsequently, the camera is fixed to the mounting plate inside the forearm, ensuring its optical axis remains parallel to the spring plane. We adjust the optical path using a planar mirror to ensure that the virtual image plane of all reflective markers is perpendicular to the camera’s optical axis. Since the actuation units are arranged in a circular layout and the mirror brackets are uniformly installed, the virtual images remain coplanar, establishing a fixed proportional relationship between single-pixel distance and real-world distance. Finally, since slider B and slider b are rigidly connected by a rod, the actual distance between them is known and can be used to calculate the scaling factor K (K = actual distance / pixel distance), thereby completing the calibration.
Characterization of the tendon elongation
We installed angle encoders (AS5600, 12-bit) on the joints of the fingers and obtained the actual angle through PWM sampling at 100 Hz (see Supplementary Fig. 3a), which was then sent to the dexterous hand’s controller through the Serial protocol. The actual angle can be converted to the tendon output displacement \(l\) by Eq. (1). Note that the angle encoders will be removed once tendon calibration is complete. The tendon input displacement \(\delta m\) is provided by feedback from the actuation-perception forearm at a frequency of 150 Hz. By controlling the position of the servo motor, the joint angle is rotated to its maximum angle and then returned to the starting position, with tendon displacement \(\delta m\) and joint angles recorded in real-time. The tendon displacement \(\delta m\) was filtered using a Butterworth low-pass filter (cut-off frequency: 50 Hz), and tendon velocity \(\delta \dot{m}\) was derived through differentiation of displacement followed by moving average filtering (window length: 35). To establish a mapping model \(\varGamma (\cdot )\) between joint angles and tendon parameters, the linear polynomial regression model was employed for functional fitting.
Characterization of the tendon contact detection
In order to obtain the relationship between the marker \(m\) and \(M\) during free motion, we control the joint angle of the hand from 0 to the maximum angle and record the displacement \((\delta m,\delta M)\) during the motion. The mapping function \(F(\cdot )\) from \(m\) and \(M\) is obtained through cubic polynomial fitting.
Characterization of the tendon transmission
We developed a force measurement platform (Supplementary Fig. 7a), where a six-dimensional force sensor (K6D40, 50 N) is mounted on the surface of the platform. The specific parameters of the force transducer are shown in the Supplementary Table 5. The height of the platform can be adjusted using a knob, allowing us to configure the fingers to apply pressure to the force sensor at different joint configurations. The external force \({{{\bf{F}}}}_{ext}\) applied by the fingertip is provided by feedback from the force sensor, while the camera outputs the spring deformation \(\delta x\) in real time. The signals from the six-dimensional force sensor are converted to digital values using a high-precision digital amplifier (GSV-8) and are ultimately transmitted to the dexterous hand’s controller via a Serial protocol at a frequency of 500 Hz. The joint angle is calculated by substituting the displacement \(\delta m\) from the base into the position measurement model, as shown in (3). For each joint controlled by active tendons, control the fingertip to press the six-dimensional force sensor in five different joint configurations, and record the spring deformation \(\delta x\), joint angle \(q\), and external torque \({{{\boldsymbol{\tau }}}}_{ext}={{{\bf{J}}}}^{T}{{{\bf{F}}}}_{ext}\) during the experiment (Supplementary Fig. 7b). The gray wolf optimization algorithm is used to fit the multi-objective optimization function \(\psi (\cdot )\).
Data acquisition and processing
The controller of the dexterous hand system utilizes an NVIDIA Xavier NX board to run the visual detection and motion control programs. The only input source is a monocular camera, connected to the controller via USB 3.0 for communication and power supply. The motion control program sends commands to the circular PWM circuit board through a serial port with a baud rate of 115200, operating at a communication frequency of 100 Hz. Upon receiving the commands, the PWM circuit board outputs 13 PWM signals to the servos. The camera can achieve a frame rate of 150 fps in RGB image output mode, and the optimized visual processing program allows for real-time processing of each frame.
Data availability
All data supporting the findings of this study are available within the article and its supplementary files. Source data are provided with this paper.
Code availability
All the relevant codes can be directed to, and will be fulfilled by, the corresponding authors.
References
Cui, J. & Trinkle, J. Toward next-generation learned robot manipulation. Sci. Robot. 6, eabd9461 (2021).
Billard, A. & Kragic, D. Trends and challenges in robot manipulation. Science 364, eaat8414 (2019).
Piazza, C., Grioli, G., Catalano, M. G. & Bicchi, A. A century of robotic hands. Annu. Rev. Control, Robot., Auton. Syst. 2, 1–32 (2019).
Kim, U. et al. Integrated linkage-driven dexterous anthropomorphic robotic hand. Nat. Commun. 12, 7177 (2021).
Cerruti, G., Chablat, D., Gouaillier, D. & Sakka, S. ALPHA: A hybrid self-adaptable hand for a social humanoid robot. In 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 900–906 (IEEE, 2016).
Schmitz, A. et al. Design, realization and sensorization of the dexterous iCub hand. In 2010 10th IEEE-RAS International Conference on Humanoid Robots, 186–191 (IEEE, 2010).
Prensilia. IH2 Azzurra Series Self-Contained Robotic Hand Basic User Guide, https://www.prensilia.com/wp-content/uploads/support/doc/PRENSILIA_IH2_basic_12.pdfA3 (2025).
Butterfass, J., Grebenstein, M., Liu, H. & Hirzinger, G. DLR-Hand II: next generation of a dextrous robot hand. In Proceedings 2001 ICRA. IEEE International Conference on Robotics and Automation (Cat. No.01CH37164), Vol. 101, 109–114 (IEEE, 2001).
Liu, H. et al. Multisensory five-finger dexterous hand: The DLR/HIT Hand II. In 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, 3692–3697 (IEEE, 2008).
Bridgwater, L. B. et al. The Robonaut 2 hand - designed to do work with tools. In 2012 IEEE International Conference on Robotics and Automation, 3425–3430 (IEEE, 2012).
Inspire-robots. The-dexterous-hands:RH56BFX, https://en.inspire-robots.com/product-category/the-dexterous-hands (2025).
seedrobotics. RH8D Hand, https://www.seedrobotics.com/rh8d-adult-robot-hand (2025).
Gu, G. et al. A soft neuroprosthetic hand providing simultaneous myoelectric control and tactile feedback. Nat. Biomed. Eng. 7, 589–598 (2023).
George, J. A. et al. Biomimetic sensory feedback through peripheral nerve stimulation improves dexterous use of a bionic hand. Sci. Robotics 4 https://doi.org/10.1126/scirobotics.aax2352 (2019).
Yang, H. et al. A lightweight prosthetic hand with 19-DOF dexterity and human-level functions. Nat. Commun. 16, 955 (2025).
Andrychowicz, M. et al. Learning dexterous in-hand manipulation. Int. J. Robot. Res. 39, 3–20 (2020).
Charlesworth, H. J. & Montana, G. Solving challenging dexterous manipulation tasks with trajectory optimisation and reinforcement learning. In International Conference on Machine Learning, 1496–1506 (PMLR, 2021).
shadowrobot. Shadow Hand, https://www.shadowrobot.com/dexterous-hand-series/ (2025).
Wang, H., Totaro, M. & Beccai, L. Toward perceptive soft robots: progress and challenges. Adv. Sci. 5, 1800541 (2018).
Li, Y. et al. A survey of multifingered robotic manipulation: biological results, structural evolvements, and learning methods. Front Neurorobotics 16, 843267 (2022).
Majidi, C. Soft sensors that can feel it all. Sci. Robot. 5, eabf0894 (2020).
Seong, J., Lee, J.-H. & Han, M.-W. Soft sensors via conductive textile stitching: enabling strain, tactile, and volumetric sensing. Adv. Mater. Technol. 10, 2401306 (2025).
Guo, X., Sun, Z., Zhu, Y. & Lee, C. Zero-biased bionic fingertip e-skin with multimodal tactile perception and artificial intelligence for augmented touch awareness. Adv. Mater. 36, 2406778 (2024).
Lee, G. et al. Fingerpad-inspired multimodal electronic skin for material discrimination and texture recognition. Adv. Sci. 8, 2002606 (2021).
Liu, Z. et al. A three-dimensionally architected electronic skin mimicking human mechanosensation. Science 384, 987–994 (2024).
Zhao, X., Sun, Z. & Lee, C. Augmented tactile perception of robotic fingers enabled by AI-enhanced triboelectric multimodal sensors. Adv. Funct. Mater. 34, 2409558 (2024).
Morrow, J. et al. Improving soft pneumatic actuator fingers through integration of soft sensors, position and force control, and rigid fingernails. In 2016 IEEE international conference on robotics and automation (ICRA), 5024–5031 (IEEE, 2016).
Park, Y.-L., Majidi, C., Kramer, R., Bérard, P. & Wood, R. J. Hyperelastic pressure sensing with a liquid-embedded elastomer. J. Micromech. Microeng. 20, 125029 (2010).
Truby, R. L. et al. Soft somatosensitive actuators via embedded 3D printing. Adv. Mater. 30, 1706383 (2018).
Yang, Y. & Chen, Y. Innovative design of embedded pressure and position sensors for soft actuators. IEEE Robot. Autom. Lett. 3, 656–663 (2017).
Rocha, R. P., Lopes, P. A., De Almeida, A. T., Tavakoli, M. & Majidi, C. Fabrication and characterization of bending and pressure sensors for a soft prosthetic hand. J. Micromech. Microeng. 28, 034001 (2018).
Zhang, H. & Wang, M. Y. Multi-axis soft sensors based on dielectric elastomer. Soft Robot. 3, 3–12 (2016).
Felt, W. & Remy, C. D. Smart braid: air muscles that measure force and displacement. In 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, 2821–2826 (IEEE, 2014).
Felt, W., Chin, K. Y. & Remy, C. D. Smart braid feedback for the closed-loop control of soft robotic systems. Soft Robot. 4, 261–273 (2017).
Felt, W., Chin, K. Y. & Remy, C. D. Contraction sensing with smart braid McKibben muscles. IEEE/ASME Trans. Mechatron. 21, 1201–1209 (2015).
Zhao, H., O’Brien, K., Li, S. & Shepherd, R. F. Optoelectronically innervated soft prosthetic hand via stretchable optical waveguides. Sci. Robot. 1, eaai7529 (2016).
Thuruthel, T. G., Shih, B., Laschi, C. & Tolley, M. T. Soft robot perception using embedded soft sensors and recurrent neural networks. Sci. Robot. 4, eaav1488 (2019).
Kim, T. et al. Heterogeneous sensing in a multifunctional soft sensor for human-robot interfaces. Sci. Robot. 5, eabc6878 (2020).
Ito, Y., Kim, Y., Nagai, C. & Obinata, G. Shape sensing by vision-based tactile sensor for dexterous handling of robot hands. In 2010 IEEE International Conference on Automation Science and Engineering, 574–579 (IEEE, 2010).
Lambeta, M. et al. DIGIT: a novel design for a low-cost compact high-resolution tactile sensor with application to in-hand manipulation. IEEE Robot. Autom. Lett. 5, 3838–3845 (2020).
Qu, J. et al. Recent progress in advanced tactile sensing technologies for soft grippers. Adv. Funct. Mate. 33. https://doi.org/10.1002/adfm.202306249 (2023).
Yamaguchi, A. & Atkeson, C. G. Recent progress in tactile sensing and sensors for robotic manipulation: can we turn tactile sensing into vision? Adv. Robot. 33, 661–673 (2019).
Yamaguchi, A. & Atkeson, C. G. Tactile Behaviors with the Vision-Based Tactile Sensor FingerVision. Int. J. Hum. Robot. 16, https://doi.org/10.1142/s0219843619400024 (2019).
Vlack, K. et al. GelForce: A traction field tactile sensor for rich human-computer interaction. In IEEE Conference on Robotics and Automation, 2004. TExCRA Technical Exhibition Based, 11–12 (IEEE, 2004).
Vlack, K. et al. in CHI ‘05 Extended Abstracts on Human Factors in Computing Systems 1154–1155 (Association for Computing Machinery, Portland, OR, USA, 2005).
Yuan, W., Dong, S. & Adelson, E. H. GelSight: high-resolution robot tactile sensors for estimating geometry and force. Sensors 17, https://doi.org/10.3390/s17122762 (2017).
Ward-Cherrier, B. et al. The TacTip family: soft optical tactile sensors with 3d-printed biomimetic morphologies. Soft Robot. 5, 216–227 (2018).
Donlon, E. et al. GelSlim: a high-resolution, compact, robust, and calibrated tactile-sensing finger. In 25th IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 1927–1934 (IEEE, 2018).
Taylor, I. H., Dong, S., Rodriguez, A. & IEEE. GelSlim 3.0: High-Resolution Measurement of Shape, Force and Slip in a Compact Tactile-Sensing Finger. In IEEE International Conference on Robotics and Automation (ICRA), 10781–10787 (IEEE, 2022).
Fang, B. et al. A dual-modal vision-based tactile sensor for robotic hand grasping. In 2018 IEEE International Conference on Robotics and Automation (ICRA), 4740-4745 (IEEE, 2018).
Fang, B., Xue, H., Sun, F., Yang, Y. & Zhu, R. A cross-modal tactile sensor design for measuring robotic grasping forces. Industrial Robot: the international journal of robotics research and application 46, 337–344 https://doi.org/10.1108/IR-08-2018-0175 (2019).
Sun, F., Fang, B., Xue, H., Liu, H. & Huang, H. A novel multi-modal tactile sensor design using thermochromic material. Sci. China Inf. Sci. 62, 214201 (2019).
Zhou, J. et al. A proprioceptive bellows (PB) actuator with position feedback and force estimation. IEEE Robot. Autom. Lett. 5, 1867–1874 (2020).
Lee, H. C. et al. A fabrication strategy for millimeter-scale, self-sensing soft-rigid hybrid robots. Nat. Commun. 15, 8456 (2024).
a, hFriedl, W., Chalon, M., Reinecke, J. & Grebenstein, M. FAS A flexible antagonistic spring element for a high performance over. In 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, 1366–1372 (IEEE, 2011).
Ogahara, Y., Kawato, Y., Takemura, K. & Maeno, T. A wire-driven miniature five fingered robot hand using elastic elements as joints. In Proceedings 2003 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2003) (Cat. No.03CH37453), Vol. 2673, 2672–2677 (IEEE, 2003).
Oliveira, J., Ferreira, A. & Reis, J. C. Design and experiments on an inflatable link robot with a built-in vision sensor. Mechatronics 65, 102305 (2020).
Faris, O. et al. Proprioception and exteroception of a soft robotic finger using neuromorphic vision-based sensing. Soft Robot. 10, 467–481 (2023).
Gilday, K., Thuruthel, T. G. & Iida, F. A vision-based collocated actuation-sensing scheme for a compliant tendon-driven robotic hand. In 2020 3rd IEEE International Conference on Soft Robotics (RoboSoft), 760–765 (IEEE, 2020).
Chen, S., Deng, Z., Gu, H. & Wei, C. A vision-based force/position fusion actuation-sensing scheme for tendon-driven mechanism. IEEE Robot. Autom. Lett. 9, 7549–7556 (2024).
Zhe, X. & Todorov, E. Design of a highly biomimetic anthropomorphic robotic hand towards artificial limb regeneration. In 2016 IEEE International Conference on Robotics and Automation (ICRA), 3485–3492 (IEEE, 2016).
Grebenstein, M. et al. The DLR hand arm system. In 2011 IEEE International Conference on Robotics and Automation (ICRA), 3175–3182 (IEEE, 2011).
Zollo, L., Roccella, S., Guglielmelli, E., Carrozza, M. C. & Dario, P. Biomechatronic design and control of an anthropomorphic artificial hand for prosthetic and robotic applications. IEEE/ASME Trans. Mechatron. 12, 418–429 (2007).
Chen, W. et al. Design and experiments of a three-fingered dexterous hand based on biomechanical characteristics of human hand synergies. IEEE/ASME Trans. Mechatron. 27, 2930–2941 (2022).
Feix, T., Romero, J., Schmiedmayer, H. B., Dollar, A. M. & Kragic, D. The GRASP taxonomy of human grasp types. IEEE Trans. Hum.-Mach. Syst. 46, 66–77 (2016).
Wang, X., Zhang, Q., Shen, X. & Li, J. Noncollocated position control of tendon-sheath actuated slender manipulator. IEEE Trans. Control Syst. Technol. 28, 688–696 (2020).
Stepanova, K. et al. Automatic self-contained calibration of an industrial dual-arm robot with cameras using self-contact, planar constraints, and self-observation. Robot. Comput. Integr. Manuf. 73, 102250 (2022).
Acknowledgements
This work is funded by the National Key Research and Development Program of China under the following grant numbers: 2024YFF0504702 (awarded to C.W.). The authors appreciate Y. Zhang (HMU) for contributing expertise in human hand anatomy and providing suggestions for the paper illustrations.
Author information
Authors and Affiliations
Contributions
S.C. fabricated the dexterous hand, designed the experiments, conducted the experiments, analyzed the experimental data, and wrote the manuscript; J.L. conducted the experiments, processed the data, edited the manuscript; Z.D. developed the visual recognition program and conducted the experiments; P.W. participated in the design and fabrication of the dexterous hand, edited the manuscript; C.W. proposed the concept, guided the experiments, and edited the manuscript. X.C. guided the theoretical research, supported the experimental validation, and reviewed the manuscript.
Corresponding authors
Ethics declarations
Competing interests
S.C., P.W., and C.W. are inventors of an invention disclosure of the patent filed by the Harbin Institute of Technology (ZL 202311262707.5, granted on 17 January 2025) related to multimodal perception principles in this work. The remaining authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Nathan Lepora, Zhuang Zhang, and Jung Kim for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Source data
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Chen, S., Li, J., Deng, Z. et al. An 18-DOF hand integrating force–position multimodal perception using a monocular camera. Nat Commun 16, 6801 (2025). https://doi.org/10.1038/s41467-025-62122-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-025-62122-0