Abstract
The demand for portable and rapid identification of liquids has challenged traditional laboratory methods. Here, we propose a high-accuracy liquid identification strategy that integrates water droplet mechanics and solid–liquid interface contact electrification. By applying non-Hookean mechanical properties of droplets, we fabricate a lotus leaf-inspired ZnO–Polydimethylsiloxane (PDMS) superhydrophobic solid–liquid sensor. Based on the special mechanical–electric coupling interface, it achieves the highest droplet pressure sensitivity of 281 mV/Pa. We have made a breakthrough in detecting diverse solution composition with a high monitoring resolution of 5 nM metal ions and 0.1% of alcohol concentration. Through the design of double-stacked devices, triboelectric signals are able to be decoupled into mechanical and contact electrification dual-mode signals. With the integration of a gated recurrent unit (GRU) model, intelligent identification of ten liquids has reached an ultrahigh accuracy of 99%, opening up a pathway for portable liquid monitoring.
Similar content being viewed by others
Introduction
Liquid identification technology is important in environmental protection, medical diagnosis, and food safety management1,2,3,4. Drop analysis technology provides a fundamental tool to understand complex hydrodynamic phenomena and interfacial effects of wettability and adsorption kinetics between solid and liquid5,6. It has been used for qualitative and quantitative identification of liquids through various means of receiving parameters on physical and chemical properties of the measured liquid7,8, including chromatography, nuclear magnetic resonance, electrochemistry, and spectroscopy9,10,11. However, these approaches typically require large and expensive instruments, making them impractical for on-the-go monitoring by non-specialists. To address these limitations, portable liquid identification methods have been developed for onsite rapid detection, offering advantages such as ease of operation, portability, and real-time capabilities, e.g., portable colorimetric methods, electrochemical sensors, optical sensors, etc12,13,14. Among them, LED-based colorimetric methods suffer from “black regions” and restrict the detection range15. Electrochemical sensors often focus on detecting specific ions or single-component organic solutions16,17. Optical sensors are often influenced by multiple environmental factors in addition to analyte concentration18,19. Therefore, a comprehensive liquid identification system offering lower detection limits, higher sensitivity, broader detection capabilities, and minimal sample consumption is expected20,21.
Based on the coupling effects of contact electrification and electrostatic induction, triboelectric sensors generate immediate electrical signals in response to dynamic stimuli, e.g., solid–liquid contact22,23,24,25,26. In recent research on contact electrification, the intrinsic charge distribution at the solid–liquid interface involves electron transfer, ionization, and Van der Waals force27,28. According to the charge transfer between liquid and solid surfaces, the concept of triboelectric spectroscopy analysis has been demonstrated29. In recent years, significant achievements have been made in taste-sensing, heavy metal detection, and amino acid monitoring30,31,32. However, for complex liquid identification, the electrical characteristic is not sufficient to achieve precise recognition. The integration of mechanical characteristics, such as surface tension and contact angle, would increase the uniqueness of liquid signals.
In this work, we propose a solid–liquid interface triboelectric sensor (SL-TS) based on mechanical–electric dual characteristics with interface enhancement to improve the sensitivity of voltage–pressure for complex liquid identification. A general mechanical–electric coupling model is developed to explore the enhancement mechanism under droplet compression. A ZnO–PDMS micro-nano superhydrophobic solid–liquid interface structure inspired by lotus leaves is designed to improve the mechanical and electrical properties. By combining non-Hookean mechanical properties of droplets with the contact-electrification properties of the solid–liquid interface, an optimal two-factor decision approach for liquid identification is proposed. The detection of various ionic concentrations, organic solution concentrations, and complex liquids was achieved. In order to decouple the mechanical and contact electrification characteristics of different liquid droplets to extract their complete features, a stacked device is designed. Based on the dual-channel one-dimensional time-series signals, we have achieved a high recognition accuracy by combining GRU-based networks.
Results
Mechanism of the solid–liquid triboelectric sensing system
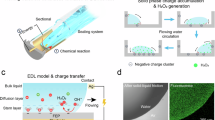
Inspired by the superhydrophobic properties of the surface of lotus leaves, we construct a micro-nanostructure ZnO–PDMS solid–liquid interface triboelectric sensor (SL-TS), see Fig. 1A. Due to the non-Hookean mechanical properties and ultralow Young’s modulus of the droplet, SL-TS exhibits ultrahigh sensitivity in the low-pressure area, making it suitable for detecting extremely weak physiological signals, such as fingertip pulses. By combining the solid–liquid interface contact electrification, the ion shielding in the liquid, and the difference in electronegativity of solid–liquid interface leads to distinct electrical signals for different liquids, establishing a universal and highly accurate liquid identification approach. Figure 1B and Supplementary Fig. 1A illustrate the structure and testing method of SL-TS. The sensor consists of an Al electrode and a ZnO–PDMS superhydrophobic interface in the lower half and a fluorinated ethylene propylene (FEP) triboelectric layer and an indium tin oxide (ITO) electrode in the upper half. The upper half of the sensor is attached to the bottom of a linear motor, which moves it up and down. Its lower half is placed on an electronic scale with a droplet of controlled volume positioned in the center. When the droplet is compressed and recovered, it produces a voltage profile as in Supplementary Fig. 1B, i.e., the voltage rises with the downward compression of the upper plate, and when the plate is released, the voltage recovers to the initial position. The details of the preparation and testing process are referred to in the “Methods” section.
A Schematic illustration of liquid recognition and fingertip pulse detection based on ZnO–PDMS micro-nanostructure SL-TS, which is inspired by the lotus leaf structure. B A mechanical measurement platform and the structure of SL-TS. C The droplet compression process model in (i) side on y–z plane and (ii) top view, where A is the point on the edge of contact line, B is the center of side contour, C is the arbitrary point on the contour, \({h}_{c}\) is the distance between the parallel plates, \(a\) is the contact radius of liquid droplets, \({F}_{c}\) is compressive force, \({F}_{{{\mathrm{capillary}}}}\) is the a resisting force of droplet, \(S\) is the contact area, \(p\) is the Laplace pressure, \(\gamma\) is the coefficient of surface tension, \(\theta=180^\circ -{CA}\) and \({CA}\) represents the contact angle. D Electrical double layer formed on the droplet–dielectric interface area. E The equivalent circuit model of the SL-TS, where CE, 1 and CE, 2 are electric double layer capacitors formed with liquid-FEP surface and liquid–ZnO–PDMS surface, Cp represents the time-invariant capacitance of dielectric materials, and \({R}_{w}\) and \({{R}}_{L}\) are the resistance of water and external load.
To elucidate the effect of droplet deformation on the electrical output of SL-TS during droplet compression, a solid–liquid mechanical–electric coupling model is established. Due to the compression characteristics of the non-Hookean behavior of droplets, a mechanical model is first constructed. As shown in Fig. 1C, on y–z plane, when the upper plate is pressed down, both the distance between the parallel plates \({h}_{c}\), and the contact radius of liquid droplets, \(a\), would change. It is subjected to the compressive force generated by the deformation of the water droplet as a resisting force, \({F}_{{{\mathrm{capillary}}}}\)33. The compressive force, \({F}_{c}\), is as below:
where \(a\) is the contact radius of the liquid droplets, \(S=\pi {a}^{2}\) is the contact area, \(p\) is the Laplace pressure, \(\gamma\) is the coefficient of surface tension, \(\theta=180^\circ -{CA}\), and \({CA}\) represents the contact angle. The detailed discussion is given in Supplementary Note 1.
As shown in Fig. 1D, after contact electrification, negative charges are generated on the FEP surface, while positive charges are generated on the liquid surface. This charge distribution shows an electric double layer, which can be modeled as a capacitor with extremely small spacing. Two distinct electric double-layer capacitors are formed to connect with the liquid-FEP surface (CE, 1) and the other with the liquid–ZnO–PDMS surface (CE, 2). Based on this, Fig. 1E shows the equivalent circuit diagram of SL-TS, where Cp represents the time-invariant capacitance of dielectric materials, such as FEP, and \({R}_{w}\) is the resistance of water. According to Kirchhoff’s law, the open-circuit voltage (\({V}_{{oc}}\)) of the device is given as (detailed information is provided in Supplementary Note 2)34:
where \({\sigma }_{b}\) and \({\sigma }_{w}\) are the charge densities of the bottom electrode and the FEP surface, \({\varepsilon }_{0}\), \({\varepsilon }_{1}\), and \({\varepsilon }_{w}\) are the permittivities of vacuum, FEP, and deionized (DI) water, respectively, \({d}_{1}\) and \({d}_{w}\) are the thicknesses of FEP and the electrical double layer capacitor. \({S}_{w}\) defines the contact area between the water and the FEP, \({S}_{b}\) represents the contact area at the water-bottom ZnO–PDMS electrode interface, and \({S}_{0}\) is the whole area of the FEP surface. From Eq. (2), its second part shows the inverse relation between \({V}_{{oc}}\) and the compressive force, \({F}_{c}\), since the first term, \(\frac{{\sigma }_{b}{d}_{w}}{{\varepsilon }_{0}{\varepsilon }_{w}}\), is a constant. Moreover, \({V}_{{oc}}\) is also influenced by Laplace pressure and the surface charge densities, both related to ion concentration and organic content of the liquid droplet.
Solid–liquid interface enhancement and its influence on droplet compression mechanics
Based on the mechanical model of the solid–liquid interface and motivated by the advantages of the superhydrophobicity33, their interface effects are investigated. Lotus leaves in nature have super high hydrophobicity due to their micro-nano structure35. Inspired by this, dual-scale micro-nano structures are prepared on the Al surface by hydrochloric acid etching and the growth of ZnO nanoparticles36, as shown in Fig. 2A. The surface is modified with PDMS through a surface vapor deposition process to form a superhydrophobic structure (the specific preparation process and materials are in the Method). Supplementary Fig. 2 shows the surface topography of the Al microstructure surface after treatment with an acidic solution (Supplementary Fig. 2A) and ZnO micro-nano structure (Supplementary Fig. 2B), which is hydrothermally grown on the surface. The high-magnification image indicates that due to the self-assembled interlocking alignment of the ZnO nanoparticles, a porous morphology is formed, and the pore diameter is less than 2 μm. The chemical composition of the ZnO–PDMS surface is examined by X-ray diffraction (XRD) and Fourier transform infrared spectrometer (FTIR). As shown in Fig. 2B, the seven peaks at 31.8°, 34.4°, 36.3°, 47.5°, 56.6°, 62.9°, and 67.9° correspond to 100, 002, 101, 102, 110, 103, and 112 diffraction peaks of the ZnO (PDF#36-1451). The ZnO with PDMS modification is further characterized by FTIR in Fig. 2C and scanning electron microscope (SEM) in Supplementary Fig. 2C. It is found that the peaks at 1550–1650 cm−1 and 3440 cm−1 correspond to the hydroxyl group on ZnO. The peaks at 799, 1025, and 1266 cm−1 belong to the asymmetric bond types of Si–C, C–C, and Si–O–C, indicating that ZnO is modified with PDMS successfully. The ZnO with PDMS modification was further characterized by FTIR in Fig. 2C and by SEM in the Supplementary Fig. 2C. After evaporating the PDMS on the surface of the ZnO micro/nanostructure, porous nanostructures were still present after the PDMS coverage was observed on the surface. The superhydrophobic contact angle of the Al–ZnO–PDMS surface is 151.9°, which is much larger than that of the etched aluminum surface of 61.5°. The Al surface after ZnO hydrothermally grew to 78.4° and the Al surface after the evaporation of the PDMS reached 95.9°, as shown in Fig. 2D. By regulating the molar ratio of the ZnO precursors (Zn(NO₃)₂:hexamethylenetetramine (HMTA) = 3:1, 2:1, 1:1, 1:2, and 1:3), a 1:1 molar ratio with PDMS evaporation results in the highest contact angle, as shown in Supplementary Fig. 3. This dual strategy leverages both surface roughness and low surface energy to achieve Cassie–Baxter state superhydrophobicity. Through COMSOL simulation, the change of stress-strain and contact area of the solid–liquid interface at different contact angles is simulated, as shown in Fig. 2E, F. When the contact angle increases from 100° to 150°, the rate of change in contact area increases with pressure. From Eq. (1), the relation between contact area and contact angle is established by adjusting the (compressive) displacement, see Fig. 2G. With the increase of the compressive distance, a larger contact angle leads to a greater change in contact area to further improve the sensitivity of the solid–liquid sensor.
A The fabrication process of ZnO–PDMS micro-nano structure (scale bar: 1 μm). B XRD of ZnO surface. C FTIR of ZnO–PDMS surface. D Comparison of contact angle between rare Al, Al–PDMS, Al–ZnO, and Al–ZnO–PDMS surfaces. E The COMSOL simulation of a compression droplet under different contact angles (CA = 100°, 130°, and 150°). F The relationship between contact area and force of droplet compression under different contact angles of solid–liquid interface through COMSOL simulation. G The relationship between contact area and compressive displacement under different contact angles of solid–liquid interface using the mechanical model. Source data is provided as a Source Data file.
Mechanical–electric coupling properties of SL-TS
Figure 3A shows the charge transfer process of SL-TS in one working cycle. It is noted that due to the electronegative property of FEP, a negative charge is generated on the FEP surface, and this layer remains charged even after the complete separation of contact surfaces. The electrode below the FEP surface will electrostatically induce opposite charges. From state i to state ii, when the top half is down-pressurized, the charged FEP surface will be gradually shielded, and the charge will flow from the bottom electrode to the top electrode by the formation of the electric double layer at the water–FEP interface. The conduction current of the external circuit keeps flowing until it reaches the lowest point of the downward pressure (state iii), where the contact area no longer changes. From states iii–iv, as the top part moves upward, the shielding effect on the FEP surface is reduced, resulting in a lower potential of the moving electrode compared with the bottom electrode. It produces a reverse current between the two electrodes until an equilibrium is maintained. A cyclic signal would be generated during the cyclic compressive and release process. Since the liquid compression modulus is smaller than solid, and it has complete and effective contact with the triboelectric surface, the sensitivity of the solid–liquid mode triboelectric pressure sensor is improved. Sensitivity represents the slope of the response curve within the small pressure range before the inflection point and is measured for different solid–liquid surfaces. By achieving a superhydrophobic solid–liquid interface, the sensitivity of SL-TS is further enhanced from 9 mV/Pa to 281 mV/Pa with a contact angle of 152°, as shown in the enlarged view of Fig. 3B. The saturation voltage to the voltage when the upper and lower part of solid–liquid sensor are about to contact, which is the final voltage value on pressure-voltage curves. The maximum detection interval with a contact angle of 152° reaches 2.4 kPa with a saturation voltage of 11.8 V. Its specific dynamic response under different pressures is shown in Fig. 3C with the minimum detection limit of 1.37 Pa and the resolution reaching 0.5 Pa. Supplementary Fig. 4 illustrates the voltage signal for a 10–50 Hz sine wave input, which reflects the device’s ability to resolve rapid mechanical inputs. Among them, the shortest response time of SL-TS is 60 ms, whereas the recovery time is 70 ms at a mechanical frequency of 50 Hz. Supplementary Fig. 5A shows good cyclic stability reflected by the stable voltage of 1.8 V during 5000 cycles by the linear motor. Supplementary Fig. 5B shows the long-term stability of SL-TS since it maintains over 95% constant voltage for 10 days at room temperature and a humidity of 20 °C and 35% RH (relative humidity). The environmental factors of temperature and humidity are studied since they affect the charge transfer during contact electrification28,37 and the liquid evaporation rate38, as shown in Supplementary Fig. 6. When the temperature increases from 20 °C to 40 °C, the sensitivity and saturation voltage are consistent. When the temperature further increases to 50 °C, the saturation voltage significantly decreases. Moreover, the stable range for the humidity effect is 25–40% RH, and the saturation voltage shows a decrease at 45% RH and 50% RH. These findings suggest an optimal operating environment for SL-TS at temperatures ranging from 20 °C to 40 °C and humidities from 25% to 40% RH. By designing a fingertip on the SL-TS (Supplementary Fig. 7), it can effectively detect a weak fingertip pulse with three characteristic peaks. This proves that the high sensitivity of SL-TS is suitable for the detection of weak signals from the human body.
A Working mechanism of the SL-TS under compression and release (i: initial state-surface charges after contact electrification, i → ii: pressing down and forward current, iii: max compression, and iii → iv: releasing and reverse current). B Voltage–pressure curves of the sensors with different contact angles of solid–liquid interface (Enlarged view for 0–500 Pa). C Repeatable response of SL-TS (contact angle of 152°) to dynamic pressures. D Voltage–pressure curves of the sensors with different concentrations of PEG droplets. E Relationship between the contact area and compressive force under different surface tensions (60 mN/m and 70 mN/m) by COMSOL simulation. The inset shows the COMSOL simulation under different surface tensions with the same compressive force (the color scale is the same as Fig. 2E). F Compressive force response to different concentrations of PEG droplets (inset: d represents the displacement on the x-axis). Source data are provided as a Source Data file.
Since the saturation voltage of SL-TS are still affected by the surface tension of the liquid solution, see Eqs. (1) and (2), we further explore its effect by increasing the concentration of polyethylene glycol (PEG) in the aqueous solution, which decreases the surface tension39. As shown in Fig. 3D, with increasing concentration of PEG from 4 wt% to 16 wt%, the saturation voltage is increased and so is the sensitivity. The rise in saturation voltage and sensitivity with increasing PEG concentration stems from enhanced charge density via PEG electropositive character and reduced surface tension40,41. By setting the surface tension at the solid–liquid interface to 60 mN/m and 70 mN/m in the COMSOL simulation, the contact area increases with decreasing surface tension (Fig. 3E). During the test, as the compressive displacement, the pressure decreases with surface tension caused by increasing PEG concentration (Fig. 3F). In particular, 4 wt% PEG solution produces a rapid increase at displacement of 3200 μm, while others are still kept at low pressure.
Mechanical–electric coupling signal characteristics of different liquids
To analyze the significant change in voltage output with increasing PEG concentration in Fig. 3D, we first isolated the effect of surface tension by simulating Eq. (2), as shown in Supplementary Fig. 8. Compared the notable change in voltage in Fig. 3D with the smaller change in Supplementary Fig. 8, it indicates that the saturation voltage is also influenced by electrical behaviors at the solid–liquid interface due to contact electrification. As shown in Fig. 4A, the contact electrification between liquid and solid involves electron transfer, ionic motion, and electric double layer formation. When a droplet is extended by pressure, electrons are first transferred from water molecules tothe FEP surface, resulting in a negative charged FEP surface and a positive charged droplet. Due to the electrostatic force, cations and anions in the liquid are further adsorbed onto the negative charged FEP surface. When the droplet retracts without pressure, some of the adsorbed cations and anions still remain on the FEP surface. Due to the difference in surface charge transfer and adsorption of ion/group types on the charged dielectric surface, SL-TS will transfer different charges, although with the same contact area, resulting in different voltages. However, similar voltage signals exist for multiple solutions at different concentrations, leading to the inability to uniquely identify the liquid from the saturation voltage.
A Contact electrification process between FEP and ionic solution. B Compressive force response to different concentrations of NaCl droplets. C, D Sensitivity and saturation voltages of different concentrations of Pb2+, Na+, Cu2+, and Cd2+ solutions. E Sensitivity and saturation voltage of different concentrations of alcohol. F–I Voltage and corresponding pressure of tap water, sparking water, white vinegar, and liquor for the compression displacement of 650 μm, 1000 μm, 1350 μm, 1700 μm, and 2050 μm. J Sensitivity and saturation voltage of tap water, sparking water, white vinegar, and liquor. Source data are provided as a Source Data file.
The increase in ion concentration will cause an increase in surface tension42. When we test NaCl solution at different concentrations, as shown in Fig. 4B, higher concentration produces greater compressive force at the same compression distance. By considering the mechanical characteristics of different liquids and Supplementary Fig. 9, where contact angles are not significantly different for some solutions, SL-TS is hence designed by combining the mechanical and electrical characteristics of solid–liquid interfacial contact electrification and compressive force for effective liquid identification. The two factors are compounded in the device output in terms of sensitivity to changes in compressive pressure and saturation voltages. We test for different ion concentration solutions and different alcohol content solutions. As shown in Fig. 4C and Supplementary Fig. 10A and 10B, with increasing Pb2+ ion concentration (1, 5, 10, 20, 30, 50, and 100 nmol/L), the sensitivity gradually decreases from 275 mV/Pa to 107 mV/Pa, and the saturation voltage decreases from 10.691 V to 4.906 V with a resolution of 5 nmol/L. Other ions are also monitored in Fig. 4D and Supplementary Figs. 10C–H. As the concentration of Na+ ions increases, both the sensitivity and saturation voltage increase from 337 mV/Pa to 510 mV/Pa and from 10.039 V to 20.809 V, respectively, and start decreasing when the concentration is increased to 1 μmol/L. For Cu2+ and Cd2+, their sensitivity and saturation voltages also show different trends. The sensitivity of the Cu2+ solution gradually decreases. Its saturation voltage increases slightly to 9.934 V with the ion concentration from 10 nmol/L to 100 nmol/L and then decreases as the concentration increases. The sensitivity and saturation voltage of the Cd2+ solution first increase to 298 mV/Pa and 9.549 V as its concentration increases from 10 nmol/L to 100 nmol/L. Both the sensitivity and saturation voltage rapidly decrease as the concentration further increases. The distinct concentration-dependent trends observed for different ions (Na⁺, Pb²⁺, Cu²⁺, and Cd²⁺) are primarily attributed to variations in their ionic radius, atomic masses, and valence states, which collectively modulate the charge transfer efficiency and liquid surface tension dynamics29,30,43. As shown in Supplementary Fig. 11A, B, an increase in the volume of liquid significantly increases the saturation voltage. Although the minimum detectable droplet volume is 10 μL since the signal between 0 Pa and 10 Pa of 5 μL cannot be recognized the limited contact area, we select 50 μL as the optimal droplet volume to balance performance and reliability.
As shown in Fig. 4E, the sensitivity is quickly increased to 397 mV/Pa when the alcohol concentration is increased from 0.1% to 2% and decreased when the concentration further rises. The saturation voltage grows slowly with the growth of alcohol concentration. When the concentration is increased to 10%, the saturation voltage is increased to 15 V. The monitoring accuracy of SL-TS for the alcohol concentration can reach as low as 0.1% by the proposed mechanical–electric coupling characteristics. As the concentration of alcohol increases, the contact angle and the surface tension of the aqueous alcohol solution decrease44, which makes it easier to produce a larger contact area at the same pressure. However, due to the surface adhesion, when the alcohol concentration increases to 5%, it is not easy to recover the initial area, so it produces a decrease in sensitivity.
For the complex solution, the voltage and pressure are subjected to a one-to-one correspondence with the same displacement downward, as in Fig. 4F–I. The output voltages and their corresponding pressures are shown at five graded compressive displacements for sparkling water, white vinegar, tap water, and liquor. All of them are colorless, transparent liquids in daily life. These figures illustrate the voltage step curve of each liquid droplet under the same displacement (650, 1000, 1350, 1700, and 2050 μm). According to the voltage–pressure curve (Supplementary Fig. 11C, D), sensitivities of tap water, liquor, sparkling water, and white vinegar are 250, 72, 129, and 63 mV/Pa, respectively. The corresponding saturation voltages are 8.9, 7.2, 4.9, and 4.6 V. Additionally, SL-TS is also able to monitor different pH levels of liquids based on the two-factor approach, as shown in Supplementary Fig.12.
Deep learning-assisted double-stacked liquid recognition
It shows that the identification of liquids performs well by voltage–pressure curves, however, it is still dependent on a pressure gauge with extra power to activate the measurement device. Moreover, the pressure-voltage curves along the full pressure range (0–2000 Pa) take a long time. Motivated by these, we propose a double-stacked structure to replace the single droplet for testing the pressure to be generated in SL-TS. As shown in Fig. 5A, the structure of the two layers is similar, and the internal droplets are changed. Device i serves for placing droplets for identification. The output voltage is obtained by the coupling of different solid–liquid contact electrification charges and mechanically induced voltages. Device ii is located at the bottom of device i. The internal liquid droplets are fixed as DI water, and it is fastened by springs at the corners. Its role is to identify the pressure changes of Device i in the pressing process that are converted into voltages. The voltages of the two devices are received through the dual-channel test platform. Figure 5B shows the working mechanism of the double-stacked device. When the uppermost plane is pressed down, the upper device will produce pressure to drive the upper surface of Device ii going down. As shown in Fig. 5C, the compression test is performed on ten liquids, including DI water, Na+, Cu2+, Cd2+, and Pb2+ solution, PEG solution, tap water, liquor, white vinegar, and sparkling water, for five cycles with fixed displacements (650, 1000, 1350, 1700, and 2050 μm). The voltages of Device i and ii are shown as blue and red lines, respectively, and it is found that each solution has its own characteristic curve.
A Illustration of the double-stacked structure SL-TS, including the device for (i) different liquids and for (ii) DI water. B Schematics of the working mechanism of the double-stacked structure SL-TS under compression and release. C Two devices’ voltage signals of DI water, Na+, Cu2+, Cd2+, Pb2+, PEG solution, tap water, sparking water, white vinegar, and liquor for the compression displacement of 650, 1000, 1350, 1700, and 2050 μm. D The comparison accuracy of a single signal of device (i), device (ii), and dual-feature input. E Confusion matrix of ten liquids by integrating features from two devices. Source data are provided as a Source Data file.
Classification is performed through the GRU network as shown in Supplementary Fig. 13, with a training set of 40 sets and a test set of 10 sets for each liquid. We first predict the liquid through a single channel (single device) as shown in Supplementary Fig. 14 and Fig. 5D. The prediction accuracies of the two single devices are 82% and 59%, respectively. The two signals are further combined to realize the accuracy of 99% (Fig. 5E). As shown in Supplementary Fig. 15, the training and testing sets have almost reached the convergence of accuracy after about 100 cycles. Compared with reported triboelectric-based liquid identification (Supplementary Table S1), SL-TS shows significant advances in all aspects, including monitoring ultralow concentration (5 nmol/L) ion solutions and alcohol concentration (0.1%), as well as achieving ultrahigh accuracy of identification in a variety of complex solutions.
Discussion
In this work, we propose a high-accuracy liquid recognition methodology based on SL-TS by combining the non-Hookean mechanical properties of the droplet with the contact electrification of the solid–liquid interface. Based on this, a ZnO–PDMS lotus leaves microstructure superhydrophobic solid–liquid interface is designed with the improvement of the voltage–pressure sensitivity to 281 mV/Pa. To the knowledge, it is the highest sensitivity achieved so far among triboelectric-based pressure sensors. Through the two-factor recognition mechanism of droplet compression and contact electrification, the detection of various ionic concentrations, organic solution concentrations, and composite liquids has been achieved. The system makes a detection resolution of 5 nM for metal ions and 0.1% for alcohol concentration. In order to decouple the mechanical and electrical properties of droplets to further extract their complete characteristics, a stacked device is proposed. By combining a GRU network, this dual-featured triboelectric solid–liquid sensing methodology is able to achieve a high liquid identification accuracy of 99%. This intelligent liquid sensing system is also able to create a droplet fingerprint library for each liquid, making a significant contribution to improving food management and chemical research.
Methods
Materials
The Al alloy plate (99.9%) was purchased from Zhengying Material, HCl, Zn(NO₃)₂⋅6H₂O and HMTA, Cd2+ selective electrode solutions, Cu2+ selective electrode solutions and Pb2+ selective electrode solutions, NaCl (99.5%), poly(ethylene glycol) (PEG 6000) and ethanol (99.7%) were purchased from Aladdin. The PDMS prepolymer (Sylgard 184 A) and curing agent (Sylgard 184B) were supplied by DOWSIL. The DI water used in the experiment was produced from a laboratory ultrapure water instrument system. Tap water was taken from the domestic water supply. In addition, white vinegar (Dingfeng vinegar, 5 g/100 mL), tap water (local municipal supply), sparkling water (Chang), and liquor (Redstarwine, 56%vol) were used.
Preparation of superhydrophobic ZnO–PDMS surface
The substrate, Al plates (20 mm × 20 mm × 1 mm), were first cleaned ultrasonically with acetone, ethanol, and DI water successively and dried with N2 gas before use. A typical etching solution with DI water and HCl (volume ratio 2:1) was prepared. The pre-treated Al substrate was immersed in the solution for 3 min at room temperature. The etched substrate was then rinsed ultrasonically with DI water, dried, and denoted as a microstructure surface. The substrate was hydrothermally treated (Hydrothermal Autoclave Reactor) in an aqueous solution (50 mL) of Zn(NO₃)₂⊠6H₂O (0.025 M, 0.371 g), HMTA (0.025 M, 0.175 g), and DI water in an oven at 90 °C for 4 h to fabricate a micro-nano structure surface. The reaction process is shown as below,
Under the same experimental conditions, the molar concentration ratios of Zn(NO₃)₂⊠6H₂O and HMTA were changed to 3:1, 2:1, 1:1, 1:2, and 1:3 to modulate different micro/nanostructures. The PDMS stamp was prepared by mixing the PDMS prepolymer with a curing agent in the proportion of 10:1 by weight and cured for 2 h at 120 °C in an oven. The PDMS stamp was then heated on a hot plate at 230 °C. After 5 min, the fabricated substrate was mounted horizontally (5 cm) above the PDMS stamp for 10 min to achieve superhydrophobicity.
Fabrication of SL-TS
The SL-TS is composed of two vertically aligned solid parts and confined droplets. The FEP layer is pasted on the ITO film to form the upper part, while the Al-based ZnO–PDMS plate is the lower part. The upper layer was fixed to a commercial linear mechanical motor (Winnemotor, WMUC512075-06-X) to move vertically, while the lower plate was fixed to a high-precision digital scale (8068-series). Different liquids, such as DI water, different concentrations of Na+, Pb2+, Cu2+, Cd2+ solutions, tap water, liquor, sparkling water, and white vinegar, are controlled through the micro-injector. The controlled volume droplets are placed at the middle of the upper and lower parts.
Characterization
Morphological characterization of the microstructure and micro-nano structure are conducted via scanning electron microscopy (SEM, Carl Zeiss Supra 55) with a gold spraying treatment prior to examination. The ZnO–PDMS sample underwent FTIR analysis using an FTIR Spectrometer (V70 & Hyperion1000) with ATR, employing a resolution of 4 cm−1 and scanning the range of 400–4000 cm−1. Static contact angles and dynamic droplet compression were measured on optical contact angle measurement equipment (OCA15) by fitting the droplet profile with the Laplace equation. To monitor the mechanical–electric coupling performance when the droplet is compressed, the upper plate was moved vertically downward to press the droplet, and the loop test was conducted using by linear mechanical motor. The high-frequency signal was tested by placing the solid–liquid sensor underneath an exciter (JZK-5). The excitation loading was amplified by a power amplifier (YE5871) and an arbitrary function generator (Tektronic-AFG1022), which combined with a piezoelectric force transducer (LDT0-028K) to ensure constant force under different frequencies. A programmable electrometer (Keithley model 6514) was used to test the electrical output signal. The mechanical data are measured by means of an electronic scale (8068-series, accuracy 0.001 g). The fluid-structure interaction and mechanical deformation were conducted by COMSOL Multiphysics software and MATLAB.
Signal processing and GRU model construction
The data from two SL-TS devices were preprocessed by adding Gaussian noise with a standard deviation of 0.01, which enhances the model to be more robust to slight changes. The dataset was then compiled from ten different liquids, each contributing 40 complete data entries per state, resulting in a training set of 400 entries. Additionally, 10 data entries per state were designated for the test set, totaling 100 test entries. The GRU model features a dual-channel architecture to process data from two devices. The data from Device i and ii are first combined into a single two-dimensional feature vector, which is defined as (batch size, T, 2). ‘Batch size’ represents the number of samples processed in each training iteration, and it is set to 64 in our model. ‘T’ represents the number of time steps and is set as 600. ‘2’ in the input means two features, e.g., contact electrification and compressive force. This combined feature vector is then fed into a shared GRU network. The network consists of four GRU layers, each with 256 hidden units. The ‘tanh’ activation function is used. The reset gate in each layer processes the hidden state from the previous time step, retaining relevant historical information to enhance short-term dependency capture within the sequence. The update gate subsequently adjusts the hidden state to help capture long-term dependencies effectively before producing the output. All data analysis was conducted within the Python programming environment using CUDA-accelerated PyTorch on an NVIDIA 4060(8G) GPU.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.
Data availability
All data supporting this study and its findings are available within the article, its Supplementary Information, and associated files. Source data are provided with this paper.
Code availability
All codes are for academic use only and available on Zenodo: https://doi.org/10.5281/zenodo.15410877.
References
Cajka, T. & Fiehn, O. Comprehensive analysis of lipids in biological systems by liquid chromatography-mass spectrometry. Trends Analyt. Chem. 61, 192–206 (2014).
Musarurwa, H. & Tavengwa, N. T. Deep eutectic solvent-based dispersive liquid-liquid micro-extraction of pesticides in food samples. Food Chem. 342, 127943 (2021).
Gao, W. et al. Fully integrated wearable sensor arrays for multiplexed in situ perspiration analysis. Nature 529, 509–514 (2016).
Liu, X. et al. Reconfigurable ferromagnetic liquid droplets. Science 365, 264–267 (2019).
Song, Q., Zhang, G. X. & Qiu, Z. R. Review of drop analysis technology for liquid property study. Opto-Electron. Rev. 13, 1–8 (2005).
Zhang, Q. et al. Atomic dynamics of electrified solid–liquid interfaces in liquid-cell TEM. Nature 630, 643–647 (2024).
Song, Q., Zhang, G. X. & Qiu, Z. R. Drop growth monitoring and drop volume measurement based on image drop analysis with CCD. Instrum. Sci. Technol. 31, 1–13 (2003).
Pannone, A. et al. Robust chemical analysis with graphene chemosensors and machine learning. Nature 634, 572–578 (2024).
Santos, A. D. C., Fonseca, F. A., Liao, L. M., Alcantara, G. B. & Barison, A. High-resolution magic angle spinning nuclear magnetic resonance in foodstuff analysis. Trac-Trends Anal. Chem. 73, 10–18 (2015).
Hayen, H. & Karst, U. Analysis of phenothiazine and its derivatives using LC/electrochemistry/MS and LC/electrochemistry/fluorescence. Anal. Chem. 75, 4833–4840 (2003).
Koel, M. Ionic liquids in chemical analysis. Crit. Rev. Anal. Chem. 35, 177–192 (2005).
Li, J. J. & Bo, X. J. Laser-enabled flexible electrochemical sensor on finger for fast food security detection. J. Hazard. Mater. 423, 127014 (2022).
Rifat, A. A. et al. Photonic crystal fiber based plasmonic sensors. Sens. Actuators B Chem. 243, 311–325 (2017).
Tu, J. et al. A wireless patch for the monitoring of C-reactive protein in sweat. Nat. Biomed. Eng. 7, 1293–1306 (2023).
Fernandes, G. M. et al. Novel approaches for colorimetric measurements in analytical chemistry—a review. Anal. Chim. Acta 1135, 187–203 (2020).
Martín, A. et al. Epidermal microfluidic electrochemical detection system: enhanced sweat sampling and metabolite detection. Acs Sens. 2, 1860–1868 (2017).
Xu, Y. C. et al. In-ear integrated sensor array for the continuous monitoring of brain activity and of lactate in sweat. Nat. Biomed. Eng. 7, 1307 (2023).
McNichols RJ, Coté GL. Optical glucose sensing in biological fluids: an overview. J. Biomed. Opt. 5, 5–16 (2000).
Zhou, Q., Pan, J., Deng, S., Xia, F. & Kim, T. Triboelectric nanogenerator-based sensor systems for chemical or biological detection. Adv. Mater. 33, 2008276 (2021).
Atkinson, J. T. et al. Real-time bioelectronic sensing of environmental contaminants. Nature 611, 548–553 (2022).
Xu, Y. et al. Bionic e-skin with precise multi-directional droplet sliding sensing for enhanced robotic perception. Nat. Commun. 15, 6022 (2024).
Willatzen, M. & Wang, Z. L. Theory of contact electrification: optical transitions in two-level systems. Nano Energy 52, 517–523 (2018).
Fan, F.-R., Tian, Z.-Q. & Wang, Z. L. Flexible triboelectric generator. Nano Energy 1, 328–334 (2012).
Lin, S., Xu, L., Chi Wang, A. & Wang, Z. L. Quantifying electron-transfer in liquid-solid contact electrification and the formation of electric double-layer. Nat. Commun. 11, 399 (2020).
Xu, W. et al. A droplet-based electricity generator with high instantaneous power density. Nature 578, 392–396 (2020).
Kwak, S. S. et al. Triboelectrification-induced large electric power generation from a single moving droplet on graphene/polytetrafluoroethylene. ACS Nano 10, 7297–7302 (2016).
Xu, C. et al. On the electron-transfer mechanism in the contact-electrification effect. Adv. Mater. 30, e1706790 (2018).
Zhan, F. et al. Electron transfer as a liquid droplet contacting a polymer surface. ACS Nano 14, 17565–17573 (2020).
Zhang, J. et al. Triboelectric spectroscopy for in situ chemical analysis of liquids. J. Am. Chem. Soc. 146, 6125–6133 (2024).
Wei, X. et al. Dual-sensory fusion self-powered triboelectric taste-sensing system towards effective and low-cost liquid identification. Nat. Food 4, 721–732 (2023).
Li, Z. et al. Triboelectrification-enabled self-powered detection and removal of heavy metal ions in wastewater. Adv. Mater. 28, 2983–2991 (2016).
Roy Barman, S. et al. Triboelectric nanosensor integrated with robotic platform for self-powered detection of chemical analytes. ACS Nano 17, 2689–2701 (2023).
Xue, L. et al. Non-Hookean droplet spring for enhancing hydropower harvest. Small 18, 2200875 (2022).
You, J. et al. High-electrification performance and mechanism of a water-solid mode triboelectric nanogenerator. ACS Nano 15, 8706–8714 (2021).
Barthlott, W., Mail, M., Bhushan, B. & Koch, K. Plant surfaces: structures and functions for biomimetic innovations. Nano-Micro Lett. 9, 23 (2017).
Liu, N. et al. High-performance piezo-electrocatalytic sensing of ascorbic acid with nanostructured wurtzite zinc oxide. Adv. Mater. 33, 2105697 (2021).
Wei, Y. et al. Contact electrification at the solid–liquid transition interface. Mater. Today 74, 2–11 (2024).
Girard, F., Antoni, M., Faure, S. & Steinchen, A. Influence of heating temperature and relative humidity in the evaporation of pinned droplets. Colloids Surf. Physicochem. Eng. Asp. 323, 36–49 (2008).
Kim, M. W. Surface activity and property of polyethyleneoxide (PEG) in water. Colloids Surf. Physicochem. Eng. Asp. 128, 145–154 (1997).
Lu, Y. et al. Liquid–liquid triboelectric nanogenerator based on the immiscible interface of an aqueous two-phase system. Nat. Commun. 13, 5316 (2022).
Yoo, D., Jang, S., Cho, S., Choi, D. & Kim, D. S. A liquid triboelectric series. Adv. Mater. 35, 2300699 (2023).
Bhatt, D., Chee, R., Newman, J. & Radke, C. J. Molecular simulation of the surface tension of simple aqueous electrolytes and the Gibbs adsorption equation. Curr. Opin. Colloid Interface Sci. 9, 145–148 (2004).
Nie, J. et al. Probing contact-electrification-induced electron and ion transfers at a liquid–solid interface. Adv. Mater. 32, 1905696 (2020).
Spencer, S. J., Andrews, G. T. & Deacon, C. G. Contact angle of ethanol–water solutions on crystalline and mesoporous silicon. Semicond. Sci. Technol. 28, 055011 (2013).
Acknowledgements
This work was supported by the National Key R&D Program of China (No. 2023YFB3208100 to Z.W.), the National Natural Science Foundation of China (No. 62526407 to Z.W., No. 62304184 to Y.L., 62174115 to Z.W., and U21A20147 to Z.W.), Natural Science Foundation of Jiangsu Province of China (No. BK20240152 to Z.W.), the Natural Science Foundation of the Jiangsu Higher Education Institutions of China (No. 24KJA430011 to Z.W.), the Research Development Fund of Xi’an Jiaotong-Liverpool University (No. RDF-SP-102 to Y.L. and REF 2301006 to Y.L.), and the Collaborative Innovation Center of Suzhou Nano Science & Technology, the 111 Project, Joint International Research Laboratory of Carbon-Based Functional Materials and Devices.
Author information
Authors and Affiliations
Contributions
L.X., Y.L., and Z.W. conceived and designed experiments. L.X. prepared the solid–liquid sensor, processed the mechanical and electrical tests, developed a mechanical–electrical coupling model, and conducted data collection and analysis. B.L., H.J., Z.G., and P.J. performed the structure design. B.L. performed simulations by COMSOL and MATLAB. Z.S. designed signal processing algorithms and conducted GRU model construction. Y.L., H.V.Z., I.Z.M., X.S., and Z.W. supervised the work. L.X., Y.L., and Z.W. wrote the manuscript. All authors discussed and commented on the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Ning Wang, Ya Yang, and Wei Zhang for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Source data
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Xie, L., Lu, B., Sima, Z. et al. Mechanical–electric dual characteristics solid–liquid interfacing sensor for accurate liquid identification. Nat Commun 16, 7069 (2025). https://doi.org/10.1038/s41467-025-62524-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-025-62524-0