Introduction

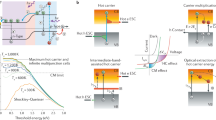
Optical hot carriers in semiconductors are light-excited electrons or holes with energies exceeding that of the energy-band edge1. Once the thermal distribution of hot carriers has been established through carrier-carrier scattering, relaxation occurs via multiple channels, predominately through optical phonon emission, but also through impact ionization and Auger recombination2,3. Hot carriers lose the energy within a few picoseconds (ps) and approximately 100 nm through fast carrier relaxation4,5,6. Consequently, the harvesting of high-energy photons in semiconductors is challenging owing to heat dissipation via free carrier-phonon scattering. Limited by this physical mechanism, the energy loss for carriers (> 50% of energy) is particularly serious in narrow-bandgap semiconductors with prevailing energy matching between carriers and phonons3,7,8. This phenomenon leads to a low quantum efficiency for semiconductor-based optoelectronic devices without external voltage bias (Fig. 1a).

Fig. 1: Spatially confined hot carrier dynamics in semiconductors.
figure 1

a In semiconductor-based optoelectronic devices, the cooling process of photoexcited hot carriers is unrestricted, and typically occurs within a few picoseconds. Hot-carrier energy loss rate is dominated by phonon emission, and intensifies with higher photon energy. This leads to rapid energy dissipation, a decline in spectral responsivity, and reduced external quantum efficiency (EQE) at shorter wavelengths for optoelectronic devices without external voltage bias. b To effectively manage the hot carrier relaxation, the spatially confined structure amplifies the local phonon bottleneck effect and prolongs the carrier diffusion lifetime, manifested as the slow decay of normalized transient reflectivity (ΔR/R). The enhanced EQE fundamentally results from the competition between hot carrier relaxation dynamics and carrier collection efficiency. Particularly in the short wavelength range, thermalized cold carriers participate more effectively in the collection process. Together, these effects lead to a significant enhancement in spectral responsivity.

Full size image

One of the solutions for improving the photons energy conversion efficiency of semiconductors is utilizing the high mobility materials9, such as graphene10,11,12, and halide perovskites6, which exhibit strong carrier-carrier scattering13,14 with a long hot carrier diffusion length15,16. In addition, spatial or dimensional control of hot-carrier cooling pathways can involve thermal isolation17,18,19,20,21 or reabsorption of hot-carrier-phonon to extend hot-carrier lifetimes or the generation of additional electron-hole pairs to bolster extraction efficiency22,23,24. The former commonly refers to the phonon relaxation bottleneck25,26, and the latter is known as carrier multiplication27,28. For example, when the transport channel of hot carriers transitions from a free plane to a quasi-unidirectional confinement structure (Fig. 1b), edge-induced hot phonon localization leads to the accumulation of acoustic phonons29. This accumulation reduces decay of hot carriers to longitudinal optical (LO) phonons25. The spatial confinement obstructs the hot carrier energy transfer pathway, amplifying the phonon bottleneck. Meanwhile, enhanced thermalization extends carrier lifetime, facilitating diffusion to the electrode and the generation of the output signal. The complex carrier-phonon and carrier-carrier interaction also depends on the hot carrier energy loss rate, typically, shorter wavelengths and weaker photon intensities correspond to higher loss rates30. However, spatial confinement of carrier generation can lead to a high-density, local carrier population and a significant carrier temperature differential. This phenomenon is beneficial for extending carrier lifetimes and enhancing their efficient utilization, particularly in shorter wavelengths, compared with conventional loss mechanisms31. Another approach for achieving high transfer efficiency of excess energy is carrier multiplication through impact ionization, commonly found in quantum dot materials32,33. However, given the multiple discrete energy levels with low density of states and the energy mismatch between carriers and optical phonons, it exhibits a low carrier multiplication efficiency34 (Supplementary Fig. 1).

Here, we select narrow bandgap lead selenide (PbSe) for this demonstration owing to its strong anharmonic interaction between optical and acoustic phonons35, as well as intrinsic strong carrier multiplication34 and brilliant thermoelectric properties36,37,38, making it feasible to enhance the photo-thermoelectric (PTE) effect by tuning the hot-carrier cooling pathways39,40. The microscopic photocurrent mapping reveals that the PTE voltage is sharply boosted by shrinking the dimensions of devices. As a result, the relaxation of thermalized carriers is blocked by the phonon relaxation bottleneck effect through strong edge phonon scattering that causes the localization of the optical-excited hot carriers. Consequently, a high blackbody responsivity of 3.6 × 103 V W−1 is obtained in the PbSe PTE device with external quantum efficiency (EQE) > 100% in the short-wave infrared region, peak sensitivity of 6.3 × 1010  cm Hz1/2 W−1 exceeding the thermoelectric theoretical limit and response speed of 33.8 μs at room temperature. Together with the successful fabrication of a highly uniform focal plane array (non-uniformity 5.6 × 10−6 %), our PbSe PTE device shows great potential in infrared imagers and thermoelectric generators.

Results

Spatial confinement-boosted photo-thermoelectric efficiency

We develop a series of spatial confinement structures based on high-quality, wafer-scale monocrystalline PbSe (Supplementary Figs. 2–6). The first set of PbSe devices feature a fixed channel depth (10 μm) and transition length (10 μm), with the width decreasing from 39 μm to 5 μm (Fig. 2a). Hall effect measurements reveal that the majority carriers in PbSe are electrons (n-type), demonstrating a carrier density of 7.13 × 1017  cm−3. The photogenerated hot carrier dynamics in spatial confinement structures can be revealed via the ultrafast transient reflection microscopy. We obtain the transient reflectivity spectra of PbSe inside the channel (Fig. 2b). Upon photoexcitation, carriers are ejected to a state above the bottom of the conduction band. This process involves electron-electron scattering, followed by electron–phonon scattering. These interactions heat up the electrons and the lattice within a few femtoseconds (fs) and ps, respectively. By fitting with the double exponential decay function, we obtain two distinct carrier lifetimes25. The fast decay (τfast), driven by carrier-phonon scattering, exhibits a similar lifetime (~ 6  ps), regardless of whether the area is spatial confined or not (Supplementary Fig. 7). Conversely, the slow decay (τslow), primarily attributed to phonon-phonon scattering, shows a significant increase as the width decreases (Fig. 2c). The influence of carrier-carrier interactions is weak in PbSe owing to its intrinsic low Auger recombination rate41. The suppression of optical-to-acoustic phonon conversion within the spatially confined channel leads to the slower relaxation of hot carriers to optical phonons, thereby increasing the lifetime and transport length of thermalized carriers in PbSe.

Fig. 2: Analyses of carrier dynamics for spatially confined PbSe microstructures.
figure 2

a Reflectance imaging of spatially confined PbSe devices. The red box indicates the confined area. Scale bar, 10 μm. b Normalized transient reflectivity ΔR/R in the confined channel. c Slow carrier lifetime (τslow) with error bars (standard deviation) calculated from (b).

Full size image

Given the results of quasi-unidirectional confinement, we then focus on the spatial distribution of photogenerated signals in another set of asymmetric T-shaped devices. These devices have one-side widths of 10, 20, 45, 70, 95, and 120 μm (without confinement) (Fig. 3a). We adopt the scanning photocurrent microscopy (SPCM, Supplementary Fig. 8) to record the micro-resolved photoexcited voltage (Voc) across the sample. With the focused laser wavelength of 4 μm (P = 60 nW and dlaser spot = 6 μm), the Voc distributions at zero bias vary significantly among the various PbSe devices (devices #1 – #6), as shown in Fig. 3b. The Voc mainly localizes at the metal/PbSe interfaces and shows strong symmetry in non-confined devices #1. Symmetrical photovoltage observed without external bias suggests a mechanism distinct from bolometric or photoconductive (PC) effects (both required a bias). To exclude the generation of photoexcited Voc caused by photovoltaic (PV) effect, we use another 808 nm laser with a smaller spot size (1.6 μm) and higher power (112 μW) for line scanning, as illustrated in Fig. 3c. Assuming the PV effect predominates, the voltage will be governed by the Schottky barrier, and its distribution should be expected to follow a Gaussian profile (the full width at half maximum is around 1 – 2 μm). Considering the non-sharp Voc near the contacts and the minimal impact of spatial confinement on the contact potential barrier, the PV effect cannot explain the failure of Gaussian fitting and the anomalously high Voc observed in Device #4 – #6. Therefore, these characteristics indicate that the PTE effect is the primary mechanism.

Fig. 3: Spatial confinement-boosted photo-thermoelectric voltage.
figure 3

a SEM images of PbSe devices with widths ranging from 10 to 120 μm. b Scanning photovoltage images of PbSe devices, showing that photovoltage increases as the channel width decreases. Scale bars, 30 μm. c Linear sweep of photovoltage applying the focused 808  nm light. The electrode positions are given by the differential of the reflectance spectrum (dR/dx, using device #1 as a reference). d Diffusion length and (e) peak Voc ratio (V+peak/V−peak) of the device as a function of channel width. The error bars represent the standard deviation. f Photovoltage versus input power under 4 μm laser illumination. g Light generated \(\Delta T\) along the middle blue dashed line in Supplementary Fig. 12a. h Experimental and simulated values of temperature ratios (T+max/T−max) of the PbSe devices.

Full size image

The key feature of Voc mapping lies in its strong correlation with spatial confinement structures: (i) the peak Voc increases by up to an order of magnitude as the channel width reduces to 10 μm; (ii) the peak photovoltage ratio, |V−peak/V+peak|, shifts from a plateau to an exponential increase when the width < 45 μm. First, in device #5 and #6, the spatial patterns of Voc hot spots differ significantly from those in the other devices, exhibiting a high peak |Voc| of 3.7 mV and 8.1 mV (compared with 1.0 mV in device #1), respectively. Moreover, the decay of Voc away from the contact can also be quantitatively described by an exponential diffusion as \({V}_{0}\exp (-\frac{x}{{L}_{{{{\rm{d}}}}}})\), where Ld represents the diffusion length (Fig. 3d). As the channel width increases, the average diffusion length grows from 3.7 μm to 14.6 μm. The increase in diffusion length within a spatial confinement device indicates a longer average carrier lifetime \(\left({L}_{{{{\rm{d}}}}}=\sqrt{D\tau }\right)\), where D is the diffusion coefficient, and \(\tau\) is the carrier lifetime. The calculated carrier lifetime increases by 16 times at a width of 10 μm compared with devices #1 (120 μm).

Then, the peak Voc ratio (Fig. 3e), rising from 1.0 (device #1) to 6.8 (device #6), indicates the broken level of spatial heat transport symmetry. The narrower channels enhance thermal localization, leading to a larger photovoltage response when sensing the surface radiation, as shown in Supplementary Fig. 9. To verify this, we investigate linear dynamic between the photoresponse and the power (Fig. 3f and Supplementary Fig. 10), which can be described by the power law \({V}_{{{{\rm{oc}}}}}\propto {P}^{{{{\rm{\gamma }}}}}\) (ref. 42). The parameter values are 0.84, 0.47, 0.45, 0.39, 0.29, and 0.17, corresponding to decreasing widths. While defect states govern sub-linearity in unconfined Device #1, Device #6 shows enhanced sub-linearity from superior local carrier heating. This generates a larger temperature difference \((\Delta T)\) and consequently stronger PTE responses.

Considering the hot carriers generated at the laser excitation spot, they will rapidly interact with optical phonons in the picosecond, transferring their energy to surrounding phonons or cold carriers through scattering. For spatial confinement devices, the broken spatial symmetry near the channel edge allows for increased horizontal phonon scattering in PbSe. As the local non-equilibrium acoustic phonon population intensifies, it inhibits the decay of optical phonons into acoustic phonons, thus extending the lifetime of thermalized carriers. When the channel width of PbSe reduces to a size comparable to the wavelength, this effect becomes more pronounced, leading to an increase in the diffusion length of thermalized carriers and an improvement in the energy transfer efficiency. To reveal insights into the mechanism of giant Voc generated in spatial-confinement devices, we position thermocouples at both ends of another set of devices to directly measure the \(\Delta T\). Thermocouples are composed of Cu/Cu-Ni alloy (Supplementary Fig. 11), known as T-type in commercial applications. Based on the Seebeck effect, we achieve micro-resolved \(\Delta T\) mapping by integrating thermocouple devices to the SPCM system, as shown in Supplementary Fig. 12a. The same features observed in both \(\Delta T\) and \(\Delta V\) distributions further prove that the origin of photogenerated Voc is the PTE effect. Below, we first focus on the mechanism of energy (temperature) transfer, and then we discuss the spatial confinement-enhanced \(\Delta T\) effect in detail.

In general, the excitation probability of hot carriers is related to the bandgap \((\Delta )\) of the material, following the Boltzmann distribution \(P\left(\Delta,T\right)\propto \exp (-\frac{\Delta }{{k}_{{{{\rm{B}}}}}T})\), where \({k}_{{{{\rm{B}}}}}\) is the Boltzmann constant, and \(T\) is the operating temperature. In this case, the exponential term in the hot carrier excitation probability of the narrow bandgap PbSe (0.27  eV) is \(3\times {10}^{-5}\) at 300  K, which is significantly higher than that of Si (~\({10}^{-19}\)), MoS2 (~\({10}^{-22}\)), and perovskites (~\({10}^{-35}\)). After excitation, hot carriers relax via phonon emission and scattering, converting kinetic energy into heat. Given the thin thickness (~ 87  nm) of the film, we reasonably assume that the electron/phonon transport behaves as a quasi-two-spatial form. When the channel width » wavelength of light (represents the range of hot carrier generation), the transport of thermalized carriers is unrestricted, making diffusion in the vertical and horizontal (across electrode pairs) directions equivalent. In contrast, when the channel width and wavelength are close, vertical diffusion is impeded by local phonon scattering (large nonequilibrium LO phonon population), which delays the conversion from optical phonons to acoustic phonons. This prolonged phonon relaxation may enhance the phonon bottleneck effect, leading to a significant conical-shaped \(\Delta T\) as a function of channel width (Fig. 3g). Although the \(\Delta T\) on the unmodified side is affected by the channel width, the variation was clearly smaller compared with the left side.

Given the critical role of the hot carrier relaxation process in thermal field redistribution, we simulate and reproduce \(\Delta T\) patterns for various PbSe devices using a two-temperature model (Supplementary Fig. 12b). We then define the peak \(\Delta T\) ratio (\({\Delta T}_{\max }^{+}/{\Delta T}_{\max }^{-}\)) to identify the intrinsic mechanism (Fig. 3h). Although both experimental and simulation results show a similar increase in this ratio with decreasing channel width, they fall short in explaining the observed super-growth phenomenon. To address this discrepancy, we simulate the additional temperature difference by assuming that the thermal conductivity \(\kappa\) varied at the spatial confined structure compared with the bulk. Specifically, the thermal conductivity near the edge is given by \(\kappa=\frac{1}{3}C{v}_{{{{\rm{edge}}}}}{\varLambda }_{{{{\rm{local}}}}}\), where C is the specific heat capacity, v is the phonon group velocity, and \(\varLambda\) is the phonon mean free path. Due to the strong phonon scattering at the edge, the group velocity \({v}_{{{{\rm{edge}}}}}\) is lower than \({v}_{{{{\rm{bulk}}}}}\). In addition, as \(\frac{1}{{\varLambda }_{{{{\rm{local}}}}}}=\frac{1}{{\varLambda }_{{{{\rm{bulk}}}}}}+\frac{1}{{\varLambda }_{{{{\rm{edge}}}}}} > \frac{1}{{\varLambda }_{{{{\rm{bulk}}}}}}\) (Matthiessen’s rule), the reduced mean free path \({\varLambda }_{{{{\rm{local}}}}}\) at the edge leads to a decrease in local thermal conductivity29. This behavior is common at the grain boundaries of thermoelectric materials43,44. With the modified \(\kappa\) (Supplementary Fig. 13), both the model and experimental data showed excellent agreement, further suggesting that the magnitude of the hot carrier-assisted PTE signals is synergistically influenced by reduced thermal conductivity and thermal localization.

Room temperature highly sensitive mid-infrared detection

The giant optical hot carrier effects caused by spatial confinement brings about potential for sensitive infrared detection applications. Below, we characterize the mid-wave infrared (MWIR) detection performance at room temperature based on spatially confined PbSe devices. Figure 4a shows the dark and photocurrent density versus voltage (J-V) characteristics with wavelengths ranging from 532  nm to 4 μm between − 1 and 1  V. The dark current density (Jdark) at zero bias is ~ 10−5  A/cm2. Figure 4b displays the current noise spectra, where the f-1 noise, with its characteristic linear descent, prevails at low frequencies (~ 10−25 A2 Hz−1 at 10  Hz), and approaches system noise (~ 10−28 A2 Hz−1) at high frequencies. The exceptionally low dark current and noise may result from high-quality monocrystalline films (reducing surface defects) and bias-free operation (avoiding g-r noise). The zero-biased \({I}_{{{{\rm{ph}}}}}\)(\(={I}_{{{{\rm{light}}}}}-{I}_{{{{\rm{dark}}}}}\)) under MWIR laser illumination (2.6, 3.1, 3.4 and 4.3 μm) is presented in Fig. 4c and Supplementary Fig. 14. \({I}_{{{{\rm{ph}}}}}\) exhibits fast photoresponse with the same magnitude, despite the relatively low power of the 4.3 μm laser. When the laser is switched on/off, the current rises/recovers steadily with the light. The rise and fall times are 33.8 and 49.6 μs, respectively, at MWIR (4.0 μm), measured from 10% to 90% of the stable photocurrent (Fig. 4d). Notably, in short-wave infrared (SWIR, 1.5 μm) irradiation, the response times improves to 11.6 and 21.9 μs, demonstrating faster performance (Supplementary Fig. 15). This aligns with the 3  dB bandwidth of ~ 0.18  MHz (Supplementary Fig. 16). Moreover, to assess the stability of the PbSe device, we measure its photoresponse over 18,000 cycles (Fig. 4e).

Fig. 4: Electrical properties and mid-wave infrared (MWIR) response of spatially confined PbSe detector.
figure 4

a J-V curves of the asymmetric PbSe device. b Noise spectrum of PbSe device and measurement system. c Photocurrent response of PbSe devices under light irradiation at various wavelengths. d Time-resolved photoresponse of PbSe device under 4 μm laser illumination demonstrates ultra-fast response speeds in the MWIR range. e Stability of PbSe device, the device was measured for 18,000 cycles at zero bias in the air. f Blackbody detection results for responsivity and detectivity versus power intensity at room temperature. g EQE for spatial confinement device at room temperature. h Comparison of detectivity with spatial confinement PbSe detector and conventional photodetectors [PV-(InGaAs, HgCdTe, InAs), PC-(PbS, PbSe), InAs/AlSb, InAs/InAsSb, HgTe QDs]. The background-limited infrared performance (BLIP) of photovoltaic and thermoelectric infrared photodetectors at 300  K is also shown.

Full size image

Blackbody detection showcases the comprehensive assessment of infrared detection capabilities. We evaluate the ability of the spatially confined PbSe devices to detect blackbody radiation (700–1200 K) at a 300  K background temperature (Fig. 4f). According to Planck’s and Wien’s law, as the blackbody temperature rises, the peak wavelength of radiation (\({\lambda }_{{{{\rm{peak}}}}}\)) decreases from ~ 4.14 (700  K) to 2.41 (1200 K) μm with increasing radiation energy. As the detector approaches the blackbody source, the responsivity increases exponentially across all blackbody temperatures (Supplementary Fig. 17). The two core figures of merit of the photodetector, responsivity (\({R}_{{{{\rm{ph}}}}}={V}_{{{{\rm{ph}}}}}/P\), where \(P\) is the power of the light) and specific detectivity (\({D}^{*}=\frac{\sqrt{A\Delta f}}{{{{\rm{NEP}}}}}\), \({{{\rm{NEP}}}}={I}_{{{{\rm{n}}}}}/{R}_{{{{\rm{ph}}}}}\), where \({I}_{{{{\rm{n}}}}}\) is the noise current of the electronic bandwidth, \(A\) is the the effective area, and \(\Delta f\) is the bandwidth, which selected as 1,000  Hz.) show a proportional relationship with the blackbody temperature, and at 1200  K, the R and D* rise to ~ 3.6 × 103  V  W−1 and 6.3 × 1010  cm Hz1/2 W−1 (NEP ~ 1.9 × 10−13  W  Hz−1/2), respectively.

The external quantum efficiency (\({{{\rm{EQE}}}}=\frac{{R}_{i}{hc}}{e\lambda }\)) of the PbSe device at room temperature is further obtained via a Fourier transform infrared spectrometer (FTIR, Fig. 4g) highlighting by ~ 116% around a wavelength of 1.9 μm, which is attributed to spatial confinement hot carrier effect and carrier multiplication through impact ionization induced by the excess energy. Figure 4h presents the spectral responsivity of the confined PbSe device. The most notable finding is the nearly monotonic decrease in the infrared response, while the D* consistently exceeds 3 × 1010  cm Hz1/2 W−1 before 4 μm. Moreover, A room temperature peak detectivity (D*) of 6.3 × 1010  cm Hz1/2 W−1 is beyond the thermoelectric theoretical limit (Fig. 4h and Supplementary Note 1). To show the infrared response capability, we compare specific detectability between the room-temperature-operated confined PbSe detector and other conventional photodetectors across a broad wavelength range. In the SWIR range, InGaAs (PV) and HgCdTe (PV) demonstrate advantages, but their response is limited to ~ 2 μm and does not extend into the MWIR range31. This limitation also applies to PbS (PC) due to its bandgap of ~0.4 eV. In the MWIR range, the D* of the confined PbSe (PTE) in this study is significantly higher than that in some other commercial PbSe detectors (typically polycrystalline films, even at low operating temperature)45, comparable to the HgTe quantum dots (QDs)46 and InAs/InAsSb superlattice47. The stability of this confined PbSe device is also excellent, ensuring no degradation for three months, outperforming that of most two-dimensional materials.

Infrared imaging and PbSe detector array

Imaging is a key application of a photodetector. To that end, Fig. 5a, b provides a schematic of the active and passive target imaging system (“Methods” section). The stability of the confined PbSe device is confirmed using a variable-frequency chopper, where Voc remains constant across different frequencies (Supplementary Fig. 18). We then perform reflective imaging on a complex NCU badge pattern, as shown in Fig. 5c. The full-spectrum imaging on a silicon wafer and metal mask under a tungsten lamp is illustrated in Supplementary Fig. 19. The imaging results under both visible light and infrared illumination are remarkably clear. In addition, Fig. 5d-g illustrates the imaging capability of a blackbody-sensitive PbSe detector under an interference object. The temperature of the heating fiber is ~ 626  K. The images show the high spatial consistency of the PbSe detector with/without the silicon wafer (cut-off wavelength of ~ 1.1 μm), clearly outlining the carbon fiber and showcasing its high dynamic range. At a higher heating temperature of ~ 1200  K, the imaging quality enhances significantly owing to the increased radiant power and the shift of the peak wavelength towards shorter wavelengths (Supplementary Fig. 20). This series of images highlights the exceptional imaging performance of the spatially confined PbSe photodetector.

Fig. 5: Infrared imaging and PbSe detector array.
figure 5

Schematic for (a) active and (b) and passive target detection. The imaging is captured by a blackbody-sensitive T-shaped PbSe device after the target (carbon fiber heating tube) is heated. c Reflective imaging through scanning patterns using lasers of 532  nm and 808  nm. Scale bars, 100  mm. d–g, Digital photograph (d) of target by a commercial CMOS camera and full spectrum image (e) of target by our PbSe photodetector. The target temperature is 626  K. With the silicon wafer in front of the target, the corresponding images are shown in (f) and (g), respectively. The white dotted line represents the position of the silicon wafer. Scale bars, 1  cm. h Optical image of the 32 × 32 pixel spatially confined PbSe detector array. Scale bar, 1.5  mm. i SEM image of red rectangular in (h). Scale bar, 360 μm. j Dark voltage and photovoltage distribution in selected 8 × 8 devices under 4 μm laser (0.17 μW) illumination. The inset is the detectivity distribution.

Full size image

We fabricate a 32 × 32 pixel focal plane array (FPA) on a PbSe wafer, as shown in Fig. 5h, to validate the high-resolution infrared imaging capability. We select 64 pixels (Fig. 5i) and calculate the distribution of dark voltage and photovoltage under the 4 μm laser illumination at zero bias (Fig. 5j). The detectivity D* of pixels shows excellent consistency, with a median value of \(2\times10^{10}\) cm Hz1/2 W−1. The pixel inhomogeneity factor is calculated to be about \(5.6\times10^{-6}\%\). It is expressed as \(\frac{1}{\bar{R}_{{{\rm{bb}}}}}\sqrt{\frac{1}{N-\left(a+b\right)}{\sum }_{i=1}^{N}{\left({R}_{{{\rm{bb}}}i}-{\bar{R}}_{{{{\rm{bb}}}}}\right)}^{2}\left)\right.}{{\times }}100\%\) where \({R}_{{{{\rm{bb}}}}i}\) represents the response of the i-th pixel, \({\bar{R}}_{{{{\rm{bb}}}}}\) is the average pixel response, and N is the total number of pixels. This low level of pixel inhomogeneity is considered acceptable in practical applications. These benefits indicate that exploiting the spatial confinement properties of PbSe wafers can significantly boost the development of high-resolution FPA and facilitate advanced hyperspectral imaging.

Discussion

In summary, we demonstrate room temperature-operated MWIR photodetectors with spatial confinement-enhanced optical hot-carriers-assisted PTE effect based on low-cost wafer-scale monocrystalline PbSe thin film (Supplementary Table 1). By controlling the carrier transport dimension, the local phonon scattering effect is amplified, which in turn makes the phonon bottleneck effect more pronounced and results in a significant increase in carrier lifetime. Meanwhile, the high concentration of photoexcited hot carriers positively influences the rapid establishment of a temperature gradient. This increased \(\Delta T\) is more pronounced due to intrinsic carrier-multiplication. The spatial confinement device shows high blackbody responsivity (3.6 × 103  V  W−1), blackbody sensitivity (6.3 × 1010  cm Hz1/2 W−1), fast photoresponse (33.8 μs), and a beyond unity EQE. We also successfully fabricated a highly uniform 32 × 32 pixel FPA with an ultralow inhomogeneity factor ~ 5.6 × 10−6%, demonstrating great potential for high-resolution infrared imaging. Our research offers a promising approach for hot carriers to be applied in highly efficient solar cells, photodetectors, thermoelectric devices, and more.

Methods

Materials synthesis and characterization

The PbSe wafer film was fabricated using the chemical vapor deposition (CVD) method. A rail-boat containing PbSe powder (Sigma-Aldrich, 99.99%) was placed in the middle of a quartz tube. Se powder (Sigma-Aldrich, 99.99%) was used as a compensating source and placed upstream of the carrier gas Ar. The SrTiO3 substrate was positioned downstream. The PbSe powder was heated to 750 °C for 75 min. The growth was maintained at 8.6 × 10−2  Pa for 5 min and then allowed to cool naturally.

The composition of the PbSe wafer was characterized using a focused ion beam-scanning electron dual beam system (Thermo Fisher Scientific Brno s.r.o.). The crystal structures of PbSe were measured by XRD (Philips Xʼpert PRO). The Raman spectra of the PbSe wafer were analyzed by a Raman spectrometer (HORIBA Jobin Yvon S.A.S) employing a 532 nm laser as the excitation source. The Bruker Fourier Transform Infrared Spectrometer (Bruker 80 v) was used to analyze the absorption spectrum. The topography and thickness of the film were characterized using a step profiler.

Device fabrication and analysis

The PbSe film was photoetched using an ultraviolet maskless lithography machine (TuoTuo technology). The film was etched by a plasma etcher (Leuven Instruments LCCP-6A) to achieve a specific shape. The metal Cr/Au (5/80  nm) was used as a contact material. The photoresponse measurement was performed by a semiconductor parameter analyzer. The PbSe detector was irradiated by different laser diodes with wavelengths of 2.6, 3.1, 3.4 and 4.3 μm. The device was coupled to a probe station. The incident powers were calibrated using the optical power meter. High time-resolution responses were measured using the 1.5 and 4.0 μm focused laser. The laser was pulsed at a frequency of 1 kHz by a chopper and recorded by the semiconductor parameter analyzer (PRIMARIUS PX600). The space distribution of photovoltage was measured using a micro-resolved photovoltage mapping system (TuoTuo Technology). The infrared response spectrum was acquired using a Fourier infrared spectrometer (Bruker VERTEX 80/80 v) at room temperature.

Micro-resolved pump-probe reflectance spectroscopy

The pump-probe measurements were performed in reflection mode under ambient conditions using a Coherent Mira 900 Ti: sapphire oscillator integrated with a Coherent Mira optical parametric oscillator (OPO). An 800  nm pump beam (1.4 μJ cm−2) generated by the Ti: sapphire oscillator was split using an 80/20 beam splitter. The weaker portion is modulated at a frequency of 1 MHz using an acousto-optic modulator. This modulated beam was then utilized to excite the device in conjunction with the internal function generator of the lock-in amplifier. The stronger portion of the beam was directed into the OPO, generating a tunable probe light with wavelengths ranging from 505–740  nm (530  nm was selected in this experiment). Two beams were spatially overlapped via a dichroic beamsplitter and then focused with a microscope objective (Olympus 60 ×, 0.9 NA). The time delay between the pump and probe beams was precisely regulated through a linear translation stage. The transient reflectivity signals were captured using a lock-in amplifier, configured with a time constant of 30  ms.

Blackbody detection and imaging system

The blackbody source (HT-P1000) was placed at varying distances from the device with a chopper modulation frequency of 1000 Hz. The blackbody radiant power is given by the formula \(P=\sigma \alpha \varepsilon {R}^{2}\frac{({T}_{{{{\rm{B}}}}}^{4}-{T}_{0}^{4})A}{{L}^{2}}\), where σ is the Stefan-Boltzmann constant, α is the modulation factor (\({2}^{-\frac{1}{2}}\)), ε represents the average emissivity (0.9 in this case), R denotes the aperture radius, TB and T0 represent the blackbody radiation source temperature and the room temperature (300  K), respectively. A is the device area, and L is the distance between the aperture and the device. In the laser and heat target imaging system, the PbSe device is mounted on a piezo x-y stage, facilitating surface scanning to capture focused light or target information. The silicon wafer was placed near the heating tube to absorb the visible light.

Numerical simulation

A two-temperature model for the PbSe PTE devices was established using the COMSOL Heat Transfer Module. This model, based on electron-phonon coupling, conveys the temperature evolution of photoexcited electrons and phonons with the following equations19:

$${C}_{{{{\rm{e}}}}}\frac{\partial {T}_{{{{\rm{e}}}}}}{\partial t}=\nabla \left({\kappa }_{{{{\rm{e}}}}}\nabla {T}_{{{{\rm{e}}}}}\right)-\gamma \left({T}_{{{{\rm{e}}}}}-{T}_{{{{\rm{ph}}}}}\right)+Q\left(x,y\right)$$
(1)
$${C}_{{{{\rm{ph}}}}}\frac{\partial {T}_{{{{\rm{ph}}}}}}{\partial t}=\nabla \left({\kappa }_{{{{\rm{ph}}}}}\nabla {T}_{{{{\rm{ph}}}}}\right)+\gamma \left({T}_{{{{\rm{e}}}}}-{T}_{{{{\rm{ph}}}}}\right)$$
(2)

where Ci is the specific heat capacity, \({\kappa }_{{{{\rm{i}}}}}\) is the thermal conductivity, \(\gamma\) is the electron-phonon coupling coefficient, and the subscripts e and ph refer to electrons and phonons, respectively. The thermal parameters for the PbSe film are sourced from literature refs. 38,48. The power intensity Q absorbed by the PbSe devices follows a Gaussian distribution, with the FWHM and half of the laser spot size assumed to be consistent. Under quasi-steady-state conditions, the temperature difference (\(\Delta T\)) between the two ends was obtained at various laser positions, and a mapping diagram of \(\Delta T\) was produced.