Introduction

Hermiticity is a fundamental concept in quantum mechanics as it ensures the reality of energies. Interestingly, it has been discovered that the requirement of Hermiticity can be relaxed in favor of considering parity-time (PT) symmetry, which also guarantees the reality of energies when the corresponding eigenstates respect the symmetry1,2,3. Notably, if a state violates the symmetry, its eigenvalue becomes complex. In a two-level system, a second-order exceptional point (EP2) appears at the transition point, where the Hamiltonian becomes nondiagonalizable4,5. The PT symmetry breaking in two-level systems has garnered significant interest across various fields, further promoting the study of diverse phenomena in non-Hermitian physics6,7,8,9,10,11,12, including single-mode lasers13,14, exceptional points, rings or knots15,16,17,18,19,20,21,22,23,24, enhanced sensing25, and unidirectional invisibility26. Moreover, experimental observations have confirmed the existence of two-mode PT symmetry breaking and related non-Hermitian topology in quantum systems27,28,29,30,31,32,33,34,35,36.

In systems with more than two levels, the PT symmetry breaking can lead to higher-order exceptional points (EPs) beyond the second order. For instance, in a ternary PT symmetric system, a third-order EP (EP3) can arise from the PT symmetry breaking, where a 3 × 3 non-Hermitian Hamiltonian has only one eigenstate. Remarkably, higher-order EPs can exhibit peculiar topological properties and sensitivity enhancement37,38,39,40. Consequently, significant efforts have been directed towards experimentally exploring EP3 and their topological properties in optical systems41,42, cavity optomechanical systems39, acoustics systems40, and Bose-Einstein condensates43. In quantum systems, two approaches are usually employed to implement a non-Hermitian Hamiltonian. One approach, named the dilation method, employs the dynamics of a Hermitian Hamiltonian involving a system qubit and an ancilla qubit to realize the non-Hermitian dynamics in a subspace27,44,45. This method has been utilized to observe a third-order exceptional line in a nitrogen-vacancy spin system46. The other method involves applying dissipation to achieve the non-Hermitian Hamiltonian, which has been applied in cold atom systems28,35,43,47, superconducting circuits29,30,48, and trapped ions31,32,49. However, the observation of the PT symmetry-breaking-induced EP3 in these systems requires two loss channels, making it difficult to describe the dynamics using an effective non-Hermitian Hamiltonian.

Here, we experimentally investigate the EP3 associated with PT symmetry breaking in a dissipative trapped-ion system. By precisely engineering the system Hamiltonian and two loss channels, we realize a three-level effective non-Hermitian Hamiltonian possessing both PT and anti-PT symmetries, which protect the existence of an EP3 within a one-dimensional parameter space. We prove that the dynamics in non-Hermitian absorption spectroscopy50 is governed by the effective non-Hermitian Hamiltonian, enabling the observation of the EP3 and the associated winding topology. In particular, we find that an off-diagonal sector of a density matrix undergoes a non-Hermitian evolution, allowing us to perform quantum state tomography across the EP3. This enables the direct observation of the coalescence of three eigenstates into a single eigenstate—an unambiguous feature of an EP3. Finally, we find that the Lindbladian, which is also a non-Hermitian matrix in Liouville space, exhibits an intrinsic EP3, and we experimentally identify this EP3 by quenching a non-physical initial state.

Results

PT symmetry-breaking-induced EP3 in a dissipative trapped ion

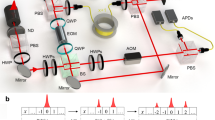
We realize a dissipative three-level system using a single trapped 171Yb+ ion, as illustrated in Fig. 1a. The three system levels are encoded in the hyperfine states \(\left\vert 0\right\rangle \equiv \left\vert F=1,{m}_{F}=1\right\rangle\), \(\left\vert 1\right\rangle \equiv \left\vert F=0,{m}_{F}=0\right\rangle\) and \(\left\vert 2\right\rangle \equiv \left\vert F=1,{m}_{F}=0\right\rangle\) within the 2S1/2 ground state manifold (see Fig. 1b). The hyperfine splitting ωHF ≈ 2π × 12.6 GHz allows us to couple \(\left\vert 1\right\rangle\) with \(\left\vert 0\right\rangle\) and \(\left\vert 2\right\rangle\) using microwaves, as indicated by the black arrows in Fig. 1b. To induce dissipation in \(\left\vert 1\right\rangle\) (\(\left\vert 2\right\rangle\)), we use a 370 nm laser B (C) to couple it with an excited state \(\left\vert {e}_{1}\right\rangle \equiv {| }^{2}{P}_{1/2},F=1,{m}_{F}=0\left.\right\rangle\) (\(\left\vert {e}_{2}\right\rangle \equiv {| }^{2}{P}_{1/2},F=1,{m}_{F}=0\left.\right\rangle\)), denoted by a dark (light) purple arrow in Fig. 1b. According to selection rules, \(\left\vert {e}_{1}\right\rangle\) (\(\left\vert {e}_{2}\right\rangle\)) spontaneously decays to \(\left\vert 0\right\rangle\), \(\left\vert 1\right\rangle\) (\(\left\vert 2\right\rangle\)), and \(\left\vert 3\right\rangle \equiv \left\vert F=0,{m}_{F}=-1\right\rangle\) with equal probabilities, as shown in Fig. 1b by the dotted (dashed) lines.

Fig. 1: Schematics of experimental configurations, and experimental results via non-Hermitian absorption spectroscopy.
figure 1

a We use a 370 nm laser beam A for cooling, optical pumping and state detection, 370 nm lasers B and C to realize the dissipation in the \(\left\vert 1\right\rangle\) and \(\left\vert 2\right\rangle\) levels, respectively, and microwaves to generate the Hermitian part of the Hamiltonian. A 411 nm laser is applied to drive the transition between the levels \(\left\vert 1\right\rangle\) and \(\left\vert a\right\rangle\) for non-Hermitian absorption spectroscopy. Laser with wavelengths of 935 nm, 3432 nm, and 976 nm are also utilized as auxiliary components in the experiments (see Supplementary Information S-1 for detailed descriptions of our experimental setup). The magnetic field has a small out-of-plane component in addition to the in-plane component so that B = B∥ + B⊥. b The main energy levels and transitions used in our experiment. Transitions driven by the microwaves, the 370 nm lasers B and C, and the 411 nm laser are described by black, purple, and blue arrows, respectively. Spontaneous decay of the excited states is shown by dotted and dashed lines. Real (c) and imaginary (d) parts of complex eigenenergies obtained by theoretical calculations (solid lines) are shown together with experimental data points (circles). e Real part of the eigenenergies near the EP3 (marked by the star) as a function of two additional detunings Δ0 and Δ1. f Theoretical (solid lines) and experimental complex eigenenergies (circles) with respect to θ defined through \({\Delta }_{0}={\Delta }_{r}\cos \theta\) and \({\Delta }_{1}={\Delta }_{r}\sin \theta\) with Δr = 2π × 0.020 MHz. The energy bands are marked with the same colors as in (e), and the starting points at θ = 0 are marked by circles in (e). In (c–f) γ = 2π × 0.040MHz, Ωa = 2π × 0.004 MHz, and the evolution time is ta = 200 μs. The experimental results are averaged over 5 rounds of experiments (each contains 200 shots) with error bars being the standard deviation of the five experimental repetitions (error bars for some data points are smaller than the symbol size).

Full size image

The dynamics of the system is described by the following master equation (ℏ = 1) (see “Methods” Adiabatic elimination for the master equation for details on deriving the equation through adiabatic elimination)

$$\frac{d\rho }{dt}={{{\mathcal{L}}}}[\rho ]=-i[H,\rho ]+{\sum }_{\mu=1}^{6}\left({L}_{\mu }\rho {L}_{\mu }^{{{\dagger}} }-\frac{1}{2}\{{L}_{\mu }^{{{\dagger}} }{L}_{\mu },\rho \}\right),$$
(1)

where \(H=\frac{{\Omega }_{1}}{\sqrt{2}}\left\vert 0\right\rangle \left\langle 1\right\vert+\frac{{\Omega }_{2}}{\sqrt{2}}\left\vert 1\right\rangle \left\langle 2\right\vert+{{{\rm{H.c.}}}}\) with Ω1,2 being the coupling strength controlled by the microwaves, \({L}_{1}={c}_{1}\left\vert 0\right\rangle \left\langle 1\right\vert\), \({L}_{2}={c}_{1}\left\vert 1\right\rangle \left\langle 1\right\vert\), \({L}_{3}={c}_{1}\left\vert 3\right\rangle \left\langle 1\right\vert\), \({L}_{4}={c}_{2}\left\vert 0\right\rangle \left\langle 2\right\vert\), \({L}_{5}={c}_{2}\left\vert 2\right\rangle \left\langle 2\right\vert\), and \({L}_{6}={c}_{2}\left\vert 3\right\rangle \left\langle 2\right\vert\) are quantum jump operators with \({c}_{n}=\sqrt{2{\gamma }_{n}/3}\), and \({\gamma }_{n}=2{J}_{n}^{2}/\Gamma\) for n = 1, 2 (J1,2 are controlled through 370 nm lasers B and C, and Γ ≈ 2π × 19.6 MHz51 arising from the short lifetime of the 2P1/2 states). If we can neglect the contribution of quantum jump terms \({\sum }_{\mu }{L}_{\mu }\rho {L}_{\mu }^{{{\dagger}} }\), then the dynamics is governed by the effective non-Hermitian Hamiltonian \({H}_{{{{\rm{eff}}}}}=H-\frac{{{{\rm{i}}}}}{2}{\sum }_{\mu }{L}_{\mu }^{{{\dagger}} }{L}_{\mu }\), which reads

$$\left(\begin{array}{ccc}0&\frac{{\Omega }_{1}}{\sqrt{2}}&0\\ \frac{{\Omega }_{1}}{\sqrt{2}}&-{{{\rm{i}}}}{\gamma }_{1}&\frac{{\Omega }_{2}}{\sqrt{2}}\\ 0&\frac{{\Omega }_{2}}{\sqrt{2}}&-{{{\rm{i}}}}{\gamma }_{2}\end{array}\right)$$
(2)

relative to the basis \(\{\left\vert 0\right\rangle,\left\vert 1\right\rangle,\left\vert 2\right\rangle \}\).

When Ω1 = Ω2 = Ω and γ1 = γ2/2 = γ, we obtain Heff = heff − iγI3 where I3 is a 3 × 3 identity matrix and heff = ΩSx +iγSz with Sx and Sz being the spin-1 matrices. In this case, heff respects both PT symmetry, \({U}_{{{{\rm{PT}}}}}{h}_{{{{\rm{eff}}}}}{U}_{{{{\rm{PT}}}}}^{-1}={h}_{{{{\rm{eff}}}}}\), and anti-PT symmetry, \({U}_{{{{\rm{APT}}}}}{h}_{{{{\rm{eff}}}}}{U}_{{{{\rm{APT}}}}}^{-1}=-{h}_{{{{\rm{eff}}}}}\), where

$${U}_{{{{\rm{PT}}}}}=\left(\begin{array}{ccc}0&0&1\\ 0&1&0\\ 1&0&0\end{array}\right)\kappa,\,\,{U}_{{{{\rm{APT}}}}}=\left(\begin{array}{ccc}1&0&0\\ 0&-1&0\\ 0&0&1\end{array}\right)\kappa,$$
(3)

with κ being the complex-conjugation operator. PT (anti-PT) symmetry ensures that an eigenenergy of heff is purely real (imaginary) when the corresponding eigenstate respects the symmetry, and the set of all eigenenergies are symmetric with respect to the real (imaginary) axis when the symmetry is broken. Consequently, as we vary a system parameter Ω/γ, if the transition for both symmetry breaking occurs at the same parameter value (e.g., Ω/γ = 1), then the eigenenergies must transition between purely real and purely imaginary values across the transition point. At this point, all three eigenenergies are zero, and an EP3 appears52. Indeed, by solving the eigenvalue problem, we obtain the eigenenergies of heff as \({E}_{\pm }=\pm \sqrt{{\Omega }^{2}-{\gamma }^{2}}\) and E0 = 0, with the corresponding right eigenstates being

$$\left\vert {\psi }_{\pm }\right\rangle ={\left(-\frac{\gamma \mp {{{\rm{i}}}}\sqrt{{\Omega }^{2}-{\gamma }^{2}}}{2\Omega },\frac{{{{\rm{i}}}}}{\sqrt{2}},\frac{\gamma \pm {{{\rm{i}}}}\sqrt{{\Omega }^{2}-{\gamma }^{2}}}{2\Omega }\right)}^{T},\\ \left\vert {\psi }_{0}\right\rangle =\frac{1}{\sqrt{{\Omega }^{2}+{\gamma }^{2}}}{\left(-\frac{\Omega }{\sqrt{2}},{{{\rm{i}}}}\gamma,\frac{\Omega }{\sqrt{2}}\right)}^{T}.$$
(4)

For Ω > γ (Ω < γ), the eigenenergies are purely real (imaginary), corresponding to preserved (broken) PT symmetry. Notably, at Ω = γ, not only do the eigenenergies become degenerate, but all three eigenstates coalesce into a single state \(\left\vert {{{\rm{EP}}}}\right\rangle=\frac{1}{2}(-1,{{{\rm{i}}}}\sqrt{2},1)\), indicating the presence of an EP3. Thus, by tuning the ratio Ω/γ, one can observe a PT transition associated with an EP3, protected by the PT and anti-PT symmetries52,53.

However, the presence of quantum jump terms \({\sum }_{\mu }{L}_{\mu }\rho {L}_{\mu }^{{{\dagger}} }\) can cause the dynamics to deviate significantly from the pure non-Hermitian evolution described by Heff. For example, 2/3 of the decayed population is returned to the system levels through the quantum jumps, which is not the case in the non-Hermitian evolution. In the following, we will employ two approaches to eliminate the effects of the quantum jump terms and experimentally detect the EP3 in Heff associated with the PT symmetry breaking. Furthermore, we find that the Lindbladian \({{{\mathcal{L}}}}\), which is also a non-Hermitian matrix in Liouville space, exhibits an intrinsic EP3 at Ω = γ. By leveraging the anti-PT symmetry of the Lindbladian, we can experimentally detect this Liouvillian EP3 by quenching a non-physical density matrix with zero trace.

Non-Hermitian absorption spectroscopy

To measure the complex eigenenergies of the effective non-Hermitian Hamiltonian, we introduce an auxiliary energy level \(\left\vert a\right\rangle \equiv {| }^{2}{D}_{5/2},F=2,m=0\left.\right\rangle\), which is coupled to the system level \(\left\vert 1\right\rangle\) by a 411 nm laser (see Fig. 1b). In this setup, the Hamiltonian is modified to

$${H}_{{{{\rm{NAS}}}}}={H}_{{{{\rm{eff}}}}}+\frac{{\Omega }_{a}}{2}(\left\vert 1\right\rangle \left\langle a\right\vert+{{{\rm{H.c.}}}})-{\delta }_{a}\left\vert a\right\rangle \left\langle a\right\vert,$$
(5)

where Ωa is the Rabi frequency, δa is the detuning, and the involved energy levels are \(\left\vert 0\right\rangle\), \(\left\vert 1\right\rangle\), \(\left\vert 2\right\rangle\), and \(\left\vert a\right\rangle\). We initially prepare the ion in the auxiliary state \(\left\vert a\right\rangle\). As time evolves, the population is transferred to the system levels and subsequently dissipates to the loss state \(\left\vert 3\right\rangle\). Finally, we measure the remaining population in \(\left\vert a\right\rangle\) with respect to the detuning δa (see Methods Sec. B), which contains information of the complex eigenenergies of the system49,50.

By setting Ωa sufficiently small, the effects of the quantum jump terms become negligible, allowing the system to undergo a non-Hermitian evolution. This is because the quantum jump terms significantly affect the dynamics only when there is sufficient population in \(\left\vert 1\right\rangle\) and \(\left\vert 2\right\rangle\). However, with a small Ωa, any population transferred to the system levels dissipates quickly to the loss state \(\left\vert 3\right\rangle\), resulting in negligible population in \(\left\vert 1\right\rangle\) and \(\left\vert 2\right\rangle\) (see “Methods” in Non-Hermitian absorption spectroscopy). As a consequence, the population in the auxiliary level at time ta is determined by the non-Hermitian evolution

$${N}_{a}={N}_{0}{\left\vert \left\langle a\right\vert {e}^{-{{{\rm{i}}}}{H}_{{{{\rm{NAS}}}}}{t}_{a}}\left\vert a\right\rangle \right\vert }^{2},$$
(6)

where we introduce a variable N0 to account for the state preparation and measurement error. We extract the complex eigenenergies of the system by fitting the experimental measurement results based on the theoretical population \({N}_{a,i}^{{{{\rm{tgt}}}}}\) calculated from Eq. (6) with slight modifications to account for the finite lifetime  (~ 7.4 ms) of \(\left\vert a\right\rangle\) (see “Methods” in Non-Hermitian absorption spectroscopy).

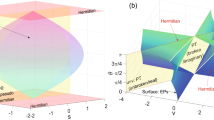
To experimentally observe the EP3 associated with the PT symmetry breaking, we tune the ratio Ω/γ from 0.4 to 1.6 across Ω/γ = 1. By measuring the remaining population in \(\left\vert a\right\rangle\) at the end of the dynamics with respect to the detuning δa (referred to as a spectral line) for each ratio and fitting these spectral lines using the method presented in Methods Non-Hermitian absorption spectroscopy, we extract the complex eigenenergies with respect to Ω/γ, with the real and imaginary components displayed in Fig. 1c and d, respectively. The measured eigenenergies closely match the theoretical values, indicating the PT symmetry-broken phase for Ω < γ and the unbroken phase for Ω > γ, with the EP3 occurring at Ω = γ.

To further confirm the existence of an EP3, we probe the spectral topology associated with the EP3. We set Ω = γ and introduce additional detuning terms (\(-{\Delta }_{0}\left\vert 0\right\rangle \left\langle 0\right\vert -{\Delta }_{1}\left\vert 1\right\rangle \left\langle 1\right\vert\)) in the system levels by varying the frequencies of the microwaves. As shown in Fig. 1e, the eigenenergies with respect to Δ0 and Δ1 exhibit a multi-sheeted structure. Starting from an arbitrary point, one needs to encircle the EP3 three times to return to the original eigenenergy (e.g., following a path defined by \({\Delta }_{0}={\Delta }_{r}\cos \theta\) and \({\Delta }_{1}={\Delta }_{r}\sin \theta\) with Δr = 2π × 0.020 MHz as shown by the solid lines in Fig. 1e), in contract to paths that do not encircle the EP3. The winding topology of the three energy bands is clearly revealed by the extracted complex eigenenergies with respect to θ, as shown in Fig. 1f through measuring the spectral lines along this path. This feature can also be characterized by the winding number relative to an energy EB inside a loop54

$$W={\int}_{0}^{2m\pi }\frac{d\theta }{2m\pi }{\partial }_{\theta }\,{{\arg }}({E}_{n}(\theta )-{E}_{B}),$$
(7)

where En is the complex eigenenergy of the nth band, and m is the smallest integer so that En(θ) = En(θ + 2πm) (here m = 3) [we define \({E}_{n}(\theta+2\pi k)={E}_{(n+k){{{\rm{mod}}}}m}(\theta )\) so that En(θ) is continuous over θ]. Our results demonstrate that W = 1/3, indicating the 6π periodicity of each band (see “Methods” in Non-Hermitian absorption spectroscopy).

Eigenstate tomography

A definitive feature of an EP3 is the coalescence of three eigenstates into a single eigenstate at this point. We now demonstrate the coalescence through eigenstate tomography, where we scan the Hilbert space to identify the eigenstates of the non-Hermitian Hamiltonian Heff without the requirement of an auxiliary level. Unfortunately, the dynamics described by Eq. (1) in the absence of an auxiliary level is not equivalent to the dynamics of a non-Hermitian Hamiltonian Heff. We address the problem by finding, based on Eq. (1), that an off-diagonal sector \(v(t)={({\rho }_{03}(t),{\rho }_{13}(t),{\rho }_{23}(t))}^{T}\) of the density matrix ρ(t) satisfies a non-Hermitian evolution: \(d{\rho }_{n3}/dt=- \! {{{\rm{i}}}}\left\langle n\right\vert {H}_{{{{\rm{eff}}}}}\rho \left\vert 3\right\rangle\) for n = 0, 1, 2 so that \(v(t)={e}^{-{{{\rm{i}}}}{H}_{{{{\rm{eff}}}}}t}v(0)\) (see “Methods” Quench dynamics for the derivation). Thus, the PT transition can be detected by initially preparing a pure state \(\rho (0)=\frac{1}{2}(\left\vert \psi \right\rangle+\left\vert 3\right\rangle ) \, (\left\langle \psi \right\vert+\left\langle 3\right\vert )\) and monitoring the dynamics of v(t) by measuring the off-diagonal sector v(t) of the evolving density matrix (see Supplementary Information S-3 on how we measure the off-diagonal elements).

If \(\left\vert \psi \right\rangle\) is an eigenstate of Heff, then v(t) will experience only an overall decay in amplitude, and the normalized off-diagonal elements \({\rho }_{i3}^{{{{\rm{n}}}}}(t)={\rho }_{i3}(t)/| v(t)|\) (i = 0, 1, 2) should remain invariant during the evolution. Therefore, the zero points of the variation of the normalized off-diagonal elements \(\Delta | {\rho }_{i3}^{{{{\rm{n}}}}}{| }^{2}=| {\rho }_{i3}^{{{{\rm{n}}}}}(\Delta t){| }^{2}-| {\rho }_{i3}^{{{{\rm{n}}}}}(0){| }^{2}\) with respect to \(\left\vert \psi \right\rangle\) reveal the eigenstates of Heff. The presence of PT and anti-PT symmetry significantly simplifies the procedure by imposing constraints that reduce the dimension of the search space. Based on these symmetries and additional constraints imposed by the Hamiltonian, we only need to scan a parameter space specified by \(\left\vert {u}_{z}(\phi )\right\rangle=\frac{1}{2}{(-{e}^{{{{\rm{i}}}}\phi },{{{\rm{i}}}}\sqrt{2},{e}^{-{{{\rm{i}}}}\phi })}^{T}\) for Ω > γ, \(\left\vert {u}_{x}(\phi )\right\rangle={(-\frac{1+\sin \phi }{2},{{{\rm{i}}}}\frac{\cos \phi }{\sqrt{2}},\frac{1-\sin \phi }{2})}^{T}\) for Ω < γ, and \(\left\vert {u}_{0}(\varphi )\right\rangle=\frac{1}{\sqrt{2}}{(-\sin \varphi,{{{\rm{i}}}}\sqrt{2}\cos \varphi,\sin \varphi )}^{T}\) for all Ω (see Methods in Eigenstate tomography). \(\left\vert {u}_{z}(\phi )\right\rangle\) and \(\left\vert {u}_{x}(\phi )\right\rangle\) become the eigenstates \(\left\vert {\psi }_{\pm }\right\rangle\) when \(\phi=\pm {\cos }^{-1}(\gamma /\Omega )\) for Ω > γ and \(\phi=\pm {\cos }^{-1}(\Omega /\gamma )\) for Ω < γ, respectively, and \(\left\vert {u}_{0}(\varphi )\right\rangle=\left\vert {\psi }_{0}\right\rangle\) when \(\varphi={\tan }^{-1}(\Omega /\gamma )\). Specifically, \(\left\vert {u}_{z}(\phi )\right\rangle=\left\vert {u}_{x}(\phi )\right\rangle=\left\vert {u}_{0}(\varphi )\right\rangle=\left\vert {{{\rm{EP}}}}\right\rangle\) when ϕ = 0 and φ = π/4.

Figure 2 a shows the variation \(\Delta | {\rho }_{23}^{{{{\rm{n}}}}}{| }^{2}\) with respect to ϕ and Ω/γ for Ω > γ with the initial state being \(\left\vert {u}_{z}(\phi )\right\rangle\), while Fig. 2b displays \(\Delta | {\rho }_{13}^{{{{\rm{n}}}}}{| }^{2}\) for Ω < γ with the initial state being \(\left\vert {u}_{x}(\phi )\right\rangle\). Regions where \(\Delta | {\rho }_{i3}^{{{{\rm{n}}}}}{| }^{2}\approx 0\) are highlighted in white. The zero points of \(\Delta | {\rho }_{i3}^{{{{\rm{n}}}}}{| }^{2}\) are determined by linear interpolation between adjacent experimental data points of opposite signs (see Methods in Eigenstate tomography). These zero points, indicated by circles, show good agreement with the theoretical values (dashed lines). We extract the eigenstates as \(\left\vert {\psi }_{\pm }\right\rangle=\left\vert {u}_{z}({\phi }_{\pm })\right\rangle\) for Ω > γ and \(\left\vert {\psi }_{\pm }\right\rangle=\left\vert {u}_{x}({\phi }_{\pm })\right\rangle\) for Ω < γ, where ϕ+ and ϕ− are the average values of the zero points in ϕ > 0 and ϕ < 0 regions, respectively. In the ϕ < 0 region of Fig. 2b, we exclude the smallest and largest zero points (marked by crosses), as they do not correspond to the eigenstates. Similarly, the eigenstate \(\left\vert {\psi }_{0}\right\rangle\) is extracted by using \(\left\vert {u}_{0}(\varphi )\right\rangle\) as the initial states (see Fig. 2c, d). The eigenstate is given by \(\left\vert {\psi }_{0}\right\rangle=\left\vert {u}_{0}({\varphi }_{0})\right\rangle\) with φ0 being the average value of the zero points, marked by circles in Fig. 2c, d. To illustrate the collapse of the three states to a single one at the EP3, we show the inner products 〈ψ−∣ψ+〉 and 〈ψ±∣ψ0〉 of the measured states for the PT symmetry-unbroken and broken regime in Fig. 2e and f, respectively. The results demonstrate that as Ω/γ approaches 1, the three eigenstates become increasingly aligned and eventually coalesce into a single vector at Ω/γ = 1, experimentally confirming the existence of an EP3.

Fig. 2: Experimental results for eigenstate tomography.
figure 2

a–d Variation of the normalized off-diagonal elements \(\Delta | {\rho }_{j3}^{{{{\rm{n}}}}}{| }^{2}\) with respect to ϕ (or φ) and Ω/γ. The initial state is \(\left\vert {u}_{z}(\phi )\right\rangle\) in (a), \(\left\vert {u}_{x}(\phi )\right\rangle\) in (b) and \(\left\vert {u}_{0}(\varphi )\right\rangle\) in (c, d) (see their definitions in the main text). In (a, c, d), j = 2, and in (b) j = 1. The circles indicate the zero points obtained by linearly interpolating the experimental data (see “Methods” in Eigenstate tomography), and the black dashed lines represent the theoretical values: \(\phi=\pm {\cos }^{-1}(\gamma /\Omega )\) for (a) \(\phi=\pm {\cos }^{-1}(\Omega /\gamma )\) for (b) and \(\varphi={\tan }^{-1}(\Omega /\gamma )\) for (c, d). The crosses in (b) also denote zero points but are excluded in the calculation of inner products since they do not correspond to the eigenstates. e, f Inner products of the eigenstates \(\left\vert {\psi }_{\pm }\right\rangle\) and \(\left\vert {\psi }_{0}\right\rangle\) for the PT symmetry-unbroken (Ω/γ > 1) and broken regime (Ω/γ < 1). The solid lines are obtained by Eq. (4), and the diamonds are experimental data.

Full size image

We further demonstrate the EP3 associated with the PT symmetry breaking through quench dynamics from an initial state \(\rho (0)=(1/2)(\left\vert 0\right\rangle+\left\vert 3\right\rangle )(\left\langle 0\right\vert+\left\langle 3\right\vert )\). We find that the density matrix element ρ03 exhibits oscillatory and decaying behaviors for Ω > γ and Ω < γ, respectively (see “Methods” in Quench dynamics), providing further evidence that all three eigenenergies transition from purely real to purely imaginary across the EP3.

Liouvillian EP3

EPs can also occur in the Liouvillian spectrum48,55,56,57,58. In fact, the non-Hermitian EP3 discussed in previous sections can be regarded as a Liouvillian EP3. Specifically, for \({\rho }_{n}^{{{{\rm{R}}}}}=\left\vert {\psi }_{n}\right\rangle \left\langle 3\right\vert\) with n = 0, + , − , we have \({{{\mathcal{L}}}}[{\rho }_{n}^{{{{\rm{R}}}}}]=-{{{\rm{i}}}}{E}_{n}{\rho }_{n}^{{{{\rm{R}}}}}\). Thus, the three eigenmatrices coalesce into a single density matrix \(\left\vert {{{\rm{EP}}}}\right\rangle \left\langle 3\right\vert\) at Ω = γ. Similarly, for \({\rho }_{n}^{{{{\rm{L}}}}}=\left\vert 3\right\rangle \left\langle {\psi }_{n}\right\vert\), we find \({{{\mathcal{L}}}}[{\rho }_{n}^{{{{\rm{L}}}}}]={{{\rm{i}}}}{E}_{n}^{*}{\rho }_{n}^{{{{\rm{L}}}}}\). This Liouvillian EP3 originates purely from the effective non-Hermitian Hamiltonian, as seen in the relation that \({{{\mathcal{L}}}}[{\rho }_{n}^{{{{\rm{R}}}}}]=- {{{\rm{i}}}}{H}_{{{{\rm{eff}}}}}{\rho }_{n}^{{{{\rm{R}}}}}\) and \({{{\mathcal{L}}}}[{\rho }_{n}^{{{{\rm{L}}}}}]={{{\rm{i}}}}{\rho }_{n}^{{{{\rm{L}}}}}{H}_{{{{\rm{eff}}}}}^{{{\dagger}} }\) (see Methods in Liouvillian EP3 for more details). This raises the question of whether an intrinsic EP3 exists for the Liouvillian itself. Interestingly, we identify three eigenmatrices, ρ± and ρ0, with eigenvalues \({\lambda }_{\pm }=-2\gamma \pm {{{\rm{i}}}}\sqrt{{\Omega }^{2}-{\gamma }^{2}}\) and λ0 = − 2γ (see “Methods” in Liouvillian EP3E. 1), distinct from the aforementioned eigenmatrices as they do not involve \(\left\vert 3\right\rangle\). These eigenmatrices coalesce into a single density matrix \({\rho }_{{{{\rm{EP}}}}}=\left\vert 0\right\rangle \left\langle 1\right\vert+\left\vert 1\right\rangle \left\langle 2\right\vert+{{{\rm{i}}}}\sqrt{2}\left\vert 0\right\rangle \left\langle 2\right\vert+{{{\rm{H.c.}}}}\) at Ω = γ, with the eigenvalues transitioning between purely real and purely imaginary up to a constant shift.

To detect the Liouvillian EP3 associated with the PT transition, we use a non-physical initial state \(\rho (0)=\left\vert {u}_{1}\right\rangle \left\langle {u}_{1}\right\vert -\left\vert {u}_{2}\right\rangle \left\langle {u}_{2}\right\vert\), where \(\left\vert {u}_{n}\right\rangle=\frac{1}{\sqrt{2}}(\left\vert 0\right\rangle+{{{\rm{i}}}}{(-1)}^{n}\left\vert 2\right\rangle )\) for n = 1, 2. Due to the anti-PT symmetry of the open quantum system, elements of ρ(t) can be detected by preparing a single state \(\sigma (0)=\left\vert {u}_{1}\right\rangle \left\langle {u}_{1}\right\vert\) and measuring the elements of σ(t) (see Methods Detection of the intrinsic Liouvillian EP3). The experimentally measured off-diagonal elements ρ12 − ρ01, shown in Fig. 3a, along with the theoretical results in Fig. 3b, reveal that ρ12 − ρ01 oscillates when Ω > γ and decays exponentially after the first peak when Ω < γ, indicating the PT symmetry breaking at Ω = γ. We further fit ρ12 − ρ01 to damped sinusoidal and hyperbolic sine functions given by \({f}_{1}(\gamma t)={A}_{1}{e}^{-2\gamma t}\sin ({B}_{1}\gamma t)\) and \({f}_{2}(\gamma t)={A}_{2}{e}^{-2\gamma t}\sinh ({B}_{2}\gamma t)\), respectively, as shown in Fig. 3c. We find that in the PT symmetry unbroken (symmetry-broken) phase, the former (latter) fitting function yields a lower error than the latter (former) with the corresponding fitted oscillation factor B1 and decay factor B2 shown in Fig. 3d. The results clearly indicates the PT transition of the Lindbladian \({{{\mathcal{L}}}}\) at Ω = γ.

Fig. 3: Results for observing a Liouvillian EP3 via quench dynamics.
figure 3

a Experimental and (b) theoretical values of ρ12 − ρ01 with respect to the normalized evolution time γt and the ratio Ω/γ. The dashed lines indicate the evolution results at the EP3. c Curve fitting using the damped sinusoidal function for experimental data (circles) at Ω/γ = 5. The inset shows the fitting results using the hyperbolic sine function at Ω/γ = 0.5. The experimental data are averaged over 1000 repetitions. d Fitted oscillation and decay factors B1 and B2 with respect to Ω/γ. The theoretical results are \({B}_{1,2}=| \sqrt{{(\Omega /\gamma )}^{2}-1}|\) (see Method in Liouvillian EP3). Error bars, some of which are smaller than the symbols, denote the 95% confidence intervals of the fit.

Full size image

In summary, we have experimentally detected an EP3 associated with PT symmetry breaking in a dissipative trapped ion system, focusing on both the non-Hermitian and Liouvillian aspects. For the non-Hermitian case, we demonstrate the existence of an EP3 and the PT transition via non-Hermitian absorption spectroscopy, eigenstate tomography, and quench dynamics. For the Liouvillian case, we show that the non-Hermitian EP3s can also be interpreted as Liouvillian EP3s. We further experimentally identify an intrinsic Liouvillian EP3 associated with a PT transition by quench dynamics. These results may enable further exploration of peculiar non-Hermitian topological properties, such as braiding of three complex energy bands59,60, and non-Hermitian applications, such as chiral state transfer48 and sensing, in a dissipative quantum system. EPs of orders higher than three can also be achieved by introducing additional energy levels and engineered losses. In addition, given that the EP3 is implemented through precise control of dissipation, this technology has the potential to advance quantum computation, quantum simulation and quantum metrology61,62.

Note added in proof. After the submission of this manuscript, we became aware of a related study reporting the experimental realization of a fourth-order exceptional point in a trapped 40Ca+ ion63.

Methods

Adiabatic elimination for the master equation

The dynamics of the full system described in Fig. 1b is governed by the Lindblad master equation (ℏ = 1)

$$\frac{d{\rho }_{f}}{dt}=-i[{H}_{f},{\rho }_{f}]+{\sum }_{\mu=1}^{6}({L}_{f,\mu }{\rho }_{f}{L}_{f,\mu }^{{{\dagger}} }-\frac{1}{2}\{{L}_{f,\mu }^{{{\dagger}} }{L}_{f,\mu },{\rho }_{f}\}),$$
(8)

where \({H}_{f}=H+({J}_{1}\left\vert 1\right\rangle \left\langle {e}_{1}\right\vert+{J}_{2}\left\vert 2\right\rangle \left\langle {e}_{2}\right\vert+{{{\rm{H.c.}}}})\) with \(H=\frac{{\Omega }_{1}}{\sqrt{2}}\left\vert 0\right\rangle \left\langle 1\right\vert+\frac{{\Omega }_{2}}{\sqrt{2}}\left\vert 1\right\rangle \left\langle 2\right\vert \!+{{{\rm{H.c.}}}}\), \({L}_{f,1}=c\left\vert 0\right\rangle \left\langle {e}_{1}\right\vert\), \({L}_{f,2}=c\left\vert 1\right\rangle \left\langle {e}_{1}\right\vert\), \({L}_{f,3}=c\left\vert 3\right\rangle \left\langle {e}_{1}\right\vert\), \({L}_{f,4}=c\left\vert 0\right\rangle \left\langle {e}_{2}\right\vert\), \({L}_{f,5}=c\left\vert 2\right\rangle \left\langle {e}_{2}\right\vert\), \({L}_{f,6}=c\left\vert 3\right\rangle \left\langle {e}_{2}\right\vert\), and \(c=\sqrt{\Gamma /3}\). Here, Ω1,2 (J1,2) are controlled by the microwaves (370 nm lasers B and C), and Γ = 1/τP ≈ 2π × 19.6 MHz with τP ≈ 8.12 ns being the lifetime of the 2P1/2 states64. Note that theoretically we have neglected the decay of the 2P1/2 states towards 2D3/2 due to the small branching ratio  (~0.5%), and experimentally we use a 935 nm laser to pump the leakage into 2D3/2 back to the 2S1/2 manifold (see Supplementary Information S-1 for details). The full system master equation [Eq. (8)] can be rewritten as

$$\frac{d{\rho }_{f}}{dt}= -{{{\rm{i}}}}[{H}_{f},{\rho }_{f}]+\frac{\Gamma }{3}{\rho }_{{e}_{1}{e}_{1}}(\left\vert 0\right\rangle \left\langle 0\right\vert+\left\vert 1\right\rangle \left\langle 1\right\vert+\left\vert 3\right\rangle \left\langle 3\right\vert )\\ +\frac{\Gamma }{3}{\rho }_{{e}_{2}{e}_{2}}(\left\vert 0\right\rangle \left\langle 0\right\vert+\left\vert 2\right\rangle \left\langle 2\right\vert+\left\vert 3\right\rangle \left\langle 3\right\vert )\\ - \frac{\Gamma }{2}\{\left\vert {e}_{1}\right\rangle \left\langle {e}_{1}\right\vert,\rho \}-\frac{\Gamma }{2}\{\left\vert {e}_{2}\right\rangle \left\langle {e}_{2}\right\vert,\rho \}.$$
(9)

Let \(P=\left\vert 0\right\rangle \left\langle 0\right\vert+\left\vert 1\right\rangle \left\langle 1\right\vert+\left\vert 2\right\rangle \left\langle 2\right\vert+\left\vert 3\right\rangle \left\langle 3\right\vert\) be the projection operator onto the 2S1/2 ground state manifold. Applying P to the master equation [Eq. (9)], we obtain

$$\frac{d\rho }{dt} = (-{{{\rm{i}}}}H\rho -{{{\rm{i}}}}{J}_{1}\left\vert 1\right\rangle \left\langle {e}_{1}\right\vert {\rho }_{f}P-{{{\rm{i}}}}{J}_{2}\left\vert 2\right\rangle \left\langle {e}_{2}\right\vert {\rho }_{f}P+\,{\mbox{H.c.}})\\ +\frac{\Gamma }{3}{\rho }_{{e}_{1}{e}_{1}}(\left\vert 0\right\rangle \left\langle 0\right\vert+\left\vert 1\right\rangle \left\langle 1\right\vert+\left\vert 3\right\rangle \left\langle 3\right\vert )\\ +\frac{\Gamma }{3}{\rho }_{{e}_{2}{e}_{2}}(\left\vert 0\right\rangle \left\langle 0\right\vert+\left\vert 2\right\rangle \left\langle 2\right\vert+\left\vert 3\right\rangle \left\langle 3\right\vert ),$$
(10)

where ρ = PρfP. Notice that Eq. (10) involves \({\rho }_{{e}_{1}\mu }\) and \({\rho }_{{e}_{2}\mu }\) (μ = 0, 1, 2, 3), as well as \({\rho }_{{e}_{1}{e}_{1}}\) and \({\rho }_{{e}_{2}{e}_{2}}\). We can derive an equation involving only the 2S1/2 levels using adiabatic elimination. From Eq. (9), we have

$$\frac{d{\rho }_{{e}_{1}0}}{dt}= -{{{\rm{i}}}}{J}_{1}{\rho }_{10}+{{{\rm{i}}}}\frac{{\Omega }_{1}}{\sqrt{2}}{\rho }_{{e}_{1}1}-\frac{\Gamma }{2}{\rho }_{{e}_{1}0},\\ \frac{d{\rho }_{{e}_{1}1}}{dt}= - {{{\rm{i}}}}{J}_{1}{\rho }_{11}+{{{\rm{i}}}}\frac{{\Omega }_{1}}{\sqrt{2}}{\rho }_{{e}_{1}0}+{{{\rm{i}}}}\frac{{\Omega }_{2}}{\sqrt{2}}{\rho }_{{e}_{1}2}+{{{\rm{i}}}}{J}_{1}{\rho }_{{e}_{1}{e}_{1}}-\frac{\Gamma }{2}{\rho }_{{e}_{1}1},\\ \frac{d{\rho }_{{e}_{1}2}}{dt}= - {{{\rm{i}}}}{J}_{1}{\rho }_{12}+{{{\rm{i}}}}\frac{{\Omega }_{2}}{\sqrt{2}}{\rho }_{{e}_{1}1}+{{{\rm{i}}}}{J}_{2}{\rho }_{{e}_{1}{e}_{2}}-\frac{\Gamma }{2}{\rho }_{{e}_{1}2},\\ \frac{d{\rho }_{{e}_{1}3}}{dt}= - {{{\rm{i}}}}{J}_{1}{\rho }_{13}-\frac{\Gamma }{2}{\rho }_{{e}_{1}3},\\ \frac{d{\rho }_{{e}_{1}{e}_{1}}}{dt}= -{{{\rm{i}}}}{J}_{1}{\rho }_{1{e}_{1}}+{{{\rm{i}}}}{J}_{1}{\rho }_{{e}_{1}1}-\Gamma {\rho }_{{e}_{1}{e}_{1}}.$$
(11)

We assume J1, J2 ≪ Γ so that the population in \(\left\vert {e}_{1}\right\rangle\) is small, giving rise to \(d{\rho }_{{e}_{1}\nu }/dt\approx 0\) for any ν. We also have \({\rho }_{{e}_{1}\nu }\ll {\rho }_{ij}\) for i, j = 0, 1, 2, 3, allowing us to omit the \({\rho }_{{e}_{1}\nu }\) terms in Eq. (11) that are not multiplied by Γ. This gives

$${\rho }_{{e}_{1}\mu } \approx -{{{\rm{i}}}}\frac{2{J}_{1}}{\Gamma }{\rho }_{1\mu },\\ {\rho }_{{e}_{1}{e}_{1}} \approx \frac{4{J}_{1}^{2}}{{\Gamma }^{2}}{\rho }_{11},$$
(12)

for μ = 0, 1, 2, 3. Similarly, for \(\left\vert {e}_{2}\right\rangle\), we obtain

$${\rho }_{{e}_{2}\mu } \approx - {{{\rm{i}}}}\frac{2{J}_{2}}{\Gamma }{\rho }_{2\mu },\\ {\rho }_{{e}_{2}{e}_{2}} \approx \frac{4{J}_{2}^{2}}{{\Gamma }^{2}}{\rho }_{22}.$$
(13)

Using Eq. (12) and Eq. (13), we have \(\left\langle {e}_{1}\right\vert {\rho }_{f}P=-{{{\rm{i}}}}(2{J}_{1}/\Gamma )\left\langle 1\right\vert \rho\) and \(\left\langle {e}_{2}\right\vert {\rho }_{f}P=-{{{\rm{i}}}}(2{J}_{2}/\Gamma )\left\langle 2\right\vert \rho\). Eq. (10) becomes

$$\frac{d\rho }{dt}= (-{{{\rm{i}}}}H\rho -{\gamma }_{1}\left\vert 1\right\rangle \left\langle 1\right\vert \rho -{\gamma }_{2}\left\vert 2\right\rangle \left\langle 2\right\vert \rho+\,{\mbox{H.c.}})\\ +\frac{2{\gamma }_{1}}{3}{\rho }_{11}(\left\vert 0\right\rangle \left\langle 0\right\vert+\left\vert 1\right\rangle \left\langle 1\right\vert+\left\vert 3\right\rangle \left\langle 3\right\vert )\\ +\frac{2{\gamma }_{2}}{3}{\rho }_{22}(\left\vert 0\right\rangle \left\langle 0\right\vert+\left\vert 2\right\rangle \left\langle 2\right\vert+\left\vert 3\right\rangle \left\langle 3\right\vert ),$$
(14)

which is the same as Eq. (1) with \({\gamma }_{1}=2{J}_{1}^{2}/\Gamma\) and \({\gamma }_{2}=2{J}_{2}^{2}/\Gamma\). We have numerically confirmed that the results from Eq. (1) agree well with those from the full dynamics [Eq. (8)] given that J1, J2 ≪ Γ.

Non-Hermitian absorption spectroscopy

By weakly coupling a system level with an auxiliary energy level \(\left\vert a\right\rangle\) and using \(\left\vert a\right\rangle\) as the initial state, we can eliminate the effects of quantum jumps. The Hamiltonian H (similarly for Hf) becomes \({H}^{{\prime} }=H+\frac{{\Omega }_{a}}{2}(\left\vert 1\right\rangle \left\langle a\right\vert+{{{\rm{H.c.}}}})-{\delta }_{a}\left\vert a\right\rangle \left\langle a\right\vert\). By a similar adiabatic elimination of \(\left\vert {e}_{1}\right\rangle\) and \(\left\vert {e}_{2}\right\rangle\) levels, one also arrives at Eq. (14) with \(H\to {H}^{{\prime} }\). We project Eq. (14) onto the subspace spanned by the system and auxiliary levels using \({P}_{a}=\left\vert 0\right\rangle \left\langle 0\right\vert+\left\vert 1\right\rangle \left\langle 1\right\vert+\left\vert 2\right\rangle \left\langle 2\right\vert+\left\vert a\right\rangle \left\langle a\right\vert\). Then we have

$$\frac{d{\rho }_{a}}{dt}=(-{{{\rm{i}}}}{H}_{{{{\rm{NAS}}}}}{\rho }_{a}+{{{\rm{H.c.}}}})+{\sum }_{n=1}^{2}\frac{2{\gamma }_{n}}{3}{\rho }_{nn}(\left\vert 0\right\rangle \left\langle 0\right\vert+\left\vert n\right\rangle \left\langle n\right\vert ),$$
(15)

with ρa = PaρPa and HNAS given by Eq. (5). The dynamics of ρ11 and ρ22 are given by

$$\frac{d{\rho }_{11}}{dt}= - \frac{4{\gamma }_{1}}{3}{\rho }_{11}-\left({{{\rm{i}}}}\frac{{\Omega }_{1}}{\sqrt{2}}{\rho }_{01}+{{{\rm{i}}}}\frac{{\Omega }_{2}}{\sqrt{2}}{\rho }_{21}+{{{\rm{i}}}}\frac{{\Omega }_{a}}{2}{\rho }_{a1}+{{{\rm{H.c.}}}}\right),\\ \frac{d{\rho }_{22}}{dt}= -\frac{4{\gamma }_{2}}{3}{\rho }_{22}-\left({{{\rm{i}}}}\frac{{\Omega }_{2}}{\sqrt{2}}{\rho }_{12}+{{{\rm{H.c.}}}}\right).$$
(16)

Given that Ωa is sufficiently small, we have ρ11 ≈ 0 and ρ22 ≈ 0 due to the dissipation terms \(-\frac{4{\gamma }_{1}}{3}{\rho }_{11}\) and \(-\frac{4{\gamma }_{2}}{3}{\rho }_{22}\) in Eq. (16). As a result, the second term on the right-hand side of Eq. (15) can be omitted, and the state satisfies a non-Hermitian evolution by HNAS.

We now derive the population in \(\left\vert a\right\rangle\) by incorporating the fact that this state has a finite lifetime. Ideally, the population in \(\left\vert a\right\rangle\) satisfies a non-Hermitian evolution given by

$${N}_{a}^{{{{\rm{nH}}}}}(t)={\left\vert \left\langle a\right\vert {e}^{-{{{\rm{i}}}}{H}_{{{{\rm{NAS}}}}}t}\left\vert a\right\rangle \right\vert }^{2}={e}^{-\kappa t},$$
(17)

where κ is the transfer rate from \(\left\vert a\right\rangle\) to the system levels. In practice, the D5/2 state \(\left\vert a\right\rangle\) has a finite lifetime of τa ≈ 7.4 ms. Considering the finite lifetime of \(\left\vert a\right\rangle\) and the state detection and measurement errors, the actual population in \(\left\vert a\right\rangle\) is approximately described by

$${N}_{a}(t)={N}_{0}{e}^{-({\gamma }_{a}+\kappa )t}={N}_{0}{e}^{-{\gamma }_{a}t}{N}_{a}^{{{{\rm{nH}}}}}(t),$$
(18)

with γa = 1/τa.

In our experiment, the measured population in \(\left\vert a\right\rangle\) is 1 subtracted by the population in the 2S1/2 manifold, given by

$${N}_{a}^{{{{\rm{tgt}}}}}(t)=1-{N}_{s}(t)={N}_{a}(t)+{N}_{F}(t),$$
(19)

where NF is the population in the 2F7/2 state. The branching ratio of D5/2 → 2F7/2 is 81.6%64, thus NF satisfies dNF/dt = 0.816γaNa. Solving the differential equation with the initial condition NF(0) = 0, we obtain

$${N}_{F}(t)= \frac{0.816{\gamma }_{a}}{{\gamma }_{a}+\kappa }{N}_{0}[1-{e}^{-({\gamma }_{a}+\kappa )t}]\\= \frac{0.816{\gamma }_{a}}{{\gamma }_{a}-\frac{1}{t}{{{\rm{ln}}}}[{N}_{a}^{{{{\rm{nH}}}}}(t)]}{N}_{0}[1-{e}^{-{\gamma }_{a}t}{N}_{a}^{{{{\rm{nH}}}}}(t)].$$
(20)

Finally, we obtain the theoretical value of the experimentally measured population in \(\left\vert a\right\rangle\) given by

$${N}_{a}^{{{{\rm{tgt}}}}}(t)= {N}_{0}{e}^{-{\gamma }_{a}t}{N}_{a}^{{{{\rm{nH}}}}}(t)\\ +\frac{0.816{\gamma }_{a}}{{\gamma }_{a}-\frac{1}{t}{{{\rm{ln}}}}[{N}_{a}^{{{{\rm{nH}}}}}(t)]}{N}_{0}[1-{e}^{-{\gamma }_{a}t}{N}_{a}^{{{{\rm{nH}}}}}(t)],$$
(21)

which is used in non-Hermitian absorption spectroscopy.

The system parameters are extracted by minimizing the loss function L = ∑iLi, with

$${L}_{i}={\sum}_{{\delta }_{a}}{\left[{N}_{a,i}^{\exp }({\delta }_{a})-{N}_{a,i}^{{{{\rm{tgt}}}}}({\delta }_{a};{{{{\boldsymbol{P}}}}}_{i})\right]}^{2}.$$
(22)

Here \({N}_{a,i}^{\exp }({\delta }_{a})\) is the experimentally measured population in the auxiliary level at detuning δa (e.g., Fig. 4a), and \({N}_{a,i}^{{{{\rm{tgt}}}}}({\delta }_{a};{{{{\boldsymbol{P}}}}}_{i})\) denotes the theoretically calculated population based on the system parameters Pi. The theoretical population \({N}_{a,i}^{{{{\rm{tgt}}}}}\) is calculated from Eq. (21). The system parameters are given by Pi = {Ω1,i, Ω2,i, γ1,i, γ2,i, N0,i} (or with additional detuning terms {Δ0,i, Δ1,i}), where i is the index for the ratio Ω/γ. We impose constraints on the fitting parameters based on the experimental setup. Specifically, we assume Ω1,i = Ω2,i since the microwave amplitudes can be controlled with high precision. For the decay rates γ1,i and γ2,i, due to the drift in the laser power, we cannot simply assume γ2,i = 2γ1,i. However, we manage to control the laser power (proportional to \({J}_{1,2}^{2}\)) within a 5% deviation from the initial value. Thus, we assume that \({\bar{\gamma }}_{2}=2{\bar{\gamma }}_{1}\), where \({\bar{\gamma }}_{n}\) denotes the average of γn,i over all i, and each γn,i is constrained to be within a 5% deviation from \({\bar{\gamma }}_{n}\). Once the system parameters are obtained through fitting, we calculate the eigenenergies of the non-Hermitian Hamiltonian.

Fig. 4: Spectral line and winding topology.
figure 4

a The spectral line (the remaining population in \(\left\vert a\right\rangle\) at the end of the dynamics at ta = 200 μs with respect to the detuning δa) for Ω/γ = 0.8. Here, the half-width of the outer dips is mainly determined by \({{{\rm{Im}}}}({E}_{0}-{{{\rm{i}}}}\gamma )\), while the half-width of the inner peak is mainly determined by \({{{\rm{Im}}}}({E}_{+}-{{{\rm{i}}}}\gamma )\). Both the theoretical results (red line) and fitted ones (black line) are calculated according to Eq. (21). The former ones are computed using the parameter Ω/γ = 0.8, while the fitted results employ parameters obtained from a fitting procedure based on the experimental data (circles). b Argument of En(θ) − EB as a function of θ with EB = − 0.016 − 0.032i plotted using the data in Fig. 1f. The y-axis is shifted so that \({{\arg }}({E}_{0}(0)-{E}_{B})=0\), and the n-th band is shifted along the x-axis by 2πn to show the spectral winding around EB. The units of energy is 2π × 1 MHz. Here, γ = 2π × 0.040 MHz and Ωa = 2π × 0.004 MHz. The experimental results are averaged over 5 rounds of experiments (each contains 200 shots) with error bars being the standard deviation of the 5 experimental repetitions.

Full size image

In Fig. 1f, we show the extracted complex eigenenergies as a function of θ. Here, we further provide \({{\arg }}({E}_{n}(\theta )-{E}_{B})\) in Fig. 4b, clearly illustrating the 6π periodicity of each band.

In addition, we note that adding the auxiliary level \(\left\vert a\right\rangle\) and its coupling with the system levels inevitably lifts the EP3 degeneracy in the total Hamiltonian HNAS. The effect vanishes in the ideal case where the coupling Ωa → 0, the evolution time ta → ∞, and \({\Omega }_{a}^{2}{t}_{a}\) remains a constant. However, due to experimental imperfections, the evolution time ta is limited by the coherence time and other errors. Consequently, a finite Ωa is required to obtain a finite signal. Although the finite coupling slightly perturbs the degeneracy, experimental errors make this perturbation negligible.

Quench dynamics

To eliminate the effects of quantum jumps, one can also utilize an off-diagonal sector in the density matrix, which follows a pure non-Hermitian evolution. We show this by writing down the density matrix in a block form,

$$\rho=\left(\begin{array}{cc}{\rho }_{{{{\rm{sys}}}}}&v\\ w&{\rho }_{33}\end{array}\right),$$
(23)

with

$${\rho }_{{{{\rm{sys}}}}}=\left(\begin{array}{ccc}{\rho }_{00}&{\rho }_{01}&{\rho }_{02}\\ {\rho }_{10}&{\rho }_{11}&{\rho }_{12}\\ {\rho }_{20}&{\rho }_{21}&{\rho }_{22}\end{array}\right),\,v=\left(\begin{array}{c}{\rho }_{03}\\ {\rho }_{13}\\ {\rho }_{23}\end{array}\right),\,w={\left(\begin{array}{c}{\rho }_{30}\\ {\rho }_{31}\\ {\rho }_{32}\end{array}\right)}^{T}.$$
(24)

The master equation in Eq. (1) can be written as

$$\frac{d}{dt}\left(\begin{array}{cc}{\rho }_{{{{\rm{sys}}}}}&v\\ w&{\rho }_{33}\end{array}\right)= - {{{\rm{i}}}}\left(\begin{array}{cc}{H}_{{{{\rm{eff}}}}}&{{{\bf{0}}}}\\ {{{\bf{0}}}}&0\end{array}\right)\left(\begin{array}{cc}{\rho }_{{{{\rm{sys}}}}}&v\\ w&{\rho }_{33}\end{array}\right)\\ +{{{\rm{i}}}}\left(\begin{array}{cc}{\rho }_{{{{\rm{sys}}}}}&v\\ w&{\rho }_{33}\end{array}\right)\left(\begin{array}{cc}{H}_{{{{\rm{eff}}}}}^{{{\dagger}} }&{{{\bf{0}}}}\\ {{{\bf{0}}}}&0\end{array}\right)+{{{\mathcal{D}}}}[\rho ],$$
(25)

where Heff is the 3 × 3 non-Hermitian matrix in Eq. (2) and

$${{{\mathcal{D}}}}[\rho ]= {\sum}_{\mu }{L}_{\mu }\rho {L}_{\mu }^{{{\dagger}} }\\ =\left(\begin{array}{cccc}{c}_{1}{\rho }_{11}+{c}_{2}{\rho }_{22}&0&0&0\\ 0&{c}_{1}{\rho }_{11}&0&0\\ 0&0&{c}_{2}{\rho }_{22}&0\\ 0&0&0&{c}_{1}{\rho }_{11}+{c}_{2}{\rho }_{22}\end{array}\right).$$
(26)

Based on this equation, we find that

$$\frac{dv}{dt}=-{{{\rm{i}}}}{H}_{{{{\rm{eff}}}}}v,$$
(27)

giving rise to

$$v(t)={e}^{-{{{\rm{i}}}}{H}_{{{{\rm{eff}}}}}t}v(0).$$
(28)

More generally, if the Hilbert space splits into two orthogonal subspaces S and \({S}^{{\prime} }\) such that the Hamiltonian acts trivially on \(\left\vert {s}^{{\prime} }\right\rangle \in {S}^{{\prime} }\), i.e.,

$$H=\left(\begin{array}{cc}{H}_{SS}&{{{\bf{0}}}}\\ {{{\bf{0}}}}&{{{\bf{0}}}}\end{array}\right),$$
(29)

and each jump operator has one of the block forms

$${L}_{\mu }=\left(\begin{array}{cc}{L}_{\mu,SS}&{{{\bf{0}}}}\\ {{{\bf{0}}}}&{{{\bf{0}}}}\end{array}\right)\quad \,{{\mbox{or}}}\,\quad {L}_{\mu }=\left(\begin{array}{cc}{{{\bf{0}}}}&{{{\bf{0}}}}\\ {L}_{\mu,{S}^{{\prime} }S}&{{{\bf{0}}}}\end{array}\right),$$
(30)

where the first and second row/column correspond to S and \({S}^{{\prime} }\), respectively, then

  1. 1.

    The effective Hamiltonian \({H}_{{{{\rm{eff}}}}}=H-\frac{{{{\rm{i}}}}}{2}{\sum }_{\mu }{L}_{\mu }^{{{\dagger}} }{L}_{\mu }\) also acts trivially on \(\left\vert {s}^{{\prime} }\right\rangle \in {S}^{{\prime} }\),

  2. 2.

    The off-diagonal sector \({\rho }_{S{S}^{{\prime} }}\) of the density matrix follows a non-Hermitian evolution \(d{\rho }_{S{S}^{{\prime} }}/dt=-{{{\rm{i}}}}{H}_{{{{\rm{eff}}}}}{\rho }_{S{S}^{{\prime} }}\) with \({\rho }_{S{S}^{{\prime} }}\) being a submatrix in the density matrix

    $$\rho=\left(\begin{array}{cc}{\rho }_{SS}&{\rho }_{S{S}^{{\prime} }}\\ {\rho }_{{S}^{{\prime} }S}&{\rho }_{{S}^{{\prime} }{S}^{{\prime} }}\end{array}\right).$$
    (31)

In our case, \(S={{{\rm{span}}}}\{\left\vert 0\right\rangle,\left\vert 1\right\rangle,\left\vert 2\right\rangle \}\) and \({S}^{{\prime} }={{{\rm{span}}}}\{\left\vert 3\right\rangle \}\). We note that this condition can always be realized by introducing an additional level that does not couple to any other levels via the Hamiltonian and the jump operators.

In the following, we show a specific application of the aforementioned technique on studying the PT-symmetry breaking in our system (such dynamics can also be used to study other non-Hermitian applications, such as state transfer48). We consider an initial state \(\rho (0)=\frac{1}{2}(\left\vert 0\right\rangle+\left\vert 3\right\rangle )(\left\langle 0\right\vert+\left\langle 3\right\vert )\), so that \(v(0)=\frac{1}{2}{(1,0,0)}^{T}=\frac{\Omega }{4({\Omega }^{2}-{\gamma }^{2})}[(\gamma -{{{\rm{i}}}}\sqrt{{\Omega }^{2}-{\gamma }^{2}})\left\vert {\psi }_{+}\right\rangle+(\gamma+{{{\rm{i}}}}\sqrt{{\Omega }^{2}-{\gamma }^{2}})\left\vert {\psi }_{-}\right\rangle -\sqrt{2({\Omega }^{2}+{\gamma }^{2})}\left\vert {\psi }_{0}\right\rangle ]\). Since the off-diagonal element ρ03 evolves as \(v(t)={e}^{-{{{\rm{i}}}}{H}_{{{{\rm{eff}}}}}t}v(0)\), we have \({\rho }_{03}(t)={[v(t)]}_{0}=\frac{{\Omega }^{2}{e}^{-\gamma t}}{4({\Omega }^{2}-{\gamma }^{2})}[1+\frac{{\Omega }^{2}-2{\gamma }^{2}}{{\Omega }^{2}} \cos (\sqrt{{\Omega }^{2}-{\gamma }^{2}}t)+\frac{2\gamma \sqrt{{\Omega }^{2}-{\gamma }^{2}}}{{\Omega }^{2}}\sin (\sqrt{{\Omega }^{2}-{\gamma }^{2}}t)]\). Further simplification gives

$${\rho }_{03}(t)=\frac{{\Omega }^{2}{e}^{-\gamma t}}{2({\Omega }^{2}-{\gamma }^{2})}{\sin }^{2}\left(\frac{\sqrt{{\Omega }^{2}-{\gamma }^{2}}}{2}t+{C}_{1}\right),$$
(32)

with \({C}_{1}={\cos }^{-1}(\gamma /\Omega )\). For Ω < γ, the equation becomes

$${\rho }_{03}(t)=\frac{{\Omega }^{2}{e}^{-\gamma t}}{2({\gamma }^{2}-{\Omega }^{2})}{\sinh }^{2}\left(\frac{\sqrt{{\gamma }^{2}-{\Omega }^{2}}}{2}t+{C}_{2}\right),$$
(33)

with \({C}_{2}={\cosh }^{-1}(\gamma /\Omega )\).

The experimentally measured off-diagonal element ∣ρ03∣, shown in Fig. 5a, agrees well with the theoretical results (Fig. 5b), providing a clear signature of the PT symmetry breaking across Ω = γ. Specifically, for Ω > γ, all eigenenergies are real (up to a constant shift), causing ∣ρ03∣ to oscillate with a frequency determined by the real eigenenergy. In contrast, for Ω < γ, the eigenenergies become purely imaginary, leading ∣ρ03∣ to experience a pure decay. Based on Eq. (32) and Eq. (33), the time evolution of ∣ρ03∣ follows a damped sinusoidal (for Ω > γ) or hyperbolic sine (for Ω < γ) behavior, described by \({f}_{1}(\gamma t)={A}_{1}{e}^{-\gamma t}{\sin }^{2}({B}_{1}\gamma t+{C}_{1})\) and \({f}_{2}(\gamma t)={A}_{2}{e}^{-\gamma t}{\sinh }^{2}({B}_{2}\gamma t+{C}_{2})\), with \({B}_{1}={B}_{2}=\frac{1}{2}| \sqrt{{(\Omega /\gamma )}^{2}-1}|\). We fit the experimental data to both functions and select the one with the smallest error. Figure 5c displays the fitting result for Ω/γ = 5, where f1(γt) fits the experimental data best, while the inset for Ω/γ = 0.5 is better characterized by f2(γt). We find that in the symmetry unbroken region, the damped sinusoidal provides a better fitting than the hyperbolic sine function. Conversely, in the symmetry broken region, the hyperbolic sine function offers a better fit, consistent with theoretical results. In addition, we plot the fitted values of B1 or B2 with respect to Ω/γ in Fig. 5d, showing excellent agreement with theoretical results. The results clearly demonstrate a PT phase transition at Ω = γ.

Fig. 5: Results for quench dynamics.
figure 5

a Experimental and (b) theoretical results of an element ∣ρ03∣ of the density matrix with respect to the normalized evolution time γt and the ratio Ω/γ. c Curve fitting using the damped sinusoidal function for experimental data (circles) at Ω/γ = 5. The inset shows the fitting results using the hyperbolic sine function at Ω/γ = 0.5. The experimental data are averaged over 400 repetitions with error bars representing the standard deviation. d Fitted oscillation and decay factors B1 or B2 with respect to Ω/γ. The error bar, which is smaller than the symbols, denotes the 95% confidence intervals of the fit.

Full size image

Eigenstate tomography

We assume that the eigenstate of the Hamiltonian is expressed as

$$\left\vert {u}_{n}\right\rangle=\left(\begin{array}{c}{a}_{n}+{{{\rm{i}}}}{b}_{n}\\ {c}_{n}+{{{\rm{i}}}}{d}_{n}\\ {e}_{n}+{{{\rm{i}}}}{f}_{n}\end{array}\right)$$
(34)

for n = 0, + , − . Due to the presence of PT and anti-PT symmetry, one of the eigenstate \(\left\vert {u}_{0}\right\rangle\) must be symmetric under both PT and anti-PT operations, that is, \({U}_{{{{\rm{PT}}}}}\left\vert {u}_{0}\right\rangle={e}^{{{{\rm{i}}}}\alpha }\left\vert {u}_{0}\right\rangle\) and \({U}_{{{{\rm{APT}}}}}\left\vert {u}_{0}\right\rangle={e}^{{{{\rm{i}}}}\beta }\left\vert {u}_{0}\right\rangle\). By choosing an appropriate gauge, we can have \({U}_{{{{\rm{PT}}}}}\left\vert {u}_{0}\right\rangle={e}^{{{{\rm{i}}}}\alpha }\left\vert {u}_{0}\right\rangle\) and \({U}_{{{{\rm{APT}}}}}\left\vert {u}_{0}\right\rangle=\left\vert {u}_{0}\right\rangle\), resulting in \(\left\vert {u}_{0}\right\rangle={(-{e}_{0},{{{\rm{i}}}}{d}_{0},{e}_{0})}^{T}\) or \(\frac{1}{\sqrt{2}}{(1,0,1)}^{T}\). We exclude the latter case, as it is unlikely to be the eigenstate of an arbitrary Hamiltonian with PT and anti-PT symmetry. Let \({e}_{0}=\frac{1}{\sqrt{2}}\sin \varphi\) and \({d}_{0}=\cos \varphi\), we arrive at a normalized state

$$\left\vert {u}_{0}(\varphi )\right\rangle=\frac{1}{\sqrt{2}}{(-\sin \varphi,{{{\rm{i}}}}\sqrt{2}\cos \varphi,\sin \varphi )}^{T},$$
(35)

which becomes the eigenstate of Heff when \(\varphi={\tan }^{-1}(\Omega /\gamma )\).

The other two states \(\left\vert {u}_{+}\right\rangle\) and \(\left\vert {u}_{-}\right\rangle\) are either PT or anti-PT symmetric. If they are PT symmetric (when Ω > γ), we have \({U}_{{{{\rm{PT}}}}}\left\vert {u}_{+}\right\rangle=-\left\vert {u}_{+}\right\rangle\), \({U}_{{{{\rm{PT}}}}}\left\vert {u}_{-}\right\rangle=-\left\vert {u}_{-}\right\rangle\), and \({U}_{{{{\rm{APT}}}}}\left\vert {u}_{+}\right\rangle={e}^{{{{\rm{i}}}}\alpha }\left\vert {u}_{-}\right\rangle\), where we have chosen a specific gauge for \(\left\vert {u}_{+}\right\rangle\) and \(\left\vert {u}_{-}\right\rangle\). These equations give rise to

$$\left\vert {u}_{\pm }\right\rangle=\frac{1}{\sqrt{2}}{\left(-r{e}^{\mp {{{\rm{i}}}}\phi },{{{\rm{i}}}}\sqrt{2(1-{r}^{2})},r{e}^{\pm {{{\rm{i}}}}\phi }\right)}^{T},$$
(36)

where r and ϕ are real numbers. In principle, one could scan the parameter space with respect to r and ϕ to identify the eigenstates. In our experiment, to reduce the amount of data required, we introduce another constraint based on the structure of the Hamiltonian. If \(\left\vert {u}_{+}\right\rangle\) is an eigenstate of Heff, then we have \(({H}_{{{{\rm{eff}}}}}+{{{\rm{i}}}}\gamma )\left\vert {u}_{+}\right\rangle=k\left\vert {u}_{+}\right\rangle\) with k being a real number, giving rise to \(r=1/\sqrt{2}\). As a result, we only need to prepare

$$\left\vert {u}_{z}(\phi )\right\rangle=\frac{1}{2}{\left(-{e}^{{{{\rm{i}}}}\phi },{{{\rm{i}}}}\sqrt{2},{e}^{-{{{\rm{i}}}}\phi }\right)}^{T}$$
(37)

for different values of ϕ to perform eigenstate tomography (see Supplementary Information S-2 for initial state preparation). \(\left\vert {u}_{z}(\phi )\right\rangle\) becomes an eigenstate of Heff when \(\phi=\pm {\cos }^{-1}(\gamma /\Omega )\).

Similarly, if \(\left\vert {u}_{+}\right\rangle\) and \(\left\vert {u}_{-}\right\rangle\) are anti-PT symmetric (when Ω < γ), then we have \({U}_{{{{\rm{APT}}}}}\left\vert {u}_{+}\right\rangle=\left\vert {u}_{+}\right\rangle\), \({U}_{{{{\rm{APT}}}}}\left\vert {u}_{-}\right\rangle=\left\vert {u}_{-}\right\rangle\), and \({U}_{{{{\rm{PT}}}}}\left\vert {u}_{+}\right\rangle={e}^{{{{\rm{i}}}}\alpha }\left\vert {u}_{-}\right\rangle\), leading to

$$\left\vert {u}_{+}\right\rangle= {\left(a,{{{\rm{i}}}}\sqrt{1-({a}^{2}+{b}^{2})},b\right)}^{T},\\ \left\vert {u}_{-}\right\rangle= {\left(-b,{{{\rm{i}}}}\sqrt{1-({a}^{2}+{b}^{2})},a\right)}^{T},$$
(38)

with a and b being real numbers. We also use \(({H}_{{{{\rm{eff}}}}}+{{{\rm{i}}}}\gamma )\left\vert {u}_{+}\right\rangle={{{\rm{i}}}}k\left\vert {u}_{+}\right\rangle\) and obtain another constraint a − b = ± 1. Therefore, we can prepare the state

$$\left\vert {u}_{x}(\phi )\right\rangle={\left(-\frac{1+\sin \phi }{2},{{{\rm{i}}}}\frac{\cos \phi }{\sqrt{2}},\frac{1-\sin \phi }{2}\right)}^{T}$$
(39)

for different ϕ, which becomes an eigenstate of Heff when \(\phi=\pm {\cos }^{-1}(\Omega /\gamma )\).

We note that these states can also be obtained by rotating the state \(\left\vert {{{\rm{EP}}}}\right\rangle\) around the z-axis (for Ω > γ) or the x-axis (for Ω < γ):

$$\left\vert {u}_{z}(\phi )\right\rangle={e}^{{{{\rm{i}}}}\phi {S}_{z}}\left\vert {{{\rm{EP}}}}\right\rangle,\\ \left\vert {u}_{x}(\phi )\right\rangle={e}^{{{{\rm{i}}}}\phi {S}_{x}}\left\vert {{{\rm{EP}}}}\right\rangle,$$
(40)

with

$${S}_{z}=\left(\begin{array}{ccc}1&0&0\\ 0&0&0\\ 0&0&-1\end{array}\right),\,\,{S}_{x}=\frac{1}{\sqrt{2}}\left(\begin{array}{ccc}0&1&0\\ 1&0&1\\ 0&1&0\end{array}\right)$$
(41)

being the spin-1 operators.

For eigenstate tomography in experiments, we determine the zero points of \(\Delta | {\rho }_{i3}^{{{{\rm{n}}}}}{| }^{2}\) by linear interpolation between adjacent experimental data points of opposite signs, as shown in Fig. 6.

Fig. 6: Determination of eigenstates in tomography.
figure 6

a \(\Delta | {\rho }_{23}^{{{{\rm{n}}}}}{| }^{2}\) as a function of ϕ with the initial state \(\left\vert {u}_{z}(\phi )\right\rangle\) at Ω/γ = 2. b \(\Delta | {\rho }_{13}^{{{{\rm{n}}}}}{| }^{2}\) as a function of ϕ with the initial state \(\left\vert {u}_{x}(\phi )\right\rangle\) at Ω/γ = 0.5. The zero points are marked by circles and crosses, determined by linear interpolation between adjacent experimental data points with opposite signs, and error bars denote the standard deviation.

Full size image

Liouvillian EP3

The Liouvillian superoperator can also be viewed as a non-Hermitian matrix in the doubled Hilbert space. By vectorizing the density matrix through Choi-Jamiolkowski isomorphism65,66,

$$\rho={\sum}_{ij}{\rho }_{ij}\left\vert i\right\rangle \left\langle j\right\vert \to \left\vert \rho \right\rangle={\sum}_{ij}{\rho }_{ij}\left\vert i\right\rangle \otimes \left\vert j\right\rangle,$$
(42)

the master equation can be written as \(d\left\vert \rho \right\rangle /dt={{{\mathscr{L}}}}\left\vert \rho \right\rangle\) with

$${{{\mathscr{L}}}}=-{{{\rm{i}}}}({H}_{{{{\rm{eff}}}}}\otimes I-I\otimes {H}{*}_{{{{\rm{eff}}}}})+{\sum}_{\mu }{L}_{\mu }\otimes {L}{*}_{\mu }.$$
(43)

In this case, the Lindbladian of our model becomes a 16 × 16 non-Hermitian matrix which can also support EP3. Notably, certain Lindbladian eigenvectors are closely related to the Hamiltonian eigenstates. Given that \(\left\vert {\psi }_{n}\right\rangle\) is the eigenstate of Heff with eigenenergy En (n = 0, ± ), \(\left\vert {\rho }_{n}^{{{{\rm{R}}}}}\right\rangle=\left\vert {\psi }_{n}\right\rangle \otimes \left\vert 3\right\rangle\) satisfies

$${{{\mathscr{L}}}}\left\vert {\rho }_{n}^{{{{\rm{R}}}}}\right\rangle=(-{{{\rm{i}}}}{H}_{{{{\rm{eff}}}}}\otimes I)\left\vert {\psi }_{n}\right\rangle \otimes \left\vert 3\right\rangle=-{{{\rm{i}}}}{E}_{n}\left\vert {\rho }_{n}^{{{{\rm{R}}}}}\right\rangle,$$
(44)

since \({H}{*}_{{{{\rm{eff}}}}}\left\vert 3\right\rangle={L}{*}_{\mu }\left\vert 3\right\rangle=0\). This means that \(\left\vert {\rho }_{n}^{{{{\rm{R}}}}}\right\rangle=\left\vert {\psi }_{n}\right\rangle \otimes \left\vert 3\right\rangle\) (\({\rho }_{n}^{{{{\rm{R}}}}}=\left\vert {\psi }_{n}\right\rangle \left\langle 3\right\vert\)) is an eigenvector (eigenmatrix) of \({{{\mathscr{L}}}}\) (\({{{\mathcal{L}}}}\)) with eigenvalue  − iEn. Similarly, one can prove that \(\left\vert {\rho }_{n}^{{{{\rm{L}}}}}\right\rangle=\left\vert 3\right\rangle \otimes \left\vert {\psi }{*}_{n}\right\rangle\) (\({\rho }_{n}^{{{{\rm{L}}}}}=\left\vert 3\right\rangle \left\langle {\psi }_{n}\right\vert\)) is an eigenvector (eigenmatrix) of \({{{\mathscr{L}}}}\) (\({{{\mathcal{L}}}}\)) with eigenvalue iEn. The three eigenmatrices \({\rho }_{0}^{M},{\rho }_{+}^{M},{\rho }_{-}^{M}\) will coalesce into a single density matrix \(\left\vert {{{\rm{EP}}}}\right\rangle \left\langle 3\right\vert\) for M = R and \(\left\vert 3\right\rangle \left\langle {{{\rm{EP}}}}\right\vert\) for M = L, giving rise to a Liouvillian EP3.

While certain Liouvillian EP3 is directly linked to the Hamiltonian EP3 (via the correspondence between eigenstates of Heff and certain eigenmatrices of \({{{\mathcal{L}}}}\)), in the following we show that there exists intrinsic Liouvillian EP3 that do not arise from the eigenstates of the effective Hamiltonian, which can be probed via quench dynamics starting from a non-physical state.

Intrinsic Liouvillian eigenmatrices

We obtain the eigenmatrices and eigenvalues of \({{{\mathcal{L}}}}\) by diagonalizing \({{{\mathcal{L}}}}\) in the doubled Hilbert space (\({{{\mathscr{L}}}}\)), from which we identify intrinsic Liouvillian eigenmatrices that do not arise from the eigenstates of Heff. Specifically, we find three eigenmatrices written as

$${\rho }_{\pm } =\left(\begin{array}{cccc}0&1\pm {{{\rm{i}}}}\sqrt{\frac{{\Omega }^{2}}{{\gamma }^{2}}-1}&{{{\rm{i}}}}\sqrt{2}\frac{\Omega }{\gamma }&0\\ 1\pm {{{\rm{i}}}}\sqrt{\frac{{\Omega }^{2}}{{\gamma }^{2}}-1}&0&1\mp {{{\rm{i}}}}\sqrt{\frac{{\Omega }^{2}}{{\gamma }^{2}}-1}&0\\ -{{{\rm{i}}}}\sqrt{2}\frac{\Omega }{\gamma }&1\mp {{{\rm{i}}}}\sqrt{\frac{{\Omega }^{2}}{{\gamma }^{2}}-1}&0&0\\ 0&0&0&0\end{array}\right),\\ {\rho }_{0}= \left(\begin{array}{cccc}0&1&{{{\rm{i}}}}\sqrt{2}\frac{\gamma }{\Omega }&0\\ 1&0&1&0\\ -{{{\rm{i}}}}\sqrt{2}\frac{\gamma }{\Omega }&1&0&0\\ 0&0&0&0\end{array}\right),$$
(45)

with the basis being \(\{\left\vert 0\right\rangle,\left\vert 1\right\rangle,\left\vert 2\right\rangle,\left\vert 3\right\rangle \}\). The corresponding eigenvalues are

$${\lambda }_{\pm } =- 2\gamma \pm {{{\rm{i}}}}\sqrt{{\Omega }^{2}-{\gamma }^{2}},\\ {\lambda }_{0} =- 2\gamma .$$
(46)

One can verify that \({{{\mathcal{L}}}}[{\rho }_{n}]={\lambda }_{n}{\rho }_{n}\) for n = ± , 0. At Ω = γ, the eigenvalues become degenerate and the eigenmatrices coalesce into a single density matrix

$${\rho }_{{{{\rm{EP}}}}}=\left(\begin{array}{cccc}0&1&{{{\rm{i}}}}\sqrt{2}&0\\ 1&0&1&0\\ -{{{\rm{i}}}}\sqrt{2}&1&0&0\\ 0&0&0&0\end{array}\right),$$
(47)

giving rise to an intrinsic Liouvillian EP3.

We further show that the Liouvillian EP3 emerges from the simultaneous breaking of the PT and anti-PT symmetry, which is the same as the Hamiltonian case. We first prove that the modular conjugation symmetry and an anti-PT symmetry and jump operator structures ensure that eigenvectors of the Lindbladian do not depend on the jump operators. Specifically, the full Lindbladian \({{{\mathcal{L}}}}\) respects the modular conjugation \({{{\mathcal{J}}}}\),

$${{{\mathcal{J}}}}{{{\mathcal{L}}}}{{{{\mathcal{J}}}}}^{-1}={{{\mathcal{L}}}},\qquad {{{\mathcal{J}}}}[\rho ]={\rho }^{{{\dagger}} }$$
(48)

and the anti-PT symmetry \({{{{\mathcal{U}}}}}_{{{{\rm{APT}}}}}\),

$${{{{\mathcal{U}}}}}_{{{{\rm{APT}}}}}{{{\mathcal{L}}}}\,{{{{\mathcal{U}}}}}_{{{{\rm{APT}}}}}^{-1}={{{\mathcal{L}}}},\qquad {{{{\mathcal{U}}}}}_{{{{\rm{APT}}}}}[\rho ]={U}_{{{{\rm{APT}}}}}^{{\prime} }\rho {({U}_{{{{\rm{APT}}}}}^{{\prime} })}^{-1}$$
(49)

with

$${U}_{{{\rm{APT}}}}^{\prime}=\left(\begin{array}{cccc}1&0&0&0\\ 0&-1&0&0\\ 0&0&1&0\\ 0&0&0&1\end{array}\right)\kappa .$$
(50)

Since both \({{{{\mathcal{U}}}}}_{{{{\rm{APT}}}}}\) and \({{{\mathcal{J}}}}\) are antiunitary symmetries, their combination \({{{{\mathcal{U}}}}}_{{{{\rm{APT}}}}}{{{\mathcal{J}}}}\) is unitary and satisfies \({({{{{\mathcal{U}}}}}_{{{{\rm{APT}}}}}{{{\mathcal{J}}}})}^{2}={{{\bf{1}}}}\). Thus, if ρ is an eigenvector of \({{{\mathcal{L}}}}\), then we have

$$({{{{\mathcal{U}}}}}_{{{{\rm{APT}}}}}{{{\mathcal{J}}}})[\rho ]={U}_{{{{\rm{APT}}}}}^{{\prime} }{\rho }^{{{\dagger}} }{({U}_{{{{\rm{APT}}}}}^{{\prime} })}^{-1}=\pm \rho .$$
(51)

We focus on the “−” branch since in our case the eigenvectors belong to this branch. Then, ρ takes the following form

$$\rho=\left(\begin{array}{cccc}0&{\rho }_{01}&{\rho }_{02}&{\rho }_{03}\\ {\rho }_{01}&0&{\rho }_{12}&{\rho }_{13}\\ -{\rho }_{02}&{\rho }_{12}&0&{\rho }_{23}\\ -{\rho }_{03}&{\rho }_{13}&-{\rho }_{23}&0\end{array}\right),\quad {\rho }_{ij}\in {\mathbb{C}}.$$
(52)

Furthermore, in our system the jump operators take the form of \({L}_{\mu }=\vert {m}_{\mu }\rangle \langle {n}_{\mu }\vert\) with mμ, nμ ∈ {0, 1, 2, 3}, leading to \({L}_{\mu }\rho {L}_{\mu }^{{{\dagger}} }=0\) since symmetries enforce the diagonal elements of ρ to be zero. In this case, ρ is an eigenvector of \({{{\mathcal{L}}}}\) if and only if it is an eigenvector of \(\tilde{{{{\mathscr{L}}}}}=-{{{\rm{i}}}}({H}_{{{{\rm{eff}}}}}\otimes I-I\otimes {H}_{{{{\rm{eff}}}}}^{*})\), or equivalently

$$\tilde{{{{\mathcal{L}}}}}[\cdot ]=-{{{\rm{i}}}}{H}_{{{{\rm{eff}}}}}[\cdot ]+{{{\rm{i}}}}[\cdot ]{H}_{{{{\rm{eff}}}}}^{{{\dagger}} },$$
(53)

where Heff is the effective Hamiltonian written in the full Hilbert space, i.e.,

$${H}_{{{{\rm{eff}}}}}=\left(\begin{array}{cccc}0&\frac{\Omega }{\sqrt{2}}&0&0\\ \frac{\Omega }{\sqrt{2}}&-{{{\rm{i}}}}\gamma &\frac{\Omega }{\sqrt{2}}&0\\ 0&\frac{\Omega }{\sqrt{2}}&-2{{{\rm{i}}}}\gamma &0\\ 0&0&0&0\end{array}\right)=\left(\begin{array}{cc}{h}_{{{{\rm{eff}}}}}-{{{\rm{i}}}}\gamma {I}_{3}&{{{\bf{0}}}}\\ {{{\bf{0}}}}&0\end{array}\right).$$
(54)

Based on the structure of Heff,

$$\tilde{\rho }=\left(\begin{array}{cccc}{\rho }_{00}&{\rho }_{01}&{\rho }_{02}&0\\ {\rho }_{10}&{\rho }_{11}&{\rho }_{12}&0\\ {\rho }_{20}&{\rho }_{21}&{\rho }_{22}&0\\ 0&0&0&0\end{array}\right)$$
(55)

is an eigenvector of \(\tilde{{{{\mathcal{L}}}}}\) with eigenvalue λ if and only if

$${\rho }_{{{{\rm{sys}}}}}=\left(\begin{array}{ccc}{\rho }_{00}&{\rho }_{01}&{\rho }_{02}\\ {\rho }_{10}&{\rho }_{11}&{\rho }_{12}\\ {\rho }_{20}&{\rho }_{21}&{\rho }_{22}\end{array}\right)$$
(56)

is an eigenvector of

$${{{{\mathcal{L}}}}}_{{{{\rm{sys}}}}}=-{{{\rm{i}}}}({h}_{{{{\rm{eff}}}}}\otimes {I}_{3}-{I}_{3}\otimes {h}_{{{{\rm{eff}}}}}^{*})$$
(57)

with eigenvalue λ + 2γ. This allows us to set ρi3 = ρ3i = 0 for i = 0, 1, 2, 3 so that

$$\rho=\left(\begin{array}{cccc}0&{\rho }_{01}&{\rho }_{02}&0\\ {\rho }_{01}&0&{\rho }_{12}&0\\ -{\rho }_{02}&{\rho }_{12}&0&0\\ 0&0&0&0\end{array}\right).$$
(58)

Since heff respects both the PT symmetry and the anti-PT symmetry, we have

$$\begin{array}{c}({U}_{{{{\rm{PT}}}}}\otimes {U}_{{{{\rm{PT}}}}}^{*}){{{{\mathcal{L}}}}}_{{{{\rm{sys}}}}}{({U}_{{{{\rm{PT}}}}}\otimes {U}_{{{{\rm{PT}}}}}^{*})}^{-1}=-{{{{\mathcal{L}}}}}_{{{{\rm{sys}}}}},\\ ({U}_{{{{\rm{APT}}}}}\otimes {U}_{{{{\rm{APT}}}}}^{*}){{{{\mathcal{L}}}}}_{{{{\rm{sys}}}}}{({U}_{{{{\rm{APT}}}}}\otimes {U}_{{{{\rm{APT}}}}}^{*})}^{-1}={{{{\mathcal{L}}}}}_{{{{\rm{sys}}}}}.\end{array}$$
(59)

We thus see that the PT symmetry represented by \({U}_{{{{\rm{PT}}}}}\otimes {U}_{{{{\rm{PT}}}}}^{*}\) and the anti-PT symmetry represented by \({U}_{{{{\rm{APT}}}}}\otimes {U}_{{{{\rm{APT}}}}}^{*}\) ensure the existence of EP3 in \({{{{\mathcal{L}}}}}_{{{{\rm{sys}}}}}\) (thus \({{{\mathcal{L}}}}\)) as the two symmetries break at the same parameter value as in the Hamiltonian case. For the winding topology of a Liouvillian EP3, see the discussion in Supplementary Information S-4.

Detection of the intrinsic Liouvillian EP3

To detect the EP3 associated with PT symmetry breaking, we adopt an initial state that can be written as a linear combination of the three eigenmatrices. We define

$$ \left\vert {u}_{1}\right\rangle=\frac{1}{\sqrt{2}}(\left\vert 0\right\rangle -{{{\rm{i}}}}\left\vert 2\right\rangle )=\frac{1}{\sqrt{2}}{\left(\begin{array}{cccc}1&0&-{{{\rm{i}}}}&0\end{array}\right)}^{T},\\ \left\vert {u}_{2}\right\rangle=\frac{1}{\sqrt{2}}(\left\vert 0\right\rangle+{{{\rm{i}}}}\left\vert 2\right\rangle )=\frac{1}{\sqrt{2}}{\left(\begin{array}{cccc}1&0&{{{\rm{i}}}}&0\end{array}\right)}^{T}.$$
(60)

The initial state is chosen as

$$\rho (0) =\left\vert {u}_{1}\right\rangle \left\langle {u}_{1}\right\vert -\left\vert {u}_{2}\right\rangle \left\langle {u}_{2}\right\vert \\ =\frac{\Omega \gamma }{\sqrt{2}({\gamma }^{2}-{\Omega }^{2})}[{\rho }_{0}-\frac{1}{2}({\rho }_{+}+{\rho }_{-})].$$
(61)

The time evolution of ρ(0) is then given by

$$\rho (t) ={e}^{{{{\mathcal{L}}}}t}[\rho (0)]\\ =\frac{\Omega \gamma }{\sqrt{2}({\gamma }^{2}-{\Omega }^{2})}[{e}^{{\lambda }_{0}t}{\rho }_{0}-\frac{1}{2}({e}^{{\lambda }_{+}t}{\rho }_{+}+{e}^{{\lambda }_{-}t}{\rho }_{-})]\\ =\frac{\Omega \gamma }{\sqrt{2}({\gamma }^{2}-{\Omega }^{2})}{e}^{-2\gamma t}\left(\begin{array}{cccc}0&A(t)&C(t)&0\\ {A}^{*}(t)&0&B(t)&0\\ {C}^{*}(t)&{B}^{*}(t)&0&0\\ 0&0&0&0\end{array}\right),$$
(62)

where

$$A(t) =1-\cos (\sqrt{{\Omega }^{2}-{\gamma }^{2}}t)+\sqrt{\frac{{\Omega }^{2}}{{\gamma }^{2}}-1}\sin (\sqrt{{\Omega }^{2}-{\gamma }^{2}}t),\\ B(t) =1-\cos (\sqrt{{\Omega }^{2}-{\gamma }^{2}}t)-\sqrt{\frac{{\Omega }^{2}}{{\gamma }^{2}}-1}\sin (\sqrt{{\Omega }^{2}-{\gamma }^{2}}t),\\ C(t) =- \frac{{{{\rm{i}}}}\sqrt{2}}{\Omega \gamma }[{\Omega }^{2}\cos (\sqrt{{\Omega }^{2}-{\gamma }^{2}}t)-{\gamma }^{2}].$$
(63)

From Eq. (62) and Eq. (63), we find

$${\rho }_{12}(t)-{\rho }_{01}(t)=\frac{\sqrt{2}\Omega }{\sqrt{{\Omega }^{2}-{\gamma }^{2}}}{e}^{-2\gamma t}\sin (\sqrt{{\Omega }^{2}-{\gamma }^{2}}t),$$
(64)

which can be used to detect the PT phase transition.

Since \({{{\rm{Tr}}}}[\rho (0)]=0\), the state ρ(0) cannot be directly prepared as it is not a physical state. To address this, we define

$$\sigma (0)=\left\vert {u}_{1}\right\rangle \left\langle {u}_{1}\right\vert,\,\,\sigma (t)={e}^{{{{\mathcal{L}}}}t}[\left\vert {u}_{1}\right\rangle \left\langle {u}_{1}\right\vert ],\\ \tau (0)=\left\vert {u}_{2}\right\rangle \left\langle {u}_{2}\right\vert,\,\,\tau (t)={e}^{{{{\mathcal{L}}}}t}[\left\vert {u}_{2}\right\rangle \left\langle {u}_{2}\right\vert ].$$
(65)

Experimentally, we can prepare the states \(\left\vert {u}_{1}\right\rangle\) and \(\left\vert {u}_{2}\right\rangle\), measure the matrix elements of σ(t) and τ(t), respectively, and then obtain ρ(t) using the relation ρ(t) = σ(t) − τ(t) (see Supplementary Information S-5 for the generic case). Furthermore, due to the anti-PT symmetry of the system, we have

$${\tau }_{01}(t) =- {\sigma }_{01}^{*}(t),\\ {\tau }_{12}(t) =- {\sigma }_{12}^{*}(t).$$
(66)

This allows us to express

$${\rho }_{12}(t)-{\rho }_{01}(t)=2{{{\rm{Re}}}}({\sigma }_{12}(t)-{\sigma }_{01}(t)),$$
(67)

which means that we only need to prepare \(\left\vert {u}_{1}\right\rangle\) and measure the off-diagonal elements of σ(t).

The proof of Eq. (66) is as follows. The anti-PT symmetry of the Lindbladian gives rise to the relation

$${U}_{{{{\rm{APT}}}}}^{{\prime} }{{{\mathcal{L}}}}[\sigma (t)]{({U}_{{{{\rm{APT}}}}}^{{\prime} })}^{-1}={{{\mathcal{L}}}}[{U}_{{{{\rm{APT}}}}}^{{\prime} }\sigma (t){({U}_{{{{\rm{APT}}}}}^{{\prime} })}^{-1}],$$
(68)

which implies that

$${U}_{{{{\rm{APT}}}}}^{{\prime} }{e}^{{{{\mathcal{L}}}}t}[\sigma (0)]{({U}_{{{{\rm{APT}}}}}^{{\prime} })}^{-1}={e}^{{{{\mathcal{L}}}}t}[{U}_{{{{\rm{APT}}}}}^{{\prime} }\sigma (0){({U}_{{{{\rm{APT}}}}}^{{\prime} })}^{-1}].$$
(69)

Since \(\tau (0)={U}_{{{{\rm{APT}}}}}^{{\prime} }\sigma (0){({U}_{{{{\rm{APT}}}}}^{{\prime} })}^{-1}\), Eq. (69) gives rise to the relation

$$\tau (t)={U}_{{{{\rm{APT}}}}}^{{\prime} }\sigma (t){({U}_{{{{\rm{APT}}}}}^{{\prime} })}^{-1},$$
(70)

which leads to Eq. (66).