Introduction

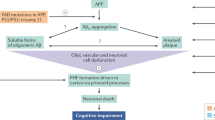
Alzheimer’s disease (AD) is biologically defined by the progressive accumulation of amyloid beta (Aβ) plaques and neurofibrillary tau (τ) tangles1. These proteinopathies develop years before symptom onset, presenting a window for early therapeutic interventions2. The temporal progression of these biomarkers also facilitates biological staging of AD, guiding treatment strategies and timing3. While amyloid positron emission tomography (PET) imaging is clinically approved for detecting Aβ, τ PET remains largely restricted to research settings4. These imaging modalities provide critical insights into disease progression but are expensive and not widely accessible, limiting their routine clinical use compared to conventional modalities such as structural magnetic resonance imaging (MRI) and neurocognitive assessments. Cerebrospinal fluid (CSF) testing offers high sensitivity for amyloid detection but lacks the ability to stage disease progression, which tau PET imaging currently provides4. PET imaging influences clinical decision-making5 and remains integral to identifying candidates for disease-modifying therapies and clinical trials6,7,8. However, its restricted accessibility in routine care settings underscores the need for cost-effective, scalable screening methods that preserve PET’s staging precision while overcoming logistical barriers.

The escalating costs associated with AD drug development underscore the necessity for precise disease staging. From 1995 to 2021, AD research and development incurred an estimated $42.5 billion expenditure, with a staggering 95% failure rate9. A large portion of these costs stems from the screening process required to determine patient eligibility based on Aβ PET positivity status9. However, emerging evidence suggests that τ pathology is more strongly linked with cognitive decline and disease progression10. The TRAILBLAZER-ALZ 2 clinical trial demonstrated that Donanemab, an amyloid-lowering therapy, was most effective in patients with lower τ PET burden6, highlighting the critical role of τ staging in determining therapeutic response. As tau’s clinical importance becomes increasingly evident, the development of predictive models that can non-invasively capture the burden and spatial distribution of tau pathology appears as a critical objective, particularly for the optimization of patient selection for novel AD therapies11,12.

Emerging technologies and frameworks, including plasma biomarkers such as p-tau 217, offer potential for early AD detection13,14. While these biomarkers can predict Aβ PET status with performance comparable to cerebrospinal fluid (CSF) analyses15, their ability to accurately predict tau PET status across diverse populations is less established14,16. Further, these biomarkers lack the ability to capture the spatial distribution of tau pathology in the brain, which is essential for accurate biological assessment of AD4,17,18. Variability due to non-neurological factors such as body mass index, cardiovascular and renal health can also affect their clinical efficacy19, and the generalizability and accuracy of cut-off points in racially and ethnically diverse samples remains to be validated20. Therefore, while promising, plasma biomarkers are not yet a standalone solution, and an integrated multimodal approach may be useful to accurately pre-screen and stratify individuals based on Aβ and τ status, as well as disease stage4,11.

Machine learning (ML) models have shown promise in addressing some of the logistical challenges of PET scans by predicting Aβ or τ PET status using less invasive data such as demographics, MRIs and cognitive assessments21,22,23,24,25,26,27,28,29. However, these models often face limitations, including development on relatively small cohorts, reliance on fluid biomarkers, lack of external validation, and dependence on complete feature sets to generate reliable predictions. By leveraging standard-of-care data, there is an opportunity to develop a cost-effective pre-screening process that estimates both amyloid and tau pathology, enabling broader access to advanced diagnostics and targeted treatments.

Here, we propose a transformer-based ML framework designed to integrate multimodal data and predict global Aβ, tau burden in a pre-defined meta-temporal region (meta-τ) encompassing medial and neocortical temporal regions30, and regional tau PET statuses. By incorporating demographic information, medical history, neuropsychological assessments, genetic markers, neuroimaging and other relevant clinically obtained data, we sought to create a flexible computational framework that explicitly accommodates missing data, reflecting the practical challenges of real-world datasets. Recognizing the synergistic relationship between Aβ and tau pathology in AD pathogenesis31, our framework jointly predicts Aβ and τ accumulation to capture their interdependent roles in disease progression. This multi-label prediction strategy addresses key methodological and scientific gaps in existing research, which often considers amyloid or tau in isolation, and serves as a demonstration of scalable participant stratification for research and clinical trials. Finally, by outputting probabilities that align with established biological staging criteria, our modeling framework offers a potential pathway to quantifying disease progression from heterogeneous clinical data.

Results

Our modeling framework was developed through training on a large, diverse dataset with multimodal features (Fig. 1 & Supplementary Tables S1–S10), and rigorously tested on an external dataset (Table 1). We evaluated our framework’s alignment with PET-estimated Aβ and τ burden and biomarker profiles, and assessed its ability to capture the synergistic relationship between Aβ and τ. In addition, we constructed a graph network using Shapley values of brain volumes for each regional tau label and validated the model’s regional tau predictions against tau PET SUVr values in the same regions. Finally, we compared the model predictions with postmortem findings, ensuring that the predicted probabilities reflected the severity of the underlying pathology.

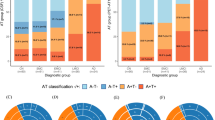
Fig. 1: Data, model development and validation strategy.
figure 1

A Our model for assessing amyloid and tau status was developed using diverse data modalities, including individual-level demographics, health history, genetic information, neuropsychological testing, physical/neurological exams, and multi-sequence MRI scans. These data sources were aggregated from seven independent cohorts: NACC, A4, OASIS3, AIBL, FHS, ADNI and HABS. All features were harmonized to the UDS3 format, and embeddings were extracted from multi-modal MRI scans. Inner concentric circles provide the sample size of cases with Aβ PET data, and outer circles denote the sample size with τ PET data. B Each feature was transformed into a set length vector through a modality-specific embedding approach before being input into the pretrained transformer. The model was then trained in two stages, first predicting Aβ and meta-τ positivity, before being finetuned to predict regional τ positivity in a second stage. C The external ADNI and HABS datasets, as well as a held-out set of NACC* data, were selected to compare pathology-specific model predicted probabilities with PET outcomes and neuropathology grades. Shapley analysis was run on the regional τ model, and a graphical network analysis was performed to detect clusters of important brain regions using the Shapley values of the T1-weighted derived volumes. A similar community detection algorithm was run on the raw regional tau PET SUVrs to enable a statistical comparison of the communities derived from Shapley values with communities derived from the regional tau SUVrs.

Full size image
Table 1 Study population
Full size table

Model accurately predicts Aβ and τ status

We first evaluated our model’s performance in predicting global Aβ and meta-τ status. The receiver operating characteristic (ROC) and precision-recall (PR) curves illustrate the model’s performance in predicting Aβ and meta-τ positivity (Fig. 2a, b). The ROC curves show that the model achieved slightly higher sensitivity and specificity for meta-τ (AUROC = 0.84) compared to Aβ (AUROC = 0.79). However, the PR curves indicate greater reliability in identifying true positive cases for Aβ (AP = 0.78) than for meta-τ (AP = 0.60), despite the higher AUROC for meta-τ. This could be attributed to class imbalance or lower prevalence of τ positivity in the dataset, leading to a higher rate of false positives in meta-τ predictions. Additional performance metrics are provided in Supplementary Table S11a. Supplementary Tables S12 and S13 detail the performance metrics for the internal validation set (NACC*) and the combined ADNI-HABS external set, respectively. Notably, the ADNI dataset had 54% fewer features than the held-out NACC* test set, and the HABS dataset had 72% fewer features. Despite these constraints in feature availability, our model maintained robust performance, highlighting its flexibility and ability to handle incomplete feature sets without significant loss of accuracy. In Supplementary Fig. S1, we reported AUROC and AP metrics stratified by age, gender, race and education. The consistent performance across these subgroups indicates that our model is potentially applicable to diverse populations.

Fig. 2: Model performance in predicting amyloid and tau positivity.
figure 2

a, b Receiver operating characteristic (ROC) and precision-recall (PR) curves for Aβ and meta-τ predictions are shown. The area under the ROC curve (AUC) and the average precision (AP) values for Aβ and meta-τ are displayed in the legends, respectively. c Heatmap presenting the AUROC and AP values for Aβ and meta-τ predictions using various combinations of clinical features, starting with person-level history alone and incrementally adding features such as MRI, neuropsychological battery, and plasma data. d Heatmap displaying the AUROC and AP values for Aβ and meta-τ predictions when specific feature sets are removed from the full model. Each row represents the model performance after excluding one feature set, showing how the absence of that data type impacts prediction accuracy. e, f ROC and PR curves showing micro-average, macro-average, and weighted-average calculations based on the regional τ labels. A portion of the NACC dataset used for internal testing, along with data from the ADNI and HABS cohorts for external validation, contributed to generating these results. In panels c and d, FAQ stands for functional activities questionnaire, and CDR stands for clinical dementia ratings.

Full size image

To assess the impact of different types of clinical features on model performance, we evaluated the model’s predictions for Aβ and meta-τ status by successively adding different feature groups. Following the typical order of assessments in neurological work-up protocols for cognitive impairment, our analyses aimed to identify incremental gains, if any, when each new test is added to the work-up process (Fig. 2c, d). The plasma biomarker available at testing, the Aβ42/40 ratio, and the APOE-ϵ4 tests are included last due to their relatively limited availability in clinical settings. For Aβ prediction, the AUROC improved from 0.59 with only person-level history to 0.79 when all features were included, with the AP values increasing in parallel from 0.55 to 0.78. Tau prediction models showed a comparable increase in AUROC from 0.53 with only patient history to 0.84 with all features. Notably, the addition of MRI data led to a substantial improvement in meta-τ AUROC from 0.53 to 0.74. Subsequent additions of neuropsychological battery scores provided additional improvements, highlighting that the integration of multiple modalities of data leads to better overall performance.

To evaluate our model’s robustness to the absence of specific feature sets, we systematically removed groups of features from the full model. For Aβ predictions, removing any single feature set had minimal impact on AUROC values, which remained between 0.74 and 0.80. This highlights the strength of our random feature masking strategy, which allowed the model to make meaningful predictions even in the absence of certain data types. Similarly, meta-τ predictions were robust across feature exclusions, with the removal of the neuropsychological battery resulting in the most significant drop in AP to 0.53. While our modeling strategy afforded the flexibility in achieving high accuracy despite the absence of certain feature sets, the importance of neuropsychological testing is underscored by the sensitivity of τ AP values to the removal of these features. The results of our Shapley analysis (Supplementary Fig. S2) provide additional support for this interpretation, with neuropsychological testing, neuroimaging and APOE-ϵ4 status having, on average, the greatest impact on model output.

We quantified our model’s performance on regional τ predictions and found that it achieved a macro-average AUROC and AP of 0.80 and 0.42, respectively (Fig. 2e, f). Individual AUROC scores ranged from 0.71 to 0.84, indicating robust discriminative ability across different regions of interest (ROIs). The medial temporal τ label achieved the highest AP of 0.60, suggesting that the model is particularly effective in identifying true positive cases in this critical region (Supplementary Table S11b). These results suggest that our transformer-based model effectively predicts regional τ accumulation, particularly excelling in the medial and lateral temporal regions, where the combined AUROC and AP values were the highest.

We conducted a comparative analysis of our transformer-based model against CatBoost, a robust machine learning approach, to evaluate performance in predicting Aβ and τ pathology. For this purpose, we tested our model without MRI embeddings, with the results detailed in Table S14. On the combined test set from ADNI, HABS, and NACC*, CatBoost achieved an AUROC of 0.81 for Aβ predictions and 0.83 for meta-τ predictions. The corresponding AP values were 0.79 for Aβ and 0.53 for meta-τ. In comparison, our model demonstrated slightly lower AUROC for Aβ predictions (0.79 vs. 0.81) but superior AP for meta-τ predictions (0.60 vs. 0.53), indicating more effective identification of true positive meta-τ cases. In addition, CatBoost’s balanced accuracy for Aβ prediction stood at 0.64, while ours was 0.68, indicating a more effective balance between sensitivity and specificity in our model. Further performance metrics for CatBoost are provided in Supplementary Table S15a. To deepen our analysis, we incrementally added features from clinical assessments in the order typically collected during neurological work-ups to the CatBoost model. This step-by-step addition is visualized in Supplementary Fig. S3, contrasting the performance of our model without MRI embeddings (panel a) to that of CatBoost (panel b). Although CatBoost initially shows higher AUROC and AP upon integrating medical history and neurological/physical examination data, our model surpasses these metrics upon adding brain regional volumes, functional assessments, and neuropsychological tests. When MRI embeddings are incorporated into our model (Fig. 2c), it achieves an AUROC comparable to CatBoost’s upon the addition of CDR scores and plasma Aβ42/40 ratios, with a marginally better AP. Overall, our transformer-based architecture, with its attention mechanism and random feature masking, provides an end-to-end framework that flexibly handles multimodal inputs and performs effectively on imbalanced datasets. This is especially evident in its superior performance for meta-τ and regional τ predictions, where CatBoost exhibits a macro-average AUROC and AP of 0.77 and 0.38, respectively (Supplementary Fig. S3, Fig. 2c, and Supplementary Tables S14, S15).

Model predictions align with biological gradients and disease progression

Even though our model was trained on binary classifications, we aimed to assess its alignment with PET-based gradients of Aβ and meta-τ accumulation (Fig. 3). As an additional step towards facilitating interpretability of our model outputs, we visualized how well the model’s predictions aligned with a commonly used clinical endpoint in AD trials, the Alzheimer’s Disease Assessment Scale-Cognitive Subscale (ADAS-Cog13 or ADAS13). We observed a positive correlation between P(Aβ) and centiloid values (Pearson’s r = 0.58, p < 0.0001; Fig. 3a), indicating that higher predicted Aβ levels are associated with increased Aβ plaque deposition, as confirmed by centiloid measurements. This relationship aligned with more severe cognitive impairment, evidenced by higher scores on the ADAS13. Similarly, we found a positive correlation between P(τ) and the log of meta-τ SUVr (Pearson’s r = 0.59, p < 0.0001; Fig. 3b), suggesting that higher model-predicted tau levels correlated with greater tau PET estimated pathology. An associated increase in ADAS-Cog13 was again visible, indicating more pronounced cognitive impairment at higher P(τ) values (Supplementary Table S16). We ran a similar analysis comparing the regional τ probabilities to the log of the corresponding regional τ SUVr values and found the strongest alignment for the medial temporal (Pearson’s r = 0.56, p < 0.0001, Supplementary Fig. S4a) and lateral temporal predictions (Pearson’s r = 0.52, p < 0.0001, Supplementary Fig. S4b). Further statistical results are reported in Supplementary Table S17.

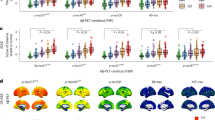
Fig. 3: Model alignment with biological outcomes.
figure 3

a The bubble plot illustrates model-predicted probabilities of amyloid PET positivity, P(Aβ), against centiloid values. Two-sided Pearson’s correlation assessed the strength of the relationship between P(Aβ) and centiloids (n = 1392, r = 0.58, p = 4.04 × 10−124). The color scale indicates ADAS-Cog 13 scores, a clinical AD staging tool not provided as model input. b Model-predicted meta-temporal tau PET positivity probabilities, P(τ), are shown against log-transformed meta-temporal SUVr values (meta-τ). A two-sided Pearson’s correlation tested the relationship between model probabilities and the log of meta-τ SUVr (n = 619, r = 0.59, p = 2.35 × 10−58). Similarly, points are colored by ADAS13 scores. Detailed statistical results can be found in Tables S16. c In cognitively unimpaired individuals (n = 853), we compared P(Aβ) between true Aβ PET negative (n = 602) and positive (n = 251) groups. A one-sided Mann-Whitney test showed significantly lower P(Aβ) for Aβ PET negative subjects (U = 53044, p = 3.36 × 10−12). d The rainclouds plot illustrates the relationship between the AT score, a composite score of model-predicted Aβ and regional τ probabilities, across PET-defined disease stages. A Kruskal-Wallis H test, followed by two-sided post hoc Dunn’s tests with Holm-Bonferroni correction revealed significant differences in AT scores among subjects who were Aβ- and τ- (A-T-, n = 411), Aβ + but τ- (A + T-, n = 139), Aβ + with tau positivity restricted to the medial temporal lobe (A + MTL +, n = 47), and Aβ positive with tau positivity extending to neocortical regions (A + NEO +, n = 101) (H = 180.73, p = 6.15   10−39). Pair-wise post hoc results are provided in Supplementary Table S18. Subjects from the ADNI cohort were used to generate the results shown in panels (a, b). Subjects from all three test cohorts were used for panel (c), and subjects from ADNI and HABS were used to generate results in panel d. All boxplots include a box presenting the median value and interquartile range (IQR), with whiskers extending from the box to the maxima and minima no further than a distance of 1.5 times the IQR. In panels c and d, significance levels are denoted as ** for p < 0.01; *** for p < 0.001; and **** for p < 0.0001.

Full size image

We also sought to evaluate our model’s sensitivity for detecting Aβ positivity in preclinical AD by comparing P(Aβ) between Aβ PET-negative (n = 602) and Aβ PET-positive (n = 251) cognitively unimpaired individuals from the ADNI, HABS, and NACC* cohorts. A Mann-Whitney U test revealed significantly lower P(Aβ) values in Aβ PET-negative cases compared to PET-positive cases (U = 53044, p = 3.36 × 10−12, Fig. 3c), demonstrating the model’s ability to distinguish between amyloid status groups even in the absence of cognitive symptoms.

Finally, we aimed to evaluate the alignment of our model probabilities with biomarker-defined disease stages (A-T-, A +T-, A + MTL +, and A + NEO +)4. A Kruskal-Wallis H test revealed that our composite AT score derived from our models’ amyloid and regional tau probabilities significantly differed across disease stages (H = 180.73, p = 6.15 × 10−39; Fig. 3d). Post-hoc analysis using Dunn’s test with Holm-Bonferroni correction for multiple comparisons demonstrated significant differences between all pairwise stage comparisons, with AT scores progressively increasing from A-T- to A + NEO + stages. This relationship suggests that our model-derived probabilities capture the biological progression of AD pathology as defined by recently proposed staging systems4. Detailed statistical results are provided in Supplementary Table S18.

Model predictions capture the synergistic relationship between Aβ and τ

To demonstrate the effectiveness of our model for pre-screening in AD clinical trials, we designed a validation approach that aligns with the emerging interest in dual targeting of Aβ and tau pathology, and in stratifying patients by disease burden. Specifically, we assessed the sensitivity of the model outputs to the co-occurring core pathological burden in amyloid PET-positive cases. First, we examined how the model’s predicted probability of Aβ positivity, P(Aβ) varied across different levels of tau PET defined pathology. Participants were categorized into two groups based on their meta-τ SUVr values: a ‘low/medium’ group (below the 67th percentile) and a ‘high’ group (at or above the 67th percentile). In Fig. 4a, the left panel serves as a reference on the relationship we expect when comparing centiloids and tau PET quantiles in our testing set, showing that centiloid values significantly increased with higher τ PET burden. The one-sided Mann-Whitney U test confirmed this trend, showing a significant difference in centiloid values across the τ PET tertiles (U = 5047, p = 1.92 × 10−13). The right panel presents P(Aβ) between these same quantiles, and similar statistically significant increases in P(Aβ) were seen between the low/medium and high groups (U = 3707, p = 4.01 × 10−20). These results indicate that the model’s Aβ predictions are sensitive to varying levels of tau burden. Similarly, we assessed how well our model’s τ probabilities related to centiloid levels in Aβ PET-positive cases. First, we tested the relationship between tau SUVr in the meta-temporal region across tertiles of Aβ centiloids to obtain a reference for the quantitative relationship between Aβ and tau pathologies, as shown in the left panel of Fig. 4b. A one-sided Mann-Whitney test indicated that meta-τ SUVr was significantly higher in the high CL group relative to the low/medium CL group (U = 5876, 6.78 × 10−10). In the right panel, the model’s predictions for tau positivity, P(τ), captured similar biological gradients, with a one-sided Mann-Whitney test showing significant differences in P(τ) across the same centiloid quantiles (6655.5, p = 3.17 × 10−07). Detailed statistical results are reported in Supplementary Table S19. Overall, these results demonstrate our model’s ability to capture the synergistic relationship between Aβ and tau pathologies, reinforcing its potential utility in patient stratification for clinical trials targeting both pathologies individually or together.

Fig. 4: Model ability to capture the synergistic relationship between Aβ and τ pathologies.
figure 4

a The panel on the left serves as a reference and shows the differences in centiloid distributions of Aβ PET + individuals between those in a low-to-medium meta-temporal τ PET group (n = 202) and those in a high (n = 102) τ PET group, with the one-sided Mann-Whitney U test indicating significant differences between the two groups (U = 5047, p = 1.92 × 10−13). The panel on the right shows the differences in our model-predicted Aβ probabilities between the same τ PET groups (U = 3707, p = 4.01 × 10−20). (b) The left panel shows the comparison of meta-temporal tau SUVr (meta-τ SUVr) between low/medium (n = 203) and high (n = 101) centiloid (CL) groups in Aβ PET + cases, with the one-sided Mann-Whitney U test pointing to significant differences between CL groups (U = 5876, p = 6.78 × 10−10). The right panel illustrates the differences in model-predicted meta-τ probabilities between the same CL groups (U = 6655.5, p = 3.17 × 10−7). Participants from the ADNI (n = 252) and HABS (n = 52) test sets were used for raincloud plots a and b. Detailed statistical results for the data presented in panels a and b can be found in Supplementary Table S19. c Kernel density plots comparing model-predicted probabilities of Aβ and meta-τ in two distinct A/T profiles (Aβ +, τ + and Aβ-, τ-) are shown. Subjects from ADNI, denoted by circles, HABS, denoted by cross symbols, and the held-out NACC* set, denoted by diamond symbols, were used for this plot. The PET-estimated Aβ +, τ + (n = 139) and Aβ −, τ − (n = 500) groups are distinguished by different shadings and contours, as indicated in the figure legend. A one-sided Mann-Whitney U test indicated significant differences in P(Aβ) between negative and positive groups (n = 639, U = 61430, p = 5.71 × 10−44) and similarly in P(τ) between negative and positive groups (n = 639, U = 60963, p = 1.63 × 10−42). All boxplots include a box presenting the median value and interquartile range (IQR), with whiskers extending from the box to the maxima and minima no further than a distance of 1.5 times the IQR. In all the panels, significance is denoted as **** for p < 0.0001.

Full size image

We further compared the distributions of our model-predicted probabilities, P(Aβ) and P(τ), between participants with the following PET-confirmed biomarker profiles: Aβ-, τ- and Aβ +, τ + (Fig. 4c). The Mann-Whitney U test revealed significant differences in both P(Aβ) and P(τ) between biomarker-positive and biomarker-negative groups (U = 61430, p = 5.71 × 10−44; U = 60963, p = 1.63 × 10−42, for Aβ and meta-τ, respectively). The scatter plots indicate that Aβ +, τ + individuals consistently exhibited higher predicted probabilities for both Aβ and τ compared to those in the Aβ-, τ- group. The associated boxplots and contour plots collectively highlight key differences between the two groups, revealing higher concentrations and a broader distribution of Aβ and τ in the Aβ +, τ + group compared to the negative group. The results also reveal a greater variability in tau levels for the Aβ +, τ + group, with the data extending to higher probabilities. In contrast, the Aβ-, τ- group showed a tighter distribution and lower biomarker values.

Regional volumes deemed important by the model align with spatial patterns of tau deposition

The accumulation and spatial progression of tau pathology in AD generally follows a stereotypical pattern, beginning in the transentorhinal region, progressing into the limbic system, and eventually spreading to the neocortical associative areas and, ultimately, the primary sensory cortices32. We created a visualization of mean Shapley values for regional volumes across predictions of regional τ positivity (Supplementary Fig. S5), ordering them following this stereotypical progression. This visualization underscores the importance of the MTL, which consistently shows high Shapley values, highlighting its role as the initial site of tau deposition and volumetric changes. To further evaluate the model’s decision-making processes when provided with brain regional volumes data, we conducted a graphical analysis to investigate the relative importance attributed to community structures in our model. We then compared the SHAP-derived community structures with tau PET-estimated graphs to assess the alignment between them. The analysis revealed a statistically significant degree of concordance, particularly in the temporal and parietal lobes, suggesting that model-based representations capture meaningful regional distinctions consistent with tau pathology (Fig. 5). Specifically, for the medial temporal τ positivity prediction, model-based and reference community structures showed moderate agreement (AMI = 0.219, p = 1.40 × 10−3). The lateral temporal region prediction demonstrated a similar pattern (AMI = 0.176, p = 5.60 × 10−3), while the medial parietal (AMI = 0.134, p = 4.84 × 10−2) and frontal (AMI = 0.138, p = 2.16 × 10−2) predictions exhibited modest similarity. The lateral parietal region achieved the highest agreement (AMI = 0.288, p = 1.60 × 10−3), and the occipital region showed moderate alignment (AMI = 0.233, p = 1.00 × 10−3). Overall, while the partitions in the model-based graphs are not identical to that of the SUVr graphs, there is a non-random correspondence between the two. This supports the idea that the model’s network of regional interactions is reflecting aspects of true tau pathology networks, rather than arbitrary groupings. These findings underscore the interpretability of our approach and its potential to bridge the gap between predictive modeling and biological markers of disease progression.

Fig. 5: Communities detected from model-derived and tau SUVr-derived graph networks.
figure 5

The dot heatmap visualizes the detected communities within graph networks constructed from normalized mutual information (NMI): one based on the Shapley values of T1-weighted regional volumetric features (SHAP), and the other based on tau PET SUVr for each of the six regional labels, including medial temporal (med-temp), lateral temporal (lat-temp), medial parietal (med-par), lateral parietal (lat-par), frontal, and occipital. Items within the same column represent a single detected community in the corresponding graph, and communities are order-invariant. Brain regions are grouped into pre-defined Braak stages (I-II, III, IV, V, and VI) on the right for visualization purposes. Statistical annotations denote the results of a one-sided spatial permutation test (n = 5000) on the adjusted mutual information (AMI) between model-based and tau SUVr-derived communities for each regional label (med-temp: AMI = 0.219, p = 1.40 × 10−3; lat-temp: AMI = 0.176, p = 5.60 × 10−3; med-par: AMI = 0.134, p = 4.84 × 10−2; lat-par: AMI = 0.288, p = 1.60 × 10−3; frontal: AMI = 0.138, p = 2.16 × 10−2; occipital: AMI = 0.233, p = 1.00 × 10−3). Significance levels are denoted as * for p < 0.05 and ** for p < 0.01. The corresponding contingency tables are provided in Supplementary Table S20.

Full size image

Model predictions align with severity of postmortem pathology

We validated our model’s predictions of Aβ and tau positivity by comparing them with neuropathological markers of AD. We observed a general increasing trend in model probabilities with increasing severity of pathological markers. Fig. 6a–d illustrate this relationship by comparing the model’s probability scores, P(Aβ) and P(τ), against key pathological markers across progressive AD stages: Thal phases of Aβ plaques, Braak stages of neurofibrillary degeneration, and CERAD (Consortium to Establish a Registry for Alzheimer’s Disease) scores for neuritic and diffuse plaques. These markers, denoted as A0–A3 (Thal phases), B0–B3 (Braak stages), and C0–C3 (CERAD scores for neuritic and diffuse plaques) all exhibited a statistically significant upward trend in the median probability of P(Aβ) and P(τ) as the stages advanced (p < 0.0001 for Thal, Braak, and CERAD stages) (Supplementary Tables S21 & S22). We also evaluated the model’s predictions in relation to cerebral amyloid angiopathy (CAA) (Fig. 6e), which is commonly observed in postmortem AD cases. The model predicted significantly higher P(Aβ) and P(τ) in individuals with mild, moderate, or severe CAA compared to those without CAA (p < 0.05) (Supplementary Table S22). These findings indicate that our model predicted probabilities for Aβ and τ positivity are closely aligned with the severity of neuropathological markers, strengthening the validity of the model to capture the underlying pathophysiology.

Fig. 6: Model alignment with postmortem findings.
figure 6

The swarm and box plots display predicted probabilities of amyloid-beta positivity, P(Aβ), and meta-temporal tau positivity, P(τ), with respect to various AD neuropathological grades in the ADNI (n = 41) and NACC (n = 147) neuropathological validation cohorts. a Kruskal-Wallis tests revealed significant differences in model-predicted probabilities across Thal phases for amyloid plaques for both P(Aβ) (H = 48.32, p = 3.05 × 10−9) and P(τ) (H = 42.02, p = 5.82 × 10−8). b With respect to Braak stage for neurofibrillary degeneration, Kruskal-Wallis tests also showed significant differences in P(Aβ) (H = 54.81, p = 5.05 × 10−10) and P(τ) (H = 54.05, p = 7.19 × 10−10). c Model probabilities were again significantly different across CERAD scores for density of neocortical neuritic plaque for P(Aβ) (H = 52.18, p = 2.74 × 10−11), and P(τ) (H = 50.37, p = 6.68 × 10−11). d For cerebral amyloid angiopathy, Kruskal-Wallis tests yielded significant differences in model-derived probabilities across pathology burden for both P(Aβ) (H = 26.46, p = 7.62 × 10−6) and P(τ) (H = 25.36, p = 1.30 × 10−5). e Finally, CERAD scores for diffuse plaques were also significantly associated with model probabilities: H = 37.84, p = 3.05 × 10−8 for P(Aβ) and H = 29.61, p = 1.66 × 10−6 for P(τ). Pairwise statistical annotations denote the results of two-sided post hoc Dunn tests with Holm-Bonferroni corrections following the Kruskal-Wallis test, with significance levels denoted as * for p < 0.05; ** for p < 0.01; *** for p < 0.001; and **** for p < 0.0001. In addition, trend lines and text boxes in the bottom right of each subplot indicate the Spearman correlation coefficient ρ and associated two-sided p-value for the overall strength of the correlation between model probabilities and neuropathological grades. Each boxplot includes a box presenting the median value and interquartile range (IQR), with whiskers extending from the box to the maxima and minima no further than a distance of 1.5 times the IQR. Detailed statistics regarding median values and IQRs can be found in Supplementary Fig. S21. Additional statistics and p-values for Spearman correlation and Kruskal-Wallis tests can be found in Supplementary Table S22.

Full size image

Discussion

In this work, we present a transformer-based machine learning model that uses multimodal data to predict individual-level Aβ and τ PET positivity status in a meta-temporal ROI and in regions associated with progressing disease. Our approach represents an advance over previous work in the field, which has typically focused on predicting amyloid or tau status independently, used smaller datasets, relied heavily on specialized biomarkers, or required full feature availability. Our model achieved strong performance on external data not used for model training, with predictions closely matching postmortem findings. We showed that our model predictions aligned with biological outcomes, as well as with disease severity staging. In addition, the model’s predictions of τ pathology in specific ROIs aligned with τ burdens derived from regional SUVr observed on PET scans.

Our modeling framework demonstrates flexibility in handling cases with missing features through the use of random feature masking. This approach allows the model to generate predictions and maintain accuracy even when some features are unavailable. The flexibility in handling various combinations of data addresses the heterogeneity encountered in real-world settings, where the exact set of assessments undergone may vary based on site-level practices, available resources, and patient-specific factors. However, our findings also highlight that certain data inputs, such as neuroimaging and APOE status, provide critical information on the underlying pathology, given the improvement in performance upon adding these features (Fig. 2c). For tau predictions, the removal of neuropsychological battery scores reduced the AP, underscoring its importance in accurate predictions. On the other hand, our analysis suggests that certain features, such as clinical dementia rating (CDR) scores, could potentially be excluded without significantly compromising the model’s predictive power. This is likely because our framework was developed by fine-tuning a model that already excels at classifying cognitive status33. This finding has practical implications, as CDR assessments require a skilled expert to conduct in-depth interviews and additional testing, which can be time-consuming and costly. Overall, our framework’s ability to maintain performance across varying scenarios without relying on a single data modality in isolation represents an important step toward practical implementation.

Our results indicate that AI models can potentially enhance biomarker-guided assessment of biological AD and facilitate participant selection in clinical trials targeting Aβ and τ, either individually or in combination. For example, in AD drug trials, models with high positive predictive values (PPV) can ensure that a higher proportion of individuals flagged as likely to have positive Aβ or tau PET scans are true positives. This could reduce the number of false positives that would need to be excluded later, improving the efficiency and cost-effectiveness of the trial. In addition, models with a high negative predictive value (NPV) are clinically desirable as they accurately rule out individuals without the condition, reducing the need for unnecessary PET scans and alleviating patient anxiety, thereby lowering both healthcare costs and patient burden. In a hypothetical scenario, our AI-based strategy could be integrated into AD screening as follows: persons undergoing neurological evaluation would first be assessed using our AI model, which utilizes clinical and imaging data to predict Aβ and τ status. The primary objective of this initial step would be to identify persons who are unlikely to have Aβ or τ pathology, thereby ruling out low-risk cases. For individuals whom the AI model does not confidently rule out as being Aβ or τ positive, PET imaging would then be recommended. This approach ensures that PET scans are focused on cases where they are most likely to provide a diagnostic benefit. In our testing cohort of 1, 833 individuals with known Aβ PET status, our model predictions demonstrate significant potential for cost savings. With an NPV of 75.35%, we can rule out 587 cases from undergoing unnecessary Aβ PET scans. Similarly, in the test cohort of 844 individuals with known tau PET status, our tau PET model achieved an NPV of 91.65%, suggesting to exclude 582 cases from requiring tau PET scans. In addition, leveraging the PPV of these models can enhance efficiency by identifying high-risk cases. Our Aβ PET model, with a PPV of 62.05%, can ensure that 654 individuals receive the necessary scans, while the tau PET model, with a PPV of 52.40%, can prioritize 109 high-risk cases for τ imaging.

In addition to predicting probabilities for Aβ and tau status, our model provides spatial characterization of the disease, which correlated with disease stage. Our findings further demonstrate that the model-derived volumetric regions of importance align with local patterns of tau deposition observed in PET imaging, thereby validating the model’s predictive capability (Fig. 5). This alignment suggests the potential to inform differential diagnosis, more precise identification of disease stages and subtypes, and support personalized treatment approaches based on regional tau pathology. While neurofibrillary tau tangles are a hallmark of AD, other dementias such as frontotemporal dementia and chronic traumatic encephalopathy can also exhibit tau accumulation34,35. The presence of Aβ and the distribution of tau pathology, however, vary by type of dementia, contributing to diverse clinical presentations and progression patterns36,37. Through providing concurrent predictions of Aβ and τ status, our model may aid in increasing specificity to biological AD. In a second stage, our regional tau model could eventually enhance differential diagnosis by allowing comparison of predicted regional tau profiles with known tau patterns of other dementias. In typical AD, tau burden gradually increases in the medial and neocortical temporal lobes before spreading to the parietal, frontal, and occipital lobes32. We have shown that our model’s composite AT score effectively differentiates between disease stages, distinguishing A + T- cases from A + MTL + cases, thereby identifying tau pathology in regions that are affected early in the disease course4,38. Because tau PET is closely associated with biological disease stage as well as cognitive decline, it has been proposed as a potential clinical endpoint for disease-modifying treatments39. Our model could thus serve as a pre-screening tool to not only identify the presence of disease but also delineate the stage of disease, refining the selection of candidates for clinical trials or treatments. While our current dataset lacked sufficient data to fully validate the subtyping potential of our model, the comprehensive regional profile of tau pathology it provides could eventually enable clinicians to determine disease stage and subtype based on established tau deposition patterns in AD40. This capability offers promising directions for future research and clinical practice, potentially transforming how AD and related disorders are diagnosed and managed.

Our study has a few limitations despite its strengths in scale, multimodal integration, and validation approach. Our model was developed and validated on seven distinct cohorts; however, its generalizability across diverse populations and clinical settings remains to be determined, as the dataset was predominantly composed of White participants. Importantly, due to the lack of non-AD and mixed dementia cases in our datasets, the generalizability of our findings to these important clinical phenotypes remains to be evaluated. While our model predicts amyloid and tau PET status as biomarkers of AD pathology, it does not directly distinguish AD from other common causes of cognitive impairment, such as vascular, Lewy body, or mixed dementias. In routine clinical settings, non-AD and mixed etiologies are prevalent, and PET positivity alone may not fully account for the complexity of real-world diagnostic challenges. Therefore, the utility of our approach should be interpreted as a tool for biomarker-based risk stratification, rather than as a comprehensive diagnostic solution for all-cause cognitive impairment. In addition, we used a binary thresholding technique to define Aβ and tau PET positivity, despite the variability in these definitions across different studies. Various studies have adopted their own criteria for PET positivity, influenced by multiple factors. Nevertheless, our modeling framework is flexible and can be adapted to different definitions of PET positivity (Fig. 3a, b). While our current model effectively provides binary classification, which aligns with how these biomarkers are often clinically interpreted, there is value in moving toward continuous quantitative predictions for more precise disease staging and monitoring. Future work should extend this binary classification to an ordinal regression task with multiple categories, providing a more quantitative approach to predicting PET status. Moreover, due to the limited number of cases with blood-based biomarker data in our training dataset (n = 255), we were unable to fully leverage these data to enhance the model’s predictive accuracy. As novel plasma biomarkers become more widely available and harmonized across assays, we anticipate that integrating them with existing medical data and neurocognitive evaluations will likely enhance the accuracy of predicting AD pathology beyond what is achieved by relying on any single modality of data. While our model could help identify individuals likely to have pathology associated with biological AD, extending this framework to select participants for clinical trials is more complex than merely identifying those who are Aβ and τ positive. Key barriers include limited awareness, fear of diagnosis, overstretched healthcare systems, poor physician awareness, lack of effective treatments, lack of fast diagnostics, and low awareness of clinical trials, causing many eligible participants to be lost before enrollment. Nevertheless, our framework can provide an important first step in identifying individuals likely to have the disease, thereby enabling more effective targeting of community outreach programs. In addition, given preliminary evidence that tau PET status and severity may impact treatment response in anti-amyloid therapies6, our model could serve as a tool to predict which patients might benefit most from specific disease-modifying drugs. By stratifying patients based on pathology severity subgroups, clinical trials can be more efficiently designed to assess treatment efficacy in targeted subgroups, potentially improving outcomes and accelerating the development of effective therapies.

In conclusion, by integrating multimodal data from standard neurological work-up, our model shows promise in identifying individuals with biological AD, reducing the reliance on expensive imaging techniques like PET scans. Our approach demonstrates the feasibility of multimodal integration for biomarker prediction, and such frameworks can ultimately contribute to reducing the burden associated with participant selection for AD clinical trials. Future studies are needed to assess the accuracy of our approach in identifying biological AD and to quantify the economic benefits of using this method in selecting participants for clinical trials.

Methods

All data were obtained in de-identified format from external study centers, each with appropriate ethical oversight. The study centers and their respective ethical approvals are as follows. The A4 study (https://www.a4studydata.org/) and the Harvard Aging Brain Study (HABS, https://habs.mgh.harvard.edu) were approved by Partners Human Research Committee; the National Alzheimer’s Coordinating Center (NACC, https://naccdata.org/) data are collected under protocols approved by institutional review boards at each participating Alzheimer’s Disease Research Center; the Open Access Series of Imaging Studies (OASIS, https://sites.wustl.edu/oasisbrains/) was approved by the Washington University Human Research Protection Office; the Australian Imaging, Biomarkers and Lifestyle study of aging (AIBL, https://aibl.org.au/) was approved by the institutional human research ethics committees of Austin Health, St. Vincent’s Health, Hollywood Private Hospital and Edith Cowan University; the Framingham Heart Study (FHS, https://www.framinghamheartstudy.org/) operates under approval from the Boston University Medical Center Institutional Review Board; the Alzheimer’s Disease Neuroimaging Initiative (ADNI, https://adni.loni.usc.edu/) was approved by institutional review boards at each participating site. All cohorts obtained appropriate informed consent from participants prior to data collection and sharing.

Study population

This study involved a total of 12, 185 participants drawn from seven different cohorts. Written informed consents were obtained from all participants or their proxies, and approval was secured from each cohort’s respective institutional ethical review boards. The training set, consisting of 10, 352 participants, included individuals from the A4 study41, NACC42, OASIS343, AIBL44, and FHS45. All subjects in this study had an amyloid PET scan, but only 3, 488 of these participants also underwent tau PET imaging. The training set was further split into training (8281 participants) and validation (2071 participants) subsets using stratified splitting across all labels, ensuring the label distribution remained consistent with the original dataset. The test set comprised 1, 833 participants from ADNI46, HABS47, and a subset of NACC subjects with neuropathological data. Data collected included demographics, medical history, neuropsychological scores, physical and neurological examinations, APOE e4 genotype, neuroimaging data, as well as CSF and blood biomarkers for model training. All model evaluations at testing were performed without using CSF. In the study sample, 7, 561 participants were Aβ PET negative, and 4, 624 were Aβ PET positive. Among those who underwent tau PET assessments (n = 3, 488), 2655 were tau PET negative and 833 were tau PET positive on a meta-temporal region of interest (ROI). Table 1 provides a detailed overview of the study population across all cohorts. Single visits were included for each participant.

Selection criterion

Participants were eligible for inclusion in the study if they had undergone at least one Aβ PET scan and had clinical or neuroimaging visits within one year of the PET scan. For cohorts with multiple eligible visits, such as ADNI, HABS, NACC, OASIS, and AIBL, visits were selected to minimize the time difference between PET scan and clinical or MRI visits. Because OASIS, ADNI, and NACC may share participants, we conducted pairwise comparisons between participants in OASIS and ADNI as well as OASIS and NACC. Specifically, we searched for similar characteristics across demographics, physical characteristics, medical history and comorbidities, functional assessment scores, neuropsychiatric symptoms, and cognitive statuses, with an error tolerance of 2 units in numerical features and excluded any such potentially duplicated participants. All subjects in the A4 cohort with an Aβ PET scan were included. In the FHS cohort, participants with an Aβ PET scan performed within one year of a clinical visit were retained. To ensure consistency across the diverse cohorts, all variables were renamed and recoded to align with the Uniform Data Set Researchers Data Dictionary (UDS) 3. Despite the unique sets of variables between cohorts, which did not always overlap, no cases were excluded due to missing data. This was facilitated by our model training approach, which incorporated random feature masking and label masking, as described below.

PET image processing

Cortical amyloid positivity was quantified using various PET imaging agents in the cohorts: dynamic 11C-PiB for FHS, late-frame 18F-florbetapen and 18F-florbetapir for ADNI, 18F-florbetapir for A4 and OASIS3, 18F-flutemetamol for AIBL, and 11C-PiB for AIBL, OASIS3, and HABS. Centiloid (CL) values were provided directly by ADNI, A4, OASIS, and a subset of NACC (n = 334), while for AIBL and HABS, an internal pipeline was used to process standard uptake value (SUV) images, following the methodology established by Klunk and colleagues48. Briefly, Aβ PET and T1-weighted (T1w) images were automatically realigned to match the orientation of the MNI152 template. We then coregistered the Aβ PET and T1w MR images to the MNI152 template, normalized to standard space, and calculated global cortical SUV ratios (SUVr) using the Global Alzheimer’s Association Interactive Network (GAAIN) masks. Our pipeline, which uses SPM12 for image realignment and normalization, differs slightly from the standard Klunk method48, which required us to process GAAIN data and regress our calculated SUVrs against Klunk’s published values to derive a scaling equation to convert SUVrs to CL for each tracer. For the FHS cohort, mean cortical 11C-PiB distribution volume ratios (DVR) images were estimated using the Logan method49 and these were subsequently processed as described above to calculate global cortical DVR values. DVR images and T1w scans were realigned to the MNI152 orientation before being co-registered and normalized to standard space. GAAIN masks were finally used to estimate the global cortical DVR. For tau PET, standardized uptake value ratios (SUVr) in Freesurfer-defined regions were made available by the A4, OASIS, FHS, ADNI, HABS and a subset of the NACC cohorts (n = 344).

PET data harmonization

Tau PET data from the various cohorts were processed using different image processing pipelines18,50,51,52. Therefore, we employed the ComBat tool to harmonize tau PET SUVr values to account for variation across cohorts53. A batch variable for cohort and several covariates were used, including age, sex, amyloid PET positivity status and diagnosis. We used an analysis of covariance (ANCOVA) framework to assess the main effects of cohorts on tau SUVr measurements across brain regions before and after ComBat harmonization, adjusting for covariates age, sex, diagnosis, and amyloid status. Raw p-values from the ANOVA results were adjusted using the Benjamini-Hochberg procedure to control for the false discovery rate across multiple comparisons. ROIs with an adjusted p-value below 0.05 were considered significant. For SUVr regions where the ANOVA indicated a significant cohort effect post-harmonization, post hoc pairwise comparisons were conducted using estimated marginal means. Pairwise contrasts between cohorts were computed with Tukey’s adjustment for multiple comparisons. Please refer to Supplementary Fig. S6 and Supplementary Tables S23–S25 for more detail on the effect of harmonization.

PET positivity thresholding and tau profiling

For Aβ PET, a pre-established threshold of 24 CL14 was applied to define positivity in A4, OASIS3, AIBL, HABS, ADNI and the subset of NACC with available CL data. For FHS, a pre-established threshold of 1.20 DVR was used to define Aβ PET positivity14. Most of the NACC subjects included in this study (n = 4, 006) were assessed using a binary UDS variable indicating Aβ positivity, and no information was available regarding site-specific thresholding. For tau PET, a meta-temporal region of interest (ROI) was constructed following established standards30. A Gaussian mixture model (GMM) with two components was run on the ComBat-harmonized tau PET SUVr data from the training set, and tau PET positivity was defined as SUVr values greater than 1.37. In addition to the meta-temporal ROI, we also defined tau ROIs associated with various AD stages and subtypes: medial temporal, lateral temporal, medial parietal, lateral parietal, frontal and occipital17,18. GMM analyses on the harmonized tau PET data set the positivity thresholds at 1.32, 1.33, 1.38, 1.29, 1.30 and 1.23, respectively. Supplementary Tables S9, S10 provides an overview of the study population broken down by regional tau positivity status.

MRI processing

T1-weighted (T1w), FLAIR, and T2*-weighted (T2*w) MRI sequences were collected from various cohorts. Table 1 details the MRI counts for each sequence across these cohorts. T1w images were segmented with Fastsurfer54, and regional volumes were estimated. A Swin UNETR architecture55,56 was further leveraged to extract features from bias field corrected volumetric T1 scans, as well as FLAIR and T2* images that were resampled to 1mm resolution. FLAIR and T2* images were additionally padded to 256 × 256 × 256 before being input to the Swin UNETR architecture. All resulting embeddings were of length 768 × 8 × 8 × 8.

Modeling framework

We utilized the framework detailed in Xue et al.,33 to analyze 443 distinct clinical features encompassing personal demographics, medical history, functional assessments, neuropsychological test scores, neuroimaging data, and fluid biomarkers (Fig. 1). Each feature was first encoded into a fixed-length vector via a modality-specific embedding technique that served as input to the transformer. The transformer then integrated these inputs to generate predictions. A key feature of this model is the implementation of a random feature masking mechanism within the transformer, which is designed to handle missing data effectively. For each sample with feature set S, we randomly permuted the features as σ and selected an index i from [1, ∣S∣]. Features σi+1 to σ∣S∣ were then masked out from the transformer input. The framework also incorporated a label masking strategy to leverage datasets with missing labels. The task was formulated as a multi-label classification problem, with separate binary heads assigned for predicting each label. To account for missing labels, the loss associated with samples lacking specific labels was masked before backpropagation. This approach significantly enhanced the model’s robustness and accuracy in real-world scenarios with incomplete datasets. We fine-tuned this model, originally trained on a 13-label classification task33, using a two-stage process. In the first stage, we trained the model to predict Aβ and meta-τ labels by transferring the weights of the transformer encoder module and the embedding modules corresponding to overlapping features. During the initial 15 epochs, only the newly initialized weights were trained, while the transferred weights remained frozen. Subsequently, we unfroze the transferred weights and included them in the training process. In the second stage, we further fine-tuned the model to predict regional τ labels. To prevent label leakage, we maintained the same training and testing splits for the NACC dataset as in the original transformer protocol33, ensuring no subject overlap between the two sets.

Loss function

Our model was trained by minimizing the “Focal Loss (FL)”57 (\({{\mathcal{L}}}\)), a variant of standard cross-entropy loss that addresses the issue of class imbalance. It assigns low weight to easy (well-classified) instances and high weight to hard-to-classify examples. This loss function was used for each of the biomarker categories. Our loss function \({{\mathcal{L}}}\) was:

$${{\mathcal{L}}}=\, \frac{1}{N}\mathop{\sum }\limits_{k=1}^{N}\mathop{\sum }\limits_{i=1}^{M}-{y}_{k,i}{\alpha }_{i}{(1-{p}_{k,i})}^{\gamma }\log ({p}_{k,i})\\ -(1-{y}_{k,i})(1-{\alpha }_{i}){({p}_{k,i})}^{\gamma }\log (1-{p}_{k,i}),$$
(1)

where N is the batch size and M is the number of biomarker categories (2 for the first stage and 6 for the second). The batch sizes N were set to 128 and 64 for the first and second stages, respectively. The focusing parameter γ was set to 2, which has been reported to perform well in previous studies33,57. The balancing parameter αi ∈ [0, 1] was set as the square of the complement of the fraction of samples labeled as 1, varying for each i due to the differing level of class imbalance across biomarker categories.

For both stages of training, the maximum number of epochs was set to 128, with early stopping applied if no improvement was observed on the validation split for 15 epochs in the first stage and 30 in the second. Mini-batch optimization was performed using the AdamW optimizer58, with learning rates of 0.001 and 0.0001, and weight decay values of 0.01 and 0.005 for the first and second stages, respectively. A cosine learning rate scheduler was employed to adjust the learning rate dynamically during training.

Interpretability analysis

To interpret the model predictions, we conducted Shapley analysis59 on the outputs for Aβ, meta-τ, and regional τ models. Shapley values quantify the contribution of each feature to the model’s predictions, effectively providing a measure of feature importance. We employed a permutation sampling strategy33,60 to efficiently estimate Shapley values across the high-dimensional feature space. This approach involves permuting feature values and measuring changes in the model’s output to approximate each feature’s impact. For each label prediction, Shapley values were calculated for all input features, including imaging-derived measures, whole brain image embeddings and clinical variables. Missing features were assigned a Shapley value of zero, indicating no contribution to the prediction. The features were then ranked by their mean Shapley values across true positive samples, identifying the most influential features driving the model’s decisions.

Traditional machine learning model

We sought to compare the performance of our model with that of a traditional machine learning framework, CatBoost61, to provide a benchmark for our approach. As a tree-based classification framework, CatBoost effectively handles missing features by assigning designated missing values when an input is absent at inference. However, CatBoost lacks support for incorporating learned embeddings from imaging data, limiting its ability to leverage spatial patterns captured in MRI scans. To address this, we used regional volumes derived from FastSurfer as the imaging-related inputs for CatBoost. In addition, unlike our transformer-based model, which performs multi-label classification in a unified manner, CatBoost requires training separate models for each output variable. As a result, we trained eight independent CatBoost models, one for each label, while our deep learning approach benefited from joint optimization across multiple tasks.

Model validation on biological outcomes

We sought to validate predicted probabilities of the model against PET estimates of amyloid and tau burden, as well as evaluate its alignment with a common clinical endpoint in AD clinical trials, the Alzheimer’s Disease Assessment Scale-Cognitive Subscale (ADAS-Cog13). Importantly, ADAS-Cog13 scores were not incorporated as input during the model’s training, ensuring independent validation of the model’s predictive capabilities. Participants from the ADNI cohort were selected for this analysis, as they both underwent amyloid and tau PET imaging and completed the ADAS-Cog13 assessment. To further evaluate our model performance in preclinical AD, we included a subset of cases who were cognitively unimpaired. We then compared model-predicted probabilities for amyloid, P(Aβ), between cases who were Aβ PET negative vs Aβ PET positive. Finally, we aimed to validate our model predictions of regional tau positivity and investigate its potential for disease staging. To derive a unified quantification of AD pathology, we employed principal component analysis (PCA). This dimensionality reduction technique allowed us to capture the shared variance across different regional tau and amyloid probabilities into a single composite score. We applied PCA and used the first principal component (PC1), which explained 97.5% of the variance, as our composite measure of AD pathology, termed the amyloid-tau (AT) score. Based on the PET binary labels, we classified participants and compared the AT scores across four distinct disease stages. These included cases who are Aβ PET negative and tau PET negative in all regions (A-T-), Aβ positive but tau negative in all regions (A + T-), Aβ positive with tau PET positivity restricted to the medial temporal lobe (A + MTL +), and Aβ positive cases with tau PET positivity in the medial temporal and neocortical regions (A + NEO +).

Subgroup analysis on biomarker profiles

We selected a subset of cases from the testing set with PET-confirmed Aβ positivity, mirroring the inclusion criteria for amyloid presence used in recent clinical trials6. Participants were then stratified into tertiles (low, medium, and high) based on their meta-τ SUVr values to evaluate the model’s predictive accuracy across a spectrum of tau burdens. We further assessed the relationship between tertile groups and centiloids to evaluate whether the model’s output is consistent with empirically measured amyloid levels. Similarly, we conducted an analysis of the model-predicted tau probabilities, P(τ), in Aβ + cases, this time stratifying participants into tertiles based on their centiloid values. Because the NACC* testing cohort did not have continuous PET data available, only ADNI and HABS were included in these analyses. Finally, to further validate our model’s ability to differentiate those who are positive on both biomarkers from those who are negative on both, we compared the distributions of P(Aβ) and P(τ) in the combined ADNI, HABS and NACC* test set between Aβ +, τ + and Aβ-, τ- cases.

Spatial analysis

Cases with positive regional τ labels and predictions were selected for this data-driven analysis. A fully-connected graph network was constructed with nodes representing individual brain regions and edges connecting the nodes. Edge weights were determined by computing pairwise normalized mutual information (NMI)62,63,64 on the Shapley values of T1-derived regional volumetric features. This quantifies the mutual dependence between two brain regions in their contribution to the model. We identified non-overlapping communities of brain regions that the model deemed important for positive predictions on each regional label using the Louvain method for community detection65. We preset the number of communities in each graph to five, corresponding to the established Braak staging of tau pathology progression, combining regions from stages 1 and 232. To address the randomness inherent in the Louvain algorithm, we employed consensus clustering with 100 draws63. Using the same set of cases, we established another graph network on the same brain regions, but with edges defined by the NMI of the tau PET SUVr values. We identified communities of brain regions in this network using the same methodology as before. To compare the T1-derived communities identified as important by the model against the communities identified in the tau PET scan, we evaluated the similarity between these two clusterings using the adjusted mutual information (AMI)66. The AMI measures the level of agreement between two clusterings with correction for random clustering agreement, and is preferred over adjusted Rand index (ARI) when the reference clustering is unbalanced and there are small clusters67 (Supplementary Table S20).

Postmortem validation

To assess the alignment of our model with neuropathological evidence, we utilized a subset of cases from the ADNI database (n = 41) for which postmortem evaluations were available. We supplemented this sample with an additional subset of cases from the NACC database (n = 147) for which neuropathological data was available, excluding these cases from the training set. Of note, this subset of NACC cases was also in the testing set of the original transformer model33 that we finetuned for this study, thus preventing potential label leakage. The mean time difference between age at death and age of neuropathological assessments was 3.05 years. On these cases, we examined the Thal phase for amyloid plaques (A score), Braak stage for neurofibrillary degeneration (B score), density of neocortical neuritic plaques (CERAD score) (C score), density of diffuse plaques (CERAD semi-quantitative score), and cerebral amyloid angiopathy, and investigated the correlation between the model-generated probability scores of Aβ and τ positivity and the grades of these neuropathological features.

Statistics and reproducibility

We conducted a series of statistical analyses to rigorously evaluate our model’s alignment with PET burden, biomarker profiles, and post-mortem neuropathological grades. No statistical method was used to predetermine sample size, and no data were excluded, as long as all features required for statistical analyses were present. When building the deep learning model, the training cases were shuffled using a consistent random seed and split into training and validation subsets using stratified splitting across all labels. The investigators were not blinded to allocation during experiments and outcome assessment. A Shapiro-Wilk test was performed prior to each analysis to assess normality. To evaluate the alignment between our model-predicted probabilities and continuous PET values, we computed both the Spearman’s ρ and Pearson’s r coefficients, log-transforming regional τ SUVr values to improve linearity. In addition, we evaluated the model’s ability to detect preclinical AD by comparing amyloid probability outputs between Aβ PET-negative and positive cognitively unimpaired cases using a one-sided Mann-Whitney U test. We then aimed to validate our model’s ability to distinguish disease stages. A Kruskal-Wallis H test, followed by post hoc Dunn’s test with Holm-Bonferroni adjustments for multiple comparisons, was performed to assess the alignment of our model’s AT score with PET-defined disease stages. We then sought to validate our model’s predictive accuracy across quantiles of disease severity. We used a one-sided Mann-Whitney U test to compare predicted probabilities, P(Aβ) and P(τ), and PET measures, centiloids and meta-T SUVr, between cases with low/medium vs. high disease burden. Similarly, we applied a one-sided Mann-Whitney U test to compare P(Aβ) and P(τ) between cases who are PET-confirmed biomarker positive and negative. In the spatial analysis, we assessed the statistical significance of the agreement between model- and tau PET SUVr graphs by performing a t test on 5000 spatial permutation draws of the AMI68,69. Spatial permutations were applied to maintain the brain’s contralateral symmetry through rotating spherically projected brain region coordinates extracted from the Desikan-Killiany atlas by a random angle along each of the x, y, and z axes. New labels were assigned by mapping the original region centroids to the closest permuted region centroid based on Euclidean distance. Finally, to evaluate differences in model probability outputs across various stages of post-mortem neuropathological scores, we employed the Kruskal-Wallis test, followed by post hoc Dunn’s tests to conduct pairwise comparisons between groups, with adjustments for multiple comparisons using the Holm-Bonferroni correction method. To further evaluate the overall correlation between model-generated probabilities and each neuropathological feature, we computed the Spearman correlation coefficient, thus assessing the strength and direction of association between the ranked neuropathological grades and model probabilities.

Performance metrics

Receiver operating characteristic (ROC) and precision-recall (PR) curves were created based on the predictions on the combined ADNI and HABS external datasets, as well as on the NACC* test set. Additional performance metrics including balanced accuracy, sensitivity, specificity, precision, also known as positive predictive value (PPV), F1 score, Matthews correlation coefficient, and negative predictive value (NPV) were computed by determining the optimal threshold for each label using Youden’s J statistic, based on the performance of the validation split.

Computational hardware and software

Our model development utilized Python (version 3.11.9) and specifically PyTorch (version 2.4.0). We used several other Python libraries to support data analysis, including pandas (version 2.2.2), numpy (version 1.26.3), matplotlib (version 3.9.1), monai (version 1.3.2), scipy (version 1.14.0), and scikit-learn (version 1.5.1). R packages were also used for data analysis and visualization, including dplyr, emmeans, and ggseg3D. Training the model on a single Tesla V100 GPU on a shared computing cluster had an average runtime of 2 minutes per epoch, while the inference task took less than a minute per instance. All figures were prepared using Canva and Adobe Illustrator.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.