Introduction

In recent years, with the increasing number of genome-wide association study (GWAS) investigations, there has been a notable increase in the public availability and utilization of GWAS summary data by researchers1,2. This inclusive dataset encompasses information from diverse populations and ethnic backgrounds3,4,5,6, a development that researchers find valuable, thus making it a current focal point of research interest. Owing to a range of influences, including geographical landscapes and varied lifestyles, genetic structures exhibit significant diversity among distinct populations7,8, also called population stratification, potentially leading to heterogeneity in GWAS summary data across different ethnic groups, such as those of European, Asian, and American descent.

Mendelian randomization (MR)2,9 is a methodology that relies on the utilization of publicly available GWAS summary data for causal inference. It uses genetic variants as instrumental variables (IVs) to infer the causal effect of one or multiple exposures on an outcome, that is, univariable or multivariable MR10,11, respectively. A valid IV must satisfy the following three assumptions: (A1) Relevance (IV is strongly associated with at least one of the exposures), (A2) Exchangeability (IV is independent of confounders between exposures and outcomes), and (A3) Exclusion restrictions (IV affects the outcome only through exposures)9. These assumptions are also mentioned in the Methods section. When we consider heterogeneous populations, one valid IV in a population may be an invalid IV in another population due to various genetic structures. For example, \({G}_{1}\) is a valid IV in population I; it may be correlated with the confounder \(U\) between exposure and outcome in population II, whereas \(U\) is not the confounder in population I. In this case, \({G}_{1}\) violates the exchangeability in population II. In addition, \({G}_{1}\) may be correlated (linkage disequilibrium (LD))12 with another SNP \({G}_{2}\), which directly affects the outcome in population II, but \({G}_{1}\) is independent of \({G}_{2}\) in population I. In this case, \({G}_{1}\) violates the exclusion restriction in population II because the LD references in different populations are different. In addition, the effects of some traits, such as body mass index, educational attainment or depression, on various disease outcomes are mediated or modified by social and environmental factors, which lead to inconsistent causal relationships in different societies or population groups. Therefore, the heterogeneity among populations includes genetic and nongenetic differences, such as social or environmental factors, also creating distinct challenges for IV validity across groups. This complexity increases the difficulty of deducing a purely causal relationship by integrating multiple heterogeneous GWAS summary datasets.

Therefore, the aim of this paper was to explore the pure causal effect, in which “pure” means that we focus on the causal effect that is not affected by social and environmental factors, i.e., the pure causal effect is invariant across heterogeneous populations. One straightforward way to infer pure causal relationships using MR is to first conduct MR analysis separately using valid IVs in different populations, obtain causal effect estimations in each population, and then combine all estimations by meta-analysis13,14. Even if there are invalid IVs in the first step, many MR methods15,16,17,18 have been proposed to eliminate the influence of invalid IVs on causal effect estimation. However, the accuracy of meta-analysis results depends on the robustness of different MR methods, and these MR methods require different assumptions15,16,17,18, which may be difficult to satisfy or cannot be tested. This may induce inconsistent causal effect estimation in different populations and make inferring pure causal relationships difficult (see Application section). Another idea is to first conduct GWAS meta-analysis for heterogeneous populations, and then select valid IVs to infer causal relationships via MR. The difficulty with this strategy is that only a short number of independent SNPs (no LD) can be selected because the LD reference panels in different populations are different8,19. These two strategies are both two-step processes, and result in doubled statistical errors, which results in a lower accuracy of causal effect estimation. In addition, meta-analysis is a statistical technique used to combine and analyze results from multiple studies20; if one result is inaccurate, the meta-analysis results are also incorrect. Meta-analysis is not a causal method in itself and does not necessarily provide causal evidence that holds true in every population included in the analysis. Therefore, we proposed a one-step method that integrates all the information, not only the MR results for each population, and provides causal evidence that holds true (also called invariant effects) in each population.

In this paper, we introduce an MR method called MR-EILLS, which utilizes the environment invariant linear least squares (EILLS)21 to integrate multiple heterogeneous GWAS summary datasets and then infer pure causal relationships. The MR-EILLS model works in both univariate and multivariate scenarios and allows for invalid IVs that violate exchangeability and exclusion restriction assumptions. In addition, MR-EILLS shows the unbiased causal effect estimation of one or multiple exposures on the outcome, whether there are valid or invalid IVs. Compared with traditional MR and meta methods, MR-EILLS yields the highest estimation accuracy, the most stable type I error rates, and greater statistical power. Finally, MR-EILLS was applied to explore the independent causal relationships between 11 blood cells and 20 disease-related outcomes, using GWAS summary statistics from five ancestries: African, East Asian, South Asian, Hispanic/Latino, and European.

Results

Method overview

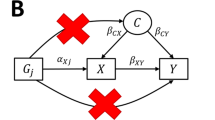
The MR-EILLS model integrates the GWAS summary statistics from multiple heterogeneous populations, and identifies the causal exposures that have invariant effects on the outcome. The GWAS summary statistics for \({E}\) heterogeneous populations include the \({G}_{j}-X\) association \({\hat{\theta }}_{p,j}^{({e})}\) and its standard error \({\sigma }_{{G}_{j}{X}_{p}}^{({e})}\), as well as the \({G}_{j}-Y\) association \({\hat{\Gamma }}_{y,j}^{({e})}\) and its standard error \({\sigma }_{y,j}^{({e})}\), where the subscript \(p\) represents the p-th exposure (\(p\in \{1,2,{\mathrm{..}}.,P\}\)), \(j\) represents the j-th IV (\(j\in \{1,2,{\mathrm{..}}.,J\}\)) and the superscript \(e\) represents the e-th population (\(e\in {\mathcal E},{\mathcal E}=\{1,2,{\mathrm{..}}.,E\}\)). We assume that the causal effects of causal exposures (\(\{{X}_{p}\},p\in P\ast \)) on \({Y}\) are invariant in different populations, that is \({\beta }_{0p}^{(1)}={\beta }_{0p}^{(2)}={\mathrm{.}}..={\beta }_{0p}^{(E)}={\beta }_{0p}^{\ast }\) for \(p\in P\ast \), where \(P\ast \) is the set of causal exposures, whereas the genetic associations between SNPs and exposures/outcome/confounders may be different, and confounders between exposures and the outcome are also different. The aim of the MR-EILLS model (Fig. 1) is to explore the pure causal effect of causal exposures on the outcome by minimizing the following objective function

$$\begin{array}{l}Q({\beta }_{0p}^{\ast };{\hat{\theta }}_{p,j}^{(e)},{\hat{\Gamma }}_{y,j}^{({e})},{\sigma }_{y,j}^{({e})2})\\={\sum }_{e\in {\mathcal E} }{w}^{({e})}{{{\rm{E}}}}_{j\in S\ast }[|{w}_{j}^{(e)}{\hat{\varepsilon }}_{j}^{(e)}{|}^{2}]+\gamma {\sum }_{p\in P}{\sum }_{e\in {\mathcal E} }{w}^{({e})}|{{{\rm{E}}}}_{j\in S\ast }[{\hat{\theta }}_{p,j}^{(e)}\cdot {w}_{j}^{(e)}{\hat{\varepsilon }}_{j}^{(e)}]{|}^{2}\end{array}$$
(1)

where \({{\rm{E}}}\) is the expectation, \({w}_{j}^{(e)}\) is the weight of IV \({G}_{j}\) on the causal effect estimation in the e-th population, and \({w}^{(e)}\) is the weight of e-th population on the pure causal effect estimation. The first part of the objective function (1) is the empirical \({L}_{2}\) loss, which is the multiple-population version of ordinary least squares in one population, and \({\hat{\varepsilon }}_{j}^{(e)}={\hat{\Gamma }}_{y,j}^{(e)}-{\sum }_{p}{\hat{\theta }}_{p,j}^{(e)}{\beta }_{0p}^{(e)}\) denotes the pleiotropic effect. Motivating simulation (Fig. 1a and Supplementary Fig. 1a) demonstrated that as the pleiotropic effect increased, the absolute value of \({\hat{\varepsilon }}_{j}^{(e)}\) increased. The pleiotropic effect includes correlated and uncorrelated pleiotropy. When only the A3 assumption (exclusion restriction) is violated, we say that an uncorrelated pleiotropic effect exists; when the A2 assumption (exchangeability) is violated, a correlated pleiotropic effect emerges. The second part of the objective function (1) is the empirical focused linear invariance regularizer, which discourages the selection of exposures with strong correlations between \({\theta }_{p,j}^{(e)}\) and \({\varepsilon }_{j}^{(e)}\) in some populations because these correlations represent correlated pleiotropy, which would distort causal effect estimation. The results of the motivating simulation (Fig. 1b and Supplementary Fig. 1b) demonstrated that as the correlated pleiotropic effect increased, the correlation between \({\hat{\varepsilon }}_{j}^{(e)}\) and \({\hat{\theta }}_{p,j}^{(e)}\) became stronger. \(\gamma > 0\) is the hyperparameter. In addition, we added the following restriction

$$S\ast=\{\;{j}:{\sum}_{e\in {\mathcal E} }|{\varepsilon }_{j}^{(e)}|+{\sum}_{p\in P}{\sum}_{e\in {\mathcal E} }|{\hat{\theta }}_{p,j}^{(e)}{\varepsilon }_{j}^{(e)}| < \lambda \}$$
(2)

to select valid IVs, that satisfy the three assumptions and have no pleiotropy. The first part of Eq. (2) represents the total pleiotropic effect for the \(j-th\) IV, and the second part of Eq. (2) represents the correlated pleiotropic effect, that is, the correlation between \({\theta }_{p,j}^{(e)}\) and \({\varepsilon }_{j}^{(e)}\) for the \(j-th\) IV. \(\lambda > 0\) is the hyperparameter controlling the strictness of filtering IVs. When there are invalid IVs, the ridge plot of \({\sum }_{e\in {\mathcal E} }|{\varepsilon }_{j}^{(e)}|+{\sum }_{p\in P}{\sum }_{e\in {\mathcal E} }|{\hat{\theta }}_{p,j}^{(e)}{\varepsilon }_{j}^{(e)}|\) has at least two peaks (Fig. 1c), whereas the ridge plot has only one peak when there is no invalid IV. The corresponding abscission value at the lowest point between the two peaks is the optimal \(\lambda \). Thus, Eq. (2) removes the invalid IVs with pleiotropic effects larger than \(\lambda \). Details for motivating the simulation are shown in Supplementary Note 1.

Fig. 1: MR-EILLS model.
figure 1

The MR-EILLS model aims to infer the causal relationships between one or multiple exposures and one outcome, integrating multiple GWAS summary datasets from heterogeneous populations. There are different pleiotropic effects and IV strengths for the same IVs in heterogeneous populations. The objective function of the MR-EILLS model considers both correlated and uncorrelated pleiotropy and removes invalid IVs. Panels a–c show the results of the motivating simulation. Panel a shows the point plot for the absolute value of \({\hat{\varepsilon }}_{j}^{(e)}\) in different populations, where a larger point indicates a larger value of \(|{\hat{\varepsilon }}_{j}^{(e)}|\). As the pleiotropic effect increases, \(|{\hat{\varepsilon }}_{j}^{(e)}|\) increases; thus, the first part of the MR-EILLS model minimizes the pleiotropic effect between different populations. Panel b shows the correlation between \({\hat{\varepsilon }}_{j}^{(e)}\) and \({\hat{\theta }}_{p,j}^{(e)}\), which represents the correlated pleiotropic effect or the violation of the InSIDE assumption. As the correlated pleiotropic effect increases, this correlation becomes stronger. This corresponds to the second part of MR-EILLS, the empirical focused linear invariance regularizer, which discourages the selection of exposures with strong correlations between \({\theta }_{p,j}^{(e)}\) and \({\varepsilon }_{j}^{(e)}\) in some populations because this correlation would distort the causal effect estimation. Panel c shows the ridge plot of \({\sum }_{e\in {{\rm E}}}|{\varepsilon }_{j}^{(e)}|+{\sum }_{p\in P}{\sum }_{e\in {{\rm E}}}|{\hat{\theta }}_{p,j}^{(e)}{\varepsilon }_{j}^{(e)}|\) when there are different proportions of invalid IVs. When there are invalid IVs, the ridge plot has two peaks, whereas the ridge plot has only one peak when there is no invalid IV. The corresponding abscission value at the lowest point between the two peaks is the optimal \(\lambda \). The third part of the MR-EILLS model removes the invalid IVs by \(\lambda \).

Full size image

Simulation

We generated GWAS summary statistics for heterogeneous populations with varying edge effects, IV strengths, and pleiotropy values under both the UVMR and MVMR scenarios. We then compared MR-EILLS with nine published methods: IVW, MR-Egger, MR-Lasso, MR-Median, MR-cML, MRAID, Cause, MR-BMA, and MR-Horse. For these MR methods, we implemented two analytical strategies: (1) metaMR, which first performs meta-analysis of GWAS summary statistics across all datasets for each variable, followed by MR analysis; and (2) mrMeta, which first conducts MR analysis separately for each dataset, followed by meta-analysis of the MR results. Both random effects and fixed effects meta-analysis approaches were employed.

In the UVMR scenario (a), with both correlated and uncorrelated pleiotropy (30% invalid IVs), MR-EILLS, Cause, and MR-cML with metaMR demonstrated unbiased causal effect estimation, whereas other methods exhibited bias (Fig. 2 and Supplementary Data 1, 2). Compared with Cause and MR-cML with metaMR, MR-EILLS showed superior performance with higher accuracy, more stable type I error rates when the causal effect was null, and greater statistical power for nonnull effects. When 80% of the IVs were invalid, all the MR methods, including MR-cML and Cause, produced biased estimates, whereas MR-EILLS maintained unbiased estimation (Supplementary Figs. 8, 9,18, 19). Notably, MR-EILLS displayed robust performance across all evaluation metrics: it maintained appropriate type I error rates for null effects and achieved >90% power with 300 IVs for nonnull effects (Supplementary Figs. 10, 11 and Supplementary Figs. 20, 21). In scenario (b), MR-IVW and MR-Egger showed significant bias, whereas the other methods performed better with smaller bias. Additionally, all methods yielded more accurate estimates under balanced pleiotropy conditions than under unbalanced pleiotropy conditions (Supplementary Figs. 22–29). For scenario (c), all methods performed similarly well, exhibiting three key characteristics: unbiased effect estimation, well-controlled type I error rates for null effects, and high power (>80%) for detecting nonnull effects (Supplementary Figs. 30–33). The complete simulation results are presented in Supplementary Figs. 2–33 (Supplementary Note 2–5).

Fig. 2: Simulation results when \({{\boldsymbol{P}}}\) = 1 (UVMR).
figure 2

a, b Results of the causal effect estimation and type I error rate when the causal effect is zero. c, d Results of causal effect estimation and statistical power when the causal effect is 0.1. The number of IVs is 100 and the proportion of invalid IVs is 30%. The number of populations is \(E=3\). 200 repeated datasets were generated in all simulations. Data in boxplots are presented as median values and interquartile range.

Full size image

For MVMR analyses with eight exposures and 30% of IVs exhibiting either correlated or uncorrelated pleiotropy (case (a)), Fig. 3 (Supplementary Data 3) demonstrates that MR-EILLS provides unbiased causal effect estimates for all exposures, whereas other methods show varying degrees of bias, including slight biases observed with MR-cML using metaMR for certain exposures. Notably, MR-EILLS achieves the highest estimation accuracy among all methods. Figure 4 (Supplementary Data 3) presents type I error rates under null effects and statistical power under nonnull effects, revealing that MR-EILLS maintains the highest statistical power for nonnull effects while showing the most stable type I error control, albeit with marginally lower than nominal rates (0.05) for some exposures—a phenomenon that diminishes with increasing population sizes (Supplementary Figs. 52, 53). Similar performance patterns are observed when \(P=3\) (Supplementary Figs. 46, 47). Under more extreme conditions with 80% invalid IVs, all MR methods produce biased estimates except MR-EILLS, which maintains unbiased estimation (Supplementary Figs. 48, 49). Furthermore, MR-EILLS demonstrates robust type I error control and achieves >90% statistical power with 300 IVs for nonnull effects (Supplementary Figs. 50, 51). For case (b), the results mirror those from UVMR analyses regardless of pleiotropy balance status (Supplementary Figs. 54–57). In the absence of pleiotropy (case (c)), all methods performed comparably well, yielding unbiased estimates, appropriate type I error rates, and high statistical power (>90%) (Supplementary Figs. 58, 59). Comprehensive simulation results are provided in Supplementary Figs. 38–59 (Supplementary Notes 6–9). When evaluating \(P=15\), Fig. 5 displays the mean F1 score, recall, and precision across methods, with MR-EILLS consistently outperforming all alternatives on these metrics.

Fig. 3: Simulation results of causal effect estimation when there is correlated and uncorrelated pleiotropy (MVMR).
figure 3

The number of IVs is 100, and the proportion of invalid IVs is 30%. The number of populations is \(E=3\). Among a total of eight exposures, two (\({X}_{1}\) and \({X}_{2}\)) are causal exposures (with a causal effect of 0.2), and the other six (\({X}_{3},{\mathrm{}}...,{X}_{8}\)) are spurious exposures (with a causal effect of 0). 200 repeated datasets were generated in all simulations. Data in boxplots are presented as median values and interquartile range.

Full size image
Fig. 4: Simulation results of the type I error rate for spurious exposures and statistical power for causal exposures when there is correlated and uncorrelated pleiotropy (MVMR).
figure 4

The number of IVs is 100, and the proportion of invalid IVs is 30%. The number of populations is \(E=3\). Among total of eight exposures, two (\({X}_{1}\) and \({X}_{2}\)) are causal exposures (with a causal effect of 0.2), and the other six (\({X}_{3},{\mathrm{}}...,{X}_{8}\)) are spurious exposures (with a causal effect of 0). This figure displays the type I error rates for \({X}_{1}\) and \({X}_{2}\), the statistical power for \({X}_{3},{\mathrm{}}...,{X}_{8}\).

Full size image
Fig. 5: Simulation results of the F1 score, precision and recall when \({{\boldsymbol{P}}}\) = 15 (MVMR).
figure 5

The number of IVs is 100 and the proportion of invalid IVs is 30%. The number of populations is \(E=3\).

Full size image

Our analyses further revealed significant heterogeneity in causal effect estimates across different populations. Supplementary Figs. 34, 60 summarizes the variation in \({I}^{2}\) across all the simulations. To illustrate this heterogeneity, we randomly selected one simulation, and the detailed forest plots of causal effect estimates for each MR method and dataset are presented in Supplementary Figs. 36, 37, 61–63. These plots demonstrate substantial inconsistencies in effect estimates among populations.

Our simulation studies were conducted under weak IV conditions, with conditional F-statistics in simulations mirroring those observed in the applied analysis (Supplementary Data 4). Compared with alternative MR methods, our proposed approach exhibits minimal variance inflation while preserving superior statistical power (Supplementary Figs. 44, 45). These findings proved robust across different genetic correlation scenarios, maintaining consistent performance when accounting for nonzero genetic correlations between populations (Supplementary Figs. 4–7, 14–17, 40–43). In terms of computational efficiency, MR-EILLS maintains high performance regardless of the number of exposures. Conversely, methods such as MR-cML and MR-BMA—particularly MR-Horse—exhibit progressively increasing computational requirements, demanding significantly greater memory allocation and processing time as the number of exposures increases (Table 1).

Table 1 Computing time for different methods in the simulation
Full size table

Application

We explored the causal relationships between a total of 11 blood cells (five red blood cells: hemoglobin (HGB) concentrations, hematocrit (HCT), mean corpuscular hemoglobin (MCH) concentrations, mean corpuscular volume (MCV), and the mean corpuscular hemoglobin concentration (MCHC); five white blood cells: white blood cell (WBC) counts, neutrophil (Neutro) counts, monocyte (Mono) counts, basophil (Baso) counts, and eosinophil (Eosin) counts; one platelets: platelet (PLT) counts) and 20 disease-related outcomes (asthma, body fat percentage, body mass index, waist circumference, weight, fasting blood glucose, HbA1c measurement, total cholesterol, type 2 diabetes, cardioembolic stroke, ischemic stroke, large artery stroke, stroke, heel bone density, pneumonia, schizophrenia, forced expiratory volume (FEV), forced vital capacity (FVC), the FEV/FVC ratio, and peak expiratory flow (PEF)) using GWAS summary statistics from five ancestries: African, East Asian, South Asian, Hispanics Latinos, and European.

First, we conducted traditional MR analysis in five ancestries, and performed heterogeneous analysis for each MR method. The results are shown in Fig. 6 (Supplementary Data 5). We found that there were large heterogeneities (\({I}^{2}\) > 0.75) for blood cells among five ancestries. We subsequently conducted multivariable MR-EILLS analysis to explore the independent causal effects of 11 blood cells on 20 disease-related outcomes. We plot ridge plots for each outcome in five ancestries, and the results are shown in Supplementary Figs. 64–66. We used the ridge plot to set the \(\lambda \) for MR-EILLS (Supplementary Data 6).

Fig. 6: Heterogeneity plot of the application results.
figure 6

The heterogeneity of MR estimations in each population using MVMR-IVW, MVMR-Egger, MVMR-Lasso, and MVMR-Median, whereas MVMR-cML and MVMR-Horse cannot output MR estimations owing to the substantial memory consumption and computational time.

Full size image

In Fig. 7 (Supplementary Data 7), we found that higher counts of some white blood cells, red blood cells or platelets were independently associated with decreased lung function. For FEV, higher WBC, Neutro counts and HGB concentrations causally induced a lower FEV (WBC: beta = −0.14, 95%CI: [−0.24, −0.04]; Neutro: beta = −0.17, 95%CI: [−0.24, −0.04]; HGB: beta = −0.29, 95%CI: [−0.54, −0.03]). The counts of Neutro and HCT were negatively associated with the level of FVC (Neutro: beta = −0.09, 95%CI: [−0.18, −0.01]; HCT: beta = −0.06, 95%CI: [−0.13, −0.002]). In addition, increases in the PLT and Neutro counts were associated with a decreased FEV/FVC ratio (PLT: beta = −0.26, 95%CI: [−0.49, −0.02]; Neutro: beta = −0.16, 95%CI: [−0.30, −0.02]). Higher MCH concentrations might result in a lower PEF level (beta = −0.08, 95%CI: [−0.16, −0.004]). James et al. reported that an increased WBC count is associated with lower levels of lung function and provided biological explanations22. A 15-year longitudinal study demonstrated that higher blood neutrophil concentrations were associated with accelerated FEV decline23. The inverse relationships of FEV and FVC with red blood cell counts were also supported by observational studies24,25. A prospective longitudinal analysis revealed that a higher baseline neutrophil count predicted a lower serially obtained FVC26. Moreover, a retrospective study revealed a strong correlation between the PLT count and the FEV/FVC ratio27.

Fig. 7: Forest plot of the application results.
figure 7

Causal effect estimations of 11 blood cells on disease-related outcomes via the MVMR-EILLS method. Data are presented as mean values and 95% confidence intervals. All the P value and confidence interval is estimated via the bootstrap method, and it is two-sided.

Full size image

Our study provides compelling evidence for causal relationships between cytokine profiles and stroke pathogenesis. Elevated PLT counts were independently correlated with increased overall stroke risk (OR = 1.93, 95%CI: [1.37, 2.71]), particularly for the cardioembolic stroke subtype. Increased Mono levels were positively associated with stroke susceptibility (OR = 1.39, 95%CI: [1.24, 1.57]), whereas elevated MCHC specifically amplified cardioembolic stroke risk (OR = 1.25, 95%CI: [1.03, 1.53]). MCH levels exhibited a marginal yet statistically significant association with ischaemic stroke incidence (OR = 1.06, 95%CI: [1.01, 1.12]). Notably, reduced WBC counts conferred protection against overall stroke risk (OR = 0.63, 95%CI: [0.47, 0.84]), with enhanced preventive efficacy observed in the large artery stroke subtype (OR = 0.55, 95%CI: [0.40, 0.75]). Protective associations were further identified across multiple hematological parameters: Eosin (OR = 0.38, 95%CI: [0.34, 0.44]), Neutro (cardioembolic: OR = 0.74, 95%CI: [0.58, 0.95]; large artery: OR = 0.54, 95%CI: [0.39, 0.76]), Baso (OR = 0.39, 95%CI: [0.31, 0.49]), HGB (OR = 0.64, 95%CI: [0.57, 0.72]), and HCT (OR = 0.69, 95%CI: [0.63, 0.76]).

These findings align with established mechanisms of inflammation-mediated vascular pathology. Mansfield et al.28 demonstrated that cytokine-driven endothelial dysfunction occurs through the IL-6/TNF-α pathway, providing mechanistic support for our observed mono-stroke associations. The neuroprotective neutrophil subset (N2) identified by ref. 29 offers a plausible explanation for the reduced stroke risk at lower Neutro counts through inflammatory modulation. Rodhe et al.30 further substantiated cytokine-mediated vascular injury through IL-8/TNF-α correlations in geriatric populations, whereas ref. 31 delineated cytokine polarization patterns affecting vascular homeostasis, which is consistent with our PLT and HGB findings. Tyagi et al.32 established chemokine-specific inflammatory cascades (e.g., CXCL10), reinforcing our conclusions that Eosin and Baso count reductions attenuate stroke risk.

Our analysis demonstrated that elevated PLT counts independently increased body fat percentage (beta = 0.01, 95%CI: [0.005, 0.02]), although no significant causal associations were detected between blood cell indices and body mass index or waist circumference. Higher MCHC values were positively related to weight (beta = 0.02, 95%CI: [0.004, 0.02]), whereas lower HCT levels were causally linked to increased weight (beta = −0.01, 95%CI: [−0.002, −0.02]). Our findings align with studies linking hematological indices to metabolic outcomes. Zhang et al.33 demonstrated that elevated HCT in obese individuals with dyslipidaemia correlates with worsened lipid profiles (higher TC, TG, LDL-C; lower HDL-C), supporting our observation that lower HCT levels are causally associated with increased weight. Similarly, ref. 34 established HCT as a key determinant of blood viscosity, which impairs insulin sensitivity and promotes adiposity—mechanisms consistent with our positive association between MCHC and body mass. These studies reinforce the role of red blood cell parameters in metabolic regulation, although causal relationships remain nuanced compared with BMI/waist circumference.

Elevated PLT (beta = 0.57, 95%CI: [0.26, 0.89]) and MCHC (beta = 0.3, 95%CI: [0.01, 0.58]) values were independently positively associated with fasting blood glucose. Conversely, Baso (beta = −0.18, 95%CI: [−0.29, −0.08]) and Mono (beta = −0.14, 95%CI: [−0.17, −0.007]) counts demonstrated inverse correlations with glucose levels. For lipid metabolism, the PLT (beta = 0.001, 95%CI: [0.002, 0.023]), WBC (beta = 0.01, 95%CI: [0.001, 0.02]), and Neutro (beta = 0.01, 95%CI: [0.002, 0.02]) counts exhibited positive dose-response relationships with total cholesterol. In contrast, HGB (HGB, beta = −0.01, 95%CI: [−0.013, −0.0001]) and HCT (beta = −0.01, 95%CI: [−0.014, −0.0007]) levels displayed protective associations against cholesterol elevation. Our findings align with the established literature linking hematological indices to metabolic outcomes. Elevated PLT and MCHC levels predict fasting blood glucose, which is consistent with studies demonstrating the role of platelet activation in insulin resistance35 and the impact of erythrocyte rigidity on endothelial function36. Lower Baso and Mono counts are correlated with increased glucose levels, supporting their anti-inflammatory roles in glucose metabolism37,38. For lipid metabolism, the PLT, WBC, and Neutro counts are positively associated with total cholesterol, mirroring leukocyte-driven atherosclerosis mechanisms39 and haemorheological contributions to dyslipidaemia40. Conversely, lower HGB and HCT levels have protective effects against hypercholesterolemia, which aligns with the role of iron metabolism in lipid regulation41.

Elevated HGB and HCT independently elevated asthma risk (HGB: OR = 1.22, 95%CI: [1.04, 1.41]; HCT: OR = 1.19, 95%CI: [1.01, 1.41]). Higher Eosin counts were positively associated with heel bone density (beta = 0.23, 95%CI: [0.02, 0.45]), whereas reduced PLT and mono counts were inversely correlated (PLT: beta = −0.25, 95%CI: [−0.47, −0.04]; Mono: beta = −0.1, 95%CI: [−0.17, −0.02]). HGB and HCT elevations were linked to pneumonia risk (HGB: OR = 1.63, 95%CI: [1.04, 2.54]; HCT: OR = 1.48, 95%CI: [1.06, 2.03]). Schizophrenia risk exhibited dose-dependent relationships with Eosin (OR = 1.27, 95%CI: [1.14, 1.42]), Baso (OR = 1.56, 95%CI: [1.21, 2.05]), and Mono (OR = 1.15, 95%CI: [1.04, 1.28]) counts, in contrast with the protective effect of a lower MCHC (OR = 0.54, 95%CI: [0.39, 0.75]). The independent elevation of asthma risk by HGB and HCT aligns with studies showing that iron deficiency anemia (proxied by low HGB/HCT) impairs lung function and increases airway hyperresponsiveness42. For bone health, the positive correlation between Eosin counts and heel bone density supports the role of eosinophils in osteoblast activation, as demonstrated by the fact that eosinophil-derived growth factors promote bone formation43. Conversely, lower PLT and Mono counts may reflect anti-inflammatory environments that reduce asthma exacerbations44. The links between HGB/HCT elevations and pneumonia risk correspond with evidence that iron overload (high HGB/HCT) promotes bacterial adherence and pulmonary inflammation45. With respect to psychiatric outcomes, the dose-dependent relationships of Eosin, Baso, and Mono counts with schizophrenia risk align with immune dysregulation theories, where proinflammatory monocytes and basophils exacerbate neuroinflammation46. Finally, the protective effect of low MCHCs against schizophrenia may reflect iron homeostasis disruption in schizophrenic patients, as elevated MCHCs are correlated with oxidative stress and dopamine dysregulation47. The details of the results are shown in Supplementary Data 5–9 and Supplementary Note 10.

Discussion

In this paper, we proposed an MR method MR-EILLS, which works in both univariable and multivariable frameworks, and it outputs the pure causal effect estimation of multiple heterogeneous populations using only GWAS summary statistics. The results of the simulation revealed the superior performance of MR-EILLS and its application in exploring causal relationships from 11 blood cells to 20 disease-related outcomes, which covered most of the expected causal links.

MR-EILLS integrates GWAS summary datasets from heterogeneous populations, and for each population, GWAS summary datasets for exposure and outcome can be from either the same individuals or different but heterogeneous individuals. This assumption is the same as that in traditional two-sample MR analysis, which requires two homogeneous but nonoverlapping samples. MR-EILLS assumes that the GWAS summary datasets for each population are from homogeneous but nonoverlapping samples. In the application, we assume that the individuals in each ancestry are homogeneous, and that the genetic diversity in different ancestries leads to heterogeneity among ancestries (different IV strengths and pleiotropy). The heterogeneity among populations includes genetic and nongenetic differences, also creating distinct challenges for IV validity across groups. Genetic architecture differences include allele frequency variations, population-specific linkage disequilibrium (LD) patterns, divergent selection pressures and unique mutation histories, etc. In addition, nongenetic modifiers—such as socioeconomic status, environmental exposures, cultural practices, and disparities in healthcare access—also play a significant role in shaping population heterogeneity. These contextual differences contribute to inconsistent causal relationships across different populations, highlighting the complex interplay between genetic predispositions and external determinants of health.

In our context, we assume that given the causal exposures, the conditional expectation of the outcome is invariant, that is, the causal effects of causal exposures on the outcome are invariant across different populations. The joint distribution of the candidate exposures and outcome may vary across different populations due to population heterogeneity. Therefore, the conditional expectation invariance structure assumption of the original EILLS method is satisfied. Another two identification conditions for identifying pure causal effect are: (1) it is necessary for identifying pre causal effect to select heterogeneous populations with large differences in social and environment factors including genetic difference; (2) a minimal identification condition related to the heterogeneity of the populations: for a exposures’ set, if \({\hat{\theta }}_{p,j}^{(e)}\) and \({\hat{\varepsilon }}_{j}^{(e)}\) is not independent in at least of one population, then there must be two populations with different causal effects. However, both of these identification conditions are untestable in practice. Therefore, when applying this method, practitioners must rely on prior knowledge to satisfy the identification assumptions as much as possible.

MR-EILLS is specifically designed for estimating causal effects in biological pathways where variables and pathway effects remain independent of social/environmental factors—either unaffected by or unmodified through these contextual influences. Taking the causal effect of hemoglobin concentration on stroke risk as an example, MR-EILLS tend to estimation the causal effect on the biological pathway like Hemoglobin level → Impaired oxygen transport → Elevated blood viscosity → Thrombosis → Stroke risk, or Hemoglobin level → Anemia development → Compensatory cardiac mechanisms → Left ventricular hypertrophy → Stroke risk, etc., but not hemoglobin level → oxygen transport efficiency → fatigue symptoms → reduced physical activity → elevated stroke risk. MR-EILLS methodology excludes such socio-environmentally mediated pathways when estimating invariant causal effects, as the mediator (“exercise”) inherently exhibits environmental variability. MR-EILLS aims to eliminate the influence of socioeconomic factors on the causal invariant effect from exposures to the outcome. The methodology does not require study populations to be globally representative, as it remains applicable to specific observational study cohorts. This is justified because socioeconomic confounders or effect modifiers inherently exist within any defined study population in observational research. Similar to MR, MR-EILLS requires no interaction assumptions for causal exposures and environmental variables. If there is an interaction between exposure and environmental variables, then this exposure tends to be considered a spurious exposure. If there is an interaction between the environmental variable and the mediator variable in the mediation pathway from exposure to outcome, then the pathway where this mediator variable is located is not included in the invariant causal effect. The additional explanation for the pure causal effect is shown in Supplementary Note 11.

MR-EILLS allows different IVs to be set in different populations. However, the strategy for metaMR, that is, first conducting GWAS meta-analysis and then performing MR analysis, requires the SNPs that are independent (i.e., no LD detected) in all populations, which reduces the number of IVs substantially; however, GWAS meta-analysis helps researchers identify more significant SNPs (i.e., \(P < 5\times {10}^{-8}\)). In addition, only a few MR methods allow the SNP set to have high LD. MR-EILLS solves this tricky issue and only requires that the IV set in each population is independent without LD.

The MR-EILLS model has two hyperparameters, which require researchers to set appropriate values to estimate the causal effects of exposures on the outcome. For \(\gamma \), we recommend \(\gamma > 0.4\) in UVMR and \(\gamma > 0\) in MVMR. The larger \(\gamma \) is, the stronger the role of the empirical focused linear invariance regularizer is. For \(\lambda \), we suggest that researchers construct ridge plots to find the optimal value. In Model (2), we keep the SNP for which the pleiotropic effect in all populations is lower than \(\lambda \). When the scales of different populations are different, the Model (2) can be modified to the following Model (2-1)

$$S\ast=\{\;{j}:|{\varepsilon }_{j}^{(e)}|+{\sum}_{p\in P}|{\hat{\theta }}_{p,j}^{(e)}{\varepsilon }_{j}^{(e)}| < {\lambda }_{e}\,{for}{any}\;{e}\}$$
(2-1)

Researchers can set different \({\lambda }_{e}\) values for different populations. For example, in our applications, we set different \({\lambda }_{e}\) values for five ancestries and five ridge plots are shown for each outcome. MR-EILLS works only if there are at least \({J}\ge {P}\) valid IVs in the IV set; this assumption is less strict than the plurality assumption17, which requires the valid IVs from the largest group of IVs sharing the same causal parameter value.

There are several limitations for MR-EILLS. The first is that MR-EILLS does not yet work in the high-dimensional case. One future key research direction is to extend MR-EILLS to high-dimensional exposure scenarios, especially for high-dimensional omics biomarkers; for this purpose, correlated IVs are also important issues to be solved. Another point is that inappropriate settings of hyperparameters may lead to incorrect inference of causal relationships between exposures and outcomes. It is important to choose the appropriate hyperparameters, especially for \(\lambda \). The value of \(\lambda \) determines whether the invalid IVs are removed, and if \(\lambda \) is too large, the causal effect estimation would be distorted. If \(\lambda \) is too small, the number of remaining IVs is small; thus, in the future, it is necessary to extend MR-EILLS to correlated IV scenarios. Our empirical application of MVMR to analyse 11 potentially correlated blood cell traits presents notable methodological challenges. The high degree of intertrait correlation, combined with the difficulty of identifying truly independent IVs for each exposure, renders this analysis particularly vulnerable to weak instrument bias. While acknowledging these fundamental limitations inherent in analyzing highly correlated traits, our proposed methodology demonstrates improved robustness by substantially reducing variance inflation compared to conventional approaches. This enhancement enables more reliable inference despite the analytical challenges posed by trait correlations.

In conclusion, we propose the MR method MR-EILLS, which integrates multiple heterogeneous GWAS summary datasets to infer the pure causal relationships between exposures and outcomes. This study has important guiding significance for the discovery of new disease-related factors. We look forward to offering constructive suggestions for disease diagnosis and applying our method beyond the scope considered here.

Methods

Ethics

Since our research solely employs de-identified, publicly accessible GWAS summary datasets, ethical approval and participant consent procedures were addressed in the primary source publications. We have therefore omitted this information from our manuscript in accordance with secondary analysis guidelines.

Overview of MR methods

For one population, assume \({P}\) exposures \({X}_{p},p\in \{1,{\mathrm{..}}.,{P}\}\) and one outcome \({Y}\). The \({J}\) independent IVs \({G}_{j},{j}\in \{1,{\mathrm{..}}.,{J}\}\) satisfy the following three assumptions:

A1. Relevance, \({G}_{j}\) is associated with at least one of the \({P}\) exposures;

A2. Exchangeability, \({G}_{j}\) is not associated with the confounder between \({P}\) exposures and the outcome;

A3. Exclusion restriction, \({G}_{j}\) affects the outcome only through exposures.

The MR model based on the individual data is as follows:

$$U= {\sum }_{j}{\omega }_{j}{G}_{j}+{\varepsilon }_{{X}_{U}}\\ {X}_{p}= {\sum }_{j}{\alpha }_{pj}{G}_{j}+{\sum }_{{X}_{k}\in pa({X}_{p})}{\beta }_{{X}_{k}{X}_{p}}{X}_{k}+{\beta }_{1p}U+{\varepsilon }_{{X}_{p}}\\ Y= {\sum }_{j}{\gamma }_{j}{G}_{j}+{\sum }_{p}{\beta }_{0p}{X}_{p}+{\beta }_{2}U+{\varepsilon }_{Y}$$
(3)

where \({\varepsilon }_{{X}_{U}},{\varepsilon }_{{X}_{p}},{\varepsilon }_{Y} \sim N(0,1)\). \({\gamma }_{j}\) represents the uncorrelated pleiotropic effect and \({\omega }_{j}\) represents the correlated pleiotropy. \({X}_{k}\in pa({X}_{p})\) is the father node of \({X}_{p}\), which is the direct cause of \({X}_{p}\), and where \({\beta }_{{X}_{k}{X}_{p}}^{(e)}\) represents the effect of \({X}_{k}\) on \({X}_{p}\). \({\beta }_{0p}\) denotes the causal effect of \({X}_{p}\) on \({Y}\). We call the exposures with \({\beta }_{0p}\ne 0\) causal exposures, which we want to discover, whereas the exposures with \({\beta }_{0p}=0\) are the spurious exposures, which are not the true cause of the outcome. We define the set of causal exposures as \(\{{X}_{p}\},p\in P\ast \subseteq \{1,{\mathrm{..}}.,{P}\}\). When \({P}\) = 1, the above model is called UVMR, whereas when \({P}\) > 1, it is called MVMR. To simplify the expression, our model below uniformly uses \({P}\) exposures, both of which are applicable to UVMR and MVMR.

The GWAS summary statistics include the \({G}_{j}-{X}_{p}\) association \({\hat{\theta }}_{p,j}\) and its variance \({\sigma }_{p,j}^{2}\), as well as the \({G}_{j}-Y\) association \({\hat{\Gamma }}_{y,j}\) and its variance \({\sigma }_{y,j}^{2}\). Based on Model (3), we have

$${\theta }_{p,j}= {\alpha }_{p,j}+{\omega }_{j}{\beta }_{1p}+{\sum }_{{X}_{k}\in pa({X}_{p})}{\theta }_{k,j}{\beta }_{{X}_{k}{X}_{p}}\\ {\Gamma }_{y,j}= {\omega }_{j}{\beta }_{2}+{\gamma }_{j}+{\sum }_{p}{\theta }_{p,j}{\beta }_{0p}$$
(4)

When \({G}_{j}\) is a valid IV (no pleiotropy), that is, \({\gamma }_{j}={\omega }_{j}=0\), then \({\varepsilon }_{j}={\Gamma }_{y,j}-{\sum }_{p}{\theta }_{{p},j}{\beta }_{0p}\) is zero and is dependent on \({\theta }_{{p},j}\). For \({j}\in \{1,{\mathrm{..}}.,{J}\}\), we can identify \({\beta }_{0p}\)\((p\in \{1,{\mathrm{..}}.,{P}\})\) by the system of linear equations \({\Gamma }_{y,j}={\sum }_{p}{\theta }_{p,j}{\beta }_{0p}\) if and only if \({J}\ge {P}\). The causal effects of exposures on the outcome \({\beta }_{0p}\) can be estimated by a weighted version of ordinary least squares (OLS), that is, the IVW regression

$${\hat{\Gamma }}_{y,j}={\sum }_{p}{\hat{\theta }}_{p,j}{\beta }_{0p}+{\zeta }_{j},{\zeta }_{j} \sim N(0,{\sigma }_{y,j}^{2})$$
(5)

which sets the intercept equal to zero. This model minimizes the empirical \({L}_{2}\) loss objective function

$$ Q({\beta }_{0p};{\hat{\theta }}_{p,j},{\hat{\Gamma }}_{y,j},{\sigma }_{y,j}^{2})\\ ={{\rm{E}}}[|{w}_{j}{\varepsilon }_{j}{|}^{2}]\\ ={{\rm{E}}}[|{w}_{j}({\hat{\Gamma }}_{y,j}-{\sum }_{p}{\hat{\theta }}_{p,j}{\beta }_{0p}){|}^{2}]$$
(6)

where \({w}_{j}\) represents the weight of IV \({G}_{j}\) in the causal effect estimation. If \({G}_{j}\) has uncorrelated pleiotropy (\({\gamma }_{j}\ne 0\)), that is, if \({G}_{j}\) is causally associated with \({Y}\) not through any \({X}_{p}\), then \({\varepsilon }_{j}={\gamma }_{j}\) is no longer equal to zero, and it represents the uncorrelated pleiotropic effect. MR-Egger regression18 is proposed to solve this problem by allowing the intercept term \(\bar{\gamma }\) in Model (5), and the intercept represents the mean pleiotropic effect. The causal effect can be estimated by minimizing

$$Q(\,{\beta }_{0p};{\hat{\theta }}_{p,j},{\hat{\Gamma }}_{y,j},{\sigma }_{y,j}^{2})={{\rm{E}}}[|{w}_{j}({\hat{\Gamma }}_{y,j}-{\sum }_{p}{\hat{\theta }}_{p,j}{\beta }_{0p}-\bar{\gamma }){|}^{2}].$$

MR-Egger regression requires the InSIDE assumption, which means that the pleiotropic effect is independent of \({\theta }_{p,j}\). If \({G}_{j}\) has correlated pleiotropy (\({\omega }_{j}\ne 0\)), that is, if \({G}_{j}\) is causally associated with the unmeasured confounding \(U\) between \({X}_{p}\) and \({Y}\), then the pleiotropic effect \({\varepsilon }_{j}={\omega }_{j}{\beta }_{2}+{\gamma }_{j}\) is not independent of \({\theta }_{p,j}\) because of the common term \({\omega }_{j}\). This is a violation of the InSIDE assumption. Equations (5–6) and MR-Egger require that \({\varepsilon }_{j}\) is independent of \({\theta }_{p,j}\) because the correlation between the intercept term and the independent variables would distort the causal effect estimation. The results of the motivating simulation for correlated and uncorrelated pleiotropy are shown in Supplementary Fig. 1.

The MR-Lasso method applies lasso-type penalization to the direct effects of IVs on the outcome. The causal estimate is described as a post-lasso estimate and is obtained via the IVW method, which uses only those IVs that are identified as valid by the lasso procedure. The objective function is as follows:

$$Q(\,{\beta }_{0p};{\hat{\theta }}_{p,j},{\hat{\Gamma }}_{y,j},{\sigma }_{y,j}^{2})={{\rm{E}}}[|{w}_{j}({\hat{\Gamma }}_{y,j}-{\sum }_{p}{\hat{\theta }}_{p,j}{\beta }_{0p}-{\gamma }_{j}){|}^{2}+{\lambda }_{L}|{\gamma }_{j}|]$$

If \({\gamma }_{j}\) shrinks to zero, the IV is treated as a valid IV. The MR-median estimator is defined as the 50th percentile of either an unweighted or IVW empirical density function of the Wald ratio, and it is consistent even when up to 50% of the information comes from an invalid IV. The aforementioned methods are classified into a category of MR methods, namely, the Wald ratio-based MR method.

The MR-cML and MRAID methods are representative of the likelihood-based MR method. MR-cML infers causal relationships using constrained maximum likelihood. It is robust to both uncorrelated and correlated pleiotropic effects, under the plurality assumption. MRAID models an initial set of candidate IVs that are in potentially high linkage disequilibrium with each other and automatically selects among them the suitable IVs for causal inference, under the joint likelihood framework. MRAID also explicitly models both uncorrelated and correlated horizontal pleiotropy.

The MR-Horse and cause methods produce unbiased causal effect estimates under the framework of Bayesian inference, while avoiding inflated false positive rates, and can account for both correlated and uncorrelated pleiotropy. The disadvantage of these two methods is that when the number of exposures is large, they require a significant amount of memory and computation time.

MR-BMA is an MVMR method used to select likely causal risk factors from high-throughput experiments. It uses Bayesian model averaging and computes the posterior probability for all possible combinations of risk factors, finally estimating the model-averaged causal estimate (MACE) by weighting and summing the causal effect estimation of each model. To some extent, MR-BMA avoids pleiotropy by considering as many risk factors as possible.

These methods are all based on a single dataset, and only information from one dataset can be used. Therefore, we proposed a method that fully exploits the information from multiple existing datasets to identify causally invariant factors, comprehensively improves the estimation precision and enhances the statistical power.

MR-EILLS model: MR integrating multiple heterogeneous populations

When there are \({E}\) heterogeneous populations, GWAS summary statistics include \({\hat{\theta }}_{p,j}^{({e})}\), \({\sigma }_{{G}_{j}{X}_{p}}^{({e})2}\), \({\hat{\Gamma }}_{y,j}^{({e})}\) and \({\sigma }_{y,j}^{({e})2}\) for \(e\in {\mathcal E} \). We define \({\varepsilon }_{j}^{(e)}={\Gamma }_{y,j}^{(e)}-{\sum }_{p}{\theta }_{p,j}^{(e)}{\beta }_{0p}^{(e)}\) and \({\hat{\varepsilon }}_{j}^{(e)}={\hat{\Gamma }}_{y,j}^{(e)}-{\sum }_{p}{\hat{\theta }}_{p,j}^{(e)}{\beta }_{0p}^{(e)}\) in the version of multiple populations. We use the superscript \(({e})\) to denote the e-th population. We assume that the pleiotropic effect, IV strength and relationships among exposures are different in heterogeneous populations, whereas the causal effects of causal exposures on \({Y}\) are invariant, that is \({\beta }_{0p}^{(1)}={\beta }_{0p}^{(2)}={\mathrm{.}}..={\beta }_{0p}^{(E)}={\beta }_{0p}^{\ast }\) for \(p\in P\ast \); this assumption is called the structure assumption21. These assumptions are rational because the IVs satisfying A1–A3 control only the unmeasured confounders between \({X}_{p}\) and \({Y}\), whereas other unmeasured confounders between IVs and exposures, or between IVs and outcomes, or between exposures are not controlled, and these unmeasured confounders are also the reason for heterogeneity between populations.

Note that a valid IV in one population may be an invalid IV in the other heterogeneous populations. On the other hand, an IV may be associated with exposure in all heterogeneous populations, while it may have different uncorrelated or correlated pleiotropy in different populations. This leads to inconsistent independence relationships between \({\theta }_{p,j}^{(e)}\) and \({\varepsilon }_{j}^{(e)}\) across different populations and inconsistent causal effect estimation of exposures on the outcome in different heterogeneous populations. Therefore, we leveraged the EILLS21, the multiple heterogeneous population version of OLS, to construct the MR-EILLS model. The MR-EILLS model integrates GWAS summary statistics from multiple heterogeneous populations and finds causal exposures that have invariant effects on the outcome in heterogeneous populations. The MR-EILLS model aims to minimize the following objective function

$$\begin{array}{l}Q({\beta }_{0p}^{\ast };{\hat{\theta }}_{p,j}^{(e)},{\hat{\Gamma }}_{y,j}^{({e})},{\sigma }_{y,j}^{({e})2})\\={\sum }_{e\in {\mathcal E} }{w}^{({e})}{{{\rm{E}}}}_{j\in S\ast }[|{w}_{j}^{(e)}{\hat{\varepsilon }}_{j}^{(e)}{|}^{2}]+\gamma {\sum }_{e\in {\mathcal E} }{w}^{({e})}{\sum }_{p\in P}|{{{\rm{E}}}}_{j\in S\ast }[{\hat{\theta }}_{p,j}^{(e)}\cdot {w}_{j}^{(e)}{\hat{\varepsilon }}_{j}^{(e)}]{|}^{2}\end{array}$$
(7)

where

$${w}_{j}^{(e)}=\frac{{\sigma }_{y,j}^{(e)-2}}{{\sum }_{j\in S\ast }{\sigma }_{y,j}^{(e)-2}}{{\rm{and}}}\;{w}^{(e)}=\frac{{N}_{e}}{N}$$
(8)

\({w}_{j}^{(e)}\) is the weight of IV \({G}_{j}\) on the causal effect estimation in the e-th population, and \({w}^{(e)}\) is the weight of the eth population on the final causal effect estimation. The first part of the objective function (1) is the empirical \({L}_{2}\) loss, which is the multiple-population version of the objective function (6) in one population. The second part of the objective function (1) is the empirical focused linear invariance regularizer, which discourages the selection of exposures with strong correlations between \({\theta }_{p,j}^{(e)}\) and \({\varepsilon }_{j}^{(e)}\) in some populations because this will distort the causal effect estimation. \(\gamma > 0\) is the hyperparameter. In addition, we added the following restriction

$$S\ast=\{\;{j}:{\sum}_{e\in {\mathcal E} }|{\varepsilon }_{j}^{(e)}|+{\sum}_{p\in P}{\sum}_{e\in {\mathcal E} }|{\hat{\theta }}_{p,j}^{(e)}{\varepsilon }_{j}^{(e)}| < \lambda \}$$
(9)

to select the valid IVs. The first part of Eq. (2) represents the uncorrelated pleiotropic effect for the \(j-th\) IV, and the second part of Eq. (2) represents the correlated pleiotropic effect for the \(j-th\) IV. \(\lambda > 0\) is the hyperparameter controlling the strictness of filtering IVs. Equation (2) removes the invalid IVs with pleiotropic effects above \(\lambda \).

The causal effects \({\beta }_{0p}^{\ast }\) can be identified under the assumption21 that there are at least \({P}\) valid IVs in the IV set, that is\({J}\ge {P}\). We use a limited-memory modification of the BFGS quasi-Newton method48 to find the optimal solution \({\beta }_{0p}^{\ast }\) of the objective function (1) under the restriction of Eq. (2). The confidence interval is estimated via bootstrap method.

Simulation

We generate the GWAS summary statistics of \(E\) heterogeneous populations via the following process:

$${\theta }_{p,j}^{(e)}= {\alpha }_{p,j}^{(e)}+{\omega }_{j}^{(e)}{\beta }_{1p}^{(e)}+{\sum }_{{X}_{k}\in pa({X}_{p})}{\theta }_{k,j}^{(e)}{\beta }_{{X}_{k}{X}_{p}}^{(e)}+{\xi }_{p,j}^{(e)}\\ {\Gamma }_{y,j}^{(e)}= {\omega }_{j}^{(e)}{\beta }_{2}^{(e)}+{\gamma }_{j}^{(e)}+{\sum }_{p}{\theta }_{p,j}^{(e)}{\beta }_{0p}^{(e)}+{\xi }_{{y},j}^{(e)}$$

where \({X}_{k}\in pa({X}_{p})\) is the father node of \({X}_{p}\), which is the direct cause of \({X}_{p}\), and where \({\beta }_{{X}_{k}{X}_{p}}^{(e)}\) represents the effect of \({X}_{k}\) on \({X}_{p}\). In total \(P\) exposures, the causal exposures are the top 30% of all exposures (e.g., \(P=8\), \(floor({P}\times 30\%)=2\), then the top two (\({X}_{1}\) and \({X}_{2}\)) are the causal exposures). The effect of causal exposure on \(Y\) (\({\beta }_{0p}^{(e)},p\in P\ast \)) is 0.2 for MVMR (\(P\) > 1) and 0.1 for UVMR (\(P\) = 1), and the effect of other spurious exposures on \(Y\) (\({\beta }_{0p}^{(e)},p\notin P\ast \)) is 0.\({\beta }_{{X}_{k}{X}_{p}}^{(e)} \sim U(-1,1)\) for the effect of edge \({X}_{k}\to {X}_{p}\).The structure between the exposures is randomly generated, and the parameter \({\beta }_{{X}_{k}{X}_{p}}^{(e)}\) represents the effect from \({X}_{k}\) to \({X}_{p}\). We set IV strength \({\alpha }_{p,j}^{(e)} \sim N(0,0.2)\) for the eth population and \({X}_{p}\); \({\xi }_{p,j}^{(e)} \sim N(0,{\sigma }_{p,j}^{({e})2})\) for eth population and \({X}_{p}\), \({\sigma }_{p,j}^{({e})2} \sim U(0.01,0.05)\) for \({X}_{p}\); \({\xi }_{{y},j}^{(e)} \sim N(0,{\sigma }_{y}^{({e})2})\) for \(E=e\), \({\sigma }_{y,j}^{({e})2} \sim U(0.05,0.1)\) and different variances represent different sample sizes; \({\beta }_{1p}^{(e)} \sim U(0.5,0.8)\) for \({X}_{p}\); and \({\beta }_{2}^{(e)} \sim U(0.5,0.8)\). We consider three scenarios:

  1. (a)

    uncorrelated and correlated pleiotropy effects, \({\gamma }_{j}^{(e)} \sim U(0,0.5)\) and \({\omega }_{j}^{(e)} \sim U(0,0.5)\);

  2. (b)

    uncorrelated pleiotropy effect (balanced pleiotropy: \({\gamma }_{j}^{(e)} \sim U(-0.5,0.5)\), unbalanced pleiotropy: \({\gamma }_{j}^{(e)} \sim U(0,0.5)\));

  3. (c)

    No pleiotropy.

The parameters of edge effects, IV strength and pleiotropy were randomly selected from a uniform distribution; thus, they are different in different datasets and represent heterogeneous datasets. We varied the number of populations to be \(E=3\) or 8; the number of IVs was 100 or 300; and the number of exposures was \(P\) = 1, 3, 8, or 15, including the cases of univariable and multivariable MR. In addition, we considered the situation in which genetic correlations among different populations are nonzero, and we generated the IV strength \({\alpha }_{p,j}^{(e)}\) in different populations using multiple normal distributions, with correlations in the covariance matrix of 0.2 or 0.6. Finally, as the number of exposures increases, weak IVs are more likely to emerge; thus, we observed the performance of our method in the presence of weak IVs, by setting the IV strength ranging from 0.01 to 0.05, and the corresponding conditional F-statistics are shown in Supplementary Data 4.

We conducted 200 repeated simulations to evaluate the performance of MR-EILLS. We also compare nine methods, including IVW, MR-Egger, MR-Lasso, MR-Median, MR-cML, MR-BMA, MARID, Cause and MR-Horse. For \(P=1\), we compare eight methods in the UVMR version except MR-BMA; for \(P\) = 3, 8, and 15, we compare seven methods in the MVMR version except MARID and Cause, because these two methods have only the UVMR version. For these MR methods, we considered two strategies: (1)metaMR, first meta all the GWAS summary statistics of \(E\) datasets for each variable and then conduct the MR analysis; and (2) mrMeta, first conduct the MR analysis (excluding MR-BMA, MARID and Cause because they cannot output the standard errors) in \(E\) datasets separately and then meta all the MR results. Meta methods include random effects and fixed effects meta-analyses.

We evaluated the performance of all methods via box-violin plots for causal effect estimation, histograms for type I errors when the causal effect is zero and statistical power when the causal effect is not zero. In addition, we calculated the \({I}^{2}\) statistics in each simulation to evaluate the heterogeneity of causal effect estimation among different datasets for each MR method. We constructed the violin plot of the \({I}^{2}\) statistics for the estimations of each variable, randomly selected three simulations to demonstrate the quartiles of estimation, and then constructed the forest plot of the estimations for each method and each variable. For \(P\) = 15, we calculated the means of the F1 score, recall and precision for each method. Recall (i.e., power, or sensitivity) measures how many relationships a method can recover from the true causal relationships, whereas precision (i.e., 1-FDR) measures how many correct relationships are recovered in the inferred relationships. The F1 score is a combined index of recall and precision. We also summarize the computing time for different methods to assess the computational efficiency.

Setting of hyperparameters \(\gamma \) and \(\lambda \)

We recommend that practitioners determine the value of \(\lambda \) by constructing a ridge plot. The abscissa is the value of \({\sum }_{e\in {\mathcal E} }|{\varepsilon }_{j}^{(e)}|+{\sum }_{p\in P}{\sum }_{e\in {{\rm E}}}|{\hat{\theta }}_{p,j}^{(e)}{\varepsilon }_{j}^{(e)}|\) for each IV in Eq. (8). We constructed the ridge plot in the simulations in Supplementary Figs. 67–71. These plots demonstrate that when there is no pleiotropy, the figure has only one peak, and \(\lambda \) only takes the value of abscission after the first peak. When there is pleiotropy, the figure has two peaks, and the corresponding abscission value at the lowest point between the two peaks is the optimal \(\lambda \). We provide the function of the ridge plot in the R package MR-EILLS.

In addition, we evaluated the root mean square error (RMSE) of causal effect estimation using a grid search: \(\gamma \) ranges from 0.1 to 200, and \(\lambda \) ranges from 0.1 to 1. The results are shown in Supplementary Figs. 72–80. We present the ranges of hyperparameters when the RMSE <0.1 in Supplementary Data 10. For UVMR, we recommend \(\gamma > 0.4\). When \(\gamma > 0.4\), the RMSE is less than 0.1, especially for the case of correlated and uncorrelated pleiotropy, whereas in other cases, the RMSE is less than 0.05. For MVMR, \(\gamma > 0\) is recommended. Compared with all valid IVs, invalid IVs increased the RMSE of causal effect estimation, regardless of whether correlated or uncorrelated pleiotropy was used. Therefore, \(\gamma \) is loosely valued, especially when \(P > 1\). The larger \(\gamma \) is, the stronger the role of the empirical focused linear invariance regularizer. Details are shown in Supplementary Note 12.

In our simulations, we employed a grid search approach to identify the optimal lambda value that minimizes the RMSE. In addition, we set \(\gamma=0.5\) for MVMR and \(\gamma=3\) for UVMR.

Application

We explored the causal effect of 11 blood cells on 20 disease-related outcomes using GWAS summary statistics from five ancestries: African, East Asian, South Asian, Hispanic/Latino, and European. GWAS summary statistics for blood cells were extracted from ref. 49, who conducted transethnic and ancestry-specific GWASs in 746,667 individuals from five populations (15,171, 151,807, 8189, 9368, and 563,947 individuals for five ancestries, respectively). GWAS summary statistics for 20 disease-related outcomes50 were extracted from the MR-Base and GWAS Catalog platforms. The details are shown in Supplementary Data 11.

First, we selected IVs for MR analysis. We separately selected SNPs with \(P < 5\times {10}^{-8}\) and clumped the LD with \({r}^{2} > 0.01\) in each population (Supplementary Data 8). In addition, we calculated the conditional F-statistics for IVs to assess the IV strength for each exposure (Supplementary Data 9). Then, we extracted the summary statistics for the IVs and conducted MR-EILLS and MR analysis for each population. We also calculated the \({I}^{2}\) statistic to evaluate the heterogeneity of causal effect estimation among different populations for each MR method. For MR-EILLS, we constructed the ridge plot in each population, and set \(\gamma=0.5\). The settings of \(\lambda \) are shown in Supplementary Data 6. The confidence interval is estimated via the bootstrap method, and details are shown in Supplementary Note 13.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.