Introduction

Quantum error correction (QEC)1,2 is essential for realizing reliable quantum computation and communication in the presence of unavoidable environmental noise3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20. While quantum information is commonly encoded in discrete variables of multiple physical qubits, single-mode bosonic encodings offer a hardware-efficient alternative by leveraging the infinite-dimensional Hilbert space of a single oscillator. Moreover, bosonic information carriers play a crucial role in transferring information over distances, making bosonic encodings indispensable in quantum communications, and distributed quantum computation and sensing21. The ability to encode and protect quantum information in bosonic modes, such as optical or microwave cavities, has attracted considerable attention in recent years. Notably, experiments with superconducting systems22 have achieved milestones by reaching the break-even point in QEC with bosonic codes23,24,25,26, demonstrating their immense potential for fault-tolerant quantum applications.

Existing bosonic QEC codes can be broadly categorized based on the symmetries they exploit in the phase space of a bosonic mode. The Gottesman-Kitaev-Preskill (GKP) codes27, for instance, leverage the displacement symmetry to correct random displacement errors in the quadrature variables. On the other hand, codes like the cat and binomial codes utilize the rotational symmetry in phase space28,29,30,31, which corresponds to a certain generalized parity of the photon number distribution. These codes are designed to tolerate photon loss or gain errors, while the code distance is determined by the photon-number parity of the codewords. However, beyond the conventional quadrature variables, the photon number and phase can also be treated as canonical variables for a bosonic mode. The potential symmetries and encoding schemes in this generalized number-phase (NP) space have not been fully explored.

In this paper, we propose a unified framework for constructing bosonic QEC codes, which embody a lattice structure in the NP space, encompassing the known cat and binomial codes as rectangular lattices. Remarkably, we uncover oblique and diamond lattice codes that exhibit a novel NP vortex effect: number-shift errors in these codes induce discrete phase rotations as error syndromes. This unique feature enables us to identify and correct errors by measuring only the phase variable of the bosonic mode. We demonstrate that our generalized codes, particularly the oblique and diamond lattice codes, exhibit enhanced performance in the presence of practically relevant noise channels that inflict both amplitude damping and dephasing. Furthermore, we propose a hardware-efficient quantum error correction protocol that is compatible with one-way quantum communication schemes. Our framework not only unifies the existing bosonic codes but also paves the way for discovering new codes with desirable properties. The NP lattice codes introduced here have the potential to significantly advance fault-tolerant quantum computation and extend the range of quantum communication32,33,34,35,36,37,38,39.

Results

Generalized number-phase encoding

Inspired by the construction of GKP codes in the quadrature phase space, we introduce generalized displacement operators in the NP space. Consider a bosonic mode described by the annihilation and creation operators \(\hat{a}\) and \({\hat{a}}^{{{\dagger}} }\), respectively, \(\hat{n}={\hat{a}}^{{{\dagger}} }\hat{a}\) represents the excitation-number operator. The NP displacement operator reads

$$\hat{{{{\mathscr{D}}}}}({{{\bf{n}}}})\equiv \exp \left(\frac{il\phi }{2}\right)\hat{R}(\phi ){\hat{\Sigma }}_{l}.$$
(1)

Here, \(\hat{R}(\phi )=\exp (i\hat{n}\phi )\) is the phase rotation operator, n = (l, ϕ) is a two-dimensional vector with the limitation \(l\in {\mathbb{Z}}\) and \(\phi \in {\mathbb{R}}\). \({\hat{\Sigma }}_{l}\equiv {\sum }_{n}\left\vert n\right\rangle \left\langle n+l\right\vert\) is the Fock ladder shift operator, which connects to the annihilation operator with the relation \(\hat{a}=\sqrt{\hat{n}+1}{\hat{\Sigma }}_{1}\). Note that \({\hat{\Sigma }}_{1}^{{{\dagger}} }=\hat{{e}^{-i\phi }}\) is the Susskind-Glogower exponential phase operator40, which is well-known to be nonunitary. Nonetheless, the nonunitary does not prevent the NP displacement operators from being a set of complete operator basis, because they satisfy the same commutation relation

$$\hat{{{{\mathscr{D}}}}}({{{\bf{n}}}})\hat{{{{\mathscr{D}}}}}({{{{\bf{n}}}}}^{{\prime} })={e}^{i{{{\bf{n}}}}\times {{{{\bf{n}}}}}^{{\prime} }}\hat{{{{\mathscr{D}}}}}({{{{\bf{n}}}}}^{{\prime} })\hat{{{{\mathscr{D}}}}}({{{\bf{n}}}}),$$
(2)

and the orthogonality relation \({{{\rm{Tr}}}}({\hat{{{{\mathscr{D}}}}}}^{{{\dagger}} }({{{{\bf{n}}}}}^{{\prime} })\hat{{{{\mathscr{D}}}}}({{{\bf{n}}}}))=2\pi {\delta }^{2}({{{\bf{n}}}}-{{{{\bf{n}}}}}^{{\prime} })\) with the conventional displacement operators. In this sense, an arbitrary operator satisfying \({{{\rm{Tr}}}}({\hat{E}}^{{{\dagger}} }E) < \infty\) can be expanded by using the NP displacement operator basis,

$$\hat{E}=\int\frac{d{{{\bf{n}}}}}{2\pi }\,{{{\rm{Tr}}}}({\hat{{{{\mathscr{D}}}}}}^{{{\dagger}} }({{{\bf{n}}}})\hat{E})\hat{{{{\mathscr{D}}}}}({{{\bf{n}}}}).$$
(3)

That is, a noise operator \(\hat{E}\) for bosonic modes can be represented as a series of NP-displacements \(\hat{{{{\mathscr{D}}}}}({{{\bf{n}}}})\) with the weight \({{{\rm{Tr}}}}({\hat{{{{\mathscr{D}}}}}}^{{{\dagger}} }({{{\bf{n}}}})\hat{E})\).

In general, a logical qudit with a finite dimension d can be encoded in a bosonic mode, which provides an infinite-dimensional Hilbert space to manage errors, thereby resulting in error-correcting bosonic codes. Here we focus on the simplest case, encoding a qubit into a bosonic mode for removing small NP displacements errors \(\hat{{{{\mathscr{D}}}}}({{{{\bf{n}}}}}_{e})\). This approach is referred to as the generalized NP encoding of a bosonic mode, with the codewords \({\left\vert 0\right\rangle }_{L}\) and \({\left\vert 1\right\rangle }_{L}\) representing two highly symmetric superposition states of NP variables. To provide a more intuitive representation of codewords in NP phase space, recall that \({{{{\mathcal{W}}}}}_{\rho }({{{\bf{c}}}})\) represents the NP Wigner function of the quantum state ρ. Here, c = (n, p) specifies arbitrary coordinates in two-dimensional NP phase space, subject to the constraints \(n\in {\mathbb{N}}\) and p ∈ [0, 2π). The detailed definition of the NP Wigner function can be found in the supplementary Note 1, including Ref. 41.

Specifically, the codewords design of such an encoding is based on Eq. (2), the commutation between two NP displacement operators results solely in a phase factor \({e}^{i{{{\bf{n}}}}\times {{{{\bf{n}}}}}^{{\prime} }}\). Here, \(| {{{\bf{n}}}}\times {{{{\bf{n}}}}}^{{\prime} }|\) should be understood as the area of a parallelogram in NP space, with n and \({{{{\bf{n}}}}}^{{\prime} }\) as its defining edges. Notably, the two NP displacement operators \(\hat{{{{\mathscr{D}}}}}({{{{\bf{n}}}}}_{x})\) and \(\hat{{{{\mathscr{D}}}}}({{{{\bf{n}}}}}_{z})\) correspond to the logical Pauli operators, satisfying the anti-commutation relation \(\bar{X}\bar{Z}=-\bar{Z}\bar{X}\) when the condition

$$| {{{{\bf{n}}}}}_{x}\times {{{{\bf{n}}}}}_{z}|=\pi$$
(4)

is satisfied. Consequently, they should be square to two stabilizers \({\hat{S}}_{x}\equiv \hat{{{{\mathscr{D}}}}}(2{{{{\bf{n}}}}}_{x})\) and \({\hat{S}}_{z}\equiv \hat{{{{\mathscr{D}}}}}(2{{{{\bf{n}}}}}_{z})\), thus the codewords of generalized NP codes are defined by the simultaneous +1 eigenstates of the two stabilizers. In other words, the codespaces \({\bar{P}}_{{{{\rm{code}}}}}=\left\vert 0\right\rangle {\left\langle 0\right\vert }_{L}+\left\vert 1\right\rangle {\left\langle 1\right\vert }_{L}\) of generalized NP codes have discrete translational invariance in NP variables, forming as a lattice with the cell area π in NP space.

Since any pair of nx, nz fulfilling Eq. (4) is valid, there are infinite types of generalized NP codes. Fortunately, due to the 2π periodicity of the phase variable, any pair of nx, nz satisfying Eq. (4) can be equivalently expressed in a gauge

$${{{{\bf{n}}}}}_{x}=\left(s,\frac{f\pi }{s}\right),\quad {{{{\bf{n}}}}}_{z}=\left(0,\frac{\pi }{s}\right).$$
(5)

Here s ≥ 1 is a positive integer that defines the rotation symmetry \({\hat{S}}_{z}=\hat{R}(2\pi /s)\) of codespaces, and ∣f = p/q∣ ∈ [0, 1) is a fractional number given by two coprime integers \(p\in {\mathbb{Z}}\) and \(q\in {{\mathbb{Z}}}^{+}\). The set of parameters (s, f) defines the lattice structure of codespaces in NP space, and the NP Wigner function of the codespaces can be directly obtained as (unnormalized)

$${{{{\mathcal{W}}}}}_{{\bar{P}}_{{{{\rm{code}}}}}}({{{\bf{c}}}})={\sum}_{r=0,t=0}^{\infty }{\delta }^{2}(r{{{{\bf{n}}}}}_{x}^{*}+t{{{{\bf{n}}}}}_{z}+{{{{\bf{n}}}}}_{0}),$$
(6)

where \({{{{\bf{n}}}}}_{x}^{*}\equiv (s,-f\pi /s)\), and \({{{{\bf{n}}}}}_{0}={\nu }_{x}{{{{\bf{n}}}}}_{x}^{*}+{\nu }_{z}{{{{\bf{n}}}}}_{z}\) with νx, νz ∈ [0, 1) serves as a selectable origin in NP space. Note that the phase coordinates on the right side of Eq. (6) may exceed the defined range [0, 2π), which is insignificant and can be returned to the defined range through the 2π periodicity of the phase variable.

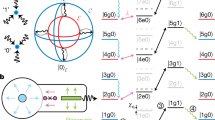
In Fig. 1a–c, we graphically illustrate the codespaces of three typical generalized NP codes in NP phase space as examples, where red and blue circles represent the peaks of the NP Wigner function of codewords \({\left\vert+\right\rangle }_{L}\) and \({\left\vert -\right\rangle }_{L}\), respectively. As expected, the codespaces of generalized NP codes are lattices in NP phase space, which can be regarded as the rectangle (R-NP), oblique (O-NP), and diamond NP (D-NP) codes determined by the shape of the lattice cell. Now, let us imagine the two-dimensional NP phase space plane rolled along the phase direction into a cylindrical surface, and the NP lattice codes will present a novel 3D physical picture, as shown in Fig. 1d, e. The R-NP codes are a series of circular rings along the number direction with an equal distance s. Conversely, NP codes with f ≠ 0 are an NP vortex along the number direction due to the non-trivial parameter f, leading to a hybridization of number and phase variables.

Fig. 1: Schematics of three types of generalized NP codes in phase space defined by canonical number and phase variables.
figure 1

a–c show the generalized NP codes with rectangle, oblique, and diamond lattice coding. Red and blue circles represent probability peaks of NP Wigner function of dual logical states \({\left\vert+\right\rangle }_{L}\) and \({\left\vert -\right\rangle }_{L}\), respectively. \(\hat{{{{\mathcal{D}}}}}({{{{\bf{n}}}}}_{x})\) and \(\hat{{{{\mathcal{D}}}}}({{{{\bf{n}}}}}_{z})\) are the logical \(\bar{X}\) and \(\bar{Z}\) operations, which are represented as deep green and orange arrows, respectively. \(\hat{{{{\mathcal{D}}}}}({{{{\bf{n}}}}}_{e})\) is the NP-shift error, represented by light green and light blue arrows. (d, e) are schematic diagrams of the generalized NP codes in NP space, which depict the codes rolling along the phase direction to form a cylindrical surface.

Full size image

Moreover, such a graphical representation of codespaces in NP phase space can directly give the code distance of the canonical number variable dN = qs (p ≠ 0) and the canonical phase variable dϕ = π/s. Thus we can define the correctable error set \(\bar{E}\) of the generalized NP codes for exactly satisfying the Knill-Laflamme (KL) conditions \(\left\langle \mu \right\vert {\hat{E}}_{j}^{{{\dagger}} }\hat{{E}_{k}}{\left\vert \nu \right\rangle }_{L}={H}_{j,k}{\delta }_{\mu,\nu }\), where H is a Hermitian matrix, and μ and ν run the logical 0 and 142. If one concentrates to remove the number-shift errors caused by excitation loss or gain, the correctable error set can be selected as \(\bar{E}=\{\hat{{{{\mathscr{D}}}}}({{{{\bf{n}}}}}_{e})\}\) with the vector ne in the region

$${{{{\bf{n}}}}}_{e}\in \left\{\,({l}_{e},{\phi }_{e})\,| -G\le {l}_{e}\le L,\,\,| {\phi }_{e}| < \frac{\pi }{2{d}_{N}}\right\},$$
(7)

where G and L are two positive integer which satisfies G + L = dN − 1. Particularly, another useful correctable error set with ne ∈ {(0, ϕe)∣∣ϕe∣ < dϕ/2} focus on removing the pure rotation errors caused by quantum dephasing, which sacrifices a portion of the ability to correct number-shift errors as a cost. The error syndromes for \(\hat{{{{\mathscr{D}}}}}({{{{\bf{n}}}}}_{e})\) need to be identified through the measurement of the generalized number parity k ∈ [0, s − 1] and the rotated phase angle \(\bar{\phi }=mf\pi /s+{\phi }_{e}\) of the noisy codespaces, thereby different ne = (le, ϕe) can be distinguished via the relation le = sm + k and \({\phi }_{e}=\bar{\phi }-mf\pi /s\) with m ∈ [⌊L/s⌋ − q + 1, ⌊L/s⌋], and ⌊ ⋅ ⌋ is the floor function. The syndromes of these NP displacement errors for generalized NP codes with different structures are summarized in Table 1. The experimental realization of the error syndrome measurement will be discussed in the following.

Table 1 Examples and comparisons of generalized NP codes
Full size table

In experiments, the ideal generalized NP codes introduced above are unavailable. Therefore, it is necessary to encode a normalized series {θn} as the amplitude of the Fock basis \(\left\vert sn\right\rangle\) to restrict the code state energy, where the normalization of θn is ∑n∣θn∣2 = 1. Then, the qubit states of generalized NP codes can be defined in a logical X basis by using the Fock states as

$${\left\vert \pm \right\rangle }_{L}(s,f,{\theta }_{n})=\exp \left(-\frac{if\pi {\hat{n}}^{2}}{2{s}^{2}}\right){\sum}_{n=0}^{\infty }{(\pm )}^{n}{\theta }_{n}\left\vert sn\right\rangle,$$
(8)

and the qubit states in logical Z basis are \({\left\vert \mu \right\rangle }_{L}=(\left\vert+\right\rangle+{(-)}^{\mu }{\left\vert -\right\rangle }_{L})/\sqrt{2}\), where μ = 0, 1 and the mean excitation of such code states is restricted as \({\bar{n}}_{{{{\rm{code}}}}}=s{\sum }_{n}n| {\theta }_{n}{| }^{2}\). Under encoding of the series {θn}, the generalized NP codes with finite energy still have the perfect discrete phase rotation invariance, but the discrete translation invariance in nx direction is approximately satisfied. In comparison to the parameters s and f, which primarily govern the ability against the excitation loss, the Fock amplitude θn dictates the capacity to resist the pure phase rotation. For R-NP codes, {θn} can give the Helovo’s phase uncertainty43Δϕ = ∣∑nθnθn+1∣−2 − 1 of the codeword \({\left\vert \pm \right\rangle }_{L}\). A smaller phase uncertainty indicates that the rotated codeword can be distinguished better by using the canonical phase measurement44,45,46,47. The positive operator-valued measure (POVM) element of the canonical phase measurement is \({\hat{{{{\mathscr{M}}}}}}_{X}={(2\pi )}^{-1}{\sum }_{n,m}{e}^{i(n-m)X}\left\vert n\right\rangle \left\langle m\right\vert\), and the associated identity relation is \(\int_{0}^{2\pi }dX{\hat{{{{\mathscr{M}}}}}}_{X}=\hat{I}\). Generally, Δϕ is the uncertainty of the codeword in the direction orthogonal to nx in NP space. On the other hand, since \(| {\sum }_{n}{\theta }_{n}{\theta }_{n+1}|=| \langle {\mu }_{L}| \hat{{{{\mathscr{D}}}}}({{{{\bf{n}}}}}_{x})| {\mu }_{L}\rangle |\) that measures the NP-version translation invariance, it also can be understood as a metric to quantify how close the code states are to the ideal NP codes. Detailed discussion on the relation between {θn} and phase uncertainty is included in the supplementary Note 2.

Though the valid choice of {θn} is endless, here we concentrate a class of Fock-amplitude that is \({\theta }_{n}=\left\langle \right.n\left\vert \alpha,r\right\rangle\), and \(\left\vert \alpha,r\right\rangle=\hat{D}(\alpha )\hat{S}(r)\left\vert 0\right\rangle\) is a pure Gaussian state, and \(\hat{S}(r)=\exp [\frac{1}{2}({r}^{*}{\hat{a}}^{2}-r{({\hat{a}}^{{{\dagger}} })}^{2})]\) is the original squeezing operator48. Unlike cat codes, NP codes with such a Fock amplitude allow the KL cost function to be exponentially suppressed as α2 increases, which is not related to the parameters s and f, that is, there does not exist a sweet spot like cat codes49. In addition, the parameters α and r of NP codes can be optimized to obtain a maximal QEC performance for a given noise channel.

The generalized NP codes defined in Eq. (8) also contain many well-known bosonic error-correcting codes. For example, the rotation-symmetric codes31, including the binomial and cat codes, are special cases of R-NP codes with different Fock amplitudes {θn}. Moreover, the phase-engineered code has been proposed to further improve the QEC performance of R-NP codes, which actually is a special case of D-NP codes50. Lastly, although NP codes and GKP codes both admit a lattice description in the phase space of a bosonic mode, these two codes are non-trivial with respect to each other. This is because a finite NP displacement (stabilizer) cannot be obtained by superposing finite quadrature displacements, and vice versa.

From Eq. (8), the mutual conversion of two different NP lattice structures (s, f1) ↔ (s, f2) of generalized NP codes can be achieved by the interface gate

$${\hat{U}}_{s}(\Delta f): \! \!=\exp \left(-\frac{i\Delta f\pi {\hat{n}}^{2}}{2{s}^{2}}\right),$$
(9)

and it’s inverse \({\hat{U}}_{s}^{{{\dagger}} }(\Delta f)\), where Δf = f2 − f1. The interface gate can change the codespace structure through modifying the Pauli X operator \(\hat{{{{\mathscr{D}}}}}({{{{\bf{n}}}}}_{x})\) to be

$${\hat{U}}_{s}(\Delta f)\hat{{{{\mathscr{D}}}}}({{{{\bf{n}}}}}_{x}){\hat{U}}_{s}^{{{\dagger}} }(\Delta f)=\hat{{{{\mathscr{D}}}}}\left[{{{{\bf{n}}}}}_{x}+\left(0,\frac{\Delta f\pi }{s}\right)\right],$$
(10)

without affecting the Pauli Z operator \(\hat{{{{\mathscr{D}}}}}({{{{\bf{n}}}}}_{z})\). This is based on the relations \({\hat{U}}_{s}(\Delta f){\hat{\Sigma }}_{s}=\hat{{{{\mathscr{D}}}}}(0,\Delta f\pi /s){\hat{\Sigma }}_{s}{\hat{U}}_{s}(\Delta f)\) and \([{\hat{U}}_{s}(\Delta f),\hat{R}(\phi )]=0\). Such a modification of codespaces can change the code distance from dN = sq1 to dN = sq2, while another code distance dϕ remains unchanged. Here, q1 and q2 are the denominator of fractions f1 and f2, respectively.

Another main use of the interface gate is to act as a bridge between the R-NP codes (s, 0) and generalized NP codes (s, f), with a shared code parameter s. Especially, since any phase rotation for generalized NP codes commutes with the interface gate, it can be effectively readout via the canonical phase measurement once the generalized NP codes are interfaced into R-NP codes to minimize the canonical phase uncertainty of the codeword \({\left\vert \pm \right\rangle }_{L}\). This is because the probability distribution of the codeword \({\left\vert \pm \right\rangle }_{L}\) is localized in the direction orthogonal to nx in NP space, as shown in the Fig. 1, and only R-NP codes satisfy the orthogonality between nx and the canonical phase axis. This method is a foundation to readout the error syndromes characterized by phase rotation for the QEC of generalized NP codes we will propose next. For simplicity, we use the notation \({\hat{U}}_{f}:={\hat{U}}_{s}(f)\) and \({\hat{U}}_{f}^{{{\dagger}} }\) to indicate the codespaces transformation (s, 0) → (s, f) and (s, f) → (s, 0), respectively. The graphical representation of the interface between generalized NP codes and R-NP codes can be found in the supplementary Note 3.

Implementation of generalized NP codes

To illustrate generalized NP codes with the familiar quadrature representation, the following discussion will return from the NP representation to the continuous variables representation, and the traditional X-P Wigner functions of the logical state \({\left\vert+\right\rangle }_{L}\) for generalized NP codes are shown in Fig. 2. Since nx direction of the logical state \({\left\vert+\right\rangle }_{L}\) of O-NP and D-NP codes are not orthogonal to the canonical phase, their quadrature representation is non-local in the canonical phase, in contrast to the R-NP codes.

Fig. 2: The X-P Wigner function of the logical state \({\left\vert+\right\rangle }_{L}\) of three generalized NP codes with the same mean excitation \({\bar{n}}_{{{{\rm{code}}}}}=6\).
figure 2

a The binomial code [s = 4; f = 0; K = 3]. b The O-NP code [s = 1; f = 1/4; r = 0]. c The D-NP code [s = 2; f = 1/2; r = 0]. Here, the parameters of these logical states are defined in Table 1, and the dual logical state \({\left\vert -\right\rangle }_{L}\) can be obtained via an additional phase rotation \(\hat{R}(\pi /s)\).

Full size image

The quantum error correction using rotation-symmetric (R-NP) codes, such as binomial codes and cat codes, has been extensively investigated in both theory and experiment. However, how to realize quantum error correction using O-NP and D-NP codes, as shown in Fig. 2b, c, respectively, has rarely been studied50. Here, we propose a standard method to remove an NP displacement error \(\hat{{{{\mathscr{D}}}}}({{{{\bf{n}}}}}_{e})\) by using the number-phase vortex effect of the O-NP codes.

As shown in Fig. 1e, the number-phase vortex effect of generalized NP codes (s, f) can be described as

$$\begin{array}{r}{\hat{\Sigma }}_{l}{\left\vert \psi \right\rangle }_{L}=\exp \left(-\frac{if{l}^{2}\pi }{2s}\right)\hat{R}\left(-\frac{lf\pi }{{s}^{2}}\right){\left\vert \tilde{{\psi }_{l}}\right\rangle }_{L}.\end{array}$$
(11)

Here, \({\left\vert \psi \right\rangle }_{L}=a{\left\vert 0\right\rangle }_{L}+b{\left\vert 1\right\rangle }_{L}\) is an arbitrary logical qubit state, and \({\left\vert \tilde{{\psi }_{l}}\right\rangle }_{L}\) (unnormalized) is the number-shifted qubit state with the Fock-basis replacement \(\left\vert sn\right\rangle \to \left\vert sn-l\right\rangle\). Due to the NP vortex effect, every number-shift error of logical qubit state will lead to a discrete phase rotation with an angle fπ/s2. In other words, this discrete phase rotation becomes syndromes of number-shift errors when the rotated code words can be correctly distinguished. Note that the syndromes formed by rotated codewords generally have a small non-zero overlap, which is different from the exactly orthogonal number parity. Nonetheless, such an overlap will tend to vanish as long as the phase uncertainty of codewords becomes small enough.

Especially, let us consider the QEC only based on the NP vortex effect of O-NP codes (s = 1), whose codeword \({\left\vert \pm \right\rangle }_{L}\) only has a trivial rotation symmetry \({\hat{S}}_{z}={e}^{i2\pi \hat{n}}\). Therefore, the identification of number-shift errors through the number-parity measurement is unavailable. Here we introduce the recovery implementation for noisy O-NP codes based on the one-step teleportation31,51,52,53:

where the irrelevant parameters s = 1 and θ are omitted, and ne = (le, ϕe) is an arbitrary vector in the region Eq. (7). \(\bar{X},\,\bar{Z},\,\bar{H}\) are logical Pauli X gate, Pauli Z gate, and Hadamard gate, respectively. The quantum gate

$${\bar{C}}_{Z}({s}_{1},{s}_{2}): \! \!=\exp \left(-i\frac{\pi }{{s}_{1}{s}_{2}}{\hat{n}}_{1}\otimes {\hat{n}}_{2}\right)$$
(13)

is the controlled-phase gate of two NP codes described by the parameters (s1, f1) and (s2, f2), respectively.

When a noise-free ancilla mode is initialized at the dual basis \({\left\vert+\right\rangle }_{L}\), the \({\bar{C}}_{Z}\) gate can entangle the data mode and the ancilla mode via the mechanism \({\bar{C}}_{Z}\left\vert {s}_{1}m\right\rangle \otimes \left\vert {s}_{2}n\right\rangle={(-1)}^{mn}\left\vert {s}_{1}m\right\rangle \otimes \left\vert {s}_{2}n\right\rangle\), where the negative sign is present only when integers m and n are both odd. Due to the NP vortex effect, unknown number shifts will lead to the rotation \(\hat{R}(-{l}_{e}f\pi )\) of the codespaces, forming as different error subspaces, and the phase difference between two adjacent error subspaces is π/dN, thereby the pure phase rotation error with ∣ϕe∣ < π/(2dN) can be treated as a distinguishable disturbance.

Further, a canonical phase measurement \({\hat{{{{\mathscr{M}}}}}}_{X}\) is performed on the data mode to identify the rotated dual basis \(\hat{R}(-{l}_{e}f\pi ){\left\vert \pm \right\rangle }_{L}\), which not only gives the error syndromes of the number-shifts le, but also indicates the projection into \({\left\vert+\right\rangle }_{L}\) or \({\left\vert -\right\rangle }_{L}\) and simultaneously teleports the quantum state from the data mode to the noise-free ancilla mode with additional logical operations \({\bar{X}}^{i}{\bar{Z}}^{{l}_{e}}\bar{H}\). Here i = 0, 1 refers to the dual basis “+”,"-”, respectively. This teleportation is successful when the rotated dual basis of the data mode can be correctly distinguished from the presence of noise. Note that the noisy qubit state \(\hat{{{{\mathscr{D}}}}}({{{{\bf{n}}}}}_{e}){\left\vert \psi \right\rangle }_{L}\) requires to be converted into the R-NP structure via the interface \({\hat{U}}_{f}^{{{\dagger}} }\) to obtain the minimal canonical phase uncertainty of the dual basis \({\left\vert \pm \right\rangle }_{L}\) before the canonical phase measurement.

Due to the code distance of phase variable dϕ = π, the identifiable number-shift error le is up to q − 1 and phase rotation error ∣ϕe∣ < π/(2q). Such a QEC ability is similar to the R-NP codes with the code distance dN = s > 1. However, instead of the R-NP codes that use the variation of number parity to identify the number-shift error, the NP vortex effect is an independent quantum resource for correcting the number-shift errors with the syndromes of discrete phase rotation.

We then discuss the QEC implementation of the generalized NP codes with non-trivial parameters s and f, which only requires adding a modular number-parity measurement before the teleportation circuit Eq. (12). The modular number-parity measurement is based on the mechanism \({\bar{C}}_{Z}^{2}\left\vert sn-k\right\rangle \otimes \left\vert \alpha \right\rangle=\left\vert sn-k\right\rangle \otimes \left\vert \alpha {e}^{-i2\pi k/s}\right\rangle\), where \({\bar{C}}_{Z}^{2}\) is the doubled phase-controlled gate and \(k=({l}_{e}\,{{{\rm{mod}}}}\,s)\) represents the detectable number-parity.The circuit representation of modular number-parity measurement is:

The k < s number shift of the data mode will cause a phase rotation with the angle 2πk/s of the coherent state stored in the ancilla mode. This phase rotation can be captured by a canonical phase measurement. The measurement result of the ancilla mode, associated with the measurement operator \(\left\vert \alpha {e}^{-i2\pi k/s}\right\rangle \left\langle \alpha {e}^{-i2\pi k/s}\right\vert\), corresponds to the application of the projective operator \({\hat{P}}_{s,k}={\sum }_{n=1}^{\infty }\left\vert ns-k\right\rangle \left\langle ns-k\right\vert\) on the data mode. The modular number-parity measurement can be exact in principle because the phase uncertainty of the coherent state can arbitrarily tend to be vanished as long as the amplitude α is large enough.

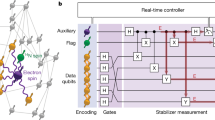
The standard QEC implementation circuit of generalized NP codes is illustrated in Fig. 3e, f. Based on the outcomes X = (X1, X2) of the modular number-parity measurement and the phase measurement in teleportation, we can recover the noisy qubit states \({{{\mathcal{N}}}}(\rho )\) after a recovery operation

$${\hat{{{{\mathscr{R}}}}}}_{{{{\bf{X}}}}}=\bar{H}{\bar{Z}}^{m}{\bar{X}}^{i}{\bar{Z}}^{\frac{k}{s}}.$$
(15)

Here the integer k ∈ [0, s − 1] is given by the outcome X1 = − 2πk/s, while the integer i and m are obtained from the outcome X2 − ϕk,s = (π/s)i − mfπ/s + ϕe. The global phase ϕk,s = − fkπ/s2 is fixed by the previous number-parity measurement, and ∣ϕe∣ < π/(2dN) is the correctable phase rotation noise. Due to the code distance dϕ = π/s of the generalized NP codes, the detectable integer m ∈ [⌊L/s⌋ − q + 1, ⌊L/s⌋] and k determine the amplitude of the number shift le = ms + k. Note that the recovery operation involves fractional order of logical \(\bar{Z}\) gate, whose implementation can be easily achieved via a simple phase rotation operation \({\bar{Z}}^{\frac{k}{s}}=\hat{R}(i\pi k/{s}^{2})\).

Fig. 3: Circuit representation of the standard QEC procedure of generalized NP codes.
figure 3

(a–d) are the Wigner functions of noisy NP codes in different error correction stages. Here, we choose the logical state \({\left\vert+\right\rangle }_{L}\) of a D-NP code \([s=2;\,f=1/2;\,r=-0.1;\,{\bar{n}}_{{{{\rm{code}}}}}=9]\) as an example. The noisy state \({{{\mathcal{N}}}}(\hat{\rho })\) [(a)] has an overlap  ~ 0.37 with the ideal logical state, which is obtained by the evolution in the error model Eq. (16) with γt = 0.1 and κt = 0.01; (b) is obtained with the single-photon loss event of code state is identified by the number parity measurement. The Wigner function (c) is obtained after performing the interface gates \({\hat{U}}_{f}^{{{\dagger}} }\), which is back to the R-NP structure, and the shallower peaks are present due to the NP vortex effect. The state (d), corrected via a perfect QEC cycle, has an overlap  ~ 0.97 with the ideal logical state. (e) and (f) are the circuit representations of the modular number-parity measurement and the teleportation-based QEC, defined in Eqs. (12) and (14), respectively. The double lines indicate the transmission of classical measurement outcomes for the recovery feedback.

Full size image

QEC performance of generalized NP codes

Based on the above implementation, we investigate the QEC performance of the generalized NP codes by considering a noise channel \({{{\mathcal{N}}}}(\hat{\rho })\) that is the solution of the master equation

$$\frac{\partial \hat{\rho }(t)}{\partial t}=\gamma {{{\mathscr{L}}}}[\hat{a}]\hat{\rho }(t)+\kappa {{{\mathscr{L}}}}[\hat{n}]\hat{\rho }(t),$$
(16)

with an integral time t, and \({{{\mathscr{L}}}}[\hat{A}]\hat{\rho (t)}=\hat{A}\hat{\rho (t)}{\hat{A}}^{{{\dagger}} }-1/2\rho (t){\hat{A}}^{{{\dagger}} }\hat{A}-1/2{\hat{A}}^{{{\dagger}} }\hat{A}\rho (t)\). Such an error model can describe the energy decay and quantum dephasing of a bosonic field stored in a cavity or transmitting in a waveguide. For the integral time t small, the physical single-photon loss and dephasing operator can be described in terms of NP displacement operators as

$$\sqrt{\gamma t}\hat{a}{e}^{-\frac{\gamma t}{2}\hat{n}}\approx \,\int_{-\pi }^{\pi }d\phi \,\frac{\sqrt{\gamma t}\exp \left(\frac{i\phi }{2}\right)}{4\sqrt{\pi }{(\gamma t/2+i\phi )}^{3/2}}\hat{{{{\mathscr{D}}}}}(1,\phi ),$$
(17)
$$\sqrt{\kappa t}\hat{n}\approx \frac{1}{2i}[\hat{{{{\mathscr{D}}}}}(0,\sqrt{\kappa t})-\hat{{{{\mathscr{D}}}}}(0,-\sqrt{\kappa t})].$$
(18)

The left side of Eq. (17) is actually the first-order Kraus operator of pure-loss channel (i.e., Eq. (16) with κ = 0)36,49. Note that the modulus of the superposition coefficient on the right side of Eq. (17) is related to a Lorentzian function with a linewidth γt. If the square root term \(\sqrt{\gamma t}\) is retained while the higher-order term γt is ignored, an unphysical representation of single-photon loss can be obtained, where the expansion coefficient diverges when ϕ = 0. The error rates must satisfy γt, κt ≪ 1 to guarantee sufficiently small NP displacements of the codewords, thereby ensuring effective QEC. Additionally, the analogous representation for the single-photon gain operator can be straightforwardly obtained as the complex conjugation of the single-photon loss.

The noisy code states then need to be sent to the QEC circuit to remove the noise and recover the logical information. As an example, we illustrate the QEC of a noisy D-NP code to demonstrate how the error correction works, as shown in Fig. 3. After the recovery process, the QEC performance of the generalized NP codes can be qualified by the channel fidelity54

$$F=\frac{1}{4}{\sum}_{{{{\bf{X}}}},j}| {{{\rm{Tr}}}}({\hat{{{{\mathscr{R}}}}}}_{{{{\bf{X}}}}}{\hat{N}}_{j}){| }^{2},$$
(19)

where \({\hat{N}}_{j}\) is the Kraus operator of the noise channel \({{{\mathcal{N}}}}\), and the Kraus-operator decomposition of the noise channel \({{{\mathcal{N}}}}\) is given in the supplementary Note 4.

In principle, the generalized NP codes with the same code distance dN = sq should perform similarly when the phase uncertainty is small enough. It indicates the mean excitation of codes \({\bar{n}}_{{{{\rm{code}}}}}\) is large, and thus the bit-flip error is dominant. However, the performance of NP codes will become different when the phase-flip error is non-negligible with the small \({\bar{n}}_{{{{\rm{code}}}}}\). This performance difference comes from both the different NP lattice structures and the Fock-amplitude series {θn}.

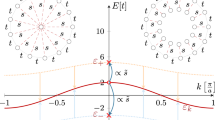
To compare the performance of NP codes with different NP lattice structures, we numerically evaluate the QEC channel infidelity as a function of the mean code excitation \({\bar{n}}_{{{{\rm{code}}}}}\), shown in Fig. 4a. As an example, here we focus on the binomial code, the O-NP code, and the D-NP code, whose Fock amplitudes are both selected as \(\left\vert {\theta }_{n}\right\rangle=\left\langle \right.n\left\vert \alpha,r\right\rangle\). Among cat and binomial codes, we selected binomial codes as the representative R-NP codes because previous research data in Refs. 31,49 indicate that binomial codes exhibit better QEC performance than cat codes under the same conditions. These NP codes have the same code distance dN = 4, and the squeezed parameter r of the O-NP and D-NP codes is optimized to minimize the channel infidelity. The numerical results show that the binomial codes and the O-NP codes have a similar performance, while the D-NP code has an outstanding performance when the mean code excitation \({\bar{n}}_{{{{\rm{code}}}}}\) is small. This phenomenon indicates that correcting number-shift errors using only the number degree (R-NP codes) or the phase degree (O-NP codes) has similar QEC performance; however, correcting number-shift errors using a hybrid number-phase degree can enhance QEC performance.

Fig. 4: QEC performance comparison of the different generalized NP codes.
figure 4

a Optimized channel infidelity as the function of the mean excitation \({\bar{n}}_{{{{\rm{code}}}}}\) of generalized NP codes which have the same code distance dN = 4. Here, we choose the error rate γt = 0.5% and κt = 0.1%. The dotted orange line corresponds to the data obtained from Eq. (20), and the break-even line is estimated using Fock states \(\left\vert 0\right\rangle\) and \(\left\vert 1\right\rangle\) for coding. b Optimized SKRPM of generalized NP codes with the fiber coupling loss rate ϵ = 1% and the dephasing error rate Γϕ = 0.1Γ. Here, the y-axis label is the generation rate of secure bits per mode. t0 is the gate operation time taken for QEC, and 1/t0 is the raw key generation rate82.

Full size image

As expected, the three types of NP codes have similar performance when \({\bar{n}}_{{{{\rm{code}}}}}\) is large enough, as shown in Fig. 4a. In such a region, the phase-flip error is negligible, and the dominant bit-flip rate can be estimated as

$$1-{\tilde{{{{\mathcal{F}}}}}}^{\gamma }\approx \mathop{\sum}_{l=1}\frac{2{\left({\bar{n}}_{{{{\rm{code}}}}}\Gamma \right)}^{l{d}_{N}}{e}^{-{\bar{n}}_{{{{\rm{code}}}}}\Gamma }}{(l{d}_{N})!}.$$
(20)

This can be derived from the QEC matrix M which is defined as \({M}_{[j\mu ],[k\nu ]}=\left\langle \mu \right\vert {\hat{N}}_{j}^{{{\dagger}} }{\hat{N}}_{k}\left\vert \nu \right\rangle\). It is based on the near-optimal performance55 of NP codes, and the detailed process can be found in the supplementary Note 5. For a given excitation-loss rate Γ = 1 − e−γt, the dominant bit-flip error rate can be suppressed by increasing the code distance dN.

On the other hand, the ability of NP codes against pure-dephasing entirely depends on the Fock amplitude θn. Though the analytical infidelity expression caused by pure dephasing for different NP codes is not trivial, they have similar performance when the phase uncertainty is very small. We can find an approximate lower bound of the QEC performance of NP codes against the pure-dephasing noise, which is obtained from the ideal NP codes, as

$${\left(1-{{{{\mathcal{F}}}}}^{\kappa }\right)}_{\min }\approx \frac{{\left(8\pi {s}^{2}\kappa t\right)}^{\frac{1}{2}}}{{\pi }^{2}}\exp \left(-\frac{{\pi }^{2}}{8{s}^{2}\kappa t}\right).$$
(21)

Here, the lower bound is dominant by a factor \({e}^{-\frac{{\pi }^{2}}{8{s}^{2}\kappa t}}\), and the remainder is an effective approximation when the dephasing rate κt ≪ 1. Though the lower bound unfortunately does not exist a simply exact expression, it already shows the key physical mechanism that the pure dephasing rate κt will be enhanced by the parameter s with a quadratic scaling. This indicates that the presence of pure dephasing prevents NP codes from working with an excessively large s. Under such a condition, phase-flip errors become the dominant error mechanism, thereby compromising the QEC performance of NP codes.

One-way quantum communication

The generalized NP codes, especially the well-known R-NP codes, have been experimentally demonstrated to have many applications. For example, the cat codes with QEC can extend the lifetime of a qubit23, and the binomial codes with QEC can protect the entanglement between two qubits26.

The generalized NP codes with repetitive QEC are also promising to execute long-distance quantum communication based on the quantum repeaters (QRs)32,33,34,35,37,38,39. One round QEC should correct the transmission loss \(1-{e}^{-{\tilde{L}}_{0}}\) and the the fiber coupling loss ϵ, where \({\tilde{L}}_{0}=L/{L}_{att}\) is the dimensionless repeater spacing, and Latt = 20km for optical fiber56. In addition, the energy attenuation in nonlinear optical fibers with Kerr medium can lead to pure phase rotation errors of the quantum states, which are usually ignored by previous studies36,56. In the QEC process shown in Fig. 3, the imperfect quantum gates and measurements also result in dephasing errors57,58. Given that the commutation of all dephasing errors with both the interface gate and the controlled-phase gate, these errors can be theoretically treated as occurring before the ideal QEC process. Therefore, the excitation-loss and dephasing errors can be collectively modeled by the Eq. (16), and the excitation-loss rate of one instance QEC is \(\Gamma=1-{e}^{-{\tilde{L}}_{0}}+\epsilon\), while the secondary dephasing error rate is modeled as Γϕ = hΓ with h < 1.

For the communication distance as far as possible, the NP codes should be optimized to minimize the error accumulation rate

$$\tau (s,f,\theta,\Gamma,{\Gamma }_{\phi })=\frac{1-F}{{\tilde{L}}_{0}}.$$
(22)

We quantify the QR performance of three types of NP codes by considering the quantum key distribution. In Fig. 4b, we compare the optimized secure key rate per mode (SKRPM) of three NP codes, where the fiber coupling loss ϵ = 1%, and the dephasing error rate is selected as Γϕ = 0.1Γ. The three types of NP codes yield an SKRPM  > 0.01 for a near-thousand-kilometer quantum communication. As expected, the binomial codes and the O-NP codes have similar performance for quantum communication, while the D-NP codes have an outstanding performance. The slight advantage of O-NP codes over binomial codes arises from their superior tolerance to pure rotation errors when the code distance dϕ = π/s of the binomial code is small enough. Moreover, we also simulate their QRs performance with Γϕ = 0.05Γ, where the communication distance is significantly extended as the dephasing error rate Γϕ is further suppressed, and the behavior of performance remains unchanged. The detailed numerical results are summarized in supplementary Table 1, which contains the Refs. 59,60.

Experimental feasibility and limitations

The simulated QEC performance of generalized NP codes presented above assumes an ideal, error-free cycle, demonstrating their theoretical potential for practical applications. For experimental implementation, superconducting quantum circuits currently represent the most viable platform due to their advanced control capabilities and scalability. Here, we provide a comprehensive analysis of the experimental requirements and practical limitations for realizing these codes in state-of-the-art superconducting quantum circuit systems.

In experiments, the encoded bosonic mode is usually stored in a high-quality microwave cavity with a lifetime T1 ~ 1 ms61, and a coupled two-level ancilla transmon with T1 ~ 0.1 ms is introduced to manipulate the bosonic mode25. In our case, the teleportation-based QEC protocol for generalized NP codes requires the operations set

$$\{{{{{\mathscr{P}}}}}_{s}(\left\vert+\right\rangle ),\,\bar{H},\,\bar{Z}( \, \beta ),\,{\hat{U}}_{f},\,{\bar{C}}_{Z},\,{\hat{{{{\mathscr{M}}}}}}_{X}\}$$
(23)

on bosonic modes. Here \(\bar{Z}(\beta )={{{\rm{diag}}}}(1,{e}^{i\beta })\) represents the arbitrary rotation of generalized NP codes (s, f) around the Z-axis in the logical level, which includes the phase gates \(\bar{S}={{{\rm{diag}}}}(1,i)\) and \(\bar{T}={{{\rm{diag}}}}(1,{e}^{i\pi /4})\). The combination of \(\bar{Z}(\beta )\) and Hadamard gate \(\bar{H}\) can realize universal rotation on a single logical qubit. In addition, \({{{{\mathcal{P}}}}}_{s}(\left\vert+\right\rangle )\) denote the preparation for the logical state \({\left\vert+\right\rangle }_{L}(s,0)\) of R-NP codes, then the corresponding logical state \({\left\vert+\right\rangle }_{L}(s,f)\) of generalized NP codes can be obtained via the interface gate \({\left\vert+\right\rangle }_{L}(s,f)={\hat{U}}_{f}{\left\vert+\right\rangle }_{L}(s,0)\).

Among these required operations, the crucial challenge is the experimental implementation of destructive canonical phase measurement \({\hat{{{{\mathscr{M}}}}}}_{X}\), which is used to identify error syndromes and teleport the quantum state. A related experiment has been demonstrated for a qubit encoded by Fock states \(\left\vert 0\right\rangle\) and \(\left\vert 1\right\rangle\) in superconducting quantum circuits47. However, the discrimination for rotated codewords of NP codes still needs to extend this experiment beyond the single-photon regime. In the absence of implementing a canonical phase measurement, heterodyne detection is a convenient method to readout the phase of an unknown signal with lower precision. The heterodyne is the well-know Gaussian POVMs with element \(\hat{E}(\alpha )={\pi }^{-1}\left\vert \alpha \right\rangle \left\langle \alpha \right\vert\), which projects the bosonic mode onto a coherent state \(\left\vert \alpha \right\rangle\) and the phase is estimated as \({{{\rm{Arg}}}}(\alpha )\), while the number information ∣α∣ is wasted. In addition, a more practical limitation is the finite readout efficiency of microwave cavities47,62,63. A detailed discussion of the reduced QEC performance in R-NP codes resulting from imperfect phase measurements is presented in Ref. 64.

The above phase measurements are independent of the encoding, offering generality for NP codes with different {θn}. When the mean code excitation \({\bar{n}}_{{{{\rm{code}}}}}\) is large enough, the intrinsic canonical phase uncertainty of the codeword \({\left\vert \pm \right\rangle }_{L}(s,0)\) will tend to vanish, thereby the rotated codewords can be effectively discriminated via the canonical phase measurement or heterodyne detection. However, in the low-excitation regime, the intrinsic canonical phase uncertainty of the codewords will limit the phase measurement accuracy, even if the phase measurement is perfect. These mechanisms are intuitively reflected in the variation of QEC performance and KL cost function for NP codes with \({\bar{n}}_{{{{\rm{code}}}}}\), as shown in Fig. 4a and in Supplementary Fig. 2, respectively.

On the other hand, a technology proposed by our previous work65 can serve as an alternative phase measurement for specific NP codes with \({\theta }_{n}=\left\langle \right.n\left\vert \alpha,r\right\rangle\). The noisy NP codes with such a Fock-amplitude θn behave as a mixture of rotated coherent-like states due to the NP vortex effect, following the interface gate operation, as shown in Fig. 3(c). Coincidentally, this technology has achieved the unambiguous discrimination of up to six coherent states (∣α∣≤2) uniformly distributed on a phase circle, corresponding to the required phase measurement for NP codes with dN = 3. It is a potential way to unambiguously identify error subspaces formed by rotated coherent-like states with a low excitation, and the measurement time is around \({\log }_{2}(2{d}_{N})\,\mu {{{\rm{s}}}}\).

Additionally, a key step in implementing generalized NP codes is the state preparation of logical states \({\left\vert+\right\rangle }_{L}(s,0)\) for R-NP codes. It is not a trivial task to prepare such a state with a large Fock space interval s. In circuit QED, a universal method for preparing an arbitrary state of a target cavity mode is available in principle. It involves the strong dispersive interaction between the cavity mode and an ancilla transmon, combined with quadrature displacement operations performed on the cavity mode66,67,68,69. In experiments, this method performs well for preparing high-fidelity logical states with several photons in  ~ 1μs23,25. However, preparing logical states with good phase distinguishability for high-order R-NP codes remains challenging via this method, as such states typically contain tens of photons. This arises because the process involves long operation times and complex controls, where the photon decay of the short-lifetime ancilla transmon introduces more noise, leading to errors in the state preparation.

The transformation from the R-NP codes (s, 0) to generalized NP codes (s, f) is based on the interface gate, as shown in Eq. (9), which is also frequently used in teleportation-based QEC. Its implementation requires controlled self-Kerr interaction \(H=K{\hat{n}}^{/}2\) for the data mode. This technology has been achieved in a Kerr-tunable superconducting resonator70, where the self-Kerr interaction strength K/2π can be adjusted from  − 5 MHz to 6 MHz, and the special logical state \({\left\vert+\right\rangle }_{L}(1,f)={\hat{U}}_{f}\left\vert \alpha \right\rangle\) of the O-NP code (with f = 1/2, 1/3, 1/4 and \({\bar{n}}_{{{{\rm{code}}}}}=2\)) is prepared within a gate time of  ~ 0.1μs. However, this experimental work was conducted in the strong dissipation regime (\(\gamma /{K}_{\max }\approx 0.1\)). Therefore, the realization of interface gates still requires the extension of the data mode lifetime to ensure that noise caused by photon loss during operations is negligible (\(\gamma /{K}_{\max }\ll 1\)). In a recent experiment71, a comparable superconducting resonator device achieved a lifetime of T1 ~ 40μs, presenting a promising platform to implement the feasible interface gate with an estimated \(\gamma /{K}_{\max }\) ratio of  ~ 2.5 × 10−3.

In Fig. 3, we present a QEC scheme only using bosonic modes, which is expected to perform QEC under bosonic-level noise and is promising for realizing fault-tolerant quantum computation based on bosonic modes. However, such a scheme requires entangling gates implemented by cross-Kerr interaction between two bosonic modes, which is typically weak (Kc/2π ~ 10 kHz) for two cavities in the current experiments. Therefore, Fig. 3 represents a long-term goal to realize QEC with all bosonic elements. For the current experimental considerations, we introduce a general method to conditionally implement universal logical rotation of an NP code, and the logical entangling \({\bar{C}}_{Z}\) gate of any two NP codes stored in different cavities. It is based on a gadget that a generalized NP code (s, f) stored in a data mode entangles an ancilla transmon prepared in \({\left\vert+\right\rangle }_{q}=(\left\vert e\right\rangle+\left\vert g\right\rangle )/\sqrt{2}\) through the gate

$${\bar{C}}_{q}(s): \! \!=\exp \left(-i\frac{\pi }{s}\hat{n}\otimes \left\vert e\right\rangle \left\langle e\right\vert \right),$$
(24)

where \(\left\vert e\right\rangle\) and \(\left\vert g\right\rangle\) denote the excited state and the ground state of the ancilla transmon, respectively. This gate serves the same role as the controlled phase gate \({\bar{C}}_{Z}(s,1)\) between two NP codes (s, f) and (1, 0) described by Eq. (13), and here the transmon replaces the trivial NP code (1, 0) with codewords are Fock state \(\left\vert 0\right\rangle\) and \(\left\vert 1\right\rangle\). In contrast to the direct cross-Kerr interaction between two cavities, the dispersive interaction \(\chi {\hat{n}}_{1}\otimes \left\vert e\right\rangle \left\langle e\right\vert\) between a cavity and a transmon is more natural and strong (χ/2π ~ 4 MHz)25.

By using the gadget that the NP code (s, f) entangles the ancilla transmon through the gate \({\bar{C}}_{q}\), one can conditionally realize the logical rotation \(\bar{Z}(\beta )\) through the teleportation circuit

Here \({\hat{X}}_{q}(\beta /2):=\exp (-i\beta {\hat{\sigma }}_{x}/2)\) is the single-qubit rotation of the transmon and \(\hat{{\sigma }_{x}}=\left\vert g\right\rangle \left\langle e\right\vert+\left\vert e\right\rangle \left\langle g\right\vert\). After measuring \(\left\vert e\right\rangle\) and \(\left\vert g\right\rangle\) basis of the transmon via \({\hat{M}}_{q}\), the logical rotation \(\bar{Z}(\beta )\) can be conditionally applied for the dada mode. Here an additional logical rotation \(\bar{Z}(C\pi )={\bar{Z}}^{C}\) with C = 0 or C = 1 arises depending on the measurement outcome: \(\left\vert g\right\rangle\) or \(\left\vert e\right\rangle\), respectively. The gate operation time of \(\bar{Z}(\beta )\) is limited by the implementation of \({\bar{C}}_{q}\), which can be estimated as 1/χ ~ 0.1μs.

To achieve the universal logical rotation of the generalized NP codes (s, f), it is necessary to implement the logical Hadamard gate. This task can be conditionally realized through the cascaded teleportation circuit

Here \({\bar{H}}_{q}\) is the Hadamard gate of the transmon qubit. This circuit can be interpreted as follows: the measurement for basis \({\left\vert \pm \right\rangle }_{q}\) conducted on the middle rail effectively induces a controlled-phase gate \({\bar{C}}_{Z}\) between the top and bottom rails. Although this method induces a conditional logical Pauli operation \({\bar{Z}}^{i}\) (not shown) on the bottom rail, where i = 0, 1 corresponds to the measurement outcome “ + ” and “ − ”, respectively, it represents a more practical approach to realizing the entangling \({\bar{C}}_{Z}\) gate than directly manipulating the cross-Kerr interaction between two cavities. This controlled-phase gate protocol is also limited by two successive gates of \({\bar{C}}_{q}\), resulting in an estimated gate time  ~ 0.2μs.

Then, the logical Hadamard gate \(\bar{H}\) can be conditionally implemented via identifying the basis \({\left\vert \pm \right\rangle }_{L}\) of the bottom rail via the phase measurement. This scheme is equivalent to Eq. (12) in the absence of noise. A logical operation \({\bar{X}}^{j}\) is present after the Hadamard gate, wherej = 0, 1 corresponds to the measurement outcome “ + ” and “ − ”, respectively. The operation time of this gate protocol is constrained by the phase measurement, which takes approximately 2 ~ 4μs for corresponding code distance dN = 2 ~ 10 using unambiguous state discrimination technology65 or even less for heterodyne detection.

We summarize the experimental reference durations T for these required operations in Table 2. Compared to the lifetimes of the cavity modes and ancilla transmon, these operations are sufficiently fast to render the implementation of generalized NP codes with current technology entirely feasible. Notably, we construct the universal logical rotation for a generalized NP code and the logical controlled-phase gate between two generalized NP codes, both based on quantum teleportation. Such a scheme inevitably introduces conditionally additional Pauli operations. A straightforward solution is to apply corresponding recovery feedback to remove these additional logical Pauli operations based on measurement outcomes, where the logical Pauli Z of NP codes (s, f) can be easily implemented via the phase rotation \(\hat{R}(\pi /s)\), while the logical Pauli X operation \(\hat{{{{\mathscr{D}}}}}({{{{\bf{n}}}}}_{x})\) of NP codes (s, f) involves multi-photon transitions between Fock states, rendering it difficult to directly realize on bosonic modes.

Table 2 Reference durations T for required QEC operations in superconducting circuit experiments
Full size table

A more practical approach was proposed in Ref. 31, where fault-tolerant quantum computation using R-NP codes is comprehensively considered. It suggests that rather than explicitly correcting the additional Pauli operations via complex procedures during teleportation-based QEC and quantum computation with magic state injection \({{{{\mathcal{P}}}}}_{\left\vert T\right\rangle }\) and \({{{{\mathcal{P}}}}}_{\left\vert S\right\rangle }\), these operations can be marked by each measurement outcome and tracked in software.

Lastly, due to the photon loss of the ancilla transmon, the required operations for bosonic modes may be faulty. Therefore, we simulate the noisy QEC cycle shown in Fig. 3 with experimental limitations. It demonstrates that the transmon dissipation during the gate operations introduces uncorrectable logical errors, thereby limiting the QEC performance of generalized NP codes. However, the main physical mechanism (number-phase vortex effect) of these codes is not significantly affected by imperfect gate operations. The detailed simulation results can be found in the supplementary Note 7. In a short-term consideration, the photon loss of an ancilla transmon can already be suppressed to the second order by replacing the employed excited state \(\left\vert e\right\rangle\) with a higher excited state \(\left\vert f\right\rangle\) of a three-level transmon72. Furthermore, the fundamental solution for these operational imperfections would require the development of fault-tolerant operations for these codes, which is a challenging but crucial long-term objective. Nonetheless, there are several theoretical frameworks that can be extended to achieve fault-tolerance for generalized NP codes31,73,74.

The QEC of a generalized NP code is based on the one-step teleportation, as shown in Eq. (12). Notably, the teleportation between two physical qubits can be extended to achieve fault-tolerance for biased noise by encoding the physical qubits into repetition codes, as proposed in Ref. 73. For generalized NP codes, after partial number-shift errors are strictly identified by the non-destructive number-parity measurement, the remaining errors are all phase rotation errors that are similar to biased noise. Therefore, a natural ideal is to extend the teleportation between two individual generalized NP codes to fault-tolerant teleportation between two repetition codes encoded by condensed generalized NP codes. For R-NP codes, this method for achieving fault-tolerance has been comprehensively discussed in Ref. 31.

Another promising scheme for implementing fault-tolerant operations on single-mode bosonic codes with discrete-variable ancillae is based on the path-independent quantum control 74. Compared with the previous scheme dedicated to NP codes, this scheme has stronger universality and lower resource consumption, maintaining the hardware efficiency of single-mode bosonic quantum codes.

Discussion

So far, we have introduced the definition, error correction, and applications of the generalized NP encoding of a bosonic mode. Here, we discuss and compare their respective advantages in experiments.

Among the three types of generalized NP codes, the state preparation of O-NP codes is the simplest when the feasible interface gate \({\hat{U}}_{f}\) is available. The preparation of code states (\({\left\vert \pm \right\rangle }_{L}(1,f)={\hat{U}}_{f}\left\vert \pm \alpha,r\right\rangle\)) and modulation of the code distance (dN) for O-NP codes solely necessitate the application of a unitary operator \({\hat{U}}_{f}\) on displaced squeezed states. While the state preparation of generalized NP codes (s, f) with a large Fork states interval s is usually difficult, which involves multi-photon transition. Another feature of the O-NP codes is the convenient implementation of approximate logical Pauli X operation \(\bar{X}\approx {\hat{U}}_{f}\hat{D}[i\pi /(2\alpha )]{\hat{U}}_{f}^{{{\dagger}} }\) with the gate infidelity \(\propto \exp (-2{\alpha }^{2})\). This is based on the commutation relations between quadrature displacement operators, and the similar gate protocol for two-leg cat codes is proposed in Ref. 28. In addition, the logical Pauli Z operation can be easily realized by a phase rotation \(\hat{R}(\pi /s)\) for all generalized NP codes (s, f).

Based on above features of O-NP codes, they can be easily implemented in optical systems. The interface gate may be realized by propagating a light field in a Kerr nonlinearity medium, and the generation of optical cat states have been widely studied in experiments75,76,77,78,79. Moreover, the most challenging aspect of realizing the one-step-teleportation QEC scheme [Eq. (12)] for O-NP codes is the correct identification of rotated codewords following the interface gate operation, analogous to the scenario depicted in Fig. 3c. In essence, this task constitutes a phase estimation problem for rotated coherent states, and the required phase measurement is also fast-growing in experiments47,65,80,81. Consequently, large-sized O-NP encoding of an optical mode is very suitable for executing long-distance quantum communication and interconnection.

On the other hand, the R-NP codes with non-trivial rotation symmetry, such as the cat codes and binomial codes, may suitably implement fault-tolerant quantum computation by encoding the microwave field stored in a superconducting cavity. The code state preparation and universal control for these codes can be achieved by manipulating the microwave cavity with a coupled discrete-variable ancillae. This allows for the strict identification of error syndromes in these codes, followed by the restoration of quantum information. The relevant experimental demonstration and theoretical proposal had a flourishing development in past decades. Moreover, the QEC performance of R-NP codes may be further improved by performing an additional unitary \({\hat{U}}_{f=1/2}\) on the code states, namely, encoding to be the D-NP codes. The truth that the D-NP codes have higher performance than R-NP and O-NP codes is analogous to which the hexagonal GKP codes have higher performance than square GKP codes. Based on the relative advantages of generalized NP codes in experiments, the faithful quantum computer and the long-distance quantum communication in a quantum network may be achieved using hybrid generalized NP encoding of bosonic modes.

In summary, we construct a novel framework of bosonic encoding, which defines the logical states via discrete number-phase translation symmetry. It is designed to against the number-phase shift error of a bosonic mode, which involves the energy decay and the quantum dephasing. The framework contains many well-known bosonic codes, such as cat codes and binomial codes, and it also guides us to find the O-NP codes and D-NP codes, which can be imagined as number-phase vortex in NP space. Crucially, such a number-phase vortex effect is an independent quantum resource, which paves a new way to correct the number-shift errors using phase degrees. Moreover, the O-NP codes are easily generated and implemented QEC for optical modes, which may allow it to suitably implement long-distance quantum communication in a hybrid quantum network or any application scenarios required to resist the NP-shifts noise in a bosonic mode. We believe that the framework can inspire the experiments and guide more discoveries of error-correcting codes.