One-shot learning for solution operators of partial differential equations

Abstract

Learning and solving governing equations of a physical system, represented by partial differential equations (PDEs), from data is a central challenge in many areas of science and engineering. Traditional numerical methods can be computationally expensive for complex systems and require complete governing equations. Existing data-driven machine learning methods require large datasets to learn a surrogate solution operator, which could be impractical. Here, we propose a solution operator learning method that requires only one PDE solution, i.e., one-shot learning, along with suitable initial and boundary conditions. Leveraging the locality of derivatives, we define a local solution operator in small local domains, train it using a neural network, and use it to predict solutions of new input functions via mesh-based fixed-point iteration or meshfree neural-network based approaches. We test our method on various PDEs, complex geometries, and a practical spatial infection spread application, demonstrating its effectiveness and generalization capabilities.

Introduction

Learning and solving governing equations of a physical system from data is a central challenge in a variety of areas of science and engineering. These governing equations are usually represented by partial differential equations (PDEs). In real-world applications, however, most PDEs lack analytical solutions. Consequently, various approaches on solving PDEs have been developed over the years. Traditional numerical methods including finite element method, finite difference method, and spectral methods have been well established. However, the computational costs of these numerical methods are prohibitively expensive for complex systems. Moreover, these methods typically require spatial discretization on some mesh of nodes, and evaluation of the solution at any other point requires interpolation or some other reconstruction method. More importantly, numerical methods require a complete understanding of the underlying PDEs.

Recently, physics-informed machine learning (PIML) has obtained great attention and provides alternative approaches for solving PDEs or approximating solution operators for PDEs¹. By integrating physics into the loss function of a neural network using automatic differentiation, physics-informed neural networks (PINNs) have been successfully applied to solve forward problems of various types of PDEs across multiple fields^{2,3,4,5,6,7,8,9,10,11}. PINN is able to generate differentiable PDE solutions at any point without a mesh. However, solving a new PDE requires the training of a new neural network, which is still computationally expensive. To address this issue, deep neural operators have been developed very recently to learn PDE solution operators by using neural networks, such as deep operator network (DeepONet)^{12,13,14,15,16,17,18} and Fourier neural operator^14,19. Deep neural operators enable fast prediction of PDE solutions under varying conditions, such as different boundary and initial conditions.

Training deep neural operators requires large amounts of data, which is either experimental data or data from computational simulations of physical systems²⁰. However, in practice, it can be expensive or infeasible to obtain or store large amounts of such data. For instance, in geophysics applications, it is quite expensive to measure seismic activity, resistivity, ground penetrating radar, and magnetic fields²¹. Similarly, in climate modeling, observed climate records are insufficient and running a long-term high-resolution climate simulation is not feasible with current computational power²². The field of fluid dynamics faces analogous challenges, as the complexity of simulating fluid flow and heat transfer in various engineering applications requires high-performance computing resources, which are economically and computationally expensive. When the governing PDEs are known, physics-informed DeepONet (PI-DeepONet)¹³ has been proposed to reduce the data requirement by incorporating PDEs into the loss function. PI-DeepONet has been applied to long-time integration of parametric evolution equations, in which the temporal domain is decomposed and a single network is trained only within a short-time interval²³. However, in many complex real problems, the explicit form of the PDEs may be unknown due to the complexity or insufficient understanding of physics. Given these challenges, it would be highly beneficial if we develop methods aiming to minimize the amount of training data and the associated computational costs for learning PDE solution operators without knowledge of the underlying PDEs. This motivates our focus on an intriguing scenario: one-shot learning, which involves network training based on only a single data point.

One-shot learning methods have been proposed to learn from a single example usually by utilizing previously acquired knowledge^24,25,26,27. One-shot learning is mainly used in the computer vision field and its usage in scientific machine learning (SciML) is very limited^28,29. To the best of our knowledge, no one-shot learning method has been developed for learning PDE solution operators. In this work, we propose a one-shot learning approach to learn PDE solution operators from only one data point, and there are no existing methods that address the aforementioned challenges. In our method, we abstract some “general knowledge” from only one PDE configuration and its solution, and make it possible to predict PDE solutions with other parameters or conditions.

We define the scope of problems and highlight the challenges we aim to address as follows.

• Our goal is to learn the solution operator of an unknown underlying PDE system that maps variable inputs to the corresponding solutions. We only consider PDEs that are well-posed with suitable initial and boundary conditions (IC/BCs). We do not consider nonlocal PDEs such as integral equations and fractional differential equations.

• We address scenarios where obtaining a large amount of paired input-output function data points are infeasible, but a single data point is available. Hence, existing data-driven methods (which require large datasets) are inapplicable. Moreover, there is no extra information (e.g., relevant tasks) available for transfer learning or meta-learning.

• While the explicit PDE form is unknown, the IC/BCs are known, as is typical when dealing with physical systems. In such cases, traditional numerical methods and physics-informed machine learning (which require the PDE form) are inapplicable. We explain why the existing data-efficient methods (physics-informed operator learning, multi-fidelity operator learning, meta-learning, transfer learning, and self-supervised learning) cannot be applied to our setting in Supplementary Section S1.

From another perspective, our method can also be viewed as an approach for discovering PDEs. When discovering PDEs, in one scenario, where we know all the terms of the PDE and only need to infer unknown coefficients from data, many neural network-based methods have been proposed. For example, we can enforce physics-based constraints to train neural networks that can solve inverse problems of PDEs^{3,5,30,31,32,33,34,35}. In the second scenario, where we do not know all the PDE terms, but have a prior knowledge of all possible candidate terms, several approaches on PDE discovery have also been developed^36,37. The kernel frameworks for learning PDEs^38,39 are proposed with kernel smoothing followed by kernel regression to learn the functional form of the differential operator with low training data requirements. In a general setup, discovering PDEs only from data without any prior knowledge is much more difficult^40,41. To address this challenge, instead of discovering the PDE in an explicit form, we use a neural network as an implicit representation of the physics laws.

Our one-shot learning method first leverages the locality of (partial) derivatives and uses a neural network to learn the local solution operator of the PDE system defined at a small computational domain. Then for a new PDE condition (e.g., a new source/forcing term or PDE coefficient field), we find the global PDE solution by coupling all local domains using the following mesh-based or neural network approaches, constrained by the IC/BCs. Specifically, a mesh-based fixed-point iteration (FPI) approach is proposed to obtain the PDE solution that satisfies the boundary/initial conditions and local PDE constraints. In this iterative approach, the computation on local stencil of mesh elements is in the same spirit as traditional PDE solvers. We also propose two versions of local-solution-operator informed neural networks (LOINNs), which are meshfree, to improve the stability and flexibility of finding the solution. Moreover, our one-shot learning method has been applied to solve multi-dimensional linear and nonlinear PDEs, PDEs defined on a complex geometry, a spatial infection spread problem, and has been generalized to a new geometry. In this paper, we demonstrate our one-shot learning method for solution operators on different PDEs for a range of conditions in “Results” section, and then describe the details of our method.

Results

We demonstrate the capability and potential of our proposed one-shot learning method through various problems, and discuss choices of the local solution operator $\widetilde{{\mathcal{G}}}$, variations in Δf, effectiveness of our method, different mesh resolutions, and generalization. We first introduce the problem setup of learning solution operators for PDEs using one-shot learning method and then present the results.

Learning solution operators for PDEs

We consider a physical system governed by a PDE defined on a spatio-temporal domain $\Omega \subset {{\mathbb{R}}}^{d}$:

$${\mathcal{F}}[u({\bf{x}});f({\bf{x}})]=0,\quad {\bf{x}}=({x}_{1},{x}_{2},\ldots,{x}_{d})\in \Omega$$

with suitable initial and boundary conditions

$${\mathcal{B}}(u({\bf{x}}),{\bf{x}})=0,$$

(1)

where u(x) is the solution of the PDE and f(x) is a forcing term. The solution u depends on f, and thus we define the solution operator as

$${\mathcal{G}}:f({\bf{x}})\mapsto u({\bf{x}}).$$

For nonlinear PDEs, ${\mathcal{G}}$ is a nonlinear operator.

In many problems, the PDE of a physical system is unknown or computationally expensive to solve, and instead, sparse data representing the physical system is available. Specifically, we consider a dataset ${\mathcal{T}}={\{({f}_{i},{u}_{i})\}}_{i=1}^{| {\mathcal{T}}| }$, and (f_i, u_i) is the i-th data point, where ${u}_{i}={\mathcal{G}}({f}_{i})$ is the PDE solution for f_i. Our goal is to learn ${\mathcal{G}}$ from the training dataset ${\mathcal{T}}$, such that for a new f, we can predict the corresponding solution $u={\mathcal{G}}(f)$. When ${\mathcal{T}}$ is sufficiently large, then we can learn ${\mathcal{G}}$ straightforwardly by using neural networks, whose input and output are f and u, respectively. Many networks have been proposed in this manner such as DeepONet¹² and Fourier neural operator¹⁹. In this study, we consider a very challenging scenario where we have only one data point for training, i.e., one-shot learning with $| {\mathcal{T}}|=1$, and we let ${\mathcal{T}}=\{({f}_{{\mathcal{T}}},{u}_{{\mathcal{T}}})\}$. Note that here “one-shot” represents one input-output data pair in the context of operator learning.

One-shot learning method based on the principle of locality

It is impossible in general to learn the PDE solution operator ${\mathcal{G}}$ from a single data point. To address this challenge, here we consider that ${\mathcal{T}}$ is not specified, and we can select ${f}_{{\mathcal{T}}}$. In addition, instead of learning ${\mathcal{G}}$ for the entire input space, we only aim to predict ${\mathcal{G}}(f)$ in a neighborhood of some f₀.

To overcome the difficulty of training a machine learning model based on only one data point, we leverage the principle of locality that (partial) derivatives in the PDEs are mathematically defined locally, i.e., the same PDE is satisfied in an arbitrary-shaped small domain inside Ω. Based on this fact, instead of considering the entire computational domain, we consider a “canonical” small local domain $\tilde{\Omega }$, and we define a local solution operator $\tilde{{\mathcal{G}}}$ at $\tilde{\Omega }$. In our method, we can place $\tilde{\Omega }$ at any specific location inside Ω, and each placement/realization leads to one training point for $\tilde{{\mathcal{G}}}$. In this way, we could easily generate a large training dataset for $\tilde{{\mathcal{G}}}$. Therefore, we transform the one-shot learning of ${\mathcal{G}}$ into a classical learning of $\tilde{{\mathcal{G}}}$. Once $\tilde{{\mathcal{G}}}$ is well trained, we predict ${\mathcal{G}}(f)$ for a new f by applying $\tilde{{\mathcal{G}}}$ as a constraint at arbitrary local domains of the PDE solution $u={\mathcal{G}}(f)$. We enforce IC/BCs in this process by hard or soft constraints, which ensure that the predicted solutions are not only locally accurate but also globally consistent across the entire domain. Specifically, our method includes the following four steps (Fig. 1). The details of each step can be found in “Methods” section.

Fig. 1: Workflow of the one-shot learning method for solution operators.

(Step 1) We select a suitable polygon, such as a rectangle, on a local mesh with step size Δx₁ and Δx₂, and thus define a local domain $\tilde{\Omega }$ (the black nodes). (Step 2) We select a target mesh node x^* and define a local solution operator $\tilde{{\mathcal{G}}}$. (Step 3) We learn $\tilde{{\mathcal{G}}}$ using a neural network from a dataset constructed from ${\mathcal{T}}=({f}_{{\mathcal{T}}},{u}_{{\mathcal{T}}})$. (Step 4) For a new PDE condition (i.e., a new input function f), we utilize the pre-trained $\tilde{{\mathcal{G}}}$ to find the corresponding PDE solution by using one of the following approaches. (Approach 1, FPI) We consider points on an equispaced global mesh. Starting with an initial guess u₀(x), we apply $\tilde{{\mathcal{G}}}$ iteratively to update the PDE solution until it is converged. (Approach 2, LOINN) We use a network to approximate the PDE solution. We apply $\tilde{{\mathcal{G}}}$ at different random locations to compute the loss function. (Approach 3, cLOINN) We use a network to approximate the difference between the PDE solution and the given u₀(x).

• Select a “canonical” local domain $\tilde{\Omega }$. We consider a virtual background equispaced mesh and select a polygon on this local mesh. We denote the set of all the mesh nodes that lie on the edges and within the interior of the chosen polygon (marked as black nodes in Fig. 1) as $\tilde{\Omega }$. We show a general choice of $\tilde{\Omega }$ in Fig. 2a (left) by black nodes.

  Fig. 2: Selecting local domains and learning local solution operators.

  

  a A general choice of the local domain $\tilde{\Omega }$ is a set of nodes on a polygon. $\tilde{\Omega }$ can have different shapes and sizes according to a specific PDE. A local solution operator $\tilde{{\mathcal{G}}}$ is defined on $\tilde{\Omega }$. b–f Examples of local domains and local solution operators used in this paper. g, h When learning $\tilde{{\mathcal{G}}}$, the training points based on $\tilde{\Omega }$ are either (g) selected on a global mesh or (h) randomly sampled.

• Select a local solution operator $\tilde{{\mathcal{G}}}$. We choose a specific location x^* (the red node in Fig. 1) from the local domain $\tilde{\Omega }$ in step 1, and then the other points ${\tilde{\Omega }}_{{\rm{aux}}}=\{{\bf{x}}\in \tilde{\Omega }| {\bf{x}}\ne {{\bf{x}}}^{*}\}$ are called “auxiliary points” (the blue nodes in Fig. 1). We construct a local solution operator

  $$\tilde{{\mathcal{G}}}:\left(\{u({\bf{x}}):{\bf{x}}\in {\tilde{\Omega }}_{{\rm{aux}}}\},\{f({\bf{x}}):{\bf{x}}\in \tilde{\Omega }\}\right)\mapsto u({{\bf{x}}}^{*}).$$

  This local solution operator $\tilde{{\mathcal{G}}}$ is learned by a fully-connected neural network that takes u values of auxiliary points and f values in $\tilde{\Omega }$ as inputs and output u values of x^*, which captures the local relationship of the PDE. The choice of the shape and size of $\tilde{\Omega }$ and $\tilde{{\mathcal{G}}}$ is problem dependent. In Figs. 2b–f, we present several choices of $\tilde{\Omega }$ and $\tilde{{\mathcal{G}}}$ used in this paper. The principles for selecting the local domain $\tilde{\Omega }$ and local solution operator $\tilde{{\mathcal{G}}}$ are summarized as follows. First, the shape of $\tilde{\Omega }$ should align with the dimensional structure of the data. For example, one-dimensional problems, $\tilde{\Omega }$ could be a line segment, while in two-dimensional scenarios, it could be a polygon. Second, for time-dependent system, in additional to spatial domain, $\tilde{\Omega }$ should also include past temporal states.

• Train the local solution operator $\tilde{{\mathcal{G}}}$. Utilizing the dataset ${\mathcal{T}}=({f}_{{\mathcal{T}}},{u}_{{\mathcal{T}}})$, we place the local domain $\tilde{\Omega }$ at different locations of Ω, which can be either a global structured mesh or randomly sampled locations (Figs. 2g and h). This process generates many input-output data pairs for training $\tilde{{\mathcal{G}}}$.

• Predict the solution u for a new input function f with suitable IC/BCs. For a new PDE condition f, we choose one of the three approaches to find the global PDE solution using the pre-trained local solution operator $\tilde{{\mathcal{G}}}$: fixed-point iteration (FPI), local-solution-operator informed neural network (LOINN) or local-solution-operator informed neural network with correction (cLOINN).

FPI is a mesh-based approach, and we can only use the structured equispaced global mesh to predict the solution. In contrast, with LOINN and cLOINN, it is possible to train the neural networks using randomly sampled data points in the domain. When we use equispaced global grid in LOINN and cLOINN, we denote the methods as LOINN-grid and cLOINN-grid, respectively. When we use randomly sampled point locations, we denote the methods as LOINN-random and cLOINN-random. The technical and implementation details of each step are provided in “Methods” section and the Supplementary Section S2.

Our numerical experiments cover a range of representative scenarios, including multi-dimensional, linear and nonlinear PDE systems, PDEs with f either as a source term or a coefficient field, and PDEs defined in a complex geometry. Notably, there are no existing methods to compare with for the problem we are addressing. In each experiment, we first obtain the training dataset via finite difference methods on an equispaced dense mesh. The parameters for generating datasets and the hyperparameters of pre-trained neural networks are listed in Supplementary Section S2. To test the developed method, we randomly sample 100 new f by f  = f₀ + Δf, in which Δf is sampled from a Gaussian random field (GRF) with a correlation length l_test = 0.1 and various amplitude σ_test. We compute the geometric mean and standard deviation of the L² relative errors for the 100 test cases (Table 1). For all experiments, the Python library DeepXDE³ is utilized to implement the neural networks.

Table 1 L² relative errors of one-shot learning method

Learning the solution operator for a linear PDE

We first demonstrate the capability of our method with a pedagogical example of a one-dimensional Poisson equation

$$\Delta u=100f(x),\quad x\in [0,1]$$

with the zero Dirichlet boundary condition, and the solution operator is ${\mathcal{G}}:f\mapsto u$.

As described in the one-shot learning method based on the principle of locality, we first need to select a “canonical” local domain $\tilde{\Omega }$, which is a line segment in 1D case. We choose the simplest local solution operator using 3 nodes (Fig. 2b) $\widetilde{{\mathcal{G}}}:\{u(x-\Delta x),u(x+\Delta x),f(x)\}\mapsto u(x)$ with Δx = 0.01 from $\tilde{\Omega }$. The training dataset ${\mathcal{T}}$ only has one data point $({f}_{{\mathcal{T}}},{u}_{{\mathcal{T}}})$ (Fig. 3a), where ${f}_{{\mathcal{T}}}$ is generated based on ${f}_{0}=\sin (2\pi x)$. Using the training dataset, we place $\tilde{\Omega }$ at different locations to generate data points and train the local solution operator. For a new PDE condition f, we apply our trained $\widetilde{{\mathcal{G}}}$ and enforce the zero Dirichlet boundary condition at x = 0 and x = 1 to find the solution. In Fig. 3c, we show examples of testing cases f = f₀ + Δf with different σ_test. When σ_test is larger, there is a more significant discrepancy between f₀ and f.

Fig. 3: 1D Poisson equation.

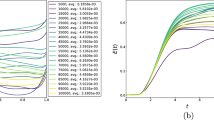
a The training data includes a random ${f}_{{\mathcal{T}}}$ generated from GRF and the corresponding solution ${u}_{{\mathcal{T}}}$. b The convergence of L² relative errors of different approaches for various test cases. The shaded regions represent one standard deviation of the L² relative errors from 100 test cases. c Testing examples of random f = f₀ + Δf with Δf sampled from GRF of σ_test = 0.02, 0.05, 0.10, 0.15 and l_test = 0.1. d Prediction example of different approaches for various test cases. e Prediction errors (the geometric mean and standard deviation) when training by f_random with amplitude σ_train and testing on functions with amplitude σ_test. The length scales l_train= 0.01 and l_test = 0.10 are fixed. f Prediction errors (the geometric mean and standard deviation) when training by f_random with different length scale l_train and amplitude σ_train = 0.10, and testing on functions with amplitude σ_test = 0.10 and l_test = 0.10.

We evaluate the performance of FPI, LOINN and cLOINN approaches on the grid data, as well as LOINN and cLOINN using randomly sampled data points (Fig. 3b). For FPI, LOINN-grid, and cLOINN-grid, we use a mesh with 101 equispaced points. For LOINN-random and cLOINN-random, we use 101 random points. We report the geometric mean of L² relative errors of all cases in Table 1 for different σ_test. As expected, the smaller σ_test we use, the better the performance. When σ_test = 0.02, all approaches achieve an L² relative error of around 1%. In Fig. 3d, we show prediction examples of using FPI and cLOINN-random approaches. For this simple case, the results of using different approaches and data sampling are similar. It is observed that in this experiment, cLOINN converges faster than LOINN and FPI.

Discussion on the choice of training data

Given that we use only one training data point, the selection of ${f}_{{\mathcal{T}}}$ in ${\mathcal{T}}$ is critical. Ideally, ${f}_{{\mathcal{T}}}$ should exhibit patterns similar to those we aim to predict, yet contain some randomness to enrich the information to be extracted. In our experiments, we use ${f}_{{\mathcal{T}}}(x)={f}_{{\rm{random}}}(x)+{f}_{0}(x)$, where ${f}_{{\rm{random}}}(x) \sim {\mathcal{GP}}(0,k({x}_{1},{x}_{2}))$ (see “Methods” section for more details). We now study the effect of ${f}_{{\mathcal{T}}}$ chosen with different amplitude σ_train and length scale l_train different from the test datasets, as well as the influence of changing the general shape of training forcing function ${f}_{{\mathcal{T}}}$.

First, we explore how the amplitude σ_train influences prediction accuracy for various σ_test (Fig. 3e). We randomly sample f_random with a fixed l_train = 0.01 across different σ_train  = 0.02, 0.05, 0.10, 0.15, and train one local solution operator for each σ_train. We then fix l_test = 0.10, and test 100 cases using σ_test  = 0.02, 0.05, 0.10, or 0.15. Here we only show the results of FPI, since performance of other methods is similar. We find that the errors are generally larger for test functions with larger σ_test (i.e., higher variability). Furthermore, we observe that the prediction accuracy is robust against different σ_train.

Second, we are interested in how different l_train impact the performance of local solution operators (Fig. 3f). We train one local solution operator for each l_train = 0.005, 0.01, 0.05, 0.10, 0.15 and σ_train = 0.10, then test them using FPI on 100 test cases with σ_test  = 0.10 and l_test  = 0.10. When l_train is too small (e.g., 0.005) or too large (e.g., 0.15), the prediction errors tend to increase with large standard deviations. The reasonable range of l_train for f_random is between 0.01 to 0.1 in this example. These results suggest that effective training data should have a length scale l_train that introduce sufficient randomness without inducing overly rapid fluctuations.

Next, we study the influence of training forcing function ${f}_{{\mathcal{T}}}$. Instead of using local solution operators trained from the sine wave ${f}_{{\mathcal{T}}}(x)={f}_{{\rm{random}}}(x)+\sin (2\pi x)$, we consider three alternatives: (1) a phase-shifted sine wave, ${f}_{{\mathcal{T}}}(x)={f}_{{\rm{random}}}(x)+\sin (2\pi x+\pi )$ (Supplementary Fig. S3a), (2) a cosine wave, ${f}_{{\mathcal{T}}}(x)={f}_{{\rm{random}}}(x)+\cos (2\pi x)$ (Supplementary Fig. S3b), and (3) a fully random function ${f}_{{\mathcal{T}}}(x)={f}_{{\rm{random}}}(x)$ with σ_train = 1.0 and l_train = 0.01 (Supplementary Fig. S3c). In both (1) and (2), we randomly sample f_random(x) with l_train = 0.01 and σ_train = 0.10 for training local solution operators. We test them on 100 test cases with σ_test = 0.10 and l_test = 0.10. For the phase-shifted sine wave, the overall shape remains similar but is flipped with respect to the x-axis. We observe a similar error 3.58 ± 6.40% with a larger standard deviation, compared to 3.71 ± 2.96% for the original sine wave. For the cosine wave, the phase is different, and the error is 8.73 ± 2.78% which is larger. For the fully random function without any information of f₀, the error further increases to 9.68 ± 0.73%. These results suggest that variations of the training data can affect predictive accuracy. Nonetheless, our method performs reasonably successful, demonstrating robustness to such changes.

Effectiveness of our method and comparison with the baselines

Our approach solves a unique challenging scenario where traditional numerical methods, which depend on known PDE forms, and traditional data-driven methods, which typically require large datasets, do not apply. There are no existing methods directly comparable to ours for this setting. Nonetheless, it would be helpful to provide baselines as comparisons.

Since a new test case is f = f₀ + Δf, u₀ in the data pair (f₀, u₀) can be used as a baseline. Notably, u₀ serves as the initial guess of FPI approach, so the convergence of the L² relative errors in FPI itself reflects the effectiveness of our approach. Take the 1D Poisson equation as an example, when σ_test = 0.10, the L² relative errors for the baseline u₀ is 16.29 ± 10.77%, which is significantly higher than the errors achieved by our method (all below 5% in Fig. 3e).

We also consider DeepONet¹² as the second baseline. With only one data pair $({f}_{{\mathcal{T}}},{u}_{{\mathcal{T}}})$, the error in predicting u from f with σ_test = 0.10 using DeepONet is very large at 20.73 ± 14.02%. Even when using both (f₀, u₀) and $({f}_{{\mathcal{T}}},{u}_{{\mathcal{T}}})$ as the training data, the error remains high at 15.83 ± 10.26%.

Learning the solution operator for a time-dependent PDE

We then consider a time-dependent linear diffusion equation

$$\frac{\partial u}{\partial t}=D\frac{{\partial }^{2}u}{\partial {x}^{2}}+f(x),\quad x\in [0,1],\quad t\in [0,1]$$

with zero boundary and initial conditions, where D = 0.01 is the diffusion coefficient. We aim to learn the solution operator ${\mathcal{G}}:f\mapsto u$ for a class of f = f₀ + Δf with ${f}_{0}=0.9\sin (2\pi x)$.

We select the simplest local solution operator defined on a local domain with 4 spatial-temporal nodes (Fig. 2d):

$$\widetilde{{\mathcal{G}}}:\{u(x,t-\Delta t),u(x-\Delta x,t),u(x+\Delta x,t),f(x,t)\}\mapsto u(x,t).$$

Since it is a time-dependent problem, we also include the previous temporal node. To generate the training dataset ${\mathcal{T}}$, we randomly sample ${f}_{{\mathcal{T}}}$ shown in Supplementary Fig. S2a. FPI and LOINN/cLOINN-grid use an equispaced mesh of 101 × 101, and LOINN/cLOINN-random use 101² random point locations.

We test these approaches for Δf sampled from GRF with σ_test = 0.1, 0.3, 0.5, and 0.8. The details of error convergence are shown in Supplementary Fig. S2b. For a fixed σ_test, FPI and cLOINN-grid both work well and outperform LOINN-grid (Table 1). LOINN-random and cLOINN-random both achieve better accuracy than LOINN/cLOINN-grid (e.g., an L² relative error smaller than 1% when σ_test = 0.1). When σ_test is increased from 0.1 to 0.8, all approaches can an achieve an L² relative error smaller than 8%. In this experiment, we conclude that cLOINN performs better and converges faster than LOINN. Also, the performance of LOINN and cLOINN with randomly sampled points are better than that with mesh points. In Supplementary Fig. S2c, we show a test example for σ_test = 0.8 and the predictions and pointwise errors using FPI, LOINN-grid, cLOINN-grid, LOINN-random, and cLOINN-random.

Learning the solution operator for a nonlinear PDE

We have shown the capability of our one-shot operator learning method on linear PDEs. Now we consider a nonlinear diffusion-reaction equation with a source term f(x):

$$\frac{\partial u}{\partial t}=D\frac{{\partial }^{2}u}{\partial {x}^{2}}+k{u}^{2}+f(x),\quad x\in [0,1],t\in [0,1]$$

with zero initial and boundary conditions, where D = 0.01 is the diffusion coefficient, and k = 0.01 is the reaction rate. The solution operator we aim to learn is ${\mathcal{G}}:f\mapsto u$, where f = f₀ + Δf with ${f}_{0}=\sin (2\pi x)$.

We select the same $\widetilde{{\mathcal{G}}}$ as the previous linear diffusion equation example (Fig. 2d), and randomly sample ${f}_{{\mathcal{T}}}$ shown in Fig. 4a to train a local solution operator. FPI and LOINN/cLOINN-grid use an equispaced mesh of 101 × 101, and LOINN/cLOINN-random use 101² random point locations. We also test these approaches for Δf sampled from GRF with σ_test = 0.1, 0.3, 0.5, and 0.8 (Fig. 4b). FPI and LOINN/cLOINN-random achieve better accuracy than the others (e.g., L² relative error smaller than 0.5% when σ_test= 0.1). When σ_test is increased from 0.1 to 0.8, all the approaches can achieve an L² relative error smaller than 5%. In Fig. 4c, we show a test example for σ_test= 0.8 and the predictions and pointwise errors using FPI, LOINN-grid, cLOINN-grid, LOINN-random, and cLOINN-random.

Fig. 4: Learning the nonlinear diffusion-reaction equation.

a The training data includes a random ${f}_{{\mathcal{T}}}$ generated from GRF and the corresponding solution ${u}_{{\mathcal{T}}}$. b The convergence of L² relative errors of different approaches for various test cases. c Prediction example of different approaches for a test case with σ_test = 0.8. d L² relative error of different test functions with σ_test = 0.1, 0.3, 0.5, 0.8 when using different numbers of point locations to show the effect of mesh resolutions.

Generalization of the local solution operator to very different testing functions

We evaluate the generalization capability of the local solution operator $\widetilde{{\mathcal{G}}}$, which is trained from the sine wave ${f}_{{\mathcal{T}}}(x)={f}_{{\rm{random}}}(x)+\sin (2\pi x)$ and the corresponding ${u}_{{\mathcal{T}}}(x)$. We test it on various new f, including (1) a phase-shifted sine wave, $f=\sin (2\pi x+\pi )$ (Fig. 5a), (2) a cosine wave, $f=\cos (2\pi x)$ (Fig. 5b), (3) a higher-frequency sine wave, $f=\sin (3\pi x)$ (Fig. 5c), (4) a sine wave with very high frequency, $f=2\sin (9\pi x)$ (Fig. 5d), (5) a sum of two sine waves at moderate and high frequencies, $f=\sin (6\pi x)+\sin (14\pi x)$ (Fig. 5e), and (6) a sum of multiple weighted sine waves at different frequencies, $f=0.8\sin (6\pi x)+0.6\sin (14\pi x)+0.4\sin (26\pi x)+0.2\sin (42\pi x)$ (Fig. 5f). The corresponding test errors for these cases are 0.18%, 2.19%, 1.80%, 6.01%, 5.20%, 2.66%, respectively. Despite these f have a wide range of frequencies and phases (very different from the training data), the prediction errors remain low. The results indicates that the local solution operator has a good generalizability and effectively captures the local relationship of the nonlinear diffusion-reaction equation.

Fig. 5: Testing the local solution operator on diverse testing functions.

a A phase-shifted sine wave, $f=\sin (2\pi x+\pi )$. b A cosine wave, $f=\cos (2\pi x)$. c A higher-frequency sine wave, $f=\sin (3\pi x)$. d A sine wave with very high frequency, $f=2\sin (9\pi x)$. e A sum of two sine waves at moderate and high frequencies, $f=\sin (6\pi x)+\sin (14\pi x)$. f A sum of multiple weighted sine waves at different frequencies, $f=0.8\sin (6\pi x)+0.6\sin (14\pi x)+0.4\sin (26\pi x)+0.2\sin (42\pi x)$. The first column is various new f; the second column is the corresponding ground truth u; the third column is the FPI prediction for each f; and the last column is the absolute error between the ground truth u and the prediction.

Generalization of the local solution operator to noisy testing input functions

We apply the same trained local solution operator $\widetilde{{\mathcal{G}}}$ to the noisy testing functions of the cosine wave $f=\cos (2\pi x)$. We corrupt the testing function with 5%, 10%, 20%, and 30% Gaussian noise (Supplementary Fig. S5a). The test errors increase with the noise level (Supplementary Fig. S5b). Notably, even when the added noise is 30%, the error remains relatively small (8.90%).

Discussion on the choice of training data

Similar to that in the Poisson equation example, we study the influence of training function ${f}_{{\mathcal{T}}}$. We consider three alternatives for ${f}_{{\mathcal{T}}}$: (1) a phase-shifted sine wave, ${f}_{{\mathcal{T}}}(x)={f}_{{\rm{random}}}(x)+\sin (2\pi x+\pi )$ (Supplementary Fig. S4a), (2) a cosine wave, ${f}_{{\mathcal{T}}}(x)={f}_{{\rm{random}}}(x)+\cos (2\pi x)$ (Supplementary Fig. S4b), and (3) a higher-frequency sine wave ${f}_{{\mathcal{T}}}(x)={f}_{{\rm{random}}}(x)+\sin (3\pi x)$ (Supplementary Fig. S4c). In all the cases, we randomly sample f_random(x) with σ_train = 0.10 and l_train  = 0.01 for training local solution operators. We evaluate performance on 100 test cases with σ_test = 0.80 and l_test= 0.10. For the phase-shifted sine wave, the error slightly increases to 3.28 ± 2.18%, compared to 2.32 ± 1.32% for the original sine wave. The cosine wave, which differs in phase, yields a error of 3.99 ± 3.37%. For the higher-frequency sine wave, the error increases to 4.61 ± 3.44%. These results further demonstrate that the method is robust to variations in the training data.

One-shot operator learning on a coarse mesh

In all the previous examples, we use a local mesh with resolution Δx = Δt = 0.01 for learning the local solution operator $\tilde{{\mathcal{G}}}$. In this section, we investigate the performance of our methods using different mesh resolutions when training $\widetilde{{\mathcal{G}}}$ and predicting solutions in Ω. For FPI, LOINN-grid, and cLOINN-grid, we generate input-output pairs for training $\tilde{{\mathcal{G}}}$ on a structured equispaced global mesh $\hat{\Omega }$ with mesh size Δx = Δt = 0.01, 0.02, 0.04, 0.05, and 0.07 (i.e., the numbers of points are 101², 51², 26², 21², and 16²), which matches the local mesh resolutions. For LOINN-random and cLOINN-random, we randomly sample 101², 51², 26², 21², 16² point locations in Ω. We compare L² relative errors with different σ_test and resolutions. With denser mesh resolutions or more points, all approaches perform better (Fig. 4d). Even using a coarse mesh of 0.05, our methods can still achieve errors around 10% for all cases, which demonstrates the computational efficiency of our proposed methods.

Learning the solution operator for a PDE with parametric coefficient fields

We illustrate the choice of local domain using an advection equation

$$\frac{\partial s}{\partial t}+a(x)\frac{\partial s}{\partial x}=0,\quad x\in [0,1],t\in [0,1]$$

with initial condition s(x, 0) = x² and boundary conditions $s(0,t)=\sin (\pi t)$, where a(x) is the velocity coefficient. We learn the solution operator mapping from the coefficient field to the PDE solution: ${\mathcal{G}}:a\mapsto s$ for a class of a = a₀ + 0.1Δf with a₀ = 1.

The training dataset ${\mathcal{T}}$ with one data point $({a}_{{\mathcal{T}}},{s}_{{\mathcal{T}}})$ is shown in Fig.S6a. We use the local solution operator (Fig. 2c)

$$\widetilde{{\mathcal{G}}}:\{s(x,t-\Delta t),s(x-\Delta x,t),s(x-\Delta x,t-\Delta t),a(x,t)\}\mapsto s(x,t).$$

The training dataset ${\mathcal{T}}$ with one data point $({a}_{{\mathcal{T}}},{s}_{{\mathcal{T}}})$ is shown in Fig. S6a. Since FPI and cLOINN-random have shown better performance compared to LOINN and cLOINN-grid in previous experiments, we only present the results of FPI and cLOINN-random here (Fig. S6b). FPI uses an equispaced mesh of 101 × 101, and cLOINN-random use 101² random point locations. The errors of FPI and cLOINN-random both achieve less than 1% with σ_test = 0.50 (Table 1), with FPI outperforming cLOINN-random slightly. When σ_test is increased from 0.50 to 2.00, the L² relative errors are smaller than 10%. We show a test example for σ_test = 0.50 and the prediction using FPI and cLOINN-random approaches in Fig. S6c.

Analyzing the effect of local domain size for the 2D nonlinear Poisson equation

Next, we investigate the effect of the size of the local domains with a 2D nonlinear Poisson equation

$$\nabla ((1+{u}^{2})\nabla u)=10f(x,y),\quad x\in [0,1],y\in [0,1]$$

with zero Dirichlet boundary conditions. We aim to learn the solution operator ${\mathcal{G}}:f\mapsto u$ for a class of f  = f₀  + Δf with ${f}_{0}(x,y)=x\sin (y)$.

We choose two different local domains, including a simple local domain with 5 nodes (Fig. 2e)

$${\widetilde{{\mathcal{G}}}}_{1}:\{u(x,y-\Delta y),u(x-\Delta x,y),u(x+\Delta x,y),u(x,y+\Delta y),f(x,y)\}\mapsto u(x,y)$$

and a larger domain with 9 nodes (Fig. 2f)

$${\widetilde{{\mathcal{G}}}}_{2}:\{u(x,y-\Delta y),u(x-\Delta x,y),u(x+\Delta x,y),u(x,y \\+\Delta y),u(x-\Delta x,y-\Delta y),u(x-\Delta x,y+\Delta y)\},\\ \{u(x+\Delta x,y-\Delta y),u(x+\Delta x,y+\Delta y),f(x,y)\}\mapsto u(x,y).$$

For this example, the numerical solution is obtained via the finite element method.

The training dataset ${\mathcal{T}}$ with one data point $({f}_{{\mathcal{T}}},{u}_{{\mathcal{T}}})$ is shown in Fig. 6a. We compare the results of FPI and cLOINN-random using ${\widetilde{{\mathcal{G}}}}_{1}$ and ${\widetilde{{\mathcal{G}}}}_{2}$ (Table. 1). FPI performs well, and the L² relative errors achieve less than 2% when σ_test = 0.05. Compared to FPI, the performance of cLOINN-random is worse but still acceptable when σ_test is small, and the errors achieve less than 5% when σ_test = 0.05. (Fig. 6b). For both FPI and cLOINN-random, the local solution operator ${\widetilde{{\mathcal{G}}}}_{2}$ outperforms ${\widetilde{{\mathcal{G}}}}_{1}$ for σ_test = 0.05, 0.10, and 0.20. An example of the prediction using FPI and cLOINN-random approaches with ${\widetilde{{\mathcal{G}}}}_{1}$ is shown in Fig. 6c.

Fig. 6: Learning the 2D nonlinear Poisson equation.

a The training data includes a random ${f}_{{\mathcal{T}}}$ generated from GRF and the corresponding solution ${u}_{{\mathcal{T}}}$. b The convergence of L² relative errors of FPI and cLOINN-random for various test cases using ${\widetilde{{\mathcal{G}}}}_{1}$ and ${\widetilde{{\mathcal{G}}}}_{2}$. c Prediction example of different approaches for a test case with σ_test = 0.05. d Local domains with 5, 9, 13, 25, 49, and 81 nodes and corresponding solution operators. e L² relative errors of FPI for σ_test = 0.20 for different local domain sizes, compared to the baseline error between u and u₀ (black-dashed line). f Wall clock time (second) per epoch for training local solution operators for different domain sizes.

To deepen our understanding, we extend our analysis to four additional different local domains with 13, 25, 49, and 81 nodes, in addition to those with 5 and 9 nodes (Fig. 6d), and conduct experiments for σ_test = 0.20 using FPI. Definitions of the local solution operators are detailed in Supplementary Section S8. Increasing the sizes of local domains potentially improves the accuracy of FPI, though improvements tend to plateau for domains larger than 49 nodes (Fig. 6e and Supplementary Table S4). However, the training time for the local solution operator increases with the number of nodes (Fig. 6f and Supplementary Table S4). This suggests that employing a local domain with more nodes can enhance accuracy, whereas a smaller domain may benefit from simpler implementation and reduced training times.

Learning the solution operator for a PDE defined in an irregular domain

Besides the regular domain, we also consider a 2D nonlinear Poisson equation in a square domain with a circle cutout of radius 0.2 (Fig. 7)

$$\nabla ((1+{u}^{2})\nabla u)=100f(x,y)$$

with zero Dirichlet boundary conditions. We learn the solution operator ${\mathcal{G}}:f\mapsto u$ for a class of f = f₀ + Δf with ${f}_{0}(x,y)=x\sin (y)$.

Fig. 7: Learning the 2D nonlinear poisson equation with a circle cutout.

a The training data includes a random ${f}_{{\mathcal{T}}}$ generated from GRF and the corresponding solution ${u}_{{\mathcal{T}}}$. b The convergence of L² relative errors of FPI and cLOINN-random for various test cases. c Prediction example of different approaches for a test case with σ_test = 0.05. d, e Test the method in a new geometry by using the local solution operator trained on the previous geometry. d The convergence of L² relative errors of FPI and cLOINN-random for test cases with σ_test = 0.10 for a smaller circle cutout. e Prediction example of different approaches for a test case.

We choose a simple local domain

$$\widetilde{{\mathcal{G}}}:\{u(x,y-\Delta y),u(x-\Delta x,y),u(x+\Delta x,y),u(x,y+\Delta y),f(x,y)\}\mapsto u(x,y)$$

with 5 nodes (Fig. 2e). For this example, the numerical solution is obtained using the finite element method. The domain is discretized using triangular elements, and the maximum size is 0.005.

The training dataset ${\mathcal{T}}$ is shown in Fig. 7a. When σ_test = 0.05, the L² relative errors achieve less than 3%. Also cLOINN-random performs slightly better than FPI while FPI converges faster, as the values of cLOINN-random solution near the circle boundary are more accurate. The comparison between these two is shown in Fig. 7b, and one example is shown in Fig. 7c. We have shown that our approaches can work well in this complex geometry.

Generalizing to a different geometry

To verify the generalization of our method, we now test the same Poisson equation in a square domain with a smaller circle cutout of radius 0.18. We use the same local solution operator $\widetilde{{\mathcal{G}}}$ trained from the previous geometry with larger circle cutout. When σ_test = 0.10, the L² relative errors achieve less than 5% for FPI and cLOINN-random. The convergences of FPI and cLOINN-random are shown in Fig. 7d, and one prediction example is shown in Fig. 7e. This demonstrate that our method can generalize well on a smaller circle cutcut.

Learning the solution operator for a PDE system

We consider a diffusion-reaction system in porous media (x ∈ [0, 1], t ∈ [0, 1])

$$\frac{\partial {C}_{A}}{\partial t}=D\frac{{\partial }^{2}{C}_{A}}{\partial {x}^{2}}-{k}_{f}{C}_{A}{C}_{B}^{2}+f(x),\quad \frac{\partial {C}_{B}}{\partial t}=D\frac{{\partial }^{2}{C}_{B}}{\partial {x}^{2}}-2{k}_{f}{C}_{A}{C}_{B}^{2}$$

with initial conditions C_A(x, 0) = C_B(x, 0) = e^−20x and zero Dirichlet boundary conditions, where D = 0.01 is the diffusion coefficient, and k_f= 0.01 is the reaction rate. The solution operator is ${\mathcal{G}}:f\mapsto ({C}_{A},{C}_{B})$. Here we predict the solutions C_A and C_B for a new $f={e}^{-\frac{{(x-0.5)}^{2}}{0.05}}+\Delta f$.

Since there are two outputs for this case, we consider the local solution operator (Fig. 2d)

$$\widetilde{{\mathcal{G}}}:\{{C}_{A}(x,t-\Delta t),{C}_{A}(x-\Delta x,t),{C}_{A}(x+\Delta x,t),{C}_{B}(x,t-\Delta t),{C}_{B} \\ (x-\Delta x,t),{C}_{B}(x+\Delta x,t),f(x,t)\}\mapsto ({C}_{A}(x,t),{C}_{B}(x,t)).$$

We show the training dataset ${\mathcal{T}}$ in Fig. 8a.

Fig. 8: Learning the diffusion-reaction system in porous media.

a The training data includes a random ${f}_{{\mathcal{T}}}$ generated from GRF and the corresponding solution ${C}_{A,{\mathcal{T}}}$ and ${C}_{B,{\mathcal{T}}}$. b The convergence of L² relative errors of FPI and cLOINN-random for various test cases of C_A and C_B. c Prediction example of different approaches for a test case with σ_test = 0.3.

In this experiment, FPI works well, and the L² relative errors achieves less than 1% when σ_test = 0.10. FPI performs better than cLOINN-random (Table 1). When σ_test = 0.10, 0.30, the accuracy of cLOINN-random is smaller than 10%. It is shown that, in this example, FPI is not only more accurate than cLOINN-random, but also converge faster (Fig. 8b). To better understand why cLOINN performs poorly sometimes, we observe that, compared with higher-error test case, for the case with low prediction error, the training loss decreases more significantly and usually reaches a lower loss value by the end of training (Supplementary Fig. S7). This observation indicates that the neural network-based approach may encounter training difficulties, which leads to poor performance for certain test cases. Given the the similarity between our neural network-based approaches to physics-informed neural networks, the training difficulties may due to optimization difficulties associated with the PDE constraint and the spectral bias^42,43. We show examples of C_A and C_B prediction using FPI and cLOINN-random approaches in Fig. 8c.

Application in spatial infection spread through heterogeneous populations

Problem setup

We present an application of our one-shot learning method to solve the spread of infectious diseases influenced by local spatio-temporal factors. Infectious diseases remain a major public health concern worldwide, particularly in the post-era of COVID-19. Mathematicians and epidemiologists have studied the the dynamics of infectious diseases and the spreading of the virus over the population. The SIR epidemic model⁴⁴ is widely used to model the spread of infectious diseases. The population is divided into three disjoint classes: susceptible (S), infected (I), and recovered (R), where susceptibles can be infected by those already infected and subsequently recover, and recovered class are immune to the disease but lose immunity over time. Various classes of individuals and their spatial interactions have been studied actively, and PDE models are used to represent different scales and interactions within the population^45,46,47. Specifically, we consider the PDE model in⁴⁷ (x ∈ [0, L], t ∈ [0, T]):

$$\frac{\partial S}{\partial t}=-D(x)\beta S\frac{{\partial }^{2}I}{\partial {x}^{2}}-\beta SI,\quad \frac{\partial I}{\partial t}=D(x)\beta S\frac{{\partial }^{2}I}{\partial {x}^{2}}+\beta SI-\gamma I,$$

where D(x) reflects the spatially variable daily travel rate due to environmental factors, β is the daily infection rate, and γ is the recovery rate of infected individuals. The recovered class R can be computed from S and I based on the population conservation in a closed system. The details of the problem setup is in Supplementary Section S10.

One-shot learning is required for this practical problem

For an infectious disease, collecting comprehensive data is challenging and time-consuming. As the disease spreads, the underlying dynamics are likely to change due to mutations in the pathogen, changes in population behavior, or public health interventions like social distancing and lockdowns. These changes affect the model parameter diffusion coefficient D(x), which captures population movement patterns. Our proposed one-shot learning approach is particularly suitable for this scenario, requiring only a single data pair-for example, current travel patterns reflected in D(x) along with the susceptible S(x, t) and infected I(x, t) populations. A model trained from this data in one setting could be quickly adapted to predict the spread for another D(x). Unlike traditional modeling approaches that generally require large datasets for training, our proposed one-shot learning method enables predictions even with limited data, which can be valuable for effective epidemic response, especially in the early stages.

One-shot learning method setup and results

We then present the setup and results of our one-shot learning method. We use L = 1, T = 10, γ = 0.2 and β = 0.8 to test our method. The initial conditions are $S(x,0)=1-0.5\cos (4\pi x)$, representing the susceptible population influenced by factors like population density or social behaviors, and $I(x,0)=0.3{e}^{\frac{-{(x-2/3)}^{2}}{0.045}}$, modeling an initial localized infection (Fig. 9a). The zero Neumann boundary conditions ensure no flux. We aim to learn a solution operator ${\mathcal{G}}:D\mapsto (S,I)$ and predict the solutions S and I for a new $D=0.001{e}^{\frac{-{(x-0.5)}^{2}}{0.08}}+0.001\Delta D$. We show the training dataset $({D}_{{\mathcal{T}}},{S}_{{\mathcal{T}}},{I}_{{\mathcal{T}}})$ in Fig. 9b.

Fig. 9: Learning the infection spread of susceptible (S) and infected (I) populations.

a The initial conditions of S and I. b The training data includes a random ${f}_{{\mathcal{T}}}$ generated from GRF and the corresponding solutions ${S}_{{\mathcal{T}}}$ and ${I}_{{\mathcal{T}}}$. c Prediction examples of FPI and cLOINN-random for a test case with σ_test =  0.3.

We use the local solution operator $\widetilde{{\mathcal{G}}}$ defined in Supplementary Section S10, and test the method for new cases with σ_test = 0.10, 0.15, 0.20, 0.30. In all cases, FPI works well, and the L² relative errors achieves below 3% (Table 1). cLOINN-random performs slightly worse than FPI. We show one example of S and I prediction using FPI and cLOINN-random approaches in Fig. 9c.

Discussion

Learning solution operators for partial differential equations (PDEs) usually requires a large amount of training data. In this study, we propose a one-shot method to learn solution operators from only one PDE solution, which remains underexplored and can potentially address the challenge of data acquisition in real applications. Considering small local domains instead of the entire computational domain of the PDE, we define and learn a local solution operator, which is then leveraged to predict a new solution via a fixed-point iteration (FPI) or local-solution-operator informed neural networks. Our method accommodates both unstructured data and grid data when training LOINN and cLOINN model.

The effectiveness of our method is demonstrated in various examples, including 1D/2D equations, linear/nonlinear equations, advection equation in which f is an coefficient, diffusion-reaction system in porous media, and complex domain with a cutout. Among the proposed approaches, FPI and cLOINN-random are demonstrated to have comparable good performance across all test cases. The neural network-based approaches, LOINN and cLOINN, allow greater flexibility on complex domains and random point locations, with cLOINN generally outperforming LOINN in most situations and converges faster. Our experiments show that using randomly sampled point locations can improve the accuracy. Additionally, we show the effect of different local solution operators, and we find including more auxiliary points improves the performance. Our method has proven effective even on very coarse grids or a small number of point locations.

The limitation of our method lies in its diminished accuracy when predicting solutions divergent from the known solution, which is an inherent challenge arising from the constraints of utilizing minimal data. In the future, we will carry out further validation on PDEs with different boundary conditions or complex domains, and improve our approaches for better accuracy, faster convergence and better computational efficiency. Moreover, our method can potentially integrate with graph neural networks (GNN)^48,49 to construct local graphs and train the local solution operator, and then combined it with FPI, LOINN or cLOINN for learning the solution operator. As noted in the introduction, our approach can also be viewed as a form of PDE discovery or representation learning. Incorporating differential terms as additional features of the local solution operator is an interesting direction^38,39. Finally, the theoretical analysis on data-efficiency remains an open and valuable problem^50,51.

Methods

In the following sections, we delve into the details of each step in our one-shot learning method for PDE solution operators.

Selecting a local domain and a local solution operator

In this section, we elaborate on the first two steps of our method. To begin with, we consider a virtual background equispaced mesh. This is not a real mesh for the solution prediction in the computational domain; instead, it is a virtual mesh that guides us to select a local domain. Taking a two-dimensional problem as an example, this local equispaced mesh has mesh size Δx₁ and Δx₂, where x₁ and x₂ are spatial or temporal dimensions corresponding to the PDE. On this local mesh, we then sketch a polygon with mesh nodes positioned on its edges or within the interior of the polygon. We denote the set of these mesh nodes as $\tilde{\Omega }$, and a general choice of $\tilde{\Omega }$ is represented by black nodes in Fig. 2a (left).

In the second step, we choose a location x^* from the local domain $\tilde{\Omega }$ as the target node, and the remaining nodes surrounded x^* are denoted as auxiliary points ${\tilde{\Omega }}_{{\rm{aux}}}=\{{\bf{x}}\in \tilde{\Omega }| {\bf{x}}\ne {{\bf{x}}}^{*}\}$. We define a local solution operator to predict the PDE solution at x^* from the information of auxiliary points and the PDE condition

$$\tilde{{\mathcal{G}}}:\left(\{u({\bf{x}}):{\bf{x}}\in {\tilde{\Omega }}_{{\rm{aux}}}\},\{f({\bf{x}}):{\bf{x}}\in \tilde{\Omega }\}\right)\mapsto u({{\bf{x}}}^{*}),$$

which is learned by a neural network. The intuition of this definition is that, for a well-defined PDE, if we know the solution u at the boundary of $\tilde{\Omega }$ and f within $\tilde{\Omega }$, then the solution u at x^* inside $\tilde{\Omega }$ is determined. We find that only using the value of f at x^* is sufficient, so in this study the local solution operator is chosen as

$$\tilde{{\mathcal{G}}}:\left(\{u({\bf{x}}):{\bf{x}}\in {\tilde{\Omega }}_{{\rm{aux}}}\},f({{\bf{x}}}^{*})\right)\mapsto u({{\bf{x}}}^{*}).$$

Learning a local solution operator

To train the local solution operator $\tilde{{\mathcal{G}}}$, we construct a training dataset from ${\mathcal{T}}=\{({f}_{{\mathcal{T}}},{u}_{{\mathcal{T}}})\}$. To make the network generalizable to different f, the selection of ${f}_{{\mathcal{T}}}$ in ${\mathcal{T}}$ is important. In our study, we use ${f}_{{\mathcal{T}}}(x)={f}_{{\rm{random}}}(x)+{f}_{0}(x)$, where ${f}_{{\rm{random}}}(x) \sim {\mathcal{GP}}(0,k({x}_{1},{x}_{2}))$ is randomly sampled from a mean-zero GRF with the covariance kernel $k({x}_{1},{x}_{2})={\sigma }_{{\rm{train}}}^{2}\exp (-\parallel {x}_{1}-{x}_{2}{\parallel }^{2}/2{l}_{{\rm{train}}}^{2})$ (σ_train: amplitude; l_train: length scale). The randomness in f_random(x) is used to induce a more “diverse” training dataset so that we can extract more information from it.

Since $\tilde{{\mathcal{G}}}$ learns for the small local domain $\tilde{\Omega }$, to generate many input-output pairs for training $\tilde{{\mathcal{G}}}$, we have two approaches. In the first approach, we have a structured equispaced global mesh $\hat{\Omega }$ with mesh size Δx₁ and Δx₂ (Fig. 2g). Note that the mesh size of the global mesh matches the local mesh. We place $\tilde{\Omega }$ at different locations of the global mesh $\hat{\Omega }$, and each placement would lead to one input-output data pair. In the second approach, we randomly sample different locations in Ω (Fig. 2h). Similarly, each location leads to one data point. These approaches make it possible to learn a network from only one PDE solution by converting one-shot learning to classical learning. For example, for a PDE in a spatio-temporal domain, we may choose the local domain Fig. 2d and generate a dataset

$${\mathcal{D}}_{\mathcal{T}}=\left\{ \underbrace{\left[u(x,t-{{\Delta}} t),u(x-{{\Delta}} x,t),u(x+{{\Delta}} x,t),f(x,t)\right]}_{{\rm{Input}}},\underbrace{u(x,t)}_{{\rm{Output}}}\right\}_{(x,t)},$$

where (x, t) is sampled from the aforementioned approaches. We discuss the reasoning of using neural networks to learn the local solution operators in Supplementary Section S3.

Since the inputs of the neural network $\widetilde{{\mathcal{G}}}$ also include the solution to be predicted, we cannot predict solution for a new f = f₀ + Δf directly. To address this issue, we propose the following three approaches to predict the solution of a new f, whose computational efficiency and prediction accuracy depend on the choice of $\tilde{{\mathcal{G}}}$.

Prediction via a fixed-point iteration (FPI)

In the step 4 of the one-shot learning method, we first propose a mesh-based fixed-point iteration approach (Algorithm 1; Fig. 1, Approach 1). The solution is only considered on a equispaced global mesh $\hat{\Omega }$ with the same mesh size Δx₁ and Δx₂ that matches the local mesh $\tilde{\Omega }$. Because f is close to f₀, we use ${u}_{0}={\mathcal{G}}({f}_{0})$ as the initial guess of u, and then in each iteration, we apply the pre-trained $\tilde{{\mathcal{G}}}$ at the current solution as the input to get a updated solution. When the solution is converged, u and f are consistent with respect to the local operator $\tilde{{\mathcal{G}}}$, and thus the current u is the solution of our PDE.

Algorithm 1

Predict the solution $u={\mathcal{G}}(f)$ for a new f via FPI

Prediction via a local-solution-operator informed neural network

We also propose a neural network-based approach LOINN (Fig. 1, Approach 2), which is meshfree and has more flexibility to handle boundary/initial conditions and training points inside the computational domain. We construct a neural network with parameters θ that takes the coordinates x as the input, and output the approximated solution $\hat{u}({\bf{x}};\theta )$. To train the network, we define the loss function that constrains $\hat{u}$ to satisfy $\widetilde{{\mathcal{G}}}$ at some local domains:

$${{\mathcal{L}}}_{{\rm{PDE}}}(\theta )=\frac{1}{| {{\mathcal{T}}}_{l}| }\sum _{{\bf{x}}\in {{\mathcal{T}}}_{l}}{\left(\hat{u}({\bf{x}};\theta )-\tilde{{\mathcal{G}}}\left(\{\hat{u}(\xi ):\xi \in {\tilde{\Omega }}_{{\rm{aux,}}{\bf{x}}}\},f({\bf{x}})\right)\right)}^{2},$$

(2)

where ${{\mathcal{T}}}_{l}$ is a set of point locations in the domain. The points can be sampled on a global mesh or randomly sampled (Hammersly sequence used in this study). For the boundary and initial condition in Eq. (1), similar to physics-informed neural networks^2,3, we define another loss function

$${{\mathcal{L}}}_{{\rm{IC/BC}}}(\theta )=\frac{1}{| {{\mathcal{T}}}_{b}| }\sum _{{\bf{x}}\in {{\mathcal{T}}}_{b}}\parallel {\mathcal{B}}(\hat{u}({\bf{x}};\theta ),{\bf{x}}){\parallel }_{2}^{2},$$

(3)

where ${{\mathcal{T}}}_{b}$ is a set of point locations on the boundary or initial domain. Then the total loss is

$${\mathcal{L}}(\theta )={{\mathcal{L}}}_{{\rm{PDE}}}(\theta )+{{\mathcal{L}}}_{{\rm{IC/BC}}}(\theta ).$$

(4)

In some cases, the initial and boundary conditions can be directly imposed by modifying the network architecture³², which eliminates the necessity of the loss ${{\mathcal{L}}}_{{\rm{IC/BC}}}$.

To improve the performance of LOINN, we develop LOINN with correction (cLOINN). Specifically, we modify the network architecture by using a last layer of adding u₀ (Fig. 1, Approach 3), and then the solution is $\hat{u}({\bf{x}})={\mathcal{N}}({\bf{x}})+{u}_{0}({\bf{x}})$, where ${\mathcal{N}}({\bf{x}})$ is the original neural network output.