Connectome-constrained ligand-receptor interaction analysis for understanding brain network communication

Abstract

Both diffusion magnetic resonance imaging and transcriptomic technologies have provided unprecedented opportunities to dissect brain network communication, offering insights from structural connectivity and signaling molecules separately. However, incorporating these complementary modalities for characterizing the interregional communication remains challenging. By simplifying the communication processes into an optimal transport problem, which is defined as the ligand-receptor expression coupling constrained by structurally-derived communication cost, we develop a method called CLRIA (connectome-constrained ligand-receptor interaction analysis) to infer a low-rank representation of ligand-receptor interaction-mediated communication networks. To solve the proposed optimization problem, the block majorization minimization algorithm is adopted and proven to converge globally. We benchmark CLRIA on simulated and published data, validating its accuracy and computational efficiency. Subsequently, we demonstrate the CLRIA’s utility in evaluating communication strategies and asymmetric communication using its solution. Furthermore, CLRIA-derived communication patterns successfully decode brain state transitions. Overall, our results highlight CLRIA as a valuable tool for understanding complex communication in the brain.

Introduction

Understanding how patterns of neural signaling through the structural backbone support brain function is the central goal of network neuroscience^1,2. The brain can be conceptualized as a network of neural units interacting on multiple spatiotemporal scales^3,4. Interregional signal propagation through structural connections can be defined as brain network communication (BNC)^1,2, which can trigger synchronous activity between brain regions and support complex cognitive functions. By abstracting biological neural signaling to network communication dynamics, the brain network communication model (BNCM) offers a flexible approach to modeling interactions between neural elements^2,5. Despite the advantages of interpretability and tractability, the simplification of signaling molecules in these models poses barriers to elucidating the uncharacterized mechanisms underlying connectome communication^1,2,6. A major form of BNC is mediated by ligand-receptor pairs (LR pairs)⁷. Their interregional interactions along axons⁸ constitute communication networks that enable the integration of information, the regulation of regional activities, and the orchestration of cognitive functions^9,10,11. Yet, how to model the coupling between structural information and molecular expression to improve our understanding of BNC remains challenging.

The recent emergence of sequencing technology has enabled the quantification of ligands and receptors at unprecedented genomic coverage. Communication strength can be estimated mainly through an explicitly defined score function based on ligand and receptor levels^7,12,13, such as the product of these levels¹². Spatial transcriptomics¹⁴ also provides information about the distance between the senders and receivers in two-dimensional slices to decipher interareal communication based on a spatial proximity graph^15,16, spatial variance component analysis^17,18, or collective optimal transport¹⁹, facilitating a more profound comprehension of the inherent signaling pathways and morphological organization in tissues. Neural-specific communication analysis tools have also been developed^20,21,22 to delineate neurotransmitter signaling at the systems level. However, the application of spatially proximal constraints to reduce false positives in existing cell communication methods may not be appropriate for characterizing BNC. In fact, the existence of fiber tracts allows for both proximal and distal communication within the brain network. Neurons are capable of extending axons between areas, ensuring the efficient transfer of signaling molecules^23,24. The aberrant expression of ligands or receptors can alter interregional communication, which in turn can lead to cognitive impairment and neurological disorders^11,25,26,27. These findings suggest the existence of intrinsic coupling between the structural backbone and the expression of LR pairs. Therefore, to model their coupling, a method that employs a connectome-based measure to guide interregional ligand-receptor interaction (LRI) is needed.

Based on structural connectivity (SC) evaluated using fiber tracking, a series of BNCMs have been developed to quantify interregional communication efficiency based on hypothesized signal transmission strategies^2,5. These models can be categorized into three main families²: (1) Routing protocols, which model information transmission along single and selective accessed paths (e.g., shortest path routing); (2) Diffusion processes, which allow a signal to spread simultaneously along multiple network fronts; (3) Parametric models, which introduce tunable parameters to combine elements of routing and diffusion. Notably, recent work showed that the topology of these models generates asymmetric communication strength, which is significantly associated with the directionality of effective connectivity²⁸ and can explain the causal propagation of focal stimuli using intracranial EEG recordings⁵. Also, these models showed a significant correlation with energy cost during trans-hierarchical brain state transitions, indicating a more efficient signaling flow from lower to higher hierarchical regions²⁹. All these results provide evidence that the directionality of neural signaling can be encoded in communication models. Therefore, adopting BNCM to guide the reconstruction of LRI-mediated communication network is quite compelling and beneficial for elucidating the intrinsic association between communication strategy and the regional expression of ligands and receptors.

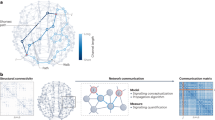
In the current study, we developed CLRIA (connectome-constrained ligand-receptor interaction analysis), which combines diffusion MRI with transcriptome data to infer LRI-mediated communication networks. We extended the canonical optimal transport framework³⁰ to be compatible with multiple LR pairs collectively. In addition, low-rank regularization was introduced to a tensor-structured transport plan for computational efficiency and robustness^{31,32,33,34,35} as well as for latent communication pattern discovery^36,37,38,39. A block majorization minimization (BMM) algorithm was implemented and proven to be globally convergent. Linear time complexity with respect to brain region can be achieved when the BNCM matrix can be factored. After evaluating CLRIA’s efficacy in recovering the latent pattern of the LRI-mediated communication networks through simulated and published data, CLRIA was applied to analyze the preference of BNC policy in light of the energy cost. Next, the extent of asymmetric communication^28,29 between region pairs was estimated to investigate the association between brain organization and trans-hierarchical signaling flow. Finally, using an unbalanced optimal transport (UOT) regression model⁴⁰ constructed on latent communication patterns, we elucidated the brain state transition during working memory (Fig. 1).

Fig. 1: Overview of CLRIA.

A CLRIA takes the communication model (M), the regional expression of ligands (L) and receptors (R) and the coupling matrix of ligand (T_L) and receptor (T_R) as input. The communication model is constructed based on structural connectivity data from diffusion MRI. The ligand and receptor expressions were calculated by the geometric mean of the composing genes. The coupling matrices record the composition relationship between LR pairs and the corresponding ligand or receptor from the ligand receptor database. CLRIA, connectome-constrained ligand-receptor interaction analysis. B CLRIA combines both diffusion MRI and transcriptomic technology to infer the low rank representation of interregional communication strength mediated by each LR pair. C Three measures produced by CLRIA for downstream analysis. (i) CLRIA distance is the Frobenius inner product between the communication model (M) and $A{\mbox{diag}}\left({C}^{T}{\mathbb{1}}\right){B}^{T}$. (ii) Transport plan is a tensor reconstructed by the tensor factor $A,{B},{C}$. (iii) Communication pattern (CP) is defined as the outer product of the corresponding columns of sender and receiver loading matrix. The contribution of LR pairs is defined as the corresponding column of the ligand-receptor (LR) loading matrix. D Communication strategy preference analysis along the diffusion to routing spectrum of the communication model. E Schematic of the asymmetric signaling analysis. (i) Trans-hierarchical asymmetric signaling of region pairs. (ii) Graph spectral analysis of an LR pair. F Summary of the methods to assess brain state transition. For further mathematical details, please see the “Methods” section.

Results

Overview of CLRIA

Overall, CLRIA (connectome-constrained ligand-receptor interaction analysis) provided a biologically meaningful approach for annotating microscale LRI information to the macroscale brain network⁶. Ligands and receptors are major signaling molecules during the communication process in the brain network. In the context of a brain network comprising $N$ regions, given the regional expression of the $i$^th pair of ligand and receptor (${l}_{i}\in {{\mathbb{R}}}^{N},\,{r}_{i}\in {{\mathbb{R}}}^{N}$), the communication process can be viewed as the transport of a ligand to its cognate receptor constrained by the (unit) transport cost ($M\in {{\mathbb{R}}}^{N\times N}$) derived from the BNCM. The resulting transport plan (${{{{\mathcal{P}}}}}_{i}\in {{\mathbb{R}}}^{N\times N}$) was designed to capture the transport/interacted abundance between each region-pair, reflecting the communication strength mediated by the LR pair. By summing the actual cost between each region pair, we obtained the total transport cost or energy consumption of transporting the $i$^th LR pair. Since the brain is an energy-efficient system, our goal was to minimize the total transport cost, which resulted in an optimal transport problem. The main difference from the canonical one is that we have multiple LR pairs that need to be optimized collectively. To solve the problem, we simply added up the total transport costs of all the LR pairs with the same weight, meaning that each LR pair was treated equally. The formulation of the initial problem is as follows:

$${\min }_{{{\mathcal{P}}}\in \Pi \left(L,R\right)}F\left({{\mathcal{P}}}\right):={\sum }_{i=1}^{\left|I\right|}{\left\langle M,{{{\mathcal{P}}}}_{i}\right\rangle }_{F}$$

(1)

where $\left|I\right|$ is the total number of LR-pairs, ${\left\langle \cdot,\cdot \right\rangle }_{F}$ is the Frobenius inner product, $L=[{l}_{1},\cdots,\,{l}_{\left|I\right|}]\in {{\mathbb{R}}}^{N\times \left|I\right|}$ and $R=[{r}_{1},\cdots,\,{r}_{\left|I\right|}]\in {{\mathbb{R}}}^{N\times \left|I\right|}$ are the regional expressions of the ligands and receptors, ${{{\mathcal{P}}}}{{{\mathscr{\in }}}}{{\mathbb{R}}}_{+}^{N\times N\times \left|I\right|}$ is the transport plan for all LR pairs, and $\Pi \left(L,R\right)=\left\{{{{\mathcal{P}}}}{{{\mathscr{\in }}}}{{\mathbb{R}}}_{+}^{N\times N\times \left|I\right|}| {{{{\mathcal{P}}}}}_{i}{{\mathbb{1}}}_{N}={l}_{i},{{{{\mathcal{P}}}}}_{i}^{T}{{\mathbb{1}}}_{N}={r}_{i},i=1,\,\cdots,\left|I\right|\right\}$ is the mass conservation constraint set.

Direct engagement with the above problem appears to be suboptimal for both biological and computational considerations. First, in a biological system, such a rigid mass conservation constraint may be empirically unjustified and operationally untenable given transcriptional measurement variability (e.g., technical noise). We used Kullback-Leibler (KL) divergence to relax this hard constraint according to UOT theory⁴¹. Second, promiscuous binding behavior, which means that single ligands may interact with multiple receptors and vice versa, necessitates the quantification of interaction abundance for each LR pair (rather than merely regional total expression). However, this is unattainable with current sequencing technology. To address this practical problem, we posited that the total interaction abundance of individual ligands or receptors would approximate its regional expression. Third, the tensor structure of the transport plan ${{{\mathcal{P}}}}$ makes direct optimization inefficient because of both computational and memory demand. The established tensor decomposition analysis frameworks had successfully disentangled biologically relevant patterns for multidimensional data^36,37,38,39, so we impose a low-rank constraint on transport plan ${{{\mathcal{P}}}}$. These modifications yielded the final optimization problem (Fig. 1A, B, See Supplementary Material for derivations):

$$\begin{array}{c}{\min }_{\left(A,B,C\right)\in \Pi \left(r\right)}F\left(A,B,C\right){{\rm{:=}}}{\left\langle M,A{{\mbox{diag}}}\left({C}^{T}{{\mathbb{1}}}_{\left|I\right|}\right){B}^{T}\right\rangle }_{F}-\varepsilon {{\mbox{H}}}\left(A,B,C\right)\\+\,{\tau }_{1}{{\mbox{KL}}}\left(A{{\mbox{diag}}}\left({B}^{T}{{\mathbb{1}}}_{N}\right){C}^{T}{T}_{L}\parallel L\right)\\+\,{\tau }_{2}{{\mbox{KL}}}\left(B{{\mbox{diag}}}\left({A}^{T}{{\mathbb{1}}}_{N}\right){C}^{T}{T}_{R}\parallel R\right)\end{array}$$

(2)

where $A,B,C$ are factor matrices decomposed from a transport plan ${{{\mathcal{P}}}}$ via rank $r$ approximation, $\Pi \left(r\right)=\left\{\left(A,B,C\right)\in {{\mathbb{R}}}_{+}^{N\times r}\times {{\mathbb{R}}}_{+}^{N\times r}\times {{\mathbb{R}}}_{+}^{\left|I\right|\times r}\right\}$ is the nonnegative constraint on the factor matrix, ${\mbox{H}}\left(.\right)$ and ${\mbox{KL}}\left(.\parallel .\right)$ are the entropy function and KL divergence, respectively, ${T}_{L}\in {{\mathbb{R}}}^{\left|I\right|\times m}$ and ${T}_{R}\in {{\mathbb{R}}}^{\left|I\right|\times n}$ are binary matrices that record the composition of ligand and receptor for each LR pair, $m$ and $n$ are the number of ligands and receptors, $\varepsilon,{\tau }_{1},{\tau }_{2}$ are the coefficients of the regularization terms.

In general, CLRIA integrates three core inputs (Fig. 1A): (1) the (unit) transport cost $M$ derived from BNCM, (2) the regional expression of each ligand $L$ and receptor $R$ from sequencing data, and (3) the coupling matrices ${T}_{L}$ and ${T}_{R},$ constructed from curated LRI databases. After solving a low-rank UOT problem with multiple LR pairs (problem (2)), CLRIA outputs a low-rank representation of the interregional communication networks mediated by LR pairs (Fig. 1B). In addition, CLRIA provides three measures for downstream analysis (Fig. 1C). First, the CLRIA distance (Fig. 1C (i)) naturally provides a measure that can be used to assess the communication strategy in the brain network by replacing the transport costs derived from different BNCMs (Fig. 1D). Second, by reconstructing the transport plan from the factor matrices $A,B,C$ (Fig. 1C (ii)), the asymmetric property of brain communication can be investigated from a molecular perspective (Fig. 1E). Finally, the outer product of the corresponding columns of $A$ and $B$ was defined as the communication patterns. Each pattern is characterized by distinct loadings of LR pairs (Fig. 1C (iii)). Based on these patterns, the UOT regression method (see Methods for details) was developed to identify the contributing regions and LR pairs during brain state transitions (Fig. 1F).

Optimization algorithm and comparative analysis

The direct application of existing UOT solvers to problem (2) is infeasible, necessitating a tailored algorithm. The objective function $F\left(A,B,C\right)$ exhibits interaction terms and block convexity, which means that it retains convexity in each variable block when the other blocks remain fixed. To leverage this structure, we implemented a BMM scheme, which sequentially minimizes majorizing surrogate functions within each variable block while keeping the others fixed, to solve problem (2) (see Methods and Supplemental Material for derivation). To establish theoretical guarantees, we applied Zangwill’s theorem⁴² to prove its global convergence ([Theorem 1] in the Supplementary Material). A further time complexity analysis revealed a linear cost with respect to the number of brain regions under the low-rank assumption of transport costs.

Subsequent to the theoretical analysis, the proposed algorithm was evaluated on simulated data based on an inverse optimal transport (iOT) method. In four synthetic datasets, both entropy-regularized and non-regularized CLRIA demonstrated superior pattern reconstruction accuracy relative to randomized solutions (Fig. S1A). A parameter sensitivity analysis demonstrated pronounced initial value dependence under reduced entropy regularization and increased marginal constraint coefficients (Fig. S1B). Therefore, subsequent evaluations employed two hyperparameter combinations ($\varepsilon=0.01,{\tau }_{1}={\tau }_{2}=1$ and $\varepsilon=0,{\tau }_{1}={\tau }_{2}=1$). Since the existing UOT solvers are incapable of directly retrieving the factor matrix, we integrated nonnegative tensor decomposition with four UOT solvers. The proposed CLRIA demonstrated comparable accuracy while achieving superior computational efficiency compared to current UOT solvers (Fig. S1C, D). These theoretical and experimental results collectively affirm the practical efficacy of the proposed algorithm.

To further evaluate the biological plausibility of CLRIA, especially the advantage of the BNCM constraint, we first conducted a comparative evaluation on real data (Fig. S2) using three approaches: (1) CLRIA with the BNCM constraint, (2) CLRIA with the Euclidean distance constraint, and (3) correlation gene expression⁴³. Building on established evidence that interregional communication fundamentally mediates the synchronization of functional activity⁴⁴, we reasoned that methods that capture more accurate communication patterns should exhibit a stronger concordance with functional connectivity. Therefore, a linear regression model was adopted and the correlation between the fitted value and empirical functional connectivity were used as the evaluation criteria. Critically, the BNCM-constrained implementation demonstrated superior alignment with functional connectivity (Fig. S3A), indicating a more reasonable constraint compared with either distance-constrained paradigms or unconstrained baseline models.

Next, we compared CLRIA with several established cell communication frameworks (CellPhone¹², CellChat^13,45, geometric mean⁴⁶, CellLinker²⁰, MEBOCOST²², and NeuronChat²¹) using identical evaluation methods and criteria. To ensure compatibility with the input requirements of these benchmarked methods, the brain regions were computationally processed as different cell types. Nonnegative tensor decomposition was then implemented on the resulting interregional communication score to obtain the communication patterns (see “Methods”). Consequently, the solution from CLRIA had a consistently higher correlation with functional connectivity (Fig. S3B), exceeding existing methods in recovering the latent communication patterns.

In addition, we compared the performance of CLRIA in inferring the direction of the signals between the cortical and subcortical regions. The subcortical regions are the major source of many neurotransmitters, and peripheral signaling inputs usually undergo essential integration processes within subcortical nuclei prior to entering the cortical functional areas²⁴. Therefore, we reasoned that the subcortical regions act as senders. To investigate whether CLRIA could accurately capture this asymmetric signaling property, the T-statistics between region-pairs were used as asymmetry indices, and then the Kolmogorov-Smirnov test was performed to quantify distributional differences between subcortex-to-cortex and cortex-to-subcortex interactions. Notably, only the result from CLRIA revealed a statistically significant subcortical-to-cortical signaling bias (KS = 0.7831, P < 1.79 × 10⁻³⁰⁸), demonstrating its potential superiority for inferring molecular signaling direction (Fig. S3C). In short, the present results indicated that the CLRIA is a relatively efficient and effective method.

Comparison of CLRIA distance between different BNCMs revealed a preference for a hybrid communication strategy

We first applied CLRIA to evaluate the brain’s biases for different communication strategies, which form the foundation for constructing BNCMs. A series of communication models was previously developed from SC based on simple dynamical processes^1,2, such as diffusion and shortest-path routing. While the significance of these models has been acknowledged and substantiated⁵, the molecular evidence supporting the selection of a specific communication strategy (e.g., diffusion or routing) is still lacking. CLRIA distance (Fig. 1D) can quantify the energy cost of the LR pairs transport based on the (unit) transport cost derived from different BNCMs. In this way, we can evaluate the preference for a communication strategy from the perspective of a minimum energy principle. Here, we focused on a biased random walk model, with the parameter $\lambda$ used to control the ratio between the local and the global information⁴⁷. This approach yielded a continuous spectrum spanning from diffusion to routing communication strategies, with hybrid strategies lying between them.

Inputting the transport costs derived from different BNCMs (rescaling to a fixed sum 10⁴) and the regional expression of all ligands and receptors into CLRIA (Figs. 1A and S2), we obtained an energy cost spectrum of the LR transport, which was quantified by the CLRIA distance. A spin permutation model⁴⁸ was used to adjust for the potential influence of spatial autocorrelation on the CLRIA distance. In contrast to the prior studies showing that the BNCM spectrum approaches a shortest path-length regime at approximately λ = 1⁴⁷, we identified an energy plateau in the intermediate λ-range under several given low-rank conditions (Fig. 2A). Consistent with previous studies showing that the hybrid strategy provides a better explanation for functional connectivity^47,49,50,51, our method provided further molecular evidence to support the use of hybrid communication strategies in the brain.

Fig. 2: Signaling preference of ligand-receptor interactions on a spectrum of communication models ranging from diffusion to routing.

A The normalized values of the CLRIA distance, ligand penalty, receptor penalty, and objective function. The spin model was used to generate the background transport cost to eliminate potential spatial autocorrelations (n = 100). The solid curves are computed by normalizing empirical values with respect to the same measures generated by spin model. The shaded regions along the solid lines denote the 95% value region. The yellow shaded regions indicate the minimum value. B The same as the CLRIA distance in (A) but for each ligand-receptor pair. The Z-score of the normalized CLRIA distance was used for visualization. Neurotransmitter and other ligand receptor pairs are marked. C The distribution of the optimal $\lambda$ that reached the minimal CLRIA distance for each ligand-receptor pair. The yellow shaded regions mark the peak regions. Source data are provided in a Source data file.

Furthermore, the contribution of each LR pair to the CLRIA distance was used to ascertain whether different communication strategies are preferred by different LR pairs. We found that the majority of LR pairs shared a similar plateau value (Fig. 2B), which was also similar to what we found for all the LR pairs combined. Additionally, a consistent communication strategy preference was observed between the neurotransmitter-receptor pairs and the other LR pairs (Fig. 2C), suggesting that a common intrinsic structural constraint dominates the signaling of all LR pairs despite their distinct modes of transport and interactions⁷. Based on all these evidences, a hybrid communication strategy preference seems to exist in terms of the minimum energy cost of LR transport.

Asymmetric signaling of LR pairs is constrained by the functional hierarchy and the SA axis

CLRIA was next applied to investigate the trans-hierarchical asymmetric communication. Neurobiological findings about the connectivity pattern between cortical areas have indicated hierarchical organization⁵². By abstracting biological signaling into network dynamics or brain states, previous studies found that hierarchy can shape asymmetric communication and the bottom-up signaling preference to enable lower energy consumption^28,29. However, the consistency with molecular behaviors remained unclear. The transport plan reconstructed using the CLRIA solution captured the interregional transport/interacted abundance of the LR pairs, revealing directional communication strengths between region pairs. (Fig. 1E (i)). To gain further insight into the trans-hierarchical asymmetric signaling from a molecular perspective, we adopted a region-pair comparison of the transport plan as an asymmetric measure (Fig. 1C, E. Methods section, “Asymmetric and trans-hierarchical signaling”), resulting in a matrix $T\in {{\mathbb{R}}}^{N\times N}$ comprising the pairwise T-statistics. After reordering this matrix based on the cortical hierarchy, the difference between the upper and lower triangle of $T$ indicated a preference for low-to-high or high-to-low trans-hierarchical signaling.

Hierarchy can be defined in different ways⁵³. To further assess the consistency of asymmetric signaling under different definitions of hierarchy, three types of metrics representing distinct neurobiological dimensions of cortex were chosen, following Sydnor et al.⁵⁴: (1) the T1w/T2w ratio, reflecting a microstructural/anatomical gradient reflecting regional differences in myelination and cortical laminar differentiation; (2) the principal gradient of functional connectivity⁵², which captures the brain’s intrinsic functional organization. (3) the SA axis (sensorimotor-association axis⁵⁴), which spans from the primary visual and somatomotor cortices to the transmodal association cortices, and captures the spatial and temporal patterning of cortical maturation proceeds throughout childhood and adolescence⁵⁵. In contrast to the T1w/T2w ratio (KS = 0.0059, P = 8.29 × 10⁻¹; Fig. 3A left), we found that the trans-hierarchical signaling strength from low to high was significantly higher than from high to low along the functional gradient (KS = 0.1055, P = 3.66 × 10⁻²⁷; Fig. 3A middle). As a vital complement to the functional gradient, a similar pattern was found for the SA axis (KS = 0.1121, P = 1.41 × 10⁻³⁰; Fig. 3A right). To adjust for the potential spatial autocorrelation, we repeated the above procedure 10,000 times using a spatial-preserving permutation model⁴⁸ and found that the trans-hierarchical asymmetric communication constrained by the Functional connectivity (FC) gradient and the SA axis were stronger than expected (Fig. 3B). These results indicate that the asymmetric signaling at the molecular level may be more constrained by functional organization and cortical maturation rather than by cortical myelination.

Fig. 3: Trans-hierarchical asymmetric signaling measured by the transport plan.

A The low-to-high hierarchical signaling propagation of the ligand-receptor interactions was more preferred than the high-to-low rank defined by the functional connectivity (FC) gradient (KS = 0.1055, P = 3.66 × 10⁻²⁷) and the sensorimotor-association (SA) axis (KS = 0.1121, P = 1.41 × 10⁻³⁰) rather than anatomical gradient (KS = 0.0059, P = 8.29 × 10⁻¹). Two-sample one-tailed Kolmogorov-Smirnov test was performed. B The trans-hierarchical asymmetric signaling was larger than expected under the spatial-preserving embedding model (10000 surrogates) for the functional connectivity gradient (P = 0.0327) and SA axis (P = 0.0329) but not the anatomical gradient (P = 0.761). Spin test was performed to adjust potential spatial autocorrelations (10000 surrogates). The red solid line is the observed values. Source data are provided in a Source data file.

Furthermore, we investigated the association between hierarchical organization and the underlying communication strategy. By reconstructing the transport plan, we were able to quantify the extent of the trans-hierarchical communication asymmetry, where greater asymmetry indicates closer alignment between interregional LRI patterns and hierarchical architecture. Interestingly, we found that the extent of asymmetry along the functional gradient and SA axis also approached a maximum around $\lambda=1$, which indicates a hybrid communication strategy and near optimal energy cost (Fig. S4). Hierarchical organization is an efficient structural paradigm. These results indicate that trans-hierarchical asymmetric communication is beneficial to both network efficiency and the energy consumption reduction of LR transport.

Asymmetric communication analysis revealed that low harmonic frequency-related LR pairs may contribute to brain development during childhood and adolescence

SC forms the physical substrate for BNC. Connectome harmonics, eigenmodes derived from the structural connectome, represent intrinsic spatial patterns of neural activity propagation. The higher frequencies encode increasingly complex and localized patterns, while the low harmonic frequency components capture the brain pattern of global and slow variations along the main geometrical axes. Connectome harmonics bridge structure and function, offering a mathematical framework for decoding brain communication. Based on the transport plan of a specific LR pair, we can quantify the asymmetric pattern of the LR interaction. We wondered whether each LR-mediated signal aligns with a specific harmonic frequency and, if so, whether we could ascertain the functional role of a specific harmonic frequency.

By projecting the asymmetric pattern onto the connectome harmonic basis, we were able to reveal the harmonic frequency property of a given LR pair. In addition, these ligand-receptor pairs can serve as “annotations” for specific frequencies, thereby resolving the potential functions of the harmonic patterns. Consequently, we classified the LR pairs into three modules according to the dominant frequency of their connectome harmonics (M1: low harmonic frequency, M2: medium harmonic frequency, M3: high harmonic frequency).

We first focused on the high harmonic frequency part and found that most LR pairs exhibited high harmonic frequency dominance (Fig. 4A). Furthermore, to explore the major functional regions of the high harmonic frequency-associated LR pairs, we analyzed their expression on seven intrinsic functional networks (IFNs) (Fig. S5). This analysis revealed high expression in transmodal regions. In combination with earlier analyses of structure-function coupling, which determined that transmodal brain regions necessitate elevated high harmonic frequency components, the present analysis provided a molecular basis for this finding⁵⁶.

Fig. 4: Energy spectrum density reveals low-frequency distributed ligand-receptor genes associated with brain development from childhood to adolescence.

A The energy spectrum density of the regional asymmetric signaling for each ligand-receptor (LR) pair. According to the graph Fourier transformation (GFT), the harmonic components can be computed by Laplacian decomposition from the structural connectome. Gene modules were classified by the dominant harmonic frequency of each LR pairs. Module M1, M2, M2 includes 101, 148, 430 genes, respectively. B Mean expression of genes in different modules and hierarchical regions during brain development. Error bars reflect ±1 standard error. The yellow shaded areas indicate stages in brain development where expression patterns differ obviously. The unimodal regions (n = 4 regions) include primary motor cortex (M1C), primary somatosensory cortex (S1C), primary auditory cortex (A1C), primary visual cortex (V1C). The transmodal regions (n = 4 regions) include dorsolateral prefrontal cortex (DFC), anterior cingulate cortex (MFC), ventrolateral prefrontal cortex (VFC), orbital frontal cortex (PFC). RPKM, reads per kilobase per million mapped reads. C Dot plot showing the enriched GO terms derived using clusterprofiler. Dot sizes are proportional to the ratio of the input genes that are annotated in a term. The dot colors represent the P-values adjusted with a Benjamini-Hochberg correction, as indicated by the colorbar. P-values were obtained from clusterprofiler using Fisher’s exact test. D Direct physical interactions between LR pairs and developmental related genes. These genes contribute to the caudal-rostral gradient and to functional specialization. Source data are provided in a Source data file.

Following the same procedure, we analyzed the low harmonic frequency-associated LR pairs. Interestingly, we found that a small number of low harmonic frequency LR pairs (M1 genes) (Fig. 4A) showed distinct expression patterns in the IFNs within IFNs, with the highest expression occurring in the sensorimotor network (Fig. S5A). To investigate the function of these low harmonic frequency LR pairs, a GO function enrichment analysis was performed and revealed that the genes in this module were involved with brain development processes, such as dendrite and nervous system development, axon regeneration, and neural precursor cell proliferation (Fig. 4C). During childhood, the sensorimotor region constitutes the pole of the first functional gradient, which then shifts to the second during adolescent brain development⁵⁷. This indicates a potential involvement of these genes in the process of brain development during early life. To validate the functional role of the M1 genes, we further investigated the regional expression along different developmental stages using data from the Brainspan atlas⁵⁸. We found that the M1 genes had a higher expression than those in the other two modules, especially during childhood (Figs. 4B and S6). Compared with transmodal regions (such as the frontal region) that descended before childhood, unimodal regions (such as M1C and S1C) exhibited a continuous increase through childhood, followed by a decline from childhood to adolescence. This pattern is coincident with the sequential maturation in the brain⁵⁷. As an important extrinsic mechanism, the thalamus drives cortical development collectively with intrinsic gene expression especially in adolescence⁵⁹. We also found that the thalamic expression of the M1 genes reached the highest point during the adolescent stage (Fig. S6). These results collectively imply a tight interconnection between the M1 genes and regional development.

Ligand receptors usually function in conjunction with downstream molecules. To further investigate the functional pathway of these genes, protein-protein interactions analyses were performed using STRING (Fig. 4D), which is a comprehensive biological database that provides information on known and predicted protein-protein interactions. Direct physical interactions were found between M1 genes and genes contributing to the caudal-rostral gradient and to arealization. Of note, knocking out the transcript factors, CUX1 and SATB2, resulted in aberrant dendritic morphology and in a failure to form the upper-layers’ projections^60,61,62. Taken together, these findings imply the regulatory role of M1 genes, linking the low harmonic frequency mode to brain development during childhood and adolescence.

Communication pattern is tied to the corresponding LR pairs and cognitive function

Prior to further investigating brain state transitions, we examined the biological plausibility of cross-dimensional associations embedded within each LRI-related communication pattern that we derived from a low-rank tensor constraint of CLRIA. For each specified rank constraint, we identified corresponding LRI-related communication patterns (Fig. 1C), each of which represents a tripartite integration of neurobiological dimensions: dominant sending regions, receiving regions, and corresponding LR pairs. Our purpose was to investigate the biological plausibility of the cross-dimensional association derived using low-rank tensor constraints. More specifically, if the principal sending-receiving regions in a given pattern exhibit functional network specificity, the corresponding dominant LR pairs should be enriched in the biological processes aligned with the functional network. Based on this premise, we first linked the sender and receiver of each communication pattern to IFNs (Fig. 5A, Methods section, “Nonnegative tensor component analysis”). In general, IFNs with higher-level cognitive functions are related to a greater number of latent communication patterns. Subsequent analyses of functional network specificity revealed that only Patterns 1 and 18 presented significant specificity (Fig. S6) with respect to vision-related functional networks. Therefore, we focused on the dominant LR pairs in Patterns 1 and 18. As expected, enrichment of the biological processes revealed significant involvement of vision-related terms (Fig. 5B), indicating a tight coupling between cortical regions and the corresponding LR loadings.

Fig. 5: Coupling between communication patterns and ligand-receptor pairs as well as cognitive function.

A The Sankey plot illustrates the source and target region in the intrinsic functional network mediated by different communication patterns. B Dot plot showing the enriched GO terms derived using clusterprofiler. The ligand-receptor pairs were ranked by loadings of corresponding communication patterns and the top 20% were selected. Dot sizes are proportional to the ratio of input genes that are annotated in a term. The dot colors represent the P-values adjusted with a Benjamini-Hochberg correction, as indicated by the colorbar. P-values were obtained from clusterprofiler using Fisher’s exact test. C A Neurosynth meta-analysis was applied to each communication pattern. Source data are provided in a Source data file.

Neurosynth is an automated meta-analysis platform for the large-scale synthesis of neuroimaging data, enabling researchers to map associations between cognitive terms and brain activation patterns across thousands of studies⁶³. To further decode the related cognitive function of each communication pattern, a Neurosynth meta-analysis based on 24 topic terms was adopted^52,64. Consistent with the link between the IFNs and enriched biological processes, Patterns 1 and 18 also showed a strong association with vision-related cognitive functions (Fig. 5C). This also revealed a spectrum of cognitive functions that loaded on communication patterns. Specifically, cognitive functions with similar neural mechanisms, e.g., attention, cognitive control, and working memory, had similar weights on the communication patterns, indicating that the communication patterns we identified were biologically meaningful.

Brain state transitions during working memory can be mediated by the underlying communication patterns

Finally, we employed CLRIA to characterize brain state transitions during working memory. A series of studies have supported the idea that proper working memory execution requires an ordered brain state transition^27,65. Therefore, we centered our investigation on a well-established N-back working memory task measured by fMRI. We defined brain states as spatial pattern estimates associated with activity across the brain regions of interest during the working memory condition (2-back) and the attention control condition (0-back). In light of the biological significance of the communication pattens, we investigated whether they could facilitate the decoding of the brain state transition using the UOT regression model included in CLRIA. In this model, we assumed that the brain state transition depends on a reconfiguration of the weights of the communication patterns. Given that assumption, a brain state transition can be viewed as a state transformation from the initial state to the target state constrained by a linear combination of the communication patterns. More concisely, it is an UOT problem with a parametric transport cost⁴⁰. By solving the weights of the communication patterns and the transport plan between the initial state and the target state, we can obtain the UOT distance (Fig. 6A, see Methods section, “UOT regression”), which quantifies the difficulty of a transition between brain states. Following this framework, we found a significantly longer UOT distance from 0-back to 2-back than the inverse transition after adjusting for age and sex using a repeated-measures ANOVA. This implied that the 2-back state is more difficult to reach (F(1075) = 163.67, P = 5.29 × 10⁻²⁹; Fig. 6B), which is consistent with the fact that 2-back is a cognitively more demanding state. To gain further insight into the transition preference of the communication patterns, we compared the coefficient of the communication patterns using the same type of statistical test (Fig. S8). The result demonstrated that Patterns 14, 15, 7, 5 were more preferred during the forward transition while Patterns 11, 20, 13, 6, 8, 9 were biased toward the reverse transition (Fig. 6C). We named these patterns transition-biased communication patterns, and most of them were mainly involved with the frontal and parietal cortices, in line with previous work showing that the PFC areas are essential for controlling transitions⁶⁶ and shifting tasks^67,68. Moreover, these functions have been shown to be modulated by dopamine receptors^27,69. We, therefore, conducted a comparison of the loading of dopamine-related LR pairs (including DRD1, DRD2, and DRD4) between the transition-biased communication patterns and the other patterns. As expected, DRD2 exhibited a higher rank in the transition-biased communication patterns (Fig. 6D), which is consistent with its role in flexible switching between states²⁷. To further quantify the preference of the LR pairs during the forward and reverse transitions, we combined the LR loadings C and coefficients $\beta$ for each communication pattern (Methods section, “UOT regression”). Following a differential analysis procedure for all the LR pairs, an obviously greater number of LR pairs showed a preference for the transition from 0-back to 2-back (Fig. 6E), which is consistent with the high energy demand of 2-back processing. All these results point to the applicability of LRI-related communication patterns to delineating regional contributions and discovering molecular cues during dynamic cognitive processes in the brain.

Fig. 6: UOT regression reveals brain state transition during working memory.

A Illustration of transport cost construction based on the communication patterns in the unbalanced optimal transport (UOT) regression. This cost was modeled as the linear combination of the communication pattern, and then the exponential transformation was performed. B Transition brain states from the attention control (0 back) condition and the working memory condition (2 back) have longer UOT distances than the reverse direction (F(1075) = 163.767, P = 5.29 × 10⁻³⁵). The repeated-measures analysis of variance (ANOVA) was performed with age and sex as covariates. The dashed red line corresponds to the zero difference between forward and reverse transition. C The Sankey plot illustrates the source and target regions in six lobes of the cortex and subcortex mediated by communication patterns that prefer forward (0 to 2) or reverse (2 to 0) transitions. D The rank percentile of the dopamine-related ligand-receptor (LR) loadings between the top-ranked communication patterns (identified in C, n = 10) and the others (n = 10). DRD1, DRD2 and DRD4 are three types of dopamine receptors. The boxplots represent the first, second (median), and third quartiles, whiskers represent the non-outlier end points, and black dots represent outliers. E Differential preference analysis between the forward and reverse transitions. The paired t-test was used to evaluate the significance of mean differences. P < 0.05 after Benjamini-Hochberg correction was regarded as significant LR pairs during transition. FDR, false discovery rate. Source data are provided in a Source data file.

Discussion

To delineate the LRI-mediated BNC, we developed CLRIA to integrate LRI into a communication model, which is based on optimal transport theory and nonnegative tensor decomposition. We highlight three key features of CLRIA: (1) The inference of interregional LRI was constrained by BNCM, a procedure that is more appropriate than adopting spatial proximity limitation in brain studies. (2) Coupling matrices were introduced to account for the promiscuous binding behavior. (3) A low-rank constraint was added to the transport plan for both computational efficiency^{31,32,33,34,35} and latent communication patterns discovery^36,37,38,39. These features demonstrate CLRIA’s capability to provide biological insights for understanding communication strategy, hierarchical organization, and transition dynamics from the perspective of signaling molecules.

Supported by the small-world property and a negative correlation between the shortest path length and functional interaction, shortest path routing was originally considered to be the principle communication strategy in the brain¹. However, the association with functional connectivity, as well as the causal interareal stimulus propagation recorded by intracranial EEG⁵, was stronger than the shortest path length^70,71 when using diffusion-based measures. This suggests that the diffusion strategy can play an important role in BNC. Therefore, recent work has attempted to combine these opposing viewpoints by using tunable parameters to provide a better explanation for functional connectivity^47,49,50,51. Although the significance of communication models has been acknowledged and demonstrated, the underlying strategy remains an open question. By introducing an additional data modality (LR expression), the CLRIA distance quantifies the energy cost of transporting multiple ligands to conjugate receptors in the brain. By comparing the CLRIA distance of different BNCMs, we showed that the brain network exhibits a bias towards a hybrid communication strategy, which can balance energy cost, signaling efficiency, and information demand². When contrasted with previous findings, our method provides a molecular perspective for comparing and validating communication models.

Next, we focused on the signaling directions between regions, which were previously found to be constrained by cortical hierarchy and exhibited bottom-up preference due to lower energy consumption^28,29. Our findings extended these studies by showing that the asymmetric signaling of LRIs also prefers a low-to-high hierarchical direction. Moreover, we quantified trans-hierarchical communication asymmetry, where greater asymmetry indicates closer alignment between interregional LRI patterns and hierarchical architecture. Our analysis demonstrated that this asymmetry also achieved a maximum around λ = 1, indicating a minimum for the energy cost of LR transport. Meanwhile, hierarchical organization represents an efficient structural paradigm⁷². Collectively, these results imply that the hierarchical organization in the brain not only improves signaling efficiency but also reduces the energy cost of transporting LR pairs. All these results revealed widespread links between microscale LRIs and macroscale topographic organization.

How to decode dynamic brain state transitions is another important aspect of BNC analysis. In contrast to brain network control theory (NCT) that models brain state transition through static SC^27,66, we proposed a UOT regression depending on the combination of LRI-related communication patterns to guide state transitions. Beyond localizing the transition to a specific region, this approach also links potential LR pairs to the process. The UOT distance also emerges as an alternative way to quantify transition difficulty between brain states. Here, we focused on working memory, which is defined as a core cognitive function involving the maintenance, updating, and manipulation of cognitive representations to support more complex tasks. The result well captured the difficult-to-reach property of the 2-back state^66,67,68 and the significant contribution of the frontoparietal regions during transition^27,73,74, as well as the role of D2 in switching between cognitive representations^27,69,75. All these results point to the applicability of LR-related communication patterns to delineating regional contributions and discovering molecular cues during dynamic cognitive processes in the brain, complementing previous work at the microscopic level.

Biologically annotated connectomes represent a valuable way to study neural connectivity in conjunction with the biological features of brain regions⁶. By combining SC and expression of paired signaling molecules in the brain, CLRIA provides a valuable computational method with the potential to delineate the interregional projection of ligands/neurotransmitters, which is experimentally difficult and expensive. With the foreseeable availability of a finer-resolution brain-wide connectome and the matching spatial transcriptome data at the cellular level, the computational efficiency and biologically meaningful solution of CLRIA will also contribute to delineating the cell type specific communication networks. If the data is usable for other species such as, such as flies^76,77, mice^78,79 and primates^80,81, cross-species comparisons of the coupling between connectome communication and molecular expression can be further conducted. This may provide a molecular perspective about how communication strategies have adapted across evolution to accomplish increasingly complex functions⁸². Moreover, the multiple LR-pairs design can be easily extended to other modal data, such as markers of pathology (e.g., tau imaging) and corresponding metabolomes, which will be useful for investigating and potentially resolving a broad range of problems. In summary, we have presented a comprehensive optimal transport-based framework ranging from static data simulation and integration to dynamic cognitive processes deconvolution, providing an avenue for investigating brain communication at the micro- and macro-scales collectively.

Methods

The full details of the theoretical background and implementation can be found in the Supplementary Information.

Ethical statement

We used the publicly available data that participated in the Human Connectome Project (HCP; S1200), and had complete MRI data including diffusion-weighted MRI, all four sessions of resting-state fMRI and task fMRI related to working memory. All participants provided informed consent as part of the HCP, and the study protocol was approved by the institutional review boards of the WU-Minn HCP Consortium. The processing of these data was approved by the medical ethical committee of the Charité Medical Center in Berlin. Ethics oversight of gene expression data was performed by the Allen institute for brain science.

HCP dataset

Structural connectivity

SC was inferred from minimally preprocessed, high-resolution diffusion-weighted MRI data from healthy young adults participating in the Human Connectome Project. Details of the diffusion MRI acquisition and preprocessing are described in Sotiropoulos et al.⁸³ and Glasser et al.⁸⁴ After estimating the orientation distribution function using a multi-shell, multi-tissue constrained spherical deconvolution model⁸⁵, whole-brain white matter tractograms of individual participants were mapped using MRtrix3⁸⁶ with the following parameters: anatomically constrained tractography (ACT⁸⁷), iFOD2 tracking algorithm⁸⁸, 5M streamlines with dynamic white-matter seeding, 300 mm maximum streamline length, and 0.1 FOD amplitude cutoff for termination. To better match the whole-brain tractograms to the diffusion properties of the observed data, we also computed streamline weights, which are designed to reduce known biases in tractography data (SIFT2⁸⁹). The human Brainnetome atlas⁹⁰ divides the cortex and subcortex into 246 regions. Connection strength between any two regions was the SIFT2-weighted sum of the streamlines connecting those regions divided by the total gray matter volume of those regions. The strengths with fewer than 10 streamlines were pruned to reduce the high false positive rate. The group-representative connectivity matrix was computed using a consensus method that combined individual-level networks while preserving the average connection density across subjects (N = 1061, 487 males, 574 females, age 22–36)⁹¹.

Functional connectivity

FC was mapped using minimally preprocessed, ICA-FIX resting-state functional MRI data from the same sample of HCP participants. For each subject, four 14 min and 33 s scans (0.72 s TR) were acquired following details described in Glasser et al.⁸⁴ and Smith et al.⁹² Following another study⁹³, motion and global signal outlier timepoints were identified using an approach adapted from Artifact Detection Tools (ART) from the CONN Toolbox⁹⁴. After removing global signaling outliers and the first 10 volumes from each scan, additional nuisance variables, e.g., including an offset term, linear trend, 6 motion parameters and their derivatives, squares, and squared derivatives (24 motion regressors), and 10 anatomical CompCor (aCompCor) regressors, were regressed out. FC matrices were calculated using the Pearson correlation between each region-pair’s average time series in the Brainnetome atlas⁹⁰, resulting in 4 FC matrices for each subject. A final group-representative FC matrix was computed as the average within subjects and then across subjects (N = 1096, 500 males, 596 females, age 22–36).

Contrast map of task fMRI

The task-evoked responses were already processed by minimal preprocessing pipelines⁸⁴. Here, we mainly focused on general linear model contrasts from working memory (0 back and 2 back). We parcellated these maps into 246 regions using the Brainnetome atlas⁹⁰ for each subject (N = 1080, 494 males, 586 females, age 22–36) and extracted the average value from each region-of-interests (ROI). Because we mainly focused on the active region, the regions with negative average values were set as zero.

AHBA gene expression processing

Human brain gene expression from AHBA (http://human.brain-map.org) was measured in six post-mortem brains, containing 3702 spatially distinct samples and 58692 probes⁹⁵. Of note, the original MNI coordinates did not take into account nonlinear deformation, so we used the coordinates from Devenyi (https://github.com/gdevenyi/AllenHumanGeneMNI/), which were registered to MNI space (ICBM 2009c). Further processing was guided by Arnatkevic et al.⁹⁶ and abagen⁹⁷. First, probes with intensities below the background in at least 50% of the samples were excluded. Based on the updated probe-to-gene annotations from Re-annotator⁹⁸, probe selection was performed based on differential stability⁹⁹. Next, expression normalization was based on the robust sigmoid method, which is robust to outliers. Finally, samples assigned to the human Brainnetome atlas⁹⁰ within 2 mm Euclidian distance of a parcel were averaged first within each donor and then across the donors. Because only two of the six donors included samples from the right hemisphere, only samples from the left hemisphere were considered¹⁰⁰, resulting in an expression matrix of 123 regions and 15634 genes.

Ligand receptor pairs

CellChatDB v2⁴⁵ is an updated version of the original CellChatDB¹³, which was expanded by more than 1000 protein and non-protein interactions based on peer reviewed literature and existing databases, such as CellPhoneDB¹² and NeuronChatDB²¹ (metabolic and synaptic signaling). This updated version contains a total of 3237 unique pairs, 1102 of which are neurotransmitters. To account for the communication between brain regions, we only retained secreted and non-protein (mainly synaptic signaling) pairs. Furthermore, ligand-receptor pairs (LR-pairs) not detected in the AHBA dataset were excluded, resulting in a final list of 1242 pairs, 663 of which are neurotransmitters. The geometric mean of their related genes was used to represent the amount of ligand or receptor.

Brainspan developmental gene expression processing

The Brainspan database quantifies the gene expression in the brain throughout development (https://www.brainspan.org/static/download.html) and includes postmortem brains from 8 post-conception weeks to 40 years⁵⁸. RNA-seq data were used to explore the expression changes along development. Referring to Hansen, et al.¹⁰⁰, we manually binned the ages into six periods: fetus (8–37 post-conception weeks), infant (4 months–1 year), child (2–8 years), adolescent (11–19 years), young adult (21–30 years), and adult (36–40 years). In each brain region and developmental stage, the log-transformed RPKMs (reads per kilobase per million mapped reads), which measure the expression of genes, were averaged across all the samples.

CLRIA

Interregional communication is constrained by the internal complex connectivity, which make signaling efficient. Ligands and receptors are major signaling molecules during the communication process. If we regarded the expression of ligands and receptors as two distributions over the brain region, then the process of BNC can be viewed as a distributional transformation from ligand to receptor constrained by the underlying anatomical connectivity. From this point of view, we initiated the following multiple sources, multiple targets, optimal transport problem to construct brain interregional communication networks through predefined LR-pairs:

$${\min }_{{{\mathcal{P}}}\in \Pi \left({L}^{{\prime} },{R}^{{\prime} }\right)}F\left({{\mathcal{P}}}\right):={\sum }_{i=1}^{\left|I\right|}{\left\langle M,{{{\mathcal{P}}}}_{i}\right\rangle }_{F}$$

where $M\in {{\mathbb{R}}}_{+}^{N\times N}$ is the transport cost constructed from the BNCM; ${{{{\mathcal{P}}}}}_{i}\in {{\mathbb{R}}}_{+}^{N\times N}$ is the transport plan of i^th LR-pair, indicating the signaling strength between brain regions; $\left|I\right|$ is the total number of LR-pairs; ${\left\langle \cdot,\cdot \right\rangle }_{F}$ is the Frobenius inner product for the matrix; ${L}^{{\prime} }\in {{\mathbb{R}}}^{N\times \left|I\right|}$ and ${R}^{{\prime} }\in {{\mathbb{R}}}^{N\times \left|I\right|}$ are the amount of ligand that interacted with the cognate receptor and vice versa; and $\Pi (L^{\prime},R^{\prime} )=\left\{\,\left.{{{\mathcal{P}}}}\in {{\mathbb{R}}}_{+}^{N\times N\times \left|I\right|}\right|{{{\mathcal{P}}}}\times 2{{\mathbb{1}}}_{N}=L{\prime},{{{\mathcal{P}}}}\times 1{{\mathbb{1}}}_{N}=R{\prime} \right\}$ is the mass preserving constraint set.

Of note, current transcriptome sequencing cannot quantify the proportions of their interactions, so we used the total expression in each brain region as a surrogate. Since the total expression and interaction part of a ligand/receptor pair may be different, we relaxed the marginal constraints by adding a KL divergence penalty term on an objective function following Chizat et al.⁴¹ We further introduced two coupling matrices ${T}_{L},{T}_{R}$, which were derived from the ligand receptor database (see Supplementary material for further details). Finally, we introduced nonnegative tensor decomposition on the transport plan as a low rank constraint for both computational efficiency and biological significance. Intuitively, this constraint reduces the number of variables to be optimized, which naturally facilitates the computational efficiency. Moreover, a recent solver of the single source-target optimal transport problem benefitted from the low rank properties of the transport cost and transplant plan and achieved remarkable success with respect to efficiency and scalability^31,33,34,35. In addition, internal associations between LR-pairs, such as multiple species interactions¹⁹ and similar gene compositions, essentially make the transport plan into a low-rank tensor. In addition, tensor decomposition (e.g., tensor component analysis, TCA) exhibits superior performance in latent pattern recovery for multi-dimensional data^36,37,38,39. Therefore, we expected that this low-rank constraint would allow us to gain details about the underlying communication patterns. Considering all the above, the final optimal transport problem can be reformulated as:

$${\min }_{\left(A,B,C\right)\in \Pi \left(r\right)}F\left(A,B,C\right):= {\left\langle M,A{{\mbox{diag}}}\left({C}^{T}{{\mathbb{1}}}_{\left|I\right|}\right){B}^{T}\right\rangle }_{F}-\varepsilon {\mbox {H}}\left(A,B,C\right) \\ +{\tau }_{1}{{\mbox{KL}}}\left(A{{\mbox{diag}}}\left({B}^{T}{{\mathbb{1}}}_{N}\right){C}^{T}{T}_{L}\parallel L\right) \\ +{\tau }_{2}{{\mbox{KL}}}\left(B{{\mbox{diag}}}\left({A}^{T}{{\mathbb{1}}}_{N}\right){C}^{T}{T}_{R}\parallel R\right)$$

where A, B and C are factor matrices decomposed from a transport plan ${{{\mathcal{P}}}}$; ${\mbox {H}}\left(A,B,C\right)={\mbox {H}}\left(A\right)+{\mbox {H}}\left(B\right)+{\mbox {H}}(C)$ is the entropy function; and $\varepsilon,{\tau }_{1},{\tau }_{2}$ are coefficients of regularization terms. $\Pi \left(r\right)=\left\{\left(A,B,C\right)\in {{\mathbb{R}}}_{+}^{N\times r}\times {{\mathbb{R}}}_{+}^{N\times r}\times {{\mathbb{R}}}_{+}^{\left|I\right|\times r}\right\}$ is the nonnegative constraint on the factor matrix. $L\in {{\mathbb{R}}}^{N\times m}$ and $R\in {{\mathbb{R}}}^{N\times n}$ are the ligand and receptor expression matrices in each brain region, respectively. For heteromeric ligands or receptors, the geometric mean of the composed genes was adopted to represent the abundance of ligands or receptors^7,101,102. We manually replaced zero with a small number (10⁻⁸⁰ as default) in the expression matrix to avoid infinity in the objective function.

BMM algorithm for CLRIA

Of note, KL terms in the objective are not well defined at ${\left(A{{\mbox{diag}}}\left({B}^{T}{{\mathbb{1}}}_{N}\right){C}^{T}{T}_{L}\right)}_{{ij}}=0$ or ${\left(B{{\mbox{diag}}}\left({A}^{T}{{\mathbb{1}}}_{N}\right){C}^{T}{T}_{R}\right)}_{{ij}}=0$, which makes the convergence analysis challenging¹⁰³. Therefore, we focused on the solution in a perturbed constraint set ${\Pi }_{{{{\rm{\delta }}}}}\left(r\right)=\left\{\left(A,B,C\right)\in {{\mathbb{R}}}_{\delta+}^{N\times r}\times {{\mathbb{R}}}_{\delta+}^{N\times r}\times {{\mathbb{R}}}_{\delta+}^{N\times \left|I\right|}\right\}$, with $\delta={10}^{-100}$ as the default. Considering the block convexity of $F\left(A,B,C\right)$ and the interaction term existing in KL divergence, we used a BMM scheme to solve the perturbed problem. The first step was to construct the surrogate function for each block. This step separated the variables and retrieved a closed form solution. Following [Lemma D 4] in the Supplemental material, we can get the surrogate function for the KL term. Based on their properties ([Proposition D 1] in the Supplemental material), we can directly get the surrogate function for each block. Starting from random initialization $\left({A}^{(0)},\,{B}^{\left(0\right)},\,{C}^{\left(0\right)}\right)\in {\Pi }_{{{{\rm{\delta }}}}}\left(r\right)$, we have the following updates by minimizing each subproblem for $k\ge 0$:

$$\begin{array}{c}{C}^{\left(k+1\right)}=\max \left\{{C}^{\left(k\right)}\odot \exp \left(-{\Omega }_{C}/{\Lambda }_{C}\right),\delta \right\}\\ {A}^{\left(k+1\right)}=\max \left\{{A}^{\left(k\right)}\odot \exp \left(-{\Omega }_{A}/{\Lambda }_{A}\right),\delta \right\}\\ {B}^{\left(k+1\right)}=\max \left\{{B}^{\left(k\right)}\odot \exp \left(-{\Omega }_{B}/{\Lambda }_{B}\right),\delta \right\}\end{array}$$

where

$${H}_{1}= A{{\mbox{diag}}}\left({B}^{T}{{\mathbb{1}}}_{N}\right){C}^{T}{T}_{L};{H}_{2}=B{{\mbox{diag}}}\left({A}^{T}{{\mathbb{1}}}_{N}\right){C}^{T}{T}_{R}\\ {\Lambda }_{C}= {\tau }_{1}{T}_{L}{{\mathbb{1}}}_{m\times N}A{{\mbox{diag}}}\left({B}^{T}{{\mathbb{1}}}_{N}\right)+{\tau }_{2}{T}_{R}{{\mathbb{1}}}_{n\times N}B{{\mbox{diag}}}\left({A}^{T}{{\mathbb{1}}}_{N}\right)\\ {\Omega }_{C}= {{\mathbb{1}}}_{\left|I\right|}{{\mathscr{D}}}\left({A}^{T}{MB}\right)+{\tau }_{1}{T}_{L}\log {\left(\frac{{H}_{1}}{L}\right)}^{T}A{{\mbox{diag}}}\left({B}^{T}{{\mathbb{1}}}_{N}\right)+{\tau }_{1}{T}_{R}\log {\left(\frac{{H}_{2}}{R}\right)}^{T}B{{\mbox{diag}}}\left({A}^{T}{{\mathbb{1}}}_{N}\right)\\ {\Lambda }_{A}= {\tau }_{1}{{\mathbb{1}}}_{N\times m}{T}_{L}^{T}C{{\mbox{diag}}}\left({B}^{T}{{\mathbb{1}}}_{N}\right)+{\tau }_{2}{{\mathbb{1}}}_{N}{\left({B}^{T}{{\mathbb{1}}}_{N}\odot {C}^{T}{T}_{R}{{\mathbb{1}}}_{n}\right)}^{T}\\ {\Lambda }_{A}= {MB}{{\mbox{diag}}}\left({C}^{T}{{\mathbb{1}}}_{\left|I\right|}\right)+{\tau }_{1}\log \left(\frac{{H}_{1}}{L}\right){T}_{L}^{T}C{{\mbox{diag}}}\left({B}^{T}{{\mathbb{1}}}_{N}\right)+{\tau }_{2}{{\mathbb{1}}}_{N}{{\mathscr{D}}}\left({C}^{T}{T}_{R}\log {\left(\frac{{H}_{2}}{R}\right)}^{T}B\right)\\ {\Lambda }_{B}= {\tau }_{1}{{\mathbb{1}}}_{N}{\left({A}^{T}{{\mathbb{1}}}_{N}\odot {C}^{T}{T}_{L}{{\mathbb{1}}}_{m}\right)}^{T}+{\tau }_{2}{{\mathbb{1}}}_{N\times n}{T}_{R}^{T}C{{\mbox{diag}}}\left({A}^{T}{{\mathbb{1}}}_{N}\right)\\ {\Omega }_{B}= {M}^{T}A{{\mbox{diag}}}\left({C}^{T}{{\mathbb{1}}}_{\left|I\right|}\right)+{\tau }_{1}{{\mathbb{1}}}_{N}{{\mathscr{D}}}\left({C}^{T}{T}_{L}\log {\left(\frac{{H}_{1}}{L}\right)}^{T}A\right)+{\tau }_{2}\log \left(\frac{{H}_{2}}{R}\right){T}_{R}^{T}C{{\mbox{diag}}}\left({A}^{T}{{\mathbb{1}}}_{N}\right)$$

The superscript for each iteration was ignored for simplicity. The derivation of the algorithm is described in the Supplemental material [Lemma 2]. The global convergence of the update rules can be proved using Zangwill’s theorem⁴² ([Theorem 1] in the Supplemental material).

Computational cost

Given a specific species (e.g., human), the number of LR-pairs ${|I|}$ and related genes of LR-pairs $m,{n}$ can be regarded as constants. Each iteration was mainly involved with vector/matrix multiplication, which requires ${{{\mathscr{O}}}}\left({N}^{2}r+N\left({mr}+n\right)\right)$, ${{{\mathscr{O}}}}\left({N}^{2}r+N\left({nr}+m\right)\right)$,${{{\rm{and}}}}$ ${{{\mathscr{O}}}}\left({N}^{2}r+{Nr}\left(m+n\right)\right)$ operations to update $A,B,C$. Writing K as the number of iterations of the BMM scheme, we ended up with a total computational cost of ${{{\mathscr{O}}}}\left(K{N}^{2}r+KN\left({mr}+{nr}\right)\right)$. If we further use factor matrices ${M}_{1}\in {{\mathbb{R}}}^{N\times d}$ and ${M}_{2}\in {{\mathbb{R}}}^{N\times d}$ such that $M={M}_{1}{M}_{2}^{T}$, which is usually meaningful for brain networks^64,104, then the algorithm requires ${{{\mathscr{O}}}}\left(KN\left({dr}+{mr}+{nr}\right)\right)$ operations. This linear cost with respect to the number of brain regions would facilitate the exploration of brain communication on a finer scale.

Comparison with other methods

We compared CLRIA against several established cell communication frameworks, including CellPhone¹², CellChat^13,45, GeoMean⁴⁶, CellLinker²⁰, MEBOCOST²² and NeuronChat²¹. CellPhone and CellChat are popular software packages for cell-cell communication analysis using single cell sequencing data, and their recent versions support distance constraints. GeoMean is short for geometric mean, which is commonly used to calculate a communication score for each LR pair between different cell types. The incorporation of metabolic processes associated with the synthesis of non-protein ligands constitutes a pivotal feature of CellLinker, MEBOCOST and NeuronChat. The ligand-receptor database ultized by CellPhone, CellChat and geometric mean was identical as CLRIA. In contrast, the self-curated ligand-receptor database were used for CellLinker, MEBOCOST and NeuronChat. To ensure compatibility with the input requirements of these benchmarked methods, brain regions were computationally processed as different cell types. Following the acquisition of the communication score, it is possible to infer the direction of signaling flow between cortex and subcortex. Furthermore, the correlation with functional connectivity was computed based on the components of tensor decomposition of communication score.

Benchmark and comparison with iOT-based simulation

Ideally, ligand receptor interactions should be validated by the spatial co-localization of the corresponding proteins, but this information is always lacking, especially at the whole brain scale. Therefore, we built a simulation method based on the iOT problem^105,106,107. Actually, given the forward problem as a map $\Phi :\left(M,L,R\right)\to \left(A,B,C\right)$, then the data synthesis is just the inverse map ${\Phi }^{-1}:\left(A,B,C\right)\to (M,L,R)$. Moreover, when $\left(A,B,C\right)$ is observed without any noise, $L,R$ are completely determined by $\left(A,B,C\right)$. Thus, the inverse map reduces to ${\Phi }^{-1}:\left(A,B,C\right)\to M$. However, this map is not well-defined since transport cost $M$ is not uniquely determined by $A,B,C$ (e.g., any two transport costs differ by an additive constant that outputs the same optimal plan)¹⁰⁷. Most existing papers focused on obtaining a unique approximation by placing constraints on the transport cost^105,108,109. Following the same idea, we added two constraints on transport cost: (1) forcing the sum of all element to a given positive constant $K$ (10⁴ as default), and (2) adding an entropy term to the objective function. Therefore, this problem can be formulated as:

$$\begin{array}{c}\min {\left\langle M,A{{\mbox{diag}}}\left({C}^{{{\rm{T}}}}{{\mathbb{1}}}_{\left|I\right|}\right){B}^{{{\rm{T}}}}\right\rangle }_{F}-\varepsilon {\mbox {H}}(M)\\ {{\mbox{s.t.}}}{\sum }_{{{\rm{ij}}}}{M}_{{{\rm{ij}}}}=K\end{array}$$

Furthermore, this problem has a closed form solution. Let $P=A{\mbox{diag}}\left({C}^{T}{{\mathbb{1}}}_{\left|I\right|}\right){B}^{T}$, we have

$$M=\frac{K\exp \left(-P/\varepsilon \right)}{{\sum }_{{ij}}{\left(\exp \left(-P/\varepsilon \right)\right)}_{{ij}}}$$

Synthetic data generation

There are two main steps for synthetic data: (1) generating a transport plan following the process that is commonly used in estimating a nonnegative tensor decomposition algorithm and (2) solving an iOT problem to get the transport cost. Specifically, the elements of $A,B,C$ were generated randomly in interval $[0,\,1)$, and column normalization was performed on A and B. The ligand and receptor expression matrices are the sums along the first and second axes of the transport plan, which can be constructed by a factor matrix. Finally, the optimal value of the above iOT problem is the transport cost, and its low-rank representation can be solved using nonnegative matrix factorization. The CLRIA algorithm was compared with brain region N chosen from $\left\{123,\,180\right\}$, number of LR-pairs chosen from $\left\{300,\,500\right\}$, and column number of factor matrix r chosen from$\left\{1,\,5,\,10,\,20,\,30\right\}$. For each case, ten independent simulations were carried out. The parameters of the entropy term and the marginal mass constraint were chosen from $\{{0,\,10}^{-4},{10}^{-2}\}$ and $\left\{1,\,2,\,5\right\}$. The low-rank constraint parameter was set the same as the r. The iteration stopped when both the relative error and the absolute error of the objective function was less than 10⁻⁵ with at least 300 iterations. For run-time comparisons, the data were simulated with brain regions in $\left\{20,\,50,\,100,\,200,\,500,\,1000,\,2000\right\}$ with a fixed number of LR-pairs $\left|I\right|=20$ and a column number $r=5$ for efficiency.

Benchmark and comparison

Considering the permutation and scaling indeterminacy of the factor matrix¹¹⁰, we used CorrIndex¹¹¹ (implemented in Tensorly¹¹², version 0.8.1, https://github.com/tensorly/tensorly) to assess the consistency between CLRIA solutions and true values as well as to compare accuracy with other methods. The CorrIndex overcame these indeterminacies and showed its reliability and computational efficiency both theoretically and experimentally compared with other indices¹¹¹. This index lies between 0 and 1, with a higher score indicating more dissimilarity. Because there is no method that can directly solve the factor matrix from the transport cost matrix (M) and the ligand and receptor expression matrices (L, R), we separated this process into two steps: (1) solving the transport plan and (2) decomposing the nonnegative tensor of the transport plan. The transport plan was solved using unbalanced OT (sinkhorn⁴¹ or MM algorithm¹¹³) and partial OT¹¹⁴ implemented in POT¹¹⁵ (version 0.9.1, https://pythonot.github.io/index.html) as well as by the collective OT¹⁹. Then, the nonnegative CP decomposition was performed by the MU or HALS algorithm, which are classical NTD algorithms implemented in Tensorly¹¹².

Brain network communication model

A communication model describes a strategy for guiding signal propagation along structural connectivity^1,2. In this paper, we mainly focused on the transmission cost, which is defined as the mean first passage time (MFPT) on a biased random walk⁴⁷. Specifically, a weighted connectome can be expressed as a matrix $W\in {{\mathbb{R}}}^{N\times N}$, where ${W}_{{ij}}$ is the weighted streamline count. The weight-to-length transformation can be defined in various ways. Following a previous work²⁸, we used $D=-{\log }_{10}\left(W/\left(\max \left(W\right)+\min \left({W}_{ > 0}\right)\right)\right)$ to attenuate extreme weights⁷⁰. The transmission cost was implemented based on the following dynamics of the system:

$${P}_{\lambda }\left(Y=j{{{\rm{| }}}}X=i,\,T=t\right)=\frac{1}{{Z}_{i}^{t}}\exp \left(-(\lambda \left({d}_{{ij}}+{g}_{{jt}}\right)+{d}_{{ij}})\right)$$

where X, Y and T are random variables indicating the current, next and target node of Markov chain, ${Z}_{i}^{t}={\sum }_{j}\exp (-(\lambda ({d}_{{ij}}+{g}_{{jt}})+{d}_{{ij}}))$ is a normalization factor, ${g}_{{jt}}$ is the shortest path length from j to t. Let transmission cost from i to t be ${C}_{\lambda }^{{trans}}(i,t)$, then we have

$${C}_{\lambda }^{{trans}}\left(i,t\right)={\sum }_{k}{n}_{\lambda }^{t}\left(i,k\right){c}_{\lambda }^{{trans}}\left(k,t\right)$$

where ${n}_{\lambda }^{t}\left(i,{k}\right)$ is the mean number of times that node k was visited by a walker starting at node i, and ${c}_{\lambda }^{{trans}}\left(k,t\right)={\sum }_{j}{P}_{\lambda }\left(Y=j| X=k,{T}=t\right){d}_{{kj}}$ is the expected distance that a walker at node i travels to its neighbor. Further computational details can be found in ref. ⁴⁷. To construct a lambda spectrum of transmission costs representing changes from diffusion to routing strategy, thirty different $\lambda$ values evenly spaced from −3 to 1.6 on a log scale were selected. To get rid of the magnitude of the transmission costs between different λ values, we rescaled the sum of all elements to 10⁴.

Null model

For each λ value, we used a spatially constrained, label-permutation null model that randomly permutes region labels while preserving their spatial embedding and autocorrelation⁴⁷. This method created a surface-based representation of cortical parcellations in fsaverage space. The fsaverage surface was then projected onto a sphere to define the spatial coordinates for each parcel. The vertices on the sphere were assigned on the basis of the shortest distance to the center of mass of each parcel. These parcel coordinates were then randomly rotated and the original parcels were reassigned the value of the closest rotated parcel. Of note, this procedure was performed at parcel resolution rather than vertex resolution to ensure that the parcel sizes were not changed during the rotation and reassignment procedure and was performed only for the left cortex. This method is available in the stats module of the netneurotools Python package (https://github.com/netneurolab/netneurotools). For the subcortical region, random shuffles were performed following the ENIGMA toolbox¹¹⁶ (https://enigma-toolbox.readthedocs.io/en/latest/pages/08.spintest/index.html).

Asymmetric and trans-hierarchical signaling

The measures for the signaling asymmetry were inspired by Seguin et al.²⁸. Specifically, given the transport plan ${{{\mathcal{P}}}}{{{\mathscr{\in }}}}{{\mathbb{R}}}^{N\times N\times \left|I\right|}$ reconstructed from tensor factor $A,B,C$, where ${{{{\mathcal{P}}}}}_{{ijk}}$ denotes the communication strength between brain regions i and j mediated by the k^th LR-pair, the difference in signaling flow between regions i and j can be defined as ${\Delta }_{{ijk}}={{{{\mathcal{P}}}}}_{{ijk}}-{{{{\mathcal{P}}}}}_{{jik}}$. We performed a one sample T-test to determine whether the mean of ${\Delta }_{{ijk}}$ across k was significantly different from 0, and the resulting T-statistics were used to quantify the extent of communication asymmetry. Repeating this test independently for all pairs of brain regions yielded a antisymmetric matrix $T\in {{\mathbb{R}}}^{N\times N}$. A Bonferroni correction was performed to control for $N\left(N-1\right)/2$ multiple comparisons and resulting P-values below 0.05 were considered as significantly asymmetric.

We used three definitions of cortical hierarchy to explore trans-hierarchy signaling: (1) anatomical hierarchy, which is defined by the T1w/T2w ratio to index the cortical microstructure and myelin content; (2) functional hierarchy, which is the gradient of functional connectivity⁵² involving the unimodal cortex at one end and the transmodal cortex at the other end; and (3) the sensorimotor-association axis (SA axis), which spans from the primary visual and somatomotor cortices to the transmodal association cortices and captures the spatial and temporal patterning of cortical maturation proceeds throughout childhood and adolescence^54,55. All these macroscale maps were obtained from the neuromaps package¹¹⁷ in fsLR space and then aggregated into the Brainnetome parcellation. We compared the distribution of T-statistics between low-to-high and high-to-low asymmetric communication by the Kolmogorov-Smirnov test and spin test.

Energy spectral density of LR-pairs

To investigate the asymmetric signaling of each LR-pair, we used the difference between the outgoing and incoming degrees of the signaling network of the k^th LR-pair as a measure. Specifically, let ${{{{\mathcal{P}}}}}_{k}\in {{\mathbb{R}}}^{N\times N}$ be the signaling network, then the difference ${d}_{k}={{{{\mathcal{P}}}}}_{k}{{\mathbb{1}}}_{N}-{{{{\mathcal{P}}}}}_{k}^{T}{{\mathbb{1}}}_{N}\in {{\mathbb{R}}}^{N}$, which can be viewed as a graph signal on the structure connectome. Following Preti et al.⁶⁴, we defined the graph Fourier transformation (GFT) by the eigen decomposition of the graph Laplacian L, where L is the Laplacian transformation of the normalized structure connectivity. The eigenvalues ${\lambda }_{i}$ can be interpreted as frequencies, and the eigenmodes ${\xi }_{i}$ as structural connectome harmonics. Eigenmodes with a low eigenvalue encode smooth signals with respect to the structural network. Let $U=\left[{\xi }_{1},\ldots,{\xi }_{N}\right]\in {{\mathbb{R}}}^{N\times N}$, the GFT converts a graph signal ${d}_{k}$ into its spectral representation ${\hat{d}}_{k}={U}^{T}{d}_{k}$, and its energy spectral density is defined as the square of ${\hat{d}}_{k}$.

Nonnegative tensor component analysis

We used the LR-pair loadings to identify the biological process by ClusterProfiler (version 4.7.1.001). Before performing the analysis, the LR-pair loadings were normalized across communication patterns to [0, 1] to remove the effect of LR-pairs expression. The genes involved with the top 20% of LR-pairs were defined as factor-related genes. The background genes were defined as all the ligand or receptor genes expressed in the brain. Terms with P-values below 0.05 after adjustment was considered to be significantly enriched functional terms.

We used the row-wise maximum of the factor matrix $A,B$ to link a brain region to each factor. The ratio of these factor-specific regions in each intrinsic function network¹¹⁸ were denoted as $p$. To further depict the specificity of a factor to the intrinsic function network, we defined a normalized entropy:

$$E\left(p\right)=-{\sum }_{i}{p}_{i}\log {p}_{i}/\log k$$

where k=8 is the number of intrinsic function network. $\log k$ is a normalized factor to rescale the entropy to [0,1].

To further investigate the related cognitive function, a Neurosynth meta-analysis (https://www.neurosynth.org) similar to the one implemented by Margulies et al.⁵² was conducted to assess topic terms associated with each factor. Values greater than 0.05 after row-sum normalization were defined as the ROI for each factor.

UOT regression

Given the i^th columns of A and B, we generated a factor-specific communication pattern as their outer product and denoted it as ${X}_{i}\in {{\mathbb{R}}}^{N\times N}$. To investigate the brain state transition mediated by these communication patterns, we formulated it as an UOT regression problem. Specifically, if $a,b\in {{\mathbb{R}}}^{N}$ are two brain states that represent stationary active patterns during the execution of cognitive processes, we aimed to minimize their transport distance:

$${\min }_{\beta,P}\;f \, \left(\beta,P\right)= {\left\langle M\left(\beta \right),P\right\rangle }_{F}-\varepsilon {\mbox {H}}\left(P\right)+{\lambda }_{1}{{\mbox{KL}}}\left(P{{\mathbb{1}}}_{N}\parallel a\right) \\ + {\lambda }_{2}{{\mbox{KL}}}\left({P}^{T}{{\mathbb{1}}}_{N}\parallel b\right)+\frac{\lambda }{2}\parallel \beta {\parallel }_{2}^{2}$$

where $M\left(\beta \right)=\exp \left(-{\sum }_{i=1}^{r}{X}_{i}{\beta }_{i}\right),\beta \in {{\mathbb{R}}}^{r}$ can be viewed as the convex combination of the communication pattern with an affinity-to-distance transform. Following balanced optimal transport regression⁴⁰, an alternative direction multiplier method was used to solve the problem, which mainly involved the following two steps:

$$\begin{array}{ccc}{P}^{(k+1)} &=& {{{{\rm{argmin}}}}}_{P}f\left({\beta }^{\left(k\right)},P\right)\\ {\beta }^{\left(k+1\right)} &=& {{{{\rm{argmin}}}}}_{\beta }f\left(\beta,{P}^{\left(k+1\right)}\right)\end{array}$$

In fact, we can obtain ${P}^{\left(k+1\right)}$ by the generalized Sinkhorn algorithm⁴¹ since it is the same as an entropic regularization optimal transport problem. By setting $\frac{\partial f\left(\beta,P\right)}{\partial {\beta }_{i}}=0$, we have

$${\beta }_{i}=\frac{1}{\lambda }{{\mbox{tr}}}\left({{{\rm{X}}}}_{{{\rm{i}}}}\left(P\odot M\left(\beta \right)\right)\right),\,i=1,\ldots,r$$

Therefore, $\beta$ can be solved by fixed point iteration and have nonnegativity. If ${T}_{i}\left(\beta \right)=\frac{1}{\lambda }{\mbox{tr}}\left({X}_{i}\left(P\odot M\left(\beta \right)\right)\right)$, it can be proved that ${T}_{i}$ is contractive mapping when $\lambda \ge {\sum }_{{ij}}{P}_{{ij}}$ (not a tight bound), and thus we can conclude that ${T}_{i}$ is linearly convergent to the unique fixed point according to the Banach fixed-point theorem.

In practice, we set $\varepsilon={\lambda }_{1}={\lambda }_{2}=1$, $\lambda=2$ and compared the individual energy cost between 0 back to 2 back and 2 back to 0 back, which was measured as the UOT distance ${\left\langle M\left(\beta \right),P\right\rangle }_{F}$ and reflected the flexibility of the brain state. The significances were assessed by a repeat measures ANOVA with sex and age as covariates. To explore the communication pattern preference during these forward and reverse transition processes, the difference of $\beta$ during the process can be used as a measure. To further investigate the underlying difference in the LR-pairs, we defined the $C\beta$ as the importance of the LR-pairs during the transition for each individual. The significance was assessed by paired t test.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.