Introduction

Spin qubits based on semiconductor quantum dots1 are considered among the most promising candidates for building blocks in quantum computers2,3. Among various quantum-dot types, hole spins in germanium combine several features favorable for encoding qubits4, including all-electrical control based on intrinsic spin–orbit interaction5,6,7,8, low effective mass that simplifies fabrication9, and reduced hyperfine interaction attributed to atomic p orbitals4 and the abundance of net-zero nuclear spin isotopes6,8. Recently, significant developments have been made, including high-quality single- and two-qubit gates10,11,12,13, singlet–triplet qubits operating at much lower magnetic field14,15,16 and a 4 × 4 two-dimensional crossbar quantum-dot array with fine tunability17. Despite these achievements, a persistent issue is that strong spin–orbit interaction is a double-edged sword, enabling ultrafast qubit control while exposing the qubit to complex noise environments4,18. In addition, anisotropic susceptibility to noise results in site-dependent qubit properties and nonuniform qubit operations, posing significant obstacles for large-scale quantum computation13. As the number of qubits scales up, semiconductor quantum computation is entering the noisy intermediate-scale quantum (NISQ) era, which demands increasingly stringent requirements for noise-resilient, uniform, and high-fidelity operations across dense arrays19. Therefore, it is a paramount challenge to improve error robustness while maintaining high-quality qubit operation20.

As a seminal and enduring example, geometric quantum computation (GQC) continues to attract significant attention in the field of quantum computation21,22,23,24. Compared to dynamical phases, geometric phases are determined by the geometry of the evolution path and are immune to perturbations that do not change the enclosed area of the path25,26, indicating their robustness against certain types of noise27,28. Taking advantage of geometric phases, geometric quantum gates can achieve noise-resilient operations. Early GQC proposals utilized adiabatic evolution to suppress unwanted transitions and state leakage22,29,30,31. However, coherence times are typically much shorter than the evolution times of adiabatic geometric gates, rendering this approach universally impractical for quantum computation. To speed up gate manipulation while still retaining robustness, nonadiabatic geometric quantum computation (NGQC) has been proposed and demonstrated. Depending on the dimension of the governing Hamiltonian and energy level configurations22,32, geometric gates are classified as Abelian-phase-based33,34,35 or non-Abelian-phase-based23,36. Notably, Abelian-phase NGQC features experimental simplicity and feasibility, paving a promising way toward universal quantum computation37. As a two-level system, hole spin qubits are well-suited for implementing NGQC schemes based on Abelian phases, benefiting from ultrafast qubit manipulations12 and easy fabrication of two-dimensional lattice structures11. By designing specific evolution paths, NGQC demonstrates the robustness against off-resonance noise (Larmor frequency noise) and systematic noise (Rabi frequency noise)38,39. Despite the implementation of Abelian-phase geometric quantum gates, their noise-resilient feature remains unverified, and the control fidelities remain far below the threshold for fault-tolerant semiconductor quantum computation24,40. Nevertheless, achieving high-fidelity, noise-resilient qubit manipulation is essential for the practical application of GQC in scalable quantum computing.

Here, we establish a hole spin qubit based on a strained germanium quantum dot. We achieve a 19 MHz Rabi frequency with a qubit dephasing time of \({T}_{2}^{*}\) = 136 ns, which can be extended to 6.75 μs through dynamical decoupling techniques. To evaluate qubit control performance, we benchmark single-qubit gate control fidelities at a series of Rabi frequencies fRabi utilizing gate set tomography (GST)41. The control fidelities of both the X/2 gate and Y/2 gate approach ~99.9% as the Rabi frequency increases, while those of I gate saturate at 97.48%, which reveals that off-resonance noise seriously affects qubit control fidelity42. Furthermore, to remove obstacles caused by noise, we introduce nonadiabatic geometric gates based on Abelian geometric phases to implement noise-resilient quantum gates37,43. To clearly compare the performance of GQC with that of dynamical gates, we characterize the control fidelities of geometric gates across a wide range of Rabi frequencies. The geometric gate control fidelities always remain above 99%, demonstrating uniform and high-quality qubit manipulation. Notably, the maximum fidelity can reach 99.9%, satisfying the demand for quantum error correction using surface code44. Moreover, we experimentally demonstrate the noise-resilient feature of geometric quantum gates by detuning the microwave frequency away from the qubit frequency. The control fidelities of geometric X/2 and Y/2 (I) gates can still reach 99% with the microwave frequency detuned by  ±2.5 MHz (±1.2 MHz), highlighting their role in reducing the need for frequent qubit frequency calibration37,45. Our results reveal that GQC is a convincing method for achieving reliable and high-fidelity qubit control in complex noise environments.

Results

Measurement techniques

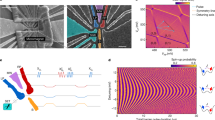
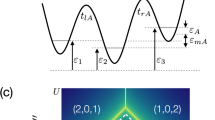
Figure 1a presents a false-colored scanning electron microscope (SEM) image of a double quantum dots (DQDs) device fabricated on an undoped strained germanium wafer46. The fabrication details are similar to those described in ref. 47. The device consists of two sections: the upper part is configured as the DQDs, and the lower portion (blue circle) serves as a charge sensor to detect the charge configuration of DQDs. An external in-plane magnetic field B0 of 1333 mT is applied to provide Zeeman splitting for defining spin qubits. Figure 1b shows a cross-section schematic of the DQDs along the white dashed line in Fig. 1a. The hole spins are confined in DQDs by selectively tuning the plunger gates P1 and P2, as well as barrier gates. Additionally, the tunnel coupling between the quantum dots and their reservoirs, and inter-dot tunnel coupling can be modified separately via three barrier gates B1, B2, and M. We apply microwave pulses to gate P2, and three-step pulses to gates P1 and P2 to initialize, control and readout the qubit state (see the “Methods” section for details). Detected by the charge sensor, the charge stability diagram of DQDs is depicted in Fig. 1c, where Ni represents the number of holes in the quantum dot under gate Pi, respectively. We select the (1, 1)−(2, 0) inter-dot tunneling region for spin state readout via enhanced latching readout (ELR)48, which is based on Pauli spin blockade (PSB)49. The latching phenomenon originates from the asymmetric coupling strengths between the two dots and their adjacent reservoirs48. By tuning the voltage on gate B2, the tunnel rate between the dot beneath P2 and the right reservoir beneath L2 can be pinched off (Supplementary Note 1), forcing holes in the dot beneath P2 to tunnel into the left reservoir via co-tunneling with the dot beneath P1, a process that also occurs slowly.

Fig. 1: Device fabrication and experimental setup.
figure 1

a False-colored SEM images of the device. The upper side is the DQD's structure, and the lower region serves as a charge sensor (blue circle). b Cross-section schematic of the device along the white dashed line in (a). Holes confined under gate P1 and P2 can tunnel to the reservoir under gate L1 and L2, with the tunnel rates adjusted by barrier gates B1 and B2. Square pulses and microwave pulses are applied to gates P1 and P2 for state readout and manipulation. c Charge stability diagram of DQDs. (N1, N2) represent the number of holes in the quantum dot under gate P1 and P2. Points E, L, and R represent the relative position of square pulses for ELR. d The latching region for ELR is indicated by parallel black dashed lines, where the distance corresponds to EST. Inset: energy level and state-ladder schematic at the latching region.

Full size image

The ELR process is explained by comparing the theoretical latching behaviors when the spin state is initialized as a singlet or triplet state50. The energy levels and state-ladder schematic in the latching region are shown in the inset of Fig. 1d, where only the singlet state S and the ground triplet state T− are considered for simplification. If T−(1, 1) is initialized, it cannot tunnel into S(2, 0) due to PSB, or into T−(2, 0) due to insufficient energy. Direct tunneling into (1, 0) is suppressed due to a slow tunnel rate, resulting in no detectable signal in the latching region. In contrast, the singlet state tunnels to (1, 0) via (2, 0) state, thereby generating a full-hole signal. Therefore, the singlet and triplet states can be clearly distinguished by monitoring hole tunneling from the dot beneath P1 to the left reservoir. The following experiments employ single-shot ELR. Figure 1c illustrates the cyclic E–L–R pulse sequence used to probe the latching region. The spin state is initialized into an S–T mixed state at stage L via the transition from (2, 1) to (1, 1). Scanning the voltage of stage R within the range shown in Fig. 1d, the latching region in (1, 0) becomes visible, as depicted by parallel black dashed lines. The energy difference between the singlet and triplet states is 0.8 meV, determined by a lever arm of 0.13 eV V−1 (see Supplementary Note 2).

Qubit Properties

Next, we focus on coherent qubit control. The spin state is initialized into T− at stage L by waiting for a sufficiently long period (see Supplementary Note 3). Qubit operations are performed via electric dipole spin resonance (EDSR) mediated by the intrinsic spin–orbit interaction (SOI)6,12. When the microwave frequency (fMW) matches the qubit resonance frequency, T− is operated to S and PSB is lifted. Consequently, a full-hole signal can be detected at stage R48,50. By applying a rectangular-shaped microwave burst (τburst) with a fixed duration of tπ (time for a π rotation), two resonance frequencies f1 = 5.60 GHz and f2 = 7.53 GHz are measured (Supplementary Note 4). Using the relation hfi = giμBB0, g-factors g1 = 0.29 and g2 = 0.39 are extracted, where h is Planck’s constant and μB is the Bohr magneton. In the following measurements, we mainly focus on the qubit with the higher frequency and characterize its properties8. Firstly, Fig. 2a shows the Rabi chevron pattern by varying τburst and Δf (defined as fMW−f2). Along the red dashed line where fMW resonates with f2 (inset of Fig. 2b), the hole spin rotates over an angle determined by τburst. Fitting the oscillation yields Rabi frequency fRabi = 11.56 MHz, \({T}_{2}^{{{\rm{Rabi}}}}\) = 1.56 μs, and a quality factor Q = 18.04 (defined by \(2 * {T}_{2}^{{{\rm{Rabi}}}} * {f}_{{{\rm{Rabi}}}}\)). As shown in Fig. 2b, increasing driving power continuously, both fRabi and the Q factor rise monotonically without saturation, as indicated by the blue triangles and red circles, respectively. At maximum driving power, fRabi reaches 19 MHz with the highest Q = 39.78. To characterize the qubit dephasing time \({T}_{2}^{*}\), we perform a Ramsey experiment with Δf = 20 MHz. By varying the idle time (τidle) between two X/2 pulses, the Ramsey decay (see Fig. 2c) yields a dephasing time \({T}_{2}^{*}=136\) ns at fRabi = 11.56 MHz. \({T}_{2}^{*}\) remains nearly constant across the measured fRabi range (Supplementary Note 5). Furthermore, we apply the Carr–Purcell–Meiboom–Gil (CPMG) sequence to alleviate the effect of noise and extend the coherence time51, in which a series of Y gates are inserted between two X/2 operations to refocus the qubit state52. Figure 2d shows a set of normalized signals with a coherence time \({T}_{2}^{{{\rm{CPMG}}}}\) of 6.75 μs for Nπ = 230 (Nπ denotes the number of Y gates in the CPMG sequence), which is 50 times longer than \({T}_{2}^{*}\). As shown in the inset of Fig. 2d, \({T}_{2}^{{{\rm{CPMG}}}}\) increases linearly with Nπ, which indicates that low-frequency noise is one of the important noise sources, as revealed through the equivalent filter functions of the CPMG pulse sequence13,51,53.

Fig. 2: Qubit properties.
figure 2

a The Rabi chevron pattern: singlet state probability PS as a function of τburst and Δf. b Rabi frequency (blue triangles) and the Q factor (red circles) measured under different microwave power \({P}_{{{\rm{MW}}}}^{1/2}\), showing no saturation. The largest fRabi of 19 MHz and Q factor of 39.78 are achieved. Inset: PS as a function of τburst along the red dashed line in (a). The red solid line represents the fitting result, yielding a Rabi frequency of 11.56 MHz and Q factor of 18.04. c Ramsey fringe obtained by varying the idle time τidle, with the fitted dephasing time \({T}_{2}^{*}\) of 136 ns. The red solid line represents the fitting result. d Coherence decay under CPMG sequences as a function of total idle time for different Nπ. Inset: \({{T}_{2}}^{{{\rm{CPMG}}}}\) as a function of Nπ. For the largest Nπ = 230, we obtain \({{T}_{2}}^{{{\rm{CPMG}}}}\) = 6.75 μs.

Full size image

Control fidelity

Among the various quantum benchmarking techniques, randomized benchmarking (RB)54 and gate set tomography (GST)41,55 stand out for their robustness against state preparation and measurement (SPAM) errors. We therefore implement both techniques to accurately assess the qubit control fidelity. RB experiment employs two types of sequences: reference sequences and interleaved sequences. The reference sequence consists of N random Clifford gates and an additional recovery gate that recovers the spin to the spin-down state. The interleaved sequences, created by inserting the target gate between adjacent random gates of the reference sequences, are used to evaluate the control fidelity of the target gate (more details shown in Supplementary Note 6). Figure 3a shows the control fidelities of single-qubit gates measured using RB. The average single-qubit gate fidelity is 99.49%, with both I, X/2 and Y/2 gate control fidelities exceeding 99%—surpassing the threshold for quantum error correction using surface codes44. Here, the I gate denotes an identity operation implemented by idling for the duration of a π/2 X or Y rotation. For GST, the default gate set contains I, X/2 and Y/2 gates. GST sequences consist of two components: fiducials for state preparation and germs for amplifying various types of gate errors. The number of total sequences depends on sequence depth. We select a sequence depth of 8, yielding a total of 448 GST sequences. Each sequence is constructed by interleaving these fiducials with germ sequences, after which we measure the singlet state probability (more details shown in Supplementary Note 6). Analyzed by the Python package pyGSTi, Fig. 3b presents the single-qubit gate fidelities across different fRabi characterized by GST56. Gate fidelities show a positive correlation with fRabi, in agreement with the Q factor trend shown in Fig. 2b. The best performance occurs at fRabi = 19 MHz, achieving control fidelity of 97.48% for I gate, 99.81% for X/2 gate and 99.88% for Y/2 gate. Note that the I gate fidelities remain substantially below 99% across the entire fRabi range, which is mainly due to the shorter \({T}_{2}^{*}\) compared to the idle time composed of multiple consecutive I gates in the GST sequence. On the one hand, the infidelity owing to Rabi decay is small, as indicated by the high-fidelity (99.49% on average) single-qubit gate characterized by RB20. On the other hand, some pulse sequences in the GST experiment include idle times much longer than \({T}_{2}^{*}\), which mainly limits the control fidelity57. Raising fRabi directly helps suppress the effect of dephasing11,20. As a result, the control fidelity of I gate improves 3.46% and those of X/2 and Y/2 gate are much closer to 99.9%. Unfortunately, when fRabi exceeds 15 MHz, the I gate fidelity appears to saturate but is still significantly below 99%. Table 1 lists the control fidelities of dynamical gates characterized by RB and GST at fRabi = 19 MHz, which are similar to each other except for the I gate. This discrepancy arises from the differences in sequence composition between the two methods (see Supplementary Note 6)11.

Fig. 3: Control fidelity and geometric quantum computation.
figure 3

a Sequence fidelities for reference (abbreviated as “Ref'') and each interleaved characterized by RB, where N represents the number of Clifford gates in the reference sequences. The control fidelity is shown below the corresponding curves. b The control fidelities of the dynamical gate set extracted by GST as a function of fRabi. The black dashed arrows guide the eyes, indicating the tendency of the fidelity. The light gray line represents the 99% control fidelity threshold. As the Rabi frequency increases, the control fidelities of X/2 and Y/2 gates gradually improve to nearly 99.9%, whereas the I gate control fidelity saturates at 97.48%. Error bars represent the 95% confidence level. c The schematic of the evolution path Path2. d The control fidelities of the geometric gate Path2 as a function of fRabi. The average control fidelity exceeds 99% at each fRabi, demonstrating the superiority of geometric gates. The light gray line denotes the 99% control fidelity threshold, consistent with panel b. The data points consistently exceed the reference line at each fRabi. This demonstrates the superior performance of the geometric gates. Error bars represent the 95% confidence level.

Full size image
Table 1 The fidelity of the dynamical single-qubit gate set
Full size table

Geometric quantum computation

Analysis of the error generator in GST reveals that the errors can be classified into coherent Hamiltonian errors and incoherent stochastic errors58,59. For coherent errors, diverse strategies can be employed to mitigate them, such as dynamical decoupling or recalibrating control58,59,60. For stochastic errors, such as dephasing and depolarizing noise, we propose a noise-resilient operation strategy to counteract uncorrelated noise58. We introduce GQC, a technique known for its superior robustness37,61 to resist various noises, enabling uniform and high-fidelity qubit manipulation.

We consider a Hamiltonian for a two-level qubit system driven by a classical microwave field,

$$H=\frac{h}{2}\left(\begin{array}{cc}\Delta f&(1+\delta ){f}_{{{\rm{Rabi}}}}{{\rm {e}}}^{-{\rm {i}}\Phi }\\ (1+\delta ){f}_{{{\rm{Rabi}}}}{{\rm {e}}}^{{\rm {i}}\Phi }&-\Delta f\end{array}\right),$$
(1)

where Δf represents the difference between fMW and f2. The corresponding terms appear in the diagonal elements of the Hamiltonian. The fluctuations in fRabi, δ, manifest in the off-diagonal elements of the Hamiltonian. To construct nonadiabatic single-qubit geometric gates, the evolution loop is designed as a closed trajectory consisting of three intervals in the experiment: 0 → τ1,τ1 → τ2,τ2 → τ3. During each interval, the microwave has different phases and amplitudes, as detailed below.

$$\begin{array}{l}\int_{0}^{{\tau }_{1}}2\pi {f}_{{{\rm{Rabi}}}}{\rm {d}}t=\theta,\Phi (t)=\phi -\pi /2,t\in [0,{\tau }_{1}],\\ \int_{{\tau }_{1}}^{{\tau }_{2}}2\pi {f}_{{{\rm{Rabi}}}}{\rm {d}}t=\pi,\Phi (t)=\phi+\gamma -\pi /2,t\in [{\tau }_{1},{\tau }_{2}],\\ \int_{{\tau }_{2}}^{{\tau }_{3}}2\pi {f}_{{{\rm{Rabi}}}}{\rm {d}}t=\pi -\theta,\Phi (t)=\phi -\pi /2,t\in [{\tau }_{2},{\tau }_{3}].\end{array}$$
(2)

The formulas above describe one of the proposals to realize a geometric gate, labeled as “Path2” in the following (see the evolution path shown in Fig. 3c). An alternative proposal, labeled as “Path1”, replaces the phase of the second interval with Φ(t) = ϕ + γ + π/2. These two proposals target different types of noise. Path1 addresses systematic noise δ, which represents fluctuations of fRabi, while Path2 resists off-resonance noise Δf, defined by the fluctuations of f237.

Following the cyclic evolution loop above, the equivalent evolution operator is

$$\begin{array}{rcl}U(\theta,\gamma,\phi )=\cos \gamma+{\rm {i}}\sin \gamma \left(\begin{array}{cc}\cos \theta &\sin \theta {{\rm {e}}}^{-{\rm {i}}\phi }\\ \sin \theta {{\rm {e}}}^{{\rm {i}}\phi }&-\cos \theta \end{array}\right)\\ {\hskip -59pt}=\exp ({\rm {i}}\gamma {{\bf{n}}}\cdot {{\boldsymbol{\sigma }}}),\end{array}$$
(3)

which determines the rotation around the axis \({{\bf{n}}}=(\sin \theta \cos \phi,\sin \theta \sin \phi,\cos \theta )\) by an angle  −2γ, where σ represents the Pauli operators. An arbitrary single-qubit geometric gate can be achieved by adjusting the parameters in the evolution loop. For example, by setting θ = π/2, ϕ = π/2, γ = 0, a geometric I gate is obtained. This geometric I gate effectively implements a 2π rotation about x-axis through three steps.

Figure 3d presents the control fidelities of single-qubit geometric gates Path2 as a function of fRabi, analyzed through GST. In contrast to dynamical gates, the average fidelities of geometric gates exceed 99% throughout the entire measurement range, highlighting the superiority of GQC. The maximum control fidelities reach 99.98%, 99.80%, and 99.97% for the I, X/2, and Y/2 gates, respectively. The detailed data shown in Fig. 3d are provided in Supplementary Table I. Especially, the fidelity of the I gate can be significantly improved even when fRabi is small. Unlike Path2, the control fidelity of the gate set achieved by Path1 is well below 99% (Supplementary Note 11). This is probably because the systematic noise targeted by Path1 is relatively weaker than the off-resonance noise here (Supplementary Note 8)24,62,63. To simultaneously resist both types of noise, we introduce an enhanced geometric gate featuring a 3π evolution path (named Path3π) that extends 1.5 times longer than Path1 and Path238. However, its performance is significantly worse than that of Path2, probably due to the longer operation time (see Supplementary Note 9).

Noise-resilient operation

After realizing high-fidelity single-qubit geometric gates, we further demonstrate their noise-resilient characteristics against Δf. As shown in the upper panels of Fig. 4, we compare the performance of the Δf-error-affected geometric gate (red triangles) with that of the corresponding dynamical counterparts ("Dyn” for short, blue circles). As expected, the gate set implemented with geometric gate Path2 is clearly superior to the conventional dynamical gate. The fidelities of the geometric X/2 and Y/2 (I) gates exceed 99% even when Δf = ±2.5 MHz (±1.2 MHz). Furthermore, Δf measurements over 55 h fall precisely within this range, verifying the ability of the geometric gate to alleviate the need for frequent calibration of qubit resonance frequency (Supplementary Note 10). Moreover, the lower panels of Fig. 4 show the differences in control fidelities between the geometric and dynamical gates. As ∣Δf∣ increases, the fidelities of the dynamical gate decrease faster than those of the geometric gate, which confirms that the geometric gate is more robust against off-resonant noise. Additionally, the robustness against Rabi error δ is displayed by comparing Path1 with the dynamical gate in Supplementary Note 11. In order to explain the noise-resilient feature of the geometric gate, we numerically simulate the fidelity with additional off-resonance noise. Based on the \({T}_{2}^{*}\) values and the GST report, we choose an appropriate noise strength as the starting point. We then calculate the probability of the singlet state for each GST sequence and analyze the fidelity. By numerical simulation, the final parameters we extracted are δfLarmor = 1.80 MHz and δfRabi = 58.48 kHz. The calculated fidelities, overlaid in Fig. 4 (Supplementary Note 7), show that the theoretical results align with the experimental results in terms of overall trends. These results clearly demonstrate the advantages of GQC in achieving high-fidelity qubit manipulations despite the presence of complex noise.

Fig. 4: Noise-resilient feature of single-qubit geometric gates.
figure 4

The upper panels of a–c show that control fidelities of the I, X/2 and Y/2 gates, realized by both geometric and dynamical approaches, as a function of Δf. The light gray lines represent a 99% control fidelity threshold. Notably, even with detuning Δf by  ±2.5 MHz (±1.2 MHz), the control fidelities of geometric X/2 and Y/2 (I) gates can still reach 99%. The differences in the control fidelities between the two approaches are displayed in the lower panels. The black dashed arrows serve as visual guides to emphasize that as Δf increases, the control fidelities of the dynamical gates decrease faster than those of the geometric gate. Error bars represent the 95% confidence level. The experimental results are consistent with the numerical simulations (blue and red dashed lines).

Full size image

Discussion

For the practical implementation of geometric quantum gates, two necessary considerations are optimal scheme selection and geometric gate operation time. The geometric gates we have implemented are tailored for different noise types. Therefore, the best scheme choice depends on the specific noise experienced by spin qubits. In semiconductor quantum computation, the dominant noise source depends on the wafer material, device architecture, and frequency domain of interest64. Through characterization of qubit coherence time, noise spectrum analysis65,66, report analyzed by gate set tomography59 or the envelope of Rabi oscillation decay67, we can make a basic assessment of noise type and noise level, enabling the efficient selection of the optimal geometric gate scheme. Otherwise, counterproductive effects may arise (Supplementary Note 8). Depending on the relative strengths of systematic and off-resonance noise, we can choose either Path1 or Path2. When the strengths of off-resonance noise and systematic noise are comparable, alternative protocols such as Path3π or nonadiabatic geometric quantum computation with noncyclic evolution paths can be employed68. On the other hand, the evolution times of all types of geometric gates implemented here are four or six times longer than those of dynamical gates. There is a trade-off between extended operation time and enhanced noise resistance. Encouragingly, a noncyclic nonadiabatic geometric quantum gate was recently proposed to shorten the evolution time, effectively avoiding the cumulative disturbances of errors due to excessive time consumption35,68.

Regarding the practical advantages of geometric gate applications, reproducible high-fidelity qubit control without frequent recalibration of control parameters is particularly attractive. In current devices with a limited number of qubits, calibration requires a considerable amount of time20,66,69. Although improvements in circuit optimization and fabrication techniques can help mitigate the noise strengths, complete elimination of noise remains challenging. Expanding to large-scale quantum computation, the varying noise environments experienced by individual qubits pose significant challenges to reproducibly achieving high-fidelity qubit control. As calibration becomes increasingly resource-demanding, it significantly hinders the efficiency of the qubit processors. Geometric gates can potentially reduce both the time and resource consumption required for recalibration in large-scale quantum computation.

In conclusion, we characterize the single-hole spin qubit in germanium DQDs and extract its control fidelity via GST. Along with increasing fRabi and the Q factor, the fidelities of the dynamical gate gradually saturated, and those of X/2 and Y/2 approach ~99.9%. However, for the I gate, the fidelity remains significantly below 99% which indicates the susceptibility of the spin qubit to off-resonance noise. In order to explore a strategy for achieving noise-resilient and high-fidelity spin qubit manipulation in future large-scale quantum computation, we introduce GQC featuring noise robustness. Two different geometric evolution loops, named Path1 and Path2, are implemented to specifically deal with systematic and off-resonance noise, respectively. Regarding geometric gate Path2, the average control fidelity of the gate set consistently reaches 99% across a wide range of fRabi, demonstrating its potential to achieve uniform qubit control under various situations. In addition, the I, X/2, and Y/2 gates exhibit maximum control fidelities of 99.98%, 99.80%, and 99.97%, respectively, despite requiring four times the operation time of dynamical gates. Furthermore, we demonstrate the robustness of geometric gates by adding off-resonance noise Δf, which currently has a more harmful impact on qubit properties. The error-affected performance of Path2 is superior to that of dynamical gates throughout the entire measurement. Calibration of the qubit resonance frequency in experiments is a time-intensive and resource-demanding process. The geometric gate, despite detuning Δf by  ±2.5 MHz (±1.2 MHz), still achieves fidelities of the X/2 and Y/2 (I) gates that reach fault-tolerant quantum computing thresholds, confirming its ability to perform high-fidelity and noise-resilient qubit operations while alleviating the need for frequent qubit frequency calibration. Consequently, the demonstrated geometric quantum gate has broad application prospects for implementing high-fidelity and robust qubit manipulations for large-scale quantum computation. Moreover, in future work, combined with two-qubit geometric gates37,70, it is expected to realize robust universal geometric quantum computation in a large-scale qubit array.

Methods

We perform the experiments using an Oxford dry dilution refrigerator with a base temperature of ~15 mK. A three-stage gate voltage pulse is generated by an arbitrary waveform generator (AWG Keysight M8190). The pulse is combined with the DC-voltages using an analog summing amplifier (SRS SIM980) and applied to plunger gates, which are connected to the DC-port of a commercial bias tee (Anritsu K251). Meanwhile, leveraging I/Q modulated signals from Tektronix AWG5208 channel pairs, we apply a microwave signal generated by a vector signal generator (Keysight E8267D) connected to the RF IN port of the bias tee. The microwave pulse modulation, generated by the AWG5208, is turned on 500 ns before and turned off 500 ns after the microwave signal. By measuring the current of the single-hole transistor, we can detect the qubit state by a charge sensing technique. Being amplified by a room-temperature amplifier (SRS SR570 and SR560), the output current can be digitized by a PCI-based waveform digitizer (AlazarTech ATS 9440) at a sampling rate of 5 MSa/s.