Introduction

Machine learning (ML) examine large datasets to develop prediction models and is known to be more popular to traditional statistical approaches1,2,3,4. The truthfulness and accuracy of data is of great importance for machine learning. However, due to the inherent variability, partial observation, or lack of information in real dynamic systems5,6, the datasets collected by machines is finite and introducing randomness to improve model generalization is critical. Traditional deep learning models are often data-driven black boxes that cannot be used freely on error-sensitive domains. For example, in the fields of autonomous driving and medical diagnostics, prediction errors would be immeasurably costly and could lead to ethical issues. In fact, it is difficult for the captured data to cover all cases, so the training dataset cannot be comprehensive, and this can lead to errors in some rare cases. On the other hand, conventional deep learning models lack transparency and interpretability due to the complex nature. Finding the reason for errors and debugging the models are difficult.

To solve the above issues, Bayesian neural networks (BayesNN) provide an alternative path to quantify uncertainty and explain loss functions. Bayesian neural networks achieve non-deterministic inference by introducing randomization of synaptic weights, and weight randomization usually consists of two dominant approaches, one of which is the Gaussian distribution of weights7,8, and the other is Monte Carlo (MC)-dropout of weights9,10. In situations where information and conditions are limited, the Bayesian method helps to predict the near-true probability of an event occurring by dynamically adjusting step-by-step. The posterior distribution inferred from previous data helps in calculating the prediction variance or entropy and thus assessing the credibility of the probabilistic model.

Gaussian weighting models are usually harder to implement with simple hardware. In CMOS circuits, Gaussian sampling needs to be implemented using linear feedback shift registers (LFSRs) and combinational logic gates11. To minimize the hardware cost, some work has utilized the conductance of resistive devices to represent the weights and cleverly used noise fluctuations to implement the Gaussian weights7,8. Lin et al. presented a Bayesian neural network implemented by exploiting the intrinsic stochasticity of RRAMs7. They used the analog conductance distribution of multiple RRAM devices fitted to a Gaussian distribution and used to represent the weights. Dalgaty et al. proposed resistive memory-based inference hardware for Bayesian neural networks8. They perform the ex-situ training of a Bayesian neural network, and then, the resulting software model is transferred in a single programming step to an array of 16,384 resistive memory devices. However, the noise fluctuations of RRAM, which refer to the low-frequency noise, decrease as the frequency and temperature increase12,13,14,15,16. This intrinsic issue is determined by the nature of the device itself and greatly restricts the application at high frequencies and temperatures. W. Schottky et al discovered that shot noise17, which has a high noise density regardless of the frequency and temperature, could be generated by the current flowing through the diode. Thus, a diode with storage capacity is exactly what is needed for Bayesian neural networks.

Here, in this work, through the systematic investigation of the noise behavior in the Fe-diode, shot noise in HRS with frequency-independent high noise density and temperature stability is selected as the entropy source. Moreover, a hierarchical BayesNN with unified entropy source and weights based on a 3D 16-layer Fe-diode array is constructed. The top layer in the 3D Fe-diode array is used to generate shot noise with high density for a high-quality entropy source. For other layers, each layer has multi-level conductance states for synapse weights. By unifying the synapse weights and entropy source through 3D integration in the same array, low energy consumption and high area efficiency can be obtained. Based on the above advantages, a low-energy-consumption, high-area efficiency BayesNN system with a wide working temperature range (− 40 °C ~ 125 °C) is experimentally demonstrated and in situ training of edge devices with properties (92.4% MNIST recognition accuracy, 0.9997 minimum entropy) is finally achieved.

Results

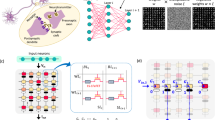
Figure 1a depicts the structure of the 3D 16-layer Fe-diode. The schematic of the fabrication process flow of the Fe-diode is provided (Supplementary Fig. 1), which comprises five main steps18. The first step (i) involves Multiple TiN/SiO2 are deposited by PVD and PECVD, the second step (ii) is dry etch to split the plane electrode, the third step (iii) is SiO2 filling in the trench, the fourth step (iv) is hole etching and the fifth step (v) is functional layer deposition. Due to its unique vertical stacking capability, implementing multi-layer 3D Fe-diodes is straightforward. This 3D Fe-diode configuration is a more area-efficient approach, which facilitates ultra-dense storage without significantly complicating the manufacturing process, compared with conventional planar Fe-diodes19,20,21,22,23,24,25. Also, our 3D Fe-diodes are designed to be fully compatible with existing CMOS technology, allowing for large-scale and cost-effective production.

Fig. 1: Device structure of 16-layer 3D Fe-diode.
figure 1

a Structure of the 16-layer 3D Fe-diode. The green color represents the insulator layer, yellow represents the plane electrode, blue represents the ferroelectric layer, and red represents the bottom electrode. b Cross-sectional TEM image of a 3D Fe-diode. The scale bar is 200 nm. Each horizontal WL was opened by selective etching successively. The area of the memory cell was defined by the thickness of the bottom electrode TiN (20 nm) and the perimeter of the hole. c Magnified TEM image of a single 3D Fe-diode highlighted by the blue box in (b) (scale bar is 10 nm). The elemental composition of each layer of the 3D Fe-diode are labeled. d Multi-level conductance states of a single cell. e Multi-level storage distribution. f Classification of different noise types in electron devices. The ideal entropy source requires frequency-independent high noise density. g Normalized current power spectral density (S/I2) of the Fe-diode in HRS measured at various bias conditions.

Full size image

The device’s structure was analyzed using cross-sectional transmission electron microscopy (TEM), which confirmed the vertical arrangement of the 16-layer Fe-diode device (Fig. 1b). In contrast to simpler devices, our Fe-diode integrates 16 layers of ferroelectric and electrode materials, creating a highly structured multi-layer device. Each layer’s precise thickness enhances the electrical performance and scaling potential, allowing for a uniform and reliable device operation. The vertical stacking of these layers addresses scaling limitations found in planar configurations, enabling a more compact design with improved energy efficiency. The zoomed-in high-resolution cross-sectional TEM image illustrates the vertical structure of a single Fe-diode (Fig. 1c).

The advantages of the Hf-based 3D 16-layer Fe-Diode lie in its potential for high-density integration, enabling selector-free cross-point architecture that simplifies circuit design. Unlike traditional 1T1C and FeFET structures26,27,28, the Fe-Diode provides inherent non-linearity and enhances read performance29,30,31,32,33. In addition, the compatibility of Hf-based materials with existing fabrication processes allows for improved miniaturization and integration34,35,36,37,38,39. Importantly, the Fe-Diode also offers significant energy efficiency with fast operation speed and low read current, as its operational mechanism reduces power consumption during read and write cycles29. This 16-layer configuration not only demonstrates the scalability of the technology but also enhances its performance capabilities. Its ability to achieve efficient data storage while minimizing complexity and energy use makes it suitable for low-energy-consumption and high-area-efficiency memory.

The multilevel storage characteristics of the 3D Fe-diode array are prominently illustrated through the statistical results obtained from the 8 kb 3D Fe-diode array (Supplementary Fig. 2 and 3), as depicted in Figs. 1d, e. Figure 1d highlights the various multilevel conductance states, which represent the synapse weights essential for neuromorphic computing applications. In Fig. 1e, we observe that States 1, 2, and 3 are situated in the low resistance state (LRS), while State 4 is in the high resistance state (HRS). This distinct separation between LRS and HRS is consistent with the observations in Fig. 1d, confirming the effectiveness of the multilevel state design.

Figure 1f shows the classification of noise in electron devices. Random Telegraph Noise (RTN), which is caused by a single trap, is difficult to activate and control. Thermal noise is frequency independent, but the density is very small, and it is easily affected by the test environment. For 1/f noise, although it has the high noise density, the density decreases as the frequency increase40.

The S/I² characteristics of the Fe-diode in the high resistance state (HRS) under various reading voltages are shown in Fig. 1g. In the high Vread region, the presence of 1/f noise is notable, suggesting fluctuations that are dependent on frequency. As Vread decreases, however, a frequency-independent high-density noise, characterized by slope (β) = 0, becomes the dominant feature. The observed noise (β = 0) is primarily linked to shot noise41.

The experimental results indicate that the multilevel states of the 3D Fe-diode exhibit uniformity, which is crucial for reliable data storage. The ability to maintain consistent resistance levels across multiple states enhances the array’s performance in terms of read accuracy and data integrity. Furthermore, the uniform distribution of resistance states allows for precise tuning of synaptic weights, making the 3D Fe-diode array suitable for high-density memory applications and advanced computing systems. In a word, the use of a 16-layer Fe-diode configuration offers several significant advantages over traditional single-layer or fewer-layer designs. Firstly, the increased number of layers enables enhanced functionality and performance due to the higher density of ferroelectric tunnel junctions. This allows for more compact integration and improved device scalability, which is crucial for high-area-efficiency applications. In addition, a 16-layer Fe-diode structure improves the overall energy efficiency of the device. By stacking multiple layers, the effective channel resistivity is optimized, reducing power consumption and heat generation compared to simpler architectures. This configuration also leverages the cumulative benefits of each individual layer, resulting in better electrical characteristics and more reliable operation, which is beneficial for low-energy-consumption applications. Moreover, the 16-layer Fe-diode maintains compatibility with standard CMOS fabrication processes, facilitating its integration into existing semiconductor technology. This makes it feasible for large-scale production and helps in lowering manufacturing costs. In summary, the 16-layer Fe-diode design provides enhanced performance, energy efficiency, and manufacturing feasibility, making it a suitable choice for low-energy-consumption and high-area-efficiency applications.

Ideal entropy source by noise in 3D Fe-diode

The temperature dependence of different types of noise is shown in Fig. 2a. The density of thermal noise and 1/f noise is affected by temperature and frequency, respectively40. Thus, a temperature and frequency independent high-density noise is required as an ideal entropy source.

Fig. 2: Entropy Source by Noise in 3D Fe-diode.
figure 2

a Classification of different noise. Compared with 1/f noise and thermal noise, the ideal entropy source requires temperature-independent high noise density. b Normalized current power spectral density (S/I2) of the Fe-diode in HRS measured at various bias conditions. c Fano factor (F = (S/I2)/2qI) at f = 102 Hz of the Fe-diode cell in the HRS. d The relationship between log(I) and V−1 in DC current measurement conforms to the TAT transport mechanism. e S/I2 @ f = 10 Hz at T = − 40, 25, and 125 °C, respectively, with increasing Vread. Shot noise keeps constant at various Ts. f S/I2 of the Fe-diode in LRS. Only 1/f noise is observed. g S/I2 sampled at 10 Hz versus current. h, i The relationship among I, V and T conforms to the Schottky Emission.

Full size image

The characteristics of shot noise in Fig. 2b can be analyzed using the Fano factor (F = (S/I2)/2qI). This factor can enhance or suppress the total shot noise represented by equation 2qI42. The calculated value of F at a frequency of 102 Hz within the low Vread region is displayed in Fig. 2c. This shift in noise behavior can be attributed to the underlying conduction mechanism, which in the HRS is governed by trap-assisted tunneling (TAT), depicted in Fig. 2d. The shot noise is generated from the TAT process43. To understand the observed phenomena better, additional context is provided (Supplementary Fig. 4). At low Vread, the conduction is dominated by TAT through fast traps, which facilitates efficient charge transport. However, as Vread increases, the involvement of slow traps becomes significant, influencing the trapping and detrapping processes and altering the overall noise characteristics44. Consequently, shot noise is predominantly observed only at lower Vread levels. These findings indicate that the shot noise observed in the HRS at low Vread levels is a valuable characteristic, making it a suitable candidate for use as an entropy source due to its frequency-independent high noise density.

Moreover, the dependence of shot noise on temperature is performed. The normalized IT power spectral densities (SIT/IT2) of the 3D Fe-diode in HRS at − 40, 25, and 125 °C are shown, respectively (Supplementary Fig. 5a–c). The behavior of SIT/IT2 changes from 1/f noise to shot noise as the read bias (Vread) decreases, regardless of T. Since that the current of TAT is mainly related to the applied voltage V rather than temperature T, the power spectral density of shot noise (S = 2qF·I) is almost constant. Therefore, in the low voltage region, the shot noise shows temperature stability, as shown in Fig. 2e (Supplementary Figs. 6, 7). In a word, shot noise in HRS at low Vread is suitable to be used as the ideal entropy source owing to its frequency and temperature-independent high noise density.

In contrast, the noise behavior of the Fe-diode cells in the low resistance state (LRS) reveals a different profile. Unlike the HRS, the LRS exhibits only 1/f noise without any indication of shot noise, and the magnitude of this noise remains nearly constant, as illustrated in Fig. 2f, g. This consistent behavior aligns with the Schottky emission mechanism, suggesting a stable conduction environment under these conditions. The electrical test results further corroborate this mechanism, as shown in Fig. 2h, i.

Surprisingly, we found that the physical properties of the Fe-diode device are exactly what is needed for edge systems with high frequencies and drastic temperature changes. The noise density of the Fe-diode can be modified by the amplitude of the read voltage and remains stable at high frequencies and temperature fluctuations. With Fe-diode devices, Bayesian neural networks with an entropy source can be implemented in high-speed, high-density silicon-based chips. The mean and standard deviation of the weight distribution of the neural network are independently tunable. The mean is represented by the conductance of the Fe-diode, while the standard deviation can be fine-tuned by the Fe-diode-based entropy source. For entropy sources, different read voltages need to be used to obtain different densities of noise. For weight reads, a constant read voltage is required. We can adjust their mean and standard deviation separately without affecting each other. Thus, hierarchical Bayesian neural network models can be easily implemented. In the hierarchical model3, we can assume that the parameters are chosen from a normal distribution with mean and standard deviation, which are the hyperparameters. In this work, these hyperparameters can be represented by the physical properties of the Fe-diode device.

Figure 3a shows the structure of the hierarchical Bayesian neural network in this work. The network is divided into five layers, and the number of neurons are 784, 480, 240, 120, 10. The number of neurons in the input layer corresponds to the number of pixels in the dataset. The dataset used for the experiments is the MNIST dataset with an image dimension of 28 × 28. The example images of the MNIST dataset are the numbers “1”, “2”, “4”, and “8” are shown at the top of Fig. 3a. When training the network model, we not only update the weight values after each epoch, but also update the standard deviation of the weights. For capturing the correlation of weights in the same layer, the weights at the same hierarchy have the same standard deviation. Limiting the network parameters in such a hierarchical manner provides a profile representation of the Bayesian neural network. As shown in Fig. 3a, σ1, σ2, σ3, and σ4 provide standard deviations for the weights connecting layer i and layer i + 1, respectively. The visualization of weights and standard deviations mapping in 16-layer arrays is shown in Supplementary Fig. 8.

Fig. 3: The hierarchical BayesNN system based on 3D 16-layer Fe-diode array.
figure 3

a The hierarchical BayesNN oriented towards MNIST recognition, with the same layer weights having the same deviation to capture weight correlations, from the input layer to the output layer, with standard deviations of the weights being, σ1, σ2, σ3 and σ4. b The workflow for in situ training based on backpropagation and expectation maximization. c The details of updating weights and hierarchical deviations. d Setup for hardware implementation of the hierarchical Bayes-NN based on 3D Fe-Diode. e 3D Fe-Diode chip. f SEM image of the test chip. g SEM image of the 16-layer 8 × 64 Fe-diode array test chip.

Full size image

Figure 3b shows the workflow for in situ training using the Fe-diode array. Energy-efficient in situ training is achieved by backpropagation with expectation maximization. For better training, the initial conductance is usually set to a random moderate value. Then, we input the image pixels and labels from the MNIST training set into the network model and perform forward inference and backpropagation. Immediately after that, the weights and hierarchical deviations represented by the Fe-diode array can be updated according to the backpropagation algorithm. The details of this step are shown in Fig. 3c. The conductance Gtarget of the target device can be calculated, and this conductance is programmed into the corresponding device of the Fe-diode array. The standard deviation σn of weights connecting layer n and layer n + 1 can also be calculated, then the noise magnitude of the weights at each hierarchy is tuned so that they obey the calculated results (Supplementary Fig. 9). The tuning of the amplitude of the noise is realized by fine-tuning the read voltage of the Fe-diode device. The Bayesian neural network in this work contains four different standard deviations, so only four different read voltages need to be set. In order to implement the entire network in one 3D array, we crop the image size and downsize the network size. (Supplementary Figs. 10 and 11).

Since MNIST is just a simple number recognition task. To validate that our technique can scale to more complex and larger tasks, we also validated it on the Fashion-MNIST dataset and the CIFAR-10 dataset with inference accuracies of 88.16% (MLP) and 88.31% (VGG-11), respectively. (Supplementary Figs. 12 and 13).

In order to verify the true randomness of the noise of the Fe-diode devices, i.e., the noises with different weights do not affect each other and has no time correlation. We extracted the noise of the devices at different locations in the array, and based on the underlying random number generator to generate random bits for NIST and ACF tests. The NIST SP800-22 test results from 5 M random bits is generated by Fe-diode devices18. The NIST 800-90B test results show the minimum entropy is 0.99965 (Supplementary Table 1). The ACF test results at a 95% confidence level (within ± 0.014) verifies that the shot noise is an independent variable18.

Figure 3d shows the setup of the hierarchical BayesNN system based on a 3D 16-layer Fe-diode array (More details in Supplementary Fig. 14). The die micrograph and SEM of the test chip are shown in Fig. 3e–g. As seen by the yellow and green waveforms in the oscilloscope, the noise of the Fe-diode device can be fine-tuned (More details in Supplementary Fig. 15). Noise in the measurement equipment, including oscilloscope and ADCs, is shielded so that it does not affect the network.

Elemental mapping confirms the precise distribution of various materials within the device18, including the ferroelectric layers, electrodes, and any intermediate spacers, revealing clear boundaries between different materials. An elemental line scan indicates the thicknesses of individual layers18, highlighting the device’s fine structural precision with reduced dimensions, leading to a highly optimized Fe-diode design.

Figure 4 shows the training results of the Bayesian neural network based on the Fe-diode array. Figure 4a–c respectively show the conductance evolution of the Fe-diodes in the output layer, including initial states, intermediate states, and final states. Validated against the MNIST dataset, we implement in situ training based on the 3D 16-layer Fe-diode array, and the recognition accuracy increases over the epochs of training. The training accuracy is severely affected by the stochasticity of the noise. When the noise stochasticity is better, its minimum entropy is larger and closer to 1.

Fig. 4: The conductance of devices at the BayesNN’s output layer. Each BL connects 16 layers, using a total of 160 BLs (80 positive, 80 negative) to store the output layer weights.
figure 4

a–c show the initial, intermediate, and final states of conductance values during in situ training, respectively. d Comparison of minimum entropy and MNIST recognition accuracy based on Fe-diode-based entropy source and CMOS Latch-based entropy source under different temperature conditions. e Accuracy trend over training epochs. In situ training results follow the software simulation closely, with a 3–5% gap. f A certain example generated by BayesNN. g An uncertain example generated by BayesNN.

Full size image

Figure 4d shows the comparison of minimum entropy and MNIST recognition accuracy based on Fe-diode-based entropy source and CMOS latch-based entropy source (Supplementary Fig. 16) under different temperature conditions. As the temperature decreases, the thermal and RTN noise densities in CMOS devices decline, leading to lower randomness of the CMOS latch-based entropy source. On the contrary, thanks to the wide temperature range of the Fe-diode, the minimum entropy remains from − 40 °C to 125 °C. The recognition accuracy also remains good over a wide temperature range.

Figure 4e shows the training accuracy over epochs. The hardware-based Bayesian neural network achieves a recognition accuracy of 93.2%, closely following the accuracy of the software simulation, with a 3–5% gap. This gap comes from hardware non-idealities and data accuracy differences. Figure 4f, g respectively show the certain and uncertain results generated by our Bayesian neural network. The method of adding noise to the network can effectively reduce the error rate in recognizing outliers. The reduction in error rate by BayesNN with noise is 5.38% (MNIST), 8.91% (Fashion-MNIST), and 8.69% (CIFAR-10). (Supplementary Table 2).

Discussion

In summary, we have experimentally demonstrated a Bayesian neural network implementation based on a 3D 16-layer Fe-diode array, where the accuracy achieved by in situ training of the network is close to the software simulation. For the five major requirements for BayesNNs: (1) High quality entropy source; (2) Multi-level conductance states; (3) Temperature stability; (4) Low energy consumption and (5) High area efficiency, we construct a hierarchical BayesNN with unified entropy source and weights based on 3D 16-layer Fe-diode array, where one single layer in the 3D Fe-diode array is used to generate shot noise with high density for high-quality entropy source and for other layers, each layer has multi-level conductance states for synapse weights.

Table 1 summaries the performance of the state-of-the-art works. The proposed Bayesian neural network, owing to the low programming energy consumption of Fe-diodes and the 3D structure, can realize a low-energy (25fJ/program), high area-efficiency (0.06F2/state), in situ training supported Bayesian neural network system. Properties including a wide working temperature range (− 40 °C ~ 125 °C), 92.4% MNIST recognition accuracy and 0.9997 minimum entropy are finally achieved.

Table 1 Benchmark of the proposed Bayesian neural network system with other reported works
Full size table

Methods

Device fabrication

Fabrication of planar metal–ferroelectric–metal (MFM) Capacitors: Planar MFM capacitors were fabricated on p-doped Si (100) substrates. Initially, 30 nm TiN bottom electrodes (BEs) were deposited using physical vapor deposition (PVD). Next, Zr-doped HfO2 films were deposited at 260 °C using thermal atomic layer deposition (ALD) with Hf[N(C2H5)CH3]4 and Zr[N(C2H5)CH3]4, applying a 1:1 precursor cycle ratio to achieve 50% Zr content in the HfO2 layers. Similarly, 30-nm TiN top electrodes (TEs) were deposited by PVD. The amorphous Zr:HfO2 films were crystallized through rapid thermal annealing in an N2 environment at 400 °C for 30 s. The top electrode was etched for PFM testing, and a SiO2 thin film was deposited on the HZO film. After optical lithography and etching, a 2 μm diameter hole was created down to the HZO film. The TiN top electrode was deposited via ALD, defining the Fe diode cell size by the contact area between TiN and HZO.

3D Integration of Fe Diode: For the preparation of a 16-layer 3D vertical memory with Fe-diode cells, multiple layers of TiN (20 nm) and SiO2 (30 nm) were deposited using PVD and PECVD, respectively. Patterning and a single-step etching were employed to create stacked wordlines (WL) with smooth sidewalls. After SiO2 was filled in the trench, a 500 nm hole was etched down to the bottom SiO2. An Hf0.5Zr0.5O2 bilayer was deposited on the sidewalls via ALD, followed by sputtering TiN/W to fill the hole as the pillar electrode (BL). Each horizontal WL was sequentially opened through selective etching, and the memory cell area was defined by the TiN bottom electrode thickness (20 nm) and the hole perimeter.

Characterizations

The DC and current noise of a self-selective cell were tested by an Agilent B1500A semiconductor parameter analyzer connected to the experimental device. The pulse measurements were performed using the HV-SPGU module of Agilent B1500A. During the electrical measurement, the W top electrode was biased, while the TiN bottom electrode was grounded.