Recombination of localized quasiparticles in disordered superconductors

Abstract

Disordered superconductors offer new impedance regimes for quantum circuits, enable a pathway to protected qubits, and can improve superconducting detectors due to their high kinetic inductance and sheet resistance. The performance of these devices can be limited, however, by quasiparticles—the fundamental excitations of a superconductor. While experiments have shown that disorder affects the relaxation of quasiparticles drastically, the microscopic mechanisms are still not understood. We address this issue by measuring quasiparticle relaxation in a disordered β-Ta film, which we pattern as the inductor of a microwave resonator. We observe that quasiparticle recombination is governed by the phonon scattering time, which is faster than conventional recombination in ordered superconductors. We interpret the results as recombination of localized quasiparticles, induced by disorder, which first delocalize via phonon absorption. We analyze quasiparticle relaxation measurements on superconductors with different degrees of disorder and conclude that this phenomenon is inherent to disordered superconductors.

Introduction

Disordered superconductors have a high resistance in their normal state, leading to a competition between electronic localization effects and the global phase coherence of superconductivity. A large amount of disorder can induce electronic granularity, pre-formed Cooper-pairs, ultimately causing a superconductor-to-insulator phase transition^1,2.

Localization effects weaken the superfluid stiffness, thereby increasing the kinetic inductance (L_k) of the superconductor. This enables new regimes in high impedance quantum circuits and the development of protected qubits³, as well as highly non-linear elements for parametric amplification⁴. For superconducting single photon detectors^5,6, the high normal state resistance of disordered superconductors increases the broadband photon absorption efficiency^7,8 and photon responsivity^9,10.

Quasiparticles, the elementary excitations in a superconductor, play a central role in these applications. In quantum circuits, quasiparticles cause decoherence and microwave loss. Considerable efforts have been made to mitigate excess quasiparticles^{11,12,13,14,15} and to explain the non-vanishing quasiparticle density at low temperatures^16,17,18,19. For superconducting radiation detectors, the relaxation of photon-generated quasiparticles dictates the detector performance²⁰.

As disorder increases, the limiting relaxation time at low temperatures becomes shorter²¹. In contrast, quasiparticle relaxation times on the order of seconds have been measured in granular Al, which is highly disordered due to oxidized grain boundaries²². Furthermore, when exciting disordered superconductors with electromagnetic radiation, an anomalous quasiparticle response has been measured^23,24 and microwave loss typically increases with L_k²⁵. This hinders the use of disordered superconductors in quantum circuits and superconducting radiation detectors. These observations suggest that disorder affects quasiparticle relaxation, but the underlying mechanisms remain poorly understood.

In this work, we demonstrate that localization effects govern the relaxation of quasiparticles in disordered superconductors. Disorder induces local gap inhomogeneities that serve as localization sites where quasiparticles rapidly recombine. Consequently, the relaxation process is not governed by recombination of mobile quasiparticles, as in ordered superconductors (Fig. 1c), but rather by delocalization and subsequent on-site recombination with a localized quasiparticle (Fig. 1d). This leads to a shorter relaxation time with a weaker temperature dependence than in the absence of localization effects. Such a short relaxation time will help to mitigate excess quasiparticles in quantum circuits¹¹. On the other hand, at low temperatures and quasiparticle generation rates, a background of localized quasiparticles may induce additional microwave loss²² and limit the response of superconducting detectors^23,24.

Fig. 1: Quasiparticle fluctuation measurement and the inferred effect of disorder on quasiparticle recombination.

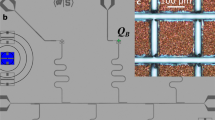
a Micrograph of the microwave resonator consisting of a NbTiN capacitor and β-Ta inductor on a membrane, which is highlighted in red. Inside the white circle, the figure is two times enlarged. We measure fluctuations in resonance frequency (δf), which are proportional to complex conductivity fluctuations (δσ₂). b Sketch of the β-Ta inductor on the 110-nm-thick SiN membrane. When two quasiparticles (green) recombine into a Cooper-pair (blue), a phonon is emitted (yellow curvy arrows). A change in the number of quasiparticles or Cooper-pairs changes σ₂, which we measure. The emitted phonon is trapped by the membrane, as indicated. We measure two resonators: one with the inductor on a SiN membrane (as sketched) and one with the SiN patch on solid Si substrate. c Sketch of traditional quasiparticle recombination with emission of a phonon with energy ≥2Δ₀, which can subsequently break a Cooper-pair. The BCS density of state (DOS) is sketched on the right, which has the same energy y-axis. d Sketch of quasiparticle recombination in disordered superconductors. Disorder can suppress the gap locally, inducing quasiparticle localization at a typical length scale of r_c ~ ξ¹⁶. Quasiparticles can delocalize via absorption of a phonon, after which they relax and rapidly recombine on-site, emitting a phonon with less than 2Δ₀ energy. Since phonon absorption is slow in disordered superconductors^27,40 and subsequent on-site recombination is fast^41,57, delocalization limits this process. On the right, the position-averaged DOS is sketched with a broadened coherence peak, parameterized by η, and a subgap tail consisting of localized states, parameterized by Γ_tail^42,44.

Results

Fluctuation measurements

We measure the quasiparticle relaxation time (τ) and density (n_qp) in a 40-nm-thick disordered β-Ta film²⁶, which is patterned as the inductor in a microwave resonator. The device is shown in Fig. 1a. The β-Ta film is disordered as the Ioffe-Regel parameter, k_Fl, is close to one, with k_F the Fermi wave number and l the electronic mean free path. We therefore expect localization effects to become important. Moreover, ql is much smaller than unity, with q the phonon wave number of a phonon with energy 2Δ₀, which is the BCS superconducting gap energy at low temperatures. This means the film is disordered with respect to electron-phonon interactions²⁷. The characterization of the film is outlined in the “Methods” section.

We cool the resonators to bath temperatures ranging from 20 mK to 300 mK. For each bath temperature, we drive the resonator at its resonance frequency and measure time streams of the complex microwave transmission in a homodyne setup (see “Methods”). From that, we extract the Power Spectral Density (PSD) of the fluctuations in σ₂, ${S}_{\delta {\sigma }_{2}/| \sigma | }(\omega )$, where σ = σ₁ − iσ₂ is the complex conductivity. This is equivalent to measuring the resonator frequency noise. These fluctuations are characterized by a Lorentzian spectrum²⁸. We fit a Lorentzian spectrum and extract the variance, s², and relaxation time, τ, as described in the “Methods” section.

The measured τ and s² are shown in Fig. 2a, b. For higher and lower bath temperatures than shown in Fig. 2, the quasiparticle fluctuations were obscured by other noise sources such as 1/f and amplifier noise.

Fig. 2: Measured relaxation time and variance compared with quasiparticle fluctuation theory.

The gray circles and red squares are determined from a fit to the measured fluctuation spectra (see “Methods”), which gives the relaxation time (a) and variance (b) of the quasiparticle fluctuation. The red squares are for the inductor on a SiN membrane (see Fig. 1b) and the gray circles on a SiN/Si solid substrate, as indicated by the legend. Error bars from statistical fit errors are smaller than the data points. The dashed lines in (a) are calculations for electron-phonon scattering time, Equation (3), which is 2D for T < 165 mK³⁵ and 3D for higher temperatures²⁷. The dashed lines in (b) are the variance of quasiparticle fluctuations for scattering events. The solid lines are for recombination. The red solid line in (a) includes the expected increase in relaxation time due to phonon trapping by the membrane (Fig. 1b). These curves are calculated without fit parameters, see “Methods”. The right axis in (b) gives the quasiparticle density corresponding to the variance of recombination events (the solid line).

Phonon scattering limited quasiparticle relaxation

We compare these measured values to the theory for quasiparticle relaxation. At low temperatures, k_BT ≪ Δ₀ with T the bath temperature and k_B the Boltzmann constant, τ is governed by electron-phonon interactions, because n_qp is low compared to the normal state carrier density²⁹. As a check, we compared the electron-electron and electron-phonon interaction times³⁰ and find that the electron-phonon interaction has the shortest relevant timescales in our system, as outlined in the Supplementary Section 1.

There are two inelastic electron-phonon processes that contribute to the relaxation of quasiparticles: recombination and scattering.

During a recombination event, two quasiparticles recombine into a Cooper-pair and emit a phonon with energy Ω ≥ 2Δ₀, as illustrated in Fig. 1c. Quasiparticle generation is the same process, but time-reversed. The recombination time, τ_rec, is proportional to 1/n_qp, which exponentially decreases with temperature, i.e.,^27,29

$${\tau }_{{{{\rm{rec}}}}}(T)={\tau }_{0}^{{{{\rm{rec}}}}}\sqrt{\frac{{T}_{{{{\rm{c}}}}}}{T}}{e}^{{\Delta }_{0}/{k}_{{{{\rm{B}}}}}T}.$$

(1)

T_c is the critical temperature and ${\tau }_{0}^{\,{\mbox{rec}}\,}$ is a proportionality constant that does not depend on temperature, but does depend on disorder and dimensionality (see “Methods”).

In our experiment, we probe the entire inductor volume and therefore measure the relaxation of an ensemble of quasiparticles. The bulk recombination time is given by³¹,

$${\tau }_{\,{\mbox{rec}}}^{*}={\tau }_{{{{\rm{rec}}}}}(1+{\tau }_{{{{\rm{esc}}}}}/{\tau }_{{{{\rm{pb}}}}})/2,$$

(2)

where τ_esc is the escape time and τ_pb is the pair-breaking time of a 2Δ₀ phonon. The last division by two in Equation (2) describes the pair-wise nature of recombination. The factor in parentheses is the phonon trapping factor and takes into account that the emitted 2Δ₀-phonon can subsequently break another pair. Quasiparticles in an ordered superconductor, like Al and α-Ta with ql ≫ 1, relax with a relaxation time given by Equation (2), which increases when phonon trapping is enhanced^21,29,32.

For the substrate case, with β-Ta on a SiN/Si substrate, we estimate the phonon trapping factor to be 2.0 from the acoustic mismatch theory set out in refs. ^33,34. Using the parameters of the film (see “Methods”), which are independently measured without fitting to the data, we obtain the solid black line in Fig. 2a. Details on the calculation of the curves in Fig. 2 are presented in Supplementary Section 1.

We increase τ_esc experimentally by etching the Si under the SiN patch of the resonators, such that the β-Ta inductor is suspended on a 110-nm-thick membrane. This is shown in Fig. 1b. Via a simple geometric calculation (Supplementary Section 1), we estimate that the membrane results in an increase of τ_esc by factor 58 compared to the substrate case. That would increase ${\tau }_{\,{\mbox{rec}}\,}^{*}$ by a factor 29, which is shown in Fig. 2a as the red solid line. We observe that the quasiparticle relaxation time is identical for both the substrate and membrane case, which is not in agreement with conventional quasiparticle recombination. Moreover, the temperature dependence of the relaxation time is much weaker than the conventional exponential temperature dependence (Equation (2)).

The dashed lines in Fig. 2a are for quasiparticle-phonon scattering. During a scattering event, a quasiparticle absorbs a thermal phonon of energy  ~k_BT. The inelastic time related to scattering, τ_scat, is proportional to the phonon occupation and therefore follows a power law versus temperature,

$${\tau }_{{{{\rm{scat}}}}}(T)={\tau }_{0}^{{\mbox{scat}}\,}{\left(\frac{T}{{T}_{{{{\rm{c}}}}}}\right)}^{-n},$$

(3)

with 2 ≤ n ≤ 9/2. n and ${\tau }_{0}^{\,{\mbox{scat}}\,}$ depend on disorder and the electron and phonon dimensionality^27,29,35,36. In our film, thermal phonons are 2D for T ≲ 165 mK and 3D for higher temperatures. This changes the exponent n from 9/2 in 3D²⁷ to 7/2 in 2D³⁵. This results in the dashed lines in Fig. 2a. We divide Equation (3) by a factor 2 in Fig. 2a to account for pair-wise recombination after the phonon scattering event, similar to Equation (2).

The agreement between the measured quasiparticle relaxation time and the power-law temperature dependence of phonon scattering indicates that quasiparticle relaxation is governed by phonon scattering. This is the main experimental result of this work and is in sharp contrast to ordered superconductors, such as Al and α-Ta^21,32.

Verification of quasiparticle generation-recombination fluctuations

To examine which relaxation process we observe, we compare the measured variance to the calculated variance of quasiparticle generation-recombination and scattering fluctuations in σ₂. This is shown in Fig. 2b. We calculate the generation-recombination noise variance with ${s}^{2}=({n}_{{{{\rm{qp}}}}}/V){(d({\sigma }_{2}/| \sigma | )/d{n}_{{{{\rm{qp}}}}})}^{2}$²⁸, where V is the β-Ta volume, and the factor in parentheses is the responsivity of the complex conductivity to changes in the quasiparticle density. This results in the solid line in Fig. 2b. This variance is equal for the membrane and substrate case, because it does not depend on phonon trapping. The responsivity factor is approximately constant with temperature (<2% deviation in our measurement regime) and known from theory^37,38, which allows us to directly measure the quasiparticle density from the variance³⁹. The right axis of Fig. 2d gives the quasiparticle density corresponding to the variance.

The dashed lines in Fig. 2b give the variance for scattering interactions. It is orders of magnitude lower than the variance for recombination events, because the energy difference of a scattering event is much less than that of a recombination event, k_BT ≪ Δ₀. The variance of the fluctuations clearly corresponds to the recombination of thermal quasiparticles²⁸. We attribute the small deviation from the thermal line at low temperatures to microwave read-out power effects¹⁷.

We performed the same analysis to the measured dissipative fluctuations, δσ₁, see “Methods”. The results show the same phenomenology as Fig. 2: a relaxation time governed by phonon scattering and a generation-recombination noise variance. This shows that we measure quasiparticle recombination events^28,39.

To summarize the above, we observe that the quasiparticle relaxation in this disordered film is governed by fast quasiparticle recombination with a time scale given by phonon scattering, which is not affected by phonon trapping. This is in sharp contrast to ordered superconductors³².

Recombination of localized quasiparticles

We explain these observations by localized quasiparticles that delocalize via phonon absorption. A delocalized quasiparticle relaxes again to another localization site and subsequently recombines on-site (Fig. 1d). Phonon absorption is relatively slow in a disordered (ql ≪ 1) metal⁴⁰ and the subsequent on-site recombination is fast, since the quasiparticles relax to the same location¹⁶. Therefore, phonon absorption limits the relaxation time, as observed in Fig. 2a. Even in the membrane case, where recombination should be slow due to phonon trapping, phonon absorption limits the relaxation time. The reason for this could be the following. The phonon that is emitted during on-site recombination has an energy below 2Δ₀, since the delocalized quasiparticle relaxes further into a localization site (Fig. 1d). The chance for such a phonon to break a Cooper-pair is very low, because the density of localized states with E < Δ₀ is very low (inset of Fig. 1d). Therefore, the phonon trapping effect for on-site recombination should be largely reduced⁴¹. This is consistent with Fig. 2, where we observe the relaxation time to be equal to the scattering time for both the membrane and substrate case.

To support this interpretation of the results, we modeled the quasiparticle fluctuations with the master equation approach described in ref. ²⁸. We describe the quasiparticles as localized such that their recombination rate depends on the average distance between two quasiparticles, as set out in ref. ¹⁶. For vanishing temperatures, this results in an exponentially long relaxation time and an excess quasiparticle density¹⁶. We however measure at a finite temperature where quasiparticles can delocalize via inelastic phonon scattering. We therefore include a second quasiparticle level to describe mobile quasiparticles, and set the delocalization time to τ_scat from Equation (3). We assume the localization time to be much shorter, such that the mobile quasiparticle density is small. We include an on-site recombination term, where a mobile quasiparticle relaxes and recombines on-site with a localized quasiparticle (Fig. 1d). We set the characteristic time for on-site recombination, ${\tau }_{0}^{\,{\mbox{os}}\,}$ c.f. ${\tau }_{0}^{\,{\mbox{rec}}\,}$ in Equation (1), such that on-site recombination is much faster than localization.

The resulting fluctuation spectra for the total number of quasiparticles follow the observed behavior, see “Methods”. When analytically examining this model, we see that in the limit of fast on-site recombination, the quasiparticle relaxation time is given by τ_scat/2 (the dashed lines in Fig. 2a) and the variance is equal to n_qp (black line in Fig. 2b). For details on the model calculations, see Supplementary Section 5.

The proposed origin of the localized states is local gap variations induced by disorder. This is described by the theory of refs. ^42,43, which extends the Larkin-Ovchinnikov inhomogeneous pairing theory⁴⁴. Such gap variations have been measured in highly disordered TiN⁴⁵. The effect of inhomogeneous pairing on the density of states is two-fold: (1) the coherence peak is broadened with a pair-breaking parameter η, which is equivalent to the Abrikosov-Gor’kov description of magnetic impurities⁴⁶, and (2) the density of states acquires an exponential subgap tail of localized states, characterized by Γ_tail. This is sketched in the inset of Fig. 1d. The values of η and Γ_tail depend on the strength of the local gap variations.

Because the thickness of our β-Ta film is on the order of the coherence length, ξ (see “Methods”), we take both Coulomb-induced mesoscopic fluctuations and finite thickness effects into account and obtain η ≈ 2.4 × 10⁻⁵⁴². To estimate Γ_tail, we consider our film quasi-2D, in which case Coulomb-enhanced mesoscopic fluctuations dominate and give Γ_tail/Δ₀ ≈ 1.5 × 10⁻⁴⁴². Quasiparticle states in this subgap tail overlap, and quasiparticles in these states will relax further. The effective localization radius at which this process stops can be estimated from Γ_tail and η and is on the order of ξ¹⁶. With the values mentioned above, r_c ≈ 3.5ξ ≈ 65 nm. This gives an estimate of density of localized quasiparticle states of ${\tilde{n}}_{\,{\mbox{qp}}}^{{{{\rm{loc}}}}}=3/(4\pi {r}_{{\mbox{c}}\,}^{3})\approx 8.5\times 1{0}^{2}\,\mu {{\mbox{m}}}^{-3}$. For details see Supplementary Section 6.

Comparing this number to the right axis of Fig. 2b, we conclude that the thermally generated quasiparticles localize due to gap variations for temperatures T < 178 mK. This leads to the situation in Fig. 1d. For higher temperatures, the thermal quasiparticle density is larger than the density of localized states. This alters the quasiparticle localization dynamics and might be related to the plateau we observe in Fig. 2a for T > 175 mK.

Discussion

Following the same line of reasoning, we expect to see the same phenomenology in other disordered superconductors. Indeed, a weak temperature dependence of the quasiparticle relaxation time is also observed in TiN for different levels of disorder⁴⁷, which was not understood before. The electron-phonon scattering time at T_c has also been measured for these films⁴⁸, which provides an accurate estimate of ${\tau }_{0}^{\,{\mbox{scat}}\,}$ and ${\tau }_{0}^{\,{\mbox{rec}}\,}$ in Equations (1) and (3). We analyzed those results and found that static scatterers cause a power law temperature dependence of the phonon scattering time with n = 2³⁶. Taking this into account, the relaxation times for these TiN films follow both the temperature and disorder dependence of electron-phonon scattering, similar to Fig. 2a, see Supplementary Section 3. With r_c ~ ξ^TiN16 these films are in the same regime as β-Ta, where ${n}_{{{{\rm{qp}}}}}(T) < {\tilde{n}}_{\,{\mbox{qp}}}^{{\mbox{loc}}\,}$ and ql < 1. Therefore, also in these films, thermal quasiparticles localize, and the recombination process is limited to delocalization via phonon absorption (Fig. 1d).

Even in an ordered superconductor, a small amount of disorder could induce quasiparticle localization at low temperatures¹⁶. In ref. ³², we observed for Al that there is no effect of phonon trapping on the relaxation time in the saturation regime at low temperatures. We explained that by the presence of an excess number of localized quasiparticles. We estimate that the density of localized quasiparticle states for the quasi-2D Al film is given by, ${\tilde{n}}_{\,{\mbox{qp}}}^{{{{\rm{loc}}}}}\simeq 1/(\pi {r}_{{\mbox{c}}\,}^{2}d)\approx 160\,\mu {{\mbox{m}}}^{-3}$, where we take r_c ~ ξ^Al ≈ 200 nm. If all these states are filled due to a non-equilibrium generation process, the quasiparticle density corresponds to the observed saturation time of 1 ms in ref. ³². An increase in disorder increases the number of localized quasiparticle states and decreases this saturation time. This is experimentally shown in ref. ²¹ for Al and α-Ta. Furthermore, the most disordered Al film in ref. ²¹ shows a weaker temperature dependence of τ, which points toward the same phenomenology as observed in Fig. 2a.

In Fig. 3, we sketch these different quasiparticle recombination regimes. Above the solid line, the thermal quasiparticle density is larger than the density of localized quasiparticle states. In that regime, the relaxation time follows the free quasiparticle recombination time, ${\tau }_{\,{\mbox{rec}}\,}^{*}(T)$ given by Equations (1) and (2) and shown in Fig. 1c. Below the solid line, quasiparticles recombine within a localization site. The relaxation time saturates to the recombination time at a quasiparticle density equal to the number of localization sites, ${\tilde{n}}_{\,{\mbox{qp}}}^{{\mbox{loc}}\,}$, as observed in refs. ^21,32. However, if the phonon scattering time is longer than this saturation time, quasiparticle localization via phonon absorption limits the relaxation, and the temperature dependence of the relaxation time is altered to the power-law of τ_scat, Equation (3). This regime is indicated as the light gray area in Fig. 3. The results of refs. ^21,32,47, which were previously unexplained, and Fig. 2 are shown in the appropriate disorder and temperature regimes and are consistent with the observed temperature dependence of the measured relaxation times.

Fig. 3: Different regimes of quasiparticle recombination as a function of temperature and disorder.

Each regime (indicated in a shade of gray) is characterized by a different temperature dependence of the quasiparticle (QP) relaxation time. The x-axis is chosen such that the dotted vertical line, ql = 1 for 2Δ₀ phonons, is approximately on the same point for different superconductors. For simplicity, we take ql for 2Δ₀ phonons only in this sketch, such that on the right side of the ql = 1 dotted line, both recombination and scattering interactions are disordered. The solid line gives the values at which the thermal quasiparticle number equals the number of localized quasiparticle states, which we estimate as ${\tilde{n}}_{\,{\mbox{qp}}}^{{\mbox{loc}}\,}=3/(4\pi {\xi }^{3})$. Below this solid line, quasiparticles will localize and recombine on-site. Below the dashed line, the scattering time, Equation (3), is longer than the recombination time, Equation (1), at a quasiparticle density equal to ${\tilde{n}}_{\,{\mbox{qp}}}^{{\mbox{loc}}\,}$, i.e., ${\tau }_{{{{\rm{rec}}}}}({\tilde{n}}_{\,{\mbox{qp}}}^{{\mbox{loc}}\,})$^27,29. In that regime, delocalization via phonon absorption limits quasiparticle recombination (Fig. 1d), which is indicated in light gray. For ql < 1 (the right side of the dotted line), phonon absorption is always slower than recombination at ${\tilde{n}}_{\,{\mbox{qp}}}^{{\mbox{loc}}\,}$. The colored areas give the experimental conditions of refs. ^21,32,47 and Fig. 2. The fade at lower temperatures for refs. ^21,47 are added because these are measurements via a pulsed excitation, which does not give information on the quasiparticle temperature. In ref. ²¹, disorder is increased by implanting ions. There is however no data on how much $1/\sqrt{\xi \Delta }$ increased in these films, which we indicated by an additional fade to higher disorder. The recombination regimes are consistent with the observed temperature dependence of the relaxation time in the respective experiments.

A saturation of the quasiparticle relaxation time requires a non-equilibrium quasiparticle generation process such as microwave read-out power¹⁷, cosmic rays¹³, radioactivity¹⁵ and stray light¹⁴. In Fig. 3, this can be viewed as a saturation of T/T_c, when T is an effective quasiparticle temperature. We assume that there is a number of excess quasiparticles present in our experiment due to the continuous microwave read-out¹⁷, which is small compared to the thermal quasiparticle density. To verify this, we measure τ and s² in the same way, but for higher read-out powers, see “Methods”. We observe that the excess quasiparticle generated by read-out power is minimized at a read-out power equivalent to a number of photons in the resonator of ${\bar{n}}_{{{{\rm{ph}}}}}\approx 6\times 1{0}^{4}$, which was used to obtain Fig. 2. For an estimation of the read-out power effects at this read-out power, see Supplementary Section 7. If we would reduce the bath temperature and minimize this generation process further, quasiparticles can become fully localized, which enhances the relaxation time exponentially¹⁶. For example, a relaxation time in granular Al on the order of seconds has been measured with ${\bar{n}}_{{{{\rm{ph}}}}}\approx 1-300$ at 25 mK²². This relaxation time decreases with increasing ${\bar{n}}_{{{{\rm{ph}}}}}$, indicating a saturated excess quasiparticle density that is sustained by microwave power. To verify that this originates from the localized quasiparticle dynamics presented in ref. ¹⁶, an experiment that independently probes both the relaxation rate and the quasiparticle effective temperature is needed. Such an experiment would be similar to this work, but at much lower temperatures and generation rates.

During the review process of this article, some related studies became available, which we reference here for completeness^49,50,51.

To conclude, we showed that quasiparticle relaxation in a disordered superconductor (with ql < 1) is governed by quasiparticle localization. After delocalization via phonon absorption, quasiparticles relax and recombine rapidly on-site (Fig. 1d), which enhances the relaxation rate. This impacts the performance of superconducting devices. For radiation detectors that measure the presence of photon-generated quasiparticles, the signal will be reduced as a result of the faster relaxation time. This presents a trade-off between photon absorption efficiency (increasing with disorder) and signal (decreasing with disorder). In quantum circuits, the short relaxation time will help eliminate excess quasiparticles at critical elements such as Josephson junctions, thereby improving coherence⁵². At low temperatures and small quasiparticle generation rates, localized quasiparticles could however increase microwave loss^22,44. Therefore, the fundamentally different quasiparticle dynamics presented in this work must be considered when implementing disordered superconductors in quantum circuits and radiation detectors.

Methods

Device design and fabrication

The capacitive part of the resonator is an interdigitated capacitor (IDC), with 20 μm wide fingers and 10 μm wide gap. It is patterned using an SF₆ Reactive Ion Etch (RIE) in a 150-nm-thick NbTiN film⁵³ with a critical temperature of 14.0 K and resistivity of 260 μΩcm. This design minimizes noise from Two Level Systems (TLS)⁵⁴ and ensures that the resonance frequency is highly sensitive to changes in the inductive β-Ta section, where the current density is high. The inductor is a strip of β-Ta, see Table 1, patterned with an SF₆ RIE etch. We place the β-Ta film on a SiN patch, which serves as a membrane for one of the resonators after the Si wafer is etched away from the backside using KOH, see Fig. 2a, b. The inductor is shorted at the end to the NbTiN ground plane to make a quarter-wave resonator. Quasiparticles in the β-Ta are confined to the inductor volume due to the higher superconducting gap of the NbTiN.

The resonance frequency is 5.1 GHz for the membrane resonator and 5.3 GHz for the substrate resonator, which is set by the finger lengths of the IDC. We set the coupling quality factor, Q_c, to  ~10,000 by tuning the length of the coupling bar next to the read-out line. The internal quality factor, Q_i, at 20 mK is approximately 400,000.

Film characterization

To obtain a measure of disorder and electron and phonon dimensionalities, we performed a measurement of the resistance versus temperature, which provides the normal state resistivity, ρ_N, and T_c, the Hall resistance at 1 K, which provides the charge carrier density, n_e, and the upper critical field as a function of temperature, which provides the diffusion constant, D. The results can be found in Table 1 and the details of these measurements are given in Supplementary Section 2. The Ioffe-Regel parameter, k_Fl, with k_F the Fermi wave number and l the electron mean free path, is of order unity. Therefore, the film is electronically disordered and we expect localization effects become important. References ^42,43 describe what electronic disorder does to the superconducting state: it introduces a broadening of the density of states and a subgap tail, consisting of localized quasiparticle states (see Fig. 1d).

Table 1 Geometry, electronic properties and phonon properties for β-Ta

For phonon-mediated superconductivity, disorder is characterized with respect to the electron-phonon interaction, i.e., ql, with q the phonon wave number. We calculate ql at two phonon energies: 2Δ₀, corresponding to recombination phonons and k_BT, typical phonon energies for scattering. We use the mass density, $\hat{\rho }$, and the longitudinal and transverse phonon velocities, c_L and c_T, from ref. ⁵⁵, see Table 1. We only consider transverse phonons because these are the fastest relaxation rates in our case, as ${({c}_{{{{\rm{T}}}}}/{c}_{{{{\rm{L}}}}})}^{3}\ll 1$^27,36. With that, we calculate q(2Δ₀)l = 0.070 and q(0.2 K)l = 0.0046: both much smaller than 1, so the film is disordered with respect to electron-phonon interactions. We therefore use quasiparticle relaxation time calculations of Reizer and Sergeyev²⁷ and Devereaux and Belitz³⁵ which are in the disordered limit (ql ≪ 1), instead of the widely used pure limit (ql ≫ 1) results of Kaplan et al.²⁹. The main difference is that the scattering time (Equation (3)) has a steeper temperature dependence in the disordered case (n → n + 1) and the proportionality constants in Equations (1) and (3), ${\tau }_{\,{\mbox{rec}}\,}^{0}$ and ${\tau }_{\,{\mbox{scat}}\,}^{0}$, become proportional to 1/ρ_N, which reflects the weakening of the electron-phonon coupling as disorder increases⁴⁰.

For electronic dimensionality, the dirty limit coherence length divided by the film thickness is, $\xi /d=\sqrt{l{\xi }_{0}}/d=0.39 < 1$, with l = 0.30 nm and ξ₀ = 0.79 μm, the Pippard coherence length. Therefore, the β-Ta film is a 3D superconductor, although it is close to 2D.

For the phonon dimensionality, we compare the phonon wavenumbers to the film thickness, qd. For recombination phonons, the film is 3D (q(2Δ₀)d = 9.3 > 1), and we can use the results of ref. ²⁷ for ${\tau }_{\,{\mbox{rec}}\,}^{0}$. For scattering phonons, the film is 2D for T < 165 mK (when q(k_BT)d ≤ 1/2) and 3D for higher temperatures. The phonon dimensionality dictates the temperature dependence, while the electronic dimensionality dictates the disorder dependence³⁵. We therefore use the 2D results of ref. ³⁵ with n = 7/2 for the low temperature regime and the 3D result of ref. ²⁷ with n = 9/2 for the high temperatures.

Setup

The sample is cooled in a dilution refrigerator, shielded from stray light with a box-in-a-box setup¹⁴. Magnetic interference is reduced by a factor of 10⁻⁶ by a CRYOPHY and superconducting niobium shield. The forward transmission measurement is performed in a homodyne setup. The microwave signal is attenuated at each temperature stage before it reaches the sample. After the signal passes the sample, it is amplified by a HEMT amplifier at 3 K and by a room temperature amplifier before it is mixed with the original microwave signal by an IQ mixer. For details on all the components, see ref. ⁵⁶.

Fluctuation measurement

Before each fluctuation measurement, we sweep the probe frequency to find the resonance frequency, f₀, and calibrate the complex forward transmission to an amplitude, δA, and phase, θ, with respect to the resonance circle⁵⁶. We set the microwave power of the on-chip probe tone relatively low at  − 98dBm to limit non-equilibrium effects such as quasiparticle redistribution¹⁷. We measure θ during 40 s at 50 kHz sampling frequency and 1 s at 1 MHz. We disregard parts of the time traces that contain pulses from cosmic rays and calculate the Power Spectral Densities (PSDs)³² and stitch the two PSDs from the 50 kHz and 1 MHz data at 20 kHz and downsample the spectrum to 30 points per decade to obtain S_θ(ω) for a single bath temperature. The fluctuations in σ₂, f₀ and θ are related via,

$${S}_{\delta {\sigma }_{2}/| \sigma | }(\omega )= {\left(\frac{4}{{\alpha }_{{{{\rm{k}}}}}\beta }\right)}^{2}{S}_{\delta f/{f}_{0}}(\omega ) \\= {\left(\frac{1}{{\alpha }_{{{{\rm{k}}}}}\beta Q}\right)}^{2}{S}_{\theta }(\omega ).$$

(4)

Here, σ = σ₁ − iσ₂ is the complex conductivity and ∣σ∣ is the absolute mean value at the set bath temperature. At low temperatures (k_BT ≪ Δ₀) ∣σ∣ ≈ σ₂. $Q={(1/{Q}_{{{{\rm{i}}}}}+1/{Q}_{{{{\rm{c}}}}})}^{-1}$ is the loaded quality factor and α_k = L_k/L_tot is the kinetic inductance fraction of the β-Ta volume with respect to the entire resonator. β is a correction factor for the film thickness, which we set to 2 since we are in the thin film limit (λ ≫ d, with λ ≈ 1.6 μm, the penetration depth)⁵⁶.

Q and α_k are measured in a separate measurement where we sweep the probe frequency to get the resonance curve at each bath temperature. We fit a Lorentzian resonance dip to those curves and extract f₀, Q_i and Q_c versus temperature. From f₀(T), we determine α_k⁵⁶, which in our case is α_k ≈ 0.44.

We disregard the 50 Hz, amplifier and 1/f noise contributions in the PSD, see Supplementary Section 4. This results in the PSDs shown in Fig. 4a, b. Panels c and d of Fig. 4 show the calculated PSDs from a fluctuation model that includes localized recombination, see Supplementary Section 5. We fit a Lorentzian spectrum to the measured ${S}_{\delta {\sigma }_{2}/| \sigma | }(\omega )$ with,

$${S}_{{{{\rm{fit}}}}}(\omega )=\frac{4{s}^{2}\tau }{1+{(\omega \tau )}^{2}},$$

(5)

to extract the variance s² and relaxation time τ from the fluctuations. An example fit is shown in Fig. 4b as the dashed line. The relaxation time and variance obtained this way are shown in Fig. 2. Following the same measurement procedure for σ₁ results in the relaxation time and variance shown in Fig. 5. Using higher microwave powers for the probe tone alters the relaxation time and variance as shown in Fig. 6.

Fig. 4: Measured and simulated power spectral densities of the complex conductivity.

Different colors are for different bath temperatures, as indicated by the colorbar. Other noise sources, such as amplifier noise and 1/f-noise have been subtracted from the measured spectra in (a) and (b), as explained in the Supplementary Section 4. The dashed black line in (b) is an example fit using Equation (5). c, d Calculated power spectral densities for quasiparticle fluctuations at the same bath temperatures as the measurements. The quasiparticle fluctuation spectra are calculated with the framework described in ref. ²⁸, including the localized quasiparticle dynamics described in ref. ¹⁶. The quasiparticle density fluctuations are analytically converted to σ₂/∣σ∣-fluctuations. For details on the model and calculations, see Supplementary Section 6.

Fig. 5: Fluctuation measurement of σ₁.

Quasiparticle relaxation time (a) and the variance (b) are obtained the same way as in Fig. 2, but from the fluctuations of the dissipative part of the complex conductivity, δσ₁. Error bars indicating statistical fit errors are smaller than the data points. The quasiparticle signal in σ₁ is a few times lower than in σ₂³⁸, which results in a smaller usable temperature range. For the substrate resonator, we did not observe any Lorentzian signatures in the PSDs of σ₁.

Fig. 6: Read-out power dependence of the relaxation time and variance.

a Relaxation time versus temperature for the membrane resonator at different on-chip read-out powers, indicated by the colors. The red data points and theory lines are the same as in Fig. 2. b Corresponding variances extracted from the same fits to σ₂-fluctuations. Error bars indicating the statistical fit errors are smaller than the data points, for both panels. A higher read-out power leads to a larger variance and smaller lifetime, which is consistent with microwave power-induced excess quasiparticles¹⁷. To limit these effects, we set the read-out power to the minimal value in this figure (red data set) and obtain the data in Fig. 2. See Supplementary Section 7 for an estimation of the read-out power effects at this lowest read-out power.

The resonance frequencies and quality factors result in a resonator bandwidth of Δf = f₀/(2Q) ≈ 0.3MHz (or equivalently, a resonator ring time of  ~0.6 μs), which is outside of the frequency range used for the fits. We therefore do not consider the effects of the resonator roll-off on the PSDs.

The datasets for membrane and substrate have been measured at two different times in the same setup and experimental conditions.