Evidence for single variant in altermagnetic RuO₂(101) thin films

Abstract

Altermagnetism presents intriguing possibilities for spintronic devices due to its unique combination of strong spin-splitting and zero net magnetization. However, realizing its full potential hinges on fabricating single-variant altermagnetic thin films. In this work, we present definitive evidence for formation of single-variant altermagnetic RuO₂(101) thin films with fully epitaxial growth on Al₂O₃(1$\bar{1}$02) r-plane substrates, confirmed through rigorous structural analyses using X-ray diffraction, atomic-resolution transmission electron microscopy and X-ray magnetic linear dichroism. The mutual correspondence of the occupancy of oxygen atoms on the surfaces of RuO₂(101)[010] and Al₂O₃(1$\bar{1}$02)[11$\bar{2}$0] plays a decisive role in the formation of the single-variant RuO₂, which is also supported by our first-principles density functional theory calculations. We further observed spin-splitting magnetoresistance in the single-variant RuO₂(101)/CoFeB bilayers, highlighting the characteristic effect of single variant on spin transport. The demonstration of single-variant RuO₂(101) films marks a significant advancement in the field of altermagnetism and paves the way for exploring their potential applications.

Introduction

Altermagnetism represents a unique phase of magnetism, distinct from the conventional characteristics of ferromagnetism and antiferromagnetism^1,2,3,4. Unlike traditional magnetic materials, altermagnets exhibit large spin splitting but maintain zero net magnetization due to the combined protection of spin and real-space group symmetry^{5,6,7,8,9,10,11,12}. In essence, they exhibit the strong spin polarization typical of ferromagnets, while retaining the antiparallel magnetic ordering characteristic of antiferromagnets. This intriguing combination of ferromagnetic-like spin polarization and antiferromagnetic order holds immense potential for spintronic applications, such as spin-orbit torque (SOT) and magnetoresistive devices^{13,14,15,16,17,18,19}. The number of potential altermagnetic materials is steadily growing, with candidates ranging from insulators to metals^{1,9,12,20,21,22,23}. Among them, tetragonal RuO₂ has emerged as a particularly exciting altermagnet. It is a conductive rutile oxide and was considered a paramagnet, but later proved to be an itinerant antiferromagnet^24,25, and more recently demonstrated to have strong time-reversal symmetry breaking in the band structure of altermagnetic RuO₂¹². A prominent anomalous Hall effect was reported in RuO₂ thin films due to the altermagnetic phase^26,27. Néel spin currents and tunneling magnetoresistance effect have also been proposed in RuO₂/TiO₂/RuO₂(001)^17,19 and RuO₂/TiO₂/CrO₂(110)²⁸ heterostructures. Further, it was demonstrated that RuO₂ enabled efficient generation of spin currents due to its spin splitting effect^13,14,15,16. The efficiencies of the spin current generation and the spin direction of the resulting spin currents are strongly dependent on the crystallographic orientation of the RuO₂ tetragonal lattice as well as the Néel vector orientation.

Among the various crystal facets of RuO₂, the (101)-oriented RuO₂ film stands out as a promising platform for spintronics applications, as it has recently been used to achieve SOT-induced magnetization switching without applying any external magnetic field¹⁵. In RuO₂(101) films, thanks to the tilting of the Néel vector with respect to the film surface, tilted spin currents are generated when the charge current is applied along the RuO₂[010] direction^13,15,16, which is crucial to achieve magnetic-field-free magnetization switching. Figure 1a shows the illustration of the crystal structure of the altermagnetic RuO₂, where the Néel vector is parallel to the [001] direction. The (101) atomic plane is indicated by a gray color, and it has an angle of about 55° with respect to the Néel vector. We name it variant A. In crystallography, RuO₂(101) has an equivalent variant B, i.e., RuO₂$(\bar{1}01)$, as shown in Fig. 1b. However, the orientations of the Néel vectors of the two variants are not identical, but instead related by mirror symmetry. Since the (101) and $(\bar{1}01)$ lattice planes are crystallographically equivalent and have the same lattice constants, two variants with different oriented Néel vectors might exist in the film, which will have important implications for spin transport. The schematic of the prototype band structure of RuO₂ is illustrated in Fig. 1c in which the spin-splitting Fermi surface is clearly shown for up-spin and down-spin. Once two variants are present in a thin film, they complicate materials design and hinder precise control over spin transport properties. Thus, a single variant RuO₂ is essential to unlock the full potential of spin splitting nature to revolutionize spintronics and facilitate the design of novel devices. To date, there has been no direct evidence confirming the existence of a single variant of RuO₂(101).

Fig. 1: Illustration of altermagnetic RuO₂ and structural and transport properties.

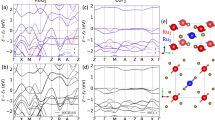
a, b, Illustrations of RuO₂ crystal structure labeled with spin directions and (a) Variant A with (101) lattice plane and (b) Variant B with $(\bar{1}01)$ lattice plane. c, Spin-splitting Fermi surface of the altermagnetic RuO₂. d, e Out-of-plane XRD analysis of the RuO₂ (30 nm) thin films grown on the r-plane sapphire substrate at 300 °C and then annealed at T_a = 300, 500, 600 or 700 °C for 15 min. f–h In-plane XRD (φ-scan) patterns of the (002), $(10\bar{1})$, and (200) planes of the RuO₂(101) film. i RHEED pattern of the film after the annealing at 600 °C. j First and second derivatives of resistivity as a function of measuring temperature for the RuO₂ thin films with different T_a. The dashed lines indicate the continuity changes corresponding to the Néel temperature of the antiferromagnetic-paramagnetic transition.

In this work, we fabricated RuO₂(101) epitaxial thin films on Al₂O₃(1$\bar{1}$02) r-plane substrates and utilized exhaustive structural analyses, including X-ray diffraction (XRD), atomic-resolution scanning transmission electron microscopy (STEM) and X-ray magnetic linear dichroism (XMLD) techniques, to provide direct evidence for the existence of a single variant in the RuO₂(101) films. We discovered that the precise matching of oxygen atom arrangements on the surfaces of RuO₂(101) and Al₂O₃(1$\bar{1}$02) is crucial in determining the formation of the single-variant RuO₂(101). First-principles density functional theory (DFT) calculations also proved its stability. XMLD can distinguish compensated magnetic structures and the formation of charge quadrupoles, undetectable by X-ray magnetic circular dichroism (XMCD). We performed XMLD with angular dependence to detect the Néel vector direction by probing the charge distributions coupled with linearly polarized synchrotron beams, which revealed a single-variant altermagnetic RuO₂(101) film with finite charge quadrupole and spin moment, in agreement with our theoretical calculations. We further demonstrated the spin-splitting magnetoresistance (SSMR) in the single-variant altermagnetic RuO₂(101)/CoFeB heterostructures associated with the distinctive single variant and titled spin current.

Results and discussion

A. Structural and electronic transport characterizations

Figure 1d shows the out-of-plane XRD scan results for the films deposited on the r-plane sapphire substrate at 300 °C and subsequently annealed at T_a = 300, 500, 600, and 700 °C. Apart from the substrate peaks, distinct diffraction peaks along the RuO₂[101] orientation were observed, indicating favorable growth in this orientation. Note that here, the (101) can also be equivalent to the $(\bar{1}01)$ considering the crystallographic symmetry. Figure 1e indicates the variation in full width at half maximum (FWHM) and diffraction intensity of 101 and 202 peaks to assess film crystallinity with annealing temperature. It is observed that higher annealing temperatures enhance crystallinity, evidenced by reduced FWHM and increased intensity. The interplanar lattice spacing of RuO₂(101) in the films is measured to be 0.2538 nm, slightly smaller than its bulk counterpart (0.2555 nm). In order to distinguish whether the film contains variant A or B or both, we further performed in-plane XRD measurements. The detailed description of the measurement setup and method are shown in Supplementary Materials. We firstly set up the configuration of X-ray incidence and reflection for RuO₂(002) plane by rotating the sample to χ = 34.08°, 2θ = 59.62°, then carried out the in-plane φ scan. The X-ray incident slit used in the measurement is 10 mm in size, which is large enough to obtain information about the crystal structure of the entire thin film. The result of the in-plane XRD scan for RuO₂(002) lattice plane of the RuO₂(101) thin film is shown in Fig. 1f. A single peak was clearly observed, which indicates a single-variant film. Note that we would see two peaks for the case of two variants by rotating the sample one full 360° circle in the plane of the sample surface because of the reverse variant RuO₂($\bar{1}$01). In order to further confirm this single variant feature, we also performed the in-plane XRD scan measurements for RuO₂(10$\bar{1}$) and (200) lattice planes at χ = 68.85°, 2θ = 35.29°, and χ = 55.28°, 2θ = 40.47°, respectively. The XRD patterns are shown in Fig. 1g, h. Both cases show a characteristic single peak. The above results indicate that only variant A exists in the RuO₂(101) thin film deposited on an Al₂O₃(1$\bar{1}$02) substrate. Figure 1i displays the reflection high-energy electron diffraction (RHEED) pattern along the RuO₂[10$\bar{1}$] direction, showing prominent streaks indicative of high-quality film preparation with a very flat surface morphology. We also investigated RuO₂ thin films grown on various substrates under different conditions and found that films on Al₂O₃(1$\bar{1}$02) exhibited the highest conductivity of 2.1 × 10⁶ Ω⁻¹m⁻¹ achieved at T_a = 600 °C. In addition, Fig. 1j shows the analysis of temperature-dependent resistivity, which reveals a Néel temperature around 390 K for films, indicating the transition from antiferromagnetic to paramagnetic states. More structure and electronic transport characterizations of the samples are in Supplementary Materials.

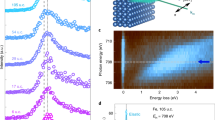
We further employed high-angle annular dark-field STEM (HAADF-STEM) for atomic-resolution structural analysis for the single variant RuO₂(101) film. The geometric relationship among the Néel vectors, RuO₂(101) and ($\bar{1}$01) planes are shown in Fig. 2a where the angle between the Néel vector and (101) or ($\bar{1}$01) plane is about 55°. If two types of variants were both formed in the RuO₂ film, two sets of Néel vectors would be obtained, among which one Néel vector deviates about 70° from the other. The HAADF-STEM image in Fig. 2b shows the atomic-resolution cross-sectional microstructure of the altermagnetic RuO₂ film grown on the r-plane Al₂O₃ substrate, with the viewing direction being parallel to the RuO₂[010] direction. A much larger scale of HAADF-STEM image is shown in Supplementary Materials. The corresponding nano beam electron diffraction (NBED) patterns collected from the film and substrate are shown in the upper-right and lower-right corners, respectively, which is also consistent with the epitaxial relationship by the XRD results. Figure 2c displays the enlarged HAADF-STEM image at the interface between the Al₂O₃ substrate and the RuO₂ film, where a good lattice matching is readily detected. The orange line is the trace direction of its Néel vector, having an angle of about 55° relative to the film plane. The specific atomic-matching scenario at the interface of Al₂O₃(1$\bar{1}$02)/RuO₂(101) is shown in the schematic diagram in Fig. 2d, which is consistent with the experimental result in Fig. 2c. This can be attributed to the fact that the RuO₂(101) plane, rather than the RuO₂($\bar{1}$01) (see the schematic of the cross-sectional lattice matching between RuO₂($\bar{1}$01) and Al₂O₃(1$\bar{1}$02) in Supplementary Materials), was formed on the surface of Al₂O₃(1$\bar{1}$02) substrate. The in-plane atomic lattice matching among Al₂O₃(1$\bar{1}$02), RuO₂(101) and RuO₂($\bar{1}$01) is shown in Fig. 2e–g, where only a single atomic plane of Ru atoms, and two layers of O atoms close to the Ru atomic layer are shown. Our crystallographic analysis clearly reveals that the in-plane atomic arrangement of RuO₂(101) is nearly the same as that of Al₂O₃(1$\bar{1}$02). The O atomic position in the RuO₂($\bar{1}$01) in-plane atomic arrangement, however, is different from that in the Al₂O₃(1$\bar{1}$02) case. To be specific, the two layers of O atoms have reversed their positions, i.e., the previous O layer above the Ru atoms now becomes the O layer below Ru, as highlighted by the dashed blue circles in Fig. 2e–g. Therefore, on the surface of Al₂O₃(1$\bar{1}$02) substrate, the growth of RuO₂(101) plane is preferable. We also conducted first-principles DFT calculations to clarify the stability of the Al₂O₃($1\bar{1}02$) surface (See Supplementary Materials). The calculations reveal that the substrate surface terminated with Al and O (z = + 0.5) atoms (Fig. 2e) is the most stable. We further calculated the stability of the RuO₂(101) and RuO₂($\bar{1}01$) variants by stacking RuO₂($101$) and RuO₂($\bar{1}01$) cells on the Al₂O₃($1\bar{1}02$) surface, corresponding to Fig. 2f [Al₂O₃($1\bar{1}02$)/RuO₂($101$)] and Fig. 2g [Al₂O₃($1\bar{1}02$)/RuO₂($\bar{1}01$)]. It is found that Al₂O₃($1\bar{1}02$)/RuO₂(101) has a lower total formation energy density by 1.2 J/m² compared to Al₂O₃($1\bar{1}02$)/RuO₂($\bar{1}01$). This result confirms that the Al₂O₃($1\bar{1}02$)/RuO₂(101) is the more favorable configuration, aligning with experimental observations. We note that the possibility of mixed surface terminations, due to thermodynamic competition and kinetic factors, may affect the stabilization of RuO₂(101) versus RuO₂($\bar{1}$01) variants. Once two variants exist, one would detect two peaks in the in-plane XRD φ scan (Fig. 1f–h). Therefore, surface treatment of the substrate and precise control of growth conditions are crucial for achieving single-variant RuO₂(101) thin films.

Fig. 2: Atomic-resolution STEM observations.

a Schematic diagram showing the geometric relationship among the Néel vector, RuO₂(101) and ($\bar{1}$01) planes. b HAADF-STEM image showing the cross-sectional microstructure of RuO₂ film grown on r-plane Al₂O₃ single crystalline substrate. The upper-right and lower-right insets show the NBED patterns of RuO₂ and Al₂O₃, collected from RuO₂[010] and Al₂O₃[11$\bar{2}$0], respectively. c Enlarged image showing the atomic arrangements at the interface between RuO₂(101) and Al₂O₃(1$\bar{1}$02). d Schematic diagram of the lattice match between RuO₂ and Al₂O₃, corresponding to the HAADF image in (c). e–g Schematic diagrams of the in-plane atomic arrangements in Al₂O₃(1$\bar{1}$02), RuO₂(101) and RuO₂($\bar{1}$01), respectively. The dashed blue circles in the black boxes highlight the positions of O atoms.

B. Detecting magnetic states of altermagnetic RuO₂(101) thin films by angular-dependent XMLD

Figure 3 shows the X-ray absorption spectroscopy (XAS), XMCD, and XMLD at Ru M-edges. In the XAS, both 3p to 4d and 3p to 5s absorption peaks with spin-orbit splitting of 3p_3/2 (M₃) and 3p_1/2 (M₂) levels are observed. Although the cross-sections in M-edge absorption are smaller than those in L-edges, finite signals of XAS and differences between linear polarized beams along horizontal and vertical directions can be detected, overlapping with linear background components of negative slope as displayed in Fig. 3a. The satellite peaks at 475 and 500 eV correspond to the 3p to 5s absorption. In the case of circularly polarized beams, no XMCD signals are detected as shown in Fig. 3b because of completely compensated antiferromagnetic order, which is different from the previous reports of Ru M-edge XMCD in Ru-based ferromagnetic compounds^29,30,31. Next, the XMLD signals detected by linearly polarized beams are displayed with sample angular dependence. Since the electric-field components of linearly polarized beams couple with those of magnetization, it depends on the rotation angles along in-plane between the beam and the antiferromagnetic Néel vectors. Figure 3c–h display the angular dependence of XMLD, which clearly shows the difference between positive and negative angles. Here, the angle between the sample surface normal and beam direction is defined as θ, and the angle that the sample is rotated in the plane of the film surface is φ. The geometry of θ = 0° corresponds to the normal incidence case in Fig. 3d, g. Clear differential XMLD line shapes are also observed. The XMLD signal intensities are most enhanced in the case of θ = − 55° tilt and gradually suppressed at 0° and + 35°, which can determine the Néel vector orientation along the [001] direction and the $3{z}^{2}-{r}^{2}$ orbital states are coupled mainly with the linearly polarized beam. To confirm these facts, the sample is rotated at φ = 90°, the spins are orthogonal, and canted components can couple with the linearly polarized beams as shown in the insets of Fig. 3f–h. With the sample rotation, the XMLD intensities are almost identical because of canting along the orthogonal direction. Since the beam spot size is on the order of micrometers, systematic changes in XMLD result from the formation of single variants as probed by XRD. Therefore, these results indicate that (i) the linear dichroism components arising from lattice symmetry are minimal, (ii) the antiferromagnetic ordering in the Ru sites with finite magnetic moments is endured, and (iii) the Néel vector orientation of RuO₂ is aligned along the [001] direction. Note that since the XMLD signals may include the structural information as X-ray linear dichroism (XLD), we performed the temperature-dependent XMLD measurements up to 400 K, higher than the Néel temperature of RuO₂, to eliminate the XLD contribution, as shown in Supplementary Materials. The results show a monotonic decrease in XMLD signal amplitude with increasing temperature and a significant suppression at 400 K. The weak spectrum at 400 K above the Néel temperature can reflect the structural contribution. To our knowledge, the structural component of XMLD (i.e., XLD) is generally temperature-independent unless a structural phase transition occurs. Since our temperature-dependent resistivity measurements indicate no such structural transitions, the significant temperature-dependent XMLD signal supports the magnetic origin and provides evidence of antiferromagnetic ordering in our RuO₂(101) samples. Although the magnetism in the RuO₂ is still controversial in recent experimental reports^32,33, the discrepancies may be due to sample-to-sample variations, especially differences in growth conditions, Ru or O vacancies, and structural uniformity.

Fig. 3: X-ray magnetic spectroscopies with angular dependence in RuO₂(101) thin films.

a XAS taken by linearly polarized beams at θ = −55°. b XMCD by the difference of circularly polarized beams. c–h XMLD with angular dependence. In the top three panels, the sample was rotated along the in-plane axis of θ = − 55°, 0°, and + 35° as displayed in the illustrations. The directions of the Néel vectors in RuO₂ are also illustrated (red arrows). The bottom three panels display the cases of sample rotation φ = 90° along the sample surface normal. Vertical axis scales are unified for all XMCD and XMLD panels. All measurements were performed at 80 K.

The XMLD spectral line shape analyses provide the quadrupole components (Q_zz) of the Ru sites using an XMLD magneto-optical sum rule^34,35,36. Since the Q_zz represents the degree of magnetically polarized charge anisotropy at the atomic sites, the electronic structure of the distorted Ru sites can be probed. The integrals of the XMLD spectra, excluding the 3p to 5s absorption contributions, can monitor the values of Q_zz, where asymmetric L₃ and L₂ line shapes result in the finite converged values of Q_zz (See Supplementary Materials). In the XMLD shown in Fig. 3c, positive converged values are estimated, suggesting that the quadrupoles elongating along the axial directions as a function of $3{z}^{2}-{r}^{2}$ are predominant. The Ru atoms are surrounded by octahedral oxygen sites with distortion along the axial oxygen atoms and are alternately aligned with the rotation of 90°. Since the XMLD (XLD) probes the sums of two kinds of Ru sites, the charge distortions of up and down spin sites are almost canceled, as suggested by the theoretical calculations shown in Fig. 4, and XMLD in RuO₂ probes only magnetically polarized information. Therefore, the systematic changes of angle-dependent XMLD suggest the single variant feature in the altermagnetic RuO₂(101) thin film.

Fig. 4: DFT calculations for altermagnetic RuO₂.

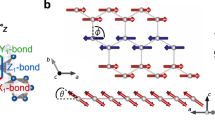
a, b Schematic illustration of the sites of Ru and O in RuO₂, as well as the quadrupole and spin moments for the perpendicular magnetization from (a) the y-direction and (b) the z-direction. x, y, and z indicate the [100], [010], and [001] directions, respectively. c MAE contribution of each atom by the second-order perturbation calculation in RuO₂. d Spin quadrupole $-\left\langle {Q}_{{\rm{zz}}}{S}_{{\rm{z}}}\right\rangle$ and orbital moment anisotropy $\left\langle {L}_{{\rm{z}}}\right\rangle -\left\langle {L}_{{\rm{x}}}\right\rangle$ of Ru and O atoms in RuO₂. e Band dispersion with and without spin-orbit interaction (SOI) of RuO₂ along high symmetry lines. f The MAE contribution of the Ru atoms by the second order perturbation calculation along the high symmetry line along X$\left(0,\,\tfrac{1}{2},0\right)$, $\Gamma \left(0,\,0,\,0\right)$, M$\left(\tfrac{1}{2},\,\tfrac{1}{2},0\right)$, and A$\left(\tfrac{1}{2},\,\tfrac{1}{2},\tfrac{1}{2}\right)$. Inset shows the first Brillouin zone with the k paths and the high symmetry lines.

C. DFT calculations for the altermagnetic RuO₂

The magneto-crystalline anisotropy energy (MAE) between the [001] and [100] magnetization directions in altermagnetic RuO₂ was investigated by the first-principles DFT calculations. We found that RuO₂ has the [001] easy axis with respect to the [100] magnetization direction, which corresponds to the MAE of 1.44 × 10⁷J/m³. Here, the spin magnetic moments are estimated to be 1.12 μ_B for each Ru site and antiferromagnetically aligned to compensate for the total net spins. The MAE value is comparable to that of L1₀-FePt based on the DFT calculations, implying that altermagnetic RuO₂ has a strong MAE along the [001] direction. To clarify the origin of the MAE of RuO₂, a second-order perturbation analysis in terms of the spin-orbit interaction was performed. The MAE of each Ru atomic site I (Ru₁, Ru₂) can be formulated as

$${E}_{{\rm{MAE}}}^{I}=\pm \frac{{\xi }_{I}}{4}\left(\left\langle {L}_{{\rm{z}}}\right\rangle -\left\langle {L}_{{\rm{x}}}\right\rangle \right)\pm \frac{21}{8}\frac{{\xi }_{I}^{2}}{{\Delta }_{{\rm{ex}}}^{I}}\left(-\left\langle {Q}_{{\rm{zz}}}{S}_{{\rm{z}}}\right\rangle \right),$$

(1)

where the first term $\left\langle {L}_{{\rm{z}}}\right\rangle -\left\langle {L}_{{\rm{x}}}\right\rangle$ and the second term $-\left\langle {Q}_{{\rm{zz}}}{S}_{{\rm{z}}}\right\rangle$ represent the expected values of orbital moment anisotropy and spin quadrupole moment, respectively. ${\xi }_{I}$ and ${\Delta }_{{\rm{ex}}}^{I}$ are the spin-orbit coupling constant and exchange splitting of each atomic site, respectively³⁷. Note that the plus ($+$) and minus ($-$) signs depend on positive and negative values of the spin moment$\,\left\langle {S}_{{\rm{z}}}\right\rangle$, since the direction of the spin quantum axis at each atomic site depends on the direction of the local spin moment. Figures 4a, b illustrate the Ru and O sites in the units of RuO₂ used in this calculations with the quadrupole and spin moments. The contribution to the MAE of the first term (spin-conserving) and the second term (spin-flipping) within the Ru sites are shown in Fig. 4c. The positive and negative values indicate the [001] and [100] easy axes of the magnetization, respectively. It is found that the Ru atoms mainly contribute to the MAE along the [001] direction, while the contribution of oxygen to the MAE is negligible. In particular, the spin-flip term contributes more than twice as much to the MAE as the spin-conserving term. This suggests that the spin quadrupole of the Ru sites has a cigar-type distribution along the [001] direction, as shown in Fig. 4a, which mainly contributes to the MAE of RuO₂. Note that the spin-conserving term is also positive. The fact that both spin-flip and spin-conserving terms contribute to the MAE is unique and identical for altermagnetism-based antiferromagnets. Figure 4d shows the orbital moment anisotropy (difference between the [001] and [100] directions) and the spin quadrupole moment ($-\left\langle {Q}_{{\rm{zz}}}{S}_{{\rm{z}}}\right\rangle$) for the Ru atom. It is clear that the quadrupole term is larger than the orbital moment anisotropy, which is consistent with the dominant contribution of the spin-flip term in Fig. 4c. The band dispersions and MAE contributions along the high symmetric lines of rutile-type RuO₂ (P4₂/mnm) are shown in Fig. 4e, f. Looking at the spin quadrupole moments from the z-axis ([001] direction), one would expect anisotropy in the [110] and [$\bar{1}10$] directions due to the anisotropic oxygen bonding in the rutile structure. However, the in-plane anisotropies are counteracted by the antiferromagnetic magnetic structure of the Ru₁ and Ru₂ sites. Thus, there remain the cigar-type spin quadrupole moments in the z-axis caused by the distorted tetragonal structure of RuO₂. This cigar-type spin quadrupole moment of Ru has been observed experimentally and is considered to be the origin of the strong magneto-crystalline anisotropy along the [001] direction. The spin-dependent band dispersions of RuO₂, especially along the Γ-M line around the Fermi level, which is a distinctive feature of altermagnetism and is consistent with the previous report⁶. Non-zero MAE contributions of the spin-conserving and spin-flip terms are also found along the Γ-M line, as shown in Fig. 4f, which indicates that the MAE contribution will be enhanced in the Brillouin zone with the spin-polarized band dispersion. Therefore, the DFT calculations of single-variant RuO₂ indicate that the large MAE with antiferromagnetic order originates from the stability by forming spin quadrupole states along the Néel vector direction.

D. Spin-splitting magnetoresistance in RuO₂(101)/CoFeB heterostructures

We further investigated the effect of this single variant of RuO₂(101) on the spin transport in the RuO₂(101)/CoFeB heterostructure. It is known that spin accumulation at the interface between a spin current source layer and a ferromagnetic layer alters the chemical potential of the ferromagnetic layer, which leads to a change in the resistance of the heterostructure when the spin-polarization (s) direction of the spin current is parallel (P) and antiparallel (AP) to the magnetization (M) direction of the ferromagnetic layer, the so-called unidirectional spin Hall magnetoresistance (USMR)³⁸. In the RuO₂(101) thin film, when the charge current (electric field, E) is applied in the [10$\bar{1}$] direction (x direction), the generated spins are along the y = z × Ê direction, independent of the Néel vector¹³. The P and AP states for M and s can be achieved when the M of the CoFeB layer is aligned in the film plane at 0 and 180° to the s, as illustrated in Fig. 5a, b. We performed the second harmonic method³⁸ to measure the longitudinal resistance of a Hall bar device of the RuO₂(101)/CoFeB sample. We rotated the M of CoFeB in the (10$\bar{1}$) plane of RuO₂ under a magnetic field of 10 kOe, see the geometry in the top panel of Fig. 5c. The longitudinal second-harmonic resistance (R_2ω) of RuO₂(10 nm)/CoFeB (2 nm) as a function of the rotation angle θ is shown in Fig. 5c. By fitting the curve, we find that it exhibits a sinusoidal dependence, i.e., R_2ω ~ sinθ, which is consistent with the USMR curves in Pt and Ta³⁸. The lowest and highest resistances appear at θ = 90° and 270°, corresponding to the AP and P states, respectively.

Fig. 5: SSMR in the RuO₂/CoFeB bilayers.

a, b Illustration of spin current generation when the E is along the [10$\bar{1}$] direction, and M and s are in (a) P and (b) AP states. c Angular dependence of R_2ω of RuO₂(101)/CoFeB bilayers measured with rotating the M in the (10$\bar{1}$) plane. d, e Illustration of tilted spin current when the E is applied in the [010] direction. M and s have (d) P and (e) AP states. f R_2ω as a function of the rotation angle of M in the (010) plane. The solid lines are the fitting results.

Afterwards, we changed the charge current to the [010] direction. In this case, the E applied along the [010] direction produces a tilted spin current due to the spin-splitting effect^13,15. The tilted spin current can contribute to the spin accumulation at the interface with its spin direction angled to the film surface. Thus, when the M is rotated in the (010) plane, the rotation angles that realize the P and AP states for M and s are different from the former case. The P and AP states of M and s are realized when the M is rotated to a certain angle outside the film surface, as shown in Fig. 5d, e. From the resistance versus the rotation angle shown in Fig. 5f, we can clearly find that there is an angular shift with respect to the data curve in Fig. 5c, with the lowest and highest resistances at 70° and 250°, respectively. To further understand the angular dependence, we fit the curve with a composite formula, i.e., R_2ω = $a\sin \left(\theta+35^\circ \right)+b\sin \theta$. Here, the first term gives rise to the spin current generation associated with the antiferromagnetic order, i.e., the Néel vector, while the second term results from the spin current generation from the unpolarized bands of the oxygen sites, which is not associated with the antiferromagnetic order. a and b are the parameters representing the magnitude of the contribution of these two terms to the total spin current. The red solid line in Fig. 5f shows a well-fitted result, with a ratio of a and b of 1.4. The result of the angle shift for realizing the P and AP states is evidence for the tilt spin current from the spin splitting effect. We refer to this effect as SSMR, a new member of the family of spin-splitting effects, which is the contribution of the single variant of RuO₂(101) to the spin transport. We note that the first harmonic resistance R_ω, as a linear response to current, is typically attributed to the combined action of both the spin-splitting effect and the inverse spin-splitting effect in this system, which may also exhibit an angle shift linked to the Néel vector of RuO₂ in its angular dependence.

In conclusion, we present compelling evidence for the synthesis of single-variant altermagnetic RuO₂(101) thin films, epitaxially grown on Al₂O₃ (1$\bar{1}$02) substrates. Using atomic resolution transmission electron microscopy, we find the alignment of oxygen atoms at the RuO₂(101) and Al₂O₃(1$\bar{1}$02) interfaces plays a critical role in single-variant formation. The unique ability of XMLD was utilized to detect the square of the element-specific magnetization proves essential for observing altermagnetism, which is hidden from conventional techniques due to its compensated magnetic order. Our single-variant films exhibit SSMR, making them potential for spin current generation in spintronic devices. The above results indicate the single variant features, while a multi-domain formation cannot explain such anisotropic properties. The DFT calculations also suggest the MAE with finite Ru magnetic moments. This work provides an intriguing correlation between altermagnetic features with magnetic spectroscopies and spin transport and may inspire further exploration for potential spintronic applications of altermagnetic materials. Note added: During the review process, we became aware of relevant work reporting XMLD signals in (110)- and (100)-oriented RuO₂ films³⁹, as well as SSMR results corresponding to the first harmonic resistance in (101)-oriented RuO₂/Co bilayers⁴⁰.

Methods

Material deposition and characterizations

All the thin films were prepared using an ultra-high vacuum magnetron co-sputtering system with a base pressure of 6 × 10⁻⁷ Pa. Pure Ru was used as the sputtering target. The Al₂O₃($1\bar{1}02$) substrates were treated in a muffle furnace at 1000 °C for one hour in an atmospheric environment. RuO₂ films were grown on Al₂O₃(1$\bar{1}$02) substrates by rf magnetron sputtering in a reactive sputtering atmosphere of Ar (30 sccm) + O₂ (2.5 sccm) at 300 °C. Post-annealing in a high vacuum was performed to improve the crystallinity and resistivity. A combination of techniques was applied to characterize the films: in-situ RHEED, ex-situ atomic force microscopy (AFM), and XRD using Cu K_α1 radiation. Further detailed microstructural characterization was performed using high-resolution HAADF-STEM, and energy dispersive X-ray spectroscopy (EDS) on an FEI Titan G2 80–200 ChemiSTEM system.

Measurement of X-ray magnetic spectroscopies

The XAS, XMCD, and XMLD measurements were performed at BL-7A and 16A in the Photon Factory at the High-Energy Accelerator Research Organization (KEK). The total electron yield mode was adopted, and measurements were performed from 80 K to 400 K. For the XMCD measurements, the photon helicities of the incident beams were switched. The XMCD measurement geometries were set to 45° tilted from the normal incidence. In XMLD measurements, the direction of the electric field component of the incident synchrotron beam E was tuned horizontally and vertically with respect to the antiferromagnetic Néel vector direction M. We defined the sign of the XMLD by subtracting (M∥E) − (M⊥E) spectra. For the angle dependences, the sample was rotated with the rotation axis in the in-plane and out-of-plane of the sample.

Device fabrication and transport measurements

In the microfabrication, the films were patterned into bar devices (width: 10 μm, length: 25 μm) for second harmonic measurements. Electrodes consisting of a Ta (5 nm)/Au (100 nm) layer were then applied to the structures using sputtering followed by a lift-off process. The second harmonic measurements were conducted at room temperature with a Keithley 6221 and a lock-in amplifier LI 5660. In addition, an external magnetic field of 10 kOe was applied, and the sample was rotated as θ = 0 − 360°. Transport properties of RuO₂ thin films deposited at various conditions were measured (Supplementary Materials). Spin-torque ferromagnetic resonance experiments were also performed to examine the generation of titled spin currents (see details in Supplementary Materials).

First-principles calculations

We investigated the MAE of rutile-type RuO₂ by the density-functional theory including the spin-orbit interactions (SOI), which is implemented in the Vienna ab initio simulation program (VASP)⁴¹. We adopted the spin-polarized generalized gradient approximation (GGA)⁴² for the exchange-correlation energy and used the projector augmented wave (PAW) potential^37,43 to treat the effect of core electrons properly. We considered the on-site Coulomb interaction⁴⁴ U = 3 eV for the Ru atom, which is a necessary condition to obtain the altermagnetic state for RuO₂²¹. The lattice constants of rutile-type RuO₂ were used, a = b = 0.4523 nm and c = 0.3115 nm, which are obtained by a structure optimization with the VASP-PAW calculation. Furthermore, we performed second-order perturbation calculations of SOI for a more detailed understanding of the MAE mechanism. The theoretical details of the perturbation calculations can be found in previous works^45,46. The convergence of these calculations was confirmed by 30 × 30 × 42 k-points in the Brillouin zone, which are sufficient to accurately estimate the MAE energy. For the calculation of the stability of the RuO₂(101) and RuO₂($\bar{1}01$) variants by stacking RuO₂($101$) and RuO₂($\bar{1}01$) cells on the oxygen-terminated Al₂O₃($1\bar{1}02$) surface, a supercell containing 162 atoms (Al, O, and Ru) was used, with 4 monolayers of RuO₂ modeled as either RuO₂(101) or RuO₂($\bar{1}01$).