Introduction

The evolution of radiofrequency and microwave networks for advanced communications and radar systems toward increasingly complex devices demands powerful digital signal processors to enable real-time data processing and rapid decision-making. On the other hand, fundamental limitations of digital electronics in bandwidth and power consumption have resurfaced interest in analog logic. An analog computing engine can utilize fundamental properties of electromagnetic waves for massive parallel processing to enable signal processing literally at the speed of light. On the other hand, the very nature of an analog processor can facilitate dramatic reduction in size, weight and power compared to its digital counterpart. In the past decade, there has been substantial progress in the development of units that perform linear operations leveraging electromagnetic waves in free space and in guided wave structures1,2,3,4,5,6,7. However, less attention is paid to reconfigurable on-chip structures that could be programmed on-demand to perform the desired transfer function between a number of ports in radiofrequency and microwave networks. In this vein, linear transforms play a pivotal role in signal processing as a large number of the relevant signal manipulations lie in this regime8.

In the optical domain, interest in physical realizing linear operations on multimode light beams was driven by applications in optical computing, expanded significantly after realizations with nanophotonic circuits9,10,11,12,13. Photonic units also find exciting new applications as a promising platform for quantum computing and simulations14, including photons in the microwave domain for large-scale quantum communication channels15,16,17. Furthermore, reconfigurable photonic integrated circuits have evolved toward various architectures and configurations, coining the term programmable photonics, holding promise for applications in classical photonic signal processing18,19,20,21,22,23. In a similar fashion, the development of programmable analog matrix computing cores at radio and microwave frequencies can provide real-time, low-power data processing solutions that circumvent the fundamental limitations of purely digital systems24,25. By merging reconfigurable electromagnetic wave manipulation with analog computing, these architectures could pave the way for next-generation, high-speed signal processing applications26. Solutions in this regard include phase-array radars27,28, lensless Fourier networks29, computational imaging30, microwave beamforming31,32, and frequency filters and synthesizers33,34,35. There is thus an interest for integrated and programmable microwave units capable of dynamically adjusting their functionalities to accommodate various of these application scenarios.

While programmable photonic systems have successfully implemented linear transformations in the optical and infrared domains, they typically require optical sources and detectors, leading to increased latency, system complexity, and power consumption. In contrast, the proposed RF-domain solution processes signals natively without optical-electrical conversion, offering reduced latency and seamless integration with existing radiofrequency (RF) front-end hardware. Additionally, the ability to implement such architectures using printed circuit boards or MMICs facilitates compact, scalable integration for embedded and low-power applications.

In this work, we introduce, design, and experimentally demonstrate a programmable microwave circuit device that performs universal unitary matrix transformations. The proposed solution operates on an interlaced structure composed of fixed networks of power dividers and tunable phase shifter arrays. The programmable phase elements provide the required degrees of freedom to represent a desired unitary operation. These results are experimentally validated by a four-port device with five layers of phase shifters, operating at the central frequency of 2.1 GHz. A time-multiplexing scheme enabled design- and power-efficient programming of the phase shifter network in series using a simple microcontroller. In addition, the self-calibration properties of the proposed circuit configuration allow for high-fidelity representation of desired matrix operations even with coarse resolution of the underlying phase shifters. The device performance is demonstrated through exemplary operations including Hadamard matrix.

Results

Theoretical background

To better understand the underlying structure of the proposed linear unitary transform device, Fig. 1a presents a schematic of the interlaced structure intertwining layers of non-tunable (passive) and tunable (active) components, represented through the unitary operators \(F\) and \({P}^{(m)}\), respectively. In the latter, \(F\) is considered as fixed and \({P}^{(m)}\) is a diagonal matrix with diagonal elements \({p}_{n}^{\left(m\right)}={e}^{i{\phi }_{n}^{(m)}}\), with \(m\in \{1,\ldots,M\}\) and \(n\in \{1,\ldots,N\}\), where \(M\) is the total number of layers and \(N\) the total number of ports. From these considerations, the proposed \(N\)-th port device follows from the interlaced universal unitary operation

$${\mathcal{U}}(\Phi ){\rm{:=}}F{P}^{\left(N+1\right)}F\ldots F{P}^{\left(1\right)}F,$$
(1)

where \({\mathcal{U}}(\Phi )\in U(N)\), and \(\Phi\) is the set of trainable phase parameters.

Fig. 1: Device structure, design, and performance.
figure 1

a Block diagram of the proposed universal unitary device inspired by a photonic interlaced structure where non-tunable (F) and tunable layers are intertwined in a cascaded fashion. b Sketch of the final device comprising non-tunable 50:50 power dividers (dashed-white) that mix incoming signals across all the channels so that the tunable phase elements (long-dashed-red) steer the signal to the required operation. The choice of the non-tunable layer is not restricted to a specific form, and the theoretical form of the corresponding transmission matrix can be deformed due to external fabrication defects. c Figure of merit \(L(\Phi)={{||}{\mathcal{U}}\left(\Phi\right)-{{\mathcal{U}}}_{t}{||}}^{2}/{N}^{2}\) for the interlaced structure using the theoretical \(F\) (see Methods section). The latter is depicted as a function of the number of layers (M), showing a sudden drop in the figure of merit at \(M=5\) layers. In this process, 500 Haard random matrices are generated for each M, presenting only the mean (dot) and standard deviation (shaded area). d Percentage error \(({{\mathcal{U}}\left(\Phi \right)-{{\mathcal{U}}}_{t}{||}}^{2}/{{||}{{\mathcal{U}}}_{t}{||}}^{2})\times 100{\boldsymbol{\%}}\,\) between the target and the reconstructed matrices when the previously optimized phases are replaced by 6-bit discretized phase shifters (upper panel). The lower panel presents the calibrated operation, where the discrete nature of the phase shifters is incorporated during the optimization process.

Full size image

The theoretical design in Eq. (1) is versatile, as the sequence of multiplications produces a device with components that are sequentially connected, as shown in Fig. 1a Furthermore, the non-tunable layer, F, only needs to be designed once and can then be replicated throughout the device. Fabrication errors should also be considered in the design of such a layer, which changes the overall functionality of the device. As pointed out in previous works36, this interlaced device can be further tuned to mitigate fabrication errors through the phase elements. For the current design, the non-tunable layer is constructed using a sequence of two-port 50:50 Power Divider Units (PDUs). The number and placement of these units must be determined based on the required universality of the complete device. Although fewer power dividers are ideal for reducing the overall footprint, the total number shall be selected so that the resulting mixing layer \(F\) fulfills the density criterion for unitary interlaced architectures23. This procedure is done by using the S-parameter specification of each power-divider provided by the manufacturer. We fabricate a four-port device (\(N=4\)) comprising \(M=5\) phase layer, and consequently 20 tunable phase elements, the overall device of which is illustrated in Fig. 1b. In this case, the non-tunable mixing layer \(F\) reduces to a minimum of two layers of power dividers (dashed-white area in Fig. 1b) without jeopardizing the universality of the proposed device. Since \(F\) is non-tunable, its proper design and characterization are fundamental to the overall device performance (up to mild deviations), as once manufactured, it cannot be further modified.

To assess the performance of the proposed device, 500 Haar random unitary \(4\times 4\) matrices are created, and the device is tuned to reconstruct each target by optimizing the training parameters \(\Phi\) in Eq. (1) for each \(M\in \{1,\ldots,9\}\). This is performed using gradient-based optimization algorithms, as shown in the Methods section and Supplementary Note 1. The results are summarized in Fig. 1c, where a phase transition in the figure of merit is observed at \(M=N+1=5\) layers. It is not surprising that higher errors are obtained for \(M < 4\), as the total number of active phase elements is lower than \({N}^{2}=16\), the total required to fully parameterize any arbitrary target in \(U(4)\). For \(M=N=4\), the system is still effectively under-parameterized, as a global phase can be factored out per layer, reducing the size of the parameterization space36. We thus have selected M = N + 1 = 5 layers to balance performance with hardware complexity. This configuration maintains reconstruction errors within acceptable tolerance for key unitary operations while enabling a more compact and energy-efficient implementation suitable for practical fabrication. The acceptable error tolerance for the number of layers M is fundamentally application dependent. While communication and radar systems can tolerate moderate errors without impairing functionality, more sensitive quantum or coding applications may require lower error levels, motivating higher M values. Therefore, MMM should be selected to balance system performance requirements and hardware complexity. It is worth mentioning that the device performance is achieved even if deviation on the non-tunable layer \(F\) are present in the actual device. This follows from the fact that mild defects can be compensated by steering the tunable phase elements to reach the desired performance36. See Supplementary Note 1 for more information.

Fabrication and experimental realization

The proposed unitary matrix solver device is fabricated following the interlaced design in Fig. 1a, where six layers of mixing \(F\) matrices and five layers of active phase elements are implemented. The \(F\) matrix layers are devised with a network of power dividers. Specifically engineered for 5G applications37, these power dividers offer low loss, tight amplitude balance, and high isolation within the 1.5–2.3 GHz frequency range. Constructed from ceramic-filled Polytetrafluoroethylene (PTFE) composites, they provide excellent electrical and mechanical stability, ensuring reliable circuit performance. For the phase layers, we opted for 6-bit digital phase shifters that feature integral CMOS drivers and low DC power consumption, making them ideal for energy-efficient designs38. These phase shifters offer a step size of 5.6°, providing complete 360° coverage with minimal attenuation variation. In addition, a low-cost, low-power consumption system-on-chip microcontroller facilitated phase shifter control, enabling serial configuration with minimal interface requirements. This serial configuration allows connecting all the phase shifters in a cascade setup from a serial bus perspective, minimizing control pin usage. See Supplementary Notes 2, 3 for more details.

The 6-bit phase shifters with 5.6° step size provide sufficient resolution for accurately implementing universal unitary operations in a 4-port device. Phase discretization errors are mitigated through digital optimization and calibration, enabling high-fidelity matrix synthesis. The upper panel in Fig. 1d depicts the percentage error of the reconstructed target when the previously optimized phases are replaced by their discrete counterpart. Indeed, a penalization is incurred in the phase discretization process, yielding an average error of 6.41% across all the 500 samples. However, by reoptimizing the device while taking into account the discrete nature of the device, the percentage error drops to a mean of 2.97%, as shown in the lower panel of Fig. 1d. Higher resolution may benefit larger-scale systems but entails increased hardware complexity. Potential mismatches between phase shifter chips are addressed through a self-calibration procedure that measures the effective device response and optimizes phase control bits to compensate for deviations. The use of integrated 6-bit digital phase shifters with CMOS drivers further enhances uniformity across phase elements, supporting stable and repeatable operation.

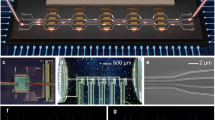
Figure 2a shows the manufactured PCB of a \(4\times 4\) unitary matrix multiplier. A replica of the power-divider unit is separately fabricated for benchmarking and calibration, which is shown in this figure and fully characterized before running the complete unitary matrix solver. In the latter, a layout of the power divider unit is presented, which was designed and simulated using the Advanced Design System (ADS) suit software before production. The layout for this layer was specifically designed to operate optimally at 2.1 GHz, which is the subsequent target operation of the unitary matrix solver.

Fig. 2: Fabricated unitary universal device and its power-divider layer.
figure 2

a PCB of the fabricated unitary matrix solver comprising power-divider unit layers (yellow-dashed) and the independent active phase elements (red-dot-dashed) and individually fabricated power-divider layer. This layer is experimentally tested to properly characterize the full unitary matrix solver. b Experimental results of the real parts of the S-matrix for the individually fabricated power-divider layer (matrix F). c Transmission matrix (normalized) of the individually fabricated power-divider unit at selected frequency points, including the target operational frequency (red-dashed).

Full size image

The individual fabricated power-divider unit is thoroughly benchmarked using a four-port vector network analyzer (VNA) to fully characterize it in the frequency spectrum 1.5–2.3 GHz. Since the power-divider layer is the only non-tunable layer, it is fundamental to properly characterize it independently so that we can estimate the required phases on the tunable layer required for the unitary matrix solver functionality. The measured transmission components of the S-parameters are summarized in Fig. 2b, where the reflection components were ignored, as their contribution is negligible. See Supplementary Note 4 for full characterization of the S-parameters. To clearly illustrate the behavior of the power-divider unit, its transmission matrix components (in normalized units) are shown in Fig. 2c for specific frequencies, including the operational frequency at 2.1 GHz used across the fully connected device. The latter shows mild deviation on the intensity of the transmission components, which is in good agreement with the ideal case show in Supplementary Note 1. In turn, deviations are expected on the phase components, as the differences in optical paths at different frequencies contribute to different phases.

Experimental results

Individual characterization of the fixed layer of power splitter networks permits precise measurement of the intervening operator \({F}_{\exp }\). This allows us to use the formula in Eq. (1) by replacing \(F={F}_{\exp }\) in order to realize the desired unitary evolution \({U}_{\exp }\) by properly steering the phase elements. The latter phases are optimized according to the desired target operation by minimizing the experimental figure of merit shown in the Methods Section. Indeed, the phase elements used in the experimental setup have a limited tuning capability; however, their accuracy is sufficient for proper device operation.

Since the network analyzer has four ports and both the proposed unitary matrix multiplier has eight ports (four inputs and four outputs), a set of two \(2\times 4\) RF switch arrays were employed at both the input and output to properly excite and gather signals from all the ports of the device. Calibration procedures utilizing RF switches ensured the precise extraction of the device’s S-parameters, while calibrated cables minimized cable losses in the measurement setup. The port switching, phase-shifter microcontroller operation, and data collection from the network analyzer are ultimately performed on a personal computer. This setup is summarized and illustrated in Fig. 3a.

Fig. 3: Experimental setup and results.
figure 3

a Schematic of the experimental setup. This setup involves a four-port vector network analyzer (VNA) composed of two inputs and two output channels. Since the device has eight ports in total (four inputs and four outputs), two 2 × 4 radiofrequency switches are interlaced between the VNA and the input and output ports of the device under test. The phase-shifters are electronically controlled in a series connection through the ESP32 microcontroller. b Measured (unnormalized) S-matrix of the constructed universal interlaced architecture operated so that the phase elements render the Hadamard matrix. c Frequency performance of the device assessed by computing the figure of merit in terms of the operational frequency for the identity, anti-diagonal, and Hadamard matrix as targets. The minimal error is located at the optimal frequency of 2.1 GHz. Theoretical (red) and measured (blue) normalized transmission matrices \({T}_{{n}_{1},{n}_{2}}\) for the identity (d), antidiagonal (e), and Hadamard (f) configurations when the device is operated at 2.1 GHz.

Full size image

We establish a benchmark scenario by configuring the device to perform three exemplary unitary operations. That is, we consider the \(4\times 4\) identity matrix and the anti-diagonal matrix, which are among the sparsest matrices in the unitary group \(U\left(4\right)\). The identity matrix steers the device into a pass-through operation (bar configuration), whereas the anti-diagonal shuffles the channel order (cross configuration). Furthermore, we consider the Hadamard matrix, \({U}^{(H)}\), which has the same density as the discrete Fourier transform but is more accessible for computation. See the Discussion section. Additionally, the 4 × 4 Hadamard matrix is commonly used to implement Hamming codes, simple error-correcting codes that can detect single-bit errors in digital communication39. The Hadamard transform is also used in image compression and feature extraction.

The optimized phases required to achieve the desired targets are loaded into the device, and the corresponding S-matrix is measured over a frequency sweep in the range of 1.5–3 GHz. The real part of the unnormalized experimental results is shown in Fig. 3b for the Hadamard matrix as a target (see Supplementary Note 3 for the full S-matrix). In the latter, it can be noted that the components Re\([{S}_{\mathrm{5,1}}]\), Re\([{S}_{\mathrm{5,2}}]\), Re\([{S}_{\mathrm{5,3}}]\), and Re\([{S}_{\mathrm{5,4}}]\) reach approximately the same values at 2.1 GHz, which is expected for a Hadamard matrix (a real-valued matrix with equal intensities). To better assess the performance of the Hadamard matrix and the other two targets, the frequency response of the reconstructed error, computed using the figure-of-merit described in Methods Section, is depicted in Fig. 3c. This reveals a minimum error for the previously optimized phases at the operational frequency of 2.1 GHz, deviations for other frequencies are due to the phases observed in Fig. 2c. For illustration, the normalized target and measured transmission matrices at 2.1 GHz are shown in Fig. 3d–f, revealing the expected performance at the optimal frequency. This not only corroborates the previous findings but also provides insight into the operational bandwidth of the device around the optimal frequency at 2.1 GHz.

The fabricated four-port prototype demonstrated robust unitary transformations, including Hadamard and identity matrices, over a 1.5–3.0 GHz frequency sweep. Despite the use of 6-bit phase shifters with coarse resolution, high-fidelity performance was achieved at low power levels (~330 μW) owing to a self-calibration scheme that compensates for fabrication-induced deviations in the fixed mixing layer. Furthermore, as shown in Fig. 3, we measured and characterized the proposed ASP system across the wide frequency range 1.5–3 GHz. Since the frequency response is well-characterized, frequency-dependent calibration can be applied. In practical scenarios, this allows us to flatten and equalize the response over a 1 GHz bandwidth centered around 2.1 GHz, making real-time wideband operation feasible and reliable within this range.

Discussion

The implementation of arbitrary unitary transformations has been explored in the context of integrated photonics for light in the optical and infrared domains. However, a fully self-contained solution that operates directly with RF signals, without the need for external optical signals, has proven elusive. Our device aims to fill this gap by introducing an integrated solution that performs unitary operations on signals in the RF domain. Unlike RAM-based analog computing40, which relies on digital memory elements and requires conversion stages, the proposed analog RF matrix processor operates natively at microwave frequencies. This approach enables real-time processing with lower latency and power consumption. By allowing direct wave-based manipulation, our device provides scalable and programmable unitary transformations, offering a complementary alternative to existing RAM-centric analog computing methods.

While the present design focuses on unitary transformations, arbitrary linear (non-unitary) matrices can be implemented using a Singular Value Decomposition (SVD) approach, i.e., A = U1ΣU2, where U1 and U2 are unitary and implemented using the current interlaced phase-coupler topology. The diagonal scaling matrix Σ can be realized by inserting a layer of variable gain or attenuation elements. Directly replacing 3-dB couplers with variable gain amplifiers (VGAs) is theoretically possible, but presents practical limitations including stability, power consumption, and control complexity.

This solution does not require any external calibration light signal and can be programmed on the fly as needed. Although the device switching capabilities are limited by the electronic elements used as the phase-element, once the architecture is fully programmed, it can fully process any number of signals. The 6-bit digital phase-shifters utilized in our experimental demonstration operate at 3.3 \({\rm{V}}\). The total current for the 20 phase shifters involved was measured to be 0.1 \({\rm{mA}}\), which leaves the total power of the device at 330 \({\rm{\mu }}{\rm{W}}\).

The device was proved to achieve pass-through (diagonal matrix) and cross (antidiagonal matrix) operations within the prescribed accuracy at the operational frequency of 2.1 GHz. These matrices are particular cases of the sparsest matrices in the \(U(4)\) group, which makes the device a signal rerouting solution while also serving as a benchmark for testing the device’s operation. In turn, the Hadamard matrix tested in the manuscript is an example of a dense matrix. Experimental results also show excellent agreement with the required target, achieving the same accuracy as in the sparse cases. Furthermore, the Hadamard matrix is used in image compression and feature extraction, which is computationally simpler than the Fourier transform39. Implementations of the discrete fractional Fourier transform, and its applications have been shown to be feasible in the optical and microwave domain29,41, which can be deployed in the current RF device by tuning the proper phase elements. This is particularly useful for beamforming applications31,32.

Although there is a higher reconstruction error for other frequencies (Fig. 3c), one can reoptimize the phase elements by using the non-tunable F layer of Fig. 2 at a different operational frequency. Since the transmission matrix intensity of F is stable over the frequency spectrum 1.5–3.0 GHz (Fig. 2b, c), one can, in principle, program our unitary matrix solver at any other frequency if needed. This makes the proposed device flexible to operate at different frequencies. The observed performance degradation beyond 2.5 GHz is attributed to phase mismatches in the fixed-layer transmission network. Extending broadband performance can be achieved through optimized wideband power divider designs or dynamic reprogramming of the phase layers to compensate for frequency-dependent variations, an important avenue for future development. The reconstruction error between the theoretical and experimental transmission matrices at 2.1 GHz is visually illustrated in Fig. 3d–f, including the percentage error is also included for reference. This showcases a high-fidelity performance, rendering a percentage error of around 0.2% for all configurations. It is worth mentioning that such accuracy was achieved by considering both the measured amplitude and phases (up to a global factor). Moreover, robustness against temperature and fabrication variations is supported using stable materials and components in the fixed power divider layers and fine-resolution digitally controlled phase shifters. The self-calibration procedure allows dynamic compensation of performance drifts, enabling consistent high-fidelity operation under varying environmental conditions.

The present device is intended as a proof of concept, designed to demonstrate its potential, and it is thus not limited to the applications discussed here. Indeed, further linear non-unitary transformations can be deployed via the SVD of the operation in question and by cascading unitary devices, such as the one proposed in this manuscript. This has been previously reported in the optical domain9,22. Beyond the current implementation, the device can be extended to millimeter-wave (mm-wave) and terahertz (THz) frequencies. The demonstrated programmable analog matrix circuit is especially suitable for RF signal processing tasks that demand real-time, low-latency, and low-power operation, such as phased-array beamforming, signal routing in radar and communication systems, and microwave quantum information processing. While the device currently targets unitary transformations, its underlying principles can be extended to more complex linear operations to meet application-specific demands. Future work will explore tailoring the architecture to domain-specific requirements including bandwidth, noise resilience, and integration density. For instance, in mm-wave communications, the device can enhance data transmission rates and improve the performance of wireless links in dense urban environments and inter-satellite communication links. The device can further enable ultra-high-speed data transfer in THz systems and support scientific research in material characterization and molecular spectroscopy42.

Although the present architecture scales with O(N2) phase elements, posing integration challenges for large-port systems, future implementations using monolithic microwave integrated circuits (MMICs) or hybrid photonic-assisted RF processors may offer practical pathways to scalable, low-overhead integration. Though direct amplitude and phase control on each input-output path is possible, it scales quadratically with the number of ports, leading to increased device complexity and power consumption. The proposed interlaced architecture, based on cascaded passive power dividers and programmable phase shifters, reduces the active element count to O(\({N}^{2}\)), enabling more compact and energy-efficient implementations. Additionally, the natural enforcement of unitarity through cascaded interference ensures signal integrity and facilitates robust calibration and compensation, advantages not easily achieved in direct amplitude-phase control arrays. Scalability to higher port counts entails increased circuit size and insertion loss, as well as potentially amplified mismatch effects. Our experimental results with a 4-port device suggest that M = N + 1 phase shifter layers suffice for universality, but practical system design must balance these factors. Future work will focus on optimizing component selection, minimizing loss through MMIC integration, and exploring advanced calibration schemes to support larger-scale implementations.

To better contextualize the advantages of the proposed analog matrix circuit, we provide a comparative analysis against conventional digital signal processing systems. Table 1 summarizes key differences in terms of relevant metrics bandwidth, latency, power efficiency, scalability, and integration approach.

Table 1 Comparison between Digital Signal Processor (DSP)43,44 and the proposed Analog Signal Processor (ASP)
Full size table

Methods

Model optimization for theoretical and experimental setup

Numerical optimization techniques are used to maximize or minimize a figure of merit that quantitative measures the performance of a theoretical model or a parametric device. Throughout the manuscript, we test the theoretical device architecture in Eq. (1) and the fabricated device, which in both cases depends on the preliminary selection of testing unitary matrices as targets. For this task, we use the customary figure of merit

$$L(\Phi )=\frac{{{||X}\left(\Phi \,\right)-{X}_{{\rm{target}}}{||}}^{2}}{{N}^{2}},$$
(2)

where \(X(\Phi )\) is the trainable quantity, \(\Phi\) the set tunable parameters, and ||\(\cdot {\rm{||}}\) the Frobenius norm.

For the theoretical analysis, Eq. (2) is combined with Eq. (1) by using the ideal and perturbed F mixing matrix. In such a case, each power divider is represented by \({U}_{{PD}}=\frac{{\sigma }_{0}-i{\sigma }_{1}}{\sqrt{2}\,}\), with \({\sigma }_{j}\) the Paulli matrices. The latter corresponds to the ideal manufacturer specification for the power-divider unit. Thus, the ideal mixing matrix becomes \(F=\left({{\mathbb{I}}}_{2}\otimes {U}_{{PD}}\right)({{\mathbb{I}}}_{1}\oplus {U}_{{PD}}\oplus {{\mathbb{I}}}_{1})\), with \(\otimes\) and \(\oplus\) the direct-product and direct-sum operations, respectively. For the experimental calibration, the S-parameters of the F matrix are extracted and used in the optimization routine to extract the phases to be set in the experimental run.