Introduction

In complex physical systems, diagnostic measurements are often intricately interconnected through fundamental physical principles. These connections arise from the laws of nature that govern the behavior of matter and energy. Electromagnetic phenomena can couple measured signals, while equations of state link variables such as pressure, volume, and temperature, enabling one quantity to be inferred from another. Similarly, coupled differential equations in fluid dynamics or plasma physics describe how multiple parameters evolve interdependently over time. Such relationships are particularly evident in fusion energy, the focus of this work, which is defined by the interplay of diverse physical processes.

Fusion energy and diagnostics: Achieving controlled fusion requires precise, real-time knowledge of plasma conditions to guide and optimize reactor performance. Modern fusion experiments meet this need by deploying a wide array of diagnostics and actuators, each measuring or influencing a different aspect of the plasma state. Recent advances have shown that Artificial Intelligence (AI) can effectively leverage these data streams to enhance plasma control1,2,3,4. Facilities such as DIII-D5 integrate diverse diagnostics to support such AI-driven control strategies6. However, limitations in the spatial and temporal resolution of many diagnostics continue to obscure fast-evolving plasma dynamics that are critical for achieving robust and optimized control7,8,9.

For example, a multi-diagnostic approach is essential to construct a complete picture of electron transport, confinement, and stability in DIII-D discharges. Thomson Scattering (TS)10,11, which employs a high-powered laser beam that scatters off plasma electrons, measures the local electron temperature and density from the scattered light spectrum. Electron Cyclotron Emission (ECE)12 provides spatially localized measurements of the electron temperature, whereas a CO2 Interferometer13 offers line-integrated measurements of the global electron density. Additionally, some diagnostics, though primarily designed for other purposes, can yield indirect yet valuable information on electrons. For instance, the Motional Stark Effect (MSE)14, used to determine the internal magnetic field pitch angle and current distribution, enhances equilibrium reconstructions, which in turn facilitate deeper insights into electron transport and confinement. Each different measurement captures different physical properties, and together form a complementary set for extracting as much information from the plasma as possible. Although it is likely that there is some kind of correlation or coupling between the measurements of different diagnostics (examples in section “Discussion” subsection “Physical basis for multimodal diagnostic coupling”), our current scientific understanding is still not capable of specifying some of these relationships analytically. Utilizing machine learning (ML) to identify such hidden relationships among different diagnostics would be a great asset to enhance their measurements, and it may also help to find a minimal set of diagnostics for a future reactor in which the availability of diagnostics is limited due to cost and hardware constraints.

Diagnostic challenges in capturing plasma instabilities: One of the most critical issues for fusion reactors is the edge-localized mode (ELM), an instability that occurs at the plasma edge under high-confinement conditions. This edge instability delivers transient and intense heat flux outward, which can cause unacceptable levels of erosion of plasma-facing materials in a reactor-scale device. Therefore, understanding and controlling this phenomenon is a major challenge that must be resolved2. However, the detailed physical mechanism of ELMs and the structure of the response to the external field occurring within milliseconds are still subjects of ongoing debate. High-frequency diagnostics like ECE and Interferometer possess sufficient time resolution to track these fast dynamics, but their limited spatial resolution and measurement conditions pose challenges in clearly observing the structural characteristics of ELMs. On the other hand, TS offers high spatial resolution near the plasma edge capable of observing detailed structures, but its temporal resolution is too low to elucidate the exact mechanism of ELMs.

The current remedy to this issue is a specific operational method for TS, known as “burst mode,” to increase the sampling rate of up to 10 kHz15,16. Despite its high pulse repetition, firing TS in “burst mode” is limited by the heat capacity of the laser medium and limited measurement repetition (see the section “Methods” subsection “Diagnostic constraints in ELM measurements” for more details). Therefore, such an approach is typically reserved for very short periods of time or specific experiments where high-resolution temporal data is crucial16.

Need for new approaches: Overcoming these diagnostic limitations calls for methods capable of generating high-resolution measurements from the limited and imperfect diagnostics already available. Various fields have developed ML-based spatial or temporal resolution enhancement techniques, but these mostly involve resolution enhancement by learning linear or nonlinear interpolation within single or limited types of data17,18,19,20,21. These are (1) applicable only to regularly sampled data, (2) largely dependent on the availability of the target sensor measurement for interpolation, and (3) challenging to generate finer-scale phenomena undetectable at the time resolution of the target sensor (more details in the section “Discussion” subsection “Relation to previous super-resolution methods”).

Contribution: We hypothesize that a data-driven ML model, so-called Diag2Diag, with multimodal inputs comprising the high-frequency diagnostics can effectively make use of internal correlations in order to estimate TS accurately. This can enhance the temporal resolution of the existing TS diagnostics without upgrading hardware, so-called Multimodal Super-Resolution TS (SRTS) diagnostics, which enable deeper physical analysis of plasma behavior.

Figure 1 summarizes the main methodology for this work. DIII-D is a well-diagnosed tokamak equipped with more than eighty distinct diagnostic systems. Many of these systems include multiple measurement channels or chords, collectively producing several hundred data streams that monitor different aspects of the plasma. These diagnostics measure various characteristics of plasma at different spatial and temporal resolutions. A potential ML model can learn the intrinsic correlations among diagnostic data and thus generate one from the others. This works for both time series and spectrograms, although different variants of artificial neural network (ANN) are used. The design choices, the optimization, and training strategies are described in the following sections.

Fig. 1: Overview of the Diag2Diag multimodal super-resolution framework.
figure 1

DiagA is essential to capture fast transient events near the edge of plasma. But due to its low temporal resolution and accuracy, it fails to track the evolution of such events. Diag2Diag solves this problem by generating a synthetic super-resolution of DiagA by learning the correlation between DiagA data and other diagnostic measurements with higher resolutions and better accuracy.

Full size image

In this work, we demonstrate that a multimodal super-resolution framework can reconstruct missing or low-resolution diagnostic signals with high fidelity by learning underlying correlations among multiple diagnostics. We show that this method enables synthetic SRTS signals, an inferred representation of TS, revealing experimental evidence of plasma profile flattening due to magnetic islands. These findings provide crucial insights into the mechanisms of ELM suppression via resonant magnetic perturbation (RMP), support robust ELM control strategies for future reactors like ITER, and establish a generalizable framework for diagnosing complex systems with limited sensor resolution. Our approach extends beyond interpolation by reconstructing and enhancing the resolution of a target diagnostic using complementary data from multiple other diagnostics. Specifically, the model learns the underlying physical correlations among different measurements in the fusion device, enabling it to generate a synthetic, high-resolution representation of the target diagnostic without requiring that diagnostic’s own data as input. As a result, this method remains effective even if the target diagnostic is unavailable or not reliable during inference (e.g., due to hardware degradation or failure). Moreover, because the input diagnostics measure different aspects of plasma at higher resolutions, the model can recover events that the target diagnostic might miss due to its intrinsic resolution limits. To our knowledge, this constitutes the first multimodal super-resolution framework of its kind in the context of fusion diagnostics.

Results

Learning diagnostic correlations: ECE to Interferometer reconstruction

Before investigating a multimodal ML-based model to generate synthetic SRTS using other diagnostics, it is crucial to first verify the existence, strength, and robustness of their underlying correlations. We therefore begin by demonstrating a fundamental capability of ML: leveraging one diagnostic’s measurements to reconstruct another’s. Specifically, we use ECE spectrograms, spatially resolved measurements with about 40 channels from edge to core, to reconstruct the line-integrated density fluctuation signals of the Interferometer. Because certain plasma instabilities and modes, such as Alfvén Eigenmode (AE), manifest in both temperature and density measurements, it is reasonable to expect that correlations exist between ECE and Interferometer measurements during such events. Here, we show that a convolutional neural network (CNN) can learn these correlations and reconstruct Interferometer spectrograms from ECE spectrograms, as illustrated in Fig. 2.

Fig. 2: Reconstructing Interferometer spectrograms from ECE spectrograms using convolutional neural networks.
figure 2

a The configuration of four Interferometer chords (R0, V1-3) and 40 ECE probes at DIII-D. b A tensor of (40 × time × frequency) is supplied to CNN. c The configuration of CNN. d Visual comparison of measured and reconstructed spectrograms for DIII-D discharge 170669. e Comparison of the Alfven Eigenmode detector output23 supplied with the measured and reconstructed spectrograms.

Full size image

Figure 2a shows the measurement positions and paths of ECE and Interferometer, as well as example spectrograms obtained from their raw signals (Fig. 2b, d). We designed and trained a CNN that takes 40 ECE spectrograms as input and reconstructs 4 target Interferometer spectrograms. The reconstructed synthetic Interferometer spectrograms visually confirm the plausible reconstruction of features such as frequency chirping and harmonics, especially during the AE events22, as seen in Fig. 2d.

To evaluate how well the underlying physical content is preserved in the reconstructed spectrograms, we employ both quantitative and physics-based assessments. First, achieving an \({{\mathscr{L}}}1\) loss of 1.2 × 10−3 on the validation set determines how closely the CNN reconstructions match the Interferometer’s amplitude and time-frequency distribution (see the section “Methods” subsection “Spectrogram model development” for more details). Second, to verify that the essential physics is captured, we apply a previously published AE detection algorithm23, originally designed for interferometer data, to both the original and reconstructed spectrograms. The resulting average F1 score of 0.82 on the validation set after applying a threshold of 0.15, as suggested in ref. 23, indicates that the model largely reproduces the AE modes, reflecting a high degree of physics fidelity in the reconstructed signals. These findings confirm that neural networks can extract and retain the intrinsic correlations among diagnostic data, even when only one diagnostic serves as input.

Having established the efficacy of this unimodal-to-unimodal reconstruction using spectrogram data, we next extend our approach to raw time-series inputs and expand to multimodal cases. In the subsequent sections, we focus on generating TS signals from a diverse set of diagnostics, illustrating the broader potential of our method for super-resolution diagnostic reconstruction.

Generating super-resolution Thomson Scattering from complementary diagnostics

In this section, we switch from spectrograms to time-series signals and show that the amplitude of a diagnostic can be reconstructed from other diagnostics, while preserving intrinsic physics. More importantly, we will show that if the input diagnostics are of much higher temporal resolution compared to the target one, such a model can be used to increase the time resolution of the target signals in a much more intelligent way compared to the conventional unimodal interpolations. As a use case, we target TS, one of the most important diagnostics that measures the electron density and electron temperature profile of plasma. However, as mentioned earlier, its low temporal resolution is a bottleneck in studying the plasma evolution in the rapidly changing events such as ELM.

Figure 3 demonstrates a diagram of the data processing pipeline during training and inference of Diag2Diag. We consider a suite of input diagnostics available at DIII-D, including Interferometer, ECE, Magnetic probes (Magnetics), Charge Exchange Recombination (CER), and MSE with typical sampling rates of 1.66 MHz, 500 kHz, 2 MHz, 200 Hz, and 4 kHz, respectively. Since our aim is not only to enhance TS but also to reconstruct it from other diagnostics, we do not use the available measurement of TS as input to Diag2Diag. To obtain a dataset that can be used to train and validate the model with the available TS measurements, all the included diagnostics are aligned with the TS sampling time steps by matching their most recent measured sample.

Fig. 3: Data processing pipeline and inference architecture for super-resolution Thomson Scattering.
figure 3

a During the training, the inputs are aligned and resampled with respect to TS timing, to have a ground truth for training and validation of the model. b During the inference, the inputs are resampled to 1 MHz, which will be the resolution of synthetic SRTS. Since there is no ground truth for data-driven validation, we validate the SRTS by studying its behavior during fast physics phenomena, which are challenging to analyze with measured TS due to its low temporal resolution.

Full size image

Since the sampling steps of TS, which is also used to align the inputs for training the model, are not always uniform in time, we opted for a feed-forward neural network instead of recurrent neural networks, which are commonly used in time-series analysis. However, we included the first and second derivatives of the high-resolution input diagnostics, ECE and Interferometer, to include the temporal evolution information. During the inference, the input diagnostics are aligned to a fixed sampling rate of 1 MHz to generate synthetic SRTS. The neural network consists of three dense layers with 512, 256, and 128 nodes per hidden layer. More details about the dataset preparation, model optimization, and uncertainty quantification are provided in sections “Methods” subsection “Time-series model development” and “Discussion” “Assessing model and measurement uncertainty”.

Figure 4 shows, in blue, synthetic SRTS signals generated through the inference of Diag2Diag for the DIII-D discharge 153761, and the original TS measurements are also shown with black dots. For this discharge, TS was fired in the highest possible temporal resolution, so-called “burst mode” (see section “Methods” subsection “Diagnostic constraints in ELM measurements” for more details). We can observe that the synthetic signals closely follow the original measurements, achieving an R2 score of 0.92 in reconstructing the available TS measurement on the validation set. Diag2Diag’s ability to reconstruct TS from other diagnostics ensures that crucial information is not lost, even in the absence of direct measurements. Furthermore, while the original TS measurement sometimes fails to capture ELM events, the synthetic SRTS accurately captures the events missed by TS.

Fig. 4: Benchmarking SRTS against high-resolution burst mode TS measurements.
figure 4

a Comparison of the electron density by the measured TS and SRTS, for discharge 15376115 near the edge (Z = 0.71 m). The spectral emission, Dα, is plotted as an indicator of ELMs. b, c An example of an ELM event captured by both diagnostics, and examples only captured by SRTS are highlighted in green and red, respectively.

Full size image

Here, we note that our objective is not to replicate the entire physics of Magnetohydrodynamics (MHD) turbulence in plasma24 from first principles, but rather to learn empirically grounded correlations among multiple diagnostics. Our aim is to show that even a modestly sized neural network can reliably capture significant nonlinear relationships, for instance, shared fluctuations or mode signatures, by training on experimental data where these diagnostic measurements overlap in time and space. Crucially, the model does not need a complete, fundamental understanding of turbulence; instead, it identifies and exploits observed patterns that consistently appear across diagnostics, as confirmed by its alignment with known plasma behaviors and successful performance on held-out data. Thus, while the network’s architecture may be relatively straightforward, it remains effective in generating physically meaningful reconstructions in a manner that is both computationally efficient and broadly adaptable, complementing (rather than replacing) fundamental physics-based models of MHD turbulence.

Benchmarking super-resolution TS against ELM cycle dynamics at DIII-D

When ELM instability occurs, a large amount of plasma quickly escapes from the boundary within milliseconds, and then the plasma gradually recovers. TS diagnostics can observe the density and temperature structure at this edge region, but are limited in capturing dynamics occurring over milliseconds. Recent research overcame these resolution limits by statistical analysis and aggregating the measurements from multiple repeated cycles of the fast activity under almost identical conditions to observe a complete evolution25. In that work, over 20 highly reproduced cycles of ELM crash and recovery were aggregated from DIII-D discharge 174823 to assume a ground truth of a complete evolution of an ELM cycle.

The aggregated density and temperature evolution measured by TS in three locations of plasma near the edge are shown in Fig. 5a, b with transparent crosses, while measurements from a single cycle are shown with circles and different colors for different measurement locations. In a more typical tokamak discharge, the plasma state continually changes, and ELMs occur more irregularly, as shown in Fig. 4. In such cases, it is not possible to reconstruct a single ELM cycle by aggregating multiple cycles, and our SRTS method will be highly beneficial.

Fig. 5: Benchmarking synthetic super-resolution Thomson Scattering against ELM cycles.
figure 5

a, b Aggregating the measured TS density and temperature in three locations of plasma near the edge for several ELM cycles of the DIII-D discharge 174823. The circle highlights the measures TS for one selected ELM cycle, and the solid lines present the SRTS, which agreeably match the measured TS. t = 0 represents the time when ELM is identified by Dα. c, d The evolution of SRTS between two consecutive measured TS near one ELM cycle across the plasma location.

Full size image

We used the Diag2Diag model to generate synthetic SRTS, shown with solid lines in Fig. 5a, b. The SRTS signal from a single cycle around time 3795 ms not only follows the trend of the aggregated multiple TS measurements but also well overlays the TS measurements within that cycle. Fig. 5c, d shows the detailed evolution of plasma density and temperature across the plasma location captured by SRTS in the same ELM cycle at 3795 ms, which is missed by TS between its two consecutive measurements at 3791 ms and 3800 ms.

Science discovery: unveiling diagnostic evidence of the RMP mechanism on the plasma boundary

In what follows, we investigate whether the synthetic super-resolution diagnostics can help to verify the hypotheses on the mechanism of plasma response to external field perturbations in fusion plasma physics that have been proposed theoretically or by simulations but have never been visualized with experimental data due to the lack of diagnostic resolution.

One promising strategy to control ELMs is employing RMPs26,27,28,29,30,31 generated by external 3D field coils depicted in Fig. 6a. These fields effectively reduce the temperature and density at the confinement pedestal, stabilizing the energy bursts in the edge region. Consequently, ITER will rely on RMPs to maintain a burst-free burning plasma in a tokamak, making it essential for the fusion community to understand and predict its physics mechanism32. However, this issue has remained a challenge for decades.

Fig. 6: Experimental evidence of RMP-induced magnetic island formation revealed by SRTS.
figure 6

Structure of 3D coils and islands by perturbed field (a), along with the evidence in the simulation (b–d) and SRTS diagnostic (e–g) for RMP-induced island mechanism on the plasma boundary in DIII-D discharge 157545.

Full size image

The leading theory33,34,35,36 for explaining the reduced pedestal by RMPs is the formation of magnetic islands by an external 3D field. The magnetic island is a ubiquitous feature in an electromagnetic system with plasmas37 formed by field reconnection38,39. This structure allows rapid heat (or temperature) and particle (or density) transport between adjacent magnetic field lines, strongly reducing the gradient of local heat and particle distribution, or, in other words, profile flattening40. The existing theories explain that RMP forms static magnetic islands at the pedestal top and foot region, therefore reducing the pedestal by local profile flattening. As illustrated in Fig. 6a, the theory predicts that RMPs can create magnetic islands near the plasma boundary where the pedestal sits. This model has been successful in quantitatively explaining and predicting the RMP-induced pedestal degradation in real experiments35,41, reinforcing magnetic islands as a promising mechanism for RMP-induced pedestal degradation. Nevertheless, measuring evidence of island or local profile flattening still remains a challenge. Extensive experimental efforts have been conducted for this reason and were able to capture the local flattening electron temperature profile42 near the pedestal top, strongly supporting this theory. However, simultaneously measuring electron temperature and density both at the pedestal top and foot was not possible. In a previous study, rough evidence was observed in TS36, but it was insufficient to derive a concrete conclusion, mainly due to a large uncertainty of measurement originating from the narrow structure (expected from theory, see Fig. 6a) and oscillatory nature of the plasma boundary. To address the diagnostic uncertainties caused by such system oscillation, one method is to increase the time sampling rate and use time averaging. However, in conventional TS, increasing the time resolution results in a trade-off with measured accuracy, eventually leading to observational limitations.

Interestingly, the SRTS has once again illuminated the profile evolution by RMP application, providing the novel evidence of “simultaneous” flattening of temperature and density profile at both the top and the foot of the pedestal, strongly supporting the theoretical prediction of the magnetic islands effect. This is possible by capturing the statically reliable time trace of the profile with the Chebyshev time filter, leveraging the enhanced temporal resolution by SRTS.

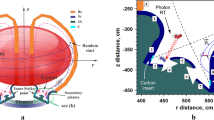
Figure 6b–g illustrates the recovery of temperature and density pedestals within 10 ms after deactivating RMP, as captured through numerical modeling (Fig. 6b–d) and SRTS (Fig. 6e–g). The simulations reveal that the recovery of temperature and density pedestals begins at the top and foot, coinciding with the disappearance of islands. As depicted in Fig. 6d, g, the profile gradient recovers at these island locations, enhancing the overall profile. For instance, the measured temperature pedestal shows recovery at both the top and the foot through an increasing gradient, displaying qualitative alignment with the simulation results. However, some discrepancies are noted, particularly in the density evolution at the pedestal foot in the SRTS, even though its gradient remains consistent with the modeling. These quantitative differences may stem from the TS’s limited spatial resolution at the boundary and the modeling assumptions, such as fixed boundary conditions43. Nevertheless, the gradient evolution directly indicates a change in transport due to the RMP-induced islands during this perturbative profile evolution, highlighting that the SRTS successfully reveals the experimental island effect. This provides the new diagnostic evidence of profile flattening at magnetic islands, a key mechanism of RMP-induced pedestal degradation.

The strength of the SRTS in unveiling profile flattening during ELM suppression can be further highlighted with additional cases. Fig. 7 shows the time traces of plasma for DIII-D discharge 136219 when the edge safety factor (q95), the magnetic pitch angle at the plasma edge, gradually decreases. Here, all other plasma operation parameters, including the RMP field, remain the same. From Dα emission looking perturbation of plasma edge (see Fig. 7a), the bursty spikes disappear during q95 = 3.5–3.6, corresponding to the ELM-suppressed phase followed by the transient ELM-free phase. This shows the strong dependence of ELM suppression on q95. The modeling work based on the island physics42 was able to explain this behavior through the sensitivity of island width at the pedestal top, where its width abruptly increases at certain q95 values due to nonlinear RMP response44. When the island becomes bigger, it leads to local flattening of electron pressure (Pe, product of temperature and density), resulting in ELM suppression. This explanation has successfully predicted this q95 dependency in multiple devices44. However, its experimental validation remains challenging as plasma becomes perturbative while q95 changes, making the pedestal diagnostic oscillatory. Such diagnostic oscillation can be overcome by time filtering, but the temporal resolution of TS was limited for resolving pedestal evolution with q95 with filtering processing.

Fig. 7: Observation of pedestal profile flattening during ELM suppression through island widening.
figure 7

a Time evolution of edge safety factor (q95) and Dα emission at plasma edge for DIII-D discharge 136219. b Contour of electron pressure versus normalized plasma radius and time. The numerically derived width of the magnetic island at the pedestal top is illustrated as green contours. c Comparison of TS (blue), SRTS (red), and filtered SRTS (orange solid line).

Full size image

The SRTS has once again derived the profile evolution by q95 change, providing novel evidence of profile flattening of the pressure profile at the top of the pedestal, leveraging the enhanced temporal resolution by SRTS. Fig. 7b illustrates the strong flattening of the pressure profile during the ELM-suppressed phase, coinciding with the location and width of the magnetic island from numerical modeling. Fig. 7c shows the electron pedestal height measured in both TS and SRTS of the nearest channel to the pedestal top, where the filtered SRTS (orange solid line) follows TS while overcoming diagnostic oscillations. This successfully extracts a prominent impact (profile flattening) on the pedestal caused by island widening from evolving plasma, leveraging the enhanced temporal resolution. This successful application of SRTS underscores its potential to reveal new physics beyond the limitations of conventional diagnostic techniques.

Discussion

Relation to previous super-resolution methods

In recent years, different kinds of ANN have been used for upsampling visual data45,46,47,48 and for radar data49,50,51. Conceptually, our methodology shares some resemblance with such inbetweening techniques, which nonlinearly interpolate missing frames in a video48. However, traditional inbetweening is typically a unimodal technique that relies on partial information from the same data stream (e.g., adjacent video frames). In contrast, our approach is intrinsically multimodal, synthesizing data from multiple diagnostics (spatially resolved and path-integrated) to reconstruct a higher-fidelity representation of the plasma. Crucially, we do not use the target diagnostic’s own measurements as inputs, allowing us to generate a synthetic super-resolution version of that diagnostic even if it fails during operation. This capability distinguishes our method from standard inbetweening algorithms and underscores its robustness and broader utility in real-world complex systems.

More examples for ML-based upsampling were proposed for medical data52 and for audio data53,54. Similar to the video upsampling approaches, these approaches can be considered a subcategory of nonlinear interpolation as well. Yoon et al.55 suggested an alternative to interpolation for estimating the gaps in temporal data streams. It is to some extent a multimodal approach, because it fuses different kinds of information. However, the algorithm is limited towards estimating missing data or dealing with irregularly sampled data. Approaches like these work well for enhancing existing sequences, which are quasi-stationary in a way such that consecutive frames or samples do not change very fast.

However, in fusion energy, many spurious events like ELM can happen between two TS samples. By interpolating between consecutive TS samples, regardless of linear or nonlinear, it is likely that we would miss such spurious events. In our work, we thus develop a novel method to generate additional TS samples based on other diagnostics. This is roughly inspired by other multimodal ML approaches, such as ref. 56, where it was proposed to fuse Radar and camera data for an enhanced distance estimation. This is a multimodal approach and thus related to our approach, or ref. 57, where ML was used to reveal the control mechanics of an insect wing hinge. This was also a multimodal approach in a way that the ML algorithm received different features recorded from flying insects. However, similar to the other approaches, no attempts to upsample or estimate missing/in-between data are made. Also58 presents an ANN method to enhance historical electron temperature data from the decommissioned C-2U fusion device. The model significantly increases the effective sampling rate of TS temperature measurements, utilizing data from multiple diagnostics, including the measured TS. The method’s effectiveness is demonstrated through comparisons with ensemble-averaged data for the micro-burst instability study. The model’s main drawbacks include limited generalization to only the temperature profile study for one specific plasma regime. Notably, the work does not explore the model’s potential for discovering new physics in fusion plasmas.

Physical basis for multimodal diagnostic coupling

Diagnostics of electromagnetic systems involve measuring photons or waves to determine the physical quantities of these systems through post-processing. Due to the nature of the systems, these diagnostics are connected. Firstly, the measured signals are interconnected through electromagnetic interactions during system events. Additionally, the physical quantities obtained from signal processing are closely linked through momentum balances. Electromagnetic plasma quantities are governed by a series of momentum equations that encompass variables such as density, flow, temperature, and higher-order terms. Figure 8 illustrates the momentum equations for plasma density (n) and temperature (T ), where D represents particle diffusivity, v is plasma flow, Sn is the particle source, q denotes heat flux, B stands for magnetic field, j is plasma current, ST is the heat source, and (α, β) are constant coefficients determined by plasma properties59. These equations demonstrate how the measured plasma quantities are interrelated both spatially and temporally. For instance, the line-averaged density obtained from Interferometer diagnostics is geometrically linked to the local density measured by TS by its definition. Simultaneously, temperatures measured by TS and ECE diagnostics, which are positioned differently, are spatially coupled through the gradient term in the momentum equations. Although the TS density and temperature do not directly interact in the equations, they are tightly linked via diffusive fluxes influenced by turbulence, flow, and sources in a self-consistent manner. This intricate physical coupling of various diagnostic measurements allows ML to identify and predict their interconnections effectively.

Fig. 8: Underlying physical coupling among fusion diagnostics enabling multimodal learning.
figure 8

The diagnostics are connected through electromagnetic interactions between signals. Simultaneously, derived quantities from these signals are coupled via geometric definitions, momentum balances, and high-order physics, including turbulence, flow, and source in the system.

Full size image

Assessing model and measurement uncertainty

To quantify the uncertainty in SRTS, we integrate a Bayesian Neural Network (BNN) with a similar architecture described in section “Methods” subsection “Time-series model development.” The model is designed with Bayesian Dense Variational layers, where each layer approximates a posterior distribution over weights using Variational Inference60. Aleatoric uncertainty, which accounts for inherent error in TS measurement, is modeled through a heteroscedastic output that predicts both the mean and log-variance of the target variable at each time step. During inference, we perform Monte Carlo sampling by drawing multiple predictions from the Bayesian posterior, and we compute epistemic uncertainty as the variance of the outputs61. In order to have a fair comparison of the epistemic and aleatoric uncertainties, we calculated the uncertainty of the BNN outputs per channel on the validation set only on the time steps where the ground truth (measured TS) is available.

Figure 9a, b illustrates the average uncertainty of the neural network outputs for electron density (ne) and temperature (Te) per TS channel over the validation set of discharges, depicted as red error bars (Epistemic uncertainty). The TS channels are represented by their distance from the mid-plane of the tokamak (Z). For comparison, we also show the empirically measured diagnostic errors in gray (Aleatoric uncertainty). Given that the epistemic uncertainty is, on average, relatively smaller than the aleatoric uncertainty inherent in the measurements, it indicates that the model has effectively learned the data-generating patterns and is relatively confident in its predictions.

Fig. 9: Uncertainty quantification of synthetic SRTS.
figure 9

a Comparison of the Epistemic and Aleatoric Uncertainties spatially, averaged over the validation dataset for both electron density ne and temperature Te. b Zoomed-in on the plasma edge part, where TS has higher spatial resolution. c The evolution of Epistemic Uncertainty as a factor of training dataset size; as the training set grows, the average and deviation of models’ uncertainty over all TS channels decrease.

Full size image

To ensure that our estimated epistemic uncertainty is meaningful, we conducted an analysis where we trained the model with progressively larger subsets of the dataset and examined how epistemic uncertainty evolved on the validation set. Figure 9c shows the average and deviation of uncertainty across all TS channels as a factor of the percentage of training data used to train the model. The results demonstrate the expected trend where uncertainty decreases as the size of the training dataset increases. At the smallest dataset size, the epistemic uncertainty is highest, indicating that the model lacks sufficient information to make confident predictions. As the training data size increases, epistemic uncertainty steadily declines, reflecting improved model confidence and reduced variability in predictions. This behavior is characteristic of BNNs, where more data helps to refine the posterior distribution over weights, leading to reduced model uncertainty. Notably, the uncertainty reduction follows a diminishing returns pattern; while initial dataset increments lead to significant reductions, the improvements become less pronounced at larger dataset sizes. This suggests that beyond a certain dataset size, additional data contributes less to resolving uncertainty, and the model approaches its inherent learning capacity. The asymptotic nature of this trend highlights the fundamental limit of epistemic uncertainty reduction through data alone, emphasizing the importance of training dataset coverage, model architecture, feature representation, and priors in further improving prediction confidence.

With regard to the source of aleatoric uncertainty and according to the DIII-D diagnostics documentation, the uncertainty in TS measurements arises from fundamental photon counting statistics (discharge noise), imperfect background subtraction, and detector dark noise, all of which are random and inherent to the measurement process62.

During the hyperparameter optimization of our models, we considered both accuracy and uncertainty of the model’s performance. Nevertheless, as shown in Fig. 9, there is epistemic uncertainty, though statistically smaller than the aleatoric uncertainty. A hypothesis could come from the ambiguous or conflicting training data. For example, there have been reports on discrepancies between ECE and TS measurements of electron temperature at JET tokamak63 and such investigations are ongoing at DIII-D as well.

Conclusions

This study introduces a transformative approach in the field of signal processing and diagnostics through the development of a multimodal neural network, Diag2Diag, which significantly enhances temporal resolution. By leveraging the intrinsic correlations among various diagnostic measurements, we have demonstrated the potential to increase the temporal resolution of the TS diagnostics in fusion plasma from a standard 0.2 kHz to an unprecedented 1 MHz. This improvement has unlocked new potentials in analyzing fast transient phenomena in plasma, such as the ELMs and the effects of RMPs on pedestal degradation, which were previously blurred or missed in lower resolution data. The ability to inspect these dynamics in greater detail provides new insights into plasma behavior, particularly in conditions where key physics is hidden in the milliseconds. This enhancement is not merely a technical improvement but a crucial enabler for deeper insights into plasma behaviors that are pivotal for advancing fusion reactors. Furthermore, the model’s ability to reconstruct and predict diagnostics from other available diagnostics opens new avenues for measurement failure mitigation, cost-effective and less hardware-dependent diagnostic systems. This is particularly beneficial for experimental setups where space and resources are limited, such as in smaller fusion test facilities or in environments where installing multiple high-resolution diagnostics is impractical.

Looking ahead, several promising extensions and refinements stand out. First, incorporating additional physics knowledge, such as through physics-informed neural networks (PINNs), may further improve accuracy by constraining the solution space and guiding the network with relevant plasma dynamics. Second, although our current work focuses on temporal resolution enhancement of TS, the same framework can be applied to other diagnostics, potentially improving their temporal or spatial resolution. By generalizing to a broader set of diagnostics and refining the method to capture spatial structure, we can further strengthen this data-driven paradigm for a wide range of fusion applications. Ultimately, these future directions will help realize more comprehensive and high-fidelity diagnostic capabilities, offering deeper insights into complex plasma phenomena.

The implications of this work extend well beyond the immediate application to magnetic fusion. The multimodal super-resolution capabilities developed here can significantly impact areas such as laser fusion data analysis, accelerator data analysis, and molecular dynamics research. In these fields, similar challenges exist where the time and space resolution of diagnostics is inadequate to capture fast phenomena effectively. By applying our method, researchers can potentially uncover new physical phenomena or confirm theoretical predictions that were previously unverifiable through experiments due to resolution constraints.

In conclusion, the Diag2Diag model not only addresses a critical need within the fusion community but also sets a precedent for the broader application of AI and ML in physical sciences. By pushing the boundaries of what can be observed and measured, this work contributes to the foundational technologies necessary for the realization of fusion energy and advances our understanding of complex physical systems across various scientific domains.

Methods

Data acquisition

For this experiment, we used discharges from the DIII-D tokamak that include all data from the key diagnostics of interest (CER, Interferometer, ECE, MSE, and TS). We randomly selected 4000 discharges recorded between the years 2017 and 2022 to ensure a diverse and representative dataset. The diagnostic data were collected using the DIII-D MDSplus64 system. These diagnostics are generally provided as time-series data streams with varying sampling frequencies, ranging from 200 Hz for TS up to 2 MHz for Magnetics. The specific preprocessing steps applied to the data for the different experiments conducted in this study are detailed in the following sections.

Feature extraction

For the spectrogram experiments, we consider the Interferometer and ECE diagnostics. We compute a logarithmic magnitude spectrogram from a time series of the raw diagnostics. For each channel (40 ECE channels and 4 Interferometer channels), we therefore used Hamming windows of 1 ms with 0.5 ms overlap. In this way, it was ensured that the different magnitude spectrograms are aligned in time. The spectrograms were afterwards converted to a logarithmic scale, clipped, and rescaled to the range of [0, 1]. Given the noisy nature of the ECE signals and after rescaling the spectrograms to the range of [0,1], the spectrograms are enhanced using a pipeline of image processing filters that includes

  • Quantile Filtering with a threshold of 0.9,

  • Gaussian Blur Filtering on patches of size 31 × 3,

  • Subtracting the average per frequency bin.

We used the ECE spectrograms as inputs to our model. Since we treated every ECE channel independently during feature extraction, we obtained one spectrogram per channel, resulting in 40 input spectrograms. Since our model is designed to estimate the Interferometer spectrograms, it predicts four output spectrogram channels corresponding to the four Interferometer interferometer channels.

For the time-series models, the different diagnostic measurements have varying sampling rates, and some are even non-uniformly sampled in time. Since the aim of time-series data analysis was to increase the resolution of TS, we used its timestamps as a reference and aligned all diagnostic modalities to TS by matching their most recent measured samples in time. We considered the first 5s of each discharge, which resulted in approximately 3.4M data-points, split into 80%, 20% respectively, for training and validation of the models. As described in the main text, to test the model, we evaluated SRTS during the ELM and RMP mechanisms.

For Interferometer and ECE inputs of the time-series models, we also included the first and second temporal derivatives. Therefore, we smoothed the signals with a moving average window of 1 ms (1660 Interferometer samples and 500 ECE samples), and then computed the first and second temporal derivatives of the smoothed signal also with a window of 1 ms.

The diagnostics CER and MSE have relatively lower temporal resolution (200 Hz and 4 kHz, respectively). In this paper, we assume that they evolve only slowly in time. For the upsampling experiments, we thus pad these diagnostics after a measured sample with constant values until the next measured sample arrives.

The input diagnostics (CER, Interferometer, ECE, Magnetics, and MSE) consist of 58, 4, 40, 8, and 38 channels, respectively, which, together with the first and second derivatives of ECE and Interferometer, form an input feature vector of 236 elements per time step. The outputs are 80 channels of TS measurements for electron density and temperature (40 each).

Spectrogram model development

The multi-channel ECE spectrograms were used as the input to a CNN, and the multi-channel Interferometer spectrograms were used as the target outputs. We optimized all important hyperparameters based on the \({{\mathscr{L}}}1\) loss to minimize the difference between the ground truth and the estimated outputs on the validation set.

The optimization process of the model involved several key steps:

  • The model underwent training for up to 500 epochs.

  • We implemented early stopping with a patience threshold of 20 epochs, during which we monitored the validation loss for any improvements.

  • The AdamW optimizer65, known for decoupling weight decay from the learning rate, was utilized to minimize the \({{\mathscr{L}}}1\) loss function.

  • We conducted a comprehensive hyperparameter optimization through a randomized search across 1000 iterations for all hyperparameters such as batch size, kernel size, and the learning rate.

To reduce the amount of training time, we randomly selected 518 discharges from the entire dataset to conduct the hyperparameter optimization. The model with the best-performing hyperparameter setting (achieving an \({{\mathscr{L}}}1\) loss of 1.2 × 10−3 on the validation set) was then re-trained on all available discharges.

The best-performing model is a CNN that transforms the ECE spectrograms with 40 channels subsequently to 32, 16, and 8 feature maps, and finally to the Interferometer spectrograms with 4 channels. For each feature map, 2D filter kernels with a size of 7 × 7 are used. Batch normalization was used separately for each channel, and parametric ReLU activation functions were used after each batch normalization layer. The model had in total of 95,823 trainable parameters (i.e., filter kernels for each feature map, batch normalization parameters, and negative slope of the parametric ReLU activation function).

Time-series model development

For the time-series prediction task, we employed a Multilayer Perceptron (MLP) model. The input data to the MLP comprised the CER, Interferometer, ECE, MSE, and magnetic diagnostics, along with the first and second temporal derivatives of the Interferometer and ECE signals, resulting in a total input size of 236 dimensions. The target output was the TS diagnostic data, which had 80 dimensions representing electron temperature and density across various spatial locations. To take the uncertainty of TS measurements into account, the target data were augmented by factor 2 by using the upper and lower intervals of each sample as additional targets.

The MLP model was trained for a maximum of 500 epochs, with an early stopping mechanism implemented to halt the training process if the validation loss did not improve for 20 consecutive epochs. The AdamW optimizer65 was employed to minimize the \({{\mathscr{L}}}1\) loss function during training.

Similar to the approach for optimizing the spectrogram model, a comprehensive hyperparameter optimization was undertaken using a randomized search approach spanning 2000 iterations. The hyperparameters jointly optimized included the batch size, hidden layer size, dropout rate, and learning rate. The final MLP comprises three hidden layers with 512, 256, and 128 nodes, which leads to a total of 295,888 trainable parameters.

In principle, incorporating additional physical constraints in the form of a loss function or adopting a PINN framework66 could further refine such a model by reducing the solution space and enhancing accuracy. However, our primary objective is to demonstrate a broadly applicable methodology rather than a domain-specific approach. Therefore, we employed a conventional network architecture with a straightforward \({{\mathscr{L}}}1\) loss function, underscoring that the central concept, exploiting inter-diagnostic correlations for super-resolution, does not hinge on specialized physics priors. This design choice also preserves the generality of our method, making it adaptable to other domains (e.g., astrophysical observations, medical imaging) where detailed physical models may be less readily available. By showing that even a standard ML approach can yield physically meaningful results when carefully formulated, we set the stage for future improvements that may incorporate more explicit physics constraints as needed.

Validation methodology and limitations

Validating synthetic, high-resolution diagnostic reconstructions in fusion plasmas presents unique challenges. Specifically for this work, no MHz-level TS measurements exist in any tokamak, and full-discharge gyrokinetic or extended MHD simulations at MHz temporal fidelity are computationally prohibitive and not yet sufficiently reliable for validation of long-pulse behavior. Such a limitation is, in fact, a motivating factor behind our approach: to develop new data-driven inference capabilities that can extend diagnostic insights beyond what is currently achievable via direct measurement or physics-based modeling. Given these constraints, we employed a multifaceted validation strategy using the best available experimental and simulation data. This includes quantitative comparison with existing TS data using R2 score, benchmarking against the highest-resolution burst-mode TS signals, and consistency checks against known plasma phenomena such as ELMs, RMP-induced magnetic islands, and q95 profile evolution. These steps collectively support the physical relevance and robustness of the super-resolved reconstructions produced by our model.

While we do not claim that the SRTS signals are identical to the actual measurements, as reflected by an R2 score that is very high but not equal to 1, our validation results demonstrate that the synthetic outputs are sufficiently accurate to provide high-value insights. These reconstructions offer practical utility for addressing diagnostic limitations such as low resolution, degradation, and failure, supporting plasma analysis, and enabling potential new physics discovery.

Diagnostic constraints in ELM measurements

In order to let fusion energy be a viable energy source, it must achieve significant fusion gain through continuous fusion reactions. A prominent method to reach this objective is operating a tokamak in high-confinement mode (H-mode), which has a narrow edge transport barrier, also known as the pedestal. This feature significantly boosts plasma confinement within the reactor, enhancing fusion power and efficiency. However, operating in H-mode introduces a steep pressure gradient at the pedestal, leading to substantial operational risks. This gradient drives hazardous edge energy bursts due to a plasma instability known as ELMs. These bursts lead to sudden drops in the energy at the pedestal, causing severe, transient heat fluxes on the reactor walls. This results in damaging material, potential surface erosion and melting, with heat energy reaching approximately 20 MJ m−2, which is an unacceptable level for fusion reactors. From ITER, future machines will not allow even the first ELM. Therefore, to advance tokamak designs toward practical application in fusion energy, it is crucial to develop dependable methods to consistently suppress these edge burst events.

A limitation of some diagnostics, such as TS, is the low temporal resolution of only 200 Hz, which does not allow for detecting and tracking fast events like ELM (≤1 ms). Nevertheless, it is still important to detect such events reliably, as they can have a strong impact on plasma behavior.

To accurately resolve the fast transient dynamics, the TS lasers can be fired in a burst mode, which enables temporal resolution of up to 10 kHz. This increase in temporal resolution is achieved by using multiple lasers in the same path with pulses interleaved closely in time. Normally, the lasers are phased to produce pulses at fairly regular intervals (exact regularity is not possible with the specific combination of 20 Hz and 50 Hz lasers being used at DIII-D). Continuous burst mode operation is also not possible because the laser system would overheat, the optics would be stressed, and the components would wear out very quickly. Therefore, the phase shifts are adjusted so that all lasers fire in rapid succession, followed by a cool-down. This burst mode encompasses between 3 and 7 laser pulses, depending on the time in the discharge.

On the other hand, diagnostics like Interferometer and ECE have much higher temporal resolution with continuous sampling frequencies around MHz, which allows for a much more detailed analysis of the plasma. However, these diagnostics have different characteristics compared to TS. While TS offers detailed insights into both electron density and temperature with high accuracy, it requires complex setups and is usually more resource-intensive. Interferometer provides a more straightforward approach to measuring electron density, excelling in situations that require rapid response and continuous monitoring. Furthermore, ECE and TS are both pivotal diagnostic tools used in tokamaks for measuring electron temperature, yet they operate on distinctly different principles and offer unique advantages. ECE utilizes the natural microwave emissions from electrons gyrating around magnetic field lines to provide excellent temporal resolution, allowing for the monitoring of rapid plasma changes and instabilities, though its effectiveness can be limited by variations in magnetic field strength. On the other hand, TS involves firing a laser into the plasma and analyzing the scattered light, which provides robust, absolute measurements of both electron temperature and density with less susceptibility to magnetic influences. While ECE excels in continuous data collection and fine temporal analysis, TS offers superior spatial resolution and is less dependent on external conditions, making it invaluable for comprehensive, though typically less frequent, plasma evaluations. If it would be possible to find a correlation between the measurements of those high-resolution diagnostics and TS, this would be useful for developing new physical analyses.

Radial plasma profile

The radial profiles for electron temperature, density, and pressure in this study are obtained using TS and SRTS with a reconstruction for plasma equilibrium. This equilibrium is calculated from the magnetic reconstruction using the EFIT code67. Normalized poloidal magnetic flux is used as a representation of normalized radial coordinates.

Workflow and bias mitigation

To avoid any bias during model development and evaluation, each of the following steps in this research was conducted independently by separate researchers in a feed-forward manner as follows:

  1. 1.

    The data scientists developed a diagnostic dataset for training the neural network, aiming for generating synthetic SRTS. In this phase, the evaluation metric was simply the similarity between the model’s output and the measured TS, whenever the measurement was available.

  2. 2.

    For physics validation, we generated the super-resolution diagnostic for a known ELMy discharge and asked an ELM-expert physicist to validate the behavior of the super-resolution diagnostic.

  3. 3.

    The data scientist then delivered the generated super-resolution diagnostic for the target plasma discharge to an experimental physicist to extract the plasma profile from that.

  4. 4.

    We then asked another physicist with expertise in simulation to obtain the simulation results for the target plasma discharge.

  5. 5.

    In the final step, we compared the plasma profiles from our generated diagnostics with the simulation results and found a strong match.

This indicates that our results are not biased based on prior physics knowledge, and we also did not rework our ML model to match our results with the simulation.