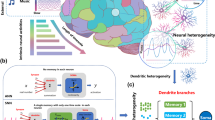
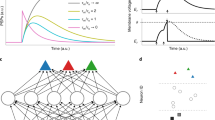
Abstract
The brain exhibits rich dynamical properties that underpin its remarkable temporal processing capabilities. However, spiking neural networks (SNNs) inspired by the brain have not yet matched their biological counterparts in temporal processing and remain vulnerable to noise perturbations. This study addresses these limitations by introducing Rhythm-SNN, which draws inspiration from the brain’s neural oscillation mechanism. Specifically, we employ heterogeneous oscillatory signals to modulate spiking neurons, enforcing them to activate periodically at distinct frequencies. This approach not only significantly reduces neuronal firing rates but also enhances the capability and robustness of SNNs in temporal processing. Extensive experiments and theoretical analyses demonstrate that Rhythm-SNN achieves state-of-the-art performance across a broad range of tasks, with a markedly reduced energy cost, even under strong perturbations. Notably, in the Intel Neuromorphic Deep Noise Suppression Challenge, Rhythm-SNN outperforms deep learning solutions by achieving over two orders of magnitude in energy reduction while delivering award-winning denoising performance.
Similar content being viewed by others
Introduction
Spiking neural networks (SNNs), which draw inspiration from the brain’s cognitive architecture and operational mechanisms, represent a promising avenue for brain-inspired artificial general intelligence1,2. When deployed on neuromorphic chips3,4,5, SNNs demonstrate exceptional processing speed and energy efficiency across various applications, such as object detection6,7, speech recognition5,8, odor recognition9, and robotics10,11. Despite these advancements, current SNNs face significant challenges in processing temporal signals characterized by complex multiscale dynamics. Moreover, they have yet to match the extraordinary efficiency and robustness of the human brain. To address these challenges, we turn our attention to the operational mechanisms of the human brain, particularly exploring neural oscillations, which may offer promising solutions to enhance the capabilities of SNNs.
Neural oscillations are rhythmic or repetitive patterns of neural activity in the brain12,13. These oscillations play critical roles in various brain functions, including synchronization and communication, perception, attention, memory, and motor control12,14,15. As illustrated in Fig. 1a, this fundamental neural mechanism provides valuable insights for addressing the challenges in SNNs. First, neural oscillations facilitate the synchronization and integration of information across various timescales. They operate across a wide range of frequencies, from the slow delta band (<4 Hz) to the rapid gamma band (>30 Hz)12. This frequency diversity enables the brain to flexibly encode, transmit, and integrate information across various timescales, thereby enhancing temporal processing capacity. For instance, neural oscillations contribute to effective speech and language processing, from the rapid encoding of phonemes to the integration of words, and the comprehension of longer linguistic constructs, such as phrases and sentences16,17. Second, neural oscillations contribute to the brain’s energy efficiency. Studies have shown that cortical neuronal activities exhibit high sparsity, with less than 1% of neurons active concurrently18. This is achieved with the assistance of neural oscillations that coordinate the timing and synchronization of neuronal firing among various neural populations. By enabling the selective activation of specific neural populations while keeping others inactive14,19, it is ensured that only relevant information is processed while minimizing unnecessary neuronal activity, thereby effectively promoting energy-efficient computation13,15. Third, neural oscillations enhance the robustness of communication and information processing in the brain amidst various noises15. The sparse neuronal activities facilitated by neural oscillations reduce the overlap between representations of different stimuli, thereby enhancing pattern separation. This improved separation enables robust decoding from noisy inputs.
a Neural oscillations spanning a wide range of frequencies have been observed across various brain regions, which play crucial roles in neural computation. Top Right: Neural oscillations operating at various frequencies enable the brain to synchronize and integrate information across diverse timescales. Bottom Left: Neural oscillations enhance energy efficiency by selectively activating distinct neural populations at specific phases of the oscillatory signal. Bottom Right: Neural oscillations promote pattern separation, allowing for robust decoding of the target signal from noisy inputs. b In the proposed Rhythm-SNN, neurons are modulated by oscillatory signals of different frequencies, which are represented by different colors. c Neuronal dynamics of rhythmic spiking neurons depicted in (b). The charging and firing behaviors of these neurons are influenced by the square wave modulation signals. Note that a constant input current is applied to these neurons in this illustration. d The unfolded computational graph of rhythmic spiking neurons is shown in (c). These neurons alternate periodically between `ON' and `OFF' states following neural modulation. During the `OFF' state, membrane potentials remain unchanged during forward propagation, thereby conserving energy. In backward propagation, gradients effectively propagate by skipping the `OFF' states, thus establishing a highway for gradient backpropagation through time.
Drawing inspiration from the key characteristics of neural oscillations, we propose a neural modulation mechanism that employs oscillatory signals to modulate the neuronal dynamics of spiking neurons. This innovation leads to the development of a new generation of SNNs, termed Rhythm-SNNs, which capitalize on the brain’s remarkable capabilities in temporal processing, energy efficiency, and robustness against perturbations. Our comprehensive experimental results indicate that Rhythm-SNNs achieve state-of-the-art (SOTA) accuracy across a wide range of challenging temporal processing tasks, while reducing energy cost by up to an order of magnitude compared to conventional SNNs that do not incorporate this neural modulation mechanism. Moreover, Rhythm-SNNs demonstrate significantly enhanced working memory capacity and improved robustness against various types of noise and adversarial attacks.
The comprehensive performance enhancements offered by the Rhythm-SNNs present significant opportunities for addressing complex temporal processing tasks at the edge. To illustrate this advantage, we applied Rhythm-SNNs to the Intel Neuromorphic Deep Noise Suppression (N-DNS) Challenge20. This challenge requires the development of neuromorphic speech enhancement models that exhibit superior temporal modeling capabilities, low latency, and minimal energy consumption – criteria that traditional signal processing and deep learning models often struggle to meet simultaneously. By leveraging the proposed rhythmic modulation mechanism, our Rhythm-SNN produces high-quality audio output that surpasses award-winning entries in the challenge, while reducing energy cost by two orders of magnitude compared to the deep learning models. This breakthrough paves the way for the next generation of neuromorphic hearing devices, such as hearing aids and headsets, capable of operating efficiently in complex environments.
Results
Rhythm-SNN: harmonizing rhythms and spikes
Neural oscillations, characterized by rhythmic patterns in membrane potentials and spike trains, are crucial for modulating neuronal activities within the brain14,19. Previous neuroscience studies have demonstrated that sensory perception and memory maintenance are selectively regulated through the modulation of neural oscillations21,22,23. Drawing inspiration from this fundamental neural mechanism, we propose a rhythmic neural modulation framework for SNNs. Within this framework, an oscillatory signal, denoted as m(t), is employed to modulate the neuronal dynamics of spiking neurons. In general, this rhythmic neural modulation can be expressed mathematically as follows:
where S(t) represents the output spike emitted at time t, I(t) denotes the input current from presynaptic neurons, and U(t) and ϑ correspond to the membrane potential and the firing threshold of the spiking neuron, respectively.
Within the proposed framework, the oscillatory signal m(t) is modeled as a periodic function. Specifically, as illustrated in Fig. 1c, we employ a square wave function for m(t) to modulate the updates to the neuron’s membrane potential and its firing activities (see “Methods” section). This approach enables the neurons to alternate between ‘ON’ and ‘OFF’ states. During the ‘ON’ state, the neurons are updated as usual, whereas in the ‘OFF’ state, the neuronal updates are halted. Neurons modulated by oscillation signals of similar period and phase are expected to synchronize in their firing activity. This synchronized firing will lead to oscillatory neural activities at the population level, aligning with observations of neural oscillation in human electrophysiological studies24,25. This design offers four notable benefits. First, as depicted in Fig. 1d, the introduction of the rhythmic modulation mechanism allows neuronal state updates to be skipped during ‘OFF’ states, significantly reducing overall neuronal activity and directly enhancing energy efficiency. Second, the ‘OFF’ states act as a shortcut during gradient backpropagation, effectively shortening the gradient propagation pathway. This mechanism is reminiscent of the residual connections commonly used in artificial neural networks (ANNs)26, which can facilitate long-term credit assignment. Third, the rhythmic modulation mechanism prevents the membrane potential of spiking neurons from being updated during ‘OFF’ states, facilitating memory preservation and hence enhancing their memory capacity. Fourth, the resulting sparse neuronal activity promotes pattern separation during signal processing, which in turn improves the model’s robustness to perturbations. Another key feature of the proposed oscillatory signals m(t) is their design to encompass diverse periods, duty cycles, and phases, as indicated by different colors in Fig. 1b. This temporal heterogeneity enriches the network dynamics, facilitating effective information synchronization and integration across a wide range of timescales.
Furthermore, we theoretically analyze the computational advantages of Rhythm-SNNs from three aspects (see “Methods” section). First, we examine the backpropagation pathways and reveal that the oscillatory modulating signal m(t) significantly alleviates the issue of exponential gradient decay with distance, a common challenge during gradient-based training of SNNs. This suggests that incorporating oscillatory modulation can improve the learning of long-term temporal dependencies. Second, we assess the memory capacity of Rhythm-SNNs using the mean recurrent length metric27. Our theoretical analysis shows that our method effectively reduces the mean recurrent length, thereby enhancing memory capacity. Third, we evaluate the robustness of Rhythm-SNNs against various types of noises and adversarial attacks through perturbation analysis of spike responses28. This analysis demonstrates that Rhythm-SNNs can enhance robustness to perturbations by reducing the spiking Lipschitz constant associated with the spike train. These theoretical advantages are also supported by the extensive experimental results presented in the following sections.
Rhythm-SNN facilitates effective and efficient temporal processing
Temporal processing is vital for accurate perception and integration of time-dependent information, which is essential for functions such as speech recognition and motor control. In this section, we evaluate the effectiveness of the proposed Rhythm-SNN across a wide range of temporal processing tasks, including visual recognition on Sequential-MNIST (S-MNIST) and Permuted Sequential-MNIST (PS-MNIST)29, speech recognition on Spiking Heidelberg Digits (SHD)30 and Google Speech Commands (GSC)31, bio-signals recognition on Electrocardiogram (ECG)32, speaker identification on VoxCeleb133, language modeling on Penn Tree Bank (PTB)34, and event stream recognition on DVS-Gesture35.
The SNN architectures evaluated in this section are state-of-the-art and serve as representative models for temporal processing tasks in the field of SNNs36,37,38. These models primarily focus on enhancing the temporal processing capabilities of SNNs by designing advanced spiking neuron models that incorporate learnable decay factors32,39,40, gating functions for neuron updates41, and dendritic structures36. To evaluate the effectiveness and broad applicability of our method, we conducted experiments by incorporating the proposed rhythmic modulation mechanism into these representative SNN architectures. As shown in Table 1 and Fig. 2a, Rhythm-SNNs consistently outperform their non-Rhythm counterparts. Notably, the performance of feedforward SNNs improves substantially upon incorporating the proposed rhythmic neural modulation mechanism, surpassing many competitive baseline models that utilize recurrent network dynamics to enhance temporal processing capacity. This highlights the significant effectiveness of the proposed mechanism in enhancing temporal processing. Following previous research32, we also conducted a detailed analysis to assess the capability of our method in facilitating multiscale temporal processing in SNNs. As shown in Fig. 2b, the accuracy of the SRNN model declines rapidly as the sequence length increases from 500 to 1500 on the DVS-Gesture dataset. In contrast, incorporating an adaptive firing threshold with a slow-decaying time constant significantly improves the performance of the ASRNN32 model over the SRNN. Even greater performance improvements are observed when our proposed rhythmic modulation mechanism is integrated into the SRNN, with our results at a sequence length of 1,500 surpassing those of the ASRNN at a sequence length of 500. Furthermore, our method can synergize with the adaptive firing threshold approach, as evidenced by further accuracy improvements in the Rhythm-ASRNN.
a Performance of Rhythm-SNNs versus non-Rhythm counterparts on the PS-MNIST and ECG datasets. b Performance of Rhythm-SNNs and non-Rhythm counterparts on the DVS-Gesture dataset, with input sequence lengths ranging from 500 to 1500. For both (a) and (b), the experiments were conducted over three runs with different random seeds, and the error bars represent the standard deviation. c Normalized temporal gradients for all hidden neurons in FFSNN, ASRNN, and their Rhythm-SNN counterparts, using a mini-batch from the PS-MNIST dataset. Rhythm-SNNs can effectively allocate more gradients to earlier time steps, facilitating the learning of long-range temporal dependencies. d Learning curves for Rhythm-SNNs and non-Rhythm counterparts under identical training conditions. Solid lines represent mean accuracies, while shaded areas indicate the standard deviation of accuracy across four runs with different random initializations. e Energy costs and corresponding accuracy of different models on the PS-MNIST dataset. The number next to the circle point of the vanilla model represents its energy cost ratio relative to its rhythmic counterpart. f Layer-wise firing rate comparison across different models depicted in (e).
To elucidate how the proposed rhythmic neural modulation effectively facilitates learning multiscale temporal dependencies, we visualize the normalized gradients of FFSNN, ASRNN, and their rhythmic counterparts on the PS-MNIST dataset. As illustrated in Fig. 2c, Rhythm-SNNs could allocate more gradients to early time steps compared to their non-Rhythm counterparts, suggesting the proposed method establishes a more effective gradient backpropagation pathway during training. More results on LSNN and SRNN are provided in Supplementary Fig. S2. Furthermore, we present two concrete examples in Supplementary Fig. S3 to demonstrate how Rhythm-SNNs improve temporal processing tasks that involve long-range dependencies. This enhancement in gradient backpropagation also accelerates training. As demonstrated in Fig. 2d, our method enables significantly faster convergence during training and exhibits greater stability, as evidenced by the smaller standard deviations across different random initializations.
We further evaluate the energy efficiency of the proposed Rhythm-SNNs. Following prior works42,43, we calculate the model’s energy cost based on Synaptic Operations (SynOps) and Neuron Operations (NeuOps) incurred during data processing and neuron updates. As shown in Fig. 2e, Rhythm-SNNs reduce energy cost compared to their non-Rhythm counterparts by up to an order of magnitude while achieving higher accuracies. This enhanced energy efficiency can be directly attributed to the sparser neuronal activity, as shown in Fig. 2f and Supplementary Fig. S4. A detailed quantitative analysis and FPGA-based neuromorphic hardware evaluation of energy efficiency between Rhythm-SNNs, conventional SNNs, and ANNs are provided in Supplementary Tables 5–7. These results highlight the significant potential of our method to enhance the energy efficiency of neuromorphic computing systems.
Rhythm-SNN enhances working memory capacity
Working memory is crucial in the neural system as it enables the temporary storage and manipulation of information necessary for complex cognitive tasks, such as reasoning, learning, and decision-making. In this section, we further assess the working memory capacity of Rhythm-SNNs using the STORE-RECALL task44,45. As illustrated in Fig. 3a and b, a sequence of binary values is randomly generated and subsequently encoded into spike trains by two groups of encoding neurons. These neurons generate spike trains within a 100 ms encoding time window for each binary value, following a Poisson distribution with an average firing rate of 50 Hz. Upon receiving the ‘STORE’ command, the network is required to store the binary value present during that period. A subsequent ‘RECALL’ command prompts the network to output the stored value. In accordance with previous research44,45, we utilize two SRNN architectures for this task, each featuring a different type of neuron model with distinct mechanisms for adaptive firing threshold updates (see Supplementary Section 2), i.e., Adaptive-Leaky Integrate and Fire (ALIF)40 and Double EXponential Adaptive Threshold (DEXAT)45, referred to as Rhythm-ALIF and Rhythm-DEXAT, respectively. More details of the experimental setup are provided in “Methods” section.
a The model architecture employed for solving the STORE-RECALL task. It consists of four groups of encoding neurons that convert input signals into spike trains, which are then processed by either a Rhythm-SRNN or a non-Rhythm-SRNN to produce the output. b Top: Input spike trains corresponding to the four groups of encoding neurons. Each input is encoded within a 100 ms encoding time window, following a Poisson distribution with an average firing rate of 50 Hz. Middle: Output spike raster of hidden neurons. Bottom: Temporal evolution of output predictions. c Comparison of recall errors between Rhythm-ALIF and Rhythm-DEXAT and their non-Rhythm counterparts across three runs with different random seeds. Error bars indicate standard deviations. d and e Loss curves and recall errors during the training process. Solid lines represent average performance, while shaded areas indicate standard deviation across three runs with different random seeds.
As shown in Fig. 3b, the rhythmic neural modulation enables Rhythm-DEXAT to maintain a lower firing rate at the hidden layer, resulting in more stable output predictions between ‘STORE’ and ‘RECALL’ commands compared to DEXAT. Similar results are observed with Rhythm-ALIF, as detailed in Supplementary Fig. S5. As illustrated in Fig. 3c, our experimental results demonstrate that Rhythm-SNNs significantly outperform their non-Rhythm counterparts in recall performance. Additionally, the reduced standard deviation of recall errors indicates that our models exhibit greater robustness. Figure 3d, e further illustrates the learning dynamics of different models, with Rhythm-SNNs converging much faster than their non-Rhythm counterparts. This demonstrates that the proposed rhythmic neural modulation mechanism effectively facilitates the learning of multiscale temporal dependencies, consistent with the observations in the previous section. To further evaluate the increased memory capacity of Rhythm-SNNs, we designed a more challenging delayed recall task in which the models are required to recall temporally encoded spike patterns after a specific delay. A comparison of recall accuracy between vanilla ALIF and Rhythm-ALIF across varying numbers of input patterns demonstrates a significantly enhanced memory capacity of our approach (see Supplementary Figs. S7 and S8). These results underscore the efficacy of our proposed method in enhancing working memory capacity and corroborate the theoretical analysis presented in “Methods” section.
Rhythm-SNN enhances robustness against perturbations
The sparse neuronal activity facilitated by Rhythm-SNNs can enhance pattern separation, potentially leading to increased model robustness. In this section, we evaluate the robustness of Rhythm-SNNs against various perturbations, including input-related Gaussian noise, network-related noises (i.e., thermal noise, silence noise, and quantization noise), and adversarial attacks. Gaussian noise simulates the disturbances that occur in the input data, whereas network-related noise represents the hardware noise commonly found in mixed-signal neuromorphic chips, affecting all neurons in the network. Additionally, adversarial attacks involve deliberate manipulations of input data aimed at deceiving machine learning models, leading them to make incorrect predictions. In our experiments, we generate input- and network-related noises in accordance with prior studies28,46, and employ the Fast Gradient Sign Method (FGSM)47 and Projected Gradient Descent (PGD)48 for black and white box attacks, respectively. More details of the experimental setup are provided in “Methods” section.
In Fig. 4, we present the test results obtained from the PS-MNIST dataset under various types of noise perturbations, where higher bars indicate more severe performance degradation. Our Rhythm-ASRNNs consistently outperform ASRNNs across all testing scenarios. Specifically, as shown in Fig. 4a, Rhythm-ASRNNs maintain stable performance across four different input noise levels, experiencing only a 0.005 accuracy drop ratio, compared to the 0.087 accuracy drop ratio obtained by ASRNNs at the highest noise level. Regarding network-related noises, Rhythm-ASRNNs exhibit a more gradual increase in accuracy drop ratio as noise level rises, as illustrated in Fig. 4b–d. To further demonstrate the effectiveness of our approach, we visualize the perturbation distance across different network layers in Fig. 4e–h. The perturbation distance is calculated as the Euclidean distance between network representations before and after introducing noise. It is evident that the perturbation distance increases in deeper layers for ASRNNs, whereas it remains significantly lower for Rhythm-ASRNNs, indicating that our model achieves more robust network representations. Additionally, visual illustrations of hidden layer representations for ASRNNs and Rhythm-ASRNNs are provided in Supplementary Figs. S11 and S12, respectively, which further demonstrate the smaller variations in network representations achieved by our Rhythm-ASRNNs.
a–d Comparison of the accuracy drop ratio of ASRNNs and Rhythm-ASRNNs under varying levels of input-related Gaussian noise and network-related noises, including thermal noise, silence noise, and quantization noise. e–h Comparison of perturbation distances for ASRNNs and Rhythm-ASRNNs across various types of noise perturbations, illustrated in (a–d). Note that the highest noise level was utilized in this analysis. The perturbation distance is quantified using the Euclidean distance between the network representations prior to and following the introduction of noise. i–l Comparison of the changes in average firing rate and average perturbation distance for ASRNNs and Rhythm-ASRNNs under various types of perturbations. Rhythm-ASRNNs with a smaller duty cycle exhibit greater robustness against noise perturbations. In the legend, `dc' represents the duty cycle of the oscillatory modulation signal used in Rhythm-ASRNNs. The numbers following the colon specify the lower and upper bounds of the initial distribution of the duty cycle. m–p Comparison of the accuracy drop ratio and perturbation distances for ASRNNs and Rhythm-ASRNNs across various types and levels of adversarial attacks. The error bars represent the standard deviation of three runs with different random seeds.
To further investigate which temporal properties of the proposed rhythmic neural modulation mechanism contribute to enhanced network robustness, we conducted experiments by adjusting the duty cycle (‘dc’) of oscillatory signals used in Rhythm-ASRNN and examined its influence on the network firing rate and network representation. As shown in Fig. 4i–l, the variability in the average firing rate decreases after incorporating the proposed rhythmic neural modulation mechanism, leading to reduced perturbations in the network representation. Additionally, we observed that a smaller duty cycle results in greater robustness against noise perturbations. These findings suggest that reducing the duty cycle of oscillatory signals, thereby promoting sparser neuronal activity, enhances the network’s robustness.
Regarding the assessment of adversarial attacks, as shown in Fig. 4m and o, ASRNNs exhibit significant performance degradation under both FGSM and PGD attacks. In contrast, Rhythm-ASRNNs consistently demonstrate a substantially lower accuracy drop ratio in both attack scenarios. This enhanced robustness can also be explained by the sparser neuronal activity achieved in Rhythm-ASRNN, with details provided in Supplementary Fig. S10. Overall, these empirical results highlight the critical importance of enforcing sparse neuronal activity in enhancing the robustness of the network. This finding is further corroborated by our theoretical analysis of the model’s robustness against perturbations (see “Methods” section).
Application in speech enhancement tasks
Human communication predominantly relies on speech, which serves as an effective medium for expressing thoughts and emotions. However, as illustrated in Fig. 5a, speech communication systems often capture unwanted environmental interferences, such as ambient noise and reverberations, which can significantly degrade the quality of the speech signal. To address these challenges, speech enhancement (SE) technologies have been developed to improve clarity and intelligibility by mitigating noise and distortions. Over the past decade, deep learning techniques have significantly enhanced SE systems. However, deploying these deep learning solutions on edge devices, such as headphones and hearing aids, remains challenging due to their substantial computational demands and latency issues. The proposed Rhythm-SNNs offer promising solutions to address these limitations inherent in deep learning approaches.
a Illustration of typical real-world acoustic environments where speech enhancement technologies are crucial for improving the clarity and intelligibility of speech signals. b The overall model architecture of the proposed Rhythm-GSNN model. c Comparison of output audio quality (measured by SI-SNR, OVR, SIG, and BAK metrics) and computational cost between Rhythm-GSNN and leading speech enhancement methods. d–f Visualization of the noisy audio spectrogram, the denoised audio spectrogram generated by Rhythm-GSNN, and the clean audio spectrogram, respectively.
Motivated by this, we evaluate the effectiveness of Rhythm-SNNs on the SE task using the latest Intel N-DNS Challenge dataset20, which provides a comprehensive evaluation across a wide range of languages, noise types, and acoustic conditions. Inspired by the winning entry of the latest Intel N-DNS Challenge, we develop a Rhythm Gated Spiking Neural Network (Rhythm-GSNN) model (see Supplementary Fig. S9 for more details). As illustrated in Fig. 5b, this model first encodes noisy speech into spike trains using a Short-Time Fourier Transform (STFT) encoder. Subsequently, the computationally intensive SE workload is handled by the Rhythm-GSNN. Finally, the output spike trains from the Rhythm-GSNN are decoded into audio signals via an inverse STFT (iSTFT) decoder. We compare our model with several SOTA approaches, including both deep learning solutions (i.e., DCCRN49, FullSubNet50) and neuromorphic solutions (i.e., Microsoft NsNet251, SDNN20, PSNN20, and GSNN52). A comprehensive set of evaluation metrics is employed in this study to ensure rigorous assessment of the generated audio samples, including Scale-Invariant Source-to-Noise Ratio (SI-SNR)53, Overall Audio Quality (OVR)54, Speech Signal Quality (SIG)54, and Background Noise Quality (BAK)54. Higher values of these metrics indicate better audio quality. More details of the experimental setup are provided in “Methods” section.
As summarized in Fig. 5c, our Rhythm-GSNN model demonstrates superior performance that is comparable to, or even surpasses, the SOTA deep learning and neuromorphic models. Notably, the integration of the proposed rhythmic neural modulation mechanism significantly enhances the performance of the original GSNN model, particularly in terms of SI-SNR and SIG metrics. Furthermore, we randomly selected a speech sample from the test set and plotted its noisy spectrogram, denoised spectrogram, and clean spectrogram in Fig. 5d–f, respectively. The denoised spectrogram produced by our Rhythm-GSNN model closely matches the reference clean spectrogram, demonstrating the high effectiveness of our method. Additionally, Rhythm-GSNN exhibits substantial advantages in energy efficiency. As reported in Fig. 5c, Rhythm-GSNN reduces energy cost by two orders of magnitude compared to the leading deep learning solution, FullSubNet50. It is also worth noting that the energy cost of Rhythm-GSNN is less than half of that of its non-rhythm counterpart. These results clearly demonstrate the superiority of our method in simultaneously enhancing the model’s denoising capability and energy efficiency. Overall, the remarkable performance achieved by our Rhythm-GSNN opens up a myriad of opportunities for deployment on edge audio devices with stringent energy and latency requirements.
Discussion
Neural oscillation mechanisms have long been identified in neuroscience studies13. Drawing inspiration from their key characteristics, we introduce Rhythm-SNN, a computational framework that incorporates rhythmic neural modulation into SNNs to enhance their temporal processing capabilities. This framework facilitates multiscale temporal processing by leveraging heterogeneous neural oscillation signals with diverse periods, duty cycles, and phases12,13,14. Our experimental results indicate that Rhythm-SNNs achieve significant improvements in temporal processing capacity, energy efficiency, and robustness against perturbations. Additionally, we provide theoretical analyses of the effective gradient backpropagation pathways, enhanced memory capacity, and improved robustness enabled by the proposed framework.
The Rhythm-SNNs represent a fundamental departure from previous studies on SNNs in the context of temporal processing. Earlier research primarily focused on modeling intrinsic neuronal variables, such as adaptive firing thresholds and heterogeneous membrane time constants, to improve the long sequence processing ability of SNNs32,39,40,45. In contrast, our approach utilizes external heterogeneous oscillatory signals to modulate neuronal dynamics, thereby facilitating the encoding, transmission, and integration of information across various timescales. The simulation results presented in Table 1 and Fig. 2 confirm the superior performance of Rhythm-SNNs across a wide range of temporal processing tasks. Additionally, we demonstrate the synergistic effect of combining external oscillatory neural modulation with intrinsic neuronal variables in enhancing the SNN’s temporal processing capacity. Furthermore, our experiments on the STORE-RECALL and delayed recall tasks have shown the benefits of our proposed method in enhancing working memory retention. These results align with previous neuroscience studies that suggest a positive correlation between memory maintenance and neural oscillations25,55. While prior work56 has explored the incorporation of an oscillatory postsynaptic potential and a phase-locking activation function into resonant spiking neurons, it primarily addressed the incompatibility between the backpropagation algorithm and SNNs, rather than enhancing the temporal processing capability of SNNs. Additionally, our design incorporates the heterogeneity of neural oscillations for multiscale temporal processing, distinguishing it from previous studies27,57, which integrated homogeneous skip connections into RNNs to address training difficulties and achieve temporal parallelization.
The proposed rhythmic modulation mechanism can also be regarded as a neuroscience-inspired periodic hard gating mechanism. This design contrasts with the continuous soft gating mechanisms used in ANN models, such as the LSTM family58,59,60 and their spiking variants7,41, and offers several notable advantages. First, unlike previous approaches that require frequent updates of the hidden states at each time step, our periodic hard gating mechanism keeps most neurons inactive during processing, thereby reducing overall neuronal activity and enhancing energy efficiency. Second, this design facilitates long-term temporal credit assignment. Our analysis indicates that it effectively mitigates the vanishing gradient problem encountered when training with long sequences by establishing multiple temporal shortcuts for gradient backpropagation. Third, the binary nature of the oscillatory gating signals is hardware-friendly, efficiently supporting the spike-driven computing paradigm and deployment in neuromorphic chips (see Supplementary Fig. S15 for more details).
Another innovative aspect of Rhythm-SNNs is their utilization of brain-like sparse coding strategies to achieve robust and energy-efficient computation. Previous efforts to enhance the robustness of SNNs have primarily relied on classical machine learning techniques, such as adding regularization terms to the loss function28,61 and developing tighter estimators to better delineate the network’s classification boundaries62. In contrast, as illustrated in Fig. 4, our model enhances robustness against various perturbations by reducing neuronal activity levels through rhythmic neural modulation. This approach aligns with neuroscience findings that suggest the sparsity of neuronal activity can enhance the robustness of neural systems in sensory processing63. Moreover, this method also allows for efficient data representation by activating only a small subset of neurons in response to stimuli.
Our approach offers an intriguing solution for efficient and robust information processing in edge devices. In our experiments on the speech enhancement task, the proposed Rhythm-GSNN demonstrated significant improvements in denoising performance while reducing energy cost by more than two orders of magnitude compared to the leading deep learning solutions. This combination of efficiency and robustness is essential for audio devices served at the edge, such as hearing aids and headsets, where low latency and ultra-low energy consumption are critical. Collectively, our method could prompt the development of more efficient, effective, and robust neuromorphic signal processing systems that could be deployed on edge devices and operate in complex real-world scenarios.
Methods
Rhythm-SNN
The proposed Rhythm-SNN utilizes heterogeneous oscillatory signals to modulate the membrane potential update and spike generation. Since these two neuronal dynamics are fundamental to all spiking neuron models, our rhythmic modulation mechanism is applicable across a wide range of such models. Here, we employ the widely used LIF64,65,66 neuron model for an illustration. Additional details on other recently developed network architectures incorporating our rhythmic modulation mechanism, along with their mathematical formulations, are provided in Supplementary Section 1. For the vanilla LIF neuron, the membrane potential of the ith neuron in layer l evolves according to:
where τm denotes the membrane time constant, Ur is the resting potential. \({U}_{i}^{l}\) and \({I}_{i}^{l}\) represent the membrane potential and input current of the neuron, respectively. Once \({U}_{i}^{l}\) exceeds the firing threshold ϑ, the neuron emits a spike \({S}_{i}^{l}\) and its potential is subtracted by the firing threshold. In fact, \({I}_{i}^{l}\) is computed by accumulating the spikes from all its presynaptic neurons, resulting in the following discrete form:
where \({w}_{ij}^{l}\) represents the connection weight from the presynaptic neuron j in layer l − 1, \({b}_{i}^{l}\) denotes the constant injected current to neuron i, and \({S}_{j}^{l-1}\) signifies the input spike from the presynaptic neuron j.
By employing the zero-order hold (ZOH) method67, we could obtain the discrete form of the membrane potential update from its continuous form illustrated in equation (2):
where α ≡ exp(−dt/τm) denotes a constant that captures the membrane potential decay, with τm as its time constant and dt as the simulation time step.
In contrast, our Rhythm-LIF neuron incorporates rhythmic modulation by utilizing oscillatory signals to modulate the membrane potential update and spike generation. Specifically, the membrane potential update is modulated by the introduced oscillatory signal \({m}_{i}^{l}\left[t\right]\) as follows:
where \({U}_{i}^{l}\left[t\right]\) is the membrane potential at time step t. Additionally, the corresponding firing activity is also modulated by the introduced oscillatory signal as described below:
where
Here, \({\varphi }_{i}^{l}\), \({c}_{i}^{l}\) and \({d}_{i}^{l}\) denote the initial phase, rhythm period, and duty cycle of the modulating signal, respectively; ⌊ ⋅ ⌋ represents the floor function; and Θ( ⋅ ) is the Heaviside step function, defined as Θ(x) = 1 for x ≥ 0 and Θ(x) = 0 for x < 0. Through this modulation mechanism, when \({m}_{i}^{l}\) equals zero, the neuron neither integrates input current from its presynaptic neurons nor emits spikes to its postsynaptic neurons, corresponding to an ‘inactivate’ state. Conversely, when \({m}_{i}^{l}\) equals one, the neuron adheres to the original dynamics of a conventional spiking neuron, representing an ‘activate’ state. The detailed computational graph of our proposed rhythmic spiking neuron is illustrated in Supplementary Fig. S1.
Collectively, the neuronal dynamics of the LIF model and the proposed Rhythm-LIF model can be summarized as follows:
Heterogeneous oscillation signals
To emulate the multiscale characteristics of neural oscillations, we parameterize the modulating signal \({m}_{i}^{l}\) by sampling its hyperparameters from diverse distributions. Specifically, given a Rhythm-SNN with L layers, the rhythmic parameters, i.e., the rhythm period \({c}_{i}^{l}\), duty cycle \({d}_{i}^{l}\), and phase \({\varphi }_{i}^{l}\) of the oscillatory signal \({m}_{i}^{l}\) of a neuron i in the layer l are generated through:
where T represents the total number of time steps and \({{{\mathcal{U}}}}\) denotes the uniform distribution. Here, we use the parameters \({c}_{\min }^{l}\), \({c}_{\max }^{l}\), \({d}_{\min }^{l}\), \({d}_{\max }^{l}\), \({\varphi }_{\min }^{l}\), and \({\varphi }_{\max }^{l}\) to define the range of the uniform distributions, which subsequently control the characteristics of the generated oscillatory signals. Since \({d}_{i}^{l}\) and \({\varphi }_{i}^{l}\) control the fraction of the duty cycle and the phase within a rhythm period, their values are constrained within the intervals (0,1] and [0,1], respectively. An ablation study on the impact of rhythm hyperparameters on Rhythm-SNNs’ performance is presented in Supplementary Figs. S13 and S14.
Training method for Rhythm-SNN
We use the backpropagation through time (BPTT) algorithm, combined with the surrogate gradient method68,69,70,71, to train the proposed Rhythm-SNN. During the training process, both the synaptic weights W and the constant injected current b are optimized. By applying the chain rule across both spatial and temporal dimensions, the derivatives of the loss function \({{{\mathcal{L}}}}\) with respect to the spike S can be formalized as follows:
Note that on the right-hand side of equation (10), the first term denotes the derivatives in the spatial dimension and the second term represents the derivatives in the temporal dimension. Similarly, the derivatives of the loss function with respect to the membrane potential U can be obtained by:
By employing equations (10) and (11) iteratively backward in time, the derivatives \(\frac{\partial {{{\mathcal{L}}}}}{\partial {b}^{l}}\) and \(\frac{\partial {{{\mathcal{L}}}}}{\partial {W}^{l}}\) can be easily obtained as per:
We use a rectangular surrogate function68,70 to approximate the non-differentiable spike activation function Θ( ⋅ ) during training, which is defined as follows:
where h( ⋅ ) represents the rectangular surrogate function. k is a hyperparameter that controls the range of the gradient flow. k is set to 0.6, in accordance with prior work46. sign( ⋅ ) denotes the sign function.
Mitigating the gradient vanishing problem with Rhythm-SNN
We next demonstrate that Rhythm-SNN can effectively address the gradient vanishing problem, a significant challenge faced by existing SNN models. To illustrate this, we first analyze the backpropagation of gradient information from time t to an arbitrary time step \(t+{c}_{i}^{l}\) in Rhythm-SNN, and compare it with a non-Rhythm-SNN that does not incorporate the rhythmic modulation mechanism.
According to equation (11), the derivative of the loss regarding the membrane potential at time step t in our Rhythm-SNN can be calculated by the following recursive formula:
Similarly, the derivative of the loss with respect to the membrane potential in the non-Rhythm-SNN is calculated as:
Given 0 < α < 1, a comparison of the coefficients of the last term in equations (15) and (16) reveals that the duty cycle \({d}_{i}^{l}\) can effectively mitigate the gradient vanishing issue during backpropagation. This property helps preserve information over a longer time span, thereby enhancing the ability to capture long-term dependencies.
Analysis of the memory capacity of Rhythm-SNN
In this part, we demonstrate the enhanced memory capacity of Rhythm-SNNs over non-Rhythm-SNNs. First, we introduce a memory capacity metric used in non-spiking RNNs27, called the mean recurrent length, which captures the average distance between inputs and outputs of the network model over multiple timescales within a cyclic period. Later, we use this metric to compare the memory capacity of Rhythm-SNNs with non-Rhythm-SNNs (see “Proposition 1”).
Definition (mean recurrent length)
Consider the minimum path length \({{{{\mathcal{D}}}}}_{t}(n)\) from an input neuron at time t to an output neuron at time t + n. The minimum path length here refers to the shortest path length of a signal propagating across a time span of n and a network depth of L. For an SNN with cyclic period C, its mean recurrent length is defined as:
Proposition 1
Consider a Rhythm-SNN consisting of L layers, with rhythm periods of oscillatory signals ranging from c1 to ck, where c1 and ck are the minimum and maximum rhythm periods, respectively. The mean recurrent length of the Rhythm-SNN is less than that of the non-Rhythm-SNN.
Proof
For a Rhythm-SNN with rhythm periods ranging from c1 to ck, its cyclic period C can be calculated as follows:
where lcm signifies the least common multiple of c1, ⋯ , ck, and c1≤ ⋯ ≤ck.
If we unfold the information propagation paths from the input neuron to the output neuron through spatial and temporal dimensions, any path from the input neuron to the output neuron spanning n time steps yields:
where \({r}_{t}\left(n\right)\) represents the shortest temporal path between the input neuron at time t and the output neuron at time t + n. Deriving \({r}_{t}\left(n\right)\) equates to solving the common change-making problem. Given denominations \(\left\{{c}_{1},\cdots \,,{c}_{k}\right\}\) and an amount n, the goal is to minimize the number of denominations summing to n. Formally, \({r}_{t}\left(n\right)\) satisfies:
where aj represents the number of banknotes of denomination cj. Following the prior work27, we use a greedy strategy to obtain an upper bound for \({r}_{t}\left(n\right)\), thereby avoiding the complex process of solving the original integer linear programming problem in equation (20). This yields:
According to equations (17), (19), and (21), the upper bound for the mean recurrent length of the Rhythm-SNN with L layers is obtained as:
For an L-layered non-Rhythm-SNN, we have:
Therefore, its mean recurrent length is:
Given that 1 < ck ≤ C, we have \(\frac{C+1}{2{c}_{k}}+L < \frac{C+1}{2}+L\). It indicates that the mean recurrent length of the Rhythm-SNN is smaller than that of the conventional SNN. According to ref. 27, a shorter mean recurrent length implies a higher network memory capacity. This can be elucidated as past information propagates along fewer edges, thus experiencing less attenuation. Consequently, the network’s memory capacity is enhanced by leveraging the proposed modulation mechanism.
Robustness analysis
We analyze the robustness of Rhythm-SNNs to various perturbations by comparing the representation distance between output spike trains in response to original patterns and those of corresponding perturbed patterns. Input perturbations mainly include adversarial attacks and random noise. Since the spiking Lipschitz constant28 provides a uniform bound on the network’s vulnerability to input perturbations, regardless of noise types, Rhythm-SNN’s robustness against these perturbations can be validated by analyzing the spiking Lipschitz constant corresponding to the distance between output spike trains.
For a Rhythm-SNN with L layers, the output spike train of the lth layer can be represented as \({{{{\bf{S}}}}}^{l}=\left\{{{{{\bf{s}}}}}^{l}\left[t\right]| t=1,2,\cdots \,,T\right\}\in {\Omega }^{T\times {N}_{l}}\left(\Omega \in \{0,1\}\right)\), where T is the inference time step, and Nl is the number of spiking neurons in layer l. We quantify the distance between the original and perturbed activations using:
where \({\hat{{{{\bf{S}}}}}}^{l}\) is the output spike train after perturbing the original input, and ∥ ⋅ ∥p is the matrix norm induced by the vector lp norm.
Previous studies72,73,74 have established the theoretical foundation for the vulnerability of neural networks to perturbations, primarily based on the magnitude of activation changes. Recent work28 has further extended this framework to spiking LIF models. We borrow this tool to analyze the distance bound of spike responses in Rhythm-SNNs and compare it with that in non-Rhythm-SNNs. According to prior work28, the upper bound of the distance between the original and perturbed spike trains for conventional SNNs can be described as:
with
where \({\gamma }^{l}={\sup }_{{{{\bf{s}}}}\ne 0,{{{\bf{s}}}}\in {\Omega }^{{N}_{l-1}}}{\left\Vert {{{{\bf{W}}}}}^{l}{{{\bf{s}}}}\right\Vert }_{\infty }+{\sup }_{{{{\bf{s}}}}\ne 0,{{{\bf{s}}}}\in {\Omega }^{{N}_{l-1}}}{\left\Vert -{{{{\bf{W}}}}}^{l}{{{\bf{s}}}}\right\Vert }_{\infty }\), Φ = {−1, 0, 1}, Ω = {0, 1}, ϑ represents the firing threshold, Wl is the weight matrix of the layer l, and α signifies the decay factor of the membrane potential. In equation (27), Λl, i.e., the Lipschitz constant, mainly bounds the variation of the original and perturbed spike outputs. For the Rhythm-SNN, its corresponding spiking Lipschitz constant can be deduced by equations (3)–(7) (see Supplementary Section 5 for more details):
Given that 0 < α < 1, the upper bound for the Rhythm-SNN’s spiking Lipschitz constant can be relaxed as follows:
The above comparison shows that our Rhythm-SNN possesses a smaller spiking Lipschitz constant compared to that of the conventional SNN. Since a smaller spiking Lipschitz constant generally leads to a decreased magnitude of network output perturbations28,72,73,74, it implies an enhanced robustness against perturbations by Rhythm-SNN.
Experimental setup for temporal processing tasks
We conduct experiments on several widely used temporal processing benchmarks, including S-MNIST29, PS-MNIST29, SHD30, ECG32, GSC31, VoxCeleb133, PTB34, and DVS-Gesture35 to validate the effectiveness of our method.
S-MNIST and PS-MNIST are built by performing a raster scan on the original MNIST digit recognition dataset in a pixel-by-pixel manner, resulting in sequences with a length of 784. Unlike S-MNIST, PS-MNIST applies a random permutation to the pixels of the original image before performing a raster scan, eliminating the original spatial structure. For both tasks, the pixel values are directly fed into the network as injected current to the neurons in the first layer. This layer functions as an encoding layer, converting non-spiking inputs into spiking outputs to enable further processing by SNNs.
The SHD dataset30 comprises approximately 10,000 audio recordings of English and German digits (0–9) from 12 speakers. Each speaker recorded approximately 40 sequences for each digit in both languages, resulting in a total of 10,420 sequences. These audios are transformed into spike-based representations using a bionic inner ear model. Following previous research36, the resulting spike trains are segmented into a sequence of 1000 frames for post-processing by an SNN. The dataset is partitioned into 8156 samples for training and 2264 samples for testing.
The ECG dataset32 contains six types of ECG waveforms, i.e., P, PQ, QR, RS, ST, and TP. We adhere to the data preprocessing procedures outlined in prior work32. Specifically, we apply a variant of the level-crossing encoding method32 on the derivative of the normalized ECG signal to convert the original continuous values into a spike train. Each channel is transformed into two distinct spike trains, representing value-increasing events and value-decreasing events, respectively.
The GSC dataset31 consists of 64,727 utterances from 1881 speakers, each pronouncing one of 35 distinct speech commands. In our experiments, we followed the dataset configuration commonly used in other works32,36, selecting 12 classes from the total of 30 available classes. These include ten specific commands: “Yes”, “No”, “Up”, “Down”, “Left”, “Right”, “On”, “Off”, “Stop”, and “Go”. Additionally, there are two extra classes: an “Unknown” class, which encompasses the remaining 25 commands, and a “Silence” class, created by randomly sampling background noise from the dataset’s audio files. For feature extraction, we followed the preprocessing approach described in prior work32. Specifically, log Mel filter coefficients were computed from the raw audio signals, and their first three derivative orders were extracted. This involved calculating the logarithm of 40 Mel filter coefficients on a Mel scale ranging from 20 Hz to 4 kHz. Each frame of the processed input is represented as a tensor with dimensions 40 × 3, corresponding to the coefficients and their derivatives. The spectrograms are normalized to ensure an appropriate input scale, and each time step in the simulation is set to 10 ms. As a result, each audio sample is transformed into a sequence of 101 frames, with each frame containing 120 channels.
The VoxCeleb1 dataset33, sourced from YouTube, includes 153,516 utterances from 1251 celebrities with diverse ethnicities, accents, professions, and ages, with balanced speaker gender, resulting in a classification task with 1251 classes. All audio is first converted to single-channel, 16-bit streams at a 16 kHz sampling rate for consistency. Spectrograms are then generated in a sliding window fashion using a Hamming window of width 25 ms and stride 10 ms.
The PTB dataset34 contains 929,000 words for training, 73,000 for validation, and 82,000 for testing, with a vocabulary size of 10,000 words. The text is segmented into sequences of fixed length 200, where each sequence serves as input for models tasked with predicting the subsequent word. To represent the words, we employ an embedding dictionary of size 650, which encodes each word into a dense vector space, capturing both semantic and syntactic relationships.
The DVS-Gesture dataset35 comprises 11 types of hand and arm movements performed by 29 individuals, recorded under three different lighting conditions using a DVS128 camera. Each frame in the dataset is a 128 × 128-sized image with two channels. Each sample in the DVS-Gesture dataset is divided into fixed-duration blocks, with each block averaged to a single frame, resulting in sequences that vary from 500 to 1500 frames depending on the block length.
The training configurations and hyperparameter settings for the above temporal processing tasks are summarized in Supplementary Table 1. We utilize the PyTorch library, which facilitates accelerated model training. All models are trained using the Adam optimizer. Our experiments are conducted using Nvidia GeForce RTX 3090 GPUs, each equipped with 24 GB of memory. In Table 1 of the main text, we provide experiment results of both Rhythm-SNNs and non-Rhythm-SNNs, which employ various spiking neuron models with both feedforward and recurrent architectures. Specifically, the tested models encompass the feedforward SNN (FFSNN)75, the SNN with recurrent connections (SRNN)70, SRNN complemented with a learnable firing threshold (LSNN)40, SRNN complemented with both learnable firing threshold and learnable time constant (ASRNN)43, and the SNN incorporating temporal dendritic heterogeneity (DH-SRNN and DH-SFNN)36. Their Rhythm-SNN counterparts are denoted as Rhythm-FFSNN, Rhythm-SRNN, Rhythm-LSNN, Rhythm-ASRNN, Rhythm-DH-SRNN, and Rhythm-DH-SFNN. The detailed mathematical formulations of these models are provided in Supplementary Section 1.
Experimental setup for the STORE-RECALL task
In this experiment, a 3-layer SRNN architecture is utilized, with each layer comprising 20 neurons. Furthermore, two types of spiking neuron models are examined, including ALIF40 and DEXAT45 neurons. For ALIF and Rhythm-ALIF models, the membrane potential decay time constant and adaptive threshold time constant are set to 20 ms and 600 ms, respectively. For DEXAT and Rhythm-DEXAT, the membrane potential decay time constant and the two adaptive threshold time constants are set to 20 ms, 30 ms, and 600 ms, respectively. These time constant settings are consistent with prior work45, as they have been chosen based on the characteristics of these two models and the task requirements. The mathematical formulations of the proposed Rhythm-ALIF and Rhythm-DEXAT models are provided in Supplementary Section 2. Input signals, composed of characters ‘0’ and ‘1’ along with ‘STORE’ and ‘RECALL’ commands, are encoded into 50 Hz Poisson spike trains by four separate neuron groups. Each neuron group contains 25 neurons and encodes each character/command with a 100 ms time window. Each ‘STORE’ command is followed by a ‘RECALL’ command with a probability of p = 1/6, leading to an average delay of 600 ms between these two commands. The output layer uses a softmax activation function, and the resulting output vector is utilized to calculate the recall error and cross-entropy loss relative to the provided label. Following previous work44,45, the network is trained for 200 epochs or until the recall error on the validation set drops below 0.05. Detailed training configurations and hyperparameter settings are provided in Supplementary Table 2.
Experimental setup for robustness evaluation tasks
We assess the robustness of Rhythm-SNNs against various perturbations, including Gaussian noise, thermal noise, silence noise, and quantization noise, and two types of adversarial attacks generated using FGSM and PGD. Gaussian noise is characterized by zero mean and variance ranging from (2/255)2 to (8/255)2. Thermal noise, which affects the input currents to spiking neurons, is simulated by adjusting variance levels from 0.05 to 0.2; silence noise, occurring when a subset of spiking neurons fails to respond, is simulated by randomly masking neuron outputs with failure rates ranging from 5% to 20%; quantization noise, resulting from the conversion of analog signals into digital signals with limited bit resolution, is simulated through post-training quantization, progressively reducing the bit number from 8 down to 2. For gradient-based attacks, the FGSM perturbs input data in the direction of the gradient of the loss relative to the input data, while the PGD operates as an iterative and more potent version of FGSM. Our evaluation is anchored on the temporal processing task employing the PS-MNIST dataset. We conduct experiments with the ASRNN and Rhythm-ASRNN models at various noise and attack levels, comprehensively evaluating their robustness against perturbations. For simplicity, we denote (ϵ/255)2 as the variance for Gaussian noise, σ as the variance for thermal noise, p as the masking rate for silence noise, and Bit as the bit resolution for quantization noise. Visual comparisons of the average perturbation distance with respect to the average firing rate changes, as displayed in Fig. 4i–l, are conducted under conditions with ϵ = 8 for Gaussian noise, σ = 0.2 for thermal noise, p = 0.2 for silence noise, and Bits = 6 for quantization noise. More details of the experimental setup and perturbation methods are provided in Supplementary Section 3.
Experimental setup for the speech enhancement task
In this task, the Intel N-DNS Challenge dataset is utilized, which includes 500 h of human speech in various languages and noise types, recorded at 16 kHz and 16-bit depth, with a synthesized signal-to-noise ratio (SNR) ranging from 20 dB to −5 dB. For performance metrics, we use Scale-Invariant Source-to-Noise Ratio (SI-SNR)53 to assess audio quality and DNSMOS54 for perceptual evaluation, with the latter considering the overall audio quality (OVR)54, speech signal quality (SIG)54, and background noise quality (BAK)54. Besides, we also evaluate the energy cost of the tested speech enhancement models. The architecture of the Rhythm-GSNN employed in this task consists of a full-band module and three sub-band modules, each of which contains two layers of the Rhythm-GSN model (see Supplementary Fig. S9). Specifically, the noisy audio is divided into three frequency bands after undergoing STFT and normalization, with each band containing an increasing number of frequencies: 32, 96, and 128, respectively. The audio is then fed into the full-band module, and its output features corresponding to each frequency band are processed by their respective sub-band modules. Finally, the features are integrated across the low-frequency, mid-frequency, and high-frequency bands, and the final denoised audio is obtained through iSTFT. More details of the training configurations and hyperparameter settings for the speech enhancement task are provided in Supplementary Table 4 and Supplementary Section 4.
Data availability
All data used in this paper are publicly available. The S-MNIST and PS-MNIST datasets can be downloaded from http://yann.lecun.com/exdb/mnist/. The SHD dataset can be accessed at https://zenkelab.org/resources/spiking-heidelberg-datasets-shd/. The ECG dataset is publicly available at https://physionet.org/content/qtdb/1.0.0/. The GSC dataset can be obtained from https://tensorflow.google.cn/datasets/catalog/speech_commands/. The DVS-Gesture dataset can be downloaded at https://research.ibm.com/interactive/dvsgesture/. The VoxCeleb1 dataset is available at https://www.tensorflow.org/datasets/catalog/voxceleb. The PTB dataset can be accessed at https://www.kaggle.com/datasets/aliakay8/penn-treebank-dataset. The Intel N-DNS Challenge dataset can be downloaded from https://github.com/IntelLabs/IntelNeuromorphicDNSChallenge.
Code availability
The source code is publicly available at https://github.com/YinsongYan/Rhythm-SNN.
References
Maass, W. Networks of spiking neurons: the third generation of neural network models. Neural Netw. 10, 1659–1671 (1997).
Roy, K., Jaiswal, A. & Panda, P. Towards spike-based machine intelligence with neuromorphic computing. Nature 575, 607–617 (2019).
Merolla, P. A. et al. A million spiking-neuron integrated circuit with a scalable communication network and interface. Science 345, 668–673 (2014).
Davies, M. et al. Loihi: a neuromorphic manycore processor with on-chip learning. IEEE Micro 38, 82–99 (2018).
Pei, J. et al. Towards artificial general intelligence with hybrid Tianjic chip architecture. Nature 572, 106–111 (2019).
Zhao, R. et al. A framework for the general design and computation of hybrid neural networks. Nat. Commun. 13, 3427 (2022).
Yin, B., Corradi, F. & Bohté, S. M. Accurate online training of dynamical spiking neural networks through forward propagation through time. Nat. Mach. Intell. 5, 518–527 (2023).
Blouw, P., Choo, X., Hunsberger, E. & Eliasmith, C. Benchmarking keyword spotting efficiency on neuromorphic hardware. In Proc. 7th Annual Neuro-inspired Computational Elements Workshop 1–8 (Association for Computing Machinery, 2019).
Imam, N. & Cleland, T. A. Rapid online learning and robust recall in a neuromorphic olfactory circuit. Nat. Mach. Intell. 2, 181–191 (2020).
Bartolozzi, C., Indiveri, G. & Donati, E. Embodied neuromorphic intelligence. Nat. Commun. 13, 1024 (2022).
Yu, F. et al. Brain-inspired multimodal hybrid neural network for robot place recognition. Sci. Robot. 8, eabm6996 (2023).
Buzsáki, G. & Draguhn, A. Neuronal oscillations in cortical networks. Science 304, 1926–1929 (2004).
Buzsáki, G. Rhythms of the Brain (Oxford Univ. Press, Oxford, 2006).
Lakatos, P., Chen, C.-M., O’Connell, M. N., Mills, A. & Schroeder, C. E. Neuronal oscillations and multisensory interaction in primary auditory cortex. Neuron 53, 279–292 (2007).
Fries, P. Rhythms for cognition: communication through coherence. Neuron 88, 220–235 (2015).
Giraud, A.-L. & Poeppel, D. Cortical oscillations and speech processing: emerging computational principles and operations. Nat. Neurosci. 15, 511–517 (2012).
Ding, N., Melloni, L., Zhang, H., Tian, X. & Poeppel, D. Cortical tracking of hierarchical linguistic structures in connected speech. Nat. Neurosci. 19, 158–164 (2016).
Lennie, P. The cost of cortical computation. Curr. Biol. 13, 493–497 (2003).
Buzsáki, G. Theta oscillations in the hippocampus. Neuron 33, 325–340 (2002).
Timcheck, J. et al. The intel neuromorphic dns challenge. Neuromorphic Comput. Eng. 3, 034005 (2023).
Hong, L. E., Buchanan, R. W., Thaker, G. K., Shepard, P. D. & Summerfelt, A. Beta (~16 Hz) frequency neural oscillations mediate auditory sensory gating in humans. Psychophysiology 45, 197–204 (2008).
Dipoppa, M. & Gutkin, B. S. Flexible frequency control of cortical oscillations enables computations required for working memory. Proc. Natl. Acad. Sci. USA 110, 12828–12833 (2013).
Dipoppa, M., Szwed, M. & Gutkin, B. S. Controlling working memory operations by selective gating: the roles of oscillations and synchrony. Adv. Cogn. Psychol. 12, 209 (2016).
Klimesch, W. Eeg alpha and theta oscillations reflect cognitive and memory performance: a review and analysis. Brain Res. Rev. 29, 169–195 (1999).
Tesche, C. & Karhu, J. Theta oscillations index human hippocampal activation during a working memory task. Proc. Natl. Acad. Sci. USA 97, 919–924 (2000).
He, K., Zhang, X., Ren, S. & Sun, J. Deep residual learning for image recognition. In Proc. IEEE Conference on Computer Vision and Pattern Recognition 770–778 (IEEE, 2016).
Chang, S. et al. Dilated recurrent neural networks. In Advances in Neural Information Processing Systems Vol. 30 (Curran Associates, 2017).
Ding, J., Bu, T., Yu, Z., Huang, T. & Liu, J. SNN-RAT: robustness-enhanced spiking neural network through regularized adversarial training. In Advances in Neural Information Processing Systems Vol. 35, 24780–24793 (Curran Associates, 2022).
Le, Q. V., Jaitly, N. & Hinton, G. E. A simple way to initialize recurrent networks of rectified linear units. Preprint at https://arxiv.org/abs/1504.00941 (2015).
Cramer, B., Stradmann, Y., Schemmel, J. & Zenke, F. The Heidelberg spiking data sets for the systematic evaluation of spiking neural networks. IEEE Trans. Neural Netw. Learn. Syst. 33, 2744–2757 (2020).
Warden, P. Speech commands: a dataset for limited-vocabulary speech recognition. Preprint at https://arxiv.org/abs/1804.03209 (2018).
Yin, B., Corradi, F. & Bohté, S. M. Accurate and efficient time-domain classification with adaptive spiking recurrent neural networks. Nat. Mach. Intell. 3, 905–913 (2021).
Nagrani, A., Chung, J. S. & Zisserman, A. VoxCeleb: a large-scale speaker identification dataset. Proc. Interspeech 2616–2620 (2017).
Marcus, M., Santorini, B. & Marcinkiewicz, M. A. Building a large annotated corpus of English: the Penn Treebank. Comput. Linguist. 19, 313–330 (1993).
Amir, A. et al. A low power, fully event-based gesture recognition system. In Proc. IEEE Conference on Computer Vision and Pattern Recognition 7243–7252 (IEEE, 2017).
Zheng, H. et al. Temporal dendritic heterogeneity incorporated with spiking neural networks for learning multi-timescale dynamics. Nat. Commun. 15, 277 (2024).
Fang, W. et al. Spikingjelly: an open-source machine learning infrastructure platform for spike-based intelligence. Sci. Adv. 9, eadi1480 (2023).
Rathi, N. et al. Exploring neuromorphic computing based on spiking neural networks: algorithms to hardware. ACM Comput. Surv. 55, 1–49 (2023).
Fang, W. et al. Incorporating learnable membrane time constant to enhance learning of spiking neural networks. In Proc. IEEE/CVF International Conference on Computer Vision 2661–2671 (IEEE, 2021).
Bellec, G., Salaj, D., Subramoney, A., Legenstein, R. & Maass, W. Long short-term memory and learning-to-learn in networks of spiking neurons. In Advances in Neural Information Processing Systems Vol. 31 (Curran Associates, 2018).
Yao, X., Li, F., Mo, Z. & Cheng, J. Glif: a unified gated leaky integrate-and-fire neuron for spiking neural networks. In Advances in Neural Information Processing Systems Vol. 35, 32160–32171 (Curran Associates, 2022).
Horowitz, M. Computing’s energy problem (and what we can do about it). In 2014 IEEE International Solid-State Circuits Conference Digest of Technical Papers 10–14 (IEEE, 2014).
Yin, B., Corradi, F. & Bohté, S. M. Effective and efficient computation with multiple-timescale spiking recurrent neural networks. In International Conference on Neuromorphic Systems 2020 1–8 (Association for Computing Machinery, 2020).
Bellec, G. et al. Biologically inspired alternatives to backpropagation through time for learning in recurrent neural nets. Preprint at https://arxiv.org/abs/1901.09049 (2019).
Shaban, A., Bezugam, S. S. & Suri, M. An adaptive threshold neuron for recurrent spiking neural networks with nanodevice hardware implementation. Nat. Commun. 12, 4234 (2021).
Yang, Q. et al. Training spiking neural networks with local tandem learning. In Advances in Neural Information Processing Systems Vol. 35, 12662–12676 (Curran Associates, 2022).
Goodfellow, I. J., Shlens, J. & Szegedy, C. Explaining and harnessing adversarial examples. Int. Conf. Learn. Representations (2015).
Madry, A., Makelov, A., Schmidt, L., Tsipras, D. & Vladu, A. Towards deep learning models resistant to adversarial attacks. Int. Conf. Learn. Representations (2018).
Hu, Y. et al. DCCRN: deep complex convolution recurrent network for phase-aware speech enhancement. Proc. Interspeech 2472–2476 (2020).
Hao, X., Su, X., Horaud, R. & Li, X. Fullsubnet: a full-band and sub-band fusion model for real-time single-channel speech enhancement. In ICASSP 2021-2021 IEEE International Conference on Acoustics, Speech, and Signal Processing 6633–6637 (IEEE, 2021).
Dubey, H. et al. Icassp 2023 deep noise suppression challenge. IEEE Open J. Signal Process. 5, 232–245 (2024).
Hao, X., Ma, C., Yang, Q., Wu, J. & Tan, K. C. Toward ultralow-power neuromorphic speech enhancement with spiking-fullsubnet. IEEE Trans. Neural Netw. Learn. Syst. 36, 17350–17364 (2025).
Bahmaninezhad, F. et al. A comprehensive study of speech separation: spectrogram vs waveform separation. Proc. Interspeech 4574–4578 (2019).
Reddy, C. K., Gopal, V. & Cutler, R. DNSMOS P.835: a non-intrusive perceptual objective speech quality metric to evaluate noise suppressors. In ICASSP 2022-2022 IEEE International Conference on Acoustics, Speech, and Signal Processing 886–890 (IEEE, 2022).
Spitzer, B., Wacker, E. & Blankenburg, F. Oscillatory correlates of vibrotactile frequency processing in human working memory. J. Neurosci. 30, 4496–4502 (2010).
Chen, Y., Qu, H., Zhang, M. & Wang, Y. Deep spiking neural network with neural oscillation and spike-phase information. Proc. AAAI Conf. Artif. Intell. 35, 7073–7080 (2021).
Campos, V., Jou, B., Giró-i Nieto, X., Torres, J. & Chang, S.-F. Skip rnn: learning to skip state updates in recurrent neural networks. Int. Conf. Learn. Representations (2018).
Hochreiter, S. & Schmidhuber, J. Long short-term memory. Neural Comput. 9, 1735–1780 (1997).
Cho, K. Learning phrase representations using RNN encoder-decoder for statistical machine translation. Proc. Conf. Empir. Methods Nat. Lang. Process. (2014).
Orvieto, A. et al. Resurrecting recurrent neural networks for long sequences. In International Conference on Machine Learning 26670–26698 (PMLR, 2023).
Ding, J., Pan, Z., Liu, Y., Yu, Z. & Huang, T. Robust stable spiking neural networks. Int. Conf. Mach. Learn. 11016–11029 (2024).
Liang, L., Xu, K., Hu, X., Deng, L. & Xie, Y. Toward robust spiking neural network against adversarial perturbation. Adv. Neural Inf. Process. Syst. 35, 10244–10256 (2022).
Yoshida, T. & Ohki, K. Natural images are reliably represented by sparse and variable populations of neurons in visual cortex. Nat. Commun. 11, 872 (2020).
Perez-Nieves, N., Leung, V. C., Dragotti, P. L. & Goodman, D. F. Neural heterogeneity promotes robust learning. Nat. Commun. 12, 5791 (2021).
Eshraghian, J. K. et al. Training spiking neural networks using lessons from deep learning. Proc. IEEE 111, 1016–1054 (2023).
Gerstner, W., Kistler, W. M., Naud, R. & Paninski, L. Neuronal Dynamics: From Single Neurons to Networks and Models of Cognition (Cambridge Univ. Press, Cambridge, 2014).
DeCarlo, R. A. Linear Systems: A State Variable Approach with Numerical Implementation (Prentice-Hall, Englewood Cliffs, 1989).
Wu, Y., Deng, L., Li, G., Zhu, J. & Shi, L. Spatio-temporal backpropagation for training high-performance spiking neural networks. Front. Neurosci. 12, 331 (2018).
Neftci, E. O., Mostafa, H. & Zenke, F. Surrogate gradient learning in spiking neural networks: bringing the power of gradient-based optimization to spiking neural networks. IEEE Signal Process. Mag. 36, 51–63 (2019).
Zenke, F. & Vogels, T. P. The remarkable robustness of surrogate gradient learning for instilling complex function in spiking neural networks. Neural Comput. 33, 899–925 (2021).
Lee, C., Sarwar, S. S., Panda, P., Srinivasan, G. & Roy, K. Enabling spike-based backpropagation for training deep neural network architectures. Front. Neurosci. 14, 497482 (2020).
Cisse, M., Bojanowski, P., Grave, E., Dauphin, Y. & Usunier, N. Parseval networks: improving robustness to adversarial examples. In International Conference on Machine Learning 854–863 (PMLR, 2017).
Weng, L. et al. Towards fast computation of certified robustness for ReLU networks. In International Conference on Machine Learning 5276–5285 (PMLR, 2018).
Fazlyab, M., Robey, A., Hassani, H., Morari, M. & Pappas, G. Efficient and accurate estimation of Lipschitz constants for deep neural networks. Adv. Neural Inf. Process. Syst. 32, 11423–11434 (2019).
Wu, Y. et al. Direct training for spiking neural networks: faster, larger, better. Proc. AAAI Conf. Artif. Intell. 33, 1311–1318 (2019).
Cramer, B. et al. Surrogate gradients for analog neuromorphic computing. Proc. Natl. Acad. Sci. USA 119, e2109194119 (2022).
Acknowledgements
We are grateful to Mr. Xiang Hao and Mr. Zeyang Song for their support with the Intel N-DNS Challenge and VoxCeleb1 tasks, respectively. We also thank Mr. Zhige Chen for his assistance in improving the visual illustrations in the manuscript. This work was partially supported by the National Natural Science Foundation of China (U21A20512, received by K.T., and Grant No. 62306259, received by J.W.), the Research Grants Council of the Hong Kong SAR (Grant No. PolyU15217424, received by J.W., PolyU25216423, received by J.W., and C5052-23G, received by K.T.), and The Hong Kong Polytechnic University (Project IDs: P0043563, received by J.W.).
Author information
Authors and Affiliations
Contributions
Y.Y., Q.Y., and J.W. conceived the work and designed the computational model. Q.Y. and Y.Y. conducted simulation experiments. Y.Y. and Y.W. performed the theoretical analysis. H.L. (Hanwen Liu) and M.Z. carried out the FPGA-based neuromorphic hardware implementation and evaluation. Y.Y., Q.Y., Y.W., H.L. (Hanwen Liu), M.Z., H.L. (Haizhou Li), K.T., and J.W. contributed to the experiment design, results discussion, and manuscript writing. J.W. supervised the whole project.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks reviewers Zeyuan Wang, Zhaofei Yu, and Basabdatta Sen Bhattacharya, who co-reviewed with Swapna Sasi, for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Yan, Y., Yang, Q., Wu, Y. et al. Efficient and robust temporal processing with neural oscillations modulated spiking neural networks. Nat Commun 16, 8651 (2025). https://doi.org/10.1038/s41467-025-63771-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-025-63771-x