Abstract
A Lite Bidirectional Encoder Representations from Transformers model is demonstrated on an analog inference chip fabricated at 14nm node with phase change memory. The 7.1 million unique analog weights shared across 12 layers are mapped to a single chip, accurately programmed into the conductance of 28.3 million devices, for this first analog hardware demonstration of a meaningfully large Transformer model. The implemented model achieved near iso-accuracy on the General Language Understanding Evaluation benchmark of seven tasks, despite the presence of weight-programming errors, hardware imperfections, readout noise, and error propagation. The average hardware accuracy was only 1.8% below that of the floating-point reference, with several tasks at full iso-accuracy. Careful fine-tuning of model weights using hardware-aware techniques contributes an average hardware accuracy improvement of 4.4%. Accuracy loss due to conductance drift – measured to be roughly 5% over 30 days – was reduced to less than 1% with a recalibration-based “drift compensation” technique.
Similar content being viewed by others
Introduction
As Deep Neural Network (DNN) model sizes continue to grow from millions to billions of weights, it has been challenging for AI hardware to keep up with the pace of this AI revolution. Analog AI accelerators based on Non-Volatile Memories (NVMs) leverage the massive parallelism in memory arrays to efficiently perform the Multiply and ACcumulate (MAC) matrix-operations that dominate these workloads. In particular, the “von Neumann bottleneck,” incurred by repeatedly moving weight data from memory to processing cores, is greatly reduced by performing computation directly at the location of data ("Compute-In-Memory” or CIM). Programming these weights into NVM devices capable of continuous analog states leads to high-density and full weight-stationarity, enabling analog AI accelerators that can offer extremely high system (not just macro) energy-efficiency [TOPS/W] at highly competitive compute-density [TOPS/mm2]1,2. Analog accelerators based on CIM have been demonstrated using various NVM technologies, e.g., Flash3,4,5, PCM6,7,8,9, RRAM10,11,12,13, MRAM14,15,16, ECRAM17,18,19, or ferroelectric devices20,21,22. A variety of bit-wise CIM macros based on high-endurance but low-density SRAM have also been proposed23,24,25,26.
In recent years, DNN-based Natural Language Processing (NLP) has transitioned from Recurrent networks such as Long Short-Term Memory (LSTM) toward Transformer-based models, which use an attention mechanism (Fig. 1a) to represent the relationships between “tokens” (e.g. words) of a data-sequence (e.g., sentences and paragraphs)27,28,29. Decoder-based transformers (such as GPT-329) can repeatedly generate a next predicted token to extend an input sequence. In contrast, Encoder-based transformers, such as BERT (Bidirectional Encoder Representations from Transformers)28 perform a single pass over each input sequence, using an attention-matrix to understand token relationships across the sequence, and thus execute NLP tasks with high accuracy.
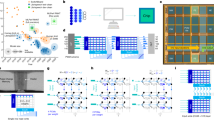
a A Transformer model relies on the attention mechanism instead of recurrence for sequence processing. b The structure of the ALBERT-base model with 12 layers of shared weights. Each layer consists of a self-attention block and a feed-forward network (FFN) block, each followed by residual addition (Add) and layer normalization (LayerNorm). The four layer-blocks implemented in hardware include inProj (mapping input activations to queries (Q), keys (K), and values (V)), outProj (mapping attention computation to output activations), and the two fully connected layer-blocks comprising the FFN (FC1, FC2). These four layer-blocks represent over 99% of the weights in the ALBERT-base model. c Seven GLUE benchmark tasks used in this paper have validation data-sets that vary considerably in size (number of examples); all but one are binary classification tasks. d The distribution of the sequence lengths for the validation datasets associated with the seven GLUE tasks. For sequences with 64 tokens, the analog accelerator is performing 98% of the required operations; for longer sequences, this percentage is slightly lower since the fully-connected layer-blocks scale linearly with sequence-length, yet the attention-compute scales quadratically. e Simulated accuracy of the seven GLUE tasks as model weights are quantized from 6-bit precision down to 2-bit (2-bit: grey; 3-bit: teal; 4-bit: lime; 5-bit: orange, 6-bit: blue), revealing significant differences in difficulty and robustness between tasks. An effective precision of 4 bits is sufficient for almost all the tasks.
This attention-matrix is dynamically generated from token-vectors emitted by large fully connected weight-layer blocks, which in turn are highly suitable for implementation with analog AI accelerators. Since BERT has achieved leading-edge performance for NLP, many approaches to reduce its model size and hardware requirements have been reported. The ALBERT (A Lite BERT) model30 significantly reduces the number of required weights by sharing the same weights across all the Transformer encoder layers. With 7.7 million unique weights, the ALBERT-base model is a Transformer-based model with meaningful industry relevance, worthy of demonstration on an analog AI accelerator. In fact, previous work has shown that ALBERT is significantly more challenging for analog AI hardware than BERT-base model31 that implements unique weight-matrices for each of the 12 layers. Thus successful demonstration of ALBERT implies that a larger chip with the same noise characteristics should have little trouble implementing BERT models. While several pure-digital accelerator macros have been introduced that focus on the attention-compute block, the associated hardware demonstrations have depended heavily on partial weight-stationarity32,33. To the best of our knowledge, this work is the largest fully weight-stationary2 CIM demonstration of a industry-relevant Transformer model to date.
In this work, we map the weights of one ALBERT layer onto a single PCM-based analog inference chip that we have demonstrated recently34. Since the weights are shared by all 12 layers, the demonstration of the entire ALBERT model can be conducted with one chip by feeding the outputs of a layer back to the chip as the inputs to the next layer, iterating the process across the 12 layers to produce the final outputs. Figure 1b shows the four fully connected layer-blocks comprising the bulk of the ALBERT model and implemented in hardware; all other operations, including the matrix computations for attention, pooler, and classifier are implemented off-chip (in software running on a control computer). Note that the weight-sharing across 12 layers in the ALBERT model provides a unique opportunity to demonstrate a complete model in a single chip. The learning about the challenges and solutions for analog AI hardware through this demonstration is broadly applicable to other models without weight-sharing.
To test the ALBERT model in hardware, we utilize seven NLP tasks in the General Language Understanding Evaluation (GLUE) benchmark (Fig. 1c)35. The size of the validation datasets associated with these tasks varies from several hundred sequences to tens of thousands, with sequence lengths ranging from ~ 10 tokens up to 128 (Fig. 1d). The accuracy of each GLUE task is measured by running embedded tokens through the 12 layers of ALBERT model, using the analog AI chip for fully-connected layers and software for attention-compute and vectorized activation-compute, followed by pooler and classifier layers implemented in software. The classifier outputs are compared with labels to calculate the final accuracy. We can examine how accuracy evolves through the 12 layers of the network by passing the outputs of these layers through the pooler and classifier to calculate the accuracy for fewer than 12 layers. For the four smaller datasets – RTE, MRPC, CoLA, and SST-2 – the entire validation datasets were used in hardware testing. For each of the larger tasks – QNLI, MNLI, and QQP – we chose a randomly sampled subset of 1000 sample-sequences for hardware testing, which exhibits the same accuracy as the entire dataset (see section “Methods”).
Inevitably there are slight errors when programming the hardware weights into PCM conductances, as well as readout noise while performing the analog MAC operations. Both of these reduce effective weight precision, which we can emulate in software by weight quantization, to rapidly assess these GLUE tasks (Fig. 1e). Most tasks can reach the accuracy of the floating-point (FP) reference at 4-bit equivalent weight precision, while 3-bit weight precision causes some accuracy degradation (Fig. 1e). GLUE tasks vary noticeably in their resilience against weight quantization, and thus to analog noise as well. For example, QNLI is robust even at 2-bit weight precision, but RTE is quite sensitive to weight precision.
Hardware-aware (HWA) training incorporates noise and hardware imperfections into the training process to produce model weights that are more resilient against hardware imperfections. Transformer-based models have been shown to be more sensitive to hardware imperfections than recurrent networks, and thus benefit considerably from HWA training31. Since the ALBERT model takes pre-trained weights and then fine-tunes them for each downstream task, we employ HWA techniques during this fine-tuning process to improve model resilience (see section “Methods” for details).
The mapping of the four layer-blocks comprising the ALBERT model (inProj, outProj, FC1, and FC2) to a single chip is shown in Fig. 2a. This mapping strategy routes signals to maximize utilization of the six input and six output landing pads (ILPs and OLPs), which are the primary throughput constraints. Figure 2b-g show the multiple phases of inputs and outputs for the four layer-blocks occurring in sequence (inProj → outProj → FC1 → FC2). Given the ILP and OLP constraints and the need for off-chip processing, these operations cannot be fully pipelined, limiting our throughput expectations for this hardware demonstration. More advanced chips with larger analog tiles (for better network mapping) and multiple compute-cores (for on-chip digital compute36) will enable pipeline design for significantly higher parallelism, utilization, throughput, and efficiency.
a The four ALBERT layer-blocks described in Fig. 1 (inProj, outProj, FC1, and FC2) are mapped onto their own tiles on a single 14nm analog inference chip. b–g The routing paths for the incoming and outgoing vectors for the four layer-blocks. Each ALBERT layer requires four phases of inputs and outputs for the layer-blocks in sequence (inProj → outProj → FC1 → FC2). b, d, f Routing paths for the independent incoming 512-element data vectors, from the six input landing pads (ILPs) across the 2D mesh over the tiles to the west-sides of one or more destination tiles; c, e, g Routing paths for outgoing 512-element vectors, from the south- or north-sides of source-tiles (or tile-pairs) to the six output landing pads (OLPs). 512-element data vectors are conveyed in duration format on 512 mesh wires in parallel8. In some cases, two 256-element vectors from two different source tiles are implicitly concatenated by the 2D-mesh before arrival at an OLP. h The mapping of each of the inProj, outProj, FC1, and FC2 layer-blocks to the requisite number of 512 × 512 weight tiles. i The percentage of weights being utilized in each of the 34 tiles for this ALBERT model (Note that the two white squares contain neither tile arrays nor 2D mesh routing wires).
However, several significant challenges that such a pipelined chip will face can be addressed in the present experiment, including the drive for sufficient MAC accuracy and the mapping of large weight matrices to fixed-size tiles. Each of the four layer-blocks are larger than one analog tile (512 × 512 weights when using 4 PCM per weight) and need to be mapped across multiple tiles. Figure 2h illustrates the multi-tile mapping of these layer-blocks. These tiles of mapped weights are carefully placed into a single chip, sometimes with two layer-blocks sharing a tile, and signal routing carefully designed to avoid any crossing of data vectors on the 2D mesh. Many tiles can be fully utilized, with only a few occupied at less than 50% (Fig. 2i). Overall, 79.4% of the weight capacity of the chip is used in the demonstration.
Results
Accuracy of the ALBERT model in hardware
The target weights in software were programmed into the on-chip PCM devices with a closed-loop tuning process34. Four PCM devices are used to program each weight and implement asymmetry balance, with positive (negative) weights programmed on the first (second) PCM-pair8. The programmed hardware (HW) weights match the target software (SW) weights quite well (see Supplementary Fig. 3 for correlation plots for all 34 tiles), with correlation coefficients (R2) > 0.98. However, correlation plots between HW MAC and SW MAC (Supplementary Fig. 4) exhibit wider spread than the raw weights. This spread visually increases with layers, and the HW-SW MAC correlation coefficients (R2) degrade steadily for all seven GLUE tasks (Supplementary Fig. 5), indicating accumulation of MAC error as tokens move through the 12 layers. Both Supplementary Figs. 4 and 5 show that these HW-SW MAC correlations improve at each inProj and FC1 layer-block as compared to outProj and FC2, which can be attributed to the restoring nature of the LayerNorm operations performed just before inProj and FC1.
Figure 3a shows the measured HW accuracy (green bars), SW accuracy (red bars), and FP accuracy (blue bars) for the seven GLUE tasks. The SW model adopts the HWA fine-tuned weights and clipping on weights and activations, thus differing from the FP model in accuracy. The average SW accuracy of the seven GLUE tasks is 0.5% below the FP accuracy. The HW imperfections degrade the average GLUE accuracy by 1.29% from this SW accuracy, resulting in an overall 1.79% accuracy loss from FP reference to HW. This FP-HW accuracy gap varies markedly across the seven GLUE tasks (Fig. 3b). Two GLUE tasks – MRPC and QNLI – reach iso-accuracy, defined as HW accuracy that exceeds 99% of FP accuracy. QQP is only slightly below this threshold. On the other hand, RTE and CoLA have the lowest HW accuracy relative to the FP reference, at 95.5% and 96.7% respectively. As the smallest dataset, RTE also shows more instability during testing in comparison with larger datasets.
a Plot and b Table of accuracy for floating-point (FP) reference (blue bars), software (SW, red bars), and hardware (HW, green bars) of the seven GLUE tasks on the ALBERT model. The HW ALBERT model achieves near iso-accuracy, with the average accuracy of seven GLUE tasks only 1.8% below the FP accuracy. MRPC and QNLI reach iso-accuracy (bold in the table). c Cumulative distributions of the error margin (defined as the difference between two classifier layer outputs) of the six binary classification tasks (RTE: red; MRPC: blue; CoLA: lime; SST-2: magenta; QNLI: aqua; QQP: black). The inset enlarges the tails (<25%) of the distributions to focus on samples with small error margin. d Median value of the MAC error (i.e., the difference between SW and HW MAC values) at layer 12 for the six binary-classification GLUE tasks. e Larger error margin and smaller MAC error lead to higher accuracy, and vice versa. f The HW accuracy of the seven GLUE tasks after layer 6 (grey), 9 (teal), 10 (lime), 11 (orange), and 12 (blue). g Histogram of the layers at which correctly-classified samples settle on that answer for the MRPC task.
The different levels of HW accuracy of the GLUE tasks can be partially explained by the intrinsic error margin of these datasets. Since six of the seven GLUE tasks use binary classification, the absolute value of the difference between the “correct” and “wrong” neurons in the classifier layer represents an error margin. A sample with large error margin is quite likely to produce the same result in the HW as FP reference – samples with small error margins are at higher risk of flipping due to noise and imperfections (Supplementary Fig. 6). Figure 3c compares the distributions of this error margin for the six binary classification GLUE tasks, focusing on the tail of the error margin distribution contributed by the most error-prone verification samples. The inset of Fig. 3c shows that tasks exhibiting higher accuracy (e.g., MRPC and QNLI) have fewer samples with small error margin than tasks with lower accuracy (e.g., RTE, CoLA).
GLUE tasks can also have poor resilience by being susceptible to producing large MAC errors. Figure 3d compares the median HW MAC error at layer 12 for the six GLUE tasks. MRPC and QNLI exhibit both high error margin and low MAC error, which explains their high accuracy. In comparison, RTE and CoLA have lower error margin and higher MAC error, and hence have lower accuracy. Figure 3e visualizes the resilience of these GLUE tasks in HW, by showing how accuracy varies with error margin and MAC error. QQP has the lowest MAC error but also has many low error margin samples; SST2 has very few low error margin samples but exhibits the highest MAC error. As a result, the accuracy of these two GLUE tasks falls in the middle. The task-specific robustness is related to how these task datasets are structured. Simulations have also shown that the smaller datasets (e.g., RTE) tend to have larger variation in training accuracy across multiple trials. The different resilience of GLUE tasks reveals the importance of intrinsic task robustness during evaluation of analog AI hardware.
Testing “early exit” in hardware
One of the strategies to both accelerate ALBERT inference and save energy is known as “early exit”37 – to redirect sequences to the pooler and classifier before passing through all 12 layers, while maintaining model accuracy. Figure 3f shows the hardware accuracy after layers 6, 9, 10, 11, and 12. The accuracy is still quite low after layer 6 and continues to increase through layers 9 and 10. The post-layer 11 accuracy is very close to the final accuracy (layer 12) for most GLUE tasks. MAC error (the difference between the HW MAC and SW MAC) also increases the most at early layers and then saturates (Supplementary Fig. 7). The average accuracy of seven GLUE tasks after layer 11 is only 0.4% below the final accuracy. “Early exit” of Transformer-based models could potentially save time and energy while also reduce unnecessary error accumulation in HW. Even larger accuracy gains could be feasible if the ALBERT model were to be explicitly fine-tuned for the target number of layers (rather than just exiting early from a model trained to expect 12 layers). Such a designed “early exit” implementation in hardware would not only use model weights fine-tuned for fewer layers, but also employ a prediction-based strategy to determine when to exit.
To examine the dynamics as sample-sequences pass through the 12 layers, Fig. 3g shows the distribution of the layers at which correctly-classified samples settle on that answer. While some samples settle on the correct answer as early as layer 2, the majority of samples become correct at layers 7-9. As sequences pass through the last few layers, only a small number of samples fix their incorrect classification, consistent with the saturation of accuracy. Supplementary Fig. 8a shows the cumulative distribution of this data – the build-up of correctly-classified samples – for all seven GLUE tasks, showing that most correctly-classified samples are obtained well before the final layers. That said, the increase of accuracy with layer is not a smooth process of adding more correct answers at every layer, since correctly-classified samples can and do flip back to the wrong class as well (Supplementary Fig. 8b).
Demonstration of the HWA training effect
HWA training has been demonstrated on smaller networks, e.g., Convolutional Neural Network (CNN), LSTM7. This implementation of the ALBERT model provides an opportunity to demonstrate the effectiveness of HWA training on Transformer-based models in actual analog inference hardware. Model weights fine-tuned with different levels of noise were programmed into the on-chip PCM devices and the hardware accuracy was measured. Figure 4a compares the hardware accuracy on all seven GLUE tasks for weights fine-tuned with noise scale of 0 ("zero-noise weights,” white bars), and for weights fine-tuned with appropriate noise scale to maximize accuracy ("HWA-tuned weights,” grey bars). These HWA-finetuned weights consistently achieve higher hardware accuracy than the zero-noise weights, driving an improvement in average GLUE-task accuracy of 4.4%. Figure 4b shows the dependence of the hardware accuracy on the noise scale used in the HWA fine-tuning for six GLUE tasks. RTE with its extremely small dataset was excluded due to excessive run-to-run instability. For each task, there exists an optimal noise scale that produces a best set of HWA-finetuned weights and the highest accuracy. Accuracy is always poor for weights finetuned with zero noise, but injecting too much noise during HWA fine-tuning also hurts accuracy. To the best of our knowledge, this work is the first hardware demonstration of the effectiveness of HWA training on a meaningfully large Transformer-based model.
a Experimentally measured HW inference accuracy with optimized (grey bars) and without any (white bars) HWA noise during fine-tuning of seven GLUE tasks. Adding the appropriate level of noise during fine-tuning improves the average HW accuracy of seven GLUE tasks by 4.4%. b The dependence of HW accuracy on the noise scale used in HWA fine-tuning for six GLUE tasks (MRPC: blue squares; CoLA: lime stars; SST-2: pink triangles; QNLI: aqua triangles; QQP: black diamonds; MNLI: brown circles). The smallest task (RTE) is excluded due to its instability. The filled-in (enlarged) symbol identifies the optimal HWA noise-scale for that task, typically in the range of 1.0–2.0. c The HW inference accuracy of the MRPC task with (red squares) and without (blue circles) recalibration over 30 days. d The distribution of MAC error from day 0 up to 3 weeks after weight programming. e The ratio of the median MAC variation over median MAC values for repeated inference attempts.
PCM conductance drift effect and mitigation
As the amorphous phase within programmed PCM devices relaxes, device-conductances decrease logarithmically over time38. Worse yet, since each device experiences this conductance drift at a slightly different decay rate, model-weight distributions broaden over time (see section “Methods”). Both (1) the decay in average conductance and (2) the broadening of weight distributions cause model-accuracy to degrade; fortunately, as we will show here, (1) can be fully compensated and (2) by itself has only a modest impact on ALBERT accuracy in HW. A comprehensive study on the impact of analog hardware nonidealities (including PCM drift) on the performance of various DNNs has been previously conducted by simulation31. Transformer-based models, including ALBERT, were shown to be slightly more robust against PCM drift than CNNs but more sensitive to drift than Recurrent Neural Networks (RNNs). This work provides an experimental assessment of the PCM drift impact and the effectiveness of the drift compensation technique.
A thorough drift test was conducted over 30 days on this hardware ALBERT model using the MRPC task. After programming the model weights into the on-chip PCM devices, the inference accuracy was measured periodically over 30 days (Fig. 4c), either using the same initial calibration (see section “Methods”) produced before the first inference test after weight programming (blue circles, “without recalibration”), or by generating a new set of recalibrated parameters before each inference test (red squares, “with recalibration”7,8). Red and blue dashed lines show simple linear fits to highlight overall trends; the black horizontal dashed line indicates the FP reference accuracy.
Without recalibration, HW accuracy degraded roughly 5% over 30 days. As expected from the logarithmic nature of conductance drift (see section “Methods”), most of this accuracy drop occurred over the first few days. Recalibration effectively performs “drift compensation”38 since the new calibration parameters measure the current states of PCM devices, thus tracking the average conductance drift. With recalibration, the HW accuracy decreases less than 1% over 30 days. Figure 4d shows how the MAC error (i.e., difference between HW and SW MAC) evolves over time. Without recalibration (upper panel), the tails of these distributions spread, driving reduced hardware accuracy. With recalibration (lower panel), there is little noticeable change of the MAC error distribution over time, thus leading to unchanged HW accuracy. As this calibration involves determining new slope and offset parameters, it requires access to calibration data and ground truth, as well as on-chip digital arithmetic circuitry. Fortunately, a system for deep learning will include on-chip digital compute cores for auxiliary operations such as normalization, activation functions etc., which can be repurposed for calibration.
Drift effect over a 30-day period is the longest hardware measurement conducted in this work. To quantify the drift effect over a longer period would require accelerated testing at elevated temperature. Note that PCM drift is an effect that is rapid immediately after programming, and then slows down significantly over time; therefore, conductance change after the first 30 days will be relatively small. Furthermore, in many business applications, the AI models are refreshed or updated within 30 days. Occasional validation examples can also be run to determine if re-calibration is needed. This drift test was conducted at room temperature. A prior study has shown that PCM-based inference accelerators are robust against ambient temperature variation (33–80 °C) with compensation techniques.39
To explore the considerable run-to-run variation in HW accuracy visible in Fig. 4c, MAC values were read out multiple times during one of the later inference tests (so drift during this experiment is negligible). To compare fairly between different layer-blocks, we normalize the MAC variation by the median MAC amplitude. This normalized read-to-read variation in MAC values (Fig. 4e) shows clear distinctions among the four layer-blocks: FC2 has the highest MAC variation and FC1 the lowest, while inProj and outProj are in the middle. These distinctions can be understood from the mapping of these layer-blocks on-chip (Fig. 2h). With its 3072 rows and 768 columns, FC2 requires summing vectors across six tiles (512 columns) or six half-tiles (final 256 columns), which each experience their own circuit noise, small tile-to-tile discrepancies in calibration coefficients, and 7-bit quantization at the OLPs. The other three layer-blocks all have 768 rows and require summation over only two tiles. FC1 has the cleanest mapping strategy, with summation performed in the analog domain within the tile-pairs before digitization at the OLPs. In contrast, the inProj and outProj layer-blocks are split across partial or shared tiles. Thus future analog accelerators that can minimize quantization and circuit noise introduced during tile-to-tile summation should significantly reduce HW variation and further improve HW accuracy.
Power and efficiency analysis
We estimate the speed and energy potential of this analog accelerator when implementing the ALBERT model, using both hardware measurements (for the energy consumption of analog operations8) and circuit simulations (for digital operations implemented in a 14nm technology36). This treatment assumes that digital compute is done in 14nm circuitry at the locations of the ILP/OLP pairs, but implements the non-pipelined dataflow used in the HW accuracy experiments (Fig. 5a), as required by the mapping strategies from Fig. 2. Both the analog compute in MAC cores ("inProj,” “outProj,” “FC1,” “FC2” in Fig. 5a) and the digital compute for auxiliary functions ("QKV,” “other ops” in Fig. 5a) are included in this analysis. Memory access involved in the digital operations (e.g., reading/writing activations) is also included in the digital compute. There are no additional external memory–access costs beyond these operations. Each sequence of tokens is processed through one layer-block of the ALBERT hardware at a time. Each layer comprises the 4 layer-blocks, the QKV compute and other operations. This is repeated 12 times to complete the 12 ALBERT layers. The next sequence of tokens (e.g. Sample 2 in Fig. 5a) may have a different sequence length, but sequence padding is not required because batch size is 1. See section “Methods” for more details. Because this particular implementation of ALBERT focused on densely packing all weights on a single chip, only a fraction of the tiles are active at any given time, which limits both peak energy efficiency and peak throughput.
a Simulated time sequence of activities in the four layer-blocks implemented in the analog accelerator (inProj, outProj, FC1, and FC2), attention computation ("QKV''), and all other digital operations. b–e show the dependence on the mean sequence-length of: (b) the ratio between analog and digital operation numbers, (c) the ratio between analog and digital energy, (d) throughput in samples-per-second, and (e) energy efficiency in samples-per-Joule. f The percentage of total energy spent on analog operations, (g) throughput, (h) task-based energy efficiency, and (i) system-level energy-efficiency in TOPS/W, across the 7 GLUE tasks.
Figures. 5b, c show that analog operations dominate both the total operation-count ( > 99% for short sequences, ≈ 98% for longer sequences) and total energy ( > 95%, Fig. 5(f)). Although the quadratic scaling of digital attention-compute operations with sequence-length noticeably affects the operation counts, the effects on energy are quite subtle. This is because the tiles in this chip-demo are only ~ 3-4 × more energy-efficient than the 14nm digital compute (~20 TOPS/W8 vs. 5–7 TOPS/W36). As tile efficiency increases, the effects of sequence-length become much more noticeable36. Although the sequence length of GLUE benchmark is limited (up to 128), additional analysis with synthetic datasets of sequence lengths up to 1000 reveals similar trends, as shown in Supplementary Fig. S10.
Throughput in samples-per-second and energy efficiency in samples-per-Joule also inherently decrease with sequence-length (Fig. 5d, e). Figure 5i shows that all seven GLUE tasks achieve a system-level energy efficiency over 3 TOPS/W, a reasonable performance considering the hardware constraints. The prior work on the demonstration of the Recurrent Neural Network Transducer (RNNT) model in this analog accelerator achieved the efficiency of 6-7 TOPS/W, a 14 × improvement over conventional digital accelerators8. In a more advanced design where digital compute units are distributed on-chip amongst the tiles, fine-grained pipelining within each layer can be expected to keep all resources continuously busy, leading to significant improvements in both energy-efficiency and throughput36. Initial pipelining studies for networks such as BERT-base and BERT-large have already been performed for such chips, showing the considerable throughput and latency benefits of “Full Weight Stationarity.”2,40 Higher tile-efficiency will help achieve higher system energy efficiency, especially for short sequence lengths.
Discussion
The Transformer architecture and the attention mechanism have dominated large language models (LLMs). To the best of our knowledge, this work is the first demonstration of a meaningfully large Transformer-based model on an analog AI accelerator. Although it is not an end-to-end demonstration, over 99% of ALBERT model weights are implemented in hardware. The ALBERT model is small in comparison with the state-of-the-art LLMs, but it is uniquely suitable for the analog accelerator in this work. The weight sharing across layers allows the mapping of all unique weights of the model (around 7 million) to a single chip and the iteration on the chip enables the implementation of the total 85 million weights in the model. As shown in the paper, this ALBERT model on analog hardware provides an important platform to examine the challenges of analog accelerators, develop mitigation techniques, and prove the feasibility of analog AI accelerators for Transformer-based models with sufficiently large size.
Analog AI accelerators are known to be susceptible to hardware imperfections and random noises. HWA training is among the most effective techniques to improve the resilience of AI models on analog accelerators. Most studies on the HWA technique are based on simulation. This work is not only a hardware demonstration of the HWA technique on a reasonably large Transformer-based NLP model across multiple benchmark tasks, but also provides experimental results to gauge key parameters in HWA simulation (e.g., weight noise). In addition, measuring the hardware performance across multiple NLP tasks reveals the importance of examining task-dependent model resilience to produce a fair and transparent evaluation of analog AI hardware.
While the analog accelerator in this work is based on PCM, lessons learned from this study are broadly applicable to other NVM technologies such as RRAM. For example, calibration is not only an essential step to convert raw MAC data from the chip to scaled MAC data for the network but also helps to compensate spatiotemporal variation in devices. Therefore, properly designed calibration is important for analog accelerators regardless of the underlining NVM technologies. The exact mapping of network weights to devices on tiles to maximize tile utilization will vary with different chip design and capacity, but the mapping methodology shown here is generally applicable to different device technologies. The closed-loop tuning of conductance to achieve high weight precision is also a technique applicable to various NVM devices.
Conductance drift is unique to PCM, but other NVM devices have retention degradation behaviors and will benefit from similar mitigation techniques. Variability is a well-known challenge for NVM devices, especially RRAM. However, the MAC variation measurement in Fig. 4e reveals the importance of circuit noise, so device variation is not the only source of variability at the network level. The relevant importance of device and circuit noise will depend on both the NVM technology and the circuit design. Note that – in contrast to the applicability of this work focused on inference to other NVM devices – training, on the other hand, involves more device-specific requirements such as the symmetry and linearity of device programming not considered here. The programming endurance of PCM is not an issue for inference accelerators where PCM devices are infrequently programmed as static weights in analog tiles for the MAC operation. In a full end-to-end inference chip, intermediate data processing will utilize SRAMs in digital compute units instead of NVMs with limited endurance. However, training will place more stringent requirements on NVM endurance since weights are frequently updated.
In summary, Transformer-based ALBERT model is demonstrated on a 14nm analog AI accelerator with 35 million PCM devices. This hardware demonstration of the ALBERT model not only provides important proof-of-feasibility of analog AI inference chips for now widely-used Transformer-based NLP models, but also enables a flexible platform to evaluate various algorithm, design, and technology solutions. Thanks to an efficient weight mapping strategy, optimized weight programming schemes, and well-designed input/output routing, the HW ALBERT model achieves near iso-accuracy as compared to the FP reference on the GLUE benchmark. This inference chip also proves that using HWA techniques during fine-tuning is important and highly effective for the ALBERT model. Although PCM conductance drift does degrade the ALBERT model accuracy over time, these effects can be greatly mitigated by recalibration. Further improvement of large network performance is expected on more advanced analog AI accelerators that can support better mapping strategies, fine-grained pipelining, and tiles with higher macro energy-efficiency.
Methods
Test platform and analog inference chip
This demonstration of the ALBERT model on the analog inference chip starts with the floating-point (FP) model, which is fine-tuned with hardware-aware (HWA) technique in software. The weights are extracted and programmed into the PCM devices in the analog chip. Digital computations are implemented in software, including the matrix computation for attention, activation functions (gelu, softmax, tanh), pooler, and classifier. The accuracy of each GLUE task is measured by running embedded tokens through the 12 layers of ALBERT model, using the analog AI chip for fully-connected layers and software for attention-compute and vectorized activation-compute, followed by pooler and classifier layers implemented in software. The classifier outputs are compared with labels to calculate the final accuracy.
The analog AI inference chip is based on Phase Change Memory (PCM) fabricated with 14nm CMOS technology. This chip contains 34 analog tiles connected with a massively-parallel 2D mesh for tile-to-tile communication34. Each tile contains 1.05 million mushroom-type PCM devices that can be parallel-programmed in row-wise fashion, with options to encode each weight across multiple PCM devices to improve precision and reduce noise. Vertically-adjacent pairs of tiles can share their peripheral capacitors, to double the number of input rows over which current integration is performed. With 35 million PCM devices, this chip has been shown capable of implementing large DNN models, e.g., Recurrent Neural Network Transducer (RNNT)8 at near software-level model accuracy.
Hardware-aware (HWA) fine-tuning
HWA techniques are employed in the fine-tuning of the ALBERT model to improve the resilience of the ALBERT model31. Supplementary Fig. 1b shows the simulated inference accuracy of the MNLI task for weights fine-tuned with different levels of noise scale during HWA fine-tuning. The HWA noise scales are multiplication factors applied on a standard PCM noise model, e.g., a noise scale of 2.0 applies “twice” the base amount of PCM noise during fine-tuning. For weights fine-tuned with an HWA noise scale of 0, the inference accuracy starts high but decreases quickly over time. For weights fine-tuned with high HWA noise scales (e.g., 3.0), the inference accuracy is stable over time although it was already low from the beginning. As shown in the bar chart of inference accuracy at 1-month (Supplementary Fig. 1c), there is an optimal range of HWA noise scale at which the model can be fine-tuned to achieve maximum inference accuracy, although this value varies from task to task. All seven GLUE tasks are fine-tuned with a range of HWA noise scales and the model weights for each noise scale were extracted to map to the analog PCM chip for hardware testing.
Sample randomization
The FP reference accuracy of a subset of 1000 samples varies depending where the 1000 samples are chosen, from within the three largest verification datasets, QNLI, QQP, and MNLI. As shown in Supplementary Fig. 2, the FP accuracy of a subset of 1000 samples can vary from subset to subset as much as 5%. Therefore, an arbitrarily chosen set of 1000 samples (e.g., the first 1000 samples of the dataset) may not be a good representation of the dataset as a whole. We choose to first randomize the samples in these larger datasets and then select a subset of 1000 samples whose accuracy closely matches that of the entire dataset, and then use this subset for all hardware testing.
Calibration
Before inference, a calibration is performed to obtain the scaling parameters that are needed to convert raw MAC data read directly from the chip to the scaled MAC data consistent with the network activation range. This step is done by passing a batch of samples from the training dataset to the model. Columnwise scale and offset parameters are calculated to best correlate the raw MAC on-chip with the target MAC in software. This calibration is needed at least once before inference but can also be done repeatedly during inference over an extended period of time (“recalibration”) to account for changing hardware weights over time (e.g., PCM drift). Note that even though the same set of weights, say for FC1, are used 12 times across the 12 layers, each usage has its own set of columnwise calibration (e.g., scale and offset) factors. This is because the excitation distributions change at each layer for the various layer-blocks.
PCM conductance drift
PCM devices depend on controlling the phase of the PCM material located in the effective device-volume – e.g., affecting the device-resistance for read current passing from a top- to a bottom-electrode through the PCM material41. PCM material can crystallize to a high-conductance state at elevated temperatures (~400–450 °C), and be quenched into the low-conductance amorphous phase by rapidly cooling molten material (hotter than ~600 °C) to temperatures low enough to suppress recrystallization (below ~ 150 °C).
PCM conductance drift occurs over time because this rapidly-quenched amorphous phase within the device volume continues to relax long after programming is completed. The overall trend is almost always from higher to lower conductance, and typically represents a stright line on a plot of \(\log G\) vs. \(\log t\), where G is conductance and t is time. Thus PCM device-conductance will drop by the same percentage within each 10 × time interval, inherently slowing down from a rapid initial decay. This can be quantified as
where G0 represents the conductance at some time t0 (as measured after programming), and ν is known as the drift coefficient, typically ranging from 0.01 to 0.10.
If this were the only problem with drift, then so long as all model weights were programmed at the same time t0, one would need only to boost readout currents by the appropriate time-dependent gain-coefficient to reproduce the original effective device-conductances. This gain-coefficient could even be applied at the end of array-columns after device read-currents were summed along bitlines. Eventually, any readout noise – coming either from the PCM devices (such as thermal, shot or random-telegraph noise) or introduced by bitline or ADC circuitry before the gain-amplification is applied – also ends up being amplified. Thus after some long time t, the signal-to-noise ratio would degrade. However, a different effect ends up degrading MAC correlation and model accuracies long before this can occur.
Beyond device-to-device variations in device width, size and material composition, every quenching event even within the same physical PCM device will encounter a different distribution of crystal grains (and stoichiometry distribution) within the device, depending on some number of its most recent programming events. This affects the device resistance through percolation paths around the amorphous plug that is undergoing relaxation, thus affecting the effective drift coefficient exhibited on both an inter- and intra-device basis. It is this shot-to-shot variability in ν coefficient that broadens distributions and makes it challenging to simply compensate all the read-currents coming from a column of PCM devices.
That said, it is still a good idea to ensure that all devices are programmed togther so that they exhibit roughly the same t0 and then scale them back up together. This allows one to boost the aggregated read currents by the average drift-coefficient, and thus maintain the same average read-signal in each array MAC. This is what the “recalibration” referred to in Fig. 4c, d accomplishes, allowing model accuracy to be maintained even as device conductances are inherently decaying.
MAC variation measurement
To measure the variation of MAC in hardware, the output from the analog chip is continuously read multiple times during one of the later inference tests (so drift during this experiment is negligible). For each array column, we have multiple samples of what should be the same MAC result, leading to a non-zero standard deviation. We can then repeat at each column to obtain the median value across a particular layer-block. The Supplementary Fig. 8c shows the median MAC value (blue bars) and the median MAC variation during the multiple-reading test (red bars) of the inProj, outProj, FC1, and FC2 layer-blocks over 12 layers. The MAC value and variation do not show layer dependence.
Power performance measurement and estimation
To estimate system-level power performance, we calculate the total energy and time to process the target workloads. System power performance is estimated in two parts: The digital compute units for all non-MAC operations are simulated using a 14nm technology, while the timing and power of the analog chip for MAC computations are experimentally measured. The analog MAC-compute time and energy includes the costs of sending activations to the edge of the chip and the conversion of activations to/from digital bits at the OLP/ILP blocks. The digital compute units are assumed to reside on the same chip, right next to the ILPs/OLPs of the analog inference chip. Analog chip power and timing measurements are illustrated in Supplementary Fig. 9.
The sequence lengths of the GLUE benchmark are relatively small, up to 128. To examine the effect of longer sequence length, synthetic datasets with sequence lengths of 150, 300, 500, and 1000 are added in the power and efficiency analysis in Supplementary Fig. 10.
Data availability
The ALBERT model is publicly available from the HuggingFace repository42. The raw data that support the findings of this study can be made available by the corresponding author upon request after IBM management approval.
Code availability
The HWA fine-tuning of the ALBERT model was conducted with an internal tool and the same capability is available in the IBM Analog Hardware Acceleration Kit at https://github.com/IBM/aihwkit43,44. (https://doi.org/10.5281/zenodo.8148598)
References
Burr, G. W., Sebastian, A., Ando, T. & Haensch, W. Ohm’s law + Kirchhoff’s current law = better AI: Neural-network processing done in memory with analog circuits will save energy. IEEE Spectrum 58, 44–49 (2021).
Burr, G. W. et al. Design of analog-AI hardware accelerators for Transformer-based language models. In Proc. 2023 International Electron Devices Meeting (IEDM) (2023).
Bavandpour, M., Mahmoodi, M. R. & Strukov, D. B. aCortex: an energy-efficient multipurpose mixed-signal inference accelerator. IEEE J. Explor. Solid State Comput. Devices Circuits 6, 98–106 (2020).
Fick, L., Skrzyniarz, S., Parikh, M., Henry, M. B. & Fick, D. Analog matrix processor for edge AI real-time video analytics. In Proc. 2022 IEEE International Solid-State Circuits Conference (ISSCC), vol. 65, 260–262 (IEEE, 2022).
Hu, H.-W. et al. A 512Gb in-memory-computing 3D-NAND flash supporting similar-vector-matching operations on edge-AI devices. In Proc. 2022 IEEE International Solid-State Circuits Conference (ISSCC), vol. 65, 138–140 (IEEE, 2022).
Cheng, H. Y. et al. State-independent low resistance drift SiSbTe phase change memory for analog in-memory computing applications. In Proc. 2024 IEEE Symposium on VLSI Technology and Circuits (VLSI Technology and Circuits), 1–2 (IEEE, 2024). https://ieeexplore.ieee.org/document/10631376/.
Le Gallo, M. et al. A 64-core mixed-signal in-memory compute chip based on phase-change memory for deep neural network inference. Nat. Electronics 6, 680–693 (2023).
Ambrogio, S. et al. An analog-AI chip for energy-efficient speech recognition and transcription. Nature 620, 768–775 (2023).
Wu, X. et al. Novel nanocomposite-superlattices for low energy and high stability nanoscale phase-change memory. Nature Communications 15, 13 (2024).
Yin, S., Sun, X., Yu, S. & Seo, J.-S. High-throughput in-memory computing for binary deep neural networks with monolithically integrated RRAM and 90-nm CMOS. IEEE Transact. Electron Devices 67, 4185–4192 (2020).
Wan, W. et al. A compute-in-memory chip based on resistive random-access memory. Nature 608, 504–512 (2022).
Zhang, W. et al. Edge learning using a fully integrated neuro-inspired memristor chip. Science 381, 1205–1211 (2023).
Song, W. et al. Programming memristor arrays with arbitrarily high precision for analog computing. Science 383, 903–910 (2024).
Deaville, P., Zhang, B. & Verma, N. A fully row/column-parallel in-memory computing macro in foundry MRAM with differential readout for noise rejection. IEEE J. Solid State Circuits. 59, 2070–2080 (2024).
Cai, H. et al. Proposal of analog in-memory computing with magnified tunnel magnetoresistance ratio and universal STT-MRAM cell. IEEE Trans. Circuits Syst. I Regul. Pap. 69, 1519–1531 (2022).
Jung, S. et al. A crossbar array of magnetoresistive memory devices for in-memory computing. Nature 601, 211–216 (2022).
Kwak, H., Kim, N., Jeon, S., Kim, S. & Woo, J. Electrochemical random-access memory: recent advances in materials, devices, and systems towards neuromorphic computing. Nano Convergence 11, 9 (2024).
Chen, P. et al. Open-loop analog programmable electrochemical memory array. Nat. Commun. 14, 6184 (2023).
Solomon, P. M. et al. Transient investigation of metal-oxide based, CMOS-compatible ECRAM. In Proc 2021 IEEE International Reliability Physics Symposium (IRPS), 1–7 (IEEE, 2021).
Soliman, T. et al. First demonstration of in-memory computing crossbar using multi-level cell FeFET. Nat. Commun. 14, 6348 (2023).
Zhang, B. et al. Multi-functional ferroelectric domain wall nanodevices for in-memory computing and light sensing. Adv. Funct. Mater. 34, 2405587 (2024).
Chen, C., Zhou, Y., Tong, L., Pang, Y. & Xu, J. Emerging 2D ferroelectric devices for in-sensor and in-memory computing. Adv. Mater. 37, 2400332 (2024).
Deaville, P., Zhang, B. & Verma, N. A 22nm 128-Kb MRAM row/column-parallel in-memory computing macro with memory-resistance boosting and multi-column ADC readout. In Proc. 2022 IEEE symposium on VLSI technology and circuits (VLSI technology and circuits), 268–269 (IEEE, 2022).
Sun, X. et al. Efficient processing of MLPerf mobile workloads using digital compute-in-memory macros. IEEE Trans. Comput Aided Des. Integr. Circuits Syst. 43, 1191–1205 (2023).
Wu, P.-C. et al. A 22nm 832Kb hybrid-domain floating-point SRAM in-memory-compute macro with 16.2-70.2 TFLOPS/W for high-accuracy AI-edge devices. In Proc. 2023 IEEE International Solid-State Circuits Conference (ISSCC), 126–128 (IEEE, 2023).
Zhang, B. et al. MACC-SRAM: a multistep accumulation capacitor-coupling in-memory computing SRAM macro for deep convolutional neural networks. IEEE J. Solid State Circuits 59, 1938–1949 (2023).
Vaswani, A. et al. Attention is all you need. 31st Conference on Neural Information Processing Systems (NIPS 2017). http://arxiv.org/abs/1706.03762 (2017).
Devlin, J., Chang, M.-W., Lee, K. & Toutanova, K. BERT: Pre-training of deep bidirectional Transformers for language understanding. http://arxiv.org/abs/1810.04805 (2019).
Floridi, L. & Chiriatti, GPT-3: Its nature, scope, limits, and consequences. Minds Mach. 30, 681–694 (2020).
Lan, Z. et al. ALBERT: A Lite BERT for self-supervised learning of language representations. International Conference on Learning Representations 2020. http://arxiv.org/abs/1909.11942. (2020).
Rasch, M. J. et al. Hardware-aware training for large-scale and diverse deep learning inference workloads using in-memory computing-based accelerators. Nat. Commun. 14, 5282 (2023).
Prabhu, K. et al. MINOTAUR: An edge Transformer inference and training accelerator with 12 MBytes on-chip resistive RAM and fine-grained spatiotemporal power gating. In 2024 IEEE Symposium on VLSI Technology and Circuits (VLSI Technology and Circuits), 1–2 (IEEE, 2024).
Tang, C. et al. A 28nm 4.35 TOPS/mm2 transformer accelerator with basis-vector based ultra storage compression, decomposed computation and unified LUT-assisted cores. In 2024 IEEE Symposium on VLSI Technology and Circuits (VLSI Technology and Circuits), 1–2 (IEEE, 2024).
Narayanan, P. et al. Fully on-chip MAC at 14 nm enabled by accurate row-wise programming of PCM-based weights and parallel vector-transport in duration-format. IEEE Trans. Electron Devices 68, 6629–6636 (2021).
Wang, A. et al. GLUE: A multi-task benchmark and analysis platform for natural language understanding. International Conference on Learning Representations 2019. http://arxiv.org/abs/1804.07461 (2019).
Jain, S. et al. A heterogeneous and programmable compute-in-memory accelerator architecture for analog-AI using dense 2D mesh. IEEE Trans. VLSI Syst. 31, 114–127 (2023).
Zhou, W. et al. BERT loses patience: Fast and robust inference with early exit. 34th Conference on Neural Information Processing Systems (NeurIPS 2020). http://arxiv.org/abs/2006.04152 (2020).
Ambrogio, S. et al. Reducing the impact of phase-change memory conductance drift on the inference of large-scale hardware neural networks. In Proc. 2019 IEEE International Electron Devices Meeting (IEDM), 6.1.1–6.1.4 (IEEE, 2019).
Boybat, I. et al. Temperature sensitivity of analog in-memory computing using phase-change memory. In Proc. 2021 IEEE International Electron Devices Meeting (IEDM), 28.3.1–28.3.4 (IEEE, 2021).
Burr, G. W. et al. Analog-AI hardware accelerators for low-latency Transformer-based language models (invited). In Proc. 2025 Custom Integrated Circuits Conference (CICC) (IEEE, 2025).
Burr, G. W. et al. Phase change memory technology. J. Vacuum Sci.Technol. B 28, 223–262 (2010).
Wolf, T. et al. HuggingFace’s Transformers: State-of-the-art natural language processing. https://arxiv.org/abs/1910.03771 (2019).
Rasch, M. J. et al. A flexible and fast PyTorch toolkit for simulating training and inference on analog crossbar arrays. In Proc 2021 IEEE 3rd International Conference on Artificial Intelligence Circuits and Systems (AICAS), 1–4 (IEEE, 2021).
Le Gallo, M. et al. Using the IBM analog in-memory hardware acceleration kit for neural network training and inference. APL Mach. Learn. 1, 041102 (2023).
Acknowledgements
We thank the IBM Research AI HW center for project support, IBM Albany Nanotech Center and IBM Bromont for device & module fabrication and W. Wilcke, S. Narayan, V. Mukherjee, S. Yamamichi, C. Osborn, J. Burns, R. Divakaruni and M. Khare for logistical and management support.
Author information
Authors and Affiliations
Contributions
G.W.B. and P.N. designed the chip architecture, including the ramp-based duration concept. G.W.B., P.N., K.H., M.I., A.O., T.Y., and T.K. developed the 2D mesh and local controller codes for mapping complex DNNs to the 14nm Analog AI Inference Chip. A.O., T.Y., A. Friz implemented the test platform and optimized I/O interfaces for fast testing. A.C. and S.A. developed the mixed MAC-software testing framework for ALBERT and conducted the accuracy experiments. S.A. developed the ALBERT weight map. A.C. conducted hardware aware training of ALBERT for GLUE with help from A. Fasoli, J.L., C.M. and M.J.R. S.A. and P.N. implemented power experiments. H.T and S.A. implemented the timing and power performance estimation. A.C., S.A., and H.T. wrote the text of the paper and C.M., P.N., T.P., S.M., V.N., G.W.B helped to revise it. S.A. and A.C. generated the figures.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Peer review
Peer review information
Nature Communications thanks Marco Pasotti, and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work is supported by the IBM Research AI Hardware Center (ibm.com/ai-hardware-center).
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Chen, A., Ambrogio, S., Narayanan, P. et al. Demonstration of transformer-based ALBERT model on a 14nm analog AI inference chip. Nat Commun 16, 8661 (2025). https://doi.org/10.1038/s41467-025-63794-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-025-63794-4