Introduction

Ordered arrays of colloidal quantum dots (QD) known as superlattices (SL) are a new generation of metamaterials which have gained significant interest due to their unique combination of optical and transport properties. The possibility of tuning the bandgap by precisely varying the size of the QD and tuning the charge transport characteristics (mobility and polarity) by ligand modification and surface passivation offers the flexibility of targeting multiple applications1,2,3,4,5,6. Furthermore, the high translational and orientational order coupled with different assembly geometries, holds promise to reveal emerging electronic properties which are of great interest for fundamental understanding of charge transport phenomena7.

The most promising candidates for the realisation of such metamaterials are epitaxially-connected lead chalcogenide (PbS, PbSe) QD SLs4,8,9. Calculations predicted both exotic electronic properties (Dirac cones, topological states in 2D assemblies)10,11 and miniband transport12, which prompted the realisation of many structures and geometries, ultimately resulting in a significant improvement of the transport properties over the past decade. A fundamental breakthrough has been the observation of homo-epitaxial necking formation between {100} facets of lead chalcogenide QD upon ligand stripping by either amines, thermal treatments or prolonged exposure to ethylene glycol (EG) or dimethyl sulfoxide (DMSO)13,14,15,16,17,18,19. This phenomenon causes a significant improvement in the collective orientational ordering of QD in the SL in both square (or simple-cubic, SC) and honeycomb geometries16,20,21. In the case of a relatively large two-dimensional SL with epitaxial necking, carrier mobilities significantly higher than in the disordered film counterpart have been measured, despite that usually high capacitance dielectric or electrolytes are needed to compensate for the high trap density induced by the ligand stripping22,23,24. Among the most relevant examples, electron mobilities of 24 cm2V−1s−1 and 18 cm2V−1s−1 for 2D square and honeycomb PbSe SL have been reported, respectively25,26,27. More recently, electron mobility of 15 cm2V−1s−1 and temperature-independent conductance have been demonstrated for a 2D square SL of PbS QD at high accumulated carrier density28. Our group recently demonstrated mobilities beyond 200 cm2V−1s−1 in both PbSe and PbS-based three-dimensional SL owing to the improved translational ordering intrinsic to the 3D crystallisation dynamics29,30.

The most advantageous and versatile fabrication method for such SL into thin films is the so-called liquid-liquid or liquid-vapour interface self-assembly31,32,33,34,35. Almost all the above-mentioned reports utilise such an approach paired with a pick-up in Langmuir-Schaefer configuration, but without any barrier compression. Whilst being simple and elegant, such an approach has a fundamental limitation which is critical for the mesoscale morphology of the films, particularly for the 2D case. While the ligand exchange (LE) or stripping is fundamental to bringing the QD close together and achieving electronic coupling, the volume loss associated with the shrinking of the SL unit cell always causes severe cracking, especially since the epitaxial necking results in very rigid percolating networks. In a static bath with a fixed area, upon shrinking, the floating film can drift on the liquid, and any interaction with the walls of the bath is lost. Therefore, single grains can separate, coverage is detrimentally affected and several structural defects arise21,36,37,38. The solution is usually to scale down the device size to avoid averaging over many sparse domains and measure the intrinsic transport properties of the SL since locally the ordered structures are preserved39. However, to be relevant for technological applications, deposition methods over large areas of several square centimetres are required.

A solution to the problem might come from the use of a full Langmuir-Schaefer (LS) approach also during the self-assembly from solution, which is very common for the deposition of monolayers (ML) of surfactants over large areas with control over the coverage and compactness of the films through surface pressure measurements40,41. In a Langmuir-Schaefer setup, two moving barriers symmetrically compress molecules (or nanocrystals) floating on a liquid surface either at a constant rate or dynamically maintaining a constant surface pressure during film pick-up. This idea has already been exploited to deposit QD of various types over very large areas, but almost exclusively for spectroscopic studies42,43,44,45,46,47,48. In these works, two important limitations are shown: (i) the film formation is carried out at the air/water interface, and (ii) the nanocrystals are always covered in (relatively) long organic ligands. These two facts exclude any possibility of transport measurements in the film due to the insulating nature of organic ligands and the tendency of most QD to oxidise in contact with air and water, hindering the optical and transport properties49. To the best of our knowledge, no report has investigated the possibility of exchanging the ligands during LS film formation, where one could utilise moving-barrier compression to compensate for the volume loss.

In the present work, we introduce an approach to the fabrication of 2D SL of PbS colloidal quantum dots over large areas. We utilise a Langmuir trough in an inert atmosphere to first form a compact oleic acid-capped QD film, which then undergoes ligand exchange and epitaxial merging. By means of the barrier’s compression, the film is further densified, and the crack formation is significantly suppressed. Changing the degree of compression before triggering the ligand stripping dramatically affects the mesoscale morphology of the film, with the higher compression resulting in smooth, homogeneous films that are crack-free over several square millimetres. The obtained SL display a hexagonal geometry despite the removal of the ligands and epitaxial connection between the QD, a previously unobserved combination. The formation of such structures is elucidated by all-atom molecular dynamics simulations, demonstrating the critical role of external pressure in arranging QD in already well-packed structures before the assembly induced by the removal of ligands. The transport properties of the 2D SL are tested in a field-effect transistor with ion-gel gating, analogously to previous literature reports. The performance of the devices is improved with higher compression, reaching electron mobilities up to 36.6 cm2V−1s−1. Overall, our results demonstrate a successful approach to fabricating 2D SL with promising transport properties over large areas approaching technological relevance. In the future, such a method could be extended to 3D SL as well, with important implications for optoelectronic applications.

Results and discussion

Superlattice fabrication with the Langmuir-Schaefer method

To fabricate 2D SL that are crack-free over large areas, we introduce an approach that combines the self-assembly at a liquid-vapour interface with a Langmuir-Schaefer deposition method, as summarised in Fig. 1a–d. An LS system with a Teflon trough is placed inside an N2 glovebox and filled with ethylene glycol (EG). Commercially available oleic-acid-capped PbS colloidal quantum dots (QD) dispersed in a highly concentrated decane solution are drop-casted at the centre of the trough and spread to cover the whole surface (Fig. 1a). The solvent is chosen to guarantee sufficient time for the colloidal solution to spread, given the large area of the trough (65 cm2). The amount of deposited QD is calculated to form a fully-spread monolayer (ML) at the starting surface area so that when compression is initiated, the surface pressure (SP) promptly starts to rise (Fig. 1b). To illustrate the effect of pre-ligand exchange compression ratio on final film properties, we fabricated samples in two different conditions determined by the surface pressure reached before the ligand exchange (LE) is initiated: low compression (LC) corresponding to an SP of 2 mN m−1 and high compression (HC) corresponding to an SP of 20 mN m−1. We hypothesise that the surface pressure at the moment of the ligand injection determines the vicinity of the QD and therefore their ordering as well as the compactness of the resulting film46.

Fig. 1: Sample fabrication.
figure 1

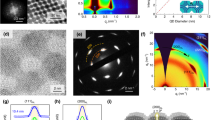
Schematic of 2D superlattice fabrication in the Langmuir-Schaefer trough: (a), the colloidal solution of PbS QD is drop-casted at the centre of the bath on the EG surface; (b), after solvent evaporation, the compression is started and the film is compacted until the desired starting surface pressure is reached; (c), the ligand exchange solution is injected in the trough from both sides underneath the barriers while compression is continued; (d), once the desired final surface pressure is reached, the SLs are transferred to the substrate of choice with the Langmuir-Schaefer method. e Exemplary surface pressure isotherms as a function of the area available per single QD. The dashed arrows indicate the points of solution injection and film pick-up on the ligand exchange curve. The coloured regions indicate the approximate timespan of ligand exchange injection. f STEM-HAADF micrograph of the OA sample fabricated at high surface pressure. The FFT is relative to the area indicated by the white square (scale bars: 200 nm, 0.5 nm−1).

Full size image

Once the desired SP is reached, the LE solution (ethylene diamine, EDA) is injected into the EG subphase from both sides of the trough by inserting the needles underneath the barriers without disrupting the floating film (Fig. 1c). The EDA ligands are known to strip off the oleic acid from the surface of the QD causing the formation of epitaxial necks through the {100} facets23,25,50,51,52. This is highly desirable to maximise the electronic coupling and the collective alignment of the QDs. This situation significantly differs from the context in which short organic molecules, such as ethanedithiol (EDT), bind to the surface of nanocrystals and cross-link them. The compression is continued at a constant rate during the approximately 15 min duration of the ligand exchange process. By the end of this treatment, the films fabricated in both conditions reached an SP of approximately 16 ± 2 mN m−1 and a similar level of compactness, so that the morphological differences between the two cases mostly depend on the surface pressure at the moment of LE start. The obtained films are then transferred via the LS method to the substrate of choice for further characterisation (optical, structural or electronic) (Fig. 1d). At all moments during the fabrication, the film looks homogeneous across the wide surface except briefly after the ligand exchange solution injection, as observable by visible inspection. The cracks formed at this point are quickly repaired by the compression, which brings the QD close together as the ligands are slowly being removed. The final films are very compact, with no visible macroscopic cracks, and noticeably darkened with respect to the pristine one, suggesting the successful removal of the ligands and a consequent increased density. We also would like to point out that this process is highly reproducible and could be easily automated in all steps, allowing for a simple and scalable deposition method for large-area films.

The dynamics of the film formation can be followed in real-time through the surface pressure isotherms measured with a Wilhelmy plate inserted in the trough. This allowed us to precisely and reproducibly trigger the LE at the correct SP for both conditions and ensure that the final SP was reached. The SP isotherms can be plotted as a function of the available area per single QD (Fig. 1e). This can be calculated with the formula:

$${A}_{{{\rm{QD}}}}=\frac{{A}_{{{\rm{t}}}}}{{c}_{{{\rm{QD}}}} \cdot {V}_{{{\rm{QD}}}} \cdot {N}_{{{\rm{A}}}}}$$
(1)

Where AQD is the area per QD, At is the area of the trough, cQD is the molar concentration of the colloidal solution (intended as moles of QD per unit volume), VQD is the volume of drop-casted colloidal solution and NA is Avogadro’s number. By knowing the size of the quantum dots, the length of the ligand shell and the assembly’s geometry, one could estimate the expected AQD for the case of a hexagonal ML with the pristine oleic acid (OA). In this way, we can predict when the SP starts to rise when the sparse film is compressed. However, we note that losses of colloidal solution and buckling of the film make these estimations less precise at higher compression rates.

Judging from the gradient of the curve, the SP isotherms display four main regions common to both sample preparations: (i) a gas phase where the QD are sparse, and the compression does not cause a rise in SP; (ii) a liquid phase when the compression closes all voids and QD are brought close together. Here, the SP increase approximately linearly with compression; (iii) after injecting EDA, the SP firstly spikes up due to the different surface tension of the LE solution and drops due to the removal of the ligands and consequent loss of volume of the film. The perturbation caused by the syringes might make the SP reading momentarily unreliable data, after which the increase with compression is restored; iv) upon further compression, the slope of the isotherm first showed a sharp increase (solid phase), followed by a saturation behaviour. This effect has been previously observed in Langmuir films undergoing buckling due to excessive compression46.

To exclude that compact films with a high density of quantum dots in close proximity (or in contact) can be fabricated with the standard LS approach and without ligand exchange, we performed scanning-transmission electron microscopy (STEM) on a highly compressed film (40 mN m−1) with pristine OA (Fig. 1f, isotherm in Supplementary Fig. 1). From the high-angle annular dark-field (HAADF) micrograph we can observe that the QD are arranged in a 2D hexagonal SL and from the Fast-Fourier Transform (FFT) of the indicated region of interest, we can determine the lattice parameter to be 7.4 nm. This means that the quantum dots have a nearest neighbour (NN) distance of approximately 1.2 nm, corresponding to the presence of a (possibly interdigitated) ligand shell. Furthermore, we conducted a systematic investigation on the effect of varying surface pressure at the moment of pick-up in the OA-capped samples (Supplementary Note 1 and Supplementary Fig. 2). Interestingly, the surface pressure is responsible for the repairing of macroscopic cracks in the film and for enhancing the coverage (although still partially). Excessive compression can result in buckling. The increase in surface pressure does not significantly decrease the lattice parameter, which remains largely unchanged between 0 and 30 mN m−1 and the superlattice geometry within single domains is preserved as well (Supplementary Fig. 3). Overall, this analysis confirms that OA-capped PbS SLs would not be viable for any optoelectronic application due to the poor coverage, large QD-QD distance, and OA shell presence which results in an insulating behaviour.

We now focus on the structural characterisation of the samples obtained with the usage of external pressure during the self-assembly and ligand exchange. As described above, we distinguish between LC and HC samples depending on the surface pressure at which the LE solution is injected. Since one of the main goals is to obtain an ordered, electronically coupled SL aiming for high charge mobility, we first studied the structure of the samples at the nanoscale. In Fig. 2a, b, we report the high magnification STEM-HAADF micrographs of the LC and HC SLs, respectively. Both SLs adopt a 2D hexagonal arrangement with lattice parameters of about 6.5 nm. This corresponds to a distance between the QD of approximately one PbS atomic layer, indicating that the ligand exchange was successful, and the nanocrystals are in direct contact with each other. This is interesting because when ML of OA-capped lead chalcogenide QD undergo ligand stripping, they tend to form square SLs with oriented attachment and epitaxial necking between {100} facets18,53,54. Here, instead, thanks to the active lateral compression, the hexagonal geometry is preserved, but with the QD also being directly in contact. This suggests that the strong shape anisotropy of the QDs, which is normally a driving force for the oriented attachment29, here does not play a major role in determining the final assembly geometry. Due to the combination of external pressure and strong interdot interaction through the bare facets upon ligand removal, the QDs do not have time to reorient before attachment.

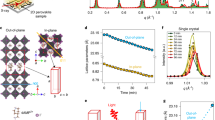
Fig. 2: Nanoscale structural characterisation.
figure 2

STEM-HAADF micrographs of the low compression (a) and high compression (b) samples, respectively. The insets show the respective FFTs of the micrograph (scale bars: 200 nm, 0.5 nm−1). c GIWAXS and inset GISAXS pattern of the LC superlattice. The bottom and left axes belong to the GISAXS pattern, while the top and right axes belong to the GIWAXS one. The intensity scale is logarithmic for GISAXS and linear for GIWAXS. Due to the high dynamic range of the detector, two different scales are needed to properly visualise features at both low and high angles. d Corresponding GISAXS and GIWAXS patterns for the HC SL. The intensity scales are the same as in (c).

Full size image

To understand whether epitaxial connections are formed in these SLs, we performed atomic-resolution STEM-HAADF to directly image such structures (Supplementary Fig. 4). While not all QD have a high symmetry plane in the zone axis, we see clear evidence of epitaxial connections and oriented attachment, especially between dimers and trimers. In a purely planar hexagonal lattice, it is not geometrically possible to have oriented attachment via {100} facets, therefore, only limited groups of QDs display it, while the majority are randomly connected. Neighbouring QD seem to always be in contact, but due to the deviation from the zone axis alignment, we cannot determine whether these are all cases of oriented attachment. While these structures are unusual, the hexagonal lattice has a higher packing fraction than the square one, and this could be beneficial for charge transport, especially in the context of hopping conduction through a percolating network.

It is now important to denote major differences between the LC and HC SLs. With lower compression (Fig. 2a), the SL is only one ML thick, as can be evinced by the contrast of the STEM-HAADF micrograph. The coverage is suboptimal, and a significant number of cracks and nano-tears can be observed36. Due to these structural defects, the diffraction spots in the FFT appear quite broad despite a single crystallographic orientation being present within relatively large domains. The grazing-incidence small-angle x-ray scattering (GISAXS) pattern shows pure Bragg rod-like diffraction, confirming that the SL has a single-layer thickness (zoomed view in the inset of Fig. 2c). The GISAXS patterns agree with the one expected for a nanocrystal ensemble with a 2D-hexagonal lattice, where the presence of multiple signal oscillations along qz is due to the modulation of the minima and maxima of the QD form factor. In the in-plane (IP) direction, two orders of reflections are present, indicating good paracrystalline order, and their reciprocal position confirms the SL hexagonal geometry as observed in the STEM (a = 6.8 ± 0.4 nm). From the broadening of the first IP peak at qy = 0.106 Å−1 we calculated the coherence length of the SL to be ε = 2π/FWHM = 103 nm. At large q-values, the grazing-incidence wide-angle x-ray scattering (GIWAXS) pattern shows arc-like diffraction signals, denoting some degree of QD collective alignment (Fig. 2c). The GIWAXS signal is related to the PbS atomic lattice (AL) and by indexing the diffraction spots, we can determine a partial collective orientation of the QD with the {100}AL planes parallel to the substrate. Thus, a non-negligible fraction of the QD forming the hexagonal epitaxially connected SL in the dry phase is preferentially oriented (possibly already at the liquid-vapour interface)55. At the same time, we cannot exclude that the fraction of QD that are randomly oriented might still be forming epitaxial connections as can be evinced by the atomic resolution STEM imaging (Supplementary Fig. 4). The combined use of these structural characterisation techniques renders well the uniqueness of such SLs: most 2D SLs reported in recent literature either adopt a square geometry with the {100}AL collective orientation of the QD or a honeycomb geometry with a {111}AL collective orientation16,21. Here, instead, the introduction of the external pressure seems to force the structure to maintain the hexagonal geometry during the ligand exchange thus maximising the packing fraction. The QD, on the other hand, adopt a preferential {100}AL orientation, possibly due to the interactions with the liquid subphase.

Between the two samples prepared, the HC SL one shows an increased coverage and compactness of the film. Its thickness is not uniformly one ML, as overlapping QD or disordered buckled domains can be observed (Fig. 2b). The FFT reveals narrower reflections with respect to the LC case, indicating an increase in the crystalline ordering induced by the large pre-LE compression. No major cracks can be observed, while some nano-tears are still present. The GISAXS pattern confirms the same spacing as in the STEM (a = 6.9 ± 0.3 nm) but shows fainter second-order reflections compared to the LC case. Nevertheless, the coherence length is in this case 148 nm, significantly higher than the LC SL and comparable to PbSe QD square SLs with oriented epitaxial attachment56. The GIWAXS pattern is analogous to the LC case except for an increased intensity of the diffraction peaks. This is partially explained by the higher density of the HC film, but the higher ratio with respect to the background also indicates an improved collective orientation of the QDs (Supplementary Fig. 5). This is evidence that the external pressure forces the QD to epitaxially connect as soon as the ligands are stripped off. With less time available for the QD to reorient, the preferential orientation, which is higher in the highly compressed SL, is preserved and enhanced with respect to the LC one. We note at this point that in both the LC and HC SLs, the QDs retain their quantum confinement as proven by the clear excitonic feature in the absorption spectra (Supplementary Fig. 6). The HC SL shows higher absorbance mostly due to the increased compactness since the buckled regions are only a minimal fraction of the area and most of the film is 1 ML as determined by AFM (Supplementary Fig. 7).

Mesoscale morphology of the superlattices

We have shown so far that applying an external pressure during the SL self-assembly and ligand exchange has an impact on the nanoscale morphology of the films. However, it is at the macroscopic scale that the most significant differences are observed, showcasing the potential of this deposition method for large-area devices. To prove this, we performed standard SEM (i.e., detecting secondary electrons (SE)) microscopy at low magnification to gain statistically relevant information on the coverage and presence of cracks in the two conditions (Fig. 3). We acquired micrographs over several areas of 2336 µm2 with a projected pixel size of 9.6 nm. Therefore, the analysis is mostly aimed at voids with a minimum size of 1-2 QDs. A full coverage (100%) corresponds to a superlattice where no QD is misplaced or missing and no macroscopic crack is observable, therefore not considering the intrinsic packing limit for spheres (or disks in the 2D projection) in a hexagonal close-packed monolayer (91%). Exemplary SEM micrographs for the LC and HC SLs are displayed in Fig. 3a, b, respectively. In this way, we could map the density and size of the voids (or cracks/tears) from a few tenths of nanometres to tenths of microns.

Fig. 3: Analysis of mesoscale morphology.
figure 3

a Low magnification SE micrograph of the low compression and (b) high compression superlattices, respectively (scale bars: 10 µm). c Exemplary void density distribution as a function of the void diameter for LC and HC samples. The inset indicates the coverage as calculated by integrating the curves and dividing the total area of the image. d Collected statistics of the two representative exponential distributions’ average void diameter as a function of pre-ligand exchange compression. Error bars represent one standard deviation. e Void density at the average void diameter and void areal fraction as a function of pre-ligand exchange compression. The bars are colour-coded with the respective axes. Error bars represent one standard deviation.

Full size image

A qualitative observation of the micrographs in the two cases immediately reveals a dramatic difference in the films’ morphology. The LC SL presents an elevated number of both buckled regions and voids of several hundredths of nanometres in diameter. The buckled regions are mostly at the edges of quasi-circular SL domains, which are sub-micrometre-sized, while the voids are homogeneously distributed around such domains. Therefore, the film is quite rough and has poor coverage. The HC SL displays a much different morphology (Fig. 3b): the film is very homogeneous and presents a few linear buckled regions that extend for tenths of microns along specific directions. We did not study this phenomenon in detail, but we hypothesise that this direction is parallel to the moving axis of the barriers. These films display voids of very small size, and clear domain borders are not observed at this magnification. Round voids are randomly distributed across the film with a significantly smaller density than the LC case.

To obtain quantitative information from the SEM micrographs, we measured the projected area of the voids with a simple thresholding method after proper correction of the raw images (Supplementary Fig. 8). For ease of interpretation, we suppose a circular nature of the voids, and we display the effective void diameter D instead of the total area. In Fig. 3c, we display a so-obtained exemplary statistical distribution of the void diameters for the LC SLs. In all cases, we found bi-exponential distributions with two distinct populations of void diameters (below and above 30 nm). The smaller voids usually account for more than 80% of the total, but the bigger voids are the most detrimental for the coverage. We assume a typical exponential distribution in the form of:

$$\frac{{{\rm{d}}}N}{{{\rm{d}}}D}\propto {e}^{-\frac{1}{\lambda } \cdot D}$$
(2)

Where λ is the mean of the distribution. By fitting the curve in Fig. 3c, we can directly obtain the mean values of the two distributions for the small and large voids (λ1 and λ2, respectively, Supplementary Fig. 8). In the reported example, λ1 is 26 nm and λ2 is 186 nm. If dN/dD is divided by the total area of the image, one obtains the void density in µm−2. By comparing the overall distribution for the LC and HC SLs, we can determine that the void density of the HC films is at least one order of magnitude lower than that of the LC ones at any given void diameter. For lower compressions, voids above 500 nm are observed, while for higher compressions, this number is less than half. The integration of these curves allows for a calculation of the coverage, which in this case is 93.3% and 99.3% for the LC and HC SLs, respectively. In Fig. 3d, e, we summarise the results of the statistical analysis of the void diameter distributions. The average λ1 decreases from 28 ± 2 nm to 7 ± 1 nm with increasing compression, while λ2 decreases from 170 ± 20 nm to 80 ± 30 nm analogously. Since the coverage is mostly affected by the larger voids, we measured the void density at λ2 and observed that, for the lower compression case, this is 2.4 times higher than for the higher compression one (Fig. 3e). Furthermore, the areal fraction of the voids over the total image area is decreased from 6.8 ± 1.5 % to 0.4 ± 0.2 % (~ 20-fold) thanks to the increased pressure. This means that the HC SL always has a coverage above 99.3%. As a final remark on the coverage over large areas, we note that in both conditions there is no evidence of macroscopic cracks in regions of up to 2.5 mm lateral dimensions (possibly even larger). To our knowledge, this is the first demonstration of an ordered SL with such high coverage over millimetre square areas.

Atomistic molecular dynamics simulations

Our experimental observations are also supported by molecular dynamics simulations of an NQD = 15 × 15 QD array, where PbS QDs of 6 nm diameter are placed in a 2D plane on a hexagonal lattice with spacing l0, random orientation, and no ligands (Fig. 4). The starting configuration in a hexagonal lattice is supported by experimental evidence (see above) (Fig. 2 and Supplementary Figs. 2 and 3) and, upon EDA injection, the experimentally verified loss of ligands justify that the ligand-ligand interaction can be omitted in the simulations. We employ a fully atomistic approach where the interaction potential between atoms is described using a combination of Morse, Lennard-Jones (LJ) and Coulombic potentials. Such interaction potential captures both short- and long-range interaction between the involved atomic species and was specifically designed for lead sulphide QD (see “Methods” for details)38,57. Given the complexity of the system, some simplifications and approximations are made by exploiting the rich structural information obtained by the experiments in order to reduce the computational cost and allow the simulation of such a large array with atomistic resolution. All QD are initialised oriented with the {100}AL parallel to the substrate (following the results from GIWAXS analysis in Fig. 2c, d) and can only rotate around their z-axis and move in the film x-y plane. Consequently, all forces along the z-axis are not calculated, and the QD motion is constrained to the x-y plane. While this approximation does not allow for the simulation of buckling, STEM micrographs at different magnifications (Figs. 2, 3 and Supplementary Figs. 2 and 4) show that this phenomenon occurs at scales larger than the simulation box (> 500 nm vs. < 200 nm). Since these simulations are limited in size and do not capture large-scale buckling effects, the packing is to be considered representative of regions far from buckling events.

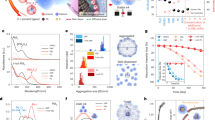
Fig. 4: Molecular dynamics simulations.
figure 4

a Snapshot and the corresponding (b) colloidal and (c) atomic FFT for the simulated PbS QD SL for the initial spacing lattice l0 = 65 Å, P = 30 atm and (d–f) l0 = 85 Å, P = 1 atm, respectively (scale bars: 0.5 nm−1; 3 nm−1). Lead atoms are represented in grey while sulphur and selenium atoms are represented in yellow. The colour scale is the same for (b, e) and (c, f) respectively. g Radial distribution functions g(r) as a function of l0 at P = 1 atm. Vertical dashed lines indicate the minimum cutoff distance used to compute the different structural descriptors. h Number of neighbours (Nneigh), orientational bond order parameter (Ψ6) and percentage of void space (Vvoid) once the system reached the equilibrium state as a function of l0 at P = 1 atm. Error bars represent one standard deviation.

Full size image

The effect of pre-LE compression is emulated by varying the initial spacing l0 (lower for higher compression). Again, for simplicity, we do not simulate ligands, counterions or dangling bonds, therefore, the QD’s surface is bare, but charge neutrality is ensured. An external pressure P in the x-y plane shrinks the simulation box until equilibrium is reached due to the rigidity of the film, thus simulating the closing of the barriers post-LE. This setup, emulates to the best of our knowledge the experimental setup during and after LE and mimics the QD self-assembly to reproduce the experimental LC and HC conditions. Note that based on a back-calculation with the surface pressure isotherms and Fig. 2, the l0 = 65 Å, P = 30 atm conditions correspond to the experimental HC and the l0 = 85 Å, P = 1 atm simulation corresponds to the experimental LC, but simulations also allow to independently vary l0 and P. Current simulations show that planar-constrained QDs are able to sustain these pressures thanks to the strong QD-QD interactions without damage to the single QD structure. Stress must then be relaxed at buckling points at scales larger than the simulation, which would be interesting to study in future work. Simulation details are reported in the Methods section. We highlight that a starting spacing of 65 Å is unrealistic with the presence of OA, but since we cannot simulate the dynamics of ligand removal, it is reasonable to think that while ligands leave the surface of the QD, their distance continuously decreases.

Figure 4a and Supplementary Movie 1 show the final structure and complete simulation for QD systems at l0 = 65 Å, P = 30 atm, whereas Fig. 4d and Supplementary Movie 2 show the final structure and simulation for systems starting at l0 = 85 Å, P = 1 atm. In both atomic and colloidal representations (i.e., by representing the centre of mass of each QD, see Supplementary Fig. 9), we clearly observe the formation of an ordered SL with few cracks/tears under HC conditions. This was corroborated by computing the diffraction pattern from the colloidal representation, which exhibited a hexagonal symmetry with several higher-order reflections (Fig. 4b). In contrast, at l0 = 85 Å, the system evolved into a stable, disordered percolating network. In this case, the colloidal diffraction pattern exhibited isotropic rings owing to the presence of a small randomly oriented SL domain with a consistent average QD distance (Fig. 4e). We also computed the diffraction pattern related to the atomic planes of all atoms in the QD, showing no preferential orientation in both conditions in agreement with the experimental results (Fig. 4c, f). We would like to notice here that the planarity constraint for the simulation is indeed not biasing the achievement of long-range order, as this does not happen for the l0 = 85 Å, P = 1 atm simulation, where the majority of the QD do not form oriented attachment through the {100} facets.

To quantify the QD spatial arrangement in all the simulated final structures, we computed the pair distribution function g(r) at different l0. In agreement with the snapshots and diffraction patterns, Fig. 4g shows that for l0 = 65 Å, the g(r) presents clear peaks beyond the first, indicating the existence of a locally ordered structure associated with length scales beyond the first shell of nearest neighbours, whereas these peaks disappear with increasing l0. As shown in the diffraction patterns and snapshots from Supplementary Fig. 9, increasing l0 inevitably leads to a more disordered structure. Furthermore, we observed that starting the assembly process at higher l0, the additional increase in pressure during the assembly process did not induce a compact crystalline structure due to the strong interactions between QD (Supplementary Fig. 9), which led to a yielding stress of the percolating network higher than the external pressure applied. We also evaluated the final self-assembled structures by computing the number of neighbouring particles Nneigh with a distance smaller than or equal to the first minimum of g(r), and the orientational bond order parameter Ψ6 (see Methods section). In addition, we computed the percentage of void space Vvoid. From Fig. 4h we observe that Nneigh is slightly below 6 for l0 = 65 Å, due to the presence of small voids; hence, the final self-assembled lattice is not a perfect crystal as manifested by Ψ6 < 1, but it is close to it (Ψ6 ~ 0.9). By increasing l0, both Nneigh and Ψ6 decreased, whereas Vvoid increased, indicating that the loss of crystalline order was due to QD sticking together to form a disordered and rigid percolating network, preventing the barrier compression to repair the voids. No significant change in structural parameters and free space was detected when changing P, highlighting the high yielding stress of the final percolating network that resists further packing of the QD. We remark that in fact, unlike in the experiments, in the simulations spacing and pressure can be decoupled, but Supplementary Figs. 9, 11 and 12 show that spacing, rather than pressure, is the main responsible for the QDs packing.

Overall, these simulations highlight the critical role of dense QD packing before the start of the LE procedure to achieve defect-free, well-ordered superlattices. The results are in line with classical theories of colloidal gels assembling into percolating networks with a yield stress proportional to the local packing and the strength of attraction between individual colloidal particles58,59. The peculiarity of these nano-colloids is their high interaction strength, leading to very strong networks at low packing, thus preventing crystalline SL formation unless a high packing fraction is reached before LE. We remark that the present results can be extended to different chemistries and are robust also at larger simulation scales (see Supplementary Methods, Supplementary Figs. 10, 11 and 12, Supplementary Movie 3 and 4). Simulations with PbSe QD of identical diameter and array size of 25 × 25 nanocrystals (~ 3 million atoms total) display analogous trends and absolute values of the parameters measured for the PbS QDs, suggesting a universality of the reported methodology.

Charge carrier transport measurements

We have so far shown how the pre-ligand exchange compression in the liquid-vapour interface assembled SL dramatically affects their structure at both the nano- and mesoscale. In particular, the increased coherence length, coverage and decreased fraction of buckling for the HC SL is expected to result in significantly improved electrical conduction through the films at a macroscopic scale. To verify such an effect, we implemented the SL into ion-gel gated field-effect transistors (IGFET) analogously to our previous reports (see Methods for details)25,29,30. The transistors, fabricated in identical conditions, were both annealed and passivated with PbI2 following our previously reported method30.

A comparison of the output curves of the LC and HC SL (Fig. 5a, b) reveals several important differences. For the LC device, the maximum current reaches 8 µA, and a significant hysteresis is present. The transistor is predominantly n-type. Nevertheless, a significant hole current contribution hinders the saturation regime, as can be noted particularly for VG = 1.5 V. This ambipolarity in the LC SL sample could be due to the poorer passivation and connectivity of the QDs, where the number of nearest neighbours is lower and therefore more facets are exposed. The abundance of buckled and disordered regions most likely contributes to the non-ideal transport observed as well. On the other side, the output curve of the HC SL presents a clear pinch-off and saturation regime as the transport is n-type dominated, and the hole contribution is also negligible at high drain-source biases. The hysteresis is dramatically reduced, and the maximum current is 4-fold higher than in the LC case. Besides the evident difference in conductivity, the transfer curves (Fig. 5c) show similar features in terms of subthreshold swing and on/off ratio (104-105).

Fig. 5: Transport measurements.
figure 5

a Output curves for the record devices of the low compression and (b) high compression superlattices, respectively (VG = 0 to 1.5 V in 300 mV steps). c Comparison of the transfer curves for the same devices as in (a, b) (VDS = 0.1 V, L = 10 µm, W = 20 µm). The thinner lines show the reverse sweep. The hysteresis is counter-clockwise due to the slow motion of the ions in the gel. The light and grey curves represent the gate leakage current for the low and high compression samples respectively. d Statistical distributions of the SLs’ electron linear mobility as a function of the compression. Box plots indicate 1 standard deviation (limits), 2 SD (whiskers), mean (square) and the median (middle line).

Full size image

The significant difference in the IGFET performances is best evidenced by the statistical distribution of the electron linear mobility (Fig. 5d). The LC SL has an average mobility of 5 ± 2 cm2V−1s−1, with the best device reaching up to 8.1 cm2V−1s−1. The higher compression increases the average mobility to 19 ± 8 cm2V−1s−1 with a maximum of 36.6 cm2V−1s−1. In both cases, the relative dispersion of the distribution is comparable (σ/µavg ~ 0.4). It is important to mention that the bias-dependent capacitance obtained from impedance spectroscopy measurements (see Methods) and, therefore, the accumulated charge has been measured for each specific device for an accurate determination of the mobility (Supplementary Fig. 13 and Supplementary Table 1). We also remark that due to the ion gel gating, high accumulated carrier densities in the order of 5–22 electrons per QD are achieved (see Supplementary Note 3). This consequently results in higher charge mobility than lower doping or gating levels (like the ones obtainable with traditional solid-state dielectrics), thanks to trap-filling and a higher number of charges available for conduction. The mobility measured for the LC SL is comparable to the ones usually measured for disordered films, and only half of the recently reported mobility for an uncompressed 2D square PbS quantum dot SL with comparable ionic-liquid gating28. This can be explained considering that the compression post-ligand exchange gives suboptimal orientational ordering and epitaxial connection in LC samples, but at the same time, it can still repair macroscopic cracks, unlike in uncompressed samples. For comparison, we fabricated IGFETs with disordered thin films fabricated via layer-by-layer spin-coating and exchanged with ethanedithiol ligands, commonly used for PbS QD photodetectors (see Supplementary Note 2 and Supplementary Fig. 14). The average electron mobility of the disordered films was found to be 4.5 ± 1.8 cm2V−1s−1 with a record device displaying a value of 7.5 cm2V−1s−1, therefore comparable with the LC superlattices. Therefore, the performance of the HC SL is significantly better and compares with the best examples of uncompressed 2D SL with epitaxial oriented attachment (with both PbS and PbSe QD)18,25,26,27.

This is possible thanks to several factors: (i) the comparable or higher translational ordering as evidenced by the noticeable coherence length of 148 nm; (ii) the higher connectivity and packing fraction due to the hexagonal geometry where 6 nearest-neighbours instead of 4 are available; (iii) the increased coverage, the lack of cracks, the limited presence of buckling and in general the excellent large scale morphology over several square millimetres present a significant advance with respect to uncompressed SL. All these factors compensate for the lower fraction of oriented attachment, which is known to dramatically improve the charge mobility in the oriented attached SL. At the same time, these measurements suggest that the so-far observed performance of these quantum dot solids might be limited by the large-scale morphology, scattering by grain boundaries and cracks, and not anymore by the limited connectivity and high energetic disorder. We expect that the charge carriers mobility could be further improved by combining the epitaxial oriented attachment with the external compression method here presented.

In this report, we present an approach to fabricating 2D SLs of PbS QD in a Langmuir-Schaefer setup with external compression, which shows large area coverage and homogeneity. We show that the degree of compression before triggering the ligand exchange is a crucial parameter for obtaining highly ordered, crack-free, hexagonal SLs. Careful structural characterisation reveals that due to the compression, the ligand-exchanged samples retain the hexagonal geometry thus maximizing the packing of the structure and the number of nearest-neighbours. The formation of these unusual SLs is predicted by a large-scale atomistic molecular dynamics simulation. The control of lateral compression, and consequently of the structural properties of the SLs, give rise to significant differences in their transport properties. Ion gel-gated FETs displayed an average electron mobility of 5 ± 2 cm2V−1s−1 for the lower compression, increasing to 19 ± 8 cm2V−1s−1 for the highly compressed ones, thanks to the better coverage, lack of cracks, better packing and increased translational ordering. This demonstrates the effectiveness of our method in achieving high carrier mobility in SLs with millimetre square coverage. Translating this approach to three-dimensional SL might have important implications for the technological applications of such metamaterials in optoelectronics.

Methods

Materials

QDot™ oleic acid-capped PbS Quantum Dots were obtained from Quantum Solutions. Decane (99%, anhydrous, Fisher), ethylene glycol (99.8%, anhydrous, Fisher), acetonitrile (99.9 + %, extra dry, Fisher), ethylenediamine (99 + %, anhydrous, Fisher), lead(II) iodide (99.99%, TCI), dimethyl sulfoxide (99.9%, anhydrous, Sigma), Poly(vinylidene fluoride-co-hexafluoropropylene) (P(VDF-HFP), Sigma), 1-Ethyl-3-methylimidazolium bis(trifluoromethyl sulfonyl)imide [EMIM][TFSI] (≥ 98%, Sigma), cyclohexanone (99.8%, Fisher). All materials were used as is and were opened and stored always in nitrogen-filled gloveboxes.

Langmuir-Schaefer deposition of superlattices

A Langmuir trough (Biolin KSV NIMA KN-2001 with Teflon barriers KN-0041) was installed inside a glovebox. The Teflon trough (80 × 5 × 0.4 cm3) and barriers were cleaned with hexane or octane after each deposition to remove residual QD and then thoroughly rinsed with acetone and isopropanol. Before the start of the experiment, the trough was filled with 48 mL of ethylene glycol (EG) ensuring to have a convex meniscus over the edges and a flat surface at the centre. Sufficient time was considered for the thermalisation of the liquid. The surface pressure isotherms were measured with a 10.3 × 2 mm2 paper Wilhelmy plate, which was previously soaked in EG to avoid drifting of the SP reading during the experiment. Before the QD deposition, a test run was performed to verify the cleanliness and purity of the liquid interface by ensuring that the SP would not rise significantly throughout the compression (< 0.3 mN m−1). A volume of 2.64 µL of 65 µM PbS QD dispersed in decane was drop-casted at the centre of the trough using a micropipette, and a waiting time of 5 minutes was considered for the spreading and solvent evaporation to take place. After verifying a constant reading of SP indicating an equilibrium condition, the SP was zeroed, and the compression was started at a constant rate of 0.8 mm min−1. The compression continued at the same rate for the whole duration of the experiment. Once the target SP (2 mN m−1 and 20 mN m−1 for the LC and HC film, respectively) was reached, ligand stripping was triggered with a 6 ml, 5 M EDA solution in EG injected below the moving barriers with two syringes simultaneously (3 mL each, with long needles and from opposite sides of the trough). The target ligand stripping duration was of 15 min after which a SP of about 16 ± 2 mN m−1 was reached. The obtained superlattices were collected on a substrate of choice with the Langmuir-Schaefer method from the centre of the trough, close to the Wilhelmy plate. The scooped samples were then washed by immersion in pure ACN solution for 30 seconds to remove the residual OA and EDA. For transistor devices, an additional immersion for 5 min in a 10 mM PbI2 solution in DMSO, and 1 min immersion in pure DMSO were performed to passivate the QD surface. A standard 20 min annealing at 120 °C was performed as well to ensure evaporation of all solvents. All samples were dried overnight in a millibar vacuum. All these steps were performed in a glovebox filled with dry nitrogen (< 0.1 ppm O2/H2O).

Deposition of disordered films via spin-coating

For the fabrication of the disordered films, a diluted solution (2 mg ml−1) of the OA-capped QD in hexane was prepared and filtered through a 0.22 µm PTFE filter. To obtain a thin film, 40 µl of the solution was spin-coated on the FET substrate with a speed of 1000 rpm, accelerating at 1000 rpm s−1 and 30 s total spin time. The sample was then flooded for 30 s with an ethanedithiol (EDT) solution of 0.02% v/v in acetonitrile to exchange the ligands and then spun with the same settings. The sample was then washed of residual ligands with pure acetonitrile for 10 s following another spinning to remove all the solvent. The washing step was repeated twice. Lead iodide passivation was omitted as thiols strongly bind to the lead atoms on the {111} facets, thus properly passivating the surface. The whole layer deposition was repeated twice to obtain a continuous film of thickness 11 nm (approximately two QD layers) and 2.5 nm roughness (Supplementary Fig. 14). The sample was annealed at 120 °C for 20 min, analogous to the SL-based FETs. All the steps were performed in a glovebox filled with dry nitrogen (< 0.1 ppm O2/H2O).

Absorption measurements

The absorption spectra were measured with a Shimadzu UV3600 spectrometer. The precise molar concentration of the QD colloidal solution was determined from the absorption spectra collected in quartz cuvettes (2 mm path length) corrected for the solvent. The extinction coefficient at 400 nm was calculated as ε400 = 0.0233 × d3 cm−1 µM−1, where d is the QD diameter. The molar concentration was then obtained from the solution absorbance at 400 nm with the formula c = A400/(ε400 × t), where t is the optical path length in the cuvette2. The LS superlattices were deposited on optical glass that was previously polished with soap and sonicated in water, acetone, and isopropanol and dried in an oven for 1 h at 100 °C. A clean glass substrate was used as a reference, and the spectra were collected using a 4 mm diameter circular mask.

Atomic force microscopy

Micrographs of the deposited films were collected with a Bruker MultiMode-8 microscope equipped with ScanAsyst® automatic image optimisation. Gwyddion software was used to correct and analyse the micrographs.

Electron microscopy

Low magnification STEM-HAADF and SE imaging was performed with an FEI Helios G4 CX operated at 30 kV (transmission) and 10 kV (secondary electrons) respectively. Atomic-resolution STEM-HAADF imaging was performed using a mono-chromated, image- and probe-corrected Thermo Fisher Scientific Themis Z S/TEM system operated at 300 kV with beam convergence of 24 mrad.

Grazing-Incidence X-ray Scattering

GISAXS and GIWAXS measurements have been performed at the I07 beamline, in DIAMOND, UK. The beamline is equipped with a 3-axis positioning system for the large area detector allowing to measure at distances suitable for either small or wide angles. The samples were measured at a 0.2° incident angle (αi) using a Pilatus 2 M detector placed 528 or 1378 mm away from the sample for GIWAXS or GISAXS, respectively. The X-ray energy of the beam was set to 12 keV, and the angular range was calibrated using the diffraction rings from standard silver behenate and silicon powder samples. The patterns were further analysed using the GIXSGUI software in MATLAB60. Supplementary GIWAXS data were collected at the multipurpose instrument for nanostructure analysis (MINA) instrument at the University of Groningen. The instrument is built on a Cu rotating anode source providing an X-ray beam with wavelength λ = 0.15413 nm. The X-ray beam path and the sample holder are kept in a rough vacuum to minimise air scattering and reduce the background in the GIWAXS configuration. 2D patterns were collected using a Vantec500 detector (2048 × 2048 pixel array with pixel size 68 × 68 µm2) located 90 mm away from the sample.

Molecular dynamic simulations

Each simulated PbS colloidal QD is created by placing Pb and S atoms into a cubic rock-salt unit cell. Then, we truncated the cubic cell to obtain a rhombicuboctahedron shape, ensuring electroneutrality. The resulting PbS QD contains N = 4760 atoms and is replicated in the x-y plane. In particular, we considered NQD = 225 (15 × 15 array) PbS QD distributed on a hexagonal lattice with spacing lattice l0, for a total of 1,071,000 charged atoms in each simulation. Each QD is initially randomly rotated along its z-axis. Molecular dynamic simulations were performed with LAMMPS61, and the interactions between atoms are described using a combination of Morse, Lennard-Jones (LJ) and Coulombic potentials, according to the expression38:

$$U={U}_{{{\rm{Morse}}}}{S}_{{{\rm{SR}}}}+\left({U}_{{{\rm{Coulomb}}}}+{U}_{{{\rm{LJ}}}}\right){S}_{{{\rm{LR}}}}$$
(3)

The Morse potential, which captures short-range (SR) attractive interactions, is given by:

$${U}_{{{\rm{Morse}}}}\left({r}_{{{\rm{ij}}}}\right)={D}_{0}[{e}^{-2\alpha \left({r}_{{ij}}-{r}_{0}\right)}-2{e}^{-\alpha \left({r}_{{ij}}-{r}_{0}\right)}]$$
(4)

where rij is the interatomic distance, D0 corresponds to the well depth, α controls the width of the potential, and r0 refers to the position of the minimum potential. On the other hand, the long-range interactions are described by the sum of the LJ potential and Coulomb part:

$$U\left({r}_{{ij}}\right)={U}_{{LJ}}\left({r}_{{ij}}\right)+{U}_{{{\rm{Coulomb}}}}\left({r}_{{ij}}\right)=4{\epsilon }_{{ij}}\left[{\left(\frac{{\sigma }_{{ij}}}{{r}_{{ij}}}\right)}^{12}-{\left(\frac{{\sigma }_{{ij}}}{{r}_{{ij}}}\right)}^{6}\right]+\frac{{q}_{i}{q}_{j}}{4\pi {\epsilon }_{0}{r}_{{ij}}}$$
(5)

where \({\sigma }_{{ij}}=\left({\sigma }_{i}+{\sigma }_{j}\right)/2\) and \({\epsilon }_{{ij}}=\sqrt{{\epsilon }_{i}{\epsilon }_{j}}\) define the distance at which the particle-particle interaction is zero and the potential well depth, respectively, whereas ϵ0 is the vacuum permittivity, and qi corresponds to the atomic charge of atom i. The functions \({S}_{{{\rm{SR}}}}({r}_{{ij}})\) and \({S}_{{{\rm{LR}}}}\left({r}_{{ij}}\right)=1-{S}_{{{\rm{SR}}}}\left({r}_{{ij}}\right)\) ensure a smooth transition between short- and long-range interactions. The short-range smoothing function is defined as

$${S}_{{{\rm{SR}}}}\left({r}_{{ij}}\right)=\left\{\begin{array}{cl}1 & \quad \quad {r}_{{ij}} < R-D \hfill \\ \frac{1}{2}-\frac{1}{2}\sin \left(\frac{\pi }{2}\frac{{r}_{{ij}}-R}{D}\right) & R-D < {r}_{{ij}} < R+D \hfill \\ 0 & \quad {r}_{{ij}} > R+D \hfill \end{array}\right.$$
(6)

where R and D are distance parameters. We adopted the parameters previously used for studying PbS QD in Chen et al.38. Thus, the partial charges are set to qPb = 1.124 e and qS = − 1.124 e. The LJ coefficients are σPb = 5.441 Å and σS = 3.161 Å regarding atom sizes, and ϵPb = 0.684 kcal mol−1 and ϵS/kB = 0.989 kcal mol−1 for the interaction parameters. In addition, the Morse potential parameters are D0 = 3.892 kcal mol−1, α = 0.470 Å−1 and r0 = 7.070 Å for the Pb-Pb interaction; D0 = 0.500 kcal mol−1, α = 0.625 Å−1 and r0 = 7.335 Å for the S-S interaction; and D0 = 73.318 kcal mol−1, α = 2.071 Å−1 and r0 = 3.030 Å for the Pb-S interaction. Finally, the smoothing parameters are R = 4.224 Å and D = 1.000 Å for the Pb-Pb interaction; R = 3.930 Å and D = 0.806 Å for the S-S interaction; and R = 5.467 Å and D = 1.000 Å for the Pb-S interaction. We fix the cut-off interaction at rc = 12 Å, and we resolve the long-range interaction due to the Coulomb part using a particle-particle particle-mesh (PPPM) with tolerance Fth = 10−562,63. Simulations of two-dimensional QD superlattices are performed in the isothermal-isobaric (NPT) ensemble using the Nosé-Hoover thermostat with a time step δt = 2 fs and total runtime of 0.8 ns, until the system reaches an equilibrium configuration (Supplementary Fig. 15 for PbS QD, Supplementary Fig. 16 for the PbSe ones). In particular, we consider temperature T = 300 K and explore the superlattice assembly at different pressure P conditions. For each state point, determined by (l0, P), we run three independent simulations by the randomisation of the QD orientations. We add a constraint of planarity, meaning that all forces along the z-axis are not calculated, and the QD motion is constrained to the x-y plane. The full code and settings are also available at the GitHub and Zenodo repositories (see Code Availability statement for the link).

Quantitative analysis of the self-assembled structures

We reduce the simulated PbS quantum dots (QD) to their corresponding centres of mass to evaluate various static properties. In particular, we compute the pair distribution function defined as

$$g\left(r\right)=\frac{A}{{N}_{{{\rm{QD}}}}^{2}} < {\sum}_{i}{\sum }_{j\ne i}\delta \left(r-{r}_{{ij}}\right) > $$
(7)

where \({r}_{{ij}}=\left|{r}_{i}-{r}_{j}\right|\) is the distance between i- and j-QD and A indicates the area of the simulation box. Likewise, we compute the diffraction pattern using the structure factor

$$S\left(q\right)={N}_{{{\rm{QD}}}}^{-1} < \rho \left(q\right)\rho \left(-q\right) > $$
(8)

where ρ(q) represents the density fluctuations in the reciprocal space and \(q=2\pi \left(\frac{{n}_{x}}{{L}_{x}},\frac{{n}_{y}}{{L}_{y}}\right)\) is the wave-vector with \({n}_{x,y}\in Z\). Here, Lx and Ly are the box lengths in the two-space directions. In addition, we compute the void space by dividing the simulation box into square bins of length lbox = 60 Å and counting the number of empty bins. We normalise the number of empty bins by the total number of bins. Finally, we characterise the system’s structural states using the orientational bond order parameter

$${\varPsi }_{6}=\frac{1}{{N}_{{{\rm{QD}}}}} {\sum}_{i=1}^{{N}_{{{\rm{QD}}}}}\left| {\sum}_{j=1}^{{N}_{{{\rm{neigh}}}}^{(i)}}{e}^{i6{\theta }_{{ij}}}\right|$$
(9)

where \({N}_{{{\rm{neigh}}}}^{(i)}\) is the number of neighbouring particles with rij smaller or equal to the first minimum of g(r), and θij expresses the angle between a fixed axis and the vector distance between particles i and j. The parameter Ψ6 = 1 corresponds to each particle being surrounded by six symmetrical arranged nearest neighbours.

IGFET characterisation

To prepare the ion gel solution, poly(vinylidene fluoride-co-hexafluoropropylene) (P(VDF-HFP)) was mixed in cyclohexanone (weight ratio 1:7) and stirred at 70 °C and 1000 rpm overnight. 1-Ethyl-3-methylimidazolium bis (trifluoromethylsulfonyl)imide [EMIM][TFSI] was added, in a weight ratio 4:1 with the polymer, several hours prior to deposition and the solution was kept at 70 °C29,30. Ion-gel deposition was performed in a glovebox by drop-casting 0.3 µl of the solution on each FET area, followed by 1 hour annealing at 70 °C and vacuum-drying overnight at millibar pressure. The devices were characterised with an Agilent E5270B SPA in a glovebox. The gating was achieved with a platinum foil placed on top of the ion-gel droplet, while the potential across the electrolyte/superlattice interface (Vref) was measured with a thin platinum wire inserted in the ion-gel. For the transfer curves, the gate voltage sweep rate was 5.7 mVs−1 at a fixed drain-source bias of 100 mV. Linear mobilities were calculated with the formula:

$${\mu }_{{{\rm{lin}}}}={\left.\frac{{{\rm{d}}}{I}_{{{\rm{DS}}}}}{{{\rm{d}}}{V}_{{{\rm{ref}}}}}\right|}_{{V}_{{{\rm{DS}}}}}\frac{1}{{V}_{{{\rm{DS}}}}}\frac{L}{{{WC}}_{{{\rm{sp}}}}}$$
(10)

Impedance spectroscopy

Impedance spectroscopy was performed on the complete device stack (Pt/SL/IG/Pt) with a Solartron 1260 impedance analyser. Frequency sweeps at a fixed gate voltage of 1.5 V were acquired in a frequency range of 10−2 − 106 Hz with an AC voltage amplitude of 20 mV. The acquired spectra were fitted by modelling the ionic gel as a constant-phase element and therefore determining the capacitance25,29,30. Gate voltage sweeps at a fixed frequency of 570 mHz were performed in the range of − 0.4 V to 1.5 V, analogously to the transfer curves with an AC voltage amplitude of 20 mV. The accumulated carrier density is estimated with the formula:

$$n\left({V}_{{{\rm{G}}}}\right)=\frac{1}{e} \cdot {\int }_{0}^{{V}_{{{\rm{G}}}}}C\left({V}_{{{\rm{G}}}}\right) \cdot d{V}_{{{\rm{G}}}}$$
(11)

Where e is the elementary charge and VG is the voltage applied to the gate28. Both methods yield comparable results.