Introduction

The imperative pursuit of high-performance energy storage solutions has driven extensive research into the fundamental processes governing lithium-ion batteries (LIBs)1. The transport of lithium within active materials determines the rate performance, capacity, and longevity of LIBs2. Conveniently, lithium diffusion within solid-solution active materials has been assumed to adhere to the classical Fick’s law, aiming to minimize concentration gradients (i.e., concentration-gradient driven diffusion;

$$J=-D({dc}/{dx})$$
(1)

where \(J\) is the diffusion flux, \(D\) is the diffusivity, and \({dc}/{dx}\) is the concentration gradient), analogous to the behavior observed in liquids or gases (Fig. 1a)3,4,5,6. Thus, it has been widely believed that lithium diffusion occurs to create a uniform lithium distribution within individual solid-solution particles7,8.

Fig. 1: Schematics of diffusion dynamics in various media.
figure 1

a Molecular diffusion in gas and liquid. b Ion diffusion in crystalline solid.

Full size image

However, diffusion is not always governed solely by concentration gradients; rather, it is driven by chemical potential gradients,

$$J=-D\left(d\varphi /{dx}\right)$$
(2)

where dφ⁄dx is the chemical potential gradient9,10,11. Chemical potential gradients account for thermodynamic factors, including strain/stress, mixing free energy, and interfacial energy, in addition to the concentration gradient. Among various factors contributing to chemical potential gradients, the coupling between chemical and mechanical effects—first described by Larché and Cahn—has been particularly noted in the context of intercalation processes in battery materials12,13,14,15.

In most macroscopic views, the concentration gradient primarily influences the chemical potential, making it convenient to express diffusion in terms of concentration for solid-solution materials where mixing is thermodynamically favorable. However, battery active materials clearly undergo anisotropic lattice volume changes, inducing nanoscopic strain/stress fields during the insertion or extraction of lithium through the diffusion channels (Fig. 1b)16,17,18,19,20. Hence, it is conceivable that the lithium concentration gradient may not align with chemical potential gradients and may deviate from the diffusion direction21,22.

While this phenomenon has been studied in polycrystalline materials, where grain boundaries introduce additional complexity to lithium transport. Single-crystalline materials provide a cleaner platform for studying these effects, as the absence of grain boundaries allows us to isolate and directly observe the intrinsic coupling between strain fields and lithium transport. If diffusion were solely driven by the concentration gradient, the lithium concentration distribution would exhibit monotonic patterns during cycling. Specifically, a core-shell lithium distribution would form in a diffusion-limited regime, while a near-uniform lithium distribution would appear in a surface reaction-limited regime. Direct evidence of dynamic lithium diffusion pathways deviating from conventionally believed patterns and lithium concentration gradients has been largely missing.

Tracking nanoscale lithium transport within single-crystalline particles during cycling requires an operando imaging platform with high chemical sensitivity and spatial resolution, along with a specifically designed particle morphology and geometry. Our model material is LiNiaMnbCo1−a−bO2 (NMC, where 1/3 <a < 1/2), which is a two-dimensional lithium conductor and widely used solid-solution cathode material in LIBs7. Despite the shift toward high-Ni NMC materials in both academia and industry23, we selected NMC111 as our model system. High-Ni compositions, such as NMC811, undergo phase separation in regions like H2-H3, making diffusion studies more challenging. In contrast, NMC111 allows us to investigate fundamental lithium transport mechanisms within the H1-H2 solid solution regime.

Previously developed operando imaging techniques, such as hard X-ray and optical microscopy, indicate a core-shell lithium distribution in NMC during cycling, implying surface-to-core lithium diffusion. However, phenomena occurring due to deviations from the concentration-gradient-driven diffusion model, such as nanoscale lithium transport against the concentration-gradient direction, have not been clearly addressed to date owing to insufficient chemical sensitivity of the analysis techniques or unclear crystallographic orientation and morphology of the analyzed particles3,24. In our work, we successfully track nanoscopic lithium diffusion in well-defined platelet single-crystalline NMC indirectly by measuring the oxidation state of Ni, revealing near-uniform yet fluctuating lithium transport in the surface reaction-limited regime across a wide range of cycling rates from 0.1 C (0.207 mA/cm2) to 3C (6.216 mA/cm2), owing to the high chemical sensitivity and spatial resolution of the operando soft X-ray imaging platform25,26,27.

Results

Operando scanning transmission X-ray microscopy

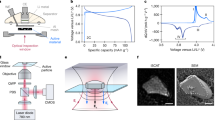
In this study, (003)-oriented single-crystalline LiNi1/3Mn1/3Co1/3O2 platelet particles (scNMC), free of internal grain boundaries unlike polycrystalline secondary particles, were utilized as model battery materials (Fig. 2a, Supplementary Figs. 1, 2, and 3)28. The scNMC morphology features two-dimensional diffusion channels along the (003) plane, characterized by a uniform thickness of approximately 150 nm and a length of approximately 1 μm. The main flat direction of scNMC serves as the lithium diffusion path, aligned parallel to the imaging plane to track nanoscale lithium diffusion. Thus, these model particles are ideal for analyzing two-dimensional lithium diffusion kinetics.

Fig. 2: Operando and ex-situ STXM results of scNMC.
figure 2

a SEM image of scNMC. b Absorption spectra (Ni L3-edge) of as-synthesized scNMC (Ni2+) and fully charged scNMC (Ni3.7+) samples. c Schematics of an operando microfluidic cell. The scNMC/Pt working electrode is positioned on the SiNx X-ray window, while the Li metal counter/reference electrode is placed outside the microdevice. The inset shows an overall cross-sectional view of the cell. d Electrochemistry curves at 0.1 C (0.207 mA/cm2), and 3 C (6.216 mA/cm2) during operando STXM. Lithium concentration maps at e, f, g 0.1 C and h 3 C cycling. Each pixel is 45 nm in size. The numbers below each frame indicate the average lithium concentration of each frame. i Ex-situ STXM results of scNMC after a relaxation period of 120 h using coin-type half-cell samples. j Evolution of the heterogeneity of particles on the same electrode during cycling. The gray trend line shows the heterogeneity changes observed at 0.1 C and 3 C rates. Source data are provided as a Source Data file.

Full size image

Operando STXM at the Ni L3-edge was employed to precisely track the local lithium concentration within scNMC particles during cycling with a pixel resolution of 45 nm (Fig. 2c, d). L-edge STXM offers substantial improvements in detecting and quantifying lithium concentrations compared to methods based on the K-edge or optical responses29. It allows for sensitive detection of Ni oxidation states through the selection-rule-allowed 2p-to-3d transition and delivers high-contrast absorption signals (~50% at L-edge vs. ~1% at K-edge for 150 nm thick scNMC)30,31. Additionally, the L-edge STXM measurements are performed in transmission mode perpendicular to the ab-plane, allowing the collection of signals integrated along the c-axis direction, where lithium diffusion does not occur. This measurement geometry enables tracking of changes in lithium distribution within the ab-plane diffusion channels during electrochemical cycling (Supplementary Fig. 4). Therefore, STXM is particularly suitable for precisely monitoring the local concentration and nanoscale diffusion of lithium within single NMC particles25,32,33. Notably, the high chemical sensitivity of STXM enabled the detection of subtle lithium heterogeneity, which has not been clearly addressed in previous publications (Supplementary Fig. 5)3,11,24,34.

The oxidation state of Ni was measured to indirectly infer lithium concentration and state-of-charge (SoC) within the voltage range of 3.0–4.3 V vs. Li/Li+ (Supplementary Figs. 6, 7 and 8)7,35. This indirect quantification was based on a calibrated linear correlation between Li concentration and Ni oxidation state. In the as-synthesized scNMC (Li1Ni1/3Mn1/3Co1/3O2), Ni was in the +2 oxidation state, while in the fully charged scNMC (Li1/2Ni1/3Mn1/3Co1/3O2), Ni was in the +3.7 oxidation state (Fig. 2b and Supplementary Fig. 9). Our DFT calculations confirm that Ni serves as the primary charge compensator during lithium insertion/extraction, as demonstrated in Supplementary Fig. 10 (Supplementary Data 1). When lithium is removed from the structure, only the directly coordinated Ni atoms undergo oxidation state changes, while Co and Mn maintain their original oxidation states. This selective charge compensation by Ni validates our approach of using Ni oxidation state as a reliable proxy for local lithium concentration. The lithium concentration at each pixel was quantified using a linear combination of X-ray absorption spectra from the end-phases (Supplementary Fig. 11).

Operando STXM results revealed intraparticle concentration heterogeneity, caused by nearly uniform yet fluctuating lithium transport across a wide range of C-rates, from 0.1 C (0.58 nA) to 5 C (2.9 nA) (Fig. 2e–h, Supplementary Figs. 12, 13, and Supplementary Video 1). Contrary to the conventional expectation of near-uniform lithium distribution in the surface-reaction-limited low C-rate regime or a core-shell distribution in the diffusion-limited high C-rate regime7, this study found that the dynamic intraparticle lithium distribution is near-uniform for both low and high C-rates. Thus, the observations at various C-rates indicate that lithium diffusion at the sub-micrometer-sized particle scale is sufficiently fast in the surface reaction-limited regime.

Although the lithium distribution became greatly homogenized, subtle heterogeneity remained, contrary to the expectation that NMC with solid solution phases would completely homogenize lithium within the particles. Nanoscale weak wavy patterns—indicative of subtle Li-dense and Li-dilute regions—were observed within the lithium distribution across a wide C-rate range owing to the high chemical sensitivity of STXM. These locally Li-dense or -dilute regions continuously relocated throughout the charge and discharge cycle (Supplementary Fig. 14). The difference in lithium composition between Li-dense and -dilute regions was typically ~0.05, less than 10% of the entire SoC range, from end-of-discharge (<x> = 1, where <x> indicates the average lithium concentration of the individual particles) to end-of-charge (<x> = 0.5). The results of ex-situ analysis conducted in an open circuit after 120 h at specific SoCs indicated significantly lower lithium-concentration heterogeneity than the operando results (Fig. 2i, j, and Supplementary Figs. 12, 13 and 15). These findings suggest that even in single-phase NMC, where lithium ions are expected to be homogeneously distributed due to maximized interionic distances, complex lithium–lithium interactions (mixing enthalpy) may persist. Such interactions can induce correlated diffusion, where lithium transport properties depend sensitively on local concentration, and we incorporated concentration-dependent diffusivity into our analysis to account for these effects.

The presence of dynamically formed Li-dense and -dilute regions was corroborated through additional experiments. First, ex situ STXM images of scNMC particles shortly after cycling (under one hour) in a composite electrode using a coin cell showed similar lithium distributions to those of operando STXM images, with a heterogeneity of 0.04 at various SoCs (Supplementary Fig. 16). Second, to exclude the possibility of measurement errors influencing heterogeneity, uniformly lithiated, as-synthesized particles (LiNi1/3Mn1/3Co1/3O2, and LiNi0.94Mn0.05Co0.01O2) were examined (Supplementary Fig. 17). These particles, representing Ni oxidation states of Ni2+ and Ni2.99+, respectively, showed near-zero heterogeneity. The quantification error for relative lithium concentration differences within a single particle is less than ±0.005 (Supplementary Figs. 18, and 19), confirming that the lithium heterogeneity results measured in our experiments are substantially above the sensitivity of STXM. Finally, controlled X-ray dosing ensured that the regions identified in particles—consistent across both freshly and repeatedly X-ray exposed samples during cycling at 0.1 C and 3 C (Supplementary Figs. 20, 21, and Supplementary Table 1)—were genuine features, not artifacts of the X-ray imaging process (Supplementary Fig. 22). All freshly imaged particles showed comparable Li-dense and Li-dilute region formation during cycling, confirming that the optimized X-ray doses used in this study neither slowed nor accelerated lithium diffusion. Moreover, we confirmed that X-ray imaging does not increase the lithium heterogeneity of 120-h-relaxed particles, indicating that the beam dose does not artificially create a heterogeneous lithium distribution. In this regard, multiple experiments confirm the presence of Li-dense and Li-dilute domains during cycling, supporting the notion that lithium undergoes real fluctuations and diffusion rather than being an imaging artifact or a speckled pattern commonly observed in optical microscopy.

Nanoscale fluctuation of lithium distribution during charge and discharge

To highlight the dynamic distribution of subtle Li-dilute and -dense regions, we mapped the concentration deviation (∆x) from the average concentration (<x>) at each pixel, defined as ∆x = x − <x >. Li-dense (∆x > 0.005) pixels are shown in orange, and Li-dilute (∆x < −0.005) pixels are shown in purple within individual particles. These nanoscopic regions collectively occupied more than 50% of the particle area during cycling (Fig. 3a, b). This observation was consistent across all eight measured particles, suggesting that these regions were recurring features during the battery cycle.

Fig. 3: Evolution of Li-dilute and Li-dense nano-regions during operation at various C-rates: comparison of experimental observations and finite element analysis (FEA) considering only concentration gradient-driven diffusion.
figure 3

a Evolution of Li-dilute and Li-dense regions during 0.1 C cycling. b Li-dilute and Li-dense regions evolution during discharge at 0.1 C and 3 C. The red dashed line indicates the position and direction of the linecut. c Evolution of Li-dilute and Li-dense regions driven solely by concentration gradient diffusion during discharge at 0.1 C and 3 C, simulated by FEA. The single particle size in FEA is 1100 nm in diameter. d Evolution of Li-dilute and Li-dense regions during discharge at 0.1 C in the presence of local structural stationary imperfections, simulated by FEA. Regions of low diffusivity, which may form due to stationary imperfections, are indicated in yellow, while regions of high diffusivity are shown in blue. The positions of these regions are assumed to remain constant. Linecut analyses for the 0.1 C condition in Fig. 3b, c, d are shown in (e), (f), and (g), respectively. The thickness in blue includes the error range of the lithium quantification process. The thickness in blue includes the error range of the lithium quantification process. The inset in Fig. 3e represents the linecut of pristine particles expected to have a uniform lithium concentration of <x> = 1. Source data are provided as a Source Data file.

Full size image

Considering the sufficiently slow C-rate and fast chemical diffusivity36, it can be inferred that lithium transport in scNMC is in the surface reaction limit regime during the 0.1 C cycle, resulting in a near-uniform lithium distribution (Fig. 3a)7. However, subtle Li-dilute and Li-dense regions cannot be adequately explained by the concentration-gradient-driven diffusion model, which considers lithium concentration only as the chemical potential factor and treats the concentration gradient as the sole driving force for diffusion. To support our argument, we demonstrated how conventional intraparticle lithium diffusion results in the spatial-temporal evolution of lithium transport when local diffusivities vary due to either stationary or dynamic structural imperfections. We showed that this does not comply with our observed near-uniform, yet fluctuating, lithium evolution at varying C-rates (Fig. 3b, e). Additionally, we observed how lithium distribution evolves during relaxation after cycling, providing clear evidence of intraparticle lithium diffusion.

First, our finite element analysis (FEA), assuming concentration gradient-driven diffusion and uniform surface insertion, did not show fluctuating lithium distribution during cycling, even when considering the anisotropic properties of the material (Supplementary Fig. 23), with ∆x reaching a maximum of 0.0017 and 0.02 at 0.1 C and 3 C, respectively (Figs. 3c, f, and Supplementary Fig. 24). This simulation considers a concentration-dependent diffusion coefficient37 ranging from 10−11 to 10−9 cm2/s, obtained from our galvanostatic intermittent titration technique (GITT) measurement (Supplementary Fig. 3). This discrepancy, combined with our strain measurements, suggests that additional factors beyond concentration gradients influence lithium transport (Supplementary Fig. 25). Although ∆x can vary depending on diffusivity measurements (e.g., 10−12 to 10−10 cm²/s from NMR measurement or 10−9 cm²/s from bulk chemical diffusivity measurement), the difference in lithium concentration between the surface and core remained minor (e.g., ∆x ~ 0.04 from NMR measurement and ∆x ~ 0.0017 from bulk chemical diffusivity measurement), supporting the fact that intraparticle lithium transport is not limited by bulk diffusion but rather more closely dictated by surface reaction in sub-micrometer particles (Supplementary Fig. 26).

Second, our FEA concluded that even with stationary regions of lower and higher diffusivity originating from locally formed stationary structural imperfections, the observed dynamic fluctuations in lithium distribution cannot be explained if diffusion is driven solely by concentration gradients. In scenarios where spatially inhomogeneous lithium diffusivity exists within the particle, global lithium maxima should still be present at the surfaces of particles during lithiation (Supplementary Figs. 27 and 28). In contrast, our experimental results frequently showed global lithium maxima in the middle of particles instead of at the surface regions. Additionally, these maxima and minima relocated during cycling (Fig. 3f), unlike what would be expected if lithium diffusion were impeded by stationary imperfections, as supported by FEA (Fig. 3d, g). Through FEA calculations, we found that in all scenarios where diffusion was driven solely by the concentration gradient, our experimental results could not be explained. This supports the conclusion that additional factors also contribute to the driving force of diffusion (Supplementary Fig. 29).

Third, we further observed lithium redistribution during relaxation by performing in situ STXM after the cycling current was paused (Fig. 4a, and Supplementary Video 2). Line-cut profiles revealed that lithium distribution continued to fluctuate around <x> ~ 0.64, with concentration maxima and minima relocating over time (Fig. 4d). This suggests that stationary imperfections may not be the major contributors to the observed dynamically relocating lithium distribution (Fig. 4f).

Fig. 4: In-situ STXM imaging during the relaxation and its comparison to hypothetical scenarios.
figure 4

a In-situ STXM imaging of lithium-ion diffusion over 4 h in a single particle charged to <x> = 0.64. b Finite element analysis simulation showing lithium distribution over 4 h, assuming diffusion occurs solely due to concentration gradients (hypothetical scenario 1), with the same particle size and initial concentration distribution as the experimental results. The average lithium concentration in the single particle remains constant in each image. c Heterogeneity changes over time obtained from experimental observations and simulations, as well as the heterogeneity of battery particles measured by ex-situ measurements of as-synthesized particles and after 120 h of relaxation. d Schematic illustration of relaxation tracked by in-situ STXM and its line-cut profiles from the particle shown in (a). The thickness in blue includes the error range of the lithium quantification process. e Schematic of the expected lithium concentration distribution changes during the relaxation process in hypothetical scenario 1, assuming diffusion is driven solely by the concentration gradient. f Schematic of the expected lithium concentration distribution changes during the relaxation process in hypothetical scenario 2, assuming an arbitrarily fixed region within the particle has either high or low diffusivity. g Schematic of the expected lithium concentration distribution changes during the relaxation process in hypothetical scenario 3, assuming regions with either high or low diffusivity dynamically change their positions within the particle. All three hypothetical scenarios assume the same initial state. Local variations in diffusivity do not fully explain the observed fluctuating lithium distribution (from Li-dense to Li-dilute or from Li-dilute to Li-dense). Source data are provided as a Source Data file.

Full size image

Lastly, spatially inhomogeneous diffusivity might dynamically change during cycling, as recent reports have discovered that structural imperfections, such as antisite defects38, dislocations39, or lattice distortion40, evolve during operation. Nonetheless, even with dynamic changes in local diffusivity, the persistent relocation and fluctuation of Li-dense and Li-dilute regions observed in our experiments cannot be explained. If local diffusivity changed randomly across the particles, Li-dense and Li-dilute regions would homogenize at varying rates governed by their local diffusivities (Fig. 4g). However, we clearly observed that these initially formed regions continuously relocated and often reversed their local concentration gradients during relaxation. For example, Fig. 4d shows that a locally Li-dense region can become Li-dilute and vice versa, indicating fluctuating lithium movement proceeding against the concentration gradient direction.

Moreover, intraparticle heterogeneity of ~0.02 was still observed after 4 h of relaxation (Fig. 4c). In the case of conventional concentration-gradient-driven diffusion, our FEA simulations indicated that the heterogeneous lithium distribution at <x> ~ 0.64 (Fig. 4b, e) should have homogenized within 20 min. This observation suggests nonclassical transport behavior that departs from Fick’s 2nd law, which predicts the homogenization timescale of inhomogeneously distributed lithium. The persistent fluctuating distribution during cycling and relaxation also suggests that lithium transport should not be explained solely by concentration gradients but rather by chemical potential gradients, such as lattice strain or stress41. In fact, this fluctuating lithium distribution likely induces strain fields as Li-dense and Li-dilute regions thermodynamically shrink and expand inter-atomic distances between neighboring oxygens along the c-axis (perpendicular to the <003> diffusion direction). However, our STXM technique is not sensitive to local strain fields, necessitating alternative characterization methods.

To investigate the presence of nanoscopic strain fields that may be associated with fluctuating lithium distribution within a single crystalline particle, we employed synchrotron-based Bragg coherent diffraction imaging (BCDI) on cycled (120 h of relaxation) and pristine particles (Fig. 5a, b). BCDI provides three-dimensional displacement fields, which can be converted into strain fields at a nanoscopic resolution (~10 nm) by applying a phase retrieval algorithm (Supplementary Fig. 30)42,43. The residual strain along the (003) crystallographic axis of scNMC in the 120 h relaxed particles after electrochemical cycle shows nonuniformly strained volumes with strain variations of ~0.1–0.4% along the (003) plane, notably greater than the maximum strain of ~0.02% observed in the as-synthesized pristine particle (Fig. 5b). These strain field magnitudes are comparable to those previously reported in related layered oxide systems using in situ and operando BCDI techniques44,45,46. While strain fields have been observed in polycrystalline NMC81145, LiCoO246, and Li-rich layered oxides44, our single-crystalline system provides a distinct advantage by eliminating grain boundary effects, allowing us to observe isolated intrinsic strain within the H1-H2 solid-solution phase evolution regime.

Fig. 5: Persistent nanoscopic non-uniform strain and fluctuating lithium distribution within a single particle.
figure 5

The Bragg coherent diffraction imaging was used to obtain the 3D strain map in the (003) direction for both the as-synthesized particle (a) and discharged particles after cycling (b). On the right-hand side of each 3D map is a slice along the (003) direction, with the black dashed lines indicating the direction of the line cut. c The change in the c-axis of scNMC during discharge, analyzed through in-situ XRD. The c-axis of the as-synthesized state was analyzed through ex-situ XRD. The inset of the figure shows an enlarged plot of the lithium concentration in the range of 0.92 to 0.96. Lithium concentration maps and line cut profiles of (d) the as-synthesized particle and (e) after-cycled (<x> = 0.95) particle. Source data are provided as a Source Data file.

Full size image

The magnitudes of strain in cycled particles align with our in situ XRD results, which show c-axis expansion during delithiation (charging) in scNMC (Fig. 5c, Supplementary Figs. 31, 32). Specifically, ∆x of ~0.02 in the discharged particle at <x> = 0.95 corresponds to a c-axis length change from ~14.25 Å to ~14.27 Å, representing a strain of ~0.15%, consistent with our BCDI results. The observed strain magnitude aligns with our FEA results, which suggest that a strain of 0.4% could theoretically lead to a concentration deviation of ∆x ~ 0.02 while maintaining uniform chemical potential (Supplementary Fig. 33). This concentration deviation is comparable to the maximum lithium concentration deviation (∆x ~ 0.02) observed in ex situ STXM of the cycled particle. The lithium concentration image and line cut profiles provide further insights into this relationship: pristine particles show highly uniform lithium distribution (∆x ~ 0.0005) (Fig. 5d), corresponding well with the minimal strain observed in BCDI measurements of pristine particles, while cycled particles at <x> = 0.95 exhibit measurable heterogeneity (Fig. 5e). Our DFT calculation also found that local strain has limited effect on shift in Ni oxidation state unless local lithium concentration shifts accordingly (Supplementary Fig. 34). Such a good agreement supports that fluctuating lithium concentration indicates intraparticle strain fields within scNMC.

In alignment with our effort to uncover the origin of strain fields, we examined how defects, such as dynamic Li-Ni cation mixing, influence strain development and Li distribution. First, we investigated whether such defects could additionally contribute to lithium distribution heterogeneity and local variations in the Ni oxidation state. For instance, atomic-scale Li-Ni mixing under dynamic conditions can modulate the local oxidation state of Ni47,48. Our DFT calculations show that Li-Ni mixing induces only a ~0.02 change in Ni oxidation state (Supplementary Fig. 35), significantly smaller than the ~0.1–0.2 fluctuations observed during in-situ STXM measurements. This suggests that cation disorder alone cannot fully account for the observed variations. Second, Li-Ni cation mixing may generate local strain fields, thereby indirectly influencing lithium distribution49. Such mixing is energetically more favorable when Ni is in the Ni²⁺ state, due to the similar ionic radii of Ni²⁺ (0.69 Å) and Li⁺ (0.76 Å), and becomes less favorable as Ni oxidizes to Ni³⁺ (0.56 Å). Our DFT calculations (Supplementary Fig. 36) further confirm that cation disorder is energetically suppressed at higher Ni oxidation states. Consistent with this, our operando STXM observations (Supplementary Fig. 37) show that dynamic lithium heterogeneity is governed by local SoC, which controls the extent of Li-Ni mixing, rather than by cycling rate (0.1 C to 3 C). In addition, lithium heterogeneity diminishes near 0.5 SoC (corresponding to Ni³⁺), consistent with reduced Li-Ni mixing. It supports the idea that reduced strain, resulting from decreased Li-Ni disorder, may contribute to the more uniform lithium distribution observed at intermediate states. Overall, while the full origin of the dynamic strain fields requires further investigation, dynamic Li-Ni mixing emerges as a plausible contributing factor that aligns with our observation.

The role of Li-dilute/-dense regions near the insertion surface

Dynamically formed Li-dilute and -dense regions near insertion surfaces influence lithium (de)insertion kinetics and significantly influence the battery rate capability. During relaxation, the heterogeneity of lithium distribution at the surface (insertion boundary) decreased, correlating with leading to an increase in the surface charge-transfer resistance (Rct) as measured by in-situ galvanostatic electrochemical impedance spectroscopy (GEIS). The coverage of these regions in individual particles was monitored via in-situ STXM during relaxation, immediately after full discharge (Fig. 6a). The surface lithium concentration is expected to control the surface charge-transfer resistance, with Li-dilute surface regions providing paths of lower resistance for charge transfer. These regions become critical for efficient battery kinetics near the end of discharge. Before relaxation, Li-dilute regions near the surface (surface pixels at the particle insertion boundary) covered ~33% of the boundary at an average lithium concentration of <x> ~ 0.94 (Fig. 6b). Over a 4-h relaxation process, their coverage reduced to <18%. This reduction in Li-dilute regions coincided with a significant increase in Rct during a 12-h relaxation period at <x> = ~0.95, demonstrating the relationship between surface heterogeneity and charge transfer kinetics at constant average lithium concentration (Fig. 6c, Supplementary Fig. 38, and Supplementary Table 2).

Fig. 6: Coverage of Li-dense and -dilute regions near the surface influences the overall lithium insertion impedance.
figure 6

a Histogram of lithium concentration distribution on the surfaces of all measured particles, comparing 0-hour and 4-h relaxation periods. b A representative particle during relaxation at <x> = 0.95 after complete discharge. The pixel nearest to the surface is referred to as the surface pixel, and only these pixels are shown. Below each image, the surface coverage of Li-dilute (purple) and Li-dense (orange) pixels is indicated. c Evolution of charge-transfer resistance during discharge and subsequent relaxation processes. The inset schematic shows the electrical circuit used for in-situ GEIS fitting. d Overpotential derived from the bulk electrochemical curve of a 5 C charge after various relaxation times in the fully discharged state. e Schematics illustrating the expected changes in overall resistance with relaxation due to redistributions in the surface lithium concentration. Source data are provided as a Source Data file.

Full size image

We further tested the rate capability of our scNCM in coin-cell geometry to better represent average behavior. In-situ potentiostatic electrochemical impedance spectroscopy (PEIS) indicated a notable increase in Rct on approaching the completion of discharge (Fig. 6c and Supplementary Fig. 39)50,51. This increase in Rct corresponded to a decrease in the exchange current density (or an increase in overpotential) in Butler-Volmer kinetics, which became very pronounced as the average lithium fraction <x> in the scNMC approached ~1 (Supplementary Figs. 40 and 41). On extending the relaxation period of the post-discharged electrode from 0 to 12 h, a significantly high overpotential (>400 mV) was observed during subsequent charging at 5 C due to the reduction of Li-dilute surface regions during relaxation (Fig. 6d). Several other commercialized layered oxides, such as polycrystalline NMC111 and Ni-rich NMC, exhibit a similar overpotential increment after relaxation (Supplementary Fig. 42). Subsequently, the surface coverage of Li-dilute regions was confirmed to decrease during relaxation after charging, consistent with the reduction in rate capability with the relaxation time on discharging (Supplementary Fig. 43) with the relaxation time. Figure 6e illustrates the analogy of a parallel resistor circuit; in this system, a wide Rct distribution at the surface decreases the overall Rct more effectively than a narrow Rct distribution. Therefore, abundant Li-dilute regions (low Rct) on the surface can facilitate lithium transport in scNMC.

Discussion

In this study, our operando STXM successfully revealed near-uniform yet fluctuating nanoscale lithium transport in scNMC during both cycling and relaxation, owing to its high chemical sensitivity. Across a wide range of C-rates (0.1 C to 3 C), consistent battery performance and near-uniform lithium transport indicate that lithium diffusion at the sub-particle scale sufficiently fast in surface-reaction-limited regime. Correlative three-dimensional strain imaging further shows that lithium distribution fluctuations are associated with internal strain fields, suggesting that local strain contributes to lithium concentration fluctuations although the precise origin of the dynamic strain fields evolving during cycling remains elucidated. Our observations imply that lithium diffusion can proceed against the lithium concentration gradient, and that deviations between the chemical potential gradient and the lithium concentration gradient may partially originate from strain-induced effects during cycling.

Moreover, the fluctuating lithium distribution at the surface was confirmed to control the surface (de)insertion kinetics of lithium and rate capability; a reduction in the population of kinetically fast Li-dilute surface regions increased the surface Rct significantly. This study highlights the significance of regulating the surface coverage of Li-dilute and -dense regions to modulate the overpotential and rate capability of scNMC systems. Our findings provide a foundational understanding of nanoscale lithium transport, offering insights for the development of materials that utilize solid-state ion transport, such as batteries, solid-state fuel cells, and memristors.

Methods

Material synthesis

Single-crystalline platelet-shaped NMC particles were synthesized using the molten-salt method with water containing cesium chloride as the solvent. Stoichiometric amounts of Ni(NO3)2⋅6H2O (Alfa Aesar, >99%), Mn(NO3)2⋅6H2O (Alfa Aesar, >99%), and Co(NO3)2⋅6H2O (Alfa Aesar, >99%) were dissolved in 25 mL of distilled water containing 0.01 mol of CsCl (Alfa Aesar, 99.9%) flux. The mixture was then thoroughly mixed with excess Li precursor (5 mol%) and LiNO3 (Alfa Aesar, 99%). Excess Li precursor was used to compensate for the Li loss that typically occurs on high-temperature heating. The mixture was then heated at 120 °C for 4 h followed by heating at 850 °C for 16 h at a ramp rate of 3 °C/min in ambient air. The final product was collected via filtration and washed with distilled water.

General characterization (SEM, XRD, and TEM)

Samples for scanning electron microscopy (SEM) and transmission electron microscopy (TEM) were prepared in an Ar-filled glovebox. A vacuum-transfer holder was used for transporting samples to the TEM column to avoid air and moisture exposure.

Ex-situ high-resolution XRD patterns of pristine scNMC were obtained from the 9B-HRPD beamline of the Pohang Light Source-II (PLS-II).

Bulk electrochemistry

For bulk-electrochemistry (coin half-cell) analysis, active material, polyvinylidene fluoride, and Super P (TIMCAL) in the ratio of 92.5:4:3.5 wt% were homogeneously dispersed in N-methyl-pyrrolidone (Acros Organics, 99%) using a planetary mixer (Thinky) at 2000 rpm for 15 min. The positive electrode composite was cast on an aluminum current collector (20 µm) with a thickness of 40 µm using a doctor blade and dried for 12 h under dry air conditions (dew point of <−50 °C) at 80 °C. The dried electrode was calendered (Rotech, MP200) with the roll gap set to 60 µm to achieve a final electrode thickness of 40 µm. The electrode was then stored under dry air conditions.

1.0 M LiClO4 in EC/DMC = 50/50 (Enchem) was used as the electrolyte. CR2032-type coin cells were assembled with the positive electrode, Celgard 2320 separator, and Li metal in a dry room (dew point <−50 °C). Li metal (supplier, 30 μm) was used as the counter electrode. Both electrode diameters (positive and negative) were 10 mm, the separator diameter was 14 mm, and the electrolyte volume was 100 μL.

The coin-half cells were cycled at 25 °C using a battery cycler (WBCS3000L, WonATech, Korea) within the voltage range of 3.0–4.3 V vs. Li/Li+. The electrodes underwent electrochemical testing, including formation cycles, rate tests, and GITT, all performed under constant current conditions. The synthesized scNMC exhibited an areal capacity of ~2.15 mAh/cm2, and its rate performance and lithium-ion diffusivity (ranging from 10−11 to 10−9 cm2/s) were comparable to those of commercialized polycrystalline NMC particles (Supplementary Fig. 3).

The diffusivity and rate performances of single-crystalline and polycrystalline NMC were compared by electrochemical methods. A constant current of 0.1 C (0.207 mA/cm2) was used for GITT. The electrochemical cells were charged and discharged for 30 min, and the voltage was monitored with a 90 min rest time. The apparent chemical diffusivity of lithium was calculated using Fick’s law. The diffusion process within the electrode was assumed to obey Fick’s second law of diffusion; after a series of assumptions and simplifications, the following equation was derived for calculating the chemical diffusion coefficient of lithium ions:

$${D}_{L{i}^{+}}=\frac{4}{\pi \tau }{\left(\frac{{m}_{B}{V}_{M}}{{M}_{B}S}\right)}^{2}{\left(\frac{\Delta {E}_{s}}{\Delta {E}_{\tau }}\right)}^{2}$$
(3)

where τ is the constant current pulse time, ΔEs is the change of the steady state voltage, ΔEτ is the total change of cell voltage during a constant current pulse, MB is the molar mass of active material, VM is the molar volume of active material, mB is the mass of the electrode material and S is the electrode area.

A VSP-300 (BioLogic) with a coin half-cell was used for electrochemical impedance spectroscopy (EIS) at 25 °C over a frequency range of 100 mHz to 1 MHz. A voltage amplitude of 10 mV was used for PEIS, while a current amplitude corresponding to a 0.1 C (dis)charge current at the electrode was used for GEIS. In-situ EIS measurements were performed within the voltage range of 3.0–4.3 V vs. Li/Li+. Each in-situ EIS measurement was preceded by a 5-s open-circuit voltage stabilization period.

STXM nanoimaging

Operando, in-situ relaxation and ex-situ STXM were mainly conducted at the 7.0.1.2 Advanced Light Source (ALS) beamline (Supplementary Fig. 44). High-resolution images were raster scanned in 45-nm steps with a dwell time of 2 ms per pixel. The temporal resolution for each frame at a single energy was 5 s for a 1 µm × 1 µm range (i.e., a total of 30 s for six energy frames). Additional ex-situ STXM images were scanned at the 10A1 beamline at the Pohang Light Source (PAL) in 45-nm steps with a dwell time of 2 ms per pixel. The external temperature of the STXM end station, where measurements were conducted, was maintained at approximately 25 °C.

For operando STXM measurement, sample preparation was performed as follows. Single-crystalline particles were dispersed perpendicular to the diffusion direction and loaded onto a microdevice housed in a microfluidic cell (Hummingbird Scientific), containing reference and counter electrodes comprising Li metal and a working electrode comprising a Pt metal film. The electrolyte (1.0 M of LiClO4 in EC/DMC = 50/50, Enchem) at a flow rate of 1 μL/min, maintaining a thickness of ~1 μm, prevented excess exposure during STXM. A container holding the electrolyte was prepared with 30 mL to ensure sufficient electrolyte flow during the experiment. Li metal (Honjo Metal, 30 μm) was used as the counter electrode.

A VSP-300 potentiostat (BioLogic) was used for the electrochemical control of each microdevice during operando STXM. During battery operation, a constant current and voltage were sequentially applied to the microdevice within the voltage range of 3.0–4.3 V vs. Li/Li+. Voltage holds were performed at 4.3 V vs. Li/Li+ for charging and 3.0 V vs. Li/Li+ for discharging until the absolute current value decreased below 0.05 C (0.29 nA). Since the amount deposited on the microdevice electrode through spin coating cannot be controlled, it is difficult to accurately determine the loaded mass. Therefore, the first formation cycle was empirically performed at a very slow constant current (0.25 nA) within the expected capacity range. The current values for the experimental process were determined based on the first cycle discharge capacity.

For in-situ relaxation STXM measurement, sample preparation was performed as follows. Using the microdevice employed in operando STXM, while tracking the charging and discharging processes, the electrochemical reaction was stopped at the state of charge (SoC) of interest. The sample was then separated from the microfluidic cell, rinsed with a sufficient amount of DMC (>50 mL), dried, and reintroduced into the high-vacuum microscope. During this process, the sample was exposed to ambient air for less than 10 min.

Ex-situ sample preparation was conducted in an Ar-filled glove box within a dry room (dew point <−50 °C). Using coin half-cells, electrochemical reactions were performed to charge or discharge to the desired SoC for measurement. After disassembling the coin cells, the electrolyte was thoroughly washed with excess DMC (>50 mL) for a sufficient duration. Following washing, samples were naturally dried within the glove box. The dried electrodes were separated from the Al current collector using a razor blade and then dispersed in 1 mL of DMC. The dispersed solution was drop-cast onto TEM grids (200-mesh copper) and naturally dried. The internal temperature of the glove box was maintained at approximately 25 °C.

Microdevice fabrication

Microdevices were fabricated by a standard photolithography technique. SiNx was grown on Si wafers (with a 4-in. diameter and thickness of 200 μm; purchased from University Wafer) by chemical vapor deposition. Next, photolithography was used to define an X-ray-transparent SiNx window on the rear side of the wafers, while reactive-ion etching (RIE) was used to remove the exposed nitride layers. After the photoresist was removed using acetone, the exposed Si was etched in a KOH bath to create a transparent SiNx window.

Photolithography was used to define working electrodes on the front side of the wafers (onto which 5 nm of Ti and 50 nm of Pt were deposited via metal sputtering). An SiNx passivation layer was grown using plasma-enhanced chemical vapor deposition to prevent the exposed Ti adhesion layer of the Pt current collector from reacting with the electrolyte. The working electrode was defined by another photolithography step and the passivation layer was removed by RIE to expose the Pt current collectors.

The fabricated wafer was diced to manufacture microdevices with a width of 5 mm and length of 6 mm, which were consecutively cleaned in acetone, isopropanol, and deionized water. After drying in a stream of dry Ar, each chip was exposed to O2 plasma treatment.

Multiple scNMC particles were separately dispersed on the current collector to enable the clear imaging of individual particles simultaneously, without any hindrance from other particles. The transmitted X-ray signal was used to quantify the lithium fraction of each 45-nm pixel along the thickness direction. Multiple scNMC particles were separately dispersed on the current collector to enable the clear imaging of individual particles simultaneously without any hindrance from other particles. The transmitted X-ray signal quantifies the lithium fraction of each 45 nm pixel along the thickness.

Finite element analysis

Two types of 2-dimensional models were used to simulate the concentration evolution during the charge and discharge of NMC primary particles. In the first model, lithium diffusion was governed only by the lithium concentration gradient. The diffusivity of lithium was determined by GITT experiments. Uniform insertion/extraction of lithium was considered at the insertion boundary.

In the second model, Li-ion diffusion was governed by the chemical potential gradient. The chemical potential was determined by the sum two components: the energy calculated by a regular solution model using the local lithium concentration and the elastic strain energy3,52. An in-situ XRD experiment was used to calculate the magnitude of volume expansion, while the stiffness coefficients and stress equations were used from the literature53. Overpotential at the insertion boundary was calculated using the Butler–Volmer equation.

Bragg coherent diffraction imaging

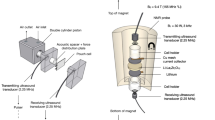
Pristine particles were loaded onto a microdevice for BCDI experiments in the 9C-CXS beamline of the PLS-II with an X-ray energy of 6 keV (λ = 2.0664 Å). The diffraction pattern was measured by a Timepix detector with a pixel size of 55 µm × 55 µm; the detector was placed at a sample-to-detector distance of ~1.07 m at 2θ = ~ 25.2° for measuring the (003) Bragg peak in the out-of-plane orientation. The θ rocking scan was conducted around the (003) Bragg peak within ±0.3° with a step of 0.01°, resulting in a total of 61 frames. Real-space images were reconstructed from coherent diffraction patterns with a phase-retrieval algorithm using error reduction and hybrid input-output algorithms54,55. ParaView was used to visualize the reconstructed results56.

First-principle calculations

All calculations in this work were performed using Density Functional Theory (DFT) with spin polarization, implemented within the Vienna Ab initio Simulation Package 57. The Projector-Augmented Wave (PAW) method was used in conjunction with the Perdew–Burke–Ernzerhof revised PBEsol2 version for the exchange-correlation functional. To account for localized 3d orbital electron-electron interactions, GGA + U parameterization was applied, with Hubbard U parameters of 3.9 eV, 5.0 eV, and 6.0 eV for Mn, Co, and Ni, respectively, as reported previously58. Structural relaxations involved full optimization until the interatomic forces converged to a threshold of less than 0.02 eV/Å, while self-consistent calculations converged to a threshold of less than 10-5 eV. Additionally, a kinetic energy cutoff of 520 eV was applied for the plane-wave basis set, along with Γ-centered k-point meshes with a density of 2000 k-points per reciprocal atom in all calculations. All the structures in this work adopt a layered structure with a space group of R-3m, following the α-NaFeO2 model. The supercell includes 72 atoms (18 Li, 6 Mn, 6 Co, 6 Ni, and 36 O) and 144 atoms (36 Li, 12 Mn, 12 Co, 12 Ni, and 72 O) for the fully lithiated structure, featuring the most favorable transition metal configuration, as previously reported59. Finally, to simulate the delithiated structure, Li vacancy formation energy was calculated for all possible configurations, and the most thermodynamically stable structure was selected at each given Li concentration. The atomic coordinates used in the DFT calculations are provided in Supplementary Data 1.