NMFGOT: a multi-view learning framework for the microbiome and metabolome integrative analysis with optimal transport plan

Abstract

The rapid development of high-throughput sequencing techniques provides an unprecedented opportunity to generate biological insights into microbiome-related diseases. However, the relationships among microbes, metabolites and human microenvironment are extremely complex, making data analysis challenging. Here, we present NMFGOT, which is a versatile toolkit for the integrative analysis of microbiome and metabolome data from the same samples. NMFGOT is an unsupervised learning framework based on nonnegative matrix factorization with graph regularized optimal transport, where it utilizes the optimal transport plan to measure the probability distance between microbiome samples, which better dealt with the nonlinear high-order interactions among microbial taxa and metabolites. Moreover, it also includes a spatial regularization term to preserve the spatial consistency of samples in the embedding space across different data modalities. We implemented NMFGOT in several multi-omics microbiome datasets from multiple cohorts. The experimental results showed that NMFGOT consistently performed well compared with several recently published multi-omics integrating methods. Moreover, NMFGOT also facilitates downstream biological analysis, including pathway enrichment analysis and disease-specific metabolite-microbe association analysis. Using NMFGOT, we identified the significantly and stable metabolite-microbe associations in GC and ESRD diseases, which improves our understanding for the mechanisms of human complex diseases.

Introduction

With the rapid evolution of multi-omics microbiome technologies, it becomes easy to collect heterogeneous data to explore biological questions and generate biological hypothesis. 16S ribosomal RNA gene amplicon and whole metagenomic shotgun sequencing (WMGS)¹ are used to detect the taxonomic composition. Simultaneously, high-throughput untargeted and targeted technologies can also be used to estimate the abundance of metabolites in the same sample². The paired metagenomic and metabolomic profiles from the same samples provide an unprecedented opportunity to explore biological mechanisms and cross-omics feature links in microbiome-related diseases.

Increasing evidences have shown that the microbial community in the human body widely involves in metabolic activities and plays an important role in host health and diseases^3,4,5. The microbial metabolic activities break down some indigestible carbohydrates and synthesize vitamins that are beneficial to host⁶. The bacterial metabolites promote gut homeostasis, and may also lead to gastrointestinal and systemic diseases⁷. However, findings from a single data view or modality usually ignore the complementary and compatible information from other views. For example, host genes and gut microbiota would act in a coordinated way when they are involved in common biological functions⁸. The metabolites generated in some bacterial taxa from the cockroach gut have antagonistic activity against certain pathogens⁹. These studies provided important evidences of metabolite-microbe interactions, but a knowledge gap still largely remains for entirety character the landscape of metabolite-microbe associations. This gap stems from the incompleteness of data, the limited characterization of bacterial genes, the metabolic “dark matter” (yet uncharacterized metabolites) and so on. Hence, there is an essential need for computational approaches and tools that can effectively integrate microbiome and metabolome data to comprehensively identify the underlying associations and patterns in the data.

Recently, a few multivariate integration methods have been developed to analyze multi-omics data obtained from the same sample^4,10, including SNF¹¹, DIABLO¹², and MVCPM¹³, but these methods were not initially designed for microbiome-metabolome joint analysis. The integration methods for paired metagenomic and metabolomic profiles mainly contain CCA-based framework and its variants: SCCA^14,15 and DCCAE¹⁶. SCCA and DCCAE assume that the projections of two sets of observations are lineally correlated and try to establish confident microbe-metabolite associations. DCCAE introduced two autoencoders and minimized the combination of CCA objective and the reconstruction error of the autoencoders. SNF and MVCPM are graph-based multi-omics integration methods, and assume that there exists a consensus sample similarity network obtained by iteratively fusing operation. However, these assumptions may not be realistic, because the interplay between bacteria, metabolites, and other factors in the complex ecosystem, renders it difficult to character the landscape of metabolite-microbe interactions with linear mapping.

In this work, we propose NMFGOT for the integrative analysis of multi-omics data, where microbiome and metabolome data are parallelly profiled from the same sample. NMFGOT is a versatile toolkit that enables clustering of the samples and facilitates downstream biological analysis, including pathway enrichment analysis and metabolite-microbe association analysis. NMFGOT is a novel unsupervised learning framework based on nonnegative matrix factorization with graph regularized optimal transport. Unlike CCA-based methods^12,14,16,17 which assume linear projection of two sets of observations, NMFGOT uses the optimal transport plan to measure the probability distance between microbiome samples, which better deals with the nonlinear high-order interactions between microbial taxa and metabolites. NMFGOT not only integrates the complementary information from different data modalities, but also includes a spatial regularization term to preserve the spatial consistency of samples in the embedding space. Through analyzing on three microbiome-related multi-omics datasets from different tissues (including gastric and gut) and diseases (including gastric cancer, end-stage renal disease, and inflammatory bowel disease), we show that NMFGOT is effective in distinguishing sample types: NMFGOT achieves superior performance in clustering and visualization. The factors for metabolome obtained in NMFGOT provide rich biological significances: they are enriched for disease-specific biological pathways, which are directly related to disease development. NMFGOT also includes a model that infers disease-specific metabolite-microbe associations, which is based on lasso penalized regression model¹⁸ and stability selection approach¹⁹. An overview of NMFGOT is shown in Fig. 1.

Fig. 1: An illustration of NMFGOT.

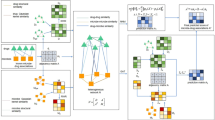
NMFGOT is designed for joint analysis of microbiome and metabolome data obtained from the same sample. a The microbial abundance and metabolite abundance profile matrices ${X}^{\left(1\right)}$ and ${X}^{\left(2\right)}$ are the inputs of NMFGOT (row represents microbial taxa or metabolite, and column represents sample). b By iteration fusion, NMFGOT learns the microbe loading matrix ${W}^{\left(1\right)}$, the metabolite loading matrix ${W}^{\left(2\right)}$, the clustering indicator matrices ${H}^{\left(1\right)}$ and ${H}^{\left(2\right)}$, and the sample-sample similarity matrix $S$. c The enrichment analysis provides biological insights of the top metabolites identified in the matrix ${W}^{\left(2\right)}$. d Lasso penalized regression and stability selection are performed to identify significant and stable metabolite-microbe pairs, which provide an avenue to understand complicated disease mechanisms. e The sample-sample similarity matrix $S$ facilitates visualization and data clustering.

Results

NMFGOT achieves good clustering performance on multiple disease-specific microbiome-metabolome datasets

We evaluated the performance of NMFGOT on three microbiome-metabolome datasets: Gastric cancer (GC) dataset, End-stage renal disease (ESRD) dataset and Inflammatory bowel disease (IBD) dataset, where microbial and metabolite abundance are simultaneously profiled for the same samples.

We compared NMFGOT with several baselines and state-of-the-art methods for microbiome-metabolome data integration, including SCCA¹⁴, SNF²⁰, MVCPM²¹ and a deep learning algorithm DCCAE¹⁶. For SCCA, we utilized grid search to determine the optimal regularization parameters and implemented k-means clustering on the canonical variables for microbiome and metabolome data. For SNF, we evaluated its performance with its default parameters and clustering method. For MVCPM, k-means was implemented on the low-dimensional representations of samples. DCCAE consists of two autoencoders and minimizes the combination of canonical correlation objective and the reconstruction error of the autoencoders. We implemented DCCAE with the defaulted parameters and used k-means on the low-dimensional representations of samples. For NMFGOT, the k-nearest neighbor (KNN) graph with k = 20 was first established, then Louvain clustering was implemented on the k-nearest neighbor graph to obtain the final clustering assignment.

The clustering performance assessed by AC, ARI and silhouette score are presented in Fig. 2. As shown in Fig. 2, our proposed NMFGOT algorithm achieves the best performance among all the methods on the three datasets in terms of AC and ARI. For the average silhouette coefficient criterion, SCCA also performs well in IBD data. The numeric values of the clustering performance metrics are presented in Supplementary Table 1.

Fig. 2: Assessment of clustering performance.

a Evaluation of the clustering performance in terms of AC. b Evaluation of the clustering performance in terms of the average silhouette score. Silhouette score measures the clustering quality by comparing the distances between each sample and its assigned cluster and its neighboring cluster. Finally, the average silhouette score was presented above. c Evaluation of the clustering performance in terms of ARI.

To further validate the effectiveness and efficiency of NMFGOT, we also conducted comparison experiments with a simplified variant of model (5): in NMFGL, we replace Laplacian graph L_opt with traditional graph (based on similarity computation, such as Gaussian kernel function). The performance of NMFGL was not as good as model (5), which suggests that it is beneficial to model microbial data using optimal transport distance (Supplementary Table 2). Ablation studies were also implemented to investigate the roles of the spatial regularization technique and optimal transport, where we set β and γ equal to 0 in turn. The experimental results show that NMFGOT performs well in most cases. More details were presented in Supplementary Table 3.

NMFGOT facilitates data visualization

We next implement UMAP visualization²² to further evaluate their performance. For SNF and NMFGOT, the learned sample similarity matrix S were used as input of UMAP. For other methods, the low-dimensional representation matrices were used to perform UMAP. The results are presented in Fig. 3. As Fig. 3 has shown, NMFGOT identified more clear cluster structure on GC (Fig. 3a) and ESRD data (Fig. 3b).

Fig. 3: Comparison of the visualization results.

SCCA, SNF, MVCPM, DCCAE and NMFGOT are compared by implementing UMAP on two multi-omics datasets (microbiome + metabolome). a GC data. b IBD data. Samples are colored based on the true labels provided in their original publications.

Interesting, on GC datasets NMFGOT identifies what appears to be a transitional state from gastrectomy to healthy patients (left bottom of Fig. 3a). The similar situation can be also found in IBD (Fig. 3b, sample nodes in box; Supplementary Fig. 1).

NMFGOT identifies host pathways associated with disease-specific metabolites on different datasets

The factors obtained from NMFGOT provide rich biological insights, and are easy to interpret. Specifically, for metabolite profile data, we selected the top 50 metabolites with large magnitudes in each column of the metabolite loading matrix ${W}^{\left(2\right)}$, and implemented pathway enrichment analysis by using MetaboAnalyst²³. The enriched metabolite sets for metabolome data agree with the biological function of the underlying sample types that the factors represent (Supplementary Table 4). In GC data, factor 2 corresponds to GC type, which is inferred by inspecting the sample type label of the samples with large values in ${H}^{\left(2\right)}$. The second column in the metabolite loading matrix ${W}^{\left(2\right)}$ is enriched for “valine, leucine and isoleucine biosynthesis” (log10(q-value) = −14.80), “Glutathione metabolism” (log10(q-value) = −7.70), and “Phenylalanine, tyrosine and tryptophan biosynthesis” (log10(q-value) = −5.67). The enriched pathways are consistent with the previous studies^24,25,26. In ESRD data, factor 1 corresponds ESRD sample type. The first column in the metabolite loading matrix ${W}^{\left(2\right)}$ is enriched for “Pyruvate metabolism” (log10(q-value) = −6.68), “Glycolysis / Gluconeogenesis” (log10(q-value) = −6.68), These results are also consistent with the previous studies^27,28 (: Supplementary Table 4).

We further validated the metabolite markers by retrieving related literatures from PubMed. The results were presented in Supplementary Table 5-6. Most of enriched metabolites included in these pathways were found to be related to GC and ESRD.

Fig. 4 shows the top enriched metabolite sets in each of these two diseases.

Fig. 4: Enrichment analysis for GC dataset and ESRD dataset.

Enrichment analysis for GC data (a) and End-stage renal disease ESRD data (b). The enriched metabolite sets are sorted by p-value (FDR < 0.5).

To summarize, NMFGOT facilitates the identification of host pathways associated with disease-specific metabolites. The enrichment analyses for the metabolite loading matrix obtained from NMFGOT provide rich and consistent biological insights on the identified sample types.

NMFGOT identifies disease-specific metabolite-microbe association

Microbial taxa and metabolites involved in common biological functions may act in a coordinated manner. Based on this hypothesis, we used the factors obtained from NMFGOT to character molecular-level associations between microbiome and metabolome in each of these three diseases. More specifically, by inspecting the sample labels with large values in ${H}^{\left(i\right)}$, sample types can be assigned to the factors in NMFGOT. We selected top 100 microbial taxa for microbial abundance data and top 50 metabolites for metabolite abundance data, and then computed the spearman correlation coefficients between microbial taxa and metabolites. Fig. 5a represents the overall pattern of correlation between microbial taxa and metabolites identified by NMFGOT in GC, ESRD and IBD (p-value < 0.05).

Fig. 5: Associations between specific microbes and individual metabolites in each disease.

a Heatmap showing the overall pattern of correlation between top microbial taxa (rows) and metabolites (columns) in factors identified by NMFGOT for GC, ESRD and IBD (p-value < 0.05). b Correlation network for significantly and stability-selected metabolites and microbial taxa in GC and ESRD. The red nodes represent metabolites, the blue nodes represent microbes. Edges represent metabolite-microbe associations. The red line indicates positive correlation, and green line indicates negative correlation.

Inferring disease-specific metabolite-microbe associations may be valuable for understanding the mechanisms of complex diseases and functions of microbes. Next, we further explored associations between metabolites and microbes based on factors obtained from NMFGOT in GC and ERSD. To do so, we firstly used lasso penalized regression model to identify specific microbes whose abundances are associated with the abundance of certain metabolite¹⁸. Specifically, we used the abundances of the microbes as predictors and the abundance of metabolite as response variable to fit the model. Then, stability selection was applied to select robust associations¹⁹. Finally, an intersection between associations identified by the lasso penalized regression model and stability selection above was performed to retain significant and stability-selected metabolite-microbe associations. Using this way, we found 40 and 54 robust metabolite-microbe associations in GC and ESRD, respectively (Fig. 5b). In GC data, these associations consist of 17 microbes and 35metabolites, 33 microbes and 35 metabolites in ESRD data.

Next, we also implemented the additional experiments on holdout dataset to validate the effectiveness and reproducibility of some markers. Specifically, we first split ESRD data into two parts, the one is used to train (50%), the other is used as holdout dataset. Then, on the train data we implemented NMFGOT algorithm and detected the significant and stability-selected metabolite-microbe associations. Meanwhile, we also implemented the same operation on the holdout dataset to identify the significant and stability-selected metabolite-microbe associations. Finally, we compared the results obtained from these two datasets and obtained the shared metabolite-microbe associations. 16 significant and stability-selected metabolite-microbe associations were supported by these two parts of data (Supplementary Table 7).

Taken together, these findings demonstrate the effectiveness of NMFGOT in identifying the latent metabolite-microbe associations.

Discussion

Advances in multi-omics sequencing technologies provide an unprecedented opportunity to explore metabolite-microbe associations and understand the mechanism in human complex diseases. To this end, we proposed NMFGOT, which integrates microbiome and metabolome data from the same samples. CCA based methods used in multi-omics data analysis (including SCCA and DCCAE) typically assume that the projections of two sets of observations are lineally correlated. Unlike these approaches, NMFGOT assumes that there exist complicated nonlinear interactions among microbial taxa, metabolites, and human gut environment, and uses OT plan to encode the complex relationships between samples. We demonstrate through three multi-omics microbiome datasets that NMFGOT consistently performs well when benchmarked with several recently published multi-omics integrating methods. NMFGOT also takes advantage of OT, which characters the probability distance between samples, as well as integrates spatial regularizations to preserve the spatial consistency of samples. Moreover, NMFGOT facilitates downstream biological analysis, including pathway enrichment analysis and disease-specific metabolite-microbe association analysis. With NMFGOT, we identified significantly and stable metabolite-microbe associations in GC and ESRD diseases. The results further show disease-specific microbial taxa can regulate synthesis of host metabolites.

In the whole experiments, we set the number of factors in NMFGOT equal to the number of sample types: $k=2$ in each of the three datasets. Experimental results show that NMFGOT achieves the best performance. we also tested the robustness of each method on the values of k, where we varied the values of k in the range {2,3,4,5,6} on different datasets. However, we found that the clustering performance of these methods evaluated by silhouette score are sensitivities for these three datasets, which is likely because microbiome multi-omics data tends to have high level of noise. For datasets with multiple groups of samples, NMFGOT also performs well in terms of silhouette score. The experimental results are also presented in Supplementary Fig. 2.

We also implemented the side-by-side comparison experiments in which single modality compositional data (microbial abundance data or metabolite abundance data) and multi-omics data are used to test the effectiveness of NMFGOT. The experimental results show that NMFGOT has better performance on AC, ARI, and silhouette score metrics (Supplementary Table 8). We further analyzed a colorectal cancer data, where microbial abundance profile and metabolite abundance data are simultaneously profiled in the same samples⁴. The 70 percent of samples are used to train, and 30 percent of samples are used as validation. The experimental results showed that the samples were reasonably separated by NMFGOT, and it obtained the high average silhouette score of samples (0.9310). The results were presented in Supplementary Fig. 3.

In the future, we will extend NMFGOT to integrate more molecular modalities to capture complementary biological insights into complex mechanisms underlying multi-omics crosstalk¹⁵. In addition, extending NMFGOT to analyze gene expression data may also be another interesting direction: gene abundance can be considered as a modality and using the gene loading and microbe loading matrices in NMFGOT to analyze gene-microbe association.

Methods

Datasets description and data preprocessing

Gastric cancer (GC) data²⁹: This dataset used in this manuscript was downloaded from (https://github.com/borenstein-lab/microbiome-metabolome-curated-data)³⁰. 96 faecal samples from 54 healthy individuals and 42 patients with gastrectomy for gastric cancer were collected. Shotgun metagenomic sequencing and targeted metabolites quantification for the same faecal samples are parallelly profiled.

End-stage renal disease (ESRD) data²⁸: This data downloaded from the literature²⁸ includes 287 samples from 223 haemodialysis patients with ESRD and 69 healthy volunteers. Microbial abundance and metabolite abundance are simultaneously profiled by shotgun metagenomics sequencing and a headspace solid phase microextraction–gas chromatography-MS (GC-MS) method, respectively.

Inflammatory bowel disease (IBD) data³: The dataset were taken from a published study of patients with IBD. It includes 121 samples with IBD and 34 controls. Microbial abundance and metabolite abundance data are parallelly profiled for the same sample. The statistical information of datasets is presented in Supplementary Table 9.

The original microbial abundance data were normalized such that the total counts of all species in each sample equal to 1. The metabolite abundance data were log-transformed with a pseudo-count of 1. For the microbial abundance data, taxa appear in less than 3 samples were removed. For the metabolite abundance data, metabolites appear in less than 2 samples were removed.

Overview of NMF

Given a nonnegative data matrix $X\in {R}_{+}^{p\times n}$, NMF factorizes $X$ into two low-rank matrices $W\in {R}_{+}^{p\times k}$ and $H\in {R}_{+}^{k\times n}$, where p is the number of features, n is the number of observations and $k\ll \min (p,n)$ is the number of factors³¹. The objective function of NMF is written as follows.

$$\mathop{\min }\limits_{W,H\ge 0}{{\|}X-{WH}{\|}}_{F}^{2},$$

(1)

where $W$ is basis matrix, $H$ is coefficient matrix and can be used as clustering indicator. ${{||}\cdot {||}}_{F}$ indicates the Frobenius norm of a matrix.

Optimal transport - Earth mover’s distance

Optimal transport plan has been successfully applied to some fields, including cell-cell communication^32,33, domain adaptation^34,35 and single-cell multi-omics data integration³⁶. Given a cost matrix $M\in {R}^{d\times d}$, probability vectors $r$ and $c$ belong to the simplex ${\sum }_{d}:= \left\{x\in {R}_{+}^{d}:{x}^{T}{{\boldsymbol{1}}}_{d}=1\right\}$, where ${{\boldsymbol{1}}}_{d}$ is the $d$ dimensional vector with all its elements to be 1 s, the optimal transport plan aims to find a transport matrix $P$ that maps $r$ to $c$. The optimal transport problem can be defined as follows³⁷.

$$\mathop{\min }\limits_{P}\left\langle P,M\right\rangle ,\,{\rm{s}}.{\rm{t}}.P\in U\left(r,c\right),$$

(2)

Here, $\left\langle \cdot ,\,\cdot \right\rangle$ is Frobenius dot-product, $U(r,c)$ denotes the transport polytope for $r$ and $c$. $U(r,c)$ can be defined as the follows.

$$U\left(r,c\right)\,{\rm{:= }}\left\{P\in {R}_{+}^{d\times d}{|}P{{\bf{1}}}_{d}=r,{P}^{T}{{\bf{1}}}_{d}=c\right\}.$$

(3)

The optimal transport distance between $r$ and $c$ is defined as follows.

$${d}_{M}\left(r,c\right)=\mathop{\min }\limits_{P\in U\left(r,c\right)}\left\langle P,M\right\rangle .$$

(4)

In this paper, ${d}_{M}\left(r,c\right)$ is used to compute the probability distance between samples from different conditions.

Multi-view learning with graph regularized optimal transport plan

To dissect heterogeneity of samples from both microbiome abundance and metabolite abundance layers, we introduce an unsupervised learning framework, named nonnegative matrix factorization with graph regularized optimal transport (NMFGOT). Considering a multi-view dataset which consists of microbial abundance profile matrix ${X}^{\left(1\right)}\in {R}_{+}^{l\times n}$(l microbial species in n samples) and metabolite profile matrix ${X}^{\left(2\right)}\in {R}_{+}^{m\times n}$(m metabolites in n samples), the objective function of NMFGOT is defined as follows:

$$\begin{array}{l}\mathop{\min }\limits_{{{W}^{\left(i\right)},H}^{\left(i\right)},S}J=\mathop{\sum }\limits_{i=1}^{2}{\left\|{X}^{\left(i\right)}-{W}^{\left(i\right)}{H}^{(i)}\right\|}_{F}^{2}+\alpha \mathop{\sum }\limits_{i=1}^{2}{\left\|S-{H}^{{\left(i\right)}^{T}}{H}^{\left(i\right)}\right\|}_{F}^{2}\\\qquad\qquad\;\;+\,\beta {tr}({H}^{{\left(i\right)}^{T}}{H}^{\left(i\right)}({1}_{n\times n}-{H}^{{\left(j\right)}^{T}}{H}^{\left(j\right)}))+\varphi {\left\|S{\bf{1}}-{\bf{1}}\right\|}_{F}^{2}\\\qquad\qquad\;\;+\,\gamma \mathop{\sum }\limits_{i=1}^{2}{tr}\left({{H}^{\left(i\right)}L}_{{opt}}^{(i)}{H}^{{\left(i\right)}^{T}}\right)\end{array}$$

(5)

$$s.t.\,{W}^{\left(i\right)},{H}^{\left(i\right)},S,\alpha ,\beta ,\varphi ,\gamma \ge 0.$$

where ${W}^{\left(i\right)}$, ${H}^{(i)}$ indicate the basis matrix and coefficient matrix for the ith data modality, respectively. ${L}_{{opt}}^{(i)}\in {R}^{n\times n}$ is the Laplacian matrix for ith data modality. In this manuscript, we used the optimal transport distance defined in subsection 2.2 to compute ${L}_{{opt}}$, i.e., ${L}_{{opt}}=D-A$, ${D}_{{ii}}=\sum _{j}{A}_{{ij}}$, where D is a diagonal matrix, A is obtained via a Gaussian kernel function based optimal transport distance. In manifold learning, Laplacian graph is usually used to capture the high-order geometrical structure relationships in original data^38,39,40. $S\in {R}_{+}^{n\times n}$ represents the learned sample-sample similarity matrix. ${\boldsymbol{1}}$ is a column vector with all its elements to be 1 s. ${1}_{n\times n}$ represents a matrix of 1 s. $\varphi$ is a parameter that is used to control the strength of the constraint $S{\boldsymbol{1}}-{\boldsymbol{1}}$. $\alpha$ and $\gamma$ are graph regularization parameters. $\beta$ is spatial regularization parameter that is used to control the strength of spatial embeddings consistence, and is set $\beta =0.1$ for all datasets. We will discuss how to select $\alpha$ and $\gamma$ parameters in the following section.

In the objective function of NMFGOT (Eq. 5), the first term, $\mathop{\sum }\nolimits_{i=1}^{2}{{||}{X}^{\left(i\right)}-{W}^{\left(i\right)}{H}^{(i)}{||}}_{F}^{2}$ is the NMF loss function for microbial abundance data and metabolite abundance data. The second term, $\mathop{\sum }\nolimits_{i=1}^{2}{{||S}-{H}^{{\left(i\right)}^{T}}{H}^{\left(i\right)}{||}}_{F}^{2}$, is a consensus graph fusion strategy which aims to learn a sample similarity matrix S. Through iteratively training, generated kernel ${H}^{{\left(i\right)}^{T}}{H}^{\left(i\right)}$ from each data modality was regularized towards a consensus graph S. In the third term of the objective function, ${tr}({H}^{{\left(i\right)}^{T}}{H}^{\left(i\right)}({1}_{n\times n}-{H}^{{\left(j\right)}^{T}}{H}^{\left(j\right)}))$, we adopt a spatial regularization technique to preserve the spatial consistency of samples. For low-dimensional sample representation matrices ${H}^{\left(1\right)}$ and ${H}^{\left(2\right)}$ obtained from microbial abundance and metabolite abundance data, we assume that samples that are spatially distant in the one embedding space, should be also pushed further in the other embedding space. Meanwhile, this strategy also introduces more flexibility and allows for specificity across different molecular modalities. The fourth term, ${||}S{\boldsymbol{1}}-{\boldsymbol{1}}{||}$, encourages each row in S to have summation close to 1.

The first four terms in Eq. 5 can learn the low-dimensional representation matrices ${W}^{\left(i\right)}$ and ${H}^{(i)}$ for multi-omics microbiome data, but they may lose the high-dimensional geometrical structure information in the original data space^38,40. To solve this problem, we add the fifth term $\mathop{\sum }\limits_{i=1}^{2}{tr}({{H}^{(i)}L}_{{opt}}^{(i)}{H}^{{(i)}^{T}})$ in the object of NMFGOT. The Laplacian graph is established based on the optimal transport distance between samples (see subsection 2.3), and it can well capture the intrinsic geometry structure of feature spaces in unsupervised learning environment⁴¹.

The details of constructing Laplacian graph ${L}_{{opt}}$ are presented as follows:

We first used the optimal transport distance described above to construct the Laplacian matrix ${L}_{{opt}}$. Given the optimal transport distance matrix ${D}^{(i)}$ obtained from the ith compositional profile, the sample-sample similarity matrix ${A}^{(i)}$ are defined as follows:

$${A}_{{jl}}^{(i)}=\exp \left(-\frac{{D}_{{jl}}^{(i)}}{\mu {{(\sigma }_{{jl}}^{(i)})}^{2}}\right),$$

(6)

$${\sigma }_{{jl}}^{(i)}=\frac{{E}_{{jl}}+{mean}\left(E\left(j,{N}_{j}\right)\right)+{mean}\left(E\left(k,{N}_{l}\right)\right)}{3}.$$

(7)

where $\mu$ is a parameter that can be empirically set. In this study, we set $\mu =0.5$ for all datasets. ${\sigma }_{{jl}}^{(i)}$ is the bandwidth parameter that can be used to eliminate the scaling problem. ${E}_{{jl}}$ denotes the squared Euclidean distance between sample $j$ and $l$. ${N}_{j}$ is the set of nearest neighbors of the $j{\rm{th}}$ sample where $\left|{N}_{j}\right|=20$. ${mean}(E(j,{N}_{j}))$ denotes the average of the squared Euclidean distances between the $j{\rm{th}}$ sample and its neighbors.

Then, the Laplacian matrix ${L}_{{opt}}$ cab be defined as follows:

$${L}_{{opt}}^{(i)}={D}_{{opt}}^{(i)}-{A}^{\left(i\right)}.$$

(8)

Here, ${D}_{{opt}}^{(i)}$ is a diagonal matrix with entries ${{D}_{{opt}}^{(i)}}_{{jj}}={\sum }_{l=1}^{n}{A}_{{jl}}^{(i)}$.

We note that canonical correlations analysis (CCA) is also used to integrate multi-omics microbiome data⁸. Our proposed NMFGOT framework differs from CCA or its variants (sparse CCA) in the following three aspects. 1) CCA-based methods assume that there exists linear projection of two sets of observations, and maximize correlation between these two data modalities. However, these methods do not consider the complicated nonlinear relationships among microbial species^42,43. In NMFGOT, we used optimal transport distance to measure the relationships between microbial samples, which better dealt with the high-order interactions (more than two species) among microbial taxa or metabolites. 2) NMFGOT includes a spatial regularization term to preserve the spatial consistency of samples in the embedding space across different data modalities, and to some extent it tolerates modality specificity. Obviously, spatial regularization leads to better clustering solutions and interpretability: the elements in ${H}^{\left(1\right)}$ will tend to be consistent with the ones in ${H}^{\left(2\right)}$. 3) NMFGOT utilizes optimal transport Laplacian to encode the geometrical structure relationships of microbial samples in the original data space, and enhances the representation ability of low-dimensional sample factor matrices.

The optimization algorithm for NMFGOT

We used the alternative iteration algorithm to solve the optimization problem of NMFGOT model. The updating rules for ${W}^{\left(1\right)}$, ${W}^{\left(2\right)},$ ${H}^{\left(1\right)}$, ${H}^{\left(2\right)}$ and $S$ can be obtained as follows.

$${W}_{{ij}}^{\left(1\right)}\longleftarrow {W}_{{ij}}^{\left(1\right)}\frac{{\left({X}^{\left(1\right)}{H}^{{\left(1\right)}^{T}}\right)}_{{ij}}}{{\left({W}^{\left(1\right)}{{H}^{\left(1\right)}H}^{{\left(1\right)}^{T}}\right)}_{{ij}}}.$$

(9)

$${W}_{{ij}}^{\left(2\right)}\longleftarrow {W}_{{ij}}^{\left(2\right)}\frac{{\left({X}^{\left(2\right)}{H}^{{\left(2\right)}^{T}}\right)}_{{ij}}}{{\left({W}^{\left(2\right)}{H}^{\left(2\right)}{H}^{{\left(2\right)}^{T}}\right)}_{{ij}}}.$$

(10)

$${H}_{{ij}}^{\left(1\right)}\longleftarrow {H}_{{ij}}^{\left(1\right)}\frac{{\left({W}^{{\left(1\right)}^{T}}{X}^{\left(1\right)}+\alpha {H}^{\left(1\right)}{S}^{T}+\gamma {{H}^{\left(1\right)}A}^{\left(1\right)}+\beta {H}^{\left(1\right)}{H}^{{\left(2\right)}^{T}}{H}^{\left(2\right)}\right)}_{{ij}}}{{\left({W}^{{\left(1\right)}^{T}}{W}^{\left(1\right)}{H}^{\left(1\right)}+\alpha {H}^{\left(1\right)}{H}^{{\left(1\right)}^{T}}{H}^{\left(1\right)}+\gamma {H}^{\left(1\right)}{D}^{\left(1\right)}\right)}_{{ij}}}.$$

(11)

$${H}_{{ij}}^{\left(2\right)}\longleftarrow {H}_{{ij}}^{\left(2\right)}\frac{{\left({W}^{{\left(2\right)}^{T}}{X}^{\left(2\right)}+\alpha {H}^{\left(2\right)}{S}^{T}+\gamma {{H}^{\left(2\right)}A}^{\left(2\right)}+\beta {H}^{\left(2\right)}{H}^{{\left(1\right)}^{T}}{H}^{\left(1\right)}\right)}_{{ij}}}{{\left({W}^{{\left(2\right)}^{T}}{W}^{\left(2\right)}{H}^{\left(2\right)}+\alpha {H}^{\left(2\right)}{H}^{{\left(2\right)}^{T}}{H}^{\left(2\right)}+\gamma {H}^{\left(2\right)}{D}^{\left(2\right)}\right)}_{{ij}}}.$$

(12)

$${S}_{{ij}}\longleftarrow {S}_{{ij}}\frac{{\left(\alpha {\sum }_{l=1}^{2}{H}^{{\left(l\right)}^{T}}{H}^{\left(l\right)}+2\eta {{ee}}^{T}\right)}_{{ij}}}{{2\left(\alpha S+\eta {{ee}}^{T}S\right)}_{{ij}}}.$$

(13)

Selection of parameters α, $\varphi$ and γ

In NMFGOT, there are three parameters α, $\varphi$ and γ that need to be tuned, and they are determined as the following. The optimization problems $\mathop{\min }\limits_{{W}^{\left(1\right)},{H}^{\left(1\right)}\ge 0}{{||}{X}^{\left(1\right)}-{W}^{\left(1\right)}{H}^{{\left(1\right)}^{T}}{||}}_{F}^{2}$, $\mathop{\min }\limits_{{W}^{\left(2\right)},{H}^{\left(2\right)}\ge 0}{{||}{X}^{\left(2\right)}-{W}^{\left(2\right)}{H}^{{\left(2\right)}^{T}}{||}}_{F}^{2}$ were first solved by NNDSVD⁴⁴ and obtain the solutions ${\hat{W}}^{\left(1\right)},\,{\hat{H}}^{\left(1\right)},\,{\hat{W}}^{\left(2\right)}$ and ${\hat{H}}^{\left(2\right)}$. Then, $\hat{S}$ can be obtained using SNF²⁰, and set α, $\varphi$ and γ as follows.

$$\begin{array}{l}\alpha =\left({\left\|{X}^{\left(1\right)}-{\hat{W}}^{\left(1\right)}{\hat{H}}^{{\left(1\right)}^{T}}\right\|}_{F}^{2}+{\left\|{X}^{\left(2\right)}-{\hat{W}}^{\left(2\right)}{\hat{H}}^{{\left(2\right)}^{T}}\right\|}_{F}^{2}\right)/\left(5\mathop{\sum }\limits_{i=1}^{2}{\left\|\hat{S}-{\hat{H}}^{\left(i\right)}{\hat{H}}^{{\left(i\right)}^{T}}\right\|}_{F}^{2}\right)\\ \varphi =\left({\left\|{X}^{\left(1\right)}-{\hat{W}}^{\left(1\right)}{\hat{H}}^{{\left(1\right)}^{T}}\right\|}_{F}^{2}+{\left\|{X}^{\left(2\right)}-{\hat{W}}^{\left(2\right)}{\hat{H}}^{{\left(2\right)}^{T}}\right\|}_{F}^{2}\right)/\left(1000{\left\|\hat{S}{\bf{1}}-{\bf{1}}\right\|}_{F}^{2}\right),{\rm{and}}\\ \gamma =\left({\left\|{X}^{\left(1\right)}-{\hat{W}}^{\left(1\right)}{\hat{H}}^{{\left(1\right)}^{T}}\right\|}_{F}^{2}+{\left\|{X}^{\left(2\right)}-{\hat{W}}^{\left(2\right)}{\hat{H}}^{{\left(2\right)}^{T}}\right\|}_{F}^{2}\right)/\left(100\mathop{\sum }\limits_{i=1}^{2}{tr}\left({\hat{H}}^{{\left(i\right)}^{T}}{L}^{\left(i\right)}{\hat{H}}^{\left(i\right)}\right)\right)\end{array}$$

(14)

The sensitive analyses of $\alpha$ and $\gamma$ are presented in Supplementary Fig. 4.

Evaluation metrics

Accuracy(AC), adjusted rand index (ARI)⁴⁵ and silhouette coefficient⁴⁶ are used to assess the performance of the clustering methods. For unlabeled dataset, we use an unsupervised metric, silhouette coefficient^47,48, to evaluate the clustering performance of each method. High silhouette coefficient score indicates that the sample is close to other samples in the same cluster, and distant from samples in other clusters. The average value of silhouette scores is used as the final evaluation.

The robustness analysis of NMFGOT on the hyperparameters

To test the robustness of NMFGOT on the hyperparameters, we varied α and γ in the range $\left\{{{\rm{\alpha }}}^{* }/10,{{\rm{\alpha }}}^{* }/5,\,{{\rm{\alpha }}}^{* }/2,{{\rm{\alpha }}}^{* },\,2{{\rm{\alpha }}}^{* },5{{\rm{\alpha }}}^{* },\,10{{\rm{\alpha }}}^{* },\,\right\}$ and$\left\{{{\rm{\gamma }}}^{* }/10,{{\rm{\gamma }}}^{* }/5,{{\rm{\gamma }}}^{* }/2,{{\rm{\gamma }}}^{* },\,2{{\rm{\gamma }}}^{* },5{{\rm{\gamma }}}^{* },\,10{{\rm{\gamma }}}^{* }\right\}$, respectively. Here ${{\rm{\alpha }}}^{* }$ and ${{\rm{\gamma }}}^{* }$ are the hyperparameters chosen by the rules described in the main text. The results are presented in Supplementary Fig. 4. For IBD dataset, the silhouette score is relatively stable when the hyperparameters vary. For GC dataset, the AC is stable when the hyperparameters vary.

Extension of NMFGOT to unseen or holdout data

we extended NMFGOT to analyze the unseen or holdout data. Given the unseen or holdout data $\hat{X}$, the transformation objective function can be defined as follows:

$$\mathop{\min }\limits_{{\hat{H}}^{\left(i\right)},\check{S}}J=\mathop{\sum }\limits_{i=1}^{2}{\left\|{\hat{X}}^{\left(i\right)}-{W}^{\left(i\right)}{\hat{H}}^{(i)}\right\|}_{F}^{2}+\alpha \mathop{\sum }\limits_{i=1}^{2}{\left\|\check{S}-{\left[{\hat{H}}^{\left(i\right)}\left\|\right.{H}^{\left(i\right)}\right]}^{T}\left[{\hat{H}}^{\left(i\right)}\left\|\right.{H}^{\left(i\right)}\right]\right\|}_{F}^{2}+\beta {\left\|\check{S}{\bf{1}}-{\bf{1}}\right\|}_{F}^{2},$$

(15)

$$s.t.\,{\widehat{H}}^{(i)},\check{S},\alpha ,\beta \ge 0$$

where ${\widehat{H}}^{(i)}$ represents the low-dimensional representation of unseen data, $\check{S}=\left[\begin{array}{cc}\hat{S} & {A}^{T}\\ A & S\end{array}\right]$ is the fused similarity matrix. $\hat{S}$ is the similarity matrix between the unseen data, and $A$ is the similarity matrix between the unseen data and the training data. We used the consensus graph fusion, $\mathop{\sum }\nolimits_{i=1}^{2}{{||}\check{S}-{[{\widehat{H}}^{\left(i\right)}{||}{H}^{\left(i\right)}]}^{T}[{\widehat{H}}^{\left(i\right)}{||}{H}^{\left(i\right)}]{||}}_{F}^{2}$, to transform the unseen data into the latent space.

We analyzed a colorectal cancer data, where microbial abundance profile and metabolite abundance data are simultaneously profiled in the same samples. The experimental results were presented in Supplementary Fig. 3.

Lasso regression and stability selection approach for metabolite-microbe associations

After obtaining the factors in our NMFGOT model, the lasso penalized regression model was used to identify the association between a metabolite and a set of microbial taxa¹⁸:

$$\mathop{\sum }\limits_{i=1}^{n}{\left({y}_{i}-{\beta }_{0}-\mathop{\sum }\limits_{j=1}^{p}{\beta }_{j}{x}_{{ij}}\right)}^{2}+\lambda \mathop{\sum }\limits_{j=1}^{p}\left|{\beta }_{j}\right|,$$

(16)

where $n$ is the number of samples, $p$ is the number of microbial taxa. $y$ is the response variable (metabolite abundance), $x$ is the predictor (taxa abundance). $\lambda$ is the parameter that controls the sparseness of models.

Due to the sensitive of the lasso model, we also used stability selection approach to choose robust microbial taxa associated with a metabolite^8,19. In this manuscript, we used stability selection with lasso to select stable microbes. The process is demonstrated as follows:

Step 1. Select a random subset of the analyzed data. We used top 100 microbes with large entries in the column of the microbe loading matrix ${W}^{\left(1\right)}$ and top 50 metabolites with large entries in the column of the metabolite loading matrix ${W}^{\left(2\right)}$.

Step 2. Fit the lasso model with $\hat{\lambda }$ that is about the best penalty $\lambda$, and record the set of selected microbes.

Step 3. Repeat steps 1 and 2 t times.

Step 4. Compute the frequency ${f}_{i}$ of each microbe that was selected across all trials.

Step 5. Pick out the microbes with its ${f}_{i}\ge {f}_{{thr}}$. ${f}_{{thr}}$ is a prespecified threshold.

In this manuscript, we set the size of a random subset as $n/2$ data, $t=100$ and ${f}_{{thr}}=0.6$.