Controlling metabolic stability of food microbiome for stable indigenous liquor fermentation

Abstract

Steering microbial metabolic stability in fermentation is a recurrent goal in microbial food production. Indigenous liquor fermentation typically relies on complex microbiome metabolism, making it difficult to steer fermentation towards consistent high-quality products. Here, we conducted a three-step experiment to identify instability factors and explore ways to steer fermentation stability in lab-scale settings. We found that the metabolic stability of the microbiome fluctuates due to fermentation parameters, dynamic benefit allocation between yeasts and Lactobacilli, and metabolic network redundancy. In addition to parameters control, short-term metabolic stability requires stable microbial benefit allocation, whereas long-term stability requires proper functional redundancy. Rationally setting initial parameters and the microbial inoculation ratio is a practical way to optimize metabolic stability for stable indigenous liquor fermentation. Our study provides new insights into microbiome metabolism control and shows the feasibility of enhancing fermentation stability through appropriate initial conditions, enabling more controlled and efficient microbial food production systems.

Introduction

Global demand for microbiome-fermented products (fermented foods, etc.) is rapidly increasing^1,2,3. Stable microbiome metabolic functionality is essential for the sustainable production of consistent high-quality products^4,5. However, ensuring and determining microbiome metabolic stability is often limited by fluctuations in physiochemical parameters⁶, biodiversity⁷, complexity^8,9, and interaction types^10,11 of the microbial ecosystem. The effect of these variables can be tested in tractable food fermentation ecosystems, which enables optimization of the fermentation process to produce consistent high-quality fermented food (e.g., yogurt, bread) and beverages (e.g., beer, kefir)¹².

However, most indigenously fermented foods are currently produced through fermentation processes based on traditional, empirical knowledge. Although these systems generally achieve high organoleptic quality due to extensive experience, their productivity and technical performance can vary considerably, which in turn affects the consistency, quality, and economic viability of the processes¹³. Substantial efforts have been made to find potential key biotic (biodiversity, etc.) and abiotic (physiochemical parameters, etc.) factors, as well as the means to ensure a stable and reproducible fermentation process^{14,15,16,17,18}. Fundamental questions remain regarding which biotic and abiotic factors govern process stability^15,19.

Since the twentieth century, significant advancements have been made in controlling stability in simpler fermentations—such as soy sauce and cheese production—which utilize pure or defined mixed-culture fermentations. Evidence from both industrial and lab-scale applications indicates that regulating parameters such as temperature, pH, moisture, and nutrient supply effectively ensures stability in these less-complex systems^20,21. The principle underlying this approach is the control of microbial growth and metabolism through precise parameter management. As a result, regulating the fermentation stability is already feasible based on suggestions by well-validated mathematical models²². However, regulating abiotic parameters alone often proves insufficient for maintaining stability in complex, solid-state indigenous fermentations. Many of these fermentations take place in sealed containers, allowing control only at the beginning of the process due to limited knowledge in bioreactor design²³. Despite setting abiotic parameters at the start, unexpected fluctuations can still occur throughout the fermentation process^20,24,25. These variations are often attributed to biotic factors, such as differences in initial microbial composition and population size^26,27. Such variations in microbial starting conditions can affect the metabolic stability of the microbiome by influencing community assembly and microbial metabolic interactions^28,29. Yet, strategies for managing initial biotic factors to ensure functional stability of the microbiome remain unclear, posing a challenge to stabilizing complex indigenous fermentation.

A notable example of such high-complexity indigenous fermentations is the cereal-based fermentation used in Chinese liquor (or called baijiu in Chinese) production, which involves simultaneous saccharification and indigenous fermentation mediated by a diverse microbiome of molds, yeasts, and bacteria³⁰. Collecting extensive data on biotic and abiotic factors from baijiu production batches allows for tracking and analyzing how these variables affect the quality and stability of the final product (Supplementary Fig. 1). These industrial data provide a valuable resource for identifying correlations between process factors and fermentation stability, potentially revealing underlying mechanisms.

Therefore, our study’s aim was to gain a better understanding of how abiotic and biotic factors influence fermentation stability, with the goal of achieving more consistent baijiu fermentation. Using an integrated three-step research strategy combining machine learning-based predictive modeling, meta-omics, and culture-based validation (Fig. 1), we addressed three unresolved critical challenges: (1) classifying unstable fermentation batches based on abiotic and biotic influences; (2) determining how these factors contribute to fermentation stability; and (3) enhancing stability by managing these factors at the start of fermentation. Our findings provide valuable insights into the impact of initial conditions on microbiome metabolic heterogeneity, offering potential strategies to improve stability in complex indigenous liquor fermentations.

Fig. 1: Graphic abstract of three-step experimental design.

First, we classified unstable fermentation outcomes caused by initial abiotic factors based on statistic-machine learning combined modeling of 1009 industrial fermentation batches. Second, we revealed the short-term and long-term effects of initial biotic factors on metabolic functional stability based on time-series multi-omics sequencing in two representative fermentation batches. Three regulation principles were summarized to ensure the metabolic stability of the fermentation microbiome. Third, we conducted simulated fermentations with different initial microbial inoculation conditions to validate the feasibility of regulation principles.

Results

Unstable fermentation batches caused by abiotic factors

Figure 2 shows the fluctuating yield (proxied by the concentration of alcohols, w/w) and quality (reflected by the six parameters as indicated in materials and methods) in industrial-scale fermentation. The total concentration (mass fraction) of the six normalized parameters was 80.66 ± 1.021% (w/w) at the start of fermentation and 83.44 ± 1.112% (w/w) at the end of fermentation. The six physiochemical parameters all showed normal distribution at the start of batches. The mean value of moisture was 50.31% (w/w), starch was 23.64% (w/w), acidity was 3.838% (w/w), reducing sugar was 1.789% (w/w), alcohols was 0.923% (w/w), and acetate was 0.159% (w/w). At the end of batches, the starch and reducing sugar turned to lognormal distributions, suggesting the depletion of available carbon sources in some batches (Fig. 2a). The unstable physiochemical parameters at the end of batches showed three peaks by Gauss model-based principal component analysis (Fig. 2b). According to fusion levels of the top two principal components, we classified unstable fermentation outputs into three quality types (high, medium, and low quality) by K-means (Fig. 2c). The alcohol concentration range of high quality was from 2.43 to 3.46%, medium quality was from 2.19 to 2.42% and low quality was from 0.42 to 2.18%. There were 377 batches of high quality, 295 batches of medium quality, and 337 batches of low quality (Dataset 1).

Fig. 2: Fermentation outcomes prediction based on initial parameters.

a Distribution of input and output parameters. b Unstable parameters at the end of 1009 batches clustered by multiple Gaussians model-based principal component analysis. c Unstable batches are classified into three quality types by K-means. The number of both Gauss models and quality types was determined by fusion level. d Accuracy of yield (%, w/w) prediction by nonlinear regression model.

To predict fermentation outputs by initial input parameters, we conducted statistical modeling. We found that 30.5% fermentation batches could be precisely (at 0.1% yield error threshold) predicted based on abiotic parameters at the start of batches (Fig. 2d). The ratio of initial acidity to initial reducing sugar concentration (0.182 ≤ ratio ≤ 0.216), initial moisture (2.539 ≤ ratio ≤ 3.296) and initial starch concentration (0.079 ≤ ratio ≤ 0.085) were three key parameters to regulate fermentation stability. As the prediction accuracy increased, the prediction precision dropped rapidly. The prediction accuracy was 72.6% at 0.3% (w/w) yield error threshold and increased to 96.3% at 0.5% (w/w) yield error threshold. The large uncertain precision of yield (0.3%–0.5%, w/w) suggested that most fluctuating yields cannot be predicted barely based on physiochemical parameters at the start of batches. Nevertheless, the prediction accuracy of fermentation quality types was 77%, which was acceptable.

Representative two unstable fermentation batches caused by biotic factors

During the dynamic baijiu fermentation process, physiochemical parameters changed with fermentation time. We divided the fermentation process into three phases based on the dynamics of physiochemical parameters. Figure 3a shows the three phases during the fermentation process, that is, phase I (0–5 days), phase II (5–21 days), and phase III (21–30 days). Figure 3b shows the dynamics of parameters (normalized by the same sample weight) throughout the fermentations. We found that alcohols were mainly generated in phase I and phase II, whereas acids were mainly generated in phase III. Alcohols rapidly increased from 0.272 ± 0.092% (w/w) to 0.582 ± 0.101% in phase I and increased from 0.582 ± 0.101% (w/w) to 0.700 ± 0.086% in phase II. Acetate (from 0.475 ± 0.064% to 0.613 ± 0.105%, w/w) and acidity (from 0.465 ± 0.067% to 0.579 ± 0.124%, w/w) continuously increased during phase II and phase III. Moisture gently increased during phase I and phase II (from 0.521 ± 0.069% to 0.678 ± 0.071%, w/w), and decreased afterward. Starch showed the opposite changing trend to moisture, it gently decreased during phase I and phase II (from 0.459 ± 0.059% to 0.219 ± 0.072%, w/w). Reducing sugar decreased throughout the fermentation process (Dataset 2). Based on our predictive model, unpredictable batches could be screened by comparing physiochemical parameters in each fermentation phase.

Fig. 3: Three-phase dynamic fermentation process.

a Principal component analysis of parameters showing changes during fermentation. The samples are colored according to the three fermentation phases as determined by parameter clusters. b Dynamics of fermentation parameters (acidity, reducing sugar, moisture, acetate, starch, alcohols) during 1009 industrial fermentation batches. All parameters are normalized by sample weights. c Fermentation parameters difference (double-tailed t-test) between batch A and batch B in each fermentation phase. d The relative abundances of microbial genera in batch A are in stark contrast with those in batch B in fermentation phase I but are similar in fermentation phase II and fermentation phase III. Each point represents a microbial genus. e Microbial genera with significant (one-way ANOVA test) relative abundance differences.

We selected two representative unstable fermentation batches (named batch A and batch B) after a comparison of their parameters. We found all parameters of these two batches were similar in fermentation phase I and II, but partial parameters were significantly different in fermentation phase III (Fig. 3c). Acidity, pH, and lactate showed significant (p < 0.05, tested by one-way ANOVA) difference in phase III. We found batch B had higher acidity, lactate, and lower pH than that of batch A.

Microbial variability emerged earlier than changes in physicochemical parameters. As shown in Fig. 3d, the microbial composition of batches A and B differed significantly in Phase I, but became increasingly similar as fermentation progressed, indicating a convergent succession of the microbial community across phases. In Phase I, the co-correlation coefficient (r²) was 0.38, which increased to 0.74 in Phase II and reached 0.92 in Phase III. Supplementary Fig. 4 illustrates that both batches contained the same 12–13 dominant fungal and bacterial genera (average relative abundance >1%), though with distinct relative abundances and succession patterns. As seen in Fig. 3e, 12 microbial genera were more abundant in batch A than in batch B, including Oceanobacillus, Bacillus, Pseudogracilibacillus, Kroppenstedtia, Lentibacillus, Schizosaccharomyces, Streptomyces, Weissella, Staphylococcus, Microascus, Zygosaccharomyces, and Bradyrhizobium. In contrast, Lactobacillus and Saccharomyces were more abundant in batch B.

Additionally, Supplementary Fig. 5 shows that biotic factors contributed more than abiotic factors to eight quality-related parameters based on random forest modeling. In batch A, biotic factors contributed most significantly to ethanol production (~80% Increase in Mean Squared Error), whereas in batch B, they contributed most to acetic acid (~75% Increase in Mean Squared Error). Abiotic factors had the highest impact on lactate in batch A (~10% Increase in Mean Squared Error) and on moisture in batch B (~10% Increase in Mean Squared Error). These findings confirm that the instability observed in both fermentation batches was primarily due to biotic factors.

Microbial community assembly patterns of two representative batches

Figure 4a shows the scanning electron microscopy images of pooled fermented samples, where hyphae, yeasts, and bacteria are embedded in the grain matrix. We observed that the spatial distribution of microbial cells varied across fermentation phases, with localized areas in the images displaying significant aggregates of either fungi or bacteria. We found that microbial aggregation occurred mostly around yeasts in phase II and bacteria in phase III, showing that different species dominate at different fermentation stages.

Fig. 4: Dynamic traits of microbial assembly.

a Example image of macroscopic fermented grains (top left), and field emission scanning electron microscopy of hyphae (marked with green), yeasts (marked with yellow), bacteria (marked with blue) embedded in the grain matrix at fermentation phase I (top right), phase II (bottom left) and phase III (bottom right). b Community assembly patterns during the fermentation process. c Variance partitioning analysis of the relative contributions of determined (alcohols, acids, etc.) and stochastic variables to variation in microbial community assembly. The solid lines indicate the contribution of the variables. The dashed lines represent the assumed contribution of stochastic variables (1 – determined contributions %).

Figure 4b shows microbial community assembly was governed by a stochastic assembly process during phase I and phase III, whereas the community assembly of phase II was a determined assembly process. Although two representative batches underwent the same three-phase assembly process, i.e., a stochastic-determined-stochastic process, the timepoint of the phase shift was different. Batch B showed an earlier timepoint of phase shift and stronger environment selection than batch A during the fermentation. The assembly shifting of batch A happened in the second period of phase II (10–15 days after the start of fermentation), whereas batch B happened in the first period of phase II (5–10 days after the start of fermentation). The maximum βNTI (β-nearest taxon index) value was about 2.36 ± 1.00 in batch B, whereas the maximum βNTI value was about 1.98 ± 0.11 in batch A.

We assessed the relative contributions of deterministic factors (alcohols, pH, acidity, acids, lactate, and acetate) and stochastic factors to microbial community assembly (Fig. 4c). Although the key deterministic contributors in batches A and B were the same, their impact varied. In batch A, lactate and acetate were the strongest abiotic influences on community assembly, followed by alcohols, pH, and acidity. In batch B, lactate and acetate were also the primary contributors, but were followed by pH, acidity, and then alcohols. The combined influence of these deterministic factors accounted for 30.2% in batch A and 65.4% in batch B, indicating that stochastic factors played a larger role in community assembly in batch A than in batch B.

Collectively, unstable fermentations driven by initial biotic factors showed fluctuations in community assembly and microbial responses to fermentation parameters. The distinct outcomes of two batches with similar abiotic conditions suggest that initial microbial settings play an important role in fermentation instability.

Short-term effect of biotic factors on metabolic functional stability

To get deeper insights into community assembly patterns affecting microbial community functions and metabolic stability, we analyzed the dynamics of metabolism-related gene transcriptions. The metabolic functions of the two batches were mainly involved in functional categories of carbon, nitrogen, and sulfur metabolism. According to the FPKM (Fragments Per Kilobase of transcript per Million mapped reads) value of every functional category, we found that the main community metabolic functions changed with the fermentation phases (Fig. 5a). During phase I, the main community functions were “sulfur metabolism”, “terpenoid and polyketide metabolism”, “glyoxylate and dicarboxylate metabolism”, “lipid metabolism” and “TCA cycle”. During phase II and phase III, the main community functions changed to “carbon metabolism”, “butanoate metabolism”, “propanoate metabolism”, “methane metabolism”, “galactose metabolism”, “nitrogen metabolism” and “amino acid metabolism”. The fluctuating metabolic functions between batch A and batch B were reflected in 14 functional categories as shown in Fig. 5a. Most (12/14) microbial metabolic functional categories of batch B were more active than batch A in phase II and phase III according to FPKM values. According to Pearson’s correlations between βNTI values and FPKM, we found functional categories of “pyruvate metabolism”, “metabolism of xenobiotics” and “glycolysis/gluconeogenesis” were significantly negatively correlated with absolute values of the βNTI (Fig. 5b). Based on structure equation model, we further illustrated the causality between metabolic functional expressions and community assembly patterns (Fig. 5c). We assumed that initial biotic factors caused changes in microbiome metabolism between fermentation batches through community assembly. The results of the data fitting did not significantly deny the model assumptions (p = 0.343). Different community assembly patterns explained 89.3% fluctuation of “glycolysis”, 42.4% fluctuation of “pyruvate metabolism”, and 42.1% fluctuation of “metabolism of xenobiotics” between two unstable fermentation batches.

Fig. 5: Fermentation instability caused by dynamic microbial beneficial distribution.

a Significant (double-tailed t-test) different transcription of 18 major metabolic functional categories. b Significant correlations between metabolic functional categories and community assembly (double-tailed t-test). c The structural equation model indicates significant effects of assembly patterns on three metabolic functional categories. d Dynamic gene expression levels among fermentation phases according to FPKM (Fragments Per Kilobase of transcript per Million fragments) values. e Alternative beneficial distribution between yeasts and lactic acid bacteria (LAB) in three metabolic functional categories. F:B means fungal FPKM values: bacterial FPKM values. f Overall fungal and bacterial metabolic fold change (batch A/batch B) between two batches. The thickness of pathway lines is calculated by Abs ((log₂ fold change) × average FPKM% values). Red lines represent up-regulated pathways, whereas blue lines represent down-regulated genes (Details see Dataset 5).

Figure 5d shows the dynamics of all assembled gene transcriptions within these three function categories in each fermentation phase. There were four clusters of genes in both batch A and batch B according to different expression dynamics, that is, cluster 1 (increased and increased), cluster 2 (increased then decreased), cluster 3 (decreased then stable), and cluster 4 (decreased and decreased). Such dynamic beneficial distribution (metabolic flux) suggested that multiple alternative genes could perform the same metabolic function.

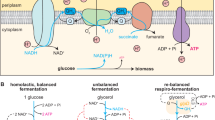
For functional categories of “pyruvate metabolism”, “xenobiotics metabolism” and “glycolysis”, we found lactic acid bacteria (Lactobacilli) occupied more than 99% genes transcription in bacteria, whereas yeasts (Pichia, Candida, Saccharomyces, Schizosaccharomyces, Zygosaccharomyces, and Torulaspora) occupied more than 97% genes transcription in fungi. The black-gray bars showed that yeasts were more active in batch A, whereas lactic acid bacteria were more active in batch B (Fig. 5e). For gene expressions of glycolysis in phase I, the cumulated FPKM value of fungi was 462.1 times bigger than that of bacteria in batch A, whereas the ratio was only 15.85 in batch B. Such gene expression difference was similar in pyruvate and xenobiotics metabolism. In addition, we observed different turnover times for the alternative metabolic interactions between fungi and bacteria in the two batches. In Batch B, the turnover occurred during phase II, whereas in Batch A, it took place in phase III (Fig. 5e). We summarized the differences in transcription of fungi and bacteria, particularly regarding primary metabolic pathways, for both batches (Supplementary Fig. 6). We found that the main consumer of substrate in “Pyruvate metabolism” and “Glycolysis” changed between the two batches. Lactobacillus was the main consumer of substrate in batch B, whereas Zygosaccharomyces was the main consumer of substrate in batch A.

As a result, different metabolic fluxes between fungi (mainly yeasts) and bacteria (mainly lactic acid bacteria) further caused the instability of overall metabolic functions (Fig. 5f and Dataset 3). We found the obvious bacterial overexpression of most genes in batch B, whereas fungal overexpression of most genes in batch A (Fig. 5f). In addition, bacterial gene overexpression focuses on fewer metabolic pathways than fungal gene overexpression. Based on the temporal stability calculated by Eq. (3), we found that the metabolic stability of the microbiome was 2% higher in batch B than in batch A for the 18 main functional categories.

Long-term effect of biotic factors on metabolic functional stability

Figure 6a shows the fluctuations in biodiversity and functional gene abundance during long-term fermentation processes. During long-term fermentation processes, we found the overall microbial functionality became more and more unstable (Fig. 6b). Compared with the functional stability index of Round 1, the index decreased by 1.33% in fermentation Round 2. The decreasing percentage of the functional stability index increased to 9.02% in fermentation Round 3. The ongoing rise in functional instability highlighted the overall differences in functional stability between the two representative batches. In addition, we found the stability of main metabolic functions in batch B was less affected than in batch A. The metabolic functional stability index of batch B was significantly (p < 0.05, Student’s t test) higher than that of batch A (Fig. 6c).

Fig. 6: Fermentation instability caused by fluctuating metabolic robustness.

a Fluctuating functional traits (top), fungal (FD), and bacterial (BD) Shannon diversity (bottom) of two batches during three-round repeated fed-batch fermentation process. b Overall functional stability index among three fermentation rounds. c Metabolic functional stability index of batch A and batch B (*p < 0.05, t-test). d Metabolic network topological properties between batch A and batch B. Robustness linear fitting (one-way ANOVA test) are cut off at 43 removed nodes.

We then compared the topology parameters of metabolic functional networks in batch A and B over the process of the long-term fermentation (Fig. 6d). Batch A showed higher values in nodes, edges, average degree of nodes, and clustering coefficient than batch B, suggesting higher network complexity in batch A. Interestingly, batch B showed better robustness but lower complexity of the metabolic functional network. When removing less than 43 nodes from the metabolic network, we found the resistance of batch A metabolic network was weaker than that of batch B. When removing more than 43 nodes from the metabolic network, batch A and batch B showed comparable network robustness.

Optimize fermentation stability by regulating initial microbial inoculation

To improve fermentation stability through initial biotic factors, we designed four inoculation ratios (conducted by dilutions) as an approach to regulate the fermentation stability. Figure 7a shows species for fermentation were isolated from three different starters (named QX [means pure aroma], NX [means strong aroma], and JX [means sauce aroma]). We found the number and the detailed express level of metabolites were affected through inoculation dilution (Fig. 7b). Dataset 4 shows that the express level of metabolites related to “pyruvate metabolism” and “glycolysis/gluconeogenesis” fluctuated among four inoculation ratios, mainly including citric acid, maltose, lactose, phenylacetic acid, and phenylalanine. The variations in metabolic profiles compared to the control group suggested that adjusting the inoculation ratio can effectively alter the metabolic flux during fermentation.

Fig. 7: Initial microbial inoculation ratio (by dilutions) affects metabolism fluctuations and community assembly within a simulated fermentation ecosystem.

a Schematic of the experimental design under different initial inoculation conditions. b Changes in metabolites during initial and medium fermentation phases reveal different patterns of metabolic expression levels. The abscissa is each comparative sample group, and the ordinate is the expression level of metabolites in groups. Each gray line represents a metabolite, and the blue line represents the average expression of all metabolites in the sub-cluster. Different metabolites detected by UPLC-MS/MS are grouped into sub-clusters via H cluster. c Bray-Curtis distance between the four groups to the control group based on volatile metabolic profiles during fermentation. SD represents the standard deviation of Bray-Curtis distances to reflect metabolic stability. d Community assembly (blue) patterns and metabolic stability (red) at four dilution gradients during the first 15 days of fermentation. The intersection of the fitted lines suggests the ideal microbial inoculation ratio.

Supplementary Fig. 7 shows that the volatile profiles were significantly influenced by inoculation dilution despite the difference in starters. Based on linear fitting results between PC1 values and different dilution degrees, we found that fermentation of the JX group was the most sensitive group to dilution conditions (R² = 0.604, p = 0.00015), whereas the QX group was the most insensitive (R² = 0.258, p = 0.022). Figure 7c shows that fermentation with low dilution tended to have high efficiency of raw material conversion. Besides, groups with lower dilution showed higher fermentation stability. For the group with ×1 dilution, the standard deviation of distances was 0.083. For the ×5, ×25, and ×50 dilutions, the standard deviations of distance were 0.160, 0.171, and 0.180, respectively.

Figure 7d shows that the dilution gradient was linearly related to fermentation stability (R² = 0.658, Slope = 0.030) and second-order linearly related to the community assembly pattern (R² = 0.401, p = 0.008). Compared with other groups, the group ×5 showed both acceptable community assembly pattern and fermentation stability. The volatile profile of group ×1 was the most stable, exhibiting the highest beta-nearest taxon index (beta-NTI) values. This determined microbial community assembly pattern likely contributed to a more efficient fermentation process. However, the accelerated fermentation process, though efficient, may was too rapid, leading to an earlier conclusion of fermentation 10 days sooner than the other groups.

Discussion

Stable indigenous food fermentation is essential for food productivity, quality, and safety as well as sustainability^24,30. The more complex a fermentation microbial ecosystem is, the more difficult it is to achieve a stable fermentation outcome due to dynamic fermentation fluctuations in time, space, and composition³¹. In our study, we demonstrated that optimization of high-complexity indigenous liquor fermentation was feasible by regulating the metabolic functional stability of the underlying microbiome through initial abiotic and biotic factors. Briefly, regulating initial fermentation parameters would help reduce the instability of the fermentation that is caused by abiotic factors. Regulating the initial microbial inoculation ratio would help reduce fermentation instability caused by biotic factors. Below, we discuss the implications of our findings and the three principles we propose for regulating microbiome metabolic functional stability in similar or less complex microbial ecosystems.

Artificial intelligence (AI) methods and quantitative regression models are effective tools to predict and ensure stable fermentation outcomes^32,33. Evaluating model input and output is important to define and classify different safety and quality types for further model prediction and control³⁴. Nevertheless, determining the minimum number of safety and quality categories that should be identified for efficient differentiation in further modeling is often challenging. In part one of our experiment, taking six parameters as a simple example, we showed that machine learning-based unsupervised analysis and clustering could help find the most suitable number of different fermentation types (Fig. 2b, c). For cases with more parameters (i.e., sensory evaluation), machine learning or deeper machine learning (i.e., neural network) analysis has the potential to help find the best classification for fermentation stability prediction and control³⁵.

Based on the statistical model combined with machine learning here, our findings showed that when input fermentation parameters have significant correlations, regulating individual parameters contributed little to fermentation outcomes (Supplementary Fig. 2 and Supplementary Table 1). Many input fermentation parameters (acidity, pH, reducing sugar, etc.) are parallel driving factors that respond simultaneously to microbial succession at different fermentation phases^36,37,38. The parameters usually exhibit non-linear interactions with one another during the dynamic liquor fermentation process³⁹. In non-linear microbial ecosystems, the phase shift of the microbiome is determined by the “energy landscape”⁴⁰. This explained why thousands of industrial liquor fermentation batches exhibited similar three-phase fermentation patterns despite fluctuations in parameters (Fig. 3a, b). We poise that the essence of unstable liquor fermentation batches was the fluctuation of fermentation parameters around the multiple attractors of the non-linear ecosystem. Such fluctuation (e.g., popularly known as the butterfly effect) is usually affected by initial conditions^41,42. Notably, regulating individual initial parameters could enhance the stability of one fermentation phase but might have a limited influence on overall fermentation stability. Supplementary Fig. 1 outlines potential approaches to help regulate initial abiotic conditions. To achieve the optimal settings suggested by the non-linear model (Fig. 2), steaming time could be adjusted to control reducing sugars, starch, and moisture content, whereas cooling adjustments, such as adding fresh liquor or hot water, could regulate acidity and moisture. Collectively, our findings from part one of this study supported the first regulation principle, that is, in microbial ecosystems with multiple driving parameters, rationally regulating the initial ratio of key parameters could help efficiently reduce metabolic instability caused by abiotic factors.

For metabolic instability caused by biotic factors, unstable fermentation outcomes may occur for a variety of reasons at different fermentation phases. For example, microbial inhibition by fermented products or physiochemical parameters often happens in the middle or later fermentation phases⁴³, and the presence of microorganisms that compete for substrate consumption often happens in the initial phase^27,44. Here, we defined the three phases of baijiu fermentation marked by dynamic physiochemical parameters. Across the three fermentation phases, the baijiu microbiome showed a convergent succession process (Fig. 3). The convergent succession in solid-state media is heavily influenced by the initial transcription of microbial genes^27,37,45. In addition, this transcription can vary depending on the microbial immigration and probabilistic spatial dispersal that occurs at the beginning of solid-state indigenous fermentation⁴⁶. A fast dispersal rate of species would benefit the uptake speed of resources^46,47,48. Thus, the convergent succession process is not only reminiscent of microbial spatial exploration theory⁴⁷ but also contains elements of consumer-resource models applied to microbial coexistence⁴⁹. At the start of two selected fermentation batches, our results showed that the different major consumers of carbon and nitrogen sources (fungi or bacteria) induced gene expression changes, suggesting regulating initial biotic factors can affect microbial succession and thus metabolism (Fig. 5 and Dataset 5). The underlying mechanism is that the same substrate can be used simultaneously by different microbes. However, differences in how these substrates are allocated among the microbes lead to variations in the types and amounts of byproducts produced. These differences create distinct community-wide metabolic phenotypes. As a result, the stability and reproducibility of these metabolic phenotypes are influenced by the dynamic distribution of substrates and metabolic benefits among the microbes. Some metabolic phenotypes can be easily reproduced under stable substrate availability and resilient microbial interactions. Stable or resilient microbial interactions can consistently maintain their metabolic characteristics over time, but unstable interactions may struggle to achieve the same outcomes, resulting in instability in fermentation results⁵⁰. Our short-term fermentation results demonstrated that batches with stable over-expression of bacterial metabolic genes (longer maintenance of stable, beneficial distribution) showed superior temporal metabolic functional stability (Fig. 5f and Dataset 5). For instance, higher stress (high acidity, etc.) caused stable overexpression of K02112 (F-type H⁺ transporting ATPase). Active primary metabolism of bacteria caused stable overexpression of D-lactate dehydrogenase and glyceraldehyde 3-phosphate dehydrogenase (Dataset 5). Collectively, our findings from part two of this study supported the second regulation principle, that is, in microbial ecosystems with a metabolic division of labor, regulating the stability of dynamic beneficial distribution for microbiota could help efficiently reduce metabolic instability caused by biotic factors.

One microbial beneficial distribution scenario in baijiu fermentation involves the co-metabolism of ethanol, lactate, and acetate. In the anaerobic baijiu fermentation process, the ethanol, lactate, and acetate are all present in high concentrations and served as major electron acceptors⁵¹. During fermentation phase II, we observed similar patterns of strong microbial inhibition by lactate and acetate, and weaker inhibition by ethanol in both unstable batches (Fig. 4b, c). However, the concentrations of these compounds differed between the two batches, leading to variations in microbial inhibition and overall fermentation dynamics. This suggests that, despite the instability, the baijiu microbiome continued to perform fermentation, albeit with some variations in efficiency between the batches. In this situation, fermentation productivity (mainly ethanol) can be predicted through a proper microbial inhibition model, helping to rationally reduce fermentation instability by adjusting the concentration of lactate and acetate³⁹.

To ensure the stability of key microbial distributions that contribute to flavor-related metabolic compounds, constraint-based metabolic modeling is essential⁵². Approaches such as flux variability analysis and flux balance analysis can provide insights into the metabolic pathways and resource allocation within microbial communities, enabling researchers to predict and stabilize metabolic outputs. Our results identified specific genes, pathways, and microbial species that can be targeted in future studies to improve fermentation stability through these modeling techniques⁵³. Recent advancements have demonstrated the effectiveness of constraint-based modeling in studying microbial interactions and optimizing metabolite production in food fermentation systems. For example, Scott et al.⁵⁴ leveraged flux balance analysis to explore the metabolic underpinnings of flavor compound biosynthesis, highlighting how pathway fluxes can be modulated to enhance specific flavor profiles. Similarly, the work by Scott et al.⁵⁵ demonstrated how modeling can predict microbial competition and cooperation within fermented communities, aiding in the design of microbial consortia with desirable metabolic properties. Lastly, Melkonian et al.⁵⁶ showcased the use of flux balance analysis for complex microbial communities in food fermentation, offering insights into maintaining functional stability across diverse microbial networks.

Another challenge that limits fermentation stability is the functional redundancy of the microbiome. This functional redundancy can provide a level of stability to the fermentation process, as the loss of one microbial species or metabolic pathway can be compensated by the presence of other species or pathways with similar functions⁵⁷. This redundancy also enhances resilience in fermentation, allowing the microbiome to adapt to changes in environmental conditions or substrate availability through various interactions among fungal and bacterial communities^58,59. However, functional redundancy can also limit the potential for optimization and improvement of the process. For example, if one microbial species or pathway is more efficient at producing a desired product than others, the presence of redundant pathways may hinder the ability to selectively enhance the desired function^60,61,62. Baijiu fermentation is a functional redundant ecosystem due to the coexistence of microbial species with similar metabolic functions¹³. Our results showed that the stably coexisted core microbial species presented more or less overlapping functional genes, suggesting that partial uncertainty of metabolic outcomes is inevitable due to microbiome functional redundancy. The modernization and standardization for completely stable indigenous liquor fermentation may need microbiome engineering technologies to precisely replace or simplify non-essential redundant microbial activities in time, space, and composition^31,63.

Simplifying the complexity of microbial ecosystems is closely associated with biodiversity and the stability of multiple metabolic functionalities^7,28. The overall ecosystem metabolic stability can be increased when biodiversity is low, but decreased when biodiversity is high⁷. In this study, we found that high bacterial diversity and topological complexity of metabolic functional network actually decreased the robustness metabolic network (Fig. 6). This finding suggested that optimizing biodiversity, rather than maximizing it, may enhance the stability of industrial baijiu fermentation³⁶.

Regulating the inoculation ratio is a practical way to change biodiversity. Notably, regulating inoculation ratio changes both fungal and bacterial diversity. In part three of this study, we found decreasing biodiversity by “inoculation ratio” strategy was not effective for optimizing fermentation stability. We argued that decreasing the inoculation ratio reduced the fungal contribution to fermentation stability⁶⁴. The “inoculation ratio” strategy may not be effective for optimizing fermentation when fungi and bacteria have opposing contributions to fermentation stability. Nevertheless, we can still enhance fermentation stability by determining the optimal inoculation ratio that maximizes the overall beneficial contributions from both fungi and bacteria.

Regulating inoculation ratio could affect microbial density that may cause different microbial assembly through a dispersal process²⁹. In the simulated fermentations, we found raising the inoculation ratio of starters (Daqu, a sort of Koji) could increase and decrease the stochasticity of community assembly (Fig. 7). High beta-NTI values will accelerate the fermentation through a determined community assembly pattern that can constrain complexity of metabolic functions^65,66. As a result, fermentation quality (flavor complexity, aroma structure, etc.) would be harmed³⁷ despite the high fermentation stability. Thus, our results suggested that we may find the optimal inoculation ratio to optimize both fermentation quality and stability⁶⁷. This finding may help future work to reduce the spatial complexity to establish the fundamental rules of designing the best microbial inoculation ratio. Collectively, the findings from part two and part three supported the third regulation principle, that is, in high functional redundancy microbial ecosystems, decreasing biodiversity while ensuring proper metabolic network complexity of the microbiome could help reduce metabolic instability caused by biotic factors.

Overall, we summarized the three traits of the fermentation microbiome and provided three regulation strategies to stabilize metabolism (Fig. 8). The fermentation microbiome is a complex ecosystem that exhibits variable metabolic stability through a combination of redundant metabolic genes, metabolic division of labor between fungi and bacteria, and the modulation of community assembly in response to parameters and environmental cues. Understanding abiotic and biotic factors that drive microbial assembly and the metabolic interactions between microbial species can help regulate microbiome metabolic stability to develop sustainable bioproduction systems.

Fig. 8: Three traits of fermentation microbiome and regulation strategies for stable metabolic functions.

Indigenous fermentation microbiome consists of abiotic factors like parameters and microbial metabolites and biotic factors like microbiota. The key parameters and metabolites drive the succession of microbiota. The fermentation microbiota has the metabolic division of labor with efforts from both fungi and bacteria. The fermentation microbiota has redundant metabolic genes to perform metabolic activities. The trinity traits make the fermentation microbiome have nonlinear parameter interactions, dynamic microbial beneficial distribution, and fluctuating robustness of metabolic networks. As a result, the fermentation microbiome acts like spheres, representing unstable solutions to achieve metabolic objectives. Three regulation strategies act like fixed blocks to stabilize the sphere, representing stability optimization of microbiome metabolism.

Methods

Research strategy

We deployed a combined strategy comprising statistical methods, machine learning, and multi-omics technologies through three research steps^52,68,69. First, machine learning and prediction modeling enabled us to calculate and classify whether abiotic or biotic factors, or both cause unstable fermentation outcomes^70,71. Second, multi-omics measurements helped understand the reason why the key factors contribute to metabolic and functional stability in the fermentation microbiome during fermentation processes⁷². Third, a combination of tools provided a basis to assess whether selected strategies for regulating metabolic and functional stability in the fermentation microbiome would be feasible.

Our three-step experiment (illustrated in Fig. 1) proceeded as follows: First, we tracked 6 abiotic parameters across 1009 industrial fermentation batches. These measurement data were mathematically modeled to correlate the parameters with fermentation yield and quality, aiming to identify potential causes of fermentation instability. Next, we selected two batches with unexpected outcomes to study whether microbial factors, beyond abiotic parameters, contributed to fermentation fluctuations. To explore the influence of biotic factors on fermentation stability over short- and long-term processes, as well as the underlying mechanisms, we used various techniques, including amplicon sequencing, meta-transcription sequencing, metagenomics, bioinformatics, statistical analysis, and electron microscopy (details below). Finally, we conducted simulated experiments to validate the impact of key factors on stability by adjusting initial microbial inoculations. We evaluated in situ fermentation stability using the metabolic functional index and assessed stability in simulated fermentations through the standard deviation of metabolic profiles.

The three parts of our strategy are described in more detail below.

Part 1: abiotic regulation

Tracking of industrial-scale fermentation

To survey and track the reasons for fluctuating fermentation yield and quality, we collected samples from 1009 batches in industrial-scale fermentation pits (a sort of solid-state fermentation reactor/chamber) in a representative baijiu factory (27.85° N; 106.38° E). The fermentation was conducted individually in 1009 sealed pits for approximately 30 days. To accommodate the large scale of the study, we adjusted the start dates of different batches, allowing us to complete sampling and tracking within 2 months. Samples were collected weekly from each batch, resulting in a total of 16,144 samples (4 time points × 4 positions × 1009 batches). After pooling the parallel samples from the four positions, we collected 4036 samples, which were transported to the laboratory within 24 h in an ice-filled bucket and stored at −20 °C for further analysis.

Physiochemical analysis of samples

The moisture of samples was measured by a gravimetric method by drying samples at 105 °C for at least 3 h to a constant weight. The acidity was determined by titration with NaOH (0.1 M), with phenolphthalein as the indicator (endpoint of pH 8.2). Starch, alcohols, acetate, and reducing sugar were monitored by the method as previously reported³⁷.

Assumptions and statistical uncertainty modeling of fermentation parameters

Mathematic modeling was conducted to reflect the fluctuating fermentation yield and quality and to find which factors (abiotic parameters or biotic triggered) governed fermentation stability. We assumed that the principal component values calculated from six parameters roughly reflected the quality of fermented products. We fitted Gauss equations to describe fluctuating yield and quality of samples at the end of a batch, as described in Eq. (1):

$${f}_{\mu ,\sigma }\left(y\right)=\frac{1}{\sigma \sqrt{2\pi }}\exp \left[-\frac{{(y-\mu )}^{2}}{2{\sigma }^{2}}\right]$$

(1)

Where y is the dependent variable (related to terminal fermentation parameters), µ is the average value, σ is the standard error and π is a constant. The fitting and calculation were conducted in MATLAB (version R2022b).

We assumed that the principal component values calculated from six parameters (moisture, starch, acidity, reducing sugar, alcohols, and acetate) roughly reflected the quality of fermented products. Based on the top two principal component values, we determined the number of clusters by machine learning-based classification (K-means). The number of multiple Gauss models fitting was same as the numbers of clusters.

To maximally predict fermentation output by initial parameters, we optimized the model several times by both linear and nonlinear fitting. The residual outlier detection methods were used for data preprocessing. A small number of fermentation batches (26 out of 1009) were removed as outliers before further modeling. We first used linear models to predict fermentation output. We found the sensitivity analysis showed an obvious difference between bottom and top marginal values by Monte Carlo sampling, suggesting potential interactions between input parameters (Supplementary Table 1). The values of the adjusted R square of all linear models were lower than 10, suggesting spline fitting rather than linear fitting would be better for prediction (Supplementary Fig. 2). Thus, we established a nonlinear regression model to describe the associations between the value of a given parameter at the start of a batch and the end of a batch. Taking fermentation yield as a quality marker, we evaluated the model accuracy of yield predictions based on three different thresholds and one classification. The multiple nonlinear regression models are second-order models as described in Eq. (2):

$$y={b}_{1}{x}_{1}^{2}+{b}_{2}{x}_{2}^{2}+{b}_{3}{x}_{3}^{2}+{b}_{4}{x}_{4}^{2}+{b}_{5}{x}_{1}{x}_{6}+{b}_{6}{x}_{2}{x}_{5}+{b}_{7}{x}_{5}{x}_{6}+{b}_{8}{x}_{2}+{b}_{9}{x}_{3}+{b}_{10}{x}_{4}+{b}_{11}{x}_{5}+{b}_{12}{x}_{6}+{b}_{13}{e}^{{x}_{2}}+{b}_{14}{e}^{{x}_{5}}+{b}_{15}{e}^{{x}_{6}}$$

(2)

Where y is the dependent variable (related to terminal fermentation parameters), x₁ through x₆ are the initial parameters, b₁ through b₁₅ are the regression coefficients, and e is a constant. The three different thresholds were alcohol concentration error thresholds of 0.5% (w/w), 0.3% (w/w), and 0.1% (w/w). The classification was three quality types that were classified by K-means. Although the model could be further optimized by Bayesian inference based on prior distribution (Supplementary Fig. 2), the improvement relies on big data rather than an understanding of fermentation mechanisms. Such continuous optimization lacks a rational basis. Therefore, we did not proceed with further improvements to the nonlinear regression model.

Part 2: biotic regulation

Screening in situ representative batches for bioprocess comparison

Using the correlation equations above, physiochemical/abiotic parameters can predict only 30.5% of fermentation batches. Thus, other factors (biotic) than abiotic/physiochemical parameters must have played a crucial role in determining the productivity and quality. To understand the mechanism behind it, we chose two in-situ representative batches according to the parameters at the start and the end of batches, named batches A and B. It did not show a significant difference in all fermentation parameters of the two batches at the start, but showed a significant (p < 0.05, double-tailed t-test) difference in partial fermentation parameters at the end of fermentation. We collected samples every 5 days during these two fermentation processes. Samples were taken from at least two locations and two depths in a pit and then pooled. We collected 84 (2 replicates × 7 time points × 2 batches × 3 rounds) samples from batches A and B during the three rounds of fermentation. The three rounds of fermentation refer to the three repeated fed-batch fermentation rounds. In baijiu production, this process is used to fully utilize the raw materials. By tracking this process, we aimed to study the long-term stability of the fermentation. All samples were transferred to the laboratory within 1 h in a bucket filled with ice. Then, we conducted fermentation parameter measurements, and RNA and DNA sequencing of time-series samples to further reveal the spatiotemporal dynamics of community metabolism.

DNA and RNA extraction

Samples were pre-treated with sterile phosphate-buffered saline (0.1 mol/L) and centrifuged at 300 × g for 5 min to obtain the supernatants. Then the supernatants were centrifuged at 11,000 × g for 5 min to obtain the sediments.

For DNA extraction, the sediments were cooled and milled in liquid nitrogen and extracted by sodium laurate buffer (sodium laurate 10 g/L, Tris-HCl 0.1 mol/L, NaCl 0.1 mol/L, and EDTA 0.02 mol/L) with phenol: chloroform: isoamyl alcohol (25:24:1) to obtain total DNA. The quality of total DNA was measured by 1% agarose gel electrophoresis and Nanodrop 8000 Spectrophotometer (Thermo Scientific, Waltham, MA) (260 nm/280 nm ratio). All genomic DNA of samples were stored at −80 °C for further procedure.

For RNA extraction, the sediments were milled with liquid nitrogen and the total RNAs were extracted with sodium laurate buffer (sodium laurate 10 g/L, Tris-HCl 0.1 mol/L, NaCl 0.1 mol/L, EDTA 0.02 mol/L) containing TRIzol (Sigma-Aldrich, St. Louis, MO). Ribo-ZeroTM rRNA Removal Kits (Bacteria) and Ribo-ZeroTM Magnetic Gold Kit (Yeast) (Epicentre, San Diego, CA) were used to remove rRNA from the total RNA. Then, the RNA of samples was stored at −80 °C for further procedure.

DNA and RNA sequencing

We conducted the DNA amplicon sequencing for 28 samples from the first fermentation round. For the DNA amplicon sequencing, the V3-V4 hypervariable region of the 16S rRNA gene and internal transcribed spacer (ITS1/ITS2) region were PCR amplified as previously described⁷³, and the resulting amplicons were quantified and sequenced on the Illumina Miseq PE300 sequencing platform (Illumina, San Diego, CA).

Based on fermentation phases, we conducted the genomic DNA sequencing only for 28 selected samples (10 samples from the 1st round fermentation; 8 samples from the 2nd round fermentation; 10 samples from the 3rd round fermentation) to evaluate the long-term effect of the initial biotic factors on functional stability. For the genomic DNA sequencing, the genomic DNA was randomly broken into fragments with a length of about 350 bp by a sonicator. Then, whole library was prepared through the steps of terminal repair, A-tail addition, sequencing connector, purification, and PCR amplification. After the qualified library pooling, the genomic sequencing was performed on Illumina HiSeq (Illumina, San Diego, CA) platform, which was conducted by the Geneseq Biotechnology Company in Nanjing, China.

Based on fermentation phases, we conducted the RNA sequencing only for 12 selected samples from the first fermentation round to evaluate the short-term effect of initial biotic factors on functional stability. For the RNA sequencing, metatranscriptomic libraries were constructed according to the NEBNext® UltraTM RNA Library Prep Kit (Illumina, New England Biolabs, MA) and sequenced on the Illumina Hiseq 2500 platform (Illumina, San Diego, CA), which was conducted by the Allwegene Technology Company in Beijing, China. All sequencing reads can be accessed in the NCBI SRA database. The DNA sequencing data have been assigned accession numbers SRR23372236 to SRR23372263. The RNA sequencing data have been assigned accession numbers SAMN29162647 to SAMN29162658.

Bioinformatic analysis

For raw DNA sequencing reads, we used Q20 as the quality standard to cut low-quality sequences³⁷. Then, overlapping reads were merged by fastq-join, and primer sequences were removed, only completely assembled reads were utilized for further analysis. The overlap length of merging was 20. The minimum length of fungal sequences was set as 50. The unique sequence set was classified under the threshold of default via Qiime2 (version, 2019-04). Chimeric sequences were identified and removed using Qiime2. The bacterial sequences were mapped to SILVA 132 database for annotation. The fungal sequences were mapped to the Unite database for annotation (version 8.2).

For metagenomic DNA sequencing reads, the raw data was filtered based on Q20. Filtered reads were assembled using MEGAHIT (v1.0.6)⁷⁴ assembly program (-- min-count 2 --k-min 27 --k-max 87 --k-step 10). Contigs with length less than 500 bp were filtered. Metabat2 was used to do the binning process based on contigs. Open reading frame prediction was performed by PRODIGAL⁷⁵, and filtered with a length shorter than 100 nt. Using CD-HIT⁷⁶ with the set (-c 0.95, -G 0, -aS 0.9, -g 1, -d 0) to remove redundancy from the predicted gene sequences. The Bowtie⁷⁷ was used to map gene sequences to a non-redundant gene catalog with 95% identity. Then the Kyoto Encyclopedia of Genes and Genomes (KEGG) database⁷⁸ was used for functional gene annotation at KEGG level 1 and KEGG level 3. We then evaluated the long-term effects of different initial biotic factors on metabolic functional stability based on the abundance of assembled genes.

For RNA sequences, we performed species classification analysis, complexity analysis, and gene expression abundance analysis. We compared high-quality reads to the nonredundant protein database (Nr) and metabolic pathway (KEGG), Gene Ontology (GO), Protein family (Pfam), homologous gene cluster (eggNOG), carbohydrate enzyme (CAZy) to obtain functional annotation information. The sequencing reads for each sample were remapped to the reference sequences using RSEM software⁷⁹. Gene expression levels were measured using the FPKM (Fragments Per Kilobase of transcript per Million fragments) method based on the number of uniquely mapped reads⁸⁰. The DESeq package (ver. 2.1.0) was used to detect DEGs between two samples⁸¹. The false discovery rate (FDR) was applied to correct the p-value threshold in multiple tests⁸². An FDR-adjusted p value (q-value) ≤0.05 and a |log2FoldChange | > 1 were used as the threshold to identify significant differences in gene expression in this study. We also evaluated the short-term effects of different initial biotic factors on metabolic functional stability based on FPKM values. We categorized 18 metabolic functions as metabolism-related gene transcriptions because their expression is closely linked to yield and flavor quality in the fermentation process.

Calculation of dynamic community assembly

βNTI was calculated to evaluate community assembly patterns, following the protocol described elsewhere^83,84. βNTI values that are >−2 or <+2 indicate a stochastic microbial community assembly pattern. We applied community assembly calculation to time-series samples. The dynamic community assembly was evaluated by the statistics of βNTI values.

Field emission scanning electron microscopy images

Field-emission SEM images were collected for ultrastructural analysis using an SU8010 instrument at 20 kV⁸⁵. Four fermentation samples from each phase (I, II, and III) were pooled and mixed individually, from which equal weights of the mixed samples were taken for electron microscopy analysis. This standardized sample preparation minimizes variability and allows for consistent comparison of images across fermentation phases. By analyzing multiple images from different angles (representative angles were displayed in Fig. 4a), we can ensure that any observed differences in microbial composition reflect true variations in the fermentation process, rather than inconsistencies arising from sample handling.

Part 3: lab-scale validation

Design of lab-scale simulated solid-state fermentations

To test the effect of microbial stochastic assembly (dispersal, etc.) on the metabolic stability of microbial communities, we designed a lab-scale simulated solid-state fermentation. Multi-species for simulated fermentation were isolated from Daqu (Fig. 7a and Supplementary Fig. 3). The Daqu are collected from three different aroma type baijiu factories, named Qingxing (QX, means pure aroma), Nongxiang (NX, means strong aroma) and Jiangxiang (JX, means sauce aroma). We first used adequate boiled (sterilized) ddH₂O to dilute Daqu into turbid liquid. Then we centrifuged liquid at 300 × g for 5 min to obtain the supernatants. Then the supernatants were centrifuged at 11,000 × g for 5 min to obtain the sediments. The sediments made from three Daqu were resuspended by ddH₂O. All suspensions of isolated species were adjusted to the same biomass by sterile water before further dilutions. We controlled biomass by ensuring that all samples were adjusted to the same weight, which allowed us to standardize the biomass across samples. Then, we created 4 dilutions (×1, ×5, ×25 and ×50) of the microbial suspension by sterilized water and individually inoculated them into steamed cereals (10%, w/w) to start the fermentation. The control group of each dilution was inoculated with the corresponding microbial solutions without any species via filtering. All fermentations were done under the same conditions (still, 30 °C) for 25 days in 100-ml centrifuge tubes. The fermentations were ended when the weight of whole fermentation tubes changed lower than 0.1 g between two sampling timepoint. Samples were taken and analyzed every 5 days. Samples of group ×1 diluted were collected only three times during the fermentation, because its fermentation ended much earlier than other groups.

(HS-SPME-GC-MS) analysis of simulated fermentation samples

To evaluate the fermentation stability, we calculated the Bray-Curtis distance of each sample based on volatile profiles. Volatiles in samples were identified by headspace-solid phase microextraction-gas chromatography-mass spectrometry (HS-SPME-GC-MS) as described in our previous work³⁸. All samples were pre-treated with 20 mL of sterile saline (1% CaCl₂, 0.85% NaCl, w/v) in 50 mL centrifuge tubes to collect supernatants after centrifuging at 5000 × g for 10 min. Supernatant (8 mL) was added into headspace bottles and mixed with 3 g of NaCl and internal standard (10 µL menthol).

(UPLC-MS/MS) analysis of simulated fermentation samples

Metabolites were separated by chromatography on an ExionLCTMAD system (AB Sciex, Framingham, MA) equipped with an ACQUITY UPLC BEH C18 column (100 mm × 2.1 mm i.d., 1.7 µm; Waters, Milford, MA). The mobile phases consisted of 0.1% (w/v) formic acid in water with formic acid (0.1%) (solvent A) and 0.1% formic acid in acetonitrile: isopropanol (1:1, v/v) (solvent B). The sample injection volume was 20 µL and the flow rate was set to 0.4 mL/min. The UPLC system was coupled to a quadrupole-time-of-flight mass spectrometer (Triple TOFTM5600+, AB Sciex, Framingham, MA) equipped with an electrospray ionization source operating in positive mode and negative mode. The detection was done over a mass range from 50 to 1000 m/z.

Statistical analysis

All statistical analysis in the three experimental parts were conducted as described below. Dynamics of physical and chemical factors were fitted with OriginPro2019. Principal component analysis (PCA), significant tests, microbial correlations, canonical-correlation analysis, random forest model, and variance partitioning analysis were conducted by the vegan package in R (http://vegan.r-forge.r-project.org/).

We calculated the structure equation model to clarify the causality and quantify the effects of microbial stochastic assembly on metabolic functions by IBM SPSS Amos 25. p values were adjusted for nonparametric analysis by the Statistical Package for Social Science (SPSS, version 22).

We constructed metabolic networks of batches A and B and evaluated network properties on an online platform (cloudtutu.com) based on the annotated functional table (KEGG level 3). We kept metabolic functions with relative abundances greater than 0.1%. Co-occurrence networks were calculated by Spearman correlation with a 0.01 cutoff threshold. Each fermentation round was set as the subgroup in the co-occurrence networks. We estimated metabolic network robustness individually by the average natural connectivity of subgroups within batch A or batch B, respectively. The natural connectivity enabled us to gauge network stability by progressively removing nodes within the static structure, allowing us to evaluate the speed at which robustness declined⁸⁶. The number 43 was determined as the intersection based on the results of our network robustness analysis. We observed that when more than 43 nodes were removed from the metabolic network, both batch A and batch B showed comparable network robustness. Prior to this point, we conducted fitting comparisons to visually illustrate the direct differences in network robustness between the two fermentation batches.

The metabolic functional stability index of the microbiome was calculated based on the average variation degree⁴. Specifically, we calculated the functional stability by taking the ratio of the mean to the standard deviation for various functional categories (KEGG level 1) and individual functional profiles (KEGG level 3) across replicated fermentation samples⁸⁷. As for main metabolic functional categories of two selected batches, we derived a function to determine the change of overall metabolic functional stability between fermentation batches as described in Eq. (3):

$${\rm{F}}.{\rm{s}}{\rm{t}}{\rm{a}}{\rm{b}}{\rm{i}}{\rm{l}}{\rm{i}}{\rm{t}}{\rm{y}}\,{\rm{c}}{\rm{h}}{\rm{a}}{\rm{n}}{\rm{g}}{\rm{e}}=\mathop{\sum }\limits_{i=f_1}^{f_n}\left(\frac{{\int }_{P1}^{P3}{(VB}_{i}/V{A}_{i})dP}{SD{(VB}_{i})/SD{(VA}_{i})}\right)$$

(3)

Where f1, f2…fn represents different metabolic functional genes. P1, P3 represents fermentation phases. VBi and VAi are the FPKM values of gene i in batches B and A. SD(VBi) and SD(VAi) are the standard deviations of the FPKM values of gene i in batches B and A.

Data visualization

Data were plotted with OriginPro2021, Microsoft® Excel, and Adobe Illustrator CS6. Different gene expressions of overall metabolic functionality mapped to the KEGG metabolic network using iPATH3⁸⁸.