Introduction

When two van der Waals (vdW) layers are stacked together, moiré patterns naturally form along with a lattice mismatch or twist angle between the constituent layers. Due to the intrinsic periodic potential, flat moiré bands can be formed1, which induce complex correlated physics, such as the superconducting and insulating states observed in twisted bilayer graphene2,3. Recently, twisted transition metal dichalcogenide (TMD) heterobilayers have gained increasing attention, where the layer degeneracy is natively broken, and the semiconducting nature provides higher electrical tunability and optical accessibility4,5,6,7,8,9,10,11. Mott-insulating and generalized Wigner crystal states were observed in half and fractionally filled TMD moiré superlattices as a result of correlated quantum physics12,13,14,15,16,17,18,19. Furthermore, displacement field-induced quantum anomalous Hall effect was predicted and observed in half hole-filled MoTe2/WSe2 moiré lattices due to the interlayer hybridization20,21,22. These works establish TMD heterobilayers as a versatile playground for forming flat bands and studying correlated quantum phenomena.

Gate-field tunable filling factor is essential in realizing the above-mentioned correlated physics in two-dimensional (2D) moiré systems. To date, most workers have adopted an assumption that doped carriers effectively tune the filling factor while not affecting the quasiparticle (QP) energies and hence the moiré potential. However, doped carriers will inevitably alter the electronic screening, which is known important in determining the strong many-electron interactions and QP energies in 2D structures23,24,25,26,27. Besides, moiré potential will naturally induce inhomogeneous carrier distributions within moiré superlattices. As a result, inhomogeneous many-electron effects are expected, which may substantially revise the moiré potential, the dispersion (kinetic energy) of electronic bands, and the subsequent correlated physics pictures.

In this work, we employ the first-principles many-body perturbation theory (MBPT) to study the renormalization of moiré potential under carrier doping. Figure 1a schematically shows the doping effects on quasielectron moiré potential and wavefunctions. Because of inhomogeneous carrier distributions, the doped area will experience lowered QP potential via QP-plasmon renormalization26,27,28,29. Thus, the moiré potential minimum further deepens, and the quasielectron wavefunction becomes more localized in the case of carrier occupation, quenching the electronic kinetic energy and forming ultra-flat bands. We take twisted MoS2/WS2 heterobilayer as an example to illustrate the mechanism of doping-enhanced quasiparticle moiré potential. Our quantitative calculations show that a moderate doping density renders an increase of the moiré potential variation from 90 to 300 meV and can reduce the low-energy moiré bandwidth by an order of magnitude. Moreover, we find that doped carriers alter the characteristic potential scales (e.g., on-site Coulomb repulsion U and charge-transfer gap ∆) in different ways. As a result, a quantum phase transition from Mott insulator to charge-transfer insulator is predicted as the twist angle varies. Therefore, besides the apparent filling factor control, doping will effectively modify the moiré potential and can serve as another tuning knob for achieving ultra-flat bands and correlated physics in 2D semiconducting moiré crystals.

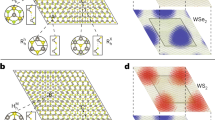
Fig. 1: Carrier plasmon-induced quasiparticle energy renormalization.
figure 1

a Schematic of doping-enhanced moiré potential in semiconducting vdW superlattices. V(r) and w(r) are the real-space moiré potential and wavefunction of quasielectrons, respectively. Under doping, the potential minimum drops due to inhomogeneous carrier distributions and QP energy renormalization. b Moiré superlattice formed by a twist between the H-type MoS2/WS2. The three high-symmetry stackings \(H_h^h\), \(H_h^X\), and \(H_h^M\) are labeled for simplicity as A, B, C, respectively. c Intrinsic moiré QP potential landscape along the three interlayer registries. The red dots represent first-principles GW results. d Bandgap, and e CBM renormalization for the three interlayer registries of H type MoS2/WS2 under electron doping. The dots are from many-body perturbation theory calculations.

Full size image

The ground-state calculations are performed with Quantum ESPRESSO30, and the intrinsic self-energies are obtained by BerkeleyGW31. The coupling between carrier plasmon and QPs are included by the generic double plasmon-pole model26,27. We do not include spin–orbit coupling, which does not significantly change self-energy corrections in TMDs and can be estimated by a rigid shift to QP energies32,33. We limit our discussions to single-particle properties here. The excitonic effects induced by quasiparticle-plasmon coupling is worthy of future studies.

Results

Moiré potential

Figure 1b shows the moiré superlattices formed by a twist between the H stacked MoS2/WS2 bilayers. Three distinct high-symmetry stacking orders \(H_h^h\), \(H_h^X\), and \(H_h^M\) can be recognized (labeled for simplicity as A, B, C in Fig. 1b, respectively), where the superscripts represent a hollow/chalcogen/metal atom center in the top layer that is vertically aligned with a hollow center in the bottom layer, respectively. The results for R-type structures can be found in Supplementary Fig. 1. The ab initio QP self-energy of the three local atomic registries are calculated under the GW approximation, \({{\Sigma }} = iGW\). The CBM for three high-symmetry stackings are all at K point in the reciprocal space. The quasiparticle band structure of the intrinsic structure is listed in Supplementary Fig. 2. The locally varying stackings cause a periodic modulation of the CBM energy. Quasielectrons in the superlattice hence experience a periodic potential, which can be interpolated by a Fourier expansion over the nearest moiré reciprocal lattice vectors

$$V\left( {{{\boldsymbol{r}}}} \right) = E_c\left( {{{\boldsymbol{r}}}} \right) = T_0 + 2V_0\mathop {\sum }\limits_{i = 1,2,3} {{{\mathrm{cos}}}}({{{\boldsymbol{b}}}}_i\cdot {{{\boldsymbol{r}}}} \pm \psi ),$$
(1)

where Ec is the local CBM. For intrinsic MoS2/WS2 heterobilayer, the fitted parameters \((T_0,\,V_0,\,\psi )\) from ab initio MBPT are \(( - 3.083\,{{{\mathrm{eV}}}},9\,{{{\mathrm{meV}}}},14^\circ )\). Figure 1c plots the QP moiré potential calculated by Eq. (1) along the three high-symmetry stacking sites. It agrees well with first-principles GW results (isolated dots), and the variation of local CBM is 90 meV. This is similar to previous DFT results6,34 since the self-energy corrections are similar for different stackings of the intrinsic heterobilayer.

Quasiparticle band renormalization

Considering the effects from doped carriers, the QP self-energy can be obtained by25,26,27,35

$${{\Sigma }} = i\left( {G_{int}W_{int} + \delta GW_{int} + G_{int}\delta W + \delta G\delta W} \right) \equiv i\left( {{{\Sigma }}_{int} + {{\Sigma }}_1 + {{\Sigma }}_2 + {{\Sigma }}_3} \right).$$
(2)

The subscript int denotes the operator in the intrinsic structure, and δ terms account for the doping effects. Σ1 is only affected by the carrier occupation

$$\Sigma _1^{n{{{\boldsymbol{k}}}}}\left( E \right) = - \Sigma _{n^\prime ,GG^\prime }\mathop {\int}\limits_{{{{\boldsymbol{q}}}} < k_f} {\frac{{d^2{{{\boldsymbol{q}}}}}}{{(2\pi )^2}}} \xi _{{{{\boldsymbol{GG}}}}^\prime }^{nn^\prime }\left( {{{{\boldsymbol{k}}}}, - {{{\boldsymbol{q}}}}} \right)W_{{\mathop{{{\rm{int}}}}} ,{{{\boldsymbol{GG}}}}^\prime }\left( {{{{\boldsymbol{q}}}},E - \varepsilon _{n{{{\boldsymbol{k}}}} - {{{\boldsymbol{q}}}}}} \right),$$
(3)

where \(\xi _{{{{\boldsymbol{GG}}}}^\prime }^{nn^\prime }\left( {k,q} \right) = M_{nn^\prime }^ \ast ({{{\boldsymbol{k}}}},{{{\boldsymbol{q}}}},{{{\boldsymbol{G}}}})M_{nn^\prime }({{{\boldsymbol{k}}}},{{{\boldsymbol{q}}}},{{{\boldsymbol{G}}}}^\prime )\) contains the band structure effect and \(M_{nn^\prime }({{{\boldsymbol{k}}}},{{{\boldsymbol{q}}}},{{{\boldsymbol{G}}}})\) is the plane-wave matrix element. kf is the Fermi wavevector. Σ2 and Σ3 have contributions from the variation of dielectric screening \(\delta W = v\delta {\it{\epsilon }}^{ - 1}\), where v is the bare Coulomb interaction. The calculation of \(\delta {\it{\epsilon }}^{ - 1}\) requires a description of the interaction between carrier plasmon and quasiparticles. As shown in previous works26,27, the dynamical screening effect can be accounted for by an approximation to the head matrix elements using the carrier-plasmon-pole model \(\delta {\it{\epsilon }}_{00}^{ - 1}\left( {q,\omega } \right) = \frac{{{{\Omega }}_d^2(q)}}{{\omega ^2 - \omega _d^2(q)}}\), where \({{\Omega }}_d(q)\) and \({\upomega}_d(q)\) are the plasmon-pole strength and frequency that can be obtained by first-principles calculations26,27. The explicit forms for Σ2 and Σ3 are thus

$$\Sigma _2^{n{{{\boldsymbol{k}}}}}\left( E \right) = \pm \mathop {\int}\limits_{q < q_c} {\frac{{d^2{{{\boldsymbol{q}}}}}}{{(2\pi )^2}}} \xi _{{{{\mathbf{00}}}}}^{nn}\left( {{{{\boldsymbol{k}}}}, - {{{\boldsymbol{q}}}}} \right)\delta W_{{{{\mathbf{00}}}}}^ \pm \,\left( {{{{\boldsymbol{q}}}},E - \varepsilon _{n{{{\boldsymbol{k}}}} - {{{\boldsymbol{q}}}}}} \right),$$
(4)
$$\Sigma _3^{n{{{\boldsymbol{k}}}}}\left( E \right) = - \mathop {\int}\limits_{q < k_f} {\frac{{d^2{{{\boldsymbol{q}}}}}}{{(2\pi )^2}}} \xi _{{{{\mathbf{00}}}}}^{nn}\left( {{{{\boldsymbol{k}}}}, - {{{\boldsymbol{q}}}}} \right)\delta W_{{{{\mathbf{00}}}}}\left( {{{{\boldsymbol{q}}}},E - \varepsilon _{n{{{\boldsymbol{k}}}} - {{{\boldsymbol{q}}}}}} \right),$$
(5)

where ± in Σ2 are for conduction and valence states, respectively. Σ1 and Σ3 include the effect of partial band filling, hence under electron doping, they only contribute to the conduction band energy renormalization, and are integrated to the Fermi wavevector kf. As a result, Σ1 roughly scales as \(- {\it{\epsilon }}_{int}^{ - 1}k_f\), and Σ3 scales as \(- \delta {\it{\epsilon }}^{ - 1}k_f\). Σ2, on the other hand, is related to the carrier screening, and contribute to the energy renormalization of both valence and conduction bands. Under the linear response theory, we integrate Σ2 up to a cutoff wavevector \(q_c = 0.16\,{{{\boldsymbol{b}}}}\) for converged self-energies in the studied heterobilayer. The individual contributions of Σ1, Σ2, and Σ3 to the on-shell QP self-energies can be found in Supplementary Fig. 3.

The QP self-energy under a self-consistent GW calculation is obtained by a rigid shift of the whole resonance profile so that the on-shell energy of Σ coincides with the QP solution26,27,36. This corresponds to a solution to the QP energy in the GW0 level (see Supplementary Fig. 4 for details). Figure 1d, e shows the bandgap and CBM renormalization for the three high-symmetry registries under doping, respectively. The results for valence band maximum are listed in Supplementary Fig. 5. As manifested by Fig. 1d, the bandgap renormalization (BGR) is most prominent in the light-doping side and gradually saturates to around 300 meV for all three stackings at high-doping densities \(\sim \!2.3 \times 10^{13}\,{{{\mathrm{cm}}}}^{ - 2}\). Compared to monolayer MoS2, whose BGR reaches about 500 meV at doping density \(\sim \!6.0 \times 10^{13}\,{{{\mathrm{cm}}}}^{ - 2}\) (see ref. 27), the bandgap reduction in heteobilayer is smaller and saturates faster. The origin of this difference is twofold. First, the intrinsic dielectric screening in a bilayer is stronger than that in a monolayer, as a result, the extra screening introduced by the doped carriers \({{\Sigma }}_2 = iG_{int}\delta W\) is weaker. Second, the CBM of the heterobilayer features a hybridized Q point along the Γ-K high-symmetry line, which lies ~100 meV above the K point (see Supplementary Fig. 1). As doping density increases, the Q point also gets occupied, thus the carrier-occupation effect \({{\Sigma }}_1^{CBM} = i\delta GW_{int}\) at K diminishes. In this regime, the carrier screening becomes the dominant mechanism of band renormalization. This effect is more evident in the evolution of CBM shown in Fig. 1e. At low-doping densities, the CBM drops dramatically, and after the onset of filling at Q, the CBM saturates with a slight uprise. The uprise is due to the transition from a holelike resonance to an electronlike resonance of \({{\Sigma }}_2^{CBM} + {{\Sigma }}_3^{CBM}\)26 and the saturation of \({{\Sigma }}_1^{CBM}\). Note that the onset of Q occupation happens at \(\sim 2.3 \times 10^{13}\,{{{\mathrm{cm}}}}^{ - 2}\) for \(H_h^h\) and \(H_h^M\) stackings, and at \(\sim \!{3.4} \times 10^{13}\,{{{\mathrm{cm}}}}^{ - 2}\) for \(H_h^X\) owing to their distinct K and Q energy difference. These two factors together cause the reduced BGR in heterobilayer and its facilitated saturation behavior.

Moiré potential landscape renormalization and ultra-flat bands

Under electron doping, the variation of the CBM at different local stackings renders an inhomogeneous carrier density within superlattices, which further modifies the moiré potential landscape according to the doping-dependent band renormalization (see Fig. 1e). We find out the doping modulated moiré potential by firstly filling electrons into the intrinsic heterobilayer potential landscape (Fig. 1c). Then we self-consistently update the quasielectron moiré potential according to the CBM renormalization at local electron densities (Fig. 1e). The typical iteration number for convergence is about 8–10.

The moiré potentials of intrinsic and doping renormalized MoS2/WS2 heterobilayer at 2° twist angle are presented in Fig. 2. The overall moiré potential variation increases from around 90 meV in the intrinsic structure and saturates to over 300 meV under a moderate doping density (\(\sim \!1.3 \times 10^{12}\,{{{\mathrm{cm}}}}^{ - 2}\) or half-filling n = 1 electron per moiré supercell). The dramatic change in the potential landscape is accompanied by an alteration of the moiré bands. The moiré band structures can be obtained by solving the moiré band Hamiltonian under the continuum model34,37,

$${{{\mathcal{H}}}} = \frac{{\hbar ^2{{{\boldsymbol{Q}}}}^2}}{{2m}} + V\left( {{{\boldsymbol{r}}}} \right),$$
(6)

where the moiré potential V(r) as defined in Eq. (1) now includes the doping renormalization effect. Figure 3a, b presents the moiré band structures at 2° twist angle for intrinsic and half-filled superlattices, respectively. The bandwidth of the lowest conduction band shrinks from 5 to 0.04 meV and becomes extremely flat under doping. The ultra-flat bands will affect a wide range of transport and optical properties, such as quenched electric conductivity due to heavy effective mass and strong excitonic effects via the enhanced van Hove singularities.

Fig. 2: Moiré potential renormalization under carrier doping.
figure 2

Real-space moiré potential of the 2° twisted MoS2/WS2 a intrinsic structure, b doped with n = 1 electron per moiré superlattice, c doped with n = 5 electrons per moiré superlattice. The charge-transfer gap ∆ is labeled in (b, c).

Full size image
Fig. 3: Isolated ultra-flat bands in a doped moiré system.
figure 3

Low-energy moiré QP band structure of 2° twisted MoS2/WS2 a intrinsic structure, b doped with n = 1 electron per moiré superlattice. c, d Real-space wavefunctions associated with the three lowest conduction bands I, II, and III shown in (a, b), respectively. e Variation of bandwidth in terms of the twist angle. f Variation of bandwidth in terms of the average doping density. The vertical axes in (c, f) are shown in the log scale for clarity.

Full size image

Meanwhile, the vanishing bandwidth indicates very weak inter-moiré-cell hoppings, pushing the system to the strong-correlated limit. Particularly, the lowest-energy flat band is isolated from the second mini band by 70 meV, while in the intrinsic structure, this energy separation is only 10 meV. As a result, the doping-enhanced moiré potential not only flattens the bands but also isolates them, so that the flat bands are more robust to external perturbations and accessible in angle-resolved photoemission spectroscopy (ARPES) measurements.

We further plot the real-space wavefunctions of the low-energy moiré bands in Fig. 3c, d. Consistent with a flat-band picture, the wavefunctions of the doped system show a much more concentrated structure. Specifically, the s orbital band I wavefunction is highly localized at the potential minimum (\(H_h^X\) site), whereas the wavefunction smears over adjacent potential minima in the intrinsic structure. Interestingly, the wavefunctions of the degenerate bands II and III show orthogonal symmetric p orbital characters as an isolated “atom”. While in the intrinsic case, the wavefunctions of the non-degenerate bands II and III are not symmetric. Therefore, due to the enhanced moiré potential, the electronic states in a doped system resemble large wavelength artificial atomic arrays. Besides, since the energy separation between the lowest flat minibands are large, the trapped periodic “cold atoms” can be stable even under room temperature.

In Fig. 3e, f, we summarize the band I width as functions of twist angle θ and average doping density n0, respectively. The shrinkage of bandwidth is significant at low-doping density. As shown in Fig. 3e, the bandwidth shrinks from around 40 to 5 meV as the twist angle varies from 4° to 2° in the intrinsic structure, whereas the bandwidth reaches less than 1 meV under 2.5° at slight doping \(n_0 = 0.7 \times 10^{12}\,{{{\mathrm{cm}}}}^{ - 2}\). The correlated physics hence is reachable in a larger range of twist angles in the doped system. Moreover, the moiré bandwidth experiences a dramatic decrease under slight carrier doping and becomes an order smaller than the intrinsic structure for 2° and 3° twist angles (see Fig. 3f). This is in accordance with Fig. 2, where the overall potential variation increases significantly at low-doping density and saturates with further doping.

It is worth justifying the validity of continuum model with our many-body calculations. First, within our studied doping density range, the quasielectron–plasmon interaction range can be estimated by the characteristic scale 2kf27, which is about 0.1 b. Hence the real-space extent of the doping-altered dielectric screening is about 10 unit cells (~3 nm), which is smaller than the studied moiré superlattices (~10 nm for a 2° twist angle). Second, the Wannier extent of the s orbitals of the localized electrons in real space can be approximated by a harmonic expansion of V(r) around the potential minimum aw = (ħ2/16π2mV0)1/4 \(\sqrt {a_M}\)34,38. At 2° twist angle and n = 1 doping, \(a_W = 1.2\,{{{\mathrm{nm}}}}\), which is significantly smaller than the moiré lattice constant and consistent with a flattened-band picture as shown in Fig. 3a–d. Thus, our many-body treatment of the local dielectric screening under carrier doping shall be valid within the studied small twist angles (up to 4°).

Phase transition between Mott and charge-transfer insulators

The substantial renormalization of moiré potential by doped carriers will impact and alter a broad range of properties. Here we take the discussion of Mott and charge-transfer insulating states as an example, which is crucial for realizing unusual superconductivity. Despite the insulating states observed in doped 2D moiré crystals, the nature of these insulating states is still in controversy38,39. Particularly, for the moiré potential with multiple minima, the formation of insulating states can have two origins. When the local Coulomb interaction U is smaller than the potential difference ∆ between minima, the ground insulating state is a Mott insulator. On the other hand, if U > ∆, it is a charge-transfer insulator. In TMD heterostructures, the on-site Coulomb interaction is typically on the order of hundreds of meV, while the DFT-calculated charge-transfer energy (∆) is generally on the order of tens of meV34,38. In this regard, the TMD heterostructures are normally within the charge-transfer picture. However, the many-body doping effect may change this picture.

The half-filling doping significantly increases the charge-transfer energy from 22 meV (Fig. 2a) to 228 meV (Fig. 2b) for 2° twisted MoS2/WS2 heterobilayer. Meanwhile, the local Coulomb interaction U can be estimated by \(U = e^2/4\sqrt {2\pi } {\it{\epsilon }}a_W\)34, where ϵ is the average dielectric constant related to the heterobilayer entities and substrate environment. The variation of U and ∆ with twist angle are summarized in Fig. 4a, b for half-filling n = 1 at ϵ = 7 and 10, respectively. For ϵ = 7 (Fig. 4a), a quantum phase transition between Mott and charge-transfer insulating states happens at around 2.5° as twist angle increases. At small twist angle (i.e., small average doping density under the same filling factor), ∆ exceeds U due to the enhanced moiré potential and charge-transfer energy as shown in Fig. 2b. Therefore, the system is in the Mott-insulating state. At larger twist angle, U increases more rapidly and exceeds Δ, the system transits to a charge-transfer state. The phase transition happens at larger twist angle for higher dielectric constant. When ϵ = 10 (Fig. 4b), as twist angle increases, the average doping density at half-filling increases because of smaller supercell size. As shown in Fig. 2c, the second potential minimum starts to get occupied, and the charge-transfer barrier ∆ is reduced. The system hence transits back to a charge-transfer-like state around the twist angle of 4.1°. Therefore, the experimentally observed insulating states at half and fractional fillings can have different origins depending on the average doping density (or twisting angle) and dielectric environment. The overall phase diagram between Mott and charge-transfer insulators at half-filling is summarized in Fig. 4c. A larger environmental dielectric constant favors the Mott state while a larger twist angle prefers the charge-transfer insulating state.

Fig. 4: Phase diagram of the half-filled heterobilayer.
figure 4

Characteristic energies of U and ∆ at half-filling over different twist angles for a ϵ = 7, b ϵ = 10. The purple line is for U, and the red line is for ∆. The background represents the ratio ∆/U. The white dashed line represents the crossing between U and ∆, which is the critical point of the transition between Mott (to the left of the dashed line) and charge-transfer (CT) insulators (to the right of the dashed line). c Phase diagram of Mott and charge-transfer (CT) insulators at half-filling under different twist angles and dielectric constants.

Full size image

The phase transition between Mott and charge-transfer insulators can be probed by optical approaches, such as the photoluminescence (PL) spectroscopy. Under those Mott-insulating states, the electronic states around the Fermi level are within the same (on-site) moiré well, and their wavefunctions significantly overlap. Thus, the optical transition can be significant, inducing sizable PL signals. On the other hand, for charge-transfer cases, those electronic states are in different moiré wells, and their spatial overlap is small. Thus, we expect weak PL signals.

We notice that the shear solitons at stacking domain boundaries will influence the different domain sizes40,41,42. This structural reconstruction around domain boundaries will introduce strain into the system, which will impact the QP energies and moiré potential. As shown in previous Raman measurements on twisted bilayer MoS243 and first-principles simulations of WSe2/WS244, the strain due to lattice reconstruction is less than 1%. This strain level will induce a change in the QP bandgap in TMD of around 100 meV, and CBM/VBM individually up to 50 meV45. Thus, strain will quantitatively affect the carrier distribution and potential renormalization, but the fundamental picture of enhanced moiré potential illustrated here will still be valid as long as the inhomogeneous doping picture sustains.

Discussion

In summary, we propose electron doping as a general way to induce enhanced moiré potential and realize pursued flat bands for quenching electronic kinetic energy in twisted semiconducting vdW structures. Combining first-principles many-body perturbation theory and continuum model, we show that the nonlinear band renormalization under doping significantly deepens the moiré potential minimum and results in isolated ultra-flat bands. Depending on the average doping density, the moiré potential landscape varies, which in turn affects the charge-transfer energy ∆ and may induce a quantum phase transition between Mott insulator and charge-transfer insulator at half-filling. Our findings are crucial for understanding the carrier filling dependent electronic structures in vdW superlattices, including heterobilayers and homobilayers, and predict that electrostatic doping can be an effective tool to tune electronic correlated physics.

Methods

The ground-state properties are calculated by density functional theory (DFT) within the general gradient approximation (GGA) using the Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional as implemented in Quantum ESPRESSO package30. A 36 × 36 × 1 k-grid is adopted, and the van der Waals (vdW) interactions are included via the semiempirical Grimme-D3 scheme46. The plane-wave energy cutoff is 65 Ry. The vacuum distance between adjacent layers is set to be 18 Å. The many-body perturbation theory (MBPT) calculations for intrinsic structures are performed with BerkeleyGW31. The intrinsic quasiparticle (QP) energies are calculated by using the single-shot G0W0 approximation, including the slab Coulomb truncation. The energy cutoff for the dielectric matrix is 10 Ry, and 224 unoccupied bands are used for the summation. For the calculation of plasmon energies, a dense k-grid of 90 × 90 × 1 is used. An energy cutoff of 2 Ry and 34 unoccupied bands are sufficient to get converged plasmon frequencies. All parameters are tested for QP energy convergence within 50 meV.

When filling electrons in the conduction band minimum (CBM) moiré potential, we sweep the Fermi energy and determine the local doping density by the energy difference between the Fermi energy and the local potential. The Fermi energy is chosen when the integrated doping density over the moiré superlattice is within 1% difference with the number of doped electrons. Then the renormalized moiré potential is determined by the CBM renormalization at local doping density as in Fig. 1e. We self-consistently run the potential renormalization process until convergence is reached (i.e., the Fermi level variation between two consecutive steps is less than 1 meV).