Introduction

Superionic conductors with high ionic conductivity are critical components of solid-state devices such as solid-state batteries and electrochemical sensors1,2,3,4,5,6. These materials are typically composed of mobile ions and a semi-rigid vibrating framework7,8,9,10. In certain materials, such as garnet Li7−xLa3Zr2−xTaxO12, perovskite LixLa2/3−x/3TiO3 and NASICON Li1+xAlxTi2−x(PO4)3, the lithium-ion concentrations can be adjusted within a certain range through aliovalent ion substitution, and the ionic conductivities are highly correlated with the ion concentrations10,11,12,13,14,15,16,17,18. In order to determine the optimal composition for achieving the highest ionic conductivity, it is essential to establish a definitive link between Li-ion concentration and ionic conductivity.

Due to the permanent and temporary site-blocking effects, not all the Li ions can contribute to the ionic conductivity. On the one hand, some Li ions may be permanently blocked by framework ions in localized regions. For example, in perovskite Li0.5La0.5TiO3 where Li-ion, La ion, and vacancy partially occupy the same crystallographic site, some of the Li ions may be blocked by La ions in adjacent sites12. Excluding the permanently blocked ions, the remaining Li ions that have the potential for long-range migration are denoted as mobile ions, also referred to as accessible ions19. On the other hand, a fraction of mobile ions may be temporarily blocked by other mobile ions during the diffusion process. This phenomenon arises because, within a specific arrangement of mobile ions over a period of time, there may not be sufficient vacancies for ion hopping17,20. For example, in cubic garnet Li7La3Zr2O12, numerous Li ions are immobile due to the temporary blockage, while only the remaining Li ions capable of jumps can be classified as effective mobile ions20,21. Therefore, it is crucial to identify which Li ions are effective mobile ions and which ones constitute the blocked ions, and further investigate their impacts on the ionic conductivity. For convenience, the definitions of the different types of Li ions and their concentrations are summarized in Section S1 of the Supplementary Material, including Li-ion concentration (\({C}_{{\rm{L}}{\rm{i}}}\)), mobile ion concentration (\({C}_{{\rm{m}}}\)), and effective mobile ion concentration (\({C}_{{\rm{e}}}\)).

The percolation theory, which is concerned with the connectivity of discrete sites, can be employed to elucidate the site-blocking effects in ion transport19,22,23. Current percolation methods are typically applied on random distributions and assume only uncorrelated single-ion jumps19. However, in many superionic conductors, Li ions adhere to specific distribution rules, and multiple-ion correlated migration is known to play a critical role, especially at non-dilute concentrations, which have been confirmed by dynamic methods such as molecular dynamics (MD) simulations and kinetic Monte Carlo (KMC) simulations24,25,26,27,28,29,30,31. Consequently, in percolation analysis, it is necessary to consider specific Li-ion distributions and their hopping behavior32. Among the dynamic methods, KMC simulations provide an efficient way to obtain reasonable Li-ion distributions and hopping behavior with acceptable accuracy and low computational cost32,33,34,35,36. By utilizing these outcomes as input parameters for percolation analysis, the accuracy and rationality of percolation analysis can be significantly enhanced.

In this work, we propose a strategy, termed P-KMC, that combines an improved percolation analysis with KMC simulations to directly calculate effective mobile ion concentration. The KMC simulations generate reasonable Li-ion distributions and hopping behavior which serve as input parameters for percolation analysis, and then the effective mobile ions and blocked ions are directly identified through the percolation analysis, which takes into account multiple-ion correlated migration when determining conduction state. We apply this method to two representative lithium superionic conductors, cubic garnet-type LixA3B2O12 (0 ≤ x ≤ 9; A and B represent different cations)37,38,39 and cubic perovskite-type LixLa2/3–x/3TiO3 (0 ≤ x ≤ 0.5)12,40,41,42,43,44,45. Our results show that the effective mobile ion concentration (\({C}_{{\rm{e}}}\)) exhibits the same trend vs. Li content (x) as the ionic conductivities in these two examples, highlighting the close association and predictability of \({C}_{{\rm{e}}}\) to ionic conductivity.

Results

Workflow of P-KMC method

The workflow of the P-KMC method is illustrated in Fig. 1. First, the lattice-gas model of the input crystal structure is constructed through topological analysis (Fig. 1a). Then, KMC simulations are performed to obtain ion trajectories (Fig. 1b), from which reasonable Li-ion distributions and hopping behavior can be extracted. Finally, the percolation analysis is performed on every distribution sample, and the effective mobile ion concentration (\({C}_{{\rm{e}}}\)) can be obtained by averaging the results of all percolation analyses (Fig. 1c).

Fig. 1: Workflow of the P-KMC method.
figure 1

a Construction of lattice-gas model. Note that the two-dimensional model depicted here is only for simplified demonstration and is not the model utilized in actual simulations. b KMC simulations to obtain reasonable distributions and hopping behavior of Li ions. c Percolation analysis to identify effective mobile ions and blocked ions. Effective mobile ion is the Li-ion within long-range bidirectional percolated pathways, while blocked ion is immobile or can only be percolated in one direction. They satisfy the relationship: \({N}_{{\rm{Li}}}={N}_{{\rm{e}}}+{N}_{{\rm{b}}}\), where \({N}_{{\rm{Li}}}\), \({N}_{{\rm{e}}}\) and \({N}_{{\rm{b}}}\) denote the number of Li ions, effective mobile ions and blocked ions, respectively. And \({N}_{{\rm{b}}}={N}_{{\rm{p}}}+{N}_{{\rm{t}}}\), where \({N}_{{\rm{p}}}\) and \({N}_{{\rm{t}}}\) are the number of permanently blocked ions and temporarily blocked ions, respectively.

Full size image

Cubic garnet

We demonstrate the applicability of P-KMC method in two representative lithium superionic conductors, cubic garnet LixA3B2O12 (0 ≤ x ≤ 9; where A and B represent a series of aliovalent cations, such as A = La and B = Zr for Li7La3Zr2O12) and cubic perovskite LixLa2/3−x/3TiO3 (0 ≤ x ≤ 0.5). The former exhibits the site-blocking effects of adjacent Li ions, while the latter exhibits the site-blocking effect of both adjacent Li ions and framework ions (La ions). The influence of the variation of Li content (x) on the ionic conductivity is assessed using the effective mobile ion concentration (\({C}_{{\rm{e}}}\)) as a proxy.

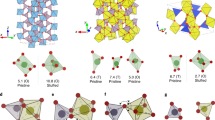
For cubic garnet LixA3B2O12, the lattice-gas model is constructed based on the Li-ion diffusion pathways, which involve the interconnections between tetrahedral and octahedral sites46. Each tetrahedral site is surrounded by four octahedrally coordinated sites, each octahedral site is surrounded by two tetrahedrally coordinated sites, and all sites are partially occupied by Li ions, as depicted in Fig. 2a, b. We disregard the effect of framework element substitution and perform KMC simulations in a 2 × 2 × 2 supercell based on the cubic Li7La3Zr2O12 crystal structure at 300 K, accommodating a maximum of 576 Li ions (equivalent to Li content x = 9, Li-ion concentration \({C}_{{\rm{Li}}}\) = 3.275 × 1028 m−3, supercell volume \(V\) = 1.759 × 10−26 m3). Although the theoretical maximum Li content reaches x = 9 per formula unit when all Li sites are occupied by Li ions32, it has been suggested that mutual locking of adjacent tetrahedral and octahedral sites imposes an upper bound of x ≤ 7.538. Figure 2b illustrates a typical distribution of Li ions in the two-dimensional topological pathways, showcasing the temporary site-blocking effect in the diffusion process. To elucidate the details of the P-KMC simulations, Table 1 summarizes the input parameters and output results for the simulation system with x = 7 and T = 300 K, corresponding to the formula Li7A3B2O12. For simplicity, the values of energy parameters \({E}_{{\rm{nn}}}\) and \({\Delta E}_{{\rm{s}}{\rm{ite}}}\) required by KMC simulation (see “Methods” section for detailed introduction) are assigned as 0.06 and 0.12 eV, respectively, which are approximately 2.3 and 4.6 kBT (when T = 300 K) in the Arrhenius equation, and the energy values remain consistent across all simulated concentrations. The results indicate a very low proportion of correlated jumps involving more than two ions (1.81%), and therefore, the percolation analysis only considers single-ion jumps (71.36%) and two-ion correlated jumps (26.83%) when evaluating the percolated state. The correlated jump percentage reported here is consistent with that found in literature28, which is approximately 25%.

Fig. 2 : The Li–O polyhedra, topological pathways and comparison of CLi, Ce and experimental ionic conductivity (σexp) in cubic garnet structure.
figure 2

a Li–O polyhedra in the crystal structure. b Different types of ions and pathways identified through percolation analysis. c The comparison of the varying trends of \({C}_{{\rm{Li}}}\), \({C}_{{\rm{e}}}\) and the experimental ionic conductivity (\({\sigma }_{\exp }\)) relative to Li content (\({x}_{{\rm{Li}}}\)) in garnet structures. The simulation conditions are \({E}_{{\rm{nn}}}\) = 0.06 eV, \(\triangle {E}_{{\rm{site}}}\) = 0.12 eV and T = 300 K. The insert plot provides a more direct comparison of \({C}_{{\rm{e}}}\) and \({\sigma }_{\exp }\) after normalization, demonstrating a high R2 value of 0.901. The values of \({\sigma }_{\exp }\) are adapted from the following compositions: Li3Er3Te2O12, Li5La3Bi2O12, Li6La3Zr1.5W0.5O12, Li6.2La3Zr1.2Sb0.8O12, Li6.4La3Zr1.4Ta0.6O12, Li6.5La3Zr1.75Te0.25O12, Li6.75La3Zr1.75Ta0.25O12, Li7La3Zr2O12 and Li7.5La2.5Sr0.5Zr2O12, all of which are measured at room-temperature except for Li3Er3Te2O12 (measured at 450 °C) due to the measurement difficulty of its negligible room-temperature ionic conductivity13,16,39.

Full size image
Table 1 Input parameters and output results of P-KMC simulations for the garnet system of x = 7 and T = 300 K
Full size table

Figure 2c reveals that the difference between \({C}_{{\rm{Li}}}\) and \({C}_{{\rm{e}}}\) is not significant in the dilute concentration region (x ≤ 3). However, as x increases, the gap between these two values widens, and the relationship \({C}_{{\rm{e}}}\,\le {C}_{{\rm{Li}}}\) is consistently observed, as indicated by the red solid line (\({C}_{{\rm{e}}}\)) and black dashed line (\({C}_{{\rm{Li}}}\)). This phenomenon is primarily attributed to the blocking effect and the enhanced correlation of ion jumps at high x region. Previous studies39 suggest that x > 3 is necessary to achieve significant ionic conductivity in garnet solid electrolytes, where the Li-ion concentration becomes non-dilute according to the divergence between \({C}_{{\rm{Li}}}\) and \({C}_{{\rm{e}}}\), highlighting the importance of distinguishing between these two concentrations in garnet structures. Hence, \({C}_{{\rm{e}}}\), rather than \({C}_{{\rm{Li}}}\), can serve as an estimation of the ionic conductivity in a superionic conductor, as it contains much more information about ion diffusion properties. The trend of \({C}_{{\rm{e}}}\) is consistent with that of the room-temperature ionic conductivity in the experimentally available x range of garnet structures (with R2 = 0.901 after normalization)39, indicating the strong predictive capability of \({C}_{{\rm{e}}}\) for ionic conductivity. Additionally, the maximum value of \({C}_{{\rm{e}}}\) appears at x = 6–7, which deviates from the trend of \({C}_{{\rm{Li}}}\), suggesting a significant blocking effect at this point, which is similar to Morgan’s previous results32.

Cubic perovskite

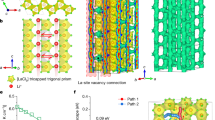
Figure 3 illustrates a schematic depiction of the second example, cubic perovskite LixLa2/3−x/3TiO3 (0 ≤ x ≤ 0.5)12,40,41,42,43, following the general chemical formula ABO3 (A = Li, La; B = Ti). In perovskite structure, the AO12 cages, referred to as A-cages, are hosted in the framework of corner-sharing BO6 octahedra, with each A-cage adjacent to six face-sharing neighboring A-cages. The lattice-gas model is constructed based on the Li-ion diffusion pathways in perovskite structure, which involve the interconnections of A-cages46. La ions are mixed occupied with Li ions in A-cages, serving as blockages in the pathways. In this work, for the sake of simplicity, the blocked sites (La ions) are randomly chosen with a fixed content of 0.5, and the impact of element substitution is not taken into account. The KMC simulations are performed in an 8 × 8 × 8 supercell based on the cubic Li0.5La0.5TiO3 crystal structure with a maximum of 256 Li ions (equivalent to x = 0.5, \({C}_{{\rm{Li}}}\) = 0.850 × 1028 m−3, \(V\) = 2.968 × 10−26 m3) at 300 K. Figure 3b shows a typical arrangement of Li and La ions, elucidating the temporary and permanent site-blocking effects in perovskite structure. An example of the input parameters and output results for the simulation system with x = 0.34 and T = 300 K (Li0.34La0.553TiO3) is presented in Table S2 of the Supplementary Material. Given that there is only one non-equivalence symmetric site in the simulated perovskite structure, \({\Delta E}_{{\rm{s}}{\rm{ite}}}\) is set to 0. The parameter \({E}_{{\rm{nn}}}\) holds a value of 0.12 eV, corresponding to approximately 4.6 kBT (T = 300 K), across all simulated concentrations. Figure 3c presents the dependence of \({C}_{{\rm{Li}}}\) and \({C}_{{\rm{e}}}\) on x, confirming the proposed relationship \({C}_{{\rm{Li}}}\,\ge \,{C}_{{\rm{e}}}\). The values of \({C}_{{\rm{Li}}}\) and \({C}_{{\rm{e}}}\) are almost equal when x ≤ 0.25, but their difference becomes increasingly larger when x > 0.25, indicating high ion correlation in non-dilute concentrations. The peak value of \({C}_{{\rm{e}}}\) occurs around x = 0.34, after which \({C}_{{\rm{e}}}\) begins to decrease. The parabolic variation of \({C}_{{\rm{e}}}\) corresponds to that of the room-temperature ionic conductivities (\({\sigma }_{\exp }\)) within the experimentally available range of x in perovskite structures (with R2 = 0.812 after normalization), revealing the close association between \({C}_{{\rm{e}}}\) and \({\sigma }_{\exp }\) 12,47.

Fig. 3: The Li–O polyhedra, topological pathways and comparison of CLi, Ce and σexp in cubic perovskite structure.
figure 3

a Li–O polyhedra in the crystal structure. b Different types of ions and pathways identified through percolation analysis. c The comparison of varying trends of \({C}_{{\rm{Li}}}\), \({C}_{{\rm{e}}}\) and \({\sigma }_{\exp }\) relative to \({x}_{{\rm{Li}}}\) in perovskite structures at room-temperature. The simulation conditions are \({E}_{{\rm{nn}}}\) = 0.12 eV and T = 300 K. Since there is only one non-equivalent sites in the structure, \({\Delta E}_{{\rm{s}}{\rm{ite}}}\) = 0. The insert plot provides a more direct comparison of \({C}_{{\rm{e}}}\) and \({\sigma }_{\exp }\) after normalization, demonstrating a high R2 value of 0.812. The values of \({\sigma }_{\exp }\) are adapted from LixLa2/3−x/3TiO318.

Full size image

Discussion

A deeper understanding of the relationship between effective mobile ion concentration and ionic conductivity is provided in Section S4 of the Supplementary Material. The aforementioned examples demonstrate that within a certain range, an increase in Li-ion concentration is beneficial for increasing effective mobile ion concentration. However, beyond this range, further increases in concentration can lead to the obstruction of diffusion pathways due to the site-blocking effect, thereby inhibiting ion jumps. The strategy of enhancing ionic conductivity by optimizing Li-ion concentration, as explored in many previous studies16,17,18, is, in fact, a process of increasing ionic conductivity by increasing the effective mobile ion concentration. The P-KMC method can identify the optimal Li-ion concentration where the effective mobile ion concentration reaches its maximum, which serves as an indicator for the highest ionic conductivity. Two approaches can be proposed to optimize ionic conductivity by increasing effective mobile ion concentration. The first approach is to regulate the Li-ion concentration. As illustrated in Fig. 2c, our P-KMC method indicates that the optimal Li content range for garnet structures is \(x\) = 6–7. This can be achieved through aliovalent substitution10. This strategy has also been applied to rhombohedral NASICON structures, where increasing Na content is found to facilitate correlated migration, thereby promoting Na ion mobility24. Another approach is to adjust the interactions between Li ions (\({E}_{{\rm{nn}}}\)) and between Li ions and framework ions (\({E}_{{\rm{site}}}\)), as demonstrated in Eq. (1) in the “Methods” section. Although there has been no experimental investigation on the direct tuning of \({E}_{{\rm{nn}}}\) and \({E}_{{\rm{site}}}\) for LLZO and LLTO, a reversible octahedral-to-tetrahedral migration of Cr in Li1.2Mn0.2Ti0.4Cr0.2O2, observed by EXAFS spectroscopy, has been found to significantly affect the interaction energies by changing the coordination environment of the ions, resulting in a boost of effect mobile ion concentration48.

In summary, we present an efficient and informative scheme to directly calculate the effective mobile ion concentration in superionic conductors by combining kinetic Monte Carlo simulation and static percolation analysis (P-KMC). Our method not only facilitates the quantitative determination of effective mobile ion concentrations but also enables the evaluation of its effect on ionic conductivity. We believe that the P-KMC method can be applied to other solid electrolytes or electrodes, as long as the migration of mobile ions in these materials can be abstracted as the motion of particles in a lattice-gas model. A suggestion of subsequent work is to accurately compute the energy parameters (\({E}_{{\rm{s}}{\rm{ite}}}\), \({E}_{{\rm{nn}}}\), energy barrier), ion distributions, and hopping behavior for KMC simulations and percolation analysis, which can be obtained through bond valence site energy (BVSE) calculations, first-principles calculations, and molecular dynamics simulations24,26,35,36,49.

Methods

Kinetic Monte Carlo simulation

The pathway networks for Li-ions, which consist of sites and connections, are represented by a lattice-gas model through topological analysis of crystal structure46,50,51,52. In KMC simulations, the total energy of the configuration is expressed as the sum of the interactions between Li ions and framework ions, and the interactions between nearest neighboring Li ions32:

$$E=\mathop{\sum }\limits_{i=1}^{n}{E}_{{\rm{sit}}{{\rm{e}}}_{i}}{k}_{i}+\frac{1}{2}\mathop{\sum }\limits_{j=1}^{n}\sum\limits_{\begin{array}{l}{i=1}\!\!\\{i{\ne}j}\end{array}}^{n} {E}_{{\rm{nn}}}{k}_{{ij}}$$
(1)

where n is the number of Li sites, \({E}_{{\rm{sit}}{{\rm{e}}}_{i}}\) is the energy associated with occupying of site i, \({E}_{{\rm{nn}}}\) is the interaction energy between the nearest Li ions, and the values of \({k}_{i}\) and \({k}_{{ij}}\) depend on the specific ion arrangement. If site i is occupied, \({k}_{i}\) = 1; otherwise, \({k}_{i}\) = 0. If site i and its neighbor site j are simultaneously occupied, \({k}_{{ij}}=1\); otherwise, \({k}_{{ij}}=0\). To determine the evolution direction of KMC simulations, the jumps are first randomly selected in a Monte Carlo step (MCS) to generate a new configuration. Subsequently, the transition probability from configuration a to configuration b (\({P}_{a\to b}\)) is calculated using the scheme proposed by Metropolis et al.53,54:

$${P}_{a\to b}=\left\{\begin{array}{ll}1 & {\Delta E}_{a\to b}\le 0\\ \;\;\;\;\;\exp \left(\frac{-{\Delta E}_{a\to b}}{{k}_{{\rm{B}}}T}\right) & {\Delta E}_{a\to b} \,>\, 0\end{array}\right.$$
(2)

where kB is the Boltzmann constant, T is the simulated temperature, and \({\triangle E}_{a\to b}\) is the energy difference between configurations a and b (\({\triangle E}_{a\to b}={E}_{b}-{E}_{a}\)). To facilitate the calculation of time-dependent properties, we adopt one Monte Carlo step as the time unit, thereby avoiding computationally expensive calculations of real time32,33,34. Considering the possibility of correlated jumps24,25,26,27,55, we classify jump modes into the following types: (1) single-ion jump, where the movement of an ion is independent of adjacent ones; (2) two-ion correlated jump, where two adjacent ions hop simultaneously (as illustrated in Fig. 1b); and similarly (3) three-ion and (4) four-ion correlated jumps. The correlated jumps involving more than four ions are disregarded due to their infrequent occurrence. To quantify the probability and significance of each jump mode, the percentage of jump mode (\({P}_{i}\)) is defined as the ratio of the number of i-ion jumps (\({n}_{i}\)) to the total number of jumps (\({n}_{{\rm{t}}{\rm{ot}}}\)): \({P}_{i}=\frac{{n}_{i}}{{n}_{{\rm{t}}{\rm{ot}}}}\), where i = 1, 2, 3, 4.

Percolation analysis

The configuration samples generated by KMC simulations are utilized to construct a series of percolation models, and percolation analysis is performed on each model, taking into account the specific jump mode. With the constrain of the site-blocking effect, graph coloring algorithm is proposed to determine the connectivity among sites and identify the percolation clusters that represent long-range diffusion pathways56. Ions within these percolated pathways are defined as effective mobile ions. The effective mobile ion concentration (\({C}_{{\rm{e}}}\)) averaged over n percolation models is calculated as:

$${C}_{{\rm{e}}}=\frac{1}{{n}_{\triangle t}}\mathop{\sum }\limits_{i=1}^{{n}_{\triangle t}}\frac{{N}_{{\rm{e}}}}{V}$$
(3)

where \({n}_{\triangle {\rm{t}}}\) is the number of time steps, \({N}_{{\rm{e}}}\) is the number of effective mobile ions during the i-th time period with a time step of \(\triangle t\) (in this work, \(\triangle t\) is selected as one Monte Carlo step) and V is the volume of simulated supercell. The calculation of \({C}_{{\rm{e}}}\) additionally incorporates dynamic ion hopping behavior compared to the current percolation analysis, thus providing more reliable information about diffusion properties. The detailed definitions of \({C}_{{\rm{e}}}\) and other types of concentrations are presented in Section S1 of the Supplementary Material.

Calculation steps of the P-KMC method

Figure 4 illustrates the detailed calculation steps of the P-KMC method, which includes two parts: KMC simulation and percolation analysis. The calculation steps are as follows:

  1. (1)

    Read input structure and settings. The input structure file should provide site coordinates and connections, which can be obtained through topological analysis.

  2. (2)

    Initialize the KMC simulation. Construct the lattice-gas model and set up simulation parameters, including temperature T, Li-ion concentration \({C}_{{\rm{Li}}}\), supercell size, simulation steps, etc.

  3. (3)

    Record the initial configuration, denoted as \({W}_{0}\), and calculate its system energy, denoted as \({E}_{0}\).

  4. (4)

    Make ions randomly jump and generate a new configuration, denoted as \({W}_{1}\), and calculate its system energy, denoted as \({E}_{1}\).

  5. (5)

    Accept the new configuration with probability \(P\) by comparing the energies before and after configuration evolution.

  6. (6)

    When the energy of configuration reaches a steady value, start collecting and saving sample data, including sample configurations, simulation time, etc.

  7. (7)

    Change the simulation parameters to repeat the above process, record multiple sets of sample data, and determine whether to end the KMC simulation.

  8. (8)

    Read external instructions to decide whether to perform percolation analysis. if “Yes”, read input settings for percolation analysis; if “No”, save the simulation data and end the program.

  9. (9)

    Read the sample data obtained from the KMC simulation and analyze the ion distribution and hopping behavior.

  10. (10)

    Analyze the site connections in the sample configuration constructed in step (9) according to the ion distribution and hopping behavior.

  11. (11)

    Perform percolation analysis on the connectivity map constructed in step (10), and record and save simulation data such as effective mobile ion concentration \({C}_{{\rm{e}}}\).

  12. (12)

    Repeat the above process until all sample data have been processed.

  13. (13)

    End the program.

Fig. 4: Detailed calculation steps of the P-KMC method.
figure 4

The calculations consist of two parts: KMC simulation and percolation analysis, with the former providing inputs for the latter.

Full size image