Introduction

High-entropy alloys (HEAs) are a novel class of alloys with intriguing properties, including high strength1,2,3,4,5,6, corrosion resistance7,8, irradiation tolerance9,10,11, and high-temperature oxidation resistance12,13,14. HEAs typically contain five or more principal elements with concentrations between 5% and 35%, holding promise for optimizing various properties. The diverse microstructures and phases in HEAs greatly influence their targeted properties. For example, face-centered cubic (FCC) phases are usually ductile, while body-centered cubic (BCC) phases exhibit high strength15,16. Therefore, accurately predicting the phases (e.g., solid solution (SS) and non-solid solution (NSS), FCC, BCC, or dual phases (DPs)) is crucial in designing HEAs.

One of the main challenges in designing HEAs is the vast unexplored composition space, resulting from the multiple components and wide range of element concentrations. Machine learning (ML) has been employed to predict the phase formation of HEAs17,18,19,20,21,22,23,24,25,26,27,28,29. Several surrogate models with prediction accuracies over 75% have been built using various physical and chemical properties of elements30,31,32,33,34,35, such as electronegativity, atomic radius, and valence electron number, as shown in Fig. 1a. Those elemental properties serve as numerical descriptions of elements, which are vectors containing particular values for different elements to describe the alloy. However, further improvement in ML predictions is hindered by the limited number of traditional numerical descriptions of elements.

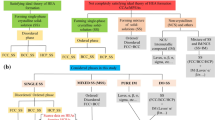
Fig. 1: The proposed strategy to generate new numerical descriptions of elements for a particular problem.
figure 1

a Common practice is to combine the composition with numerical descriptions of elements to construct material features. b The known numerical descriptions of elements, such as radius and valence electron concentration, are only a small fraction of the optimization space. Better numerical descriptions of elements are likely to be generated to improve the model's performance and extensibility. c As the optimization space is enormous, a tailored genetic algorithm framework is employed to generate better numerical descriptions of elements.

Full size image

The existing physical and chemical properties of elements represent only a small portion of the possible space, as indicated by the blue lines out of numerous orange lines in Fig. 1b. The value describing each element is not inherently restricted, forming a vast space of possibilities. Our interest lies in generating better numerical descriptions of elements within this space (as indicated by the red lines in Fig. 1b), to improve model performance for phase prediction of HEAs. Moreover, we anticipate that the generated numerical descriptions can be extended to other predictive tasks, such as estimating mechanical properties.

In the present study, we propose a strategy based on a tailored genetic algorithm (GA) to obtain new numerical descriptions. We generated four new vectors to describe the elements Al, Ti, V, Cr, Fe, Co, Ni, and Cu. Logistic regression (LR) models based on these generated numerical elemental descriptions outperformed those based on empirical features. The classification accuracy for recognizing FCC, BCC, and DP in HEAs improved by 20%, from 77% to 97%. For distinguishing SS and NSS phases, the accuracy improved from 81% to 87%. We experimentally validated our model by randomly selecting 15 new HEAs. Our model correctly labeled 8 out of 9 for FCC, BCC, and DP, and 13 out of 15 for SS and NSS phases, significantly outperforming models based on traditional empirical features. By incorporating these descriptions derived from a simple LR model, the performance of various classifiers improved by 3% to 22%. Furthermore, the generated numerical descriptions of elements were directly applied to reduce the regression errors in predicting the hardness of HEAs. Testing on six different materials datasets, including ceramics and functional alloys, demonstrated that the obtained numerical descriptions significantly improved prediction precision across various properties. This highlights the broad applicability of our strategy.

Results

Design strategy and modeling

As schematically illustrated in Fig. 1c, this study introduces a tailored GA framework to optimize numerical descriptors for elements, enhancing the predictive performance of phase classification in HEAs. The protocol consists of five key steps: initial population generation, materials feature construction, feature evaluation using a classification model, selection, and crossover & mutation.

Initial population generation

The numerical description of elements is designed to capture the inherent differences among various elements. Each element is assigned a value between 0 and 1, reflecting its relative magnitude compared to other elements. To construct the search space, this range is discretized into 100 values with an increment of 0.01. For this study, eight elements, including Al, Ti, V, Cr, Fe, Co, Ni, and Cu, are considered. Consequently, a vector (\(\vec{x}\)) containing eight values serves as the numerical description of the elements. Two numerical vectors (i.e., a pair of \(\vec{x}\)) are generated, ensuring clear physical interpretability and limiting the search space (additional details can be found in the Supplementary Discussions). Thus, each individual in the GA is represented as a string of length 16. An initial population of p = 500 strings is randomly generated as a parent generation.

Materials feature construction

Based on the two vectors (\(\vec{x}\)) in each individual, two material features (X) are calculated using the formula:

$$X=\sqrt{\mathop{\sum }\limits_{i=1}^{n}{c}_{i}{\left(1-\frac{{\overrightarrow{x}}_{i}}{\bar{X}}\right)}^{2}}$$
(1)

where i stands for different elements, ci is the concentration and \(\bar{X}\) is the mole average of \(\vec{x}\), given by

$$\bar{X}=\mathop{\sum }\limits_{i=1}^{n}{c}_{i}{\overrightarrow{x}}_{i}$$
(2)

This formula has been widely used to characterize the mismatch between elements in HEAs36,37,38,39. At this stage, 500 pairs of material features are generated, corresponding to the initial population of the GA. Each pair of features represents a unique combination of elemental descriptors that will be evaluated for their ability to predict the phase behaviour of the alloy. These material features serve as the input for the ML model in the next step, where their predictive power will be assessed.

Materials feature evaluation

An LR classifier is employed to assess the predictive performance of the material features derived from each individual in the tailored GA. The classification accuracy, calculated using the entire dataset, serves as the fitness value. The higher the classification accuracy, the better the material features are at distinguishing between different phases, indicating that the individual is more effective in representing the desired characteristics of the high-entropy alloys. This evaluation process ensures that individuals with higher fitness values, i.e., higher classification accuracy, have a greater probability of passing on to the next generation.

Selection

The Stochastic Tournament Selection method40 is employed to select individuals (numerical descriptions of elements) for reproduction based on their relative fitness values, steering the GA toward more optimal solutions. Specifically, two individuals are randomly selected from the population, and the one with the higher fitness value is retained for the next generation. This selection process is repeated 500 times to maintain a constant population size of 500 individuals.

Crossover and mutation

Uniform crossover41 and single-point mutation42 operators are employed to generate novel elemental numerical descriptions, thereby increasing the diversity of the search process. In the uniform crossover phase, 90% of the population is preselected, and two individuals are randomly chosen as parents. Each gene in the offspring’s individual is randomly selected from one of the corresponding genes of the two parents. This procedure is repeated until the required number of offspring is generated for the subsequent mutation step. Following crossover, single-point mutation is applied. A total of 800 gene loci from the entire population (16 genes locus × 500 individuals) are randomly selected, with a mutation probability of 10%. The selected genes are then replaced with new values randomly drawn from a range between 0 and 1. This introduces additional variability, ensuring a more thorough exploration of the search space.

The newly generated 500 individuals are appended to the next generation. The classification accuracies of the new generation are then evaluated, and the selection, crossover and mutation processes are repeated. This iterative process continues until a maximum of 1000 generations is reached. It is noted that besides the GA, other heuristic algorithms or cutting-edge techniques like reinforcement learning could also be incorporated into our framework. Exploring these methods is a promising direction for future work.

Elemental numerical descriptions for phase prediction of high-entropy alloys

We investigated two classification problems: classification I for SS and NSS HEAs, and classification II for FCC, BCC, and DP HEAs. We first searched for a pair of numerical descriptions of elements for classification I.

The GA strategy shown in Fig. 1c was employed. The best classification accuracy within each generation of 500 LR models was plotted as a function of the number of iterations for one GA run in Fig. 2a. As the initial population of numerical descriptions for elements was stochastically generated, resulting in ML models with low classification accuracy. The crossover and mutation of GA rapidly explored offsprings, presumably with better prediction accuracy. Such a GA process was performed 50 times to obtain a stable and superior solution, as the result of GA usually depends on its initial population. The red solid line in Fig. 2a represents the best performer of the 50 GA runs. And, the two vectors of numerical descriptions for elements with the highest classification accuracy were identified as (\({\vec{x}}_{I}^{\,1}\) and \({\vec{x}}_{I}^{\,2}\)) for classifying SS and NSS alloys, as listed in Table 1.

Fig. 2: Results of 50 GA runs and the classification performance for phase prediction of HEAs.
figure 2

a, b The classification accuracy of the logistic regression (LR) model as a function of the number of iterations within 50 GA runs for classification I and classification II, respectively. The red solid line indicates the best performer. c, e is the margin of LR model to classify the SS and NSS HEAs based on the materials features defined from the numerical descriptions of elements and traditional empirical features, respectively. d, f is the margin of the LR model to classify FCC, BCC, and DP HEAs based on the features of the material defined from the numerical descriptions of elements and traditional empirical features, respectively. The larger symbols represent the 15 newly synthesized HEAs.

Full size image
Table 1 The obtained numerical descriptions of elements for phase prediction of high-entropy alloys
Full size table

Based on \({\vec{x}}_{I}^{\,1}\) and \({\vec{x}}_{I}^{\,2}\), two materials features (\({X}_{I}^{1}\) and \({X}_{I}^{2}\)) were calculated according to Equation (1). In Fig. 2c, the data are plotted on the plane of \({X}_{I}^{1}\) and \({X}_{I}^{2}\) with a classification margin differentiating SS and NSS. The classification accuracy is 87%. We traverse all possible pairs of nine empirical material features to choose the one with the highest accuracy for separating SS and NSS in our dataset. As shown in Fig. 2e, Λ-γ has the highest accuracy of 81%. Thus using the generated two vectors of numerical descriptions of elements \({\vec{x}}_{I}^{\,1}\) and \({\vec{x}}_{I}^{\,2}\), the classification accuracy for SS and NSS is improved by 6%.

We then performed the same procedure to identify two vectors of numerical descriptions of elements for classification II. The GA rapidly converges, as shown in Fig. 2b and identifies two vectors (\({\vec{x}}_{II}^{\,1}\) and \({\vec{x}}_{II}^{\,2}\)) as listed in Table 1. Figure 2d shows the classification margin for separating FCC, BCC and DP on the plane of \({X}_{II}^{1}\) and \({X}_{II}^{2}\) calculated from \({\vec{x}}_{II}^{\,1}\) and \({\vec{x}}_{II}^{\,2}\). The classification accuracy is as high as 97%. Compared to the best empirical materials features pair of VEC and δR in Fig. 2f, the classification accuracy is improved by 20%.

Compared to previous efforts in ML-assisted phase prediction of HEAs30,31,32,33,34,35, our strategy achieved a higher classification accuracy with simpler ML models by the newly generated elemental numerical descriptions. Therefore, it is possible to generate new vectors of numerical descriptions for elements in an unlimited space, which would enhance model performance for specific problems. However, whether the generated numerical descriptions of elements provide validated predictive capability and can be extended to other problems remains unclear. In the following two subsections, we performed experiments to verify the predictive capability and then utilized the new sets of numerical descriptions for elements in the phase classification problem to improve the regression model for the mechanical properties of HEAs.

Experimental validation of classification model predictions

Fifteen compositions were randomly chosen from a large virtual space consisting of 1,697,136 candidates. This space was constructed by varying the molar fraction of elements between 0.05 and 0.35 in steps of 0.03, within a system of Al, Ti, V, Cr, Fe, Co, Ni, and Cu (considering only alloys with four to six elements). The chemical compositions of the 15 alloys (denoted as A1 to A15) are listed in Table 2.

Table 2 The composition, phase formation, and mechanical properties of the 15 newly synthesized HEAs
Full size table

Figure 3a shows the X-ray diffractometer (XRD) profiles of the 15 new HEAs. For classification I, six selected alloys (A1–A6) are labeled as NSS due to the appearance of intermetallic phase (IM) peaks, while the remaining alloys are labeled as SS. Since the IM peaks of A1-A4 alloys are not very distinct, further scanning electron microscopic (SEM) combined with energy dispersive X-ray spectroscopy (EDS) analyses, shown in Fig. 3b–e, confirm that an Al-Cr-rich IM phase exists in A1 and A2 alloys, a B2 structure IM phase appears in A3 alloy, and fine V-rich precipitates are present in A4 alloy. For classification II, A7, A8, and A9 alloys exhibit XRD peaks corresponding to FCC and are thus labeled as FCC. A10, A11, and A12 alloys show peaks for both FCC and BCC phases, leading to their classification as DP. Correspondingly, A13, A14, and A15 alloys are labeled as BCC. The actual labels and the predicted ones are compared in Table 2. It can be seen that 13 of the 15 HEAs are accurately predicted for classification I, and 8 of the 9 HEAs are accurately predicted for classification II, using LR models based on the newly generated elemental numerical descriptions. The new labels of the synthesized HEAs are also plotted in Fig. 2c–f. These new data can be fed back into the original datasets to further improve accuracy.

Fig. 3: Microstructure of newly synthesized HEAs.
figure 3

a XRD profiles of newly synthesized HEAs. b–e The SEM and EDS analysis for selected HEAs: b A1, c A2, d A3, and e A4.

Full size image

The A1 and A2 alloys were mislabeled by traditional empirical features. It may be because traditional features primarily involve information on the mismatch in atomic size (for example, δR represents atomic size difference, and γ reveals the atomic packing misfitting and topological instability43). The difference in radius of elements such as Al, Ti, V, and Cr in A1 and A2 alloys is rather small, leading to the incorrect prediction of SS formation. However, the Cr has a large negative enthalpy of mixing with Al and facilitates the formation of Al-Cr-rich intermetallic compounds, which was missed by traditional empirical features. Our features failed to predict the NSS label for A4, as a small variation in Cr and Co leads to a low fraction of fine V-rich precipitates in the A4 alloy compared to the SS phase in A7.

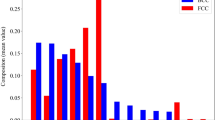
Phases significantly influence the mechanical properties of HEAs, so we conducted compression tests at room temperature on the new SS HEAs. The stress-strain curves of the nine alloys are shown in Fig. 4a. The FCC alloys, including A7, A8, and A9, exhibit low strength (yield strength σy ~ 200 MPa) but high ductility (fracture strain ϵf > 50%). In contrast, A13, A14, and A15 alloys, characterized by the BCC phase, display relatively high strength and low ductility. The DP alloys, including A10, A11, and A12, show a large variation in both strength and ductility. As illustrated in Fig. 4b, a DP structure combining BCC and FCC phases provides a good balance, trading off between strength and ductility. In summary, phase information as a priori knowledge is crucial for the targeted design of alloys.

Fig. 4: Compressive mechanical properties of the nine newly synthesized HEAs.
figure 4

a Compressive stress-strain curves. b Room temperature compressive yield strength vs fracture strain.

Full size image

Enhancing regression models for the hardness of HEAs

Next, we demonstrate the improvement in regression model performance by using the numerical descriptions of elements generated from the classification task. We hypothesized that these features capture hidden information about the HEAs phase structures, and therefore, the numerical descriptors used for phase classification are likely to enhance the prediction accuracy of materials properties. Rather than generating specific numerical descriptions tailored for the regression task, we utilized both the newly generated materials features (\({X}_{I}^{1}\), \({X}_{I}^{2}\), \({X}_{II}^{1}\), and \({X}_{II}^{2}\)), and traditional empirical features to build gradient boosting decision tree (GBDT) models for predicting the hardness of HEAs. This analysis was performed using a dataset of 173 samples. The empirical material features include the nine traditional features used for phase prediction, as well as additional mechanical property-related features, such as shear modulus (G), local modulus mismatch (D. G), difference in shear modulus (δG), energy term in the strengthening model (A), Peierls-Nabarro factor (F), modulus mismatch (η), lattice distortion energy (D. R), local size mismatch (μ), and the square of the work function (w)44,45,46,47,48,49. A detailed list of these 18 features is provided in Supplementary Table S1.

We then evaluated the performance of the GBDT models using three material features. We selected the best subset of features from the newly generated material features (\({X}_{I}^{1}\), \({X}_{I}^{2}\), \({X}_{II}^{1}\), and \({X}_{II}^{2}\)), along with the best subset of empirical features. To assess model performance, we employed both 10-fold cross-validation and the hold-out method. In the hold-out method, the original dataset was randomly split into a training set (90%) and a testing set (10%). A GBDT model was then trained on the training set, and its performance was evaluated on the testing set. Model performance was quantified using the coefficient of determination (R2) and the mean absolute error (MAE), calculated using the formula:\(\frac{1}{n}\mathop{\sum }\nolimits_{i = 1}^{n}\left\vert {y}_{i}-\hat{{y}_{i}}\right\vert\) where n is the number of data points, yi is the true value, and \(\hat{{y}_{i}}\) is the predicted value. This procedure was repeated 100 times to ensure robustness, and the average R2 and MAE values for each model were recorded as indicators of model performance.

As shown in Fig. 5a, b, the feature subset that achieved the lowest test error for hardness prediction includes \({X}_{I}^{2}\), \({X}_{II}^{1}\), and \({X}_{II}^{2}\). This subset resulted in an MAE of 45.8 HV and an R2 value of 0.88. In comparison, the best empirical feature subset, consisting of VEC, F, and δG, yielded an MAE of 58.6 HV and an R2 value of 0.79. This improvement is statistically significant, as evidenced by the t test P value, which is smaller than 0.01, as shown in Fig. 5. This confirms that the inclusion of the newly generated elemental numerical descriptors significantly enhanced model performance, reducing the MAE by 22% and increasing the R2 value from 0.79 to 0.88. These results highlight the effectiveness of the descriptors, originally designed for phase classification, in enhancing regression performance for hardness prediction. This demonstrates their versatility and broader applicability in materials property prediction (regression) tasks for HEAs.

Fig. 5: Improvement in hardness prediction with newly generated features.
figure 5

Comparison of a R2 and b MAE values for machine learning models based on material feature subsets that achieve the lowest test error, with and without the inclusion of our newly generated features. The statistical significance of the improvement is indicated by the t test P value (<0.01).

Full size image

Discussion

The generated numerical descriptions of elements are effective for both classification and regression tasks in the design of HEAs. These descriptions likely correlated with specific physical and chemical properties of elements. We conducted Pearson correlation analysis between the generated numerical descriptions and various elemental properties such as atomic radii (R), Pauling electronegativity (χP), valence electron concentration (VEC), and others. A detailed list of these properties can be found in Supplementary Table S2).

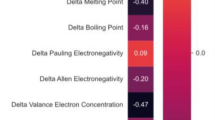
Our analysis revealed that \({\vec{x}}_{I}^{1}\) and \({\vec{x}}_{I}^{2}\) have the highest Pearson correlation coefficients with the electrical resistivity (ER) and the metallic radius (R), respectively, among all the physical properties. The results are shown in Fig. 6a, b. \({\vec{x}}_{I}^{1}\) contains similar information with ER, which is related to electronegativity, while \({\vec{x}}_{I}^{2}\) correlates with R, representing the atomic size effect. Both electronegativity and atomic size are crucial factors in the Hume-Rothery rules for evaluating the phase stability of alloys36,50,51. Thus, the generated \({\vec{x}}_{I}^{1}\) and \({\vec{x}}_{I}^{2}\) are consistent with empirical knowledge.

Fig. 6: Correlation between physical properties of elements and the generated optimal numerical descriptions of elements.
figure 6

a \({\vec{x}}_{I}^{1}\) vs electrical resistivity. b \({\vec{x}}_{I}^{2}\) vs R. c \({\vec{x}}_{II}^{1}\) vs s-electron in total VEC. d \({\vec{x}}_{II}^{2}\) vs work function.

Full size image

Figure 6c, d show that \({\vec{x}}_{II}^{1}\) and \({\vec{x}}_{II}^{2}\) are most relevant to the proportion of s-electron in total VEC (s.VEC) and the work function (WF). The WF measures how tightly a metal holds its electrons, while VEC represents the number of total electrons, including d electrons in the valence band. These parameters have been used to predict the formation of FCC and BCC phases in HEAs52,53. Our result in Fig. 6c indicates that s.VEC could be a better numerical description of elements for this classification problem as it includes both the effect of VEC and the number of easily lost s-electrons.

For classification I, materials features of δR and δER were defined by R and ER according to Equation (1). The classification accuracy of 0.81 is the same as the one from widely used empirical features (Fig. 2e). For classification II, the pair of WF and s. VEC calculated by Equation (2) improves the classification accuracy from 0.77 (using empirical features) to 0.8. The selection of Equation (2) is based on the observation that Equation (2) consistently resulted in higher classification accuracy for Classification II compared to Equation (1). This finding aligns with prior experience, as the VEC parameter, which is widely used to distinguish FCC, BCC, and DP phases, is also derived using Equation (2). Figure 7 compares the performance of classifiers based on features from our generated numerical descriptions of elements, features selected through correlation analysis, and traditional empirical features. Features from our generated numerical descriptions outperform the other two sets. A possible reason is that existing physical properties of elements may vary in complex systems due to the significant influence of physical and chemical interactions from surrounding atoms.

Fig. 7
figure 7

The performance of classifiers based on the features from our new numerical descriptions of elements, the features selected by the correlation analysis shown above, as well as traditional empirical features.

Full size image

Although the elemental numerical descriptions shown in Table 1 were generated using LR models, it is expected that incorporating these values will enhance the performance of other classifiers for phase formation in HEAs, as already utilized in previous studies30,31,32,33,34,35,54,55. Five widely used classification models were built: a decision tree model (Dtree), a Naive Bayes classifier (Bayes), a Neural Network classifier (Nnet), a random forest model, and a support vector machine with a radial basis function kernel (SVM.rbf). To estimate the performance of these ML models, we adopted a cross-validation method (10-folds with 100 repetitions) during the models’ training and testing. The final reported testing accuracy is the average of the 100 testing accuracy results.

Figure 8 presents a comparison of the five ML models using traditional empirical features versus the same models using the newly generated features. When the new features from our numerical descriptions are introduced, the accuracy of all classifiers increases. The classification accuracy can be improved by up to 15% for SS and NSS, and up to 22% for FCC, BCC, and DP, as shown in Fig. 8. Thus, the generalization ability of our generated numerical descriptions of elements was verified by the experimental results and their efficient improvement in both regression and classification tasks across different ML models.

Fig. 8: Comparison among different ML models: traditional features vs new features.
figure 8

a Classification I. b Classification II.

Full size image

The strategy developed in this study can be extended to various materials datasets, including high-temperature strength (HT strength) and fracture strain of HEAs, the piezoelectric coefficient (d33), the electrostrain and the dielectric energy storage density (DES density) of BaTiO3 ceramics, and the transformation temperatures of NiTi-based shape memory alloys (SMA TC). Detailed information about these datasets is summarized in Supplementary Table S3, and all datasets are available in the Supplementary Information. Since the datasets we used differ from the ones in the referenced studies, a direct comparison of our results with theirs would not be fair or meaningful. To ensure a more robust comparison, we focused on evaluating the impact of our feature generation strategy using the same dataset and ML models.

Following the same procedure shown in the “Design strategy and modeling” subsection, our strategy generated two new numerical descriptions of elements for each targeted property, as listed in Supplementary Table S4. We then used these descriptions to construct two materials features according to Equation (2) and built the corresponding support vector machine (SVM) regression model. For comparison, traditional materials features were selected using sequential forward selection (SFS) methods, which resulted in models with more than three features. The traditional features are detailed in Supplementary Table S3.

Figure 9 compares the performance of models using traditional features with those using the newly generated features. Figure 9a, b display the predicted values versus the measured electrostrain. The data points are closer to the diagonal line for the model using our new features (Fig. 9b). This trend is also observed for the high-temperature strength of HEAs and the transformation temperatures of SMA TC, as shown in Fig. 9c–f. Figure 9g, h presents the comparison of model performance in terms of R2 and mean absolute percentage error (MAPE), calculated as \(\frac{100 \% }{n}\mathop{\sum }\nolimits_{i = 1}^{n}\left\vert \frac{{y}_{i}-\hat{{y}_{i}}}{{y}_{i}}\right\vert\). Using only two features from the generated elemental numerical descriptions outperforms ML models that rely on multiple traditional empirical features across all datasets tested in this study.

Fig. 9: Comparison of regression models based on the features of the material defined from the generated numerical description of elements and the traditional empirical features.
figure 9

a, b For electrostrain of BaTiO3 ceramics. c, d for high-temperature strength of HEAs. e, f for transformation temperatures of NiTi-based shape memory alloys. g, h summarize the comparison of the model performance in terms of R2 and MAPE in six materials datasets.

Full size image

In summary, we proposed a strategy to generate numerical descriptions of elements to enhance the prediction accuracy of ML models for targeted properties. This strategy was applied to predict phase formation in HEAs, achieving up to a 20% improvement in classification accuracy for recognizing FCC, BCC, and dual-phase alloys. Experimental validation demonstrated that the features of the material constructed from the generated numerical descriptions accurately predicted 8 out of 9 newly synthesized alloys, outperforming traditional empirical features, which yielded 4 correct labels. The generated numerical descriptions of elements were also utilized to enhance regression models for the hardness of HEAs, improving the R2 value from 0.79 to 0.88. Additionally, the prediction accuracy of five classifiers was improved using these generated numerical descriptions, with accuracy gains ranging from 3% to 15%. The strategy was tested on six different materials datasets, consistently improving model performance for predicting targeted properties. This work provides a robust method for generating new numerical descriptions of elements and consequently enhancing the performance of ML models.

Methods

Dataset and empirical materials features

The phase information for AlTiVCrFeCoNiCu HEAs was collected from the literature, limited to as-cast samples. Our dataset comprises 301 experimentally obtained HEAs, labeled as either SS or NSS. Additionally, the 150 SS alloys were further categorized into FCC, BCC, or DP.

For comparison, we also used nine empirical material features reported to affect the phase formation of HEAs. These include the mixing enthalpy (ΔHm), the mixing entropy (ΔSm), the VEC, the difference in the Pauling electronegativities (δχP), the Allen electronegativity (δχA), the atomic size difference (δR), comprehensive descriptor (Ω) that quantifies the predominance of the entropy with respect to the enthalpy, and two geometrical descriptors (Λ) and (γ)36,37,38,39,43,52,53,56,57,58,59. A detailed list of these features is provided in Supplementary Table S1.

Experimental procedure

The experimental validation of the ML predictions was performed. The HEA ingots with a weight of 50 g were prepared by arc melting on a water-cooled copper mold in the argon atmosphere, with a mixture of raw materials of 99.9% pure elements. All the ingots were melted at least six times to improve the homogeneity. The crystalline structures were analyzed by a Bruker D8 ADVANCE XRD with Cu Kα radiation with the 2θ ranging from 30° to 100° at a speed of 3°/min. The morphology and the micro-composition of the HEAs were obtained by a Zeiss Sigma300 SEM combined with EDS. Cylinder specimens with a diameter of 3 mm and a height of 6 mm for compressive tests were prepared by spark cutting followed by grinding with sandpaper. Compressive stress-strain curves were measured by an Instron 5969 tensile machine at room temperature with a strain rate of 0.3 mm/min. Each test was repeated at least three times. The 0.2% proof strength was identified as the yield strength.