Introduction

Metallic glasses1,2,3,4,5 (MGs) are attracting ever-increasing interest for their remarkable mechanical properties, such as high strength, hardness, and wear resistance, which make them promising candidates for advanced applications6,7,8. These unique properties of MGs stem from their amorphous (disordered) atomic structure, in contrast to the crystalline (ordered) structure of traditional metals and alloys. The amorphous state is achieved by rapidly cooling the metallic liquid to prevent the atoms from organizing into a crystalline arrangement. This cooling process directly affects a critical feature called glass forming ability3,9,10,11,12,13,14,15,16 (GFA), which is the ability of a material to avoid crystallization and maintain a disordered structure during cooling. A good GFA is fundamental to making any metallic glass and possibly acquiring unique mechanical properties. However, questions remain about how cooling rates17,18,19,20, i.e., the variation of temperature with respect to time, and chemical compositions may promote a glassy disordered state (good GFA). In generic terms, while rapid cooling supports GFA, quenching or cooling from the liquid state gives better and better properties the slower the procedure is, though with an increasing risk of crystallization due to the general metastability of the glassy state. This account is for ideal MG, however, in the laboratory reality, the glass-making route is a daunting task21,22.

The exploration of metallic glass property landscapes has first and foremost concentrated on the GFA since that is the starting point for considering any particular composition and a preparation route. Here and for other properties, one faces considerable challenges in coming up with high-throughput experimental approaches for mapping or design/optimization, often using machine learning23,24. Similar composition landscape problems are presented by high-entropy (crystalline) alloys (HEAs), where the phase stability (at a given temperature) and the challenge of multi-property optimization become evident. The high complexity of MGs has, in general, received a lot of attention from ML approaches25,26,27 that help to predict promising compositions with good GFA within a large compositional space. Molecular dynamics (MD) simulations instead allow the computational investigation of MG properties after sample preparation by a given cooling method. The typical application is to compute the mechanical properties of a prepared sample, e.g., in conditions simulating nanoidentation28, deformation protocol dependence29, tensile straining30, or shear deformation31.

Moving beyond the progress in predicting GFA, a key question remains: how cooling rates and composition interact to influence the mechanical performance in metallic glasses? To answer this question, here, we systematically investigate the link between composition, cooling rate, and mechanical performance within the CuZrAl system, a ternary metallic glass with known good GFA and promising mechanical properties. This system has recently been explored for the GFA as a function of composition using MD to compute descriptors for that purpose32. Furthermore, it has been experimentally shown that the addition of small amounts of Al into the CuZr MG increases the mechanical properties, such as strength, ductility, elastic modulus, hardness, and work-hardenability. The optimal amount of Al concentrations seems to vary from 5%33,34 to exceeding 10%35,36. Additionally, some studies indicate that a decrease in the plastic strain is seen with the increase in strength and modulus37.

In this study, we aim to efficiently map the landscape of target mechanical properties using Bayesian optimization and MD simulations. Despite the fact that there are fewer compositional degrees of freedom compared, e.g., to high-entropy alloys38,39, here the sample preparation in simulations is computationally significantly more costly. This is due to the fact that glasses are history-dependent, and their properties are significantly influenced by the preparation protocols. In order to approach experimental reality in terms of realistic cooling rates, difficult to achieve in numerical simulations, Monte Carlo methods have lately become popular40,41,42. In this work, we exploit this type of protocol and vary the cooling rate and elemental compositions to explore their effects on glass properties.

To probe the high-dimensional search space even more efficiently, we employ active learning methods43,44,45,46,47. These methods aim to identify optimal compositions with minimal computational cost. Compared to other iterative sampling methods, such as Sobol sequences48,49, active learning methods take the already measured values into account in the sampling point selection and do not only consider the geometry of the search space. We use Bayesian optimization38,39,47,50,51,52 (BO) with Gaussian Process Regression53 (GPR) to explore the search space and to finally exploit the gathered information in finding the optimal composition. Gaussian process regressors require far fewer hyperparameters to be fitted compared, for example, to neural networks, and this translates to significantly smaller datasets needed during BO. We study in silico the CuZrAl metallic glass, and vary its composition around the standard Cu0.50Zr0.50 starting point. A practical reason for this is, in addition to the large interest in this system, the availability of MD potentials.

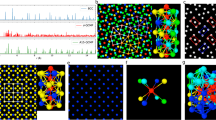
Specifically, in this work, we utilize an automated protocol38 (see Fig. 1) which combines: an online database, a Bayesian optimization algorithm for the selection of the subsequent composition, and molecular dynamics for the glass preparation and shear simulations to probe the mechanical properties. Our goal is to efficiently map the composition space of CuZrAl glasses in regard to their mechanical properties. In the following, we describe the search process, the effect of the cooling rate, and finally the optimal CuZrAl glass compositions.

Fig. 1: Workflow of the optimization process.
figure 1

The data is stored in an online Aalto Materials Digitalization Platform (AMAD) database from which the Bayesian optimization (BO) algorithm determines the next composition cn+1. In a molecular dynamics (MD) simulation, metallic glasses (MGs) of this composition are prepared, checked for crystallinity, and sheared. Finally, the database is updated with the yield stress τy and modulus G determined from the stress-strain curve. The different cooling rates \(\dot{T}\) are run in different loops. The top-right corner illustrates the composition choice made by the BO algorithm: the new composition corresponds to the maximal standard deviation of the yield stress determined by Gaussian process regression (GPR). The bottom-right corner shows the stress-strain curve and how the two yield point characteristics are derived from it.

Full size image

Results

The workflow

The search process (illustrated in Fig. 1) starts from a set of four initial compositions—represented by a point in the compositional space c = [cCu, cZr, cAl] which is just a vector of the atomic composition ci of the glass—for which the mechanical properties (yield stress τy and the shear modulus G) have been precomputed. These are stored in an online database in the Aalto Materials Digitalisation Platform (AMAD), which can be accessed both programmatically from the computational cluster (as done in the workflow) or by a human via a web interface.

The main part of the workflow is then the BO algorithm, where the mechanical properties at each point in the compositional space are represented by a probabilistic surrogate function, constructed based on known input data (read from the AMAD database), and is here a Gaussian process regressor. This probabilistic representation is then used for further measurements based on the chosen utility function: one can focus on exploration by examining points where the uncertainty in the probabilistic representation is high, or on exploitation by focusing on points where the value of the mechanical property of interest—here the yield stress τy—is expected to be high. Here we have chosen to do a purely exploratory search (as the goal is to map the search space, not only to find the maximum), and the utility function is simply the standard deviation of the yield stress Δτy given by the GPR. The BO algorithm then gives the next composition to be simulated cn+1 (corresponding to the utility function maximum), to the next part of the workflow.

The chosen glass compositions, with N = 6000, are then prepared by quenching using a hybrid molecular dynamics-Monte Carlo algorithm (see “Methods” section for details), and a shear simulation is performed using the LAMMPS54. The interaction between the atoms is given by the Embedded Atom Method (EAM), which has been extensively used for the CuZrAl system55,56,57. This is done for 20 random realizations of the composition, and the stress-strain curves resulting from the shear simulations are averaged over all the realizations to yield an average stress-strain curve (an example of which is shown in Fig. 1).

Additionally, the initial glass configuration was evaluated for crystallinity by calculating the fractions of various crystal structures (e.g., face-centered cubic (FCC), hexagonal close-packed (HCP), body-centered cubic (BCC)) using adaptive-Common Neighbor Analysis (a-CNA) (see “Methods” section). The fraction of crystal-like particles was found to be very low. Therefore, the samples analyzed here were determined to be homogeneous and non-crystalline.

For the mechanical response, samples are subjected to athermal quasi-static shear deformation. For a system with 6000 particles and onward, the yield stress is not sensitive to the system size56. The yield stress and shear modulus are then determined from the average stress-strain curve and appended to the AMAD database. The yield stress corresponds to the maximum stress value in the γ ∈ (0, 0.2) interval, and the shear modulus to the initial slope of the stress-strain curve (see Fig. 1). The workflow will then start another loop.

Mapping the mechanical properties in composition space

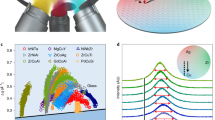
As the constraint ∑ici = 1 sets up a 2-dimensional manifold in the 3D space, we can simply do the optimization in the 2D space given by two of the compositions, concentrations of Zr and Al. Additionally, we impose the constraints 0.3 ≤ cCu, cZr ≤ 0.7 and cAl ≤ cCu, cZr. After the workflow has run for 60 iterations based on the yield stress τy at a cooling rate of \(\dot{T}=1{0}^{12}\) K/s we find the landscape shown in Fig. 2. Based on the same data we also compute the landscape of the shear modulus G. For comparison, the same sequence of compositions is simulated also for two different cooling rates, a faster (\(\dot{T}=1{0}^{13}\) K/s) and a slower (\(\dot{T}=1{0}^{11}\) K/s) one. All of the resulting landscapes are also shown in Fig. 2, with the exception that the slowest cooling rate is only run for 12 iterations due to the high computational cost.

Fig. 2: The compositional landscape and mechanical properties.
figure 2

Ternary plots of the mechanical properties obtained at the end of the workflow. The rows indicate different cooling rates \(\dot{T}\) and the columns the mechanical property considered (yield stress τy or shear modulus G.).

Full size image

The yield stress landscapes show a clear maximum at a point corresponding to intermediate Al concentration and low Zr concentration. The landscapes look pretty similar for different cooling rates, but the scale of the actual yield stress values changes with the cooling rate, the slowly cooled glasses being stronger. The landscapes of τy and G look very similar for all the cooling rates.

The optimal composition for yield stress from GPR is Cu0.53Zr0.31Al0.16, based on the original cooling rate of \(\dot{T}=1{0}^{12}\) K/s. Only minor changes are found for the different cooling rates, \(\dot{T}=1{0}^{13}\) K/s giving Cu0.55Zr0.30Al0.15 and \(\dot{T}=1{0}^{11}\) K/s giving Cu0.58Zr0.30Al0.12. The best point found in the dataset (for the original cooling rate) is Cu0.52Zr0.33Al0.15.

Another way to look at the landscapes is to see how the yield stress varies as a function of the Al concentration (see Fig. 3) for a given concentration of, e.g., Zr. It is clear that with all the cooling rates, the highest yield stresses are achieved at intermediate Al concentrations, at around 10%–20% Al content, in agreement with the experimental picture of the impact of Al addition35,36. Interestingly, with the slowest cooling case, there seems to be a second peak at high aluminum concentrations (Fig. 3c), which is not present with the faster cooling rates (Fig. 3a, b). This peak, too, corresponds to low Zr concentrations.

Fig. 3: The yield stress with varying Al content.
figure 3

The yield stress landscapes of Fig. 2 plotted as a function of the Al content for various fixed Cu/Zr ratios and for different cooling rates a \(\dot{T}=1{0}^{13}\) K/s, b \(\dot{T}=1{0}^{12}\) K/s, and c \(\dot{T}=1{0}^{11}\) K/s, showing a clear peak at cAl between 10% and 20% at low Zr concentrations.

Full size image

The effect of cooling can be seen to change with the mechanical response itself (see Fig. 4). The concentrations corresponding to the lowest yield stresses—i.e., the high-Zr and low-Cu regime—give similar values for all cooling rates (Fig. 4a) but when the yield stress increases (close to the optimal point), the effect of the cooling rate also increases. The exact same effect is seen in the shear modulus (Fig. 4b).

Fig. 4: The cooling rate effects.
figure 4

a The effect of cooling rate on the yield stresses. A dashed line is a square root dependence as a guide to the eye. b The effect of cooling rate on the shear modulus. A dashed line is a square root dependence as a guide to the eye. c A universal linear relation between the shear modulus and yield stress is found for all cooling rates.

Full size image

The yield stress and shear modulus are strongly related. A linear relation G = τy/γ0 + G0 between them is found (see Fig. 4c) with γ0 = 0.129 and G0 = 11.24 GPa. This behavior is seen for all the cooling rates and arises from the weak dependence of the yield strain γy—defined as the strain corresponding to the yield stress— on the composition (see, e.g., the stress-strain curves in Fig. 5). Generally, at the yield point

$${\gamma }_{{\rm{y}}}=\frac{{\tau }_{{\rm{y}}}}{G}+{\gamma }_{{\rm{p}}}^{{\rm{y}}},$$
(1)

where \({\gamma }_{{\rm{p}}}^{{\rm{y}}}\) is the plastic strain at the yield point, which can—using the linear relation—be written in the form

$${\gamma }_{{\rm{p}}}^{{\rm{y}}}={\gamma }_{{\rm{y}}}-\frac{{\tau }_{{\rm{y}}}}{{\tau }_{{\rm{y}}}/{\gamma }_{0}+{G}_{0}}.$$
(2)

There are two obvious limits: τy → 0, where \({\gamma }_{{\rm{p}}}^{{\rm{y}}}\to 0\), and τy → ∞ where \({\gamma }_{{\rm{p}}}^{{\rm{y}}}\to {\gamma }_{{\rm{y}}}-{\gamma }_{0}\). The value observed for γ0 is close to the observed semi-universal γy.

Fig. 5: The stress-strain behavior and structure of the optimal glass.
figure 5

a Example stress-strain curves, illustrating the difference between the starting point Cu0.50Zr0.50, the worst yield stress (Cu0.30Zr0.70), and the best yield stress (Cu0.52Zr0.33Al0.15) at \(\dot{T}=1{0}^{12}\) K/s. An example configuration of the optimal composition is illustrated in the top-left corner. b The fractions of different structures for the compositions shown in (a), indicated by the same colors.

Full size image

The optimal glass

For the original cooling rate of \(\dot{T}=1{0}^{12}\) K/s the optimal composition found in our dataset is Cu0.52Zr0.33Al0.15. Comparing the stress-strain behavior of this composition to the starting point Cu0.50Zr0.50 and the worst composition in the dataset, Cu0.30Zr0.70 shows a clear difference in behavior (see Fig. 5a). The worst glass shows practically no stress drop, but instead gradually evolves from elastic to plastic behavior. As the yield stress and shear modulus improve, the stress drop becomes more prominent. This shows clearly the impact of composition on mechanical behavior.

Structural explanations for these differences can be studied by examining local structures in these three compositions (see Fig. 5b). There are inconsequential amounts of various types of local crystalline structures, viz BCC, FCC, and HCP for the various compositions58, which suggests that we are sampling in the “amorphous-regime” of compositional space. The noticeable change in the mechanical response can be explained by the population of the locally favored icosahedral structures, which are key structural features with long lifetimes and thus provide the “stability” in the supercooled region59,60. For the various compositions, the population of the icosahedral structures clearly correlates with the dramatic change in the overall mechanical stability. This then means that the strong cooling rate effect seen in Fig. 4a, b relates to the strong cooling rate effect in the formation of icosahedral structures. Indeed, when the cooling rate decreases from 1013 K/s to 1012 K/s, we observe the ICO fraction in the optimal Cu0.52Zr0.33Al0.15 increasing from 1.4 ⋅ 10−2 to 1.9 ⋅ 10−1. For the worst composition, Cu0.30Zr0.70, the change in the ICO fraction (from 4.9 ⋅ 10−4 to 3.4 ⋅ 10−4) with the same cooling rate change is insignificant.

Search process

The landscapes shown previously (Figs. 2 and 3) omit the actual measured values and focus on the GPR prediction. Looking at the actual goodness-of-fit at the final iteration (Fig. 6) shows that the GPR actually fits the data very well. We have also quantified this by computing the Bayesian R2 metric61 (see “Methods” section for details), which can be seen in Fig. 6a, b. Interestingly, the fit is slightly worse for the yield stress (Fig. 6a, R2 = 0.97) compared to the shear modulus G (Fig. 6b, R2 = 0.99). This is likely due to the difficulty of accurately determining the yield stress as the maximum stress achieved at simulation varies strongly, which affects the maximum stress in the average stress-strain curves. The shear modulus is much more robust against this type of stochastic behavior.

Fig. 6: The goodness-of-fit.
figure 6

a The Gaussian process regression (GPR) prediction of the yield stress vs. the true value for all the points at iteration 60. The dashed line indicates the perfect prediction, and the Bayesian R2 metric is indicated by the number in the corner. b Same as panel a but for the shear modulus.

Full size image

The search process starts from the edges of the search space, as—with relatively small variations in the yield stresses observed—these points are the furthest from the measured points, and thus have the highest uncertainty. We have benchmarked our active learning approach against Sobol sequences that try to uniformly fill up the space (rigorous results48 only hold up if the number of points is a power of 2 and the domain is rectangular) and see that until around iteration 30 our approach shows more uniform convergence, while the accuracy of the Sobol sequence approach fluctuates wildly. At large iteration numbers, where most regions of the search space are sampled, the performances naturally become equal. Good glasses are found really early in the search process, the second best yield stress (3.01 GPa) being achieved already at iteration 6. The best yield stress (3.36 GPa) corresponds to iteration 54, and the third (2.94 GPa) and fourth (2.92 GPa) to iterations 23 and 29, respectively. This shows that if we were to choose to do exploitative optimization instead of the exploratory search used here, the number of iterations needed would likely be much smaller than the 60 used here. This has been previously seen in a higher-dimensional search space in the case of high-entropy alloys38.

At each iteration of the search, the GPR kernel hyperparameters (k0, ℓi, and w, see “Methods” section for details) are optimized. The evolution of these with the iteration number (Fig. 7) shows that after around ten iterations, the hyperparameter values seem to converge to roughly correct numbers. This is consistent with behavior seen in Figs. 2 and 3, where the slowest cooling rate (\(\dot{T}=1{0}^{11}\) K/s) shows similar behavior as the other cooling rates already at iteration 12 (compared to iteration 60 for the others). The only exception is the white noise level w, which stays at the minimum value (w = 10−5). In the next ten iterations, the noise level w rises, and the other hyperparameters converge to k0 ≈ 0.8 and ℓi ≈ 0.1. The length scale is practically the same for both Al and Zr. The hyperparameter values stay there for the rest of the iterations with only minor fluctuations around the values achieved at iteration 30. The white noise level w stays very low at all the iterations, signifying very low errors in the GPR fit.

Fig. 7: The kernel hyperparameters.
figure 7

The evolution of the hyperparameters a kernel strength k0, b kernel length scales ℓi, and c white noise kernel strength w as a function of the iteration number.

Full size image

Discussion

We have implemented an automated loop for exploring the compositional space of CuZr(Al) metallic glasses, studying also various cooling rates. This is done by utilizing Bayesian optimization, cooling in silico, and molecular dynamics shear simulations.

The landscape of the system (with some constraints as to the Cu/Zr content) turns out to be dominated by one maximum “peak” with the two implications of a non-equiatomic Cu/Zr ratio and an optimal Al content. This appears to be in line with the somewhat thin experimental understanding. Likewise, the idea that extra Cu content or a non-equimolar Cu/Zr composition is good for the GFA has been made with a similar qualitative twist of Cu dominance32. The effect of the cooling rate turns out to be very relevant because the optimal compositions can indeed be controlled even more by slower cooling.

Presently, we do not seek the fundamental relationship between the structure and the mechanical properties, and the structural signatures controlling the elastic modulus or yield stress. However, the question of GFA optimization alluded to above is clearly related to these. The same also applies to the eventual presence of short- or medium-range order that could be varied with cooling.

In summary, Bayesian approaches seem to be promising for the exploration of metallic glasses due to the “small data” nature of these workflows (we ran 60 iterations compared to the 813 possible grid points). The improved performance over, e.g., Sobol sequences stems from the active learning utilizing information already present in the dataset, instead of just the search space geometry. This difference would be amplified in higher-dimensional search spaces and in more exploitative optimization, where Sobol sequences are simply unsuitable. We would in particular stress the applications to experiments, where one could thus hope to avoid complex high-throughput setups by a design of the experimental search/mapping process. For our in silico case, we have selected a serial BO approach, but in experimental adaptations, it would also be an avenue to look at batch variants62 of Bayesian search to speed up the research compared to the serial exploration. The same also applies to multi-target optimization63 for combined property mappings, such as GFA and mechanical properties.

Methods

Bayesian optimization with Gaussian process regression

The Bayesian Optimization (BO) is done here using Gaussian Process Regression53 (GPR), implemented in scikit-learn software64, where the desired quantity y for each point c in the search space is represented by a Gaussian distribution with mean μy(c) and standard deviation Δy(c). The points in the search space are given by vectors c = [cZr, cAl] reduced into 2D, as the ∑ici = 1 constraint makes this possible. The kernel used in the GPR is based on the standard anisotropic radial basis function kRBF, characterized by a kernel strength k0 and two length scales ℓi corresponding to the ith component of the compositions. To account for the variation in the yield stress due to the specific atomic configuration, a white noise kernel, \({k}_{{\rm{WN}}}\left[y({\boldsymbol{c}}),y({{\boldsymbol{c}}}^{{\prime} })\right]=w\delta \left(| {\boldsymbol{c}}-{{\boldsymbol{c}}}^{{\prime} }| \right)\) where δ is the Dirac delta function and the norm the Euclidean distance, is added. The total kernel is then given by the covariance \({\rm{cov}}\left[y({\boldsymbol{c}}),y({{\boldsymbol{c}}}^{{\prime} })\right]={k}_{{\rm{RBF}}}+{k}_{{\rm{WN}}}\). The kernel hyperparameters w, k0 and ℓi optimized in the GPR algorithm are chosen to have the following initial values: w is initially the standard deviation of the yield stress in the current dataset, k0 four times this value, and the length scales ℓi are bounded by the minimum and maximum spacing of the datapoints in the dataset38,65 (i.e., the minimum and maximum difference of ci in the dataset), and initialized to the mean of these two values. The white noise level w is restricted by w ≥ 10−5 to avoid numerical issues.

The output used in the active learning part of the workflow is the yield stress τy. In addition to this, we use the shear modulus G data to do similar GPR fitting, although this is not involved in the active learning part. Finally, the same sequence of compositions is simulated also for two different cooling rates, again without the active learning component. The optimization starts from four initial inputs Cu0.50Zr0.50, Cu0.70Zr0.30, Cu0.30Zr0.70, and Cu0.34Zr0.34Al0.32, representing three commonly studied CuZr glasses at the edges of the search space, and a sample with the maximum Al content. After this, the next point is picked based on the highest value of the utility function. We have chosen to perform a purely exploratory search, and use as the utility function the standard deviation of the yield stress Δτy.

Optimization in a grid can run into a situation where the maximum of the utility function is achieved at a point already previously visited. However, this is much less likely in the purely exploratory search. We have chosen as the next point the point corresponding to the maximum utility function, in the set of points not previously visited. We run the search loop for 60 iterations, which gives a fairly good coverage of a 2D surface. For the slowest cooling rate, we have stopped the run after 12 iterations, due to the high computational cost. To quantify the goodness-of-fit, we compute the Bayesian variant of the R2 metric61, which takes into account the uncertainty in the prediction. It is defined with the explained variance Var(yGPR) and residual variance Var(y − yGPR) as \({R}^{2}={\rm{Var}}({y}_{{\rm{GPR}}})/\left[{\rm{Var}}({y}_{{\rm{GPR}}})+{\rm{Var}}(y-{y}_{{\rm{GPR}}})\right]\).

Glass formation and characterization

To prepare the glasses and test the mechanical properties of each composition, we perform MD simulations using LAMMPS54. The system size used here is 6000 atoms, and a cubic box with periodic boundary conditions is used. Glass preparation is done using a hybrid Molecular Dynamics-Monte Carlo (MD+MC) scheme under the variance-constrained semi-grand canonical ensemble (VC-SGC)66. This VC-SGC MC scheme allows exploring the configurational degrees of freedom by randomly selecting an atom and attempting to change its type, while also calculating the corresponding energy and concentration changes. It allows for targeting of specific concentration ranges while maintaining a fixed total number of particles and volume. Acceptance of these transmutations follows the Metropolis criterion, ensuring the preservation of detailed balance. On the other hand, the relaxation processes are accounted for by the MD integration steps. To maintain the desired concentration within the system66, we set the variance parameter κ = 103. The differences in chemical potential relative to Zr using hybrid MD+MC simulations under the semi-grand canonical ensemble at a temperature of 2000 K and the specific set of parameters that minimize the composition errors in relation to the desired concentration can be found in ref. 42. The hybrid scheme is also used for ZrCu by ref. 41. The interaction between the atoms is given by the embedded atom method (EAM) interatomic potential and parameters55. The quenching is performed starting from molten metals at a high temperature well above the melting point using a fixed cooling rate \(\dot{T}\) at fixed pressure. In the MD+MC scheme, an MC cycle consisting of N attempts is performed every 20 MD steps. The glasses are cooled from 2000 K to 300 K, using one of the three cooling rates (1011, 1012, or 1013 K/s) as explained in the main text.

To identify the local structural signatures, we performed adaptive-Common Neighbor Analysis (a-CNA) using OVITO software67. With a flexible cutoff for neighbors, the adaptive CNA method focuses on the bond topology of the nearest neighbors to accurately detect local order68. This allows us to identify the fractions of atoms participating in various structures, including face-centered cubic (FCC), hexagonal close-packed (HCP), body-centered cubic (BCC), and icosahedral (ICO) configurations. The fraction of crystalline particles remains minimal in this study.

We perform athermal quasi-static shear simulations under Lees–Edwards periodic boundary conditions. The simulation cell was incrementally sheared with a strain step of δγ = 10−4 and minimized using the conjugate gradient method. This setting allows us to mimic the low temperatures and low-shear rates experimental conditions. Throughout the shearing process, we record the stress-strain response, which provides a detailed stress-strain curve for analysis. The mechanical property we focus on is the yield stress τy, which is determined from the average stress-strain curve (averaged over 20 realizations of the atomic configurations) as the maximum of the shear stress. We have checked that these statistics are enough for a good estimate of the yield stress. Also, the shear modulus G, determined by averaging the positive slopes of the stress-strain curve for the first 1% of strain in each realization of the disorder, is recorded. See Fig. 1 for an illustration of the stress-strain curve analysis.

The workflow

The full workflow (illustrated in Fig. 1) starts with a database stored in the Aalto Materials Digitalization Platform (AMAD), which has an initial set of inputs and outputs. The database is read automatically by the BO algorithm, which performs the GPR in a grid with a concentration step Δc = 0.01 and boundaries 0.30 ≤ c ≤ 0.70, which is the window in which we let the concentrations vary. We also impose the additional conditions cAl < cCu and cAl < cZr. The algorithm outputs a point that corresponds to the highest value of the utility function (Δτy) in the points that have not been visited before. The composition corresponding to this point is given as an input to the shear simulation, and after the yield stress and shear modulus are determined, the composition and the corresponding yield stress are written back to the AMAD database. This process is automatically iterated.