Introduction

Over the past decade, enhanced environmental awareness and the increasing demand for renewable energy have propelled the rapid advancement of photovoltaic (PV) technology1. Solar energy, as the most prominent carbon-neutral and fastest-growing renewable energy source, has received widespread attention and application2,3. Among the various PV technologies, organic photovoltaics (OPVs) stand out as a transformative solar technology with significant potential for high-throughput manufacturing4,5. OPVs are characterized by their low manufacturing cost, light weight, mechanical flexibility, and ultra-low-loss properties, making them suitable for diverse applications such as building-integrated photovoltaics (BIPVs) and mobile device charging6,7,8. OPVs are composed of donor (electron-donating) and acceptor (electron-accepting) material, both of which are organic in nature9,10,11. According to the design principle of the combination of donor (D) and acceptor (A), organic solar cells can be divided into binary solar cells and ternary solar cells. Among them, binary solar cells are usually composed of a donor material and an acceptor material12. The combination of these materials can form a heterojunction to generate charge separation under light conditions. After the photon is absorbed, the electron transitions from the donor material to the acceptor material, forming free electrons and holes, and realizing the separation and transfer of electric charge13. Recently, ternary organic solar cells have emerged as a promising strategy to achieve high performance, due to the enhanced light-harvesting efficiency via introducing a suitable third component into the binary matrix. In general, ternary solar cells consist of a polymer as the host electron donor, a fullerene derivative as the host electron acceptor, and a third species as an infrared sensitizer14,15. The combination of donor and acceptor in binary and ternary solar cells is the key to the study of OPVs technology. Thus, the performance of OPVs hinges on the device configuration and the properties of the organic materials used16,17,18.

Historically, OPVs development has progressed through three major stages: (I) Optimization of bulk heterojunction (BHJ) morphology using poly(3-hexylthiophene) (P3HT) and fullerene-based acceptors (FAs)19; (II) Development of new donor materials for improved compatibility with FAs acceptors20,21,22; (III) Development and advancement of non-fullerene acceptors (NFAs)23,24. In comparison to FAs, the recent development of NFAs have exhibited broad light absorption ranges, strong tunability, excellent electron transport characteristics, and high photoelectric conversion efficiency (\({PCE}=\frac{{J}_{{sc}}{V}_{{oc}}{FF}}{{P}_{{in}}}\): refers to the efficiency with which input solar energy (\({P}_{{in}}\)) is converted into electric power)25,26. Currently, NFA are usually designed with a low band gap (\({E}_{g}\)) to enhance the harvest of near-infrared (NIR) light27. NFA have addressed the traditional trade-offs between energy driving force and external quantum efficiency, leading to high-efficiency charge separation. The push to replace fullerenes in OPVs has accelerated the development of various NFA materials, including polymer, macromolecule, and small organic molecule. Consequently, there is an urgent need to fabricate devices with highly optimized NFA acceptors or effective blend donors with NFA acceptor polymers to achieve high charge transport mobility, high charge generation, reduced voltage loss, and enhanced efficiency28,29. Significant progress has been made in the last few years, particularly in the development of new donors and NFAs (II and III)30,31. Notably, Zheng et al. achieved a PCE exceeding 20% for the first time in a single-junction A-DA’D-A type NFA-based OPV device using a series device structure32. Sun and co-workers designed a π-extended non-fullerene acceptor (NFA) B6Cl with large voids among the honeycomb network, which introduced into photovoltaic systems8. Despite these advances, OPV still face challenges such as lower PCE and long-term instability compared to inorganic and perovskite solar cells33,34,35. Additionally, the development process often involves extensive trial and error, requiring substantial tome and resources for fine chemical synthesis and PCE testing of new acceptors28,36.

To mitigate the resource-intensive nature of these experimental processes and shorten material development cycles, recently, machine learning (ML) is applied to predict the PCE of OPV devices and screen new OPV materials17,37,38. In materials science, ML as a data-driven approach, can effectively learn from existing data, discern underlying patterns, and establish direct relationships between a material’s chemical structure and the performance39,40,41,42,43,44,45. In the OPV field, Shinji et al. used artificial neural networks (ANN) and random forest (RF) algorithms to screen conjugated molecules for polymer fullerene applications by introducing electronic properties and PCE targets46. Similarly, Sahu et al. compiled a dataset of 270 donor molecules and correlated 13 microscopic properties of the donor material with the PCE performance using ML47. As non-fullerene acceptors (NFAs) have garnered significant attention and become research hotspots, most state-of-the-art OPVs with efficiencies ranging from 13% to 19% have been achieved using NFA-based systems in recent years. Therefore, it is essential to focus on the application of ML approaches to tackle the broader and more complex challenges associated with non-fullerene OPVs. Furthermore, despite significant efforts in applying ML for property prediction and material screening, its potential benefits are still underutilized48,49. The choice of input features is critical in ML and directly impacts the results. Transforming these features for compatibility with ML models is an essential step in predictive model development, particularly in chemical informatics and materials science50,51.

In the field of organic photovoltaic material (OPV) ML research, molecular fingerprints are crucial for predicting material performance and facilitating material selection52,53. Molecular fingerprints serve as input representations of chemical structures and play a pivotal role in research and development. Existing methods for generating molecular fingerprints have their strengths and limitations. One widely used tool for generating molecular fingerprints is the RDKIT54 toolkit, which allows the conversion of Simplified Molecular Input Line Entry System (SMILES) codes into Molecular Access System (MACCS) fingerprints (Fig. 1a). MACCS is a primitive 2D fingerprint, displayed by an array of bits of 0 s and 1 s, where each bit position indicates the presence or absence of structural fragments, such as S − N and alkali metals, providing 166 digital keys55. Although it has some interpretability, the division of fragments is too random to represent the regional irregularity of the polymer skeleton. Additionally, the molecular descriptors generated with RDKIT describe the properties of the molecule using arrays of real numbers rather than directly expressing the chemical structure56, as shown in Fig. 1c. To address these limitations, our group proposed the concept of “Polymer-Unit” for organic polymer functional materials and developed the Polymer-Unit Fingerprint (PUFp)57 that accurately represents molecular fingerprints by segmenting appropriate functional building blocks (Fig. 1b). The Python-based Polymer Unit Identification Script (PURS) is accessible via the following web pages: https://github.com/yecaichao/Python-based-polymer-unit-recognition-script-PURS-for-PUFp.

Fig. 1: Explanation of fingerprints and descriptors.
figure 1

a PUFp: Polymer-unit fingerprinting, each bit in the PUFp code represents a polymer-unit and utilizes one-hot encoding. b Descriptors: Molecular properties generated by the RDKIT toolkit. c MACCS: Each bit in the MACCS code represents a small substructure and utilizes one-hot encoding.

Full size image

In this study, we utilize the Polymer-Unit Fingerprint (PUFp) to delve into the structure-property relationships of organic photovoltaic (OPV) acceptors materials. Figure 2 outlines the workflow for analyzing these relationships, consisting of six key components, each with specific tasks:

  1. i.

    Establishment of OPV Acceptor Material Database: Initially, a database comprising experimental 1343 non-fullerene acceptor materials along with 260 donor materials for OPV is compiled.

  2. ii.

    Conversion of Structures into Polymer Unit Fingerprint (PUFp): The structures of these acceptor materials are transformed into binary representations. This involves segmenting SMILES into individual polymer units (PUs) using the PURS script, creating a PU library, and generating PUFp using PURS.

  3. iii.

    Application of Supervised Machine Learning Algorithms: Five supervised ML algorithms (Random Forest)58, Multi-Layered Perceptron, Support Vector Machine59, K-Nearest Neighbor, and Kernel Ridge Regression) are employed to train regression and classification models using the OPV acceptor material database. The best-performing model is then utilized to uncover feature-property and quantitative structure-property relationships.

  4. iv.

    Utilization of Chemical Descriptors and Other Features: Chemical descriptors computed by the RDKit Descriptors module, along with additional features such as HOMO/LUMO levels, \({E}_{g}\), and \({M}_{w}\), are employed to identify feature-property relationships.

  5. v.

    Analysis of PUFp Fingerprint: An in-house designed PUFp fingerprint, capable of expressing 413 different PUs of N-type OPVs and 209 different PUs of P-type OPVs, is utilized to assess the importance of PUs in identifying key PUs significantly impacting OPV performance.

  6. vi.

    Design of New OPV Acceptor Materials: Important PUs identified from N-type OPV materials are combined to design novel acceptor materials for OPV. The accuracy and screening capabilities of the framework are evaluated.

Fig. 2: Workflow of building, application, and evaluations of machine learning methods in this work.
figure 2

(i) Scheme of collecting experimental data. (ii) Scheme of PU fingerprint identification, form a PU library and generate fingerprints. (iii) Scheme of machine training. (iv) Scheme of the feature-property relationship analysis. (v) Scheme of the quantitative structure-property relationship analysis. (vi) Exploration and design of important combinations of polymer units for OPVs high PCE.

Full size image

Overall, by integrating machine learning techniques and PUFp Fingerprint, we develop a predictive model to discern associations between polymer-units/features and target performances, particularly Power Conversion Efficiency (PCE). The aim is to utilize this approach to design innovative materials based on the established feature/substructure-property relationships elucidated by the PUFp-ML model. These methodologies are also applicable to donor materials, thereby facilitating accelerated material discovery and providing valuable insights for designing advanced OPV materials.

Results And Discussion

The feature-selection and ML-model enhancement in PCE Prediction for OPV materials

In this study, we began with 220 molecular descriptors calculated via RDKit from the SMILES strings of each macromolecule. Facilitating the development of machine learning models by analyzing feature-property relationships is an essential initial step. To identify the macromolecule properties most closely related to power conversion efficiency (PCE), we employed a feature selection method. This combined the 220 RDKit descriptors with 17 additional microscopic properties, including normalized HOMO level, LUMO level, bandgap (\({E}_{g}\)), molecular weight (\({M}_{w}\)), and number-average molecular weight (\({M}_{n}\)), totaling 237 features.

Model learning complexity is influenced by the correlation strength60 between features and the target property, with molecular properties proving to enhance model accuracy61. Feature selection is one of the key steps in machine learning, selecting features from all features that positively impact the learning algorithm, which will reduce the difficulty of learning tasks and make the model more interpretable. As an integrated learning method based on decision tree, Random Forest (RF) regression has significant advantages in feature importance assessment. Additionally, Lasso regression, a linear model that incorporates an L1 regularization term (i.e., the sum of the absolute values of the variable coefficients) to mitigate overestimation of model performance, was utilized for efficient variable selection. In this section, we utilized the RF regression and Lasso regression to find the optimal feature subset. Figure 3a depicts the feature importance ranking of RF regression and Lasso regression. The weight ranking of each feature in the RF regression model is shown on the left side of Fig. 3a (blue bar chart), ignoring features with weights below 0.005. Top features include MaxPartialCharge, \({E}_{g}\), -HOMO_p, and -LUMO_n. The features with non-zero coefficients in Lasso regression are sorted, as shown on the right side (red bar chart) of Fig. 3a. Notably, the important features identified by Lasso regression are largely consistent with those selected for the trained model. Separate feature importance ranking plots for the two regression methods are also presented in Supporting Information. Reducing redundancy in the feature set while retaining informative elements can improve machine learning performance and mitigate overfitting.

Fig. 3: Key features analysis.
figure 3

a Feature importance ranking of RF regression and Lasso regression. b SHAP dependence plot of top 20 features of RF model. c SHAP interaction evaluation plot of top 5 features for P-type and N-type OPVs.

Full size image

Through comprehensive consideration of the screening results of feature importance by RF and Lasso regression, we selected 17 features from total 237 features, including MaxPartialCharge, \({E}_{g}\)_n, -HOMO_p, -LUMO_n, \({M}_{w}\), M, \({M}_{n}\), PEOE_VSA9, \({E}_{{\rm{LL}}}^{{\rm{DA}}}\), -HOMO_n, SMR_VSA10, NumHeteroatoms, FpDensityMorgan1, -LUMO_p, \({E}_{g}\)_p, \({E}_{{\rm{HL}}}^{{\rm{DA}}}\) and PDI (see Table 1). Among them, the primary features for P-type materials are -HOMO_p, -LUMO_p, \({E}_{g}\)_p, while N-type materials include MaxPartialCharge, \({E}_{g}\)_n, -LUMO_n, \({M}_{w}\), M, \({M}_{n}\), PEOE_VSA9, -HOMO_n, SMR_VSA10, NumHeteroatoms, FpDensityMorgan1, PDI and other 220 features. Additionally, \({E}_{{\rm{HL}}}^{{\rm{DA}}}\) represents the energetic difference between HOMO of donor and LUMO of acceptor, while \({E}_{{\rm{LL}}}^{{\rm{DA}}}\) quantifies the energetic difference between the LUMO of the donor and the LUMO of the acceptor. The SHAP (Shapley Additive exPlanations) method was then used to analyze these features’ contributions to the PCE prediction model. We use this method as a feature selection criterion and extracted the top 17 features that contribute the most to the model according to the SHAP value. Each feature’s SHAP value is shown in Fig. 3b, delineating the marginal contribution to the model’s output. The complete SHAP evaluation diagram is shown in Figure S4. Additionally, to further analyze the correlation between features of the donor and acceptor and the PCE in OPVs, the Pearson correlation coefficient is calculated to measure the linear relationship between the input feature and output feature. As shown in Figure S5, it is not difficult to find that the characteristic values strongly correlated with PCE include MaxPartialCharge, Eg_n, -LUMO_n, -HOMO_p, etc. The correlations between MaxPartialCharge, Eg_n, -LUMO_n, -HOMO_p and PCE are -0.29, -0.46, 0.43, 0.46, respectively, as depicted in Figure S5. This further verifies the evaluation results of the random forest regression model.

Table 1 The selected features and their physical interpretations
Full size table

The atom with the maximum partial charge (MaxPartialCharge) was found to contribute the most to the model and had an inhibitory effect on PCE. MaxPartialCharge refers to the local accumulation of positive or negative charge due to the uneven distribution of electron density between atoms in a molecule. The presence of a high MaxPartialCharge indicates poor electronic delocalization and low conjugation degree within the molecule, resulting in inefficient charge transport and thereby reducing the PCE. Notably, the molecular orbital energy levels significantly affect PCE. Higher HOMO_p values positively correlate with the PCE predicted by the model, while lower LUMO_n values have a negative correlation. The PCE is defined by \(\frac{{J}_{{sc}}{V}_{{oc}}{FF}}{{P}_{{in}}}\), where \({P}_{{in}}\) is the incident illumination power. Also, according to the empirical equation of \({V}_{{oc}}\) = \({e}^{-1}(\left|{{E}_{{HOMO}}}^{D}\right|-\left|{{E}_{{LUMO}}}^{A}\right|)\)-0.3 V (where e is the elementary charge), the alignment of donor’s HOMO and acceptor’s LUMO levels is crucial for estimating PCE. Figure 4a, b shows that \({V}_{{oc}}\) increases with the deepening of HOMO level of polymer donor (EHOMOD) and decreases with the deepening of LUMO level (ELUMOA), consistent with the above conclusion. A trade-off between achieving a small energy loss (\({E}_{{loss}}\)) (i.e., a high VOC) and a high charge generation efficiency (ηEQE) in OPV devices, which means they often suffer much larger energy losses (0.5–1.0 eV) than inorganic PV devices (0.3–0.4 eV). However, the emergence of NFAs has circumvented the VOC-ηEQE trade-off, enabling the attainment of a higher PCE with a much smaller \({E}_{{loss}}\). In OPV systems, a LUMO offset of ∼0.3 eV between the donor and acceptor is required to ensure efficient electron transfer and subsequent dissociation into free charge carriers. This generates a charge transfer (CT) state that consists of a hole on the HOMO of the donor and an electron on the LUMO of the acceptor, with the energy of this CT state (ECT) usually smaller than that of the narrowest band gap (\({E}_{g}\)). The VOC of the resulting device was further improved due to the greater energy difference between the HOMO of the donor and the LUMO of the acceptor. Additionally, the LUMO energy level difference between the donor and the acceptor (ΔE1) decreases, which are beneficial for reducing energy loss and improving PCE (as shown in Fig. 4f). To sum up, optimizing molecular orbital energy levels will become a key step to affect the performance of OPV devices.

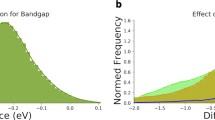
Fig. 4: Statistics of experimental device parameters (∼1343 points).
figure 4

a \({V}_{{oc}}\) versus −HOMO. b \({V}_{{oc}}\) versus −LUMO. c \({J}_{{sc}}\) versus \({{E}}_{g}\). d \({J}_{{sc}}\) versus \({M}_{w}\). e The data distribution of Eg for the N-type OPVs dataset. f Schematic illustration of band gap alignment between donor materials and NFAs. In state-of-the-art polymer: NFA systems, the \({J}_{{sc}}\) is jointly contributed by the large-band-gap polymer donor and narrow-band-gap NFA with complementary optical absorption profiles. The green arrows show the transfer of electrons upon photoexcitation. The red arrows show the transfer of holes upon photoexcitation.

Full size image

\({E}_{g}\) has a significant contribution to the in PCE and is negatively correlated with PCE62. Designing low-bandgap materials to match the solar spectrum is a common method to improve short-circuit current (\({J}_{{sc}}\)) and thus the PCE of OPV cells63. Fig. 4c plots \({J}_{{sc}}\) as a function of the polymer Eg, showing that \({J}_{{sc}}\) tends to increase as \({E}_{g}\) decreases, since a narrower \({E}_{g}\) can harvest more energy from the sunlight. The use of narrow band gap NFAs can broaden the absorption spectrum of OPVs to the near-infrared region, reducing energy loss. This further validates that controlling the \({E}_{g}\) of the chemical structure within a relatively small range (~1.5-2.5 eV) can produce OPV materials with high PCE. Figure 4e, most \({E}_{g}\) values in our database fall within this range. Additionally, molecular weight (Mw) plays a critical role in enhancing PCE. Figure 4d indicates a non-uniform positive correlation between \({J}_{{sc}}\) and the logarithm of Mw. Increasing the Mw of an identical polymer backbone is a straightforward approach to improve the PCE. In fact, a high Mw is believed to enhance the PCE of polymer OPVs due to increased crystallinity and intercrystallite connectivity. Consequently, optimizing \({E}_{g}\) and HOMO-LUMO migration levels is a reasonable strategy for designing polymer molecules, benefiting the synthesis and application of OPV materials. The LUMO energy difference between the donor and acceptor (\({E}_{{\rm{LL}}}^{{\rm{DA}}}\)) is also crucial for PCE, a large difference can lead to significant energy loss (\({V}_{{oc}}\,\)Loss) at the D/A interface (Fig. 4f), whereas \({E}_{{\rm{HL}}}^{{\rm{DA}}}\) can roughly estimate the driving force to dissociate excitons in the D/A interface. An illustration of this is shown in Fig. 3b. Similarly, the polymer dispersion index (PDI) describes the molecular weight distribution of the polymer. Defined as \({PDI}=\frac{{M}_{w}}{{M}_{n}}\), where \({M}_{w}\) and \({M}_{n}\) represent the weight average and number average molecular weights respectively, it underscores the correlation between molecular weight and PCE. We also find that atomic contributions to the monomer surface area (VSA) or polarizability (or molecular refractivity) are crucial factors influencing a polymer’s PCE. PEOE_VSA9 descriptors, which combine partial charges and surface area, are significant for OPV’s PCE. A higher PEOE_VSA value indicates a greater positive impact on the predicted PCE value. Similar patterns are observed with other combined descriptors. For instance, SMR_VSA10, the total VSA of atoms within a specific range of molecular refractivity (MR), positively affects PCE. MR values are calculated for each atom type using Wildman and Crippen’s method. If the total VSA of atoms has an MR between 4 and ∞ (SMR_VSA10), a higher PCE is likely. Key contributing atom types include C doubly bonded to a heteroatom, aromatic C with a heteroatom neighbor, aromatic bridgehead C, and aromatic C = C. Additionally, NumHeteroatoms positively impacts PCE. These 2-D topological/topochemical properties provide insights into molecular surface interactions, while FpDensityMorgan1 generates similarity fingerprints based on atomic chemical and connectivity attributes, also positively affecting PCE. Overall, this work reveals the correlation between polymer PCE and its physicochemical descriptors, such as HOMO, LUMO, molecular weight, and molecular refractivity.

OPVs are composed of donor (electron-donating) and acceptor (electron-accepting) material, both of which are organic in nature. The performance of OPVs is largely determined by the properties of the donor/acceptor (D/A) materials. In other words, the design strategy of the D/A materials and the synergistic effect of their combination are crucial to the performance of OPV devices. Therefore, to reduce the need for trial and error experiments and achieve efficient device performance (including complementary absorption and highly balanced charge transport characteristics, among others), the search for and discovery of synergistic donor/acceptor (D/A) combinations is indispensable. Herein, when we compute SHAP interaction values for all features, the dimension of SHAP is 1343*5*5 (where 1343 is the sample size and 5 is the number of features), which is used to capture the interaction effect of pairs. Additionally, the selection of the five features of the interaction is based on the ranking of the marginal contribution rate in SHAP values. The color represents the characteristic value along the vertical axis (red for high values, blue for low values). The complete interaction evaluation diagram is presented in Figure S6. The feature selection criterion of the interaction is based on the SHAP interaction value distribution (intuitively, the prominence of the red and blue regions). Specifically, the SHAP interaction value is used to represent the influence of the interaction of the two features on the model prediction. In other words, the standout red and blue regions in the interaction diagram have large interaction values and are more suitable for feature combination, while those overlapping together have no obvious interaction effect. From Fig. 3c, the variable in the green rectangle is suitable for feature combination, as indicated by the standout red and blue regions, whereas the variable in the yellow rectangle is not suitable. It is evident that the interaction between MaxPartialCharge and \({{E}}_{g}\) is relatively obvious. The narrower \({{E}}_{g}\) is, the easier it is for electrons or holes to jump from the valence band to the conduction band, and the higher the intrinsic carrier concentration, which has a positive contribution to the current. Whereas the current actually characterizes the speed of charge flow, making charge transport more efficient, which in turn increases PCE. It follows that MaxPartialCharge and \({E}_{g}\) play a synergistic role, whether it is reducing MaxPartialCharge or reducing \({E}_{g}\), it can promote charge separation and transmission, and improve PCE. Additionally, it is more interesting that the HOMO of the P-type material and the LUMO of the N-type material interact, which is consistent with the OPV mechanism. Organic materials absorb light energy to generates tightly bounded electron-hole pairs, namely, excitons. Owing to the large binding energy of exciton, thermal separation of electron and hole is hardly possible at room temperature (around 20 °C). To separate the electron and hole, OPV utilizes the D/A interface to surpass such binding energy. The energy difference between the \({{E}}_{g}\) and the charge-transfer state energy (ECT) provides the ΔE1 for exciton dissociation, which is equal to the lowest unoccupied molecular orbital (LUMO) energy level difference between the donor and the acceptor (as shown in Fig. 4f). This optimal energy level difference helps to efficiently transfer excited electrons to the N-type material, minimizing charge recombination and boosting photovoltaic conversion efficiency. Additionally, aligning the energy levels of P-type and N-type materials enhances interface stability, facilitates efficient charge separation and transport, and minimizes energy loss, thereby improving device performance. The energy level difference between the HOMO and LUMO determines the generation of photocurrent-optimal discrepancies allow for maximum photon absorption and charge carrier production, thus enhancing current output and overall device efficiency.

In summary, effective interaction between P-type’s HOMO and N-type’s LUMO is a crucial factor in achieving high-performance OPV devices, and researching and optimizing this interaction can significantly enhance the performance and photovoltaic conversion efficiency of organic photovoltaic devices.

Explicable structure-property relationship analysis in OPVs

As outlined in METHODS section, the polymer units (PU) identified by PURS are collected into the polymer-unit library (as shown in Fig. 5a), which is organized by the number of rings and element types using PURS (Fig. 5b, c). Among them, by the number of rings can be divided into branch chain, mono ring, fused ring; and are then sorted by their element composition. This classification is essential to facilitate subsequent combinations of different PUs to develop new materials. More detailed information regarding the polymer units is available in the Supporting Information.

Fig. 5: Polymer-unit library: Polymer units are classified according to the number of rings and the type of elements.
figure 5

a polymer unit (PU) identified from the OPV database by PURS. b Classify by ring number. c Classify by element type.

Full size image

To evaluate the marginal contribution of each PU to the PCE, we employed SHAP analysis on 260 donor materials and 1343 non-fullerene acceptor materials based on RF model. SHAP decomposes the prediction into the sum of contributions from each input feature, enabling the interpretability of the importance of each PU. A higher importance value indicates a greater reliance of the machine learning algorithm on a specific PU for determining the performance of an acceptor material.

Using PUFp as input, we examined the characteristics of polymer units with substantial SHAP values across three RF models (P-type, N-type, and P/N interactions) (Fig. 6b–d) and labeled them as important PU. The chemical structures corresponding to the important PUs of P-type OPV materials are depicted in Fig. 6f, and serial No. refers to its index number in the PU library (Fig. 5). The No. 200 PU is benzo[1,2-b:4,5-b’] dithiophene-4,8-dione, which has a quinone resonance structure, giving the polymer a good plane, while further improving the electron absorption capacity. More importantly, the quinone resonance structure is beneficial to enhance the charge transfer within the D-A polymer molecule. PU No. 175 is a heterocyclic structure containing S atoms, which will increase the rigidity after entering the main chain of polymerization, so that the free spin of the molecular chain segment is limited, so that the polymer has excellent photoelectric properties. The No. 24 PU contain imide groups, the electron-withdrawing groups, which contribute to lowering the LUMO level of the polymer and facilitating electron injection into the conduction band.

Fig. 6: Identification of key polymer units by using a SHAP evaluation.
figure 6

a The generation strategy of PUFp. b–e The interpretations of the ML models for P-type, N-type, P-N classification and D-A polymer-unit interaction of N-type by the SHAP evaluation. The blue and red bars on the right denote the proportional relation between the units and the prediction values. f–i Chemical structures of the PUs and their roles are identified through the importance analysis.

Full size image

The significant PUs for N-type OPVs is shown as insets in Fig. 6g. Key PUs include: PU No. 283 contains a thiazole structure, and the electrostatic attraction between the sulfur and nitrogen atoms in thiazoles is beneficial to forming a closer π-π packing structure, which is a common strategy in the D-A OPV design. The No. 305 PU is quinoxaline, as a well-known electron-deficient system, which can not only improve the coplanarity of the polymeric main chain, but also extend the length of the π-π conjugated system to a large extent and increase the intensity of π-π close packing, which is a promising acceptor unit at present. Halogenation of electron acceptor units, such as Nos.304 and 97 PUs, can enhance the intramolecular charge transfer (ICT) effect and reduce the band gap of small non-fullerene receptors, which is one of the more effective molecular design strategies.

In Fig. 6d, the characteristic interaction evaluation of polymer units of P-type and N-type OPV materials was carried out to construct characteristic combinations, and the important PU obtained was shown in Fig. 6h. The complete interactive evaluation diagram is shown in Figure S7. More information about the characteristic interaction evaluation of polymer units of P-type and N-type OPV materials can be found in the Supporting Information. Herein, when we compute SHAP interaction values for all features, the dimension of SHAP is 1343*7*7 (where 1343 is the sample size and 7 is the number of features), which is used to capture the interaction effect of pairs. From Fig. 6d, the variable in the green rectangle is suitable for the feature combination because of the red and blue parts that stand out, whereas the variable in the yellow rectangle is not suitable. As a result, we screened out five variables suitable for feature combination, whose sequence number combinations are Nos. 175 and 382, Nos. 175 and 304, Nos. 200 and 382, Nos. 24 and 382, and Nos. 135 and 304, respectively. The corresponding PU of each sequence number is given in Fig. 6h. For the No. 175, as a donor unit, 2-methylthiophene has a strong electron transfer effect, which enhances the conjugated plane gravity and reduces the π-π packing distance. Perylene diimide (PDI) plays a catalytic role. If the strong coplanar PDI unit is introduced into the main chain, the charge delocalization ability inside the molecule can be increased, the π-π packing distance can be reduced, and the PCE can be increased. For the Nos. 175 and 304 combinations, the large atomic radius and special atomic orbital arrangement of halogen atoms can disperse the electron cloud density. Conjugated polymers based on fluorine or chlorine substitution usually exhibit better FF and Voc. Introducing halogen atoms into the sealing of non-fullerene accepter materials can reduce the molecular energy level, enhance the intramolecular charge transfer, and enhance the molecular crystallization. Additionally, the introduction of two-dimensional conjugated side chains in PU No.304 can increase the molecular conjugated area, broaden the spectral absorption, promote the interaction between molecules, and facilitate the formation of nanoscale bicontinuous phase separation during the preparation of thin films to the donor-acceptor blend, thus showing good photovoltaic performance. Using PUFp as input, we analyze the Pearson coefficients for D/A materials, and the detailed thermal map is shown in Figures S8.

In Fig. 6e, the characteristic interaction evaluation of D-A polymer units of N-type OPV materials was carried out to construct characteristic combinations, and the important D-A PU obtained was shown in Fig. 6i. The complete interactive evaluation diagram is shown in Figure S9. From the interaction diagram, we can find that the units suitable for feature combination are: No.304 (A) and No.105 (D), No.151 (D) and No.382 (A), No.283 (A) and No.151 (D), No.304 (A) and No.197 (D), No.149 (A) and No.151 (D), No. 355(D) and No.305 (A), etc. It provides ideas for the next important PU combination and structure design. Using PUFp as input, we analyze the Pearson coefficients for D/A units (in type acceptor materials), and the detailed thermal map is shown in Figures S10. When there are multiple thieno[3,4-b] thiophene electron-absorbing units in the structure, the intramolecular charge transfer (ICT) can make the material better absorb sunlight and improve the photoelectric conversion efficiency. Then, the introduction of halogen atoms can enhance the ICT effect and reduce the band gap of non-fullerene acceptors, which is one of the most effective molecular design strategies. The combination of thieno[3,4-b] thiophene and thiazole forms a rigid conjugated plane with rich heteroatoms, which is conducive to electron delocalization, and is a promising PU. For D-A polymer unit, ICT is generated due to the push-pull electron interaction between D and A, which reduces the band gap and causes the absorption redshift. Meanwhile, π-bridge is often used between D and A to reduce steric hindrance and improve the molecular planarity of the polymer. More importantly, it can be found that these different types of polymer units are common building blocks in D/A polymer molecules for the synthesis of OPV materials. In brief, the optimization objectives are as follows:

  • The copolymerization of donor unit and acceptor unit was used to reduce the energy level band gap and broaden the spectral absorption.

  • The HOMO energy level is reduced by introducing electron pushing groups.

  • Through the precise introduction of fluorine/chlorine atom substitution on the polymer skeleton, the regulation of molecular energy levels, absorption, film morphology and charge dynamics can be achieved, while improving the \({J}_{{sc}}\) and FF, thereby improving the PCE and reducing energy loss.

  • By introducing conjugated side chains to construct two-dimensional molecules, the coplanarity of molecules are increased and the PCE is improved.

Design and Screening of High PCE OPV Acceptor Materials Based on Important Polymer Units

By combining important PU in N-type OPV materials, we designed new polymer molecules to test the accuracy and rapid screening capabilities of our framework. The top 20 important PUs in N-type materials were categorized into three groups: donor polymer units (D), acceptor polymer units (A), and branched chain (C), as shown in Fig. 7a. Among them, there are five types of donor polymer units, six types of acceptor polymer units, and nine types of branched chains. Without specific constraints, a vast space composed of numerous structures (~1,048,576) is generated. In Figure S12, distributions of the polymer-unit type are shown and the donor polymer units, acceptor polymer units, and branched chain categories were used as the axes for all OPVs in the studied database. Figure S12 shows many empty areas in both the N-type OPVs, and obviously, these unreported combinations generate a huge space composed of many structures. In other words, there are many new materials that have not been explored based on the combination of existing PU, leaving a lot of space to be explored. To reduce the number of unreported candidates OPV materials within this categorization, the range of D, A, and C is limited to macromolecule with a high PCE ( > 12) and the macromolecule composition of at least one macromolecule composition of type D-A or A-D. The machine learning-based scheme for high PCE prediction is shown in Fig. 7b. Using these qualifications, we generated 3336 acceptor material combinations that matched 260 donor materials and employed the trained RF model (shown in Figure S3) to predict their PCEs and identify the combination with the highest PCE. The example of screened high PCE OPV acceptor materials is shown in Fig. 7c, and PCE > 14 value about 2678 combinations are provided in Support information.

Fig. 7: Design and screening of high PCE OPV acceptor materials.
figure 7

a The top 20 important PUs in N-type and classification, abbreviation definitions for the PUs: donor polymer unit (D), acceptor polymer unit (A) and branched chain group (C). b Scheme of high PCE combination prediction by ML. c New materials generated by the PU combination process.

Full size image

Additionally, we mapped the key building blocks from these highlighted polymer units and compared them to the structures of high-performance OPV acceptor materials. Our chemical structure analysis revealed that PUs like No.283 and No.149 were prevalent in over 14% of high PCE polymer acceptor materials. Firstly, the electrostatic attraction between sulfur and nitrogen atoms in the thiazoles (Fig. 7a) promotes tighter π-π stacking, which is a common strategy for designing D-A type acceptor materials. Meanwhile, quinoline enhances the coplanarity of the main chain, and its nitrogen atoms usually share electrons through covalent bonds with empty orbital electrons in other elements. Furthermore, halogenation of electron-accepting units can enhance intramolecular charge transfer (ICT) effects and reduce the bandgaps of non-fullerene acceptors.

As shown in Fig. 7c, the structure contains chlorine-containing fused rings, which broaden light absorption and contribute to higher short-circuit currents (\({J}_{{sc}}\)). The inclusion of strong electron donor groups like alkoxy chloride in the polymer backbone improves both the processability and photoelectric properties of the conjugated polymer. Additionally, chlorination is easier to synthesize compared to fluorination. Studies have shown that molecular design involving chlorination can expand light absorption and improve output voltage. This enables modification of non-radiative energy losses in OPV cells through chemical modification of the photoactive material, providing an opportunity to design efficient OPV materials with low bandgap-voltage offsets.

More importantly, we visualized the top 1000 of the 3336 combinations (targeting the acceptor material) for which PCE > 12 had been predicted. The violin plot, a data visualization that combines features of a boxplot and a kernel density map, shows how the data is distributed. Here, red represents all OPV acceptor materials, green represents A-D-A type OPV materials, and blue represents A-DA’-D-A type OPV materials. Figure 8b shows the distribution of predicted PCE values for all top 1000 designed and screened OPV acceptor materials, A-D-A type OPV materials, and A-DA’-D-A type OPV materials, respectively. The density curve illustrates the distribution of PCE under three categories of classification. The wider parts indicate more concentrated data, while the narrower parts indicate relatively fewer data points. Notably, the overall distribution of PCE values for A-DA’-D-A type OPV materials is higher than for A-D-A type OPV materials, indicating that A-DA’-D-A type OPV materials exhibit better structural properties and are more suitable as candidate structures for OPV materials. This finding provides a reliable strategy and guideline for the design of OPV materials.

Fig. 8: New OPV acceptors and predicted performance distribution.
figure 8

a The representative OPV material acceptor structure. b Predicted PCE value distribution for the top 1000 combinations.

Full size image

In summary, by leveraging advanced machine learning (ML) technology, we studied polymers to model highly optimized, efficient, and stable polymer structures for organic photovoltaic (OPV) cells. A significant amount of photovoltaic property data was collected from reported experimental studies and used to train ML models. We developed five models using RF, MLP, KNN, KRR, and SVM algorithms, with the RF regression model demonstrating the best predictive ability. Various representations of acceptor molecules, including descriptors, MACCS, and polymer unit fingerprint (PUFp), were employed to build ML models for predicting the corresponding OPV PCE class. The results indicate that PUFp with a length greater than 600 bits provides the best representation of acceptor molecules. In feature-property analysis, the polymers’ highest occupied molecular orbital (HOMO), lowest unoccupied molecular orbital (LUMO), molecular weight (\({M}_{w}\)), and band gap (\({E}_{g}\)) emerged as the most decisive descriptors. A library of 413 polymer units was constructed, and key polymer units affecting NFA (non-fullerene acceptor) materials were identified. More importantly, by combining these key polymer units in N-type OPV materials, new polymer molecules were designed to test the accuracy and rapid screening capabilities of our framework. Our research for the relationship between feature/structure and PCE can accelerate the design of new acceptor materials, thus advancing the development of high-PCE OPVs. Our methodology offers a promising approach for screening and designing new polymer acceptors for OPVs and can be applied to a wide range of donor materials, thereby accelerating the development of high-performance OPVs.

Methods

OPV dataset preparation

The OPV database comprises 1343 real NFAs acceptor materials gathered from literature sources. To ensure data quality, missing data and inconclusive results were excluded. Available experimental data such as open-circuit voltage (\({V}_{{oc}}\)), short-circuit current (\({J}_{{sc}}\)), fill factor (\({FF}\)) microstructural characteristics, and experimental PCE trends are collected for each studied system. It also contains 1343 SMILES for polymer OPV materials (standardized by RDKit). Additional data details are available in the supplementary notes. Recognizing the importance of representing a wide PCE range in the dataset, we aimed to encompass molecules across the entire PCE spectrum. In the established database, the medium PCE value is 8.61%, with an average of 8.08% (Figure S3a). As shown in Figure S3b, PCE ranges from 0.01 to 18.22%. We divided the data into three categories (0.01-5.99%; 6.00-11.99%; 12.00-18.22%), PCE within 0.01 to 5.99% are labeled as “low performance” those within 5.99 to 11.99% as “medium performance” and those above 12.00% as “high performance” OPV materials. The distribution of PCEs across these categories is approximately 3:5:2. In the established database, approximately 80% (1074 D/A pairs) and 20% (269 D/A pairs) of the data were divided into independent training (i.e. establishing the relationship between structure and PCE) and test subsets (i.e. determining the predictive accuracy of the training model), respectively.

Generation strategy of PUFp for OPV materials

I. The organic macromolecule OPV database contains 1343 SMILES (standardized by RDKit) of the OPV materials that have been experimentally reported.

II. The PCE of organic macromolecular OPV materials can be improved by proper molecular design. PUs is considered the basic functional building blocks of the macromolecular structure construction. Using the PURS scripts, identify and divide all PU in the normalized SMILES of OPV dataset and generate corresponding fingerprints. The rules for identification and division are as follows: (1) dividing at breakpoints; (2) a single bond connecting two independent elements (mono ring, bicyclic ring, fused ring, or branched chain units) is used as a breakpoint; (3) acyclic structures are classified as chains.

III. All the PU collected include a “polymer-unit library”. The number of PUs in the polymer-unit library is T, and the maximum number of PUs in the OPV data is N. Each OPV data is contained in a node matrix of dimension (T, N).

IV. Finally, each row of node matrix is summed to generate a one-dimensional vector/fingerprint, which is PUFp. It contains information about the type and number of PUs. The generation strategy of PUFp for OPV materials as displayed in Figure S13.

In this work, the length of the generated PUFp is 413 bits, that is, 1343 OPV data is composed of 413 different PUs. Details for generation strategy of PUFp, please visit the following web pages: https://github.com/yecaichao/Python-based-polymer-unit-recognition-script-PURS-for-PUFp.

Evaluation metrics

Evaluation metrics provide a comprehensive assessment of a model’s predictive performance by comparing the actual values to the estimated values. The primary metrics used include Root Mean Square Error (RMSE) and the coefficient of determination (R²) for regression models, and accuracy for classification models.

Root Mean Square Error (RMSE)

RMSE measures the average magnitude of errors between predicted and actual values, providing insight into the deviation of the predicted values from the true values. The formula for RMSE is:

$${{RMSE}}=\sqrt{\frac{{\sum }_{i=1}^{n}{({y}_{i}^{{\prime} }-{y}_{i})}^{2}}{n}}$$
(1)

Where, n is the number of samples, \({y}_{i}^{{\prime} }\) is the true value, \({y}_{i}\) is the predicted value.

R2 score

The R² score indicates how well the regression model fits the observed data. It represents the proportion of variance in the dependent variable that is predictable from the independent variables. The R² value ranges from 0 to 1, with higher values indicating a better fit. The formula for R² is:

$${{{R}}}^{2}=1-\frac{{\sum }_{i}{({\hat{y}}_{i}-{y}_{i})}^{2}}{{\sum }_{i}{(\bar{y}-{y}_{i})}^{2}}$$
(2)

Where, \({\hat{y}}_{i}\) is the predicted value, \({y}_{i}\) is the observed value.

Accuracy

Accuracy is commonly used to assess classification models, representing the proportion of correctly predicted instances out of the total instances. It is calculated as:

$${Accuracy}=\frac{{Number\; of\; Correct\; Predictions}}{{Total\; Number\; of\; Predictions}}=\frac{{TP}+{TN}}{{TP}+{TN}+{FP}+{FN}}$$
(3)

Where, TP is true positive, TN is true negative, FP is false positive, FN is false negative.

These metrics collectively provide a robust framework for evaluating the performance and reliability of both regression and classification models.

SHAP method

The Shapley additive explanations (SHAP) is a method of model post interpretation, whose core idea is to calculate the marginal contribution of features to the model output and then explain the “black box model” from the global and local levels. To obtain the contribution of a feature \(i\), all operations by which a feature might have been added to the set (\(N!\)) and a summation over all possible sets (\(S\)) is considered. For any feature sequence, the marginal contribution through addition of feature \(i\) is given by \([f(S\cup \{i\})-f(S)]\). The resulting quantity is weighted by the different possibilities the set could have been formed prior to feature i’s addition (\(\left|S\right|!\)) and the remaining features could have been added (\(({|N|}-{|S|}-1)!\)). Hence, the importance of a given feature \(i\) is defined by the following formula:

$${\phi }_{i}=\frac{1}{N!}\sum _{S\subseteq N\setminus \{i\}}{|S|}!\,({|N|}-{|S|}-1)!\,[f(S\cup \{i\})-f(S)]$$
(4)

SHAP value is a quantitative index to measure the contribution of each feature in the machine learning model to the prediction result, which is used as an evaluation standard and it facilitate the distribution of a model’s prediction resulting from an input feature vector over the individual features.

Lasso regression

Lasso regression, a linear model that incorporates an L1 regularization term (i.e., the sum of the absolute values of the variable coefficients) to mitigate overestimation of model performance, was utilized for efficient variable selection. By introducing an adjustment parameter (\(\lambda\)), Lasso penalizes the absolute value of the coefficient, forcing some unimportant coefficient values to zero, which not only automatically selects important features, but also effectively controls the complexity of the model. The mathematical model is expressed as:

$$\mathop{\min }\limits_{\beta }\left\{\frac{1}{2n}\mathop{\sum }\limits_{i=1}^{n}{({y}_{i}-{x}_{i}^{T}\beta )}^{2}+\lambda {{||}\beta {||}}_{1}\right\}$$
(5)

Where, \({y}_{i}\) is the response variable, \({x}_{i}\) is the predictor variable, \(\beta\) is the coefficient vector, \({{||}\beta {||}}_{1}\) represents the L1 norm of the coefficient vector (that is, the sum of the absolute values of the coefficients), and \(\lambda\) is the regularization parameter, which controls the penalty intensity of the coefficients.

Supplementary material

The Supplementary material is available for: Polymer-units SMILES, Model Algorithm, Parameter Adjustment, Dataset Information, Lasso regression for features selection and Polymer-unit Structures (PDF). The Code_SI is available for: get-polymer-unit.py, polymer-unit-classify.py, structure_identity_tool.py, RF.py, SVM.py, KRR.py, con_smile.py, README.txt and OPV_exp_data (CSV). Prediction_PCE_data (PDF). Polymer_Units_Library & Ring_definition (PDF).