Introduction

The performance of structural materials in demanding environments is governed not only by their bulk composition but also by the characteristics of their microstructure—such as phase distribution, precipitate morphology, grain size, and defect interactions1,2,3,4. Realizing a specific, performance-enhancing microstructure requires an in-depth understanding of the complex, multiscale relationships between composition, thermodynamics, kinetics, and processing conditions5,6,7,8,9,10,11. While traditional alloy development has often relied on empirical experimentation or isolated modeling techniques, the need for more targeted, rapid, and mechanistically informed design strategies has driven the emergence of Integrated Computational Materials Engineering (ICME)12.

Recent advances in machine learning (ML) and data-driven approaches have further accelerated progress in computational alloy design by enabling high-throughput screening of composition spaces13,14,15,16,17. In particular, ML models trained on data from thermodynamic tools such as CALPHAD have been used to identify candidate alloys with desired phase stability or solidification ranges. However, many of these efforts focus narrowly on equilibrium descriptors and overlook the evolution of microstructural features that ultimately govern mechanical behavior. Descriptors such as diffusion-controlled phase transformation rates, lattice coherency, and lattice distortion—which directly influence precipitate coarsening, recrystallization, and phase morphology—remain underutilized in the composition screening stage.

In this work, we present a multiscale ICME framework that explicitly incorporates these nanoscale and kinetic factors into the alloy screening process. By integrating CALPHAD-based thermodynamic modeling, machine learning-driven high-throughput composition filtering, atomistic simulations using fine-tuned machine learning interatomic potentials18,19, and diffusion kinetics analysis, we establish a workflow capable of selecting compositions not only with favorable phase stability but also with microstructural characteristics known to enhance long-term performance20,21,22,23. These include low lattice misfit to reduce interfacial energy and promote intragranular γ′ precipitation, reduced atomic mobility of key precipitate-forming elements to slow coarsening, and elevated lattice distortion to facilitate dynamic recrystallization—together supporting the retention of a fine, stable γ′ dispersion within the γ matrix.

While the methodology is applied here to the case of wrought Ni-based superalloys—targeting the formation of fine, intragranular γ′ precipitates within coarse γ grains20,21,22,23—the computational framework is not restricted to this alloy class. The approach is broadly adaptable to other systems where microstructure-directed design is critical, such as steels, Co-based alloys, or high-entropy alloys. In particular, the use of atomistic-level screening to evaluate local distortion and diffusion kinetics offers a generalized path toward tailoring microstructure evolution across a wide range of materials.

This study demonstrates how advanced composition screening, driven by integrated physics-based and data-driven models, can bridge the gap between alloy chemistry and microstructural realization. Through this framework, we aim to move beyond traditional screening metrics and enable the predictive design of materials with tailored, stable microstructures optimized for application-specific performance.

Results

Machine learning model development for high-throughput screening

To enable high-throughput composition screening for selecting promising alloy candidates with tailored microstructures, machine learning models were trained using datasets exclusively derived from CALPHAD calculations performed with Thermo-Calc using the TCNI12 thermodynamic database24. The data were structured into two main categories: the first focused on alloy compositions and their corresponding solidus and liquidus temperatures (used for the Ts and Tl models), while the second incorporated temperature-dependent phase stability information. Specifically, the second dataset included indicators of whether a given composition formed a γ single-phase solid solution (γ1 model), whether topologically close-packed (TCP) phases were present (TCP model), the combined γ and γ’ phase fractions (γ + γ’ model), and the fraction of the γ’ phase alone (γ’ model).

To generate the alloy compositions, element weight percentages were randomly assigned within predefined ranges for Cr, Ni, Co, Mo, Nb, W, Ti, Al, Si, Fe, Mn, C, and B, as outlined in Table 1. Element-specific step sizes were applied to reflect the typical compositional sensitivity of each element in Ni-based superalloys: 1 wt% for Cr and Co, 0.5 wt% for Mo and W, 0.4 wt% for Fe, 0.2 wt% for Nb, Ti, Al, and Mn, 0.1 wt% for Si, 0.01 wt% for C, and 0.001 wt% for B. A total of 150,000 unique compositions were created, ensuring that the sum of all element weight fractions was less than 100 wt%. The remaining balance was allocated to Ni to reach a total of 100 wt%. Based on these step sizes, a rough approximation of the total number of combinatorially possible compositions (without accounting for the 100 wt% constraint) exceeds 5.9 × 10¹⁷, which underscores the importance of an efficient screening strategy capable of navigating such a vast design space.

Table 1 Minimum and maximum weight percentages of each element used for generating alloy compositions in the dataset
Full size table

For the dataset involving temperature-dependent phase stability, calculations were performed at five discrete temperatures: 700, 800, 900, 1000, and 1100 °C. This resulted in a total of 750,000 data points.

The compositional boundaries used for candidate generation were based on the limits of established commercial wrought Ni-based superalloys, such as Alloy 625, Alloy 230, Alloy 80A, 740H, and Haynes 282. This ensured that generated compositions were thermodynamically plausible. The actual compositions of these reference alloys are provided in the Supplementary Table 1 for comparison. Furthermore, non-physical or phase-unstable compositions were automatically filtered out during screening using machine learning models trained to predict phase stability and solidification behavior.

Although elements like Si, Mn, and Fe are often regarded as impurities in high-performance Ni-based superalloys, they were intentionally included in small amounts to explore their influence on lattice misfit, local atomic distortion, and aluminum diffusivity as part of the broader compositional design space, without the assumption that their impact would be uniformly negative.

The Ts and Tl models were used to identify alloy compositions with narrow solidification ranges to improve castability25. The γ + γ’ model ensured that the total fraction of desirable phases remained high, while the γ’ model controlled the volume fraction of γ’, a critical phase for high-temperature strength. The γ1 model was designed to reduce excessive coarsening of secondary phases during homogenization, and the TCP model was employed to eliminate compositions prone to forming topologically close-packed phases, which can be detrimental to high-temperature performance.

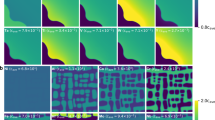
The regression models for Ts, Tl, γ + γ’, and γ’ were trained using designated training and validation datasets and were evaluated on a separate test set not used during training. Their predictive accuracy is illustrated in Fig. 1 as actual versus predicted scatter plots, using 1500 randomly selected nonzero data points from each set. The Ts model achieved a mean absolute error (MAE) of 12.4 K for the training set, 12.8 K for the validation set, and 12.6 K for the test set. The Tl model showed MAEs of 16.6 K, 16.8 K, and 16.9 K, respectively. The γ + γ’ model yielded a consistent MAE of 0.026 across all datasets. For the γ’ model, the MAE was 0.029 for the training set and 0.030 for both the validation and test sets. Although the γ’ model’s error visualization appears larger due to the high frequency of data points with a target value of zero, a separate evaluation excluding these zeros revealed an MAE of 0.046, confirming the model’s reliability in predicting nonzero γ’ fractions.

Fig. 1: Performance of regression models used for high-throughput composition screening.
figure 1

Scatter plots comparing actual versus predicted values for the four regression models used in high-throughput composition screening: (a) Ts model (solidus temperature, MAE in Kelvin), (b) Tl model (liquidus temperature, MAE in Kelvin), (c) γ + γ′ model (sum of γ and γ′ phase fractions, MAE in absolute fraction), and d γ′ model (γ′ phase fraction, MAE in absolute fraction). Each plot includes the coefficient of determination (R2) and mean absolute error (MAE) as performance metrics.

Full size image

Similarly, the classification models for γ1 and TCP phase prediction were evaluated using the independent test set. Their performance is presented in Fig. 2 as confusion matrices. The γ₁ model achieved accuracies of 99.9% for the training set and 99.3% for both the validation and test sets. The TCP model achieved 99.0% accuracy for the training set, 96.2% for the validation set, and 96.0% for the test set.

Fig. 2: Confusion matrices for classification models predicting γ single-phase formation and TCP phase stability.
figure 2

Confusion matrices for the γ1 model on the training (a), validation (b), and test sets (c), respectively. Confusion matrices for the TCP model on the training (d), validation (e), and test sets (f), respectively.

Full size image

Although the γ₁ model’s overall accuracy is high, its test recall and precision are 83.0% and 95.8%, respectively. This asymmetry arises from the extreme class imbalance in the dataset, where γ single-phase data points comprise only ~2.8% of the total. Even though class weighting was used to mitigate imbalance effects, some misclassification is inevitable. In contrast, the TCP model displays more balanced precision and recall, and its confusion matrices confirm stable generalization across data splits.

To contextualize our model performance, we note that previous studies on phase classification in complex alloy systems report lower or comparable results. For example, Huang et al. achieved up to 94.3% accuracy using artificial neural networks for binary classification tasks in high-entropy alloys26, while Singh et al. reported an average test accuracy of 92% using a SMOTE-augmented random forest classifier27. Machaka showed accuracies ranging from 94.0% to 97.5% for various classifiers including random forest, support vector machine, and artificial neural network28. While these models differ in dataset scope and objectives, our γ₁ and TCP models demonstrate competitive accuracy, further validating their utility in high-throughput alloy screening.

These results confirm that the models exhibit strong generalization capabilities and maintain high predictive performance, demonstrating their robustness and relevance for microstructure-informed alloy composition screening.

High-throughput screening for optimized microstructure

A high-throughput composition screening was conducted using six validated machine learning models to identify optimal alloy compositions for wrought Ni-based superalloys, with a focus on microstructure design suitable for high-temperature deformation processing. This effort was guided by an ICME framework, with the objective of developing alloys that promote intragranular dynamic recrystallization (DRX) and facilitate the formation of fine, intragranular γ’ precipitates within coarse γ grains. Rather than aiming to directly predict mechanical properties, the screening targeted microstructural attributes associated with improved hot workability and stability during thermomechanical processing.

The overall workflow—from initial random composition generation to ML-based screening, advanced nanoscale filtering, and final experimental validation—is illustrated in Fig. 3. This flowchart highlights how the integration of CALPHAD-informed ML models and atomistic simulations efficiently reduced a vast composition space (2 billion alloys) to a final set of experimentally promising candidates.

Fig. 3: Schematic illustration of the ICME-based alloy screening workflow.
figure 3

Starting from two billion randomly generated compositions, high-throughput machine learning models trained on CALPHAD data filtered 228 candidates based on key thermodynamic criteria. These were further refined to 12 compositions through advanced screening using molecular dynamics and diffusion kinetics, followed by experimental validation of one alloy composition.

Full size image

The initial filtering stage selected alloy compositions with a predicted solidification range of 50 K or less, based on the outputs of the Ts and Tl models. Only compositions predicted by the γ1 model to form a stable γ single phase at 1100 °C were retained, as single-phase γ is favorable for uniform deformation during hot rolling. At the target aging and processing temperature of 800 °C, the γ + γ’ and γ’ models were used to identify compositions in which the combined γ and γ’ phase fractions reached at least 99%, and the γ’ fraction fell within the range of 0.2 to 0.4. This γ’ range reflects phase distributions commonly found in commercial wrought superalloys such as Haynes 282, which are engineered for balanced workability and thermal stability. In addition, to improve oxidation and corrosion resistance during processing and service, only compositions with a minimum of 20 wt% chromium were considered.

Using these criteria, a total of 2 billion randomly generated compositions, bounded by the elemental ranges in Table 1, were evaluated. From this pool, 228 compositions satisfied all selection criteria and were retained for further analysis. These compositions are provided in the Supplementary Information.

While such a screening process could, in principle, be conducted using conventional CALPHAD methods, the machine learning models—trained on thermodynamic data—enabled a dramatic acceleration in screening speed. For comparison, performing CALPHAD calculations for 150,000 compositions required approximately 11 days (15,840 min) on an Intel(R) Core(TM) i9-14900K processor, yielding only 4 compositions that satisfied all selection criteria. In contrast, screening 2 billion compositions using the trained machine learning models took only 15 min on an NVIDIA RTX A6000 GPU, identifying 228 suitable compositions. This corresponds to a throughput of 15.2 successful candidates per minute using ML, compared to 0.00025 candidates per minute using CALPHAD, resulting in an approximate 60,000-fold improvement in screening efficiency.

It is important to note that the machine learning models are not intended to replace CALPHAD in terms of thermodynamic precision, but rather to serve as a highly efficient pre-screening tool that enables scalable exploration of vast compositional spaces. The four successful CALPHAD-screened compositions are also listed in the Supplementary Information for comparison.

Table 2 summarizes the minimum and maximum weight percentages of alloying elements in the 228 selected compositions. The trends observed in these selected alloys provide insight into the compositional boundaries favorable for wrought Ni-based alloy design. For example, elements such as Mo and W, which increase the risk of forming TCP phases, were naturally filtered out due to their negative impact on γ and γ’ phase stability at 800 °C. Similarly, all selected alloys contained less than 0.09 wt% carbon, indicating an avoidance of compositions prone to excessive carbide formation, which can compromise hot workability and grain boundary integrity. The aluminum content of the selected alloys ranged from 1 wt% to 5 wt%, reflecting aluminum’s key role in γ’ formation and its influence on microstructural evolution during thermomechanical treatment.

Table 2 Minimum and maximum weight percentages of elements in the 228 selected Ni-based superalloy compositions
Full size table

In summary, the compositional trends that emerged from this machine learning-driven screening process were not pre-assumed but resulted organically from criteria based on thermodynamic stability, processing compatibility, and microstructure control. These findings reinforce the value of advanced ICME workflows in identifying alloy chemistries optimized for wrought processing and tailored microstructural development, laying the foundation for subsequent experimental validation and performance assessment under hot working conditions.

Advanced composition screening for optimized microstructure

To further refine the 228 alloy compositions identified through high-throughput composition screening, a second phase of screening was conducted using kinetic calculation and molecular dynamics (MD) simulations. This advanced screening stage aimed to identify compositions with the targeted microstructure. The key properties evaluated in this stage were the chemical diffusion coefficient of aluminum in the γ single phase (\({D}_{\left({Al},{Al}\right)}^{{Ni}}\), m2/s) at 800 °C, the lattice misfit between the γ and γ’ phases, and the lattice distortion within the γ matrix.

Among these, diffusion kinetics plays a particularly important role in influencing γ’ evolution during thermal exposure. The γ’ phase (Ni3Al) is critical for microstructural strengthening in Ni-based superalloys, and its coarsening behavior over time can impact the long-term stability of the precipitate morphology. While the mechanical implications of γ’ coarsening were not experimentally evaluated in this study, its control is known to be essential for maintaining desirable microstructural features in service environments29.

The kinetics of γ’ coarsening can be quantitatively described by the classical Lifshitz–Slyozov–Wagner (LSW) theory:

$${\bar{r}}_{t}^{3}-{\bar{r}}_{0}^{3}=\frac{8{\gamma }_{i}D{V}_{m}^{2}{C}_{e}}{9{RT}}t$$
(1)

where \({\bar{r}}_{t}\) is the average particle radius at time t, \({\bar{r}}_{0}\) is the initial average particle radius, \({\gamma }_{i}\) is the particle surface energy, \(D\) is the diffusion coefficient of the γ’ forming element, \({V}_{m}\) is the molar volume of the γ’ phase, \({C}_{e}\) is the equilibrium solubility of the γ’ forming element in the γ phase, \(R\) is the ideal gas constant, and \(T\) is the absolute temperature. This model highlights the dominant role of diffusion kinetics in determining precipitate coarsening rates.

The growth of γ’ precipitates is driven by the diffusion of aluminum toward the γ/γ’ interface. Prior studies, including those by Tiley et al.30, have shown that aluminum diffusion is the rate-controlling mechanism in γ’ evolution. Therefore, calculating the chemical diffusion coefficient of aluminum provides a means of comparing the microstructural stability potential of different compositions.

The chemical diffusion coefficient \({D}_{\left(k,j\right)}^{n}\) provides a quantitative measure of atomic mobility, where k represents the diffusing species (Al), j represents the gradient species (Al), and n is the reference species (Ni). The aluminum flux \({J}_{{Al}}\) in an alloy can be expressed as:

$${J}_{{Al}}=-\sum _{j=\left[{Co},{Cr},\ldots ,{Al}\right]}{D}_{\left({Al},j\right)}^{{Ni}}\frac{\partial {c}_{j}}{\partial z}$$
(2)

where j includes all alloying elements except Ni, and \(\frac{\partial {c}_{j}}{\partial z}\) represents the concentration gradient of each element. However, given that the concentration gradients of elements other than aluminum are negligible at the γ/γ’ interface, this equation simplifies to:

$${J}_{{Al}}=-{D}_{\left({Al},{Al}\right)}^{{Ni}}\frac{\partial {c}_{{Al}}}{\partial z}$$
(3)

While γ′ coarsening in Ni-based superalloys can be influenced by the diffusion behavior of multiple elements—including Ti, Ta, and Nb—aluminum is often the dominant diffusing species in Ni₃Al-type precipitates. Prior studies have shown that aluminum diffusion typically governs the initial and overall kinetics of γ′ evolution, particularly in alloys with moderate concentrations of other γ′-forming elements such as Ti and Ta29,31. Therefore, in this work, we use the aluminum chemical diffusion coefficient, \({D}_{\left({Al},{Al}\right)}^{{Ni}}\), as a practical and representative metric for coarsening tendency during high-throughput composition screening.

We acknowledge, however, that this is a first-order approximation. Incorporating multicomponent diffusion would require calculating a full set of cross-diffusion coefficients—such as \({D}_{\left({Al},{Ti}\right)}^{{Ni}}\), \({D}_{\left({Al},{Ta}\right)}^{{Ni}}\), \({D}_{\left({Al},{Nb}\right)}^{{Ni}}\), and reciprocal terms—as well as resolving concentration gradients for each relevant species. Additionally, the individual and combined contributions of each species to γ′ coarsening would need to be quantified and modeled, which remains a complex and computationally intensive challenge. While such detail is important for fully resolved kinetic modeling, it is not feasible within the scope of large-scale, high-throughput screening of millions or billions of compositions.

Thus, our use of \({D}_{\left({Al},{Al}\right)}^{{Ni}}\) strikes a balance between physical relevance and computational efficiency. It enables robust and scalable filtering based on relative coarsening resistance while maintaining tractability across the large composition space examined. In future work, we plan to extend the framework to include multicomponent diffusion effects for more detailed evaluation of selected candidate compositions, particularly those with higher Ti or Ta contents.

By calculating \({D}_{\left({Al},{Al}\right)}^{{Ni}}\) for each candidate alloy using DICTRA simulations coupled with the TCNI12 thermodynamic and mobility databases, we assessed the relative mobility of aluminum atoms, which provides insight into the potential γ’ coarsening behavior. Lower values of \({D}_{\left({Al},{Al}\right)}^{{Ni}}\) indicate reduced diffusion-driven growth, supporting the formation of finer and more stable precipitate distributions. Therefore, in the context of microstructure optimization, compositions with lower aluminum diffusivity were prioritized for their potential to support thermally stable γ’ morphologies under expected service conditions.

The next key parameter in the advanced composition screening process is the lattice misfit (\(\delta\)) between the γ’ and γ phases, which quantifies coherency strain at the interface. It is defined as:

$$\delta =\frac{2\left({a}_{{\gamma }^{{\prime} }}-{a}_{\gamma }\right)}{\left({a}_{{\gamma }^{{\prime} }}+{a}_{\gamma }\right)}$$
(4)

where \({a}_{{\gamma }^{{\prime} }}\) and \({a}_{\gamma }\) are the lattice parameters of the γ’ and γ phases, respectively. These parameters were calculated using thermodynamic equilibrium compositions derived from CALPHAD at 800 °C, ensuring that the evaluated misfit reflects phase-stable, service-relevant conditions.

Lattice parameters were obtained using MD simulations with a fine-tuned machine learning interatomic potential, which was validated against density functional theory (DFT)-calculated lattice constants with high accuracy, as detailed in the “Methods” section. In this study, MD simulations are employed specifically for the estimation of static structural properties, and not for modeling microstructural evolution, defect interactions, or interface behavior. This targeted use of MD enables efficient nanoscale property evaluation across a broad compositional space, consistent with the primary objective of high-throughput, multiscale composition screening.

To evaluate lattice distortion, which supports DRX through dislocation accumulation, we calculated the mean squared atomic displacement (MSAD)32,33,34:

$${\rm{MSAD}}=\frac{1}{N}\mathop{\sum }\limits_{i=1}^{N}{\left|{x}_{{fully}-{relaxed}}^{\left(i\right)}-{x}_{{ideal}}^{\left(i\right)}\right|}^{2}$$
(5)

where \({x}_{{fully}-{relaxed}}^{\left(i\right)}\) is the position of the i-th atom in the relaxed configuration, \({x}_{{ideal}}^{\left(i\right)}\) is the corresponding position in the ideal FCC reference structure, and N is the total number of atoms. The square root of the MSAD, denoted as MSAD1/2, was calculated and expressed in picometers (pm) to facilitate comparison among different alloy compositions.

In this study, MSAD was used as a scalar, system-wide approximation of lattice distortion. It reflects the overall configurational mismatch induced by multicomponent alloying and serves as a computationally efficient proxy for the degree of local lattice irregularity. This type of distortion is known to influence dislocation storage behavior and DRX nucleation under hot working conditions35.

We note that more detailed descriptors, such as per-atom strain tensors or Voronoi volumes, could offer higher spatial resolution or species-specific insights. However, these methods introduce significant complexity and sensitivity to local structural noise, and they are not easily reducible to a scalar metric suitable for high-throughput screening. In contrast, MSAD provides a consistent and interpretable metric that can be rapidly evaluated across thousands of candidate structures. While it does not capture local variations or explicitly resolve chemical species, it enables effective early-stage filtering of alloy compositions with enhanced DRX potential.

It is important to note that this study focuses on the design and identification of alloy compositions with favorable microstructural indicators, rather than on the experimental verification of DRX or the simulation of its kinetics. Assumptions regarding DRX potential are based on widely accepted physical principles and supported by indirect evidence. Specifically, elevated lattice distortion increases resistance to dislocation motion, leading to the accumulation of dislocations within grains36. These dislocation-rich regions serve as preferential nucleation sites for DRX, thereby facilitating the formation of fine-grained microstructures35. In the context of Ni-based superalloys, such intragranular DRX is particularly advantageous for promoting the uniform precipitation of fine γ′ particles within large γ grains22. In this study, the relationship between composition, lattice distortion, and DRX behavior is leveraged as part of a computational screening framework to down-select promising compositions for future validation, rather than as a mechanistic model of recrystallization.

These three parameters were chosen because they collectively influence the key microstructural processes required to achieve the desired γ/γ′ morphology. In the context of Ni-based superalloy processing, a low aluminum diffusion coefficient helps suppress γ′ coarsening during high-temperature exposure, preserving precipitate fineness. A low lattice misfit between γ and γ′ reduces interfacial energy and promotes coherent phase boundaries37, discouraging grain boundary γ′ formation, which can be detrimental to creep resistance. Concurrently, high lattice distortion enhances dislocation accumulation during deformation, creating favorable sites for DRX nucleation. The newly recrystallized grains that form through this mechanism subsequently act as preferential zones for intragranular γ′ precipitation during aging. Together, these factors reinforce a morphology of fine, well-dispersed γ′ precipitates within coarse γ grains, which is known to enhance structural stability during high-temperature service.

Taken together, lattice misfit, lattice distortion, and aluminum diffusivity provide a physically motivated and computationally tractable basis for advanced composition screening. Used in conjunction with thermodynamic phase predictions, these nanoscale parameters enable the identification of alloys that are not only stable and castable but also structurally optimized to support the formation of high-performance microstructures under typical industrial processing conditions. This integrated, multiscale approach reflects the core objective of this work: to accelerate the design of Ni-based superalloys by linking composition to nanoscale phenomena that influence final microstructural outcomes.

For the 228 previously selected compositions, additional calculations were performed to determine the chemical diffusion coefficient, lattice misfit, and lattice distortion (expressed as MSAD¹/² in pm). These results are provided in the Supplementary Information.

To assess the capability of the computational framework in realizing the desired microstructure, 12 representative compositions were selected from the 228 screened candidates based on combined thresholds of aluminum diffusion coefficient, lattice misfit, and lattice distortion. Specifically, selected compositions exhibited aluminum diffusion coefficients below 1.04 × 10−16 m2/s, lattice misfit below 1.01%, and lattice distortion above 4.55 pm. These thresholds were statistically determined from the overall distribution of computed values and aimed to isolate compositions with the highest potential for promoting fine, stable intragranular γ′ precipitation. The compositions and corresponding property values of the selected alloys are summarized in Table 3.

Table 3 Compositions and calculated properties of the 12 selected Ni-based superalloys
Full size table

Among the 12 selected compositions, alloy #65 was chosen for experimental validation not solely for its individual property values, but because it demonstrated a well-balanced combination of the lowest lattice misfit (0.65%), moderate aluminum diffusivity (7.83 × 10⁻¹⁷ m²/s), and the highest lattice distortion (5.69 pm). Although other alloys, such as #42, showed lower aluminum diffusivity, their overall microstructural profiles—such as higher lattice misfit or lower distortion—made them less favorable in the context of achieving the desired γ/γ′ morphology. Therefore, alloy #65 was selected as a representative candidate that reflects the integrated outcome of the multiscale screening framework, balancing diffusion kinetics, interfacial strain, and DRX-promoting lattice distortion.

Experimental validation

The experimental validation of alloy #65 was conducted to assess whether the integrated computational framework could accurately predict and realize the targeted microstructure. As illustrated in Fig. 4 and Supplementary Fig. 1, microstructural analysis of both as-rolled and heat-treated specimens confirmed the formation of fine, intragranular γ′ precipitates, in agreement with computational predictions.

Fig. 4: Experimental validation of microstructure in alloy #65.
figure 4

a Scanning electron microscope (SEM) image (×50,000) of the as-rolled specimen showing ultrafine precipitates (~10 nm) within grain interiors. b SEM image (×50,000) of the heat-treated specimen (800 °C for 2 h), revealing fine intragranular precipitates (~50 nm). c Phase fraction vs. temperature profile for alloy #65. d Backscatter electron (BSE) image with corresponding EDS elemental maps for the as-rolled specimen.

Full size image

SEM imaging demonstrated the presence of ultrafine, dispersive precipitates approximately 10 nm in size within the grains of the as-rolled specimen. Upon heat treatment at 800 °C for 2 h, these features coarsened to approximately 50 nm, while maintaining a uniform intragranular distribution. Although electron backscatter diffraction (EBSD) and energy-dispersive spectroscopy (EDS) could not distinctly differentiate γ and γ′ phases due to crystallographic and spatial resolution limitations, the morphology, size scale, and thermal evolution of these precipitates are strongly consistent with secondary γ′, as previously confirmed by transmission electron microscopy (TEM) in similar microstructures reported by Lee et al.23. These findings also align with the equilibrium γ′ phase fraction predicted by CALPHAD (Fig. 4c), further reinforcing the validity of the computational predictions. While TEM analysis would provide definitive structural identification, the objective of this work is to validate the realization of the targeted microstructure using an ICME-guided pathway. In this context, the current SEM-based evidence is considered sufficient to confirm that the designed γ/γ′ morphology was successfully achieved.

To evaluate the coarsening behavior of the observed γ′ precipitates, we applied the classical LSW theory (Eq. (1)) to predict the expected growth after aging. The interfacial energy between γ and γ′ was calculated via molecular dynamics using the fine-tuned SevenNet potential, yielding \({\gamma }_{i}=0.156{\rm{J}}/{{\rm{m}}}^{2}\). The chemical diffusion coefficient of aluminum was determined as \(D={D}_{\left({Al},{Al}\right)}^{{Ni}}=7.83\times {10}^{-17}{{\rm{m}}}^{2}/{\rm{s}}\), while the molar volume of the γ′ phase was computed as \({V}_{m}=6.795\times {10}^{-6}{{\rm{m}}}^{3}/{\rm{mol}}\) from the relaxed atomic structure. The equilibrium solubility of aluminum in the γ matrix was calculated as \({C}_{e}=11468{\rm{mol}}/{{\rm{m}}}^{3}\) using CALPHAD thermodynamic analysis. Using \(R=8.314{\rm{J}}/{\rm{mol}}\cdot {\rm{K}}\), T = 1073.15 K (800 °C), and an aging time of t = 7200 s, we estimated \({\bar{r}}_{t}^{3}-{\bar{r}}_{0}^{3}=4.62\times {10}^{-24}{{\rm{m}}}^{3}\), where \({\bar{r}}_{0}\) was assumed to be 10 nm based on the as-rolled specimen. This yields a predicted average precipitate radius of approximately 17.8 nm after aging.

Although this is smaller than the experimentally observed value (~50 nm), the LSW model serves as a simplified, first-order approximation under idealized conditions. Its purpose here is not to predict exact coarsening rates, but to enable rapid, comparative evaluation of candidate compositions in terms of their relative resistance to γ′ coarsening. The smaller-than-measured prediction reflects the ideal assumptions of the model (e.g., constant diffusion field, no particle interactions), whereas the experimental data may include additional effects such as elastic interactions or solute drag.

The EDS maps in Fig. 4d confirm homogeneous elemental distribution across the observed region, with no evidence of compositional segregation or coarse intermetallic phases. This uniformity supports the conclusion that the observed precipitates are not primary γ’ or TCP phases but are instead secondary, nanoscale γ’ formed via dynamic recrystallization and subsequent aging. Due to the extremely fine scale of these precipitates and the spatial resolution limits of SEM-based EDS, performing a meaningful line scan across individual γ′ features was not feasible. We therefore rely on morphology and comparative literature evidence to support the identification. These limitations are acknowledged, and future high-resolution studies may further validate these findings using techniques such as TEM or diffraction analysis.

Grain structure analysis using inverse pole figure (IPF) maps in Supplementary Fig. 1 revealed that both the as-rolled and heat-treated specimens exhibit large, equiaxed grains. The average grain size was measured to be 146 µm in the as-rolled condition and slightly increased to 152 µm after heat treatment, indicating limited grain growth during the aging process. The dark regions in the IPF maps correspond to non-FCC phases, which are likely fine carbides such as NbC or Cr23C6, consistent with thermodynamic predictions and commonly observed secondary phases in Ni-based superalloys.

Importantly, the increase in γ’ precipitate size after heat treatment suggests continued growth beyond the DRX-induced nucleation stage. Since excessive coarsening can eventually degrade long-term creep resistance, one of the critical challenges for further optimizing the alloy is to suppress γ’ coarsening during post-deformation heat treatment. One promising strategy to achieve this is by selecting alloy compositions in which the γ’ phase fraction remains relatively stable across service temperatures. As shown in Fig. 4c, alloy #65 exhibits noticeable variation in γ’ phase fraction with temperature, indicating limited thermal stability. Refining this compositional behavior—specifically by minimizing temperature-dependent changes in the γ’ fraction—could be an effective approach to achieving sustained microstructural stability during long-term service.

While alloy #65 was the only composition experimentally validated in this study due to practical constraints, we further assessed the robustness and generalizability of our framework by retrospectively applying our screening criteria to two high-entropy alloy systems reported in the literature: one by Daoud et al. (Al10Co25Cr8Fe15Ni36Ti6) and another by Detrois et al. (ASC2 alloy)38,39. Although these alloys were not explicitly designed through our ICME workflow, they exhibit microstructures similar to our design target—fine, intragranular γ′ precipitates within a coarse γ matrix—and have demonstrated excellent tensile performance at both room and elevated temperatures. Using our computational approach, we evaluated each alloy’s key nanoscale descriptors. Specifically, Daoud’s alloy yielded a chemical diffusion coefficient of aluminum 8.86 × 10−17 m2/s, lattice misfit of 1.00%, and MSAD1/2 of 4.64 pm. Detrois’ ASC2 alloy showed values of 7.18 × 10−17 m2/s, 0.83%, and 5.08 pm, respectively. These values fall within the thresholds set by our advanced screening criteria: aluminum diffusion coefficients below 1.04 × 10−16 m²/s, lattice misfit below 1.01%, and lattice distortion above 4.55 pm. The fact that these independently developed, high-performance alloys satisfy our predictive criteria provides strong indirect validation of the framework. Moreover, their agreement with our screening metrics supports the potential generalizability of this methodology to alloy classes beyond Ni-based systems. These results suggest that integrating thermodynamic, kinetic, and atomistic descriptors offers a broadly applicable strategy for microstructure-directed alloy design.

Discussion

This study demonstrates an ICME framework that integrates CALPHAD modeling, machine learning, molecular dynamics, and diffusion kinetics to realize targeted microstructures in Ni-based alloys. Unlike prior approaches focused solely on thermodynamic stability, our method incorporates atomistic-level descriptors—such as aluminum diffusion coefficients, γ/γ′ lattice misfit, and lattice distortion—to predict and guide the formation of fine, intragranular γ′ precipitates. Through high-throughput screening of two billion compositions and multiscale refinement, we identified 12 candidate alloys, one of which was experimentally validated to exhibit the predicted γ/γ′ morphology.

The significance of this work lies in its ability to bridge thermodynamic predictions with nanoscale structural evolution, offering a robust pathway for microstructure realization. While high-temperature mechanical testing was not performed, this study focuses on validating microstructure prediction as a critical first step toward performance-based alloy design. Notably, independent studies on high-entropy alloys by Daoud and Detrois have reported similar microstructures with superior mechanical properties, and their compositions satisfy our screening criteria for diffusion, misfit, and distortion38,39. These findings provide indirect support for the relevance and broader applicability of our framework.

Although in situ TEM heating would provide valuable real-time validation of γ′ coarsening kinetics, such experiments require specialized instrumentation and significant effort. Given the scale and scope of the current study, we consider in-situ TEM a promising direction for future research rather than a necessary component of the present work. Future efforts will incorporate both mechanical testing and advanced microstructural analysis across a broader range of compositions and alloy systems to further validate and extend the predictive power of the proposed framework.

Methods

Machine learning model development

To develop a machine learning model capable of identifying promising alloy candidates with tailored microstructures, we constructed a comprehensive dataset using CALPHAD calculations performed in Thermo-Calc with the TCNI12 database24. TCNI12 was selected due to its extensive validation and widespread use in Ni-based alloy design. It includes all assessed binary subsystems relevant to the compositional space explored in this study (Cr, Ni, Co, Mo, Nb, W, Ti, Al, Si, Fe, Mn, C, and B), as well as many critically assessed ternary subsystems involving key alloying elements such as Ni, Cr, Co, and Al—for example, Co-Cr-Ni, Al-Co-Ni, Al-Cr-Ni, Al-Co-Cr, Cr-Fe-Ni, and Co-Ni-W. This level of thermodynamic assessment ensures reliable extrapolation into multicomponent phase fields and supports the accuracy of phase stability predictions for high-throughput screening.

Furthermore, TCNI12 incorporates magnetic contributions to thermodynamic properties through a mean-field model implemented within the compound energy formalism. This model captures the effects of magnetic entropy and enthalpy, including transitions such as the antiferromagnetism of chromium. However, as all CALPHAD calculations in this study were conducted at elevated temperatures (≥700 °C), which are well above the Néel temperature of chromium (~311 K), the influence of long-range magnetic ordering is expected to be negligible. Thus, while magnetic effects are implicitly included in the thermodynamic formulation, they are not expected to significantly affect the results under the high-temperature conditions considered here.

To ensure data integrity and completeness, entries with calculation errors were removed. This process resulted in two datasets: one containing 148,710 data points for liquidus and solidus temperatures, and another with 746,009 data points capturing temperature-dependent phase stability. The full dataset used in this study is available via the link provided in the “Data availability” section.

The machine learning models were developed using manually hyperparameter-tuned XGBoost and a fully connected neural network implemented in PyTorch40,41. Given that XGBoost is a decision tree-based model, input data remained unnormalized, as normalization does not significantly affect its performance. However, for the neural network, each feature was normalized using its respective minimum and maximum values to ensure stable training and improved accuracy.

The predictive models consisted of both regression and classification tasks. Neural network regression models were used to predict solidus temperature (Ts model), liquidus temperature (Tl model), the sum of γ and γ’ phase fractions (γ + γ’ model), and the γ’ fraction (γ’ model). These models were trained using the Mean Squared Error (MSE) loss function and the Adam optimizer42. For classification tasks, XGBoost-based logistic regression models were employed to predict whether a given composition forms a γ solid solution single phase (γ1 model) and whether it forms TCP phases (TCP model). The γ1 model assigned a label of 1 when the γ mole fraction was at least 0.999 and 0 otherwise, while the TCP model assigned a label of 1 if TCP phases were stable and 0 otherwise.

The dataset was divided into 80% training, 10% validation, and 10% test sets. The training set was used to fit the models, the validation set was utilized for early stopping, and the test set, which remained unseen during training, was used for final evaluation.

For XGBoost models, hyperparameters were set with a maximum tree depth of 10, a learning rate of 0.1, 500 boosting iterations, and an early stopping criterion of 10. Class imbalance was addressed by adjusting class weights based on the ratio of positive to negative labels. The neural network models were configured with a hidden layer size of 2048, a depth of 4 layers, and leaky ReLU activation functions. Training was conducted over 1000 epochs with a batch size of 128, applying an early stopping criterion of 5. To mitigate data imbalance in the γ’ model, where approximately two-thirds of the dataset had a label of 0, a weight factor of 10 was applied to the loss function for nonzero data points, enhancing the model’s predictive accuracy for values within the range of 0 to 1.

Diffusion coefficient calculation

The diffusion coefficient used for advanced composition screening was calculated using Thermo-Calc and DICTRA24. Since diffusion coefficients depend on both mobility and thermodynamic factors, it was essential to use a mutually compatible mobility and thermodynamic database to ensure accurate calculations43. To achieve this, the mobility database was specifically organized based on the TCNI12 thermodynamic database, ensuring consistency between the two.

To enhance the reliability of the calculated diffusion coefficients, mobility parameters from available literature sources were incorporated44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64. These parameters were then calibrated to match experimental diffusion coefficient data, ensuring that the computed values accurately reflected real diffusion behavior in Ni-based superalloys.

Molecular dynamics

In this study, MD simulations were conducted using the machine learning potential SevenNet (version 11July2024) within the LAMMPS simulation package65,66. SevenNet is based on the Neural Equivariant Interatomic Potentials (NequIP) framework, which has demonstrated high accuracy in predicting atomic interactions67. Although SevenNet performed well in the Matbench Discovery benchmark for universal force fields68, it was fine-tuned in this study to more accurately describe the γ and γ’ phases in Ni-based superalloys.

The fine-tuning process involved generating Ni-rich γ and γ’ structures with various compositions, each containing 32 atoms. A total of 32 γ-phase compositions and 42 γ’-phase compositions were randomly selected, and for each composition, three different atomic distributions were generated, resulting in 96 γ structures and 126 γ’ structures used for training. To validate the fine-tuned SevenNet, an additional set of 48 γ structures and 54 γ’ structures with compositions not used in the training process were generated as test structures. In the γ’ structures, Ni was enriched at site 1, while Al was enriched at site 2. The details of these compositions are provided in the Supplementary Information.

To ensure accurate energy and force calculations, all generated structures were fully relaxed using DFT with the Vienna Ab initio Simulation Package (VASP). The Perdew-Burke-Ernzerhof (PBE) exchange-correlation functional within the Projector Augmented-Wave (PAW) method was used. A 4 × 4 × 4 k-point mesh and a 520 eV energy cutoff for the plane-wave basis set were applied. The electronic self-consistency convergence was set to 10−5 eV, while the ionic relaxation forces were converged to −0.02 eV/Å. Spin polarization was enabled to account for magnetic effects, and a smearing method with a width of 0.1 eV was used. Structural relaxations were performed using the conjugate gradient algorithm with a time step of 0.3 fs and a maximum of 100 ionic relaxation steps.

While the MD simulations using SevenNet do not dynamically model magnetic ordering, the potential implicitly reflects the influence of local magnetic effects—particularly those associated with Cr—through its training on spin-polarized DFT reference data. This allows the potential to account for magnetic contributions to local atomic environments and structural distortion, which are important in high-Cr compositions.

To evaluate the accuracy of the fine-tuned SevenNet in reproducing the structural properties of Ni-based superalloys, the lattice constants of both the training and test structures were computed using LAMMPS and compared to the DFT results (Fig. 5). To mitigate errors from random alloying element distributions, the lattice constants were averaged over the three generated structures per composition before comparison. For the training structures, R2 was 0.9629, with a mean absolute error (MAE) of 0.003 Å, while for the test structures, R2 was 0.9231, with an MAE of 0.005 Å. These results confirm that the fine-tuned SevenNet accurately reproduces the structural properties of superalloys as calculated by DFT.

Fig. 5: Validation of the fine-tuned SevenNet potential against DFT-calculated lattice constants.
figure 5

Comparison of lattice constants predicted by MD simulations using the fine-tuned SevenNet machine learning potential versus DFT calculations for both training and test structures. Each data point represents the average lattice constant of three atomic configurations per composition to account for random element distributions.

Full size image

The fine-tuned SevenNet was subsequently used in MD simulations to calculate lattice misfit and lattice distortion, which are critical factors in optimizing compositions for the targeted microstructure. To perform these calculations, 228 compositions were selected from an initial pool of 2 billion randomly generated compositions based on thermodynamic screening and machine learning predictions. For each selected composition, FCC (γ) and L12 (γ’) structures containing 4000 atoms each were generated, with their compositions determined based on equilibrium phase compositions from CALPHAD calculations at 800 °C. Given the low fraction of interstitial elements (C and B) in FCC and L12 phases, their contributions were neglected.

To account for the variations in results due to different atomic arrangements, three distinct atomic configurations were generated for each composition. The final lattice misfit and lattice distortion values were then obtained by averaging the results across these configurations.

To evaluate the interfacial energy (\({\gamma }_{i}\)) between the γ and γ′ phases, MD simulations were performed using the fine-tuned SevenNet machine learning interatomic potential. The interfacial energy is defined as the excess energy required to form an interface between two phases compared to their respective bulk states. It was calculated using the relation:

$${\gamma }_{i}=\frac{{E}_{{total}}^{\gamma /{\gamma }^{{\prime} }}-{n}_{\gamma }{E}_{\gamma }^{{bulk}}-{n}_{{\gamma }^{{\prime} }}{E}_{{\gamma }^{{\prime} }}^{{bulk}}}{2A}$$
(6)

where \({E}_{{total}}^{\gamma /{\gamma }^{{\prime} }}\) is the total energy of the relaxed γ/γ′ interface structure, \({E}_{\gamma }^{{bulk}}\) and \({E}_{{\gamma }^{{\prime} }}^{{bulk}}\) are the energies per atom of bulk γ and γ′ phases respectively, and \({n}_{\gamma }\) and \({n}_{{\gamma }^{{\prime} }}\) are the number of atoms of each type in the interface system. The denominator 2A accounts for the presence of two interfaces due to periodic boundary conditions, where A is the cross-sectional area of one γ/γ′ interface.

To construct the interface model, a supercell was created by joining fully relaxed γ and γ′ structures along the x-direction, ensuring coherent lattice matching at the interface to reflect realistic epitaxial conditions. After joining, the combined structure was fully relaxed to eliminate artificial strain at the interface. All simulations were repeated three times using different random atomic arrangements for each phase to ensure statistical robustness, and the final value of \({\gamma }_{i}\) was taken as the average.

Microstructural characterization

A 5 kg ingot was fabricated using a Vacuum Induction Melting Furnace (VIM) with a composition of 20% Cr, 5% Co, 1% Nb, 2.5% W, 4% Al, 0.4% Mn, 0.03% C, and 0.005% B by weight. The ingot was processed into a rectangular shape with dimensions of 80 mm in width, 100 mm in length, and 19 mm in height for subsequent hot rolling. Prior to rolling, the ingot was homogenized at 1100 °C for 1 h. It was then hot-rolled with a 20% reduction per pass, achieving a total reduction of 60%. The hot-rolled specimens underwent an aging treatment at 800 °C for 2 h, followed by water quenching.

Microstructure characterization was performed using a Field-Emission Scanning Electron Microscope (FE-SEM, JSM-7100F, JEOL, Japan) equipped with BSE, EDS, and EBSD detectors. Samples were mechanically polished up to 1200 SiC grit paper and electropolished in a solution of 92% CH₃COOH + 8% HClO₄ at 20 V to reveal the microstructure.